2. 油气藏地质及开发工程国家重点实验室, 四川成都 610059;
3. 西华师范大学, 四川南充 637002
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu, Sichuan 610059, China;
3. China West Normal University, Nanchong, Sichuan 637002, China
如今,随着世界各国对石油、天然气等能源的需求日益增长,以裂缝型储层为代表的非常规油气藏逐渐接替常规油气藏,成为油气勘探、开发的新目标。裂缝是裂缝型储层中流体的通道,连接了储层内的溶洞和溶孔[1],可为储层预测提供重要信息[2]。因此裂缝对油气的分布具有重要影响。
目前,常规的裂缝预测方法主要包括地震属性分析方法和地震各向异性方法。基于叠后地震属性的分析技术发展相对成熟,如相干属性[3]、曲率属性[4]、蚂蚁追踪[5]等,可表征长度大于1/4地震波长的大尺度裂缝。受地震数据纵向分辨率的影响,叠后属性技术还无法识别更小尺度的微裂缝。存在微裂缝的地下介质的各向异性特征显著[6],其中具有一组竖直裂缝且对称轴水平的横向各向同性(HTI)介质是一种典型的各向异性介质[7]。在HTI介质中纵波振幅、纵波速度(走时)以及横波分裂特征随着入射角和裂缝方位角的改变而发生规律性变化。因此可以利用这三种信息反演裂缝方位角以及各向异性参数,进而估计裂缝的发育方向和相对发育密度[8-9]。
然而,利用横波分裂预测裂缝需要采集高质量的横波数据,一般采用井下三分量数据[10]或海底四分量数据[11]。利用纵波速度(走时)特征只能预测大套储层中的裂缝,导致预测结果的纵向分辨率较低[12]。利用纵波振幅各向异性特征预测裂缝的分辨率较高,稳定性强,是目前常用的方法[13],包括纵波振幅随方位角变化(AVAZ)[14]、纵波振幅随炮检距变化(AVO)[15]两类。大多数的各向异性反演方法需要建立初始模型,其中一种建模方法是将各向同性模型作为各向异性反演的初始模型[16],但建模结果与真实情况有较大偏差。此外,利用岩石物理信息[17]或测井信息[18]也可以建立各向异性参数模型,通过估算井旁道各向异性参数,并在层位约束下插值,从而得到各向异性参数初始模型。此种建模方法在井附近精度较高,但无法保证远井处的模型精度。由于三维初始模型的精度还取决于井的数量,受勘探过程中钻井数量的限制,特别是在勘探初始阶段,很难保证初始模型的准确性,从而影响最终各向异性参数反演结果[19]。
虽然利用纵波走时信息预测裂缝的纵向分辨率低,但是在地震数据的每一个成像点位置(特别是在井间)均可提取各向异性信息,较插值方法可靠。针对地震各向异性反演的初始模型的建立问题,本文在HTI介质假设下,利用炮检距矢量片(OVT)数据的走时信息获取各向异性参数(
利用叠前全方位角道集的纵波走时信息反演方位走时各向异性,首先要得到目的层纵波走时。在选取的时窗内,采用走时扫描函数获取纵波走时
| $ Q\left(T\right)=W\left({\varphi }_{n}, T\right) \left|{}_{{T}_{0}}^{{T}_{1}}\right. $ | (1) |
式中:
在选定的时窗内,当振幅取最大
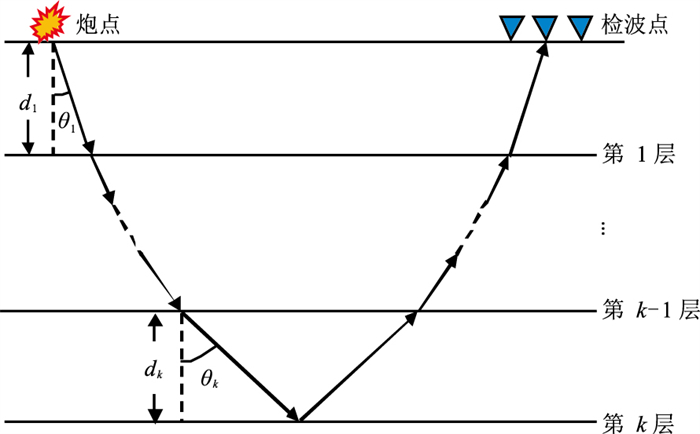
| $ T=2\sum\limits_{k=1}^{K}\frac{{d}_{k}}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{k}}{\left[{a}_{0}^{\left(n\right)}+{a}_{1}^{\left(n\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{k}+{a}_{2}^{\left(n\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{4}{\theta }_{k}\right]}^{1/2} $ | (2) |
|
图 1 多层各向异性介质射线追踪轨迹 |
其中
| $ \left\{\begin{array}{l}{a}_{0}^{\left(n\right)}={v}_{{}_{\mathrm{{\rm P}}0k}}^{-2}(1-2{\varepsilon }_{k})\\ {a}_{1}^{\left(n\right)}=2{v}_{{}_{\mathrm{{\rm P}}0k}}^{-2}(2{\varepsilon }_{k}-{\delta }_{k})\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}({\varphi }_{n}-{\phi }_{k})\\ {a}_{2}^{\left(n\right)}=2{v}_{{}_{\mathrm{{\rm P}}0k}}^{-2}({\delta }_{k}-{\varepsilon }_{k})\mathrm{c}\mathrm{o}{\mathrm{s}}^{4}(\varphi n-{\phi }_{k})\end{array}\right. $ | (3) |
式中:
式(2)是经过多次近似得到的,因此当各向异性较弱或者
根据时距关系利用Dix公式[22]计算
| $ {v}_{\mathrm{{\rm P}}{0}_{k}}^{2}=\frac{{T}_{0, k}{v}_{\mathrm{R}, k}^{2}-{T}_{0, k-1}{v}_{\mathrm{R}, k-1}^{2}}{{T}_{0, k}-{T}_{0, k-1}} $ | (4) |
式中:
| $ X=2\sum\limits_{j=1}^{k}\left({d}_{j}\mathrm{t}\mathrm{a}\mathrm{n}{\theta }_{j}\right) $ | (5) |
| $ \frac{\partial }{\partial \left({d}_{j}\mathrm{t}\mathrm{a}\mathrm{n}{\theta }_{j}\right)}\left(T-\lambda X\right)=0 $ | (6) |
式中:
式(2)表明目的层走时受上覆地层各向异性以及裂缝方位角的影响。因此为了计算目的层的各向异性参数,首先应该得到上覆地层的各向异性参数以及裂缝方位角。本文采用逐层反演方法,利用目的层走时和上覆地层的各向异性参数计算目的层的各向异性参数。首先,利用单层走时(式(2)中K=1)获取第一层的各向异性参数。然后再逐层获取下伏地层的各向异性参数。
根据式(2),得到第
| $ t=\frac{2{d}_{k}}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{k}}{\left[{a}_{0}^{\left(n\right)}+{a}_{1}^{\left(n\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{k}+{a}_{2}^{\left(n\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{4}{\theta }_{k}\right]}^{1/2} $ | (7) |
设第
| $ {\mathit{\boldsymbol{{T}}}}_{N, k-1}^{\mathrm{c}\mathrm{a}\mathrm{l}}=\left(\begin{array}{c}{t}_{\mathrm{1, 1}}+{t}_{\mathrm{1, 2}}+\cdots +{t}_{1, i}+\dots +{t}_{1, k-1}\\ {t}_{\mathrm{2, 1}}+{t}_{\mathrm{2, 2}}+\cdots +{t}_{2, i}+\dots +{t}_{2, k-1}\\ \vdots\\ {t}_{n, 1}+{t}_{n, 2}+\cdots +{t}_{n, i}+\dots +{t}_{n, k-1}\\ \vdots\\ {t}_{N, 1}+{t}_{N, 2}+\cdots +{t}_{N, i}+\dots +{t}_{N, k-1}\end{array}\right) $ | (8) |
式中
| $ {\mathit{\boldsymbol{{t}}}}_{N, k}^{\mathrm{c}\mathrm{a}\mathrm{l}}=\left(\begin{array}{c}\frac{2{d}_{k}}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{k}}{\left[{a}_{0}^{\left(1\right)}+{a}_{1}^{\left(1\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{k}+{a}_{2}^{\left(1\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{4}{\theta }_{k}\right]}^{1/2}\\ \frac{2{d}_{k}}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{k}}{\left[{a}_{0}^{\left(2\right)}+{a}_{1}^{\left(2\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{k}+{a}_{2}^{\left(2\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{4}{\theta }_{k}\right]}^{1/2}\\ \vdots\\ \frac{2{d}_{k}}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{k}}{\left[{a}_{0}^{\left(n\right)}+{a}_{1}^{\left(n\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{k}+{a}_{2}^{\left(n\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{4}{\theta }_{k}\right]}^{1/2}\\ \vdots\\ \frac{2{d}_{k}}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{k}}{\left[{a}_{0}^{\left(N\right)}+{a}_{1}^{\left(N\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{k}+{a}_{2}^{\left(N\right)}\mathrm{s}\mathrm{i}{\mathrm{n}}^{4}{\theta }_{k}\right]}^{1/2}\end{array}\right) $ | (9) |
在式(5)和式(6)的约束下,地震波在不同测线方位的炮点到检波点的总走时为
| $ {\mathit{\boldsymbol{{T}}}}_{N, k}^{\mathrm{c}\mathrm{a}\mathrm{l}}=\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{ }({\mathit{\boldsymbol{{T}}}}_{N, k-1}^{\mathrm{c}\mathrm{a}\mathrm{l}}+{\mathit{\boldsymbol{{t}}}}_{N, k}^{\mathrm{c}\mathrm{a}\mathrm{l}}) $ | (10) |
根据式(1),从叠前全方位角道集中拾取第
| $ {\mathit{\boldsymbol{{T}}}}_{N, k}^{\mathrm{o}\mathrm{b}\mathrm{s}}={\left(\begin{array}{ccc}{T}_{1, k}^{\mathrm{o}\mathrm{b}\mathrm{s}}& {T}_{2, k}^{\mathrm{o}\mathrm{b}\mathrm{s}}& \begin{array}{cc}\cdots & {T}_{N, k}^{\mathrm{o}\mathrm{b}\mathrm{s}}\end{array}\end{array}\right)}^{\mathrm{T}} $ | (11) |
根据式(10)和式(11),利用最小二乘法可反演
| $ J\left(\mathit{\boldsymbol{{m}}}\right)=\left|\right|{\mathit{\boldsymbol{{T}}}}_{N, k}^{\mathrm{o}\mathrm{b}\mathrm{s}}-{\mathit{\boldsymbol{{T}}}}_{N, k}^{\mathrm{c}\mathrm{a}\mathrm{l}}|{|}_{2}^{2} $ | (12) |
式中
通过纵波方位走时各向异性反演方法无法直接获取各向异性参数
| $ \gamma =A\times \varepsilon +B $ | (13) |
式中
通过最小二乘方法迭代计算式(12),当合成走时
在每一个成像点均可独立利用走时信息反演各向异性参数,不受层位和测井信息约束。然而,由于走时反演只能识别大套储层,并且由时距关系计算的地层速度为近似解,因此得到的参数精度以及分辨率不满足储层预测的要求[24]。为此,本文将走时反演获取的各向异性参数结果作为AVAZ反演的初始模型。
2 各向异性反演根据弱各向异性理论假设,Rüger等[25-26]推导了HTI介质纵波反射系数
| $ \begin{array}{c} R\left(\theta , \varphi \right)=\frac{1}{2}\frac{\Delta Z}{\stackrel{-}{Z}} +\frac{1}{2}\left\{\frac{\Delta {v}_{\mathrm{P}0}}{{\stackrel{-}{v}}_{\mathrm{P}0}}-{\left(\frac{2{\stackrel{-}{v}}_{\mathrm{S}0}}{{\stackrel{-}{v}}_{\mathrm{P}0}}\right)}^{2}\frac{\Delta G}{\stackrel{-}{G}}+\left[\Delta \delta +2{\left(\frac{2{\stackrel{-}{v}}_{\mathrm{S}0}}{{\stackrel{-}{v}}_{\mathrm{P}0}}\right)}^{2}\Delta \gamma \right]\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}(\varphi -\varphi )\right\}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta + \\ \frac{1}{2}\left[\frac{\Delta {v}_{\mathrm{P}0}}{{\stackrel{-}{v}}_{\mathrm{P}0}}+\Delta \varepsilon \mathrm{c}\mathrm{o}{\mathrm{s}}^{4}(\varphi -\varphi )+\Delta \delta \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}(\varphi -\varphi )\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}(\varphi -\varphi )\right]\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \end{array} $ | (14) |
式中:
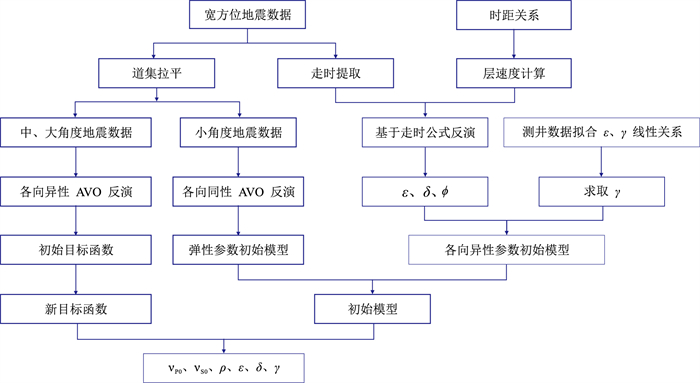
在各向异性反演中,采用高斯—牛顿法反演各向异性参数。为了提高反演精度以及解决高斯—牛顿法中的局部最小解问题,将各向异性反演分为两个阶段。同时考虑到各向异性随入射角的增加而越明显这一特性,在第一阶段使用小角度(θ < 20°)道集进行各向同性AVO反演,获得弹性参数(
| $ \Delta \mathit{\boldsymbol{{M}}}\cong {\left(\mathit{\boldsymbol{{H}}}+\mu \mathit{\boldsymbol{{I}}}\right)}^{-1}{\mathit{\boldsymbol{{J}}}}_{\mathrm{H}\mathrm{T}\mathrm{I}}^{\mathrm{T}}\left({\mathit{\boldsymbol{{R}}}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-{\mathit{\boldsymbol{{R}}}}_{0}\right) $ | (15) |
其中
| $ \mathit{\boldsymbol{J}}_{{\rm{HTI}}}^{\rm{T}} = \left( {\begin{array}{*{20}{c}} {\frac{{\partial R\left( {{\theta _1}, \phi } \right)}}{{\partial {v_{{\rm{P}}0}}}}\quad \frac{{\partial R\left( {{\theta _1}, \phi } \right)}}{{\partial {v_{{\rm{S}}0}}}}\quad \frac{{\partial R\left( {{\theta _1}, \phi } \right)}}{{\partial \rho }}\quad \frac{{\partial R\left( {{\theta _1}, \phi } \right)}}{{\partial \varepsilon }}\quad \frac{{\partial R\left( {{\theta _1}, \phi } \right)}}{{\partial \delta }}\quad \frac{{\partial R\left( {{\theta _1}, \phi } \right)}}{{\partial \gamma }}}\\ {\frac{{\partial R\left( {{\theta _2}, \phi } \right)}}{{\partial {v_{{\rm{P}}0}}}}\quad \frac{{\partial R\left( {{\theta _2}, \phi } \right)}}{{\partial {v_{{\rm{S}}0}}}}\quad \frac{{\partial R\left( {{\theta _2}, \phi } \right)}}{{\partial \rho }}\quad \frac{{\partial R\left( {{\theta _2}, \phi } \right)}}{{\partial \varepsilon }}\quad \frac{{\partial R\left( {{\theta _2}, \phi } \right)}}{{\partial \delta }}\quad \frac{{\partial R\left( {{\theta _2}, \phi } \right)}}{{\partial \gamma }}}\\ \vdots \\ {\frac{{\partial R\left( {{\theta _m}, \phi } \right)}}{{\partial {v_{{\rm{P}}0}}}}\quad \frac{{\partial R\left( {{\theta _m}, \phi } \right)}}{{\partial {v_{{\rm{S}}0}}}}\quad \frac{{\partial R\left( {{\theta _m}, \phi } \right)}}{{\partial \rho }}\quad \frac{{\partial R\left( {{\theta _m}, \phi } \right)}}{{\partial \varepsilon }}\quad \frac{{\partial R\left( {{\theta _m}, \phi } \right)}}{{\partial \delta }}\quad \frac{{\partial R\left( {{\theta _m}, \phi } \right)}}{{\partial \gamma }}} \end{array}} \right) $ | (16) |
| $ \mathit{\boldsymbol{{H}}}=\left(\begin{array}{c}\frac{\partial R(\theta , \phi )}{\partial \mathit{\boldsymbol{{E}}}}\\ \frac{\partial R(\theta , \phi )}{\partial \mathit{\boldsymbol{{A}}}}\end{array}\right)\cdot \left(\begin{array}{cc}\frac{\partial R(\theta , \phi )}{\partial \mathit{\boldsymbol{{E}}}}& \frac{\partial R(\theta , \phi )}{\partial \mathit{\boldsymbol{{A}}}}\end{array}\right) $ | (17) |
式中:
在迭代过程中,将每次迭代增量
|
图 2 基于HTI介质方位走时各向异性反演流程 |
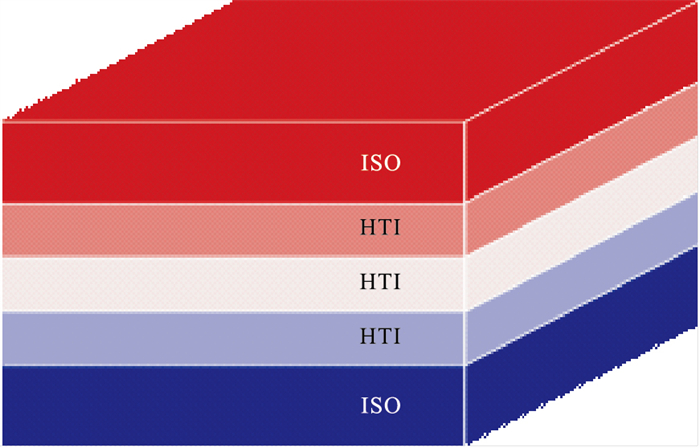
建立一个水平层状的HTI模型(图 3),其弹性参数和各向异性参数如表 1所示。Tsuneyama等[28]通过分析盐水饱和砂岩和页岩的测井数据得到式(13)中
|
图 3 水平层状模型 第1、5层为各向同性(ISO)层,第2、3、4层为HTI层。 |
|
|
表 1 水平层状模型的弹性参数和各向异性参数 |
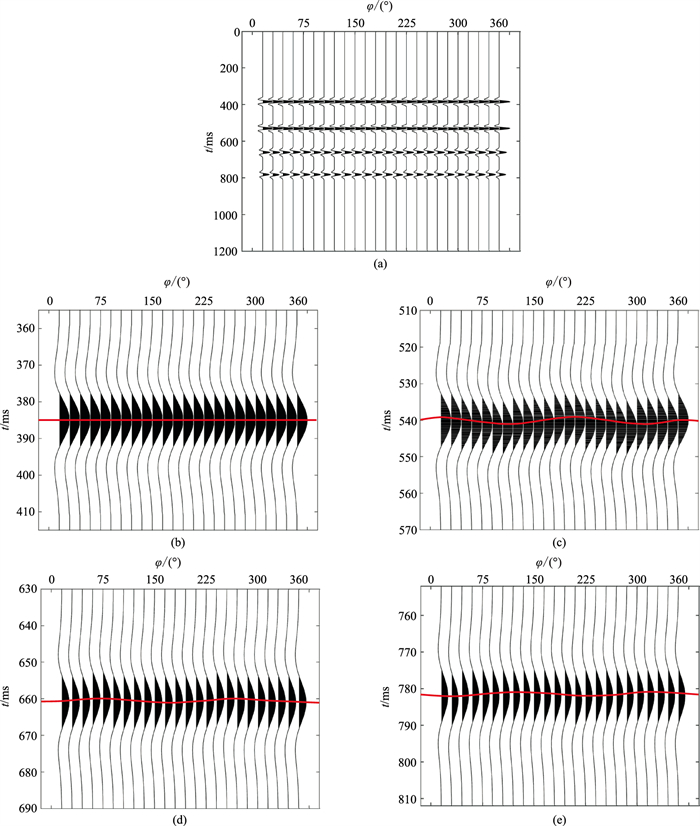
对于叠前全方位角道集,设置X=280 m以及φ间隔为15°;对于入射角道集,设置φ为0°、60°和120°以及θ为5°~40°。利用式(14)计算图 3在时域的PP波反射系数。然后,将反射系数序列与主频为30 Hz的雷克子波卷积,生成叠前全方位角道集(图 4)和入射角道集(图 5)。
|
图 4 叠前全方位角道集地震记录 (a)叠前全方位角道集地震记录;(b)D1底部同相轴;(c)D2底部同相轴;(d)D3底部同相轴;(e)D4底部同相轴 |

|
图 5 不同方位角道集 (a)φ=0°;(b)φ=60°;(c)φ=120° |
对每一层地层底界面对应的同相轴提取走时(图 4中红线)。为了验证走时反演效果,对第1层~第4层的各向异性参数的所有可能值进行最小二乘扫描,得到反演结果(表 2~表 5)。反演结果表明,走时反演的最大相对误差在10%以内,该精度对于建立初始模型是可以接受的。方位走时各向异性反演的模型测试结果表明,在没有任何约束条件下,方位走时各向异性反演依然能得到较准确的结果,说明反演方法的稳定性较高。
|
|
表 2 D1反演结果相对误差分析 |
|
|
表 3 D2反演结果相对误差分析 |
|
|
表 4 D3反演结果相对误差分析 |
|
|
表 5 D4反演结果相对误差分析 |
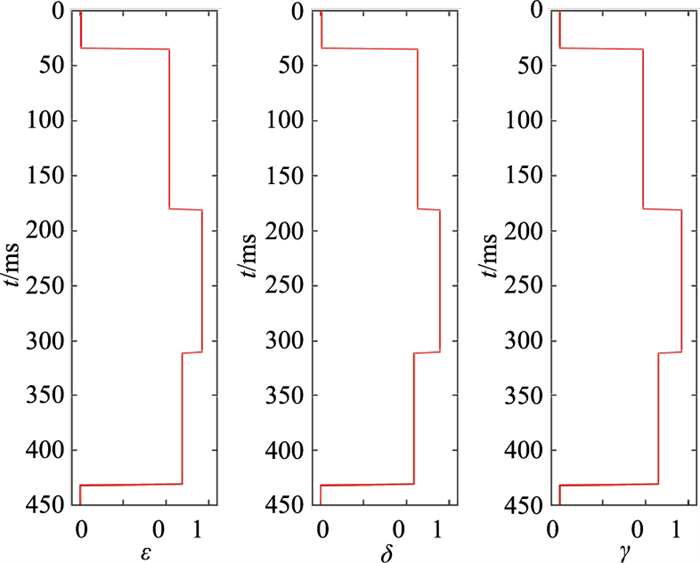
利用式(13),根据反演得到的
|
图 6 各向异性参数初始模型 |
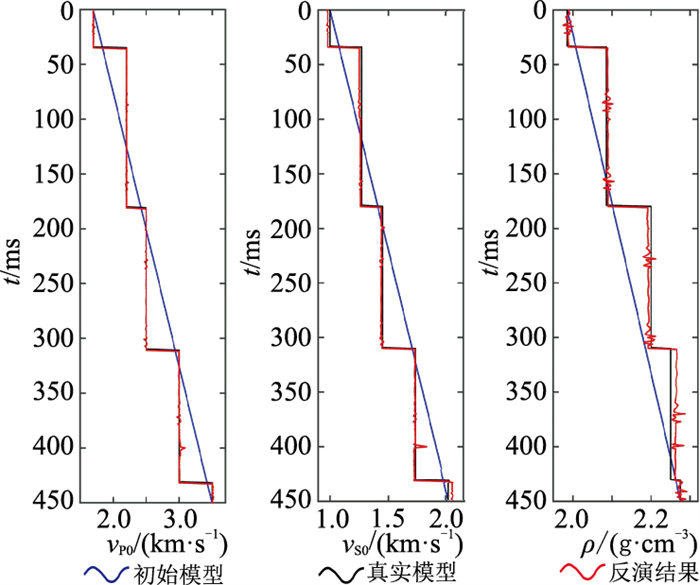
各向异性反演分两个阶段。第一阶段为各向同性反演,第二阶段为各向异性反演。对小角度(5°~20°)的入射角道集(图 5)进行各向同性反演,共迭代20次。当迭代停止时,各向同性反演残差(
|
图 7 各向同性反演结果 |
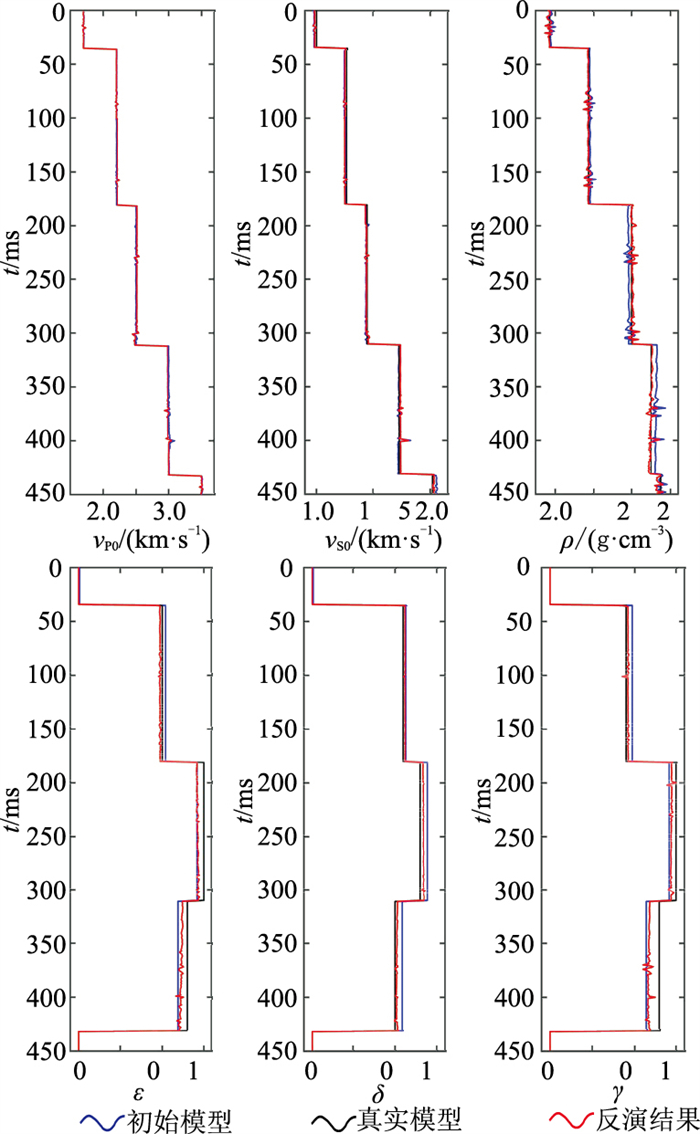
在图 6和图 7的约束下,对中、大角度(20°~40°)的入射角道集(图 5)进行各向异性AVAZ反演,共迭代了28次。当迭代停止时,各向异性AVAZ反演残差很小,约为0.32。各向异性反演结果(图 8)表明,在初始模型值误差较小的情况下,反演值始终与理论值吻合较好。因此,若能提供较精确的各向异性参数初始模型,基于HTI介质的各向异性AVAZ反演可以得到更准确的Thomsen参数。
|
图 8 各向异性反演结果 |
本文利用四川盆地某页岩油储层的OVT地震数据测试所提方法的效果。页岩储层在构造应力作用下,易产生裂缝。岩心以及地层微电阻率扫描成像(FMI)测井中均发现高角度裂缝,整体具有明显的HTI介质特征。
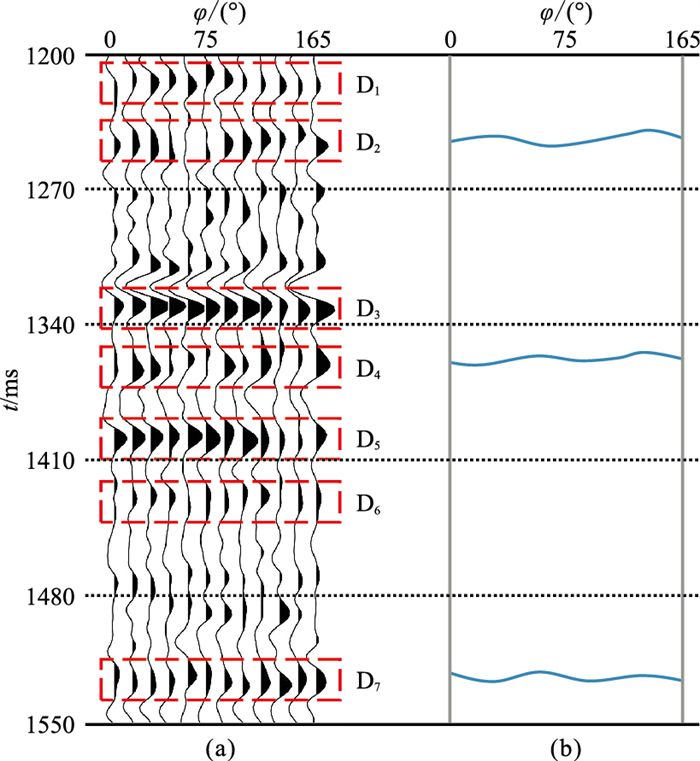
以某一个OVT为例,炮检距为1100~1150 m的方位覆盖次数较高,因此抽取炮检距为1127 m的方位角道集(图 9)进行方位走时各向异性反演。
|
图 9 分层以及走时提取结果 (a)叠前方位角道集;(b)走时提取结果 |
与常规的叠前地震数据相比,OVT数据不仅包含炮检距信息,还包含方位角信息。因此,为了减小走时拾取误差,首先根据地质资料的岩性信息以及地震记录中同相轴的连续性,将目的层细分为6层(图 9a)。其次,拾取OVT数据中同一炮检距的多个方位的走时,并且剔除异常值。即使其中有几道数据的误差较大,但对于拾取的大量走时数据而言,其影响可以忽略不计。同时,为了增加走时反演的稳定性,对拾取的走时进行方位插值,从而得到任意方位走时(图 9b)。通过图 9a以及时距关系计算分层地层参数,得到地层参数分层结果(表 6)。
|
|
表 6 地层参数分层结果 |
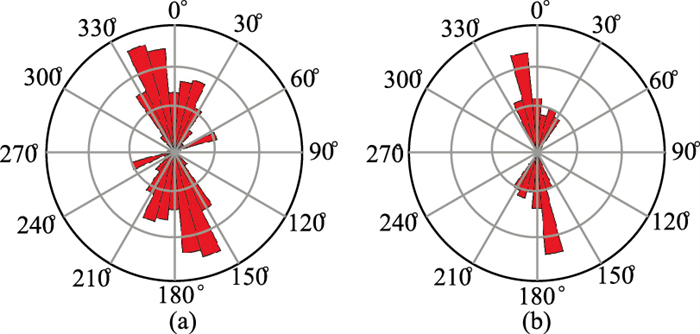
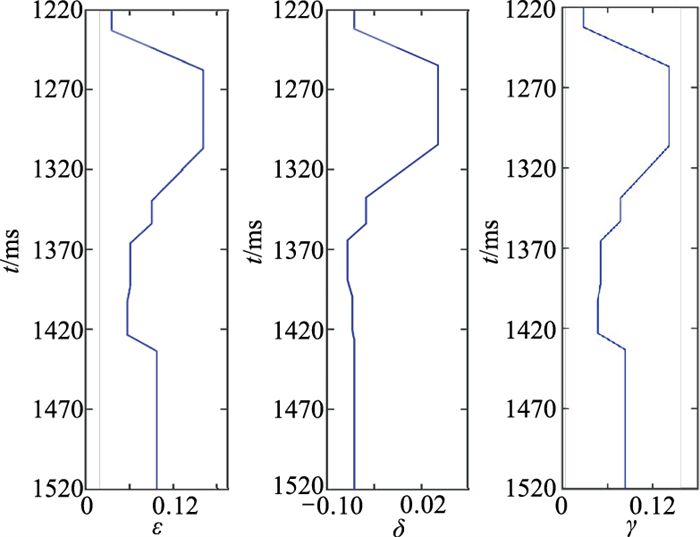
图 10为裂缝方位预测结果。可以看出,基于走时反演得到的裂缝方位(图 10b)与实际裂缝发育方位(图 10a)基本一致,为AVAZ反演提供了良好的模型基础。利用计算得到的地层参数以及走时拾取结果进行方位走时各向异性反演得到各向异性参数
|
图 10 裂缝方位预测结果 (a)岩心裂缝方位玫瑰图;(b)走时反演的裂缝方位玫瑰图 |
|
图 11 方位走时各向异性反演建模结果 |
|
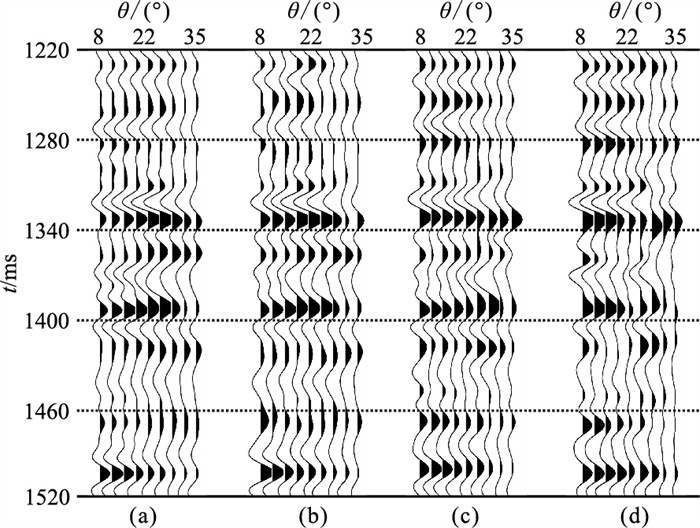
图 12 不同方位的入射角道集(a)φ=0°;(b)φ=45°;(c)φ=90°;(d)φ=135° |
|
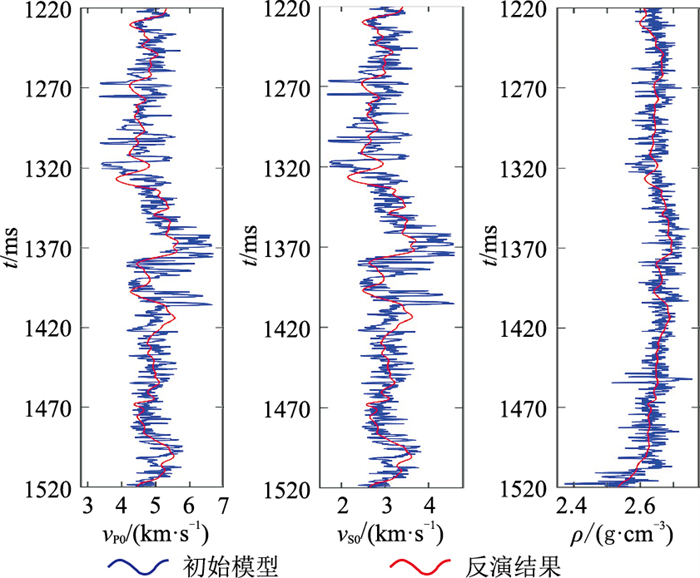
图 13 各向同性反演结果 |
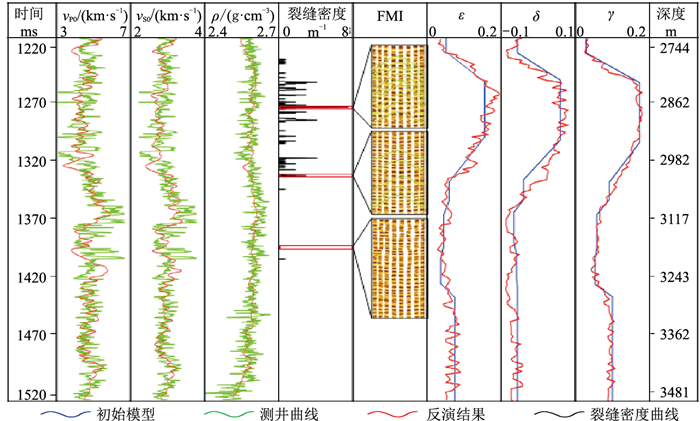
在图 11、图 13的约束下进行各向异性反演,得到各向异性反演结果(图 14)。由图可见:①弹性参数反演结果(
|
图 14 各向异性反演结果 |
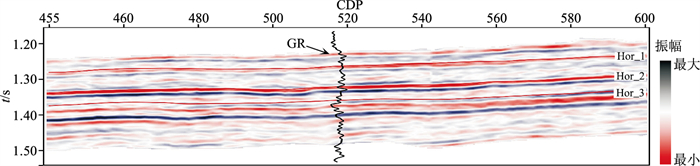
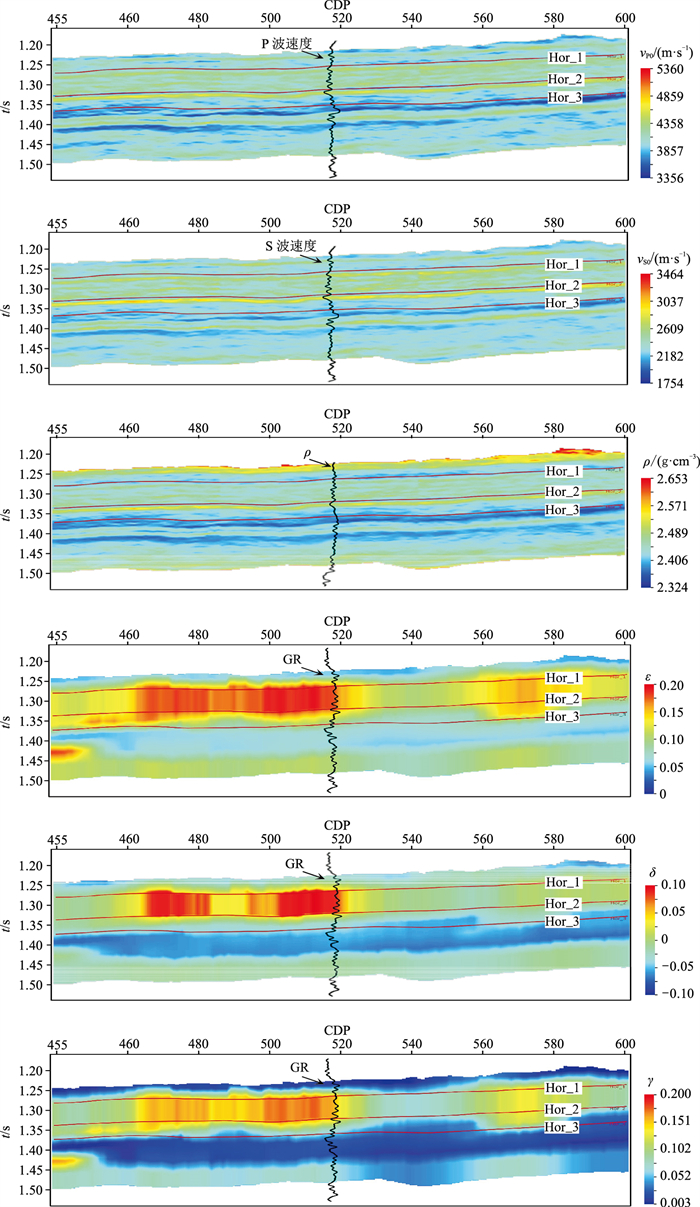
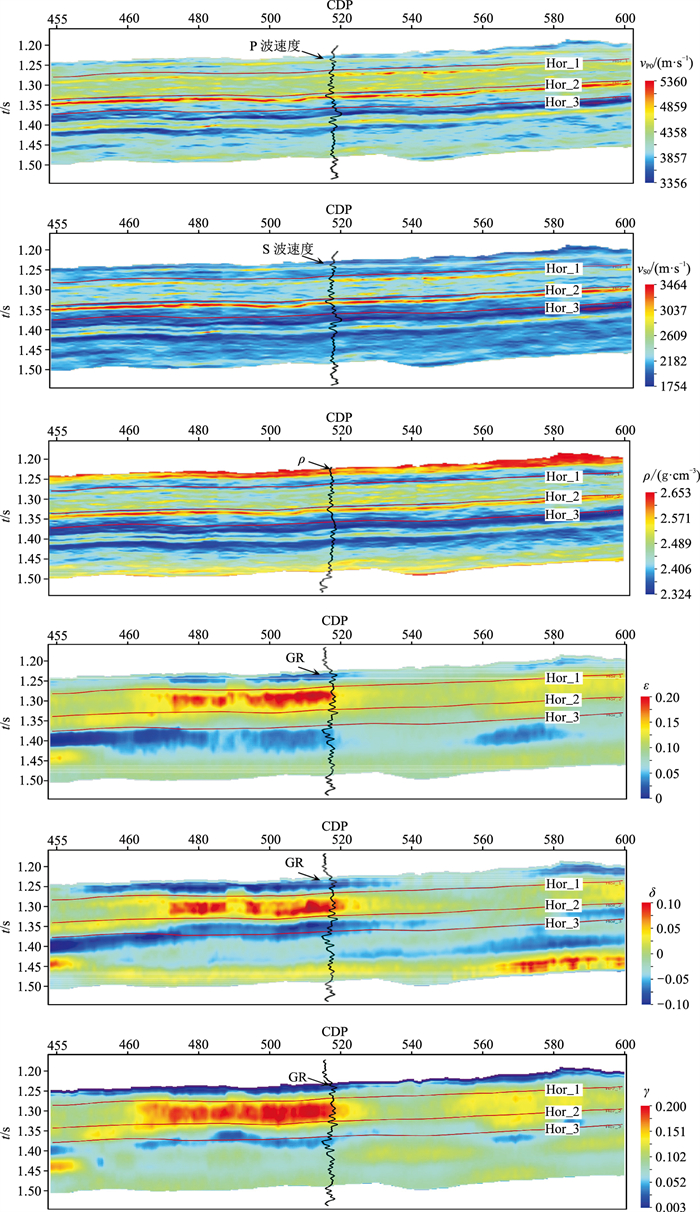
根据图 2,抽取CDP为450~600的过井叠前地震数据(叠后剖面如图 15所示)进行反演。其中,抽取炮检距为1127 m的叠前方位道集进行方位走时各向异性反演,抽取φ为0°、45°、90°、135°的入射角道集进行各向异性反演。根据方位走时各向异性反演以及各向同性反演得到初始模型剖面(图 16),根据各向异性反演得到反演剖面(图 17)。由图 17可见,各向异性参数高值区(红色区域)裂缝较发育,整体上目的层上部裂缝较下部发育,与井上裂缝发育情况吻合,证实了所提方法的可行性。
|
图 15 叠后地震剖面 |
|
图 16 各向异性反演初始模型剖面 |
|
图 17 各向异性反演剖面 |
传统反演方法利用测井资料和层位插值构建初始模型的做法导致初始模型精度较低。为此,本文充分考虑了OVT数据中的走时和振幅信息,提出了一种基于HTI介质的方位走时各向异性建模的反演方法。首先,获取各个地层的方位纵波走时。然后,利用得到的方位走时信息进行方位走时各向异性反演,并利用反演结果建立各向异性参数初始模型。最后,基于Rüger反射系数近似公式,采用高斯—牛顿法进行各向异性AVAZ反演获得各向异性参数。模型测试表明,方位走时各向异性反演可以在无测井约束的情况下获得精度较高的各向异性参数。在获取各层的各向异性参数的基础上,通过各向异性AVAZ反演得到了较为精确且分辨率更高的反演结果。四川盆地实际数据测试结果表明,利用所提方法成功地获得了储层的弹性和各向异性信息。
| [1] |
WANG L, WEI J, HUANG P, et al. Seismic prediction method of multiscale fractured reservoir[J]. Applied Geophysics, 2018, 15(2): 240-252. DOI:10.1007/s11770-018-0667-8 |
| [2] |
何峰, 龙凡, 韩刚, 等. 基于宽方位地震数据的纵、横波速度方位各向异性对比研究[J]. 石油地球物理勘探, 2021, 56(2): 289-294, 301. HE Feng, LONG Fan, HAN Gang, et al. Comparision of azimuthal anisotropy of P-wave and S-wave velocity based on wide azimuth seismic data[J]. Oil Geophysical Prospecting, 2021, 56(2): 289-294, 301. |
| [3] |
BAHORICH M S, FARMER S L. 3-D seismic discontinuity for faults and stratigraphic features: the coherence cube[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [4] |
MURRAY G H, J r. Quantitative fracture study: Sanish Pool, McKenzie County, North Dakota[J]. AAPG Bulletin, 1968, 52(1): 57-65. |
| [5] |
COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]. Proceedings of ECAL91-European Conference on Artificial Life, 1991, 134-142.
|
| [6] |
THOMSEN L. Elastic anisotropy due to aligned cracks in porous rock[J]. Geophysical Prospecting, 1995, 43(6): 805-829. DOI:10.1111/j.1365-2478.1995.tb00282.x |
| [7] |
SKOPINTSEVA L, ALKHALIFAH T. An analysis of AVO inversion for postcritical offsets in HTI media[J]. Geophysics, 2013, 78(3): N11-N20. DOI:10.1190/geo2011-0288.1 |
| [8] |
周晓越, 甘利灯, 杨昊, 等. 利用叠前振幅和速度各向异性的联合反演方法[J]. 石油地球物理勘探, 2020, 55(5): 1084-1091. ZHOU Xiaoyue, GAN Lideng, YANG Hao, et al. A joint inversion method using amplitude and velocity anisotropy[J]. Oil Geophysical Prospecting, 2020, 55(5): 1084-1091. DOI:10.13810/j.cnki.issn.1000-7210.2020.05.016 |
| [9] |
公亭, 王兆磊, 罗文山, 等. 横波源三维地震资料矢量横波四分量旋转和快慢波分离技术[J]. 石油地球物理勘探, 2022, 57(5): 1028-1034. GONG Ting, WANG Zhaolei, LUO Wenshan, et al. Four-component rotation and fast-slow wave separation techniques for 3D vector S-wave seismic data of S-wave sources[J]. Oil Geophysical Prospecting, 2022, 57(5): 1028-1034. DOI:10.13810/j.cnki.issn.1000-7210.2022.05.003 |
| [10] |
符志国, 黄建国, 廖娟, 等. 基于二维三分量资料的裂缝预测[J]. 石油物探, 2013, 52(2): 212-216, 228. FU Zhiguo, HUANG Jianguo, LIAO Juan, et al. Fracture prediction by using 2D3C seismic data[J]. Geophysical Prospecting for Petroleum, 2013, 52(2): 212-216, 228. DOI:10.3969/j.issn.1000-1441.2013.02.015 |
| [11] |
HALL S A, KENDALL J M. Fracture characterization at Valhall: Application of P-wave amplitude variation with offset and azimuth (AVOA) analysis to a 3D ocean-bottom data set[J]. Geophysics, 2003, 68(4): 1150-1160. DOI:10.1190/1.1598107 |
| [12] |
杨晓, 王真理, 喻岳钰. 裂缝型储层地震检测方法综述[J]. 地球物理学进展, 2010, 25(5): 1785-1794. YANG Xiao, WANG Zhenli, YU Yueyu. The overview of seismic techniques in prediction of fracture reservoir[J]. Progress in Geophysics, 2010, 25(5): 1785-1794. |
| [13] |
王洪求, 杨午阳, 谢春辉, 等. 不同地震属性的方位各向异性分析及裂缝预测[J]. 石油地球物理勘探, 2014, 49(5): 925-931. WANG Hongqiu, YANG Wuyang, XIE Chunhui, et al. Azimuthal anisotropy analysis of different seismic attributes and fracture prediction[J]. Oil Geophysical Prospecting, 2014, 49(5): 925-931. |
| [14] |
于晓东, 桂志先, 汪勇, 等. 叠前AVAZ裂缝预测技术在车排子凸起的应用[J]. 石油地球物理勘探, 2019, 54(3): 624-633. YU Xiaodong, GUI Zhixian, WANG Yong, et al. Prestack AVAZ fracture prediction applied in Chepaizi Uplift[J]. Oil Geophysical Prospecting, 2019, 54(3): 624-633. |
| [15] |
付欣, 张小龙, 孙云强, 等. 基于双差反演策略的时移地震AVO反演[J]. 石油地球物理勘探, 2022, 57(4): 888-896. FU Xin, ZHANG Xiaolong, SUN Yunqing, et al. Time-lapse seismic AVO inversion based on a double difference inversion strategy[J]. Oil Geophysical Prospecting, 2022, 57(4): 888-896. |
| [16] |
CAI P, TSVANKIN I. Joint migration velocity analysis of PP-and PS-waves for VTI media[J]. Geophysics, 2013, 78(5): WC123-WC135. DOI:10.1190/geo2012-0416.1 |
| [17] |
张广智, 陈怀震, 王琪, 等. 基于碳酸盐岩裂缝岩石物理模型的横波速度和各向异性参数预测[J]. 地球物理学报, 2013, 56(5): 1707-1715. ZHANG Guangzhi, CHEN Huaizhen, WANG Qi, et al. Estimation of S-wave velocity and anisotropic para- meters using fractured carbonate rock physics model[J]. Chinese Journal of Geophysics, 2013, 56(5): 1707-1715. |
| [18] |
GE Z, PAN S, LIU J, et al. Estimation of brittleness and anisotropy parameters in transversely isotropic media with vertical axis of symmetry[J]. IEEE Transactions on Geoscience & Remote Sensing, 2021. DOI:10.1109/tgrs.2021.3073162 |
| [19] |
SUN Y, CHEN S, LI Y, et al. Shale rocks brittleness index prediction method using extended elastic impedance inversion[J]. Journal of Applied Geophysics, 2021. DOI:10.1016/j.jappgeo.2021.104314 |
| [20] |
SENA A G. Seismic traveltime equations for azimuthally anisotropic and isotropic media: Estimation of interval elastic properties[J]. Geophysics, 1991, 56(12): 2090-2101. DOI:10.1190/1.1443021 |
| [21] |
赵爱华, 丁志峰. 一种弱各向异性介质地震波群速度的近似表示新方法[J]. 地球物理学进展, 2005, 20(4): 916-919. ZHAO Aihua, DING Zhifeng. New approximate expressions of seismic group velocities for weakly anisotropic media[J]. Progress in Geophysics, 2005, 20(4): 916-919. DOI:10.3969/j.issn.1004-2903.2005.04.006 |
| [22] |
DIX C H. Seismic velocities from surface measurements[J]. Geophysics, 1955, 20(1): 68-86. DOI:10.1190/1.1438126 |
| [23] |
SONDERGELD C H, RAI C S. Elastic anisotropy of shales[J]. The Leading Edge, 2011, 30(3): 324-331. DOI:10.1190/1.3567264 |
| [24] |
LU M, TANG J, YANG H, et al. P-wave travel-time analysis and Thomsen parameters inversion in orthorhombic media[J]. Chinese Journal of Geophysics, 2005, 48(5): 1247-1252. DOI:10.1002/cjg2.770 |
| [25] |
RÜGER A, Tsvankin I. Using AVO for fracture detection: Analytic basis and practical solutions[J]. The Leading Edge, 1997, 16(10): 1429-1434. DOI:10.1190/1.1437466 |
| [26] |
RÜGER A. Variation of P-wave reflectivity with offset and azimuth in anisotropic media[J]. Geophysics, 1998, 63(3): 935-947. DOI:10.1190/1.1444405 |
| [27] |
LU J, WANG Y, CHEN J, et al. Joint anisotropic amplitude variation with offset inversion of PP and PS seismic data[J]. Geophysics, 2018, 83(2): N31-N50. DOI:10.1190/geo2016-0516.1 |
| [28] |
TSUNEYAMA F, MAVKO G. Velocity anisotropy estimation for brine-saturated sandstone and shale[J]. The Leading Edge, 2005, 24(9): 882-888. DOI:10.1190/1.2056371 |
| [29] |
THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |



 杨宇勇, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院,610059。Email:
杨宇勇, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院,610059。Email: