0 引言

储层物性参数是描述储层特征的关键信息，是预测储层的含油气性、估计油气储量等的基础^[1]。在实际工作中，通常从两个方面预测储层物性参数。一方面，仅根据有限的钻井数据和(或)测井资料估算储层物性参数，无法描述整个研究区的地质特征。另一方面，虽然采集的大量地震资料蕴含了丰富的地下信息，但由地震数据直接反演物性参数往往是困难的。为此，人们引入弹性参数作为中间变量，发展了一系列物性参数的间接地震反演方法^[2]。这种方法需要建立一个正演模型描述弹性和物性参数之间的关系，进而求解对应的反问题预测物性参数。

针对物性参数预测问题，统计学方法是一种容易理解且方便的方法^{[1, 3]}，但需要大量高质量的测井或岩心数据，具有明显的数据依赖性，而且缺乏物理过程模拟，难以反映普遍规律。因此，引入考虑实际物理过程的岩石物理模型作为正演模型，可以有效弥补纯统计学方法的不足^[4-5]。自20世纪中叶以来，人们针对实际油气储层，发展了一系列岩石物理模型描述弹性参数和物性参数之间的关系，并模拟了储层介质中的地震波传播现象。Biot/Squirt(BISQ)模型^[6]是典型的岩石物理模型，起源于20世纪中叶对孔隙介质中的固—液耦合机制的研究。Biot^[7]基于数理方程和拉格朗日力学理论，率先指出孔隙双相介质存在一种动态的固—流耦合机制——Biot机制，并建立了相应的弹性波方程。然而，众所周知，Biot模型并不能充分描述在某些储层中地震波的高频散和强衰减现象^[8]。为此，Dvorkin等^[6]基于Biot模型引入喷射流机制，建立了最初的各向同性介质BISQ模型。Yang等^[9-10]系统研究了BISQ模型，建立了包含两种力学机制(固—流耦合各向异性效应和孔隙流体流动)的各向异性BISQ模型。近年来，通过引入等效介质、黏弹性等理论描述复杂油气储层特征^[11-15]。此外，大量的岩心实验数据和油田实际数据进一步证明了BISQ模型的可靠性和有效性^[16-17]。但是，在实际应用中基于岩石物理模型的反演易受噪声干扰，甚至得到完全错误的预测结果^[4]。

在地球物理反演领域，贝叶斯理论具有重要的理论和应用价值^[18]，包括量化地质结构预测的不确定性、提高地震反演精度、添加空间约束等。针对物性参数预测问题，贝叶斯反演方法也备受关注。一方面，由于贝叶斯反演是基于统计学框架的反演方法，在反演目标参数的同时给出模型参数的后验概率，进而分析预测结果的不确定性^[4]。但是，由于地下模型的特殊性，无法通过反复试验验证物性参数的不确定性估计，而且也缺乏可靠的统计检验。另一方面，根据最大后验估计理论，贝叶斯反演通过引入先验信息实现物性参数反演的正则化，进而提高了物性参数反演精度和抗噪能力^[19]。

物性参数反演经常涉及多参数优化问题，其中的最优解就是物性参数预测结果。因此，稳定、高效的优化算法也是物性参数反演的重要研究内容。如单纯形法、最速下降法、共轭梯度法等确定性算法是求解线性优化问题的常用算法。然而，对于物性参数反演这类存在多解性的优化问题，上述确定性算法往往难以找到全局最优解。因此，如遗传算法、模拟退火算法等具有全局搜索能力的随机算法通常是更好的选择，其中遗传算法的应用最广泛。Eiben等^[20]基于马尔科夫链理论，在数学上证明了遗传算法具全局收敛性，并成功应用于地球物理反问题^[21-22]。Fang等^[16]基于BISQ模型利用混合遗传算法可有效反演储层物性参数。

本文旨在发展一种间接地震反演方法，进而可靠地预测储层物性参数，其核心是根据储层弹性参数预测多种物性参数的联合非线性反演。虽然现有方法取得了一定效果，但仍存在几个问题亟待解决。一是建立可靠的岩石物理正演模型刻画弹性参数和物性参数的非线性关系。二是在岩石物理模型的基础上引入测井数据约束，以提高反演精度。为此，本文首先在BISQ理论和等效流体理论的基础上建立了岩石物理正演模型，该模型反映了孔隙介质中固体和流体的多种物理作用，可精细地刻画储层中地震波的传播过程。其次，在贝叶斯统计学的框架下，采用高斯先验模型，引入测井数据约束，进而发展了基于BISQ模型的储层物性参数贝叶斯反演方法。再次，由于反演问题的多解性，引入具有全局搜索能力的杂交遗传算法提高反演精度和效率。利用所提反演方法预测中国东部A油田目标区域的孔隙度和含水饱和度，获得了较好效果。

1 基于BISQ模型的岩石物理建模

将孔隙流体等效模型和固体骨架模量—孔隙度模型引入部分饱和的BISQ模型^[11]，建立相应的岩石物理模型刻画储层弹性参数与物性参数之间的非线性关系。

储层介质中的孔隙流体通常是石油、天然气和地层水的混合物。由于混合成分是气体或液体，其剪切模量为零。在液体充分混合的情况下，通过Reuss平均公式^[8]

$ \frac{1}{{K}_{\mathrm{f}}}=\frac{{s}_{\mathrm{w}}}{{K}_{\mathrm{w}}}+\frac{1-{s}_{\mathrm{w}}}{{K}_{\mathrm{o}}} $

(1)

计算油水混合的等效流体体积模量$ {K}_{\mathrm{f}} $。式中：$ {s}_{\mathrm{w}} $为含水饱和度；$ {K}_{\mathrm{w}} $和$ {K}_{\mathrm{o}} $分别为水和油的体积模量。

当孔隙连通性较差时，多孔岩石被分为一系列的斑块，此时孔隙流体分布不均匀。在这种复杂情况下，虽然简单的平均公式不能精确地描述液体混合物的等效作用，但是仍可用式(1)计算$ {K}_{\mathrm{f}} $下界$ {K}_{\mathrm{f}}^{\mathrm{d}} $。此外，Voigt平均公式^[8]

$ {K}_{\mathrm{f}}^{\mathrm{u}}={s}_{\mathrm{w}}{K}_{\mathrm{w}}+(1-{s}_{\mathrm{w}}){K}_{\mathrm{o}} $

(2)

给出了$ {K}_{\mathrm{f}} $上界$ {K}_{\mathrm{f}}^{\mathrm{u}} $。在实际应用中，因为$ {K}_{\mathrm{f}}^{\mathrm{u}} $和$ {K}_{\mathrm{f}}^{\mathrm{d}} $是接近的，所以可将两者视为$ {K}_{\mathrm{f}} $的有效近似值。

固体骨架是一种理想的等效模型，而不是真实的饱和气体岩石。固体骨架模量只与固体组分及其孔隙特性相关，不受孔隙流体弹性模量影响^[8]。一般情况下，人们根据现有测井资料或岩心资料建立适当的数学模型近似地计算固体骨架模量^{[4, 16]}。

Dvorkin等^[6]结合含流体孔隙岩石在宏观尺度的Biot流作用和在微观尺度的喷射流作用建立了BISQ模型。Biot流特征频率为

$ {f}_{\mathrm{b}}=\frac{\eta \phi }{2\mathrm{\pi }\kappa {\rho }_{\mathrm{f}}} $

(3)

式中：$ \eta $为流体黏度；$ \phi $为孔隙度；$ \kappa $为渗透率；$ {\rho }_{\mathrm{f}} $为孔隙流体密度。

由于实际地震波频率$ f $远小于$ {f}_{\mathrm{b}} $($ {f}_{\mathrm{b}} $≈10⁶ Hz)，Dvorkin等^[23]基于BISQ模型提出了更简洁的P波速度公式

$ {V}_{\mathrm{P}}=\frac{1}{\mathrm{R}\mathrm{e}\left(\sqrt{Y}\right)} $

(4)

其中

$\left\{\begin{array}{l} Y=\frac{\rho_{\mathrm{s}}(1-\phi)+\rho_{\mathrm{f}} \phi}{M+\frac{F_{\mathrm{sq}} \alpha^2}{\phi}} \\ F_{\mathrm{sq}}=F\left[1-\frac{2 J_1(\xi)}{\xi J_0(\xi)}\right] \\ \xi=R \sqrt{\frac{i 2 \pi f \eta \phi}{\kappa F}} \\ \alpha=1-\frac{K}{K_{\mathrm{s}}} \end{array}\right.$

(5)

式中：$ {J}_{0} $和$ {J}_{1} $分别为0阶和1阶Bessel函数；$ {\rho }_{\mathrm{s}} $为固体基质密度；$ R $为特征喷射流长度^[6]；$ F $为Biot流动系数；K为固体骨架的体积模量；$ {K}_{\mathrm{s}} $为固体基质的体积模量；$ M $为固体骨架的单轴应变模量，即

$ M=K+\frac{4}{3}G $

(6)

式中$ G $为固体骨架的剪切模量。由下式^[7]

$ \frac{1}{F}=\frac{1}{{K}_{\mathrm{f}}}+\frac{\alpha -\phi }{\phi {K}_{\mathrm{s}}} $

(7)

计算F。

在BISQ模型中，S波速度为^[11]

$ \left\{\begin{aligned} V_{\mathrm{s}} & =\frac{\sqrt{G}}{\operatorname{Re}\left(\sqrt{\rho_{\mathrm{x}}}\right)} \\ \rho_{\mathrm{x}} & =(1-\phi) \rho_{\mathrm{s}}+(1-\theta) \phi \rho_{\mathrm{f}} \\ \frac{1}{\theta} & =\frac{\rho_{\mathrm{a}} / \rho_{\mathrm{f}}+\phi}{\phi}+\mathrm{i} \frac{f_{\mathrm{b}}}{f} \end{aligned}\right.$

(8)

式中ρ_a为固—流耦合密度^[7]。

根据质量守恒定律得到含流体岩石密度ρ和ρ_f

$ \left\{\begin{array}{l}\rho =\phi {\rho }_{\mathrm{f}}+(1-\phi ){\rho }_{\mathrm{s}}\\ {\rho }_{\mathrm{f}}={s}_{\mathrm{w}}{\rho }_{\mathrm{w}}+(1-{s}_{\mathrm{w}}){\rho }_{\mathrm{o}}\end{array}\right. $

(9)

式中ρ_w和ρ_o分别为地层水和油的密度。

2 储层物性参数的贝叶斯估计

为方便书写，基于前述BISQ模型，可以将密度$ \rho $和纵、横波阻抗I_P、I_S视为关于模型参数$ \boldsymbol{l} $(待反演物性参数)和辅助参数$ \boldsymbol{m} $的非线性函数

$ \left\{\begin{array}{l}\rho ={f}_{1}(\boldsymbol{l}, \boldsymbol{m})\\ {I}_{\mathrm{P}}=\rho {V}_{\mathrm{P}}={f}_{2}(\boldsymbol{l}, \boldsymbol{m})\\ {I}_{\mathrm{S}}=\rho {V}_{\mathrm{S}}={f}_{3}(\boldsymbol{l}, \boldsymbol{m})\end{array}\right. $

(10)

其中

$ \left\{\begin{array}{l}\boldsymbol{l}=(\phi , {s}_{\mathrm{w}}{)}^{\mathrm{T}}\\ \boldsymbol{m}=({\rho }_{\mathrm{s}}, {\rho }_{\mathrm{w}}, {\rho }_{\mathrm{o}}, {K}_{\mathrm{s}}, {K}_{\mathrm{w}}, {K}_{\mathrm{o}}, \dots )\end{array}\right. $

(11)

在实际应用中，密度和弹性阻抗作为观测数据，可以视为模型计算的理论值和观测误差之和

$ \left\{\begin{array}{l}\rho ={f}_{1}(\boldsymbol{l}, \boldsymbol{m})+{e}_{1}\\ {I}_{\mathrm{P}}={f}_{2}(\boldsymbol{l}, \boldsymbol{m})+{e}_{2}\\ {I}_{\mathrm{S}}={f}_{3}(\boldsymbol{l}, \boldsymbol{m})+{e}_{3}\end{array}\right. $

(12)

式中e_i(i=1，2，3)为观测误差。设观测数据$ \boldsymbol{d}=(\rho , {I}_{\mathrm{P}}, {I}_{\mathrm{S}}) $，将式(12)改为更简洁的向量形式

$ \boldsymbol{d}=\boldsymbol{f}(\boldsymbol{l}, \boldsymbol{m})+\boldsymbol{e} $

(13)

在贝叶斯统计框架下，通过地震属性的条件分布的概率密度$ p\left(\boldsymbol{d}\right|\boldsymbol{l}, \boldsymbol{m}) $和模型参数的先验分布概率密度$ p\left(\boldsymbol{l}\right) $计算后验分布概率密度

$ p\left(\boldsymbol{l}\right|\boldsymbol{d}, \boldsymbol{m})=\frac{p\left(\boldsymbol{d}\right|\boldsymbol{l}, \boldsymbol{m}\left)p\right(\boldsymbol{l})}{p\left(\boldsymbol{d}\right|\boldsymbol{m})} $

(14)

式中$ p\left(\boldsymbol{d}\right|\boldsymbol{m}) $可视为$ p\left(\boldsymbol{l}\right|\boldsymbol{d}, \boldsymbol{m}) $的概率归一化常数

$p(\boldsymbol{d} \mid \boldsymbol{m})=\int p(\boldsymbol{d} \mid \boldsymbol{l}, \boldsymbol{m}) p(\boldsymbol{l}) \mathrm{d} \boldsymbol{l}$

(15)

最大后验(MAP)估计是贝叶斯错误率最小的预测值。根据式(14)可以计算目标参数的MAP估计

$ \begin{aligned} \hat{\boldsymbol{l}} & =\underset{l \in \boldsymbol{R}^n}{\arg \max } ~p(\boldsymbol{l} \mid \boldsymbol{d}, \boldsymbol{m}) \\ & =\underset{l \in \boldsymbol{R}^n}{\arg \max } \ln p(\boldsymbol{l} \mid \boldsymbol{d}, \boldsymbol{m}) \\ & =\underset{l \in \boldsymbol{R}^n}{\arg \max } \ln \frac{p(\boldsymbol{d} \mid \boldsymbol{l}, \boldsymbol{m}) p(\boldsymbol{l})}{p(\boldsymbol{d} \mid \boldsymbol{m})} \\ & =\underset{l \in \boldsymbol{R}^n}{\arg \max } [\ln p(\boldsymbol{d} \mid \boldsymbol{l}, \boldsymbol{m})+\ln p(\boldsymbol{l})-\ln p(\boldsymbol{d} \mid \boldsymbol{m})] \end{aligned} $

(16)

式中：$ {\boldsymbol{R}}^{n} $为$ n $维实数空间，$ n $为待反演的物性参数个数；$ \mathrm{l}\mathrm{n}p\left(\boldsymbol{d}\right|\boldsymbol{m}) $和$ \boldsymbol{l} $无关，在反演中可以忽略。

假设式(13)的随机误差e服从高斯分布N(μ_i，σ_i²)，因此

$ p\left(\boldsymbol{d}\right|\boldsymbol{l}, \boldsymbol{m})=C\mathrm{e}\mathrm{x}\mathrm{p}{-\frac{1}{2}\sum\limits _{i=1}^{3}{w}_{i}[{d}_{i}-{f}_{i}(\boldsymbol{l}, \boldsymbol{m})-{\mu }_{i}{]}^{2}} $

(17)

式中：μ_i为平均偏差；$ {w}_{i}=1/{\sigma }_{i}^{2} $为权重，σ_i²为方差；C为$ p\left(\boldsymbol{d}\right|\boldsymbol{l}, \boldsymbol{m}) $的概率归一化常数。

通常情况下，p(l)作为已知信息约束目标参数的反演，从而有效地避免物性参数反演的多解性并抑制噪声。高斯分布是一种描述先验信息的简单且有效的统计模型^[19]，其概率密度为

$ p\left(\boldsymbol{l}\right)={C}_{0}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}{D}^{2}\left(\boldsymbol{l}\right)\right] $

(18)

式中：$ {C}_{0} $为$ p\left(\boldsymbol{l}\right) $的概率归一化常数；$ D\left(\boldsymbol{l}\right) $为模型参数的马氏距离

$ D\left(\boldsymbol{l}\right)=\sqrt{(\boldsymbol{l}-{\boldsymbol{\mu }}_{0}{)}^{\mathrm{T}}{\boldsymbol{W}}_{0}(\boldsymbol{l}-{\boldsymbol{\mu }}_{0})} $

(19)

式中：$ {\boldsymbol{W}}_{0}={\boldsymbol{\varSigma }}_{0}^{-1} $为模型参数先验分布协方差矩阵的逆；$ {\boldsymbol{\mu }}_{0} $为先验分布的期望。实际问题中，模型参数空间通常是有界的，即$ \boldsymbol{l}\in \boldsymbol{L} $($ \boldsymbol{L} $表示模型参数所属的有界空间)。因此，$ p\left(\boldsymbol{l}\right) $应该是截断的高斯分布，而不是定义在无界空间的高斯分布。根据式(18)，通过修正$ {C}_{0} $可获得正确的先验分布。

将式(17)、式(18)代入式(16)，得到关于模型参数的正则化反演问题

$ \widehat{\boldsymbol{l}}=\underset{l\in {\boldsymbol{R}}^{n}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{ }\mathrm{m}\mathrm{a}\mathrm{x}}\sum\limits _{i=1}^{3}{w}_{i}[{d}_{i}-{f}_{i}(\boldsymbol{l}, \boldsymbol{m})-{\mu }_{i}{]}^{2}+{D}^{2}\left(\boldsymbol{l}\right) $

(20)

$ C $和$ {C}_{0} $与模型参数无关，可以在反演中忽略。

BISQ模型是一种非线性岩石物理模型，所以式(20)呈多局部最优解。然而，传统的基于梯度下降的反演算法通常强烈依赖初值，因此全局收敛能力弱。同时，由于BISQ模型的复杂性，梯度往往难以计算。为此，文中引入一种具有全局收敛能力的杂交遗传算法^[16]，该算法模仿了生物进化机制，将优化问题的候选解视为生物种群中的个体，并根据目标函数量化种群个体的生存能力(适应值)。该方法主要包括选择、交叉和变异运算。在遗传算法运行过程中，种群整体向适应值高的方向进化，而不同个体在不同的局部最优解附近聚集，进而找到全局最优解。

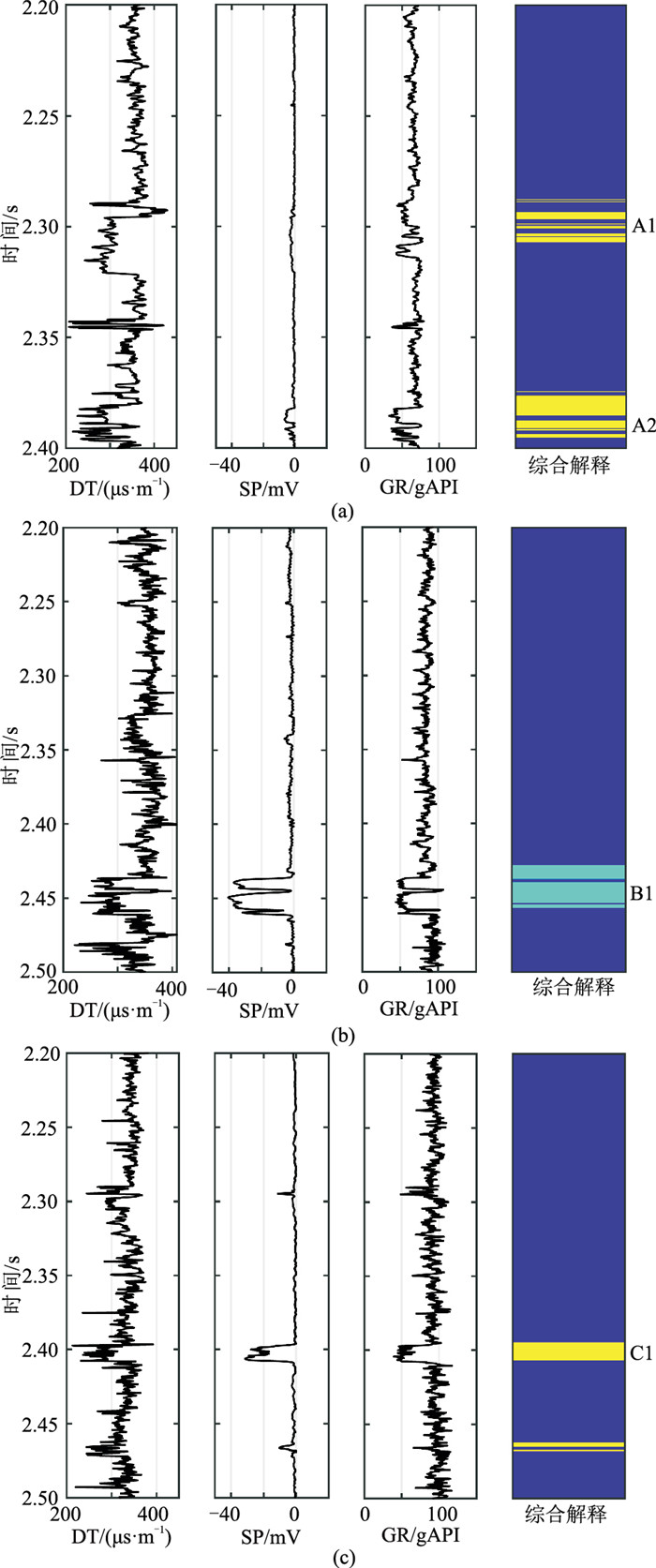
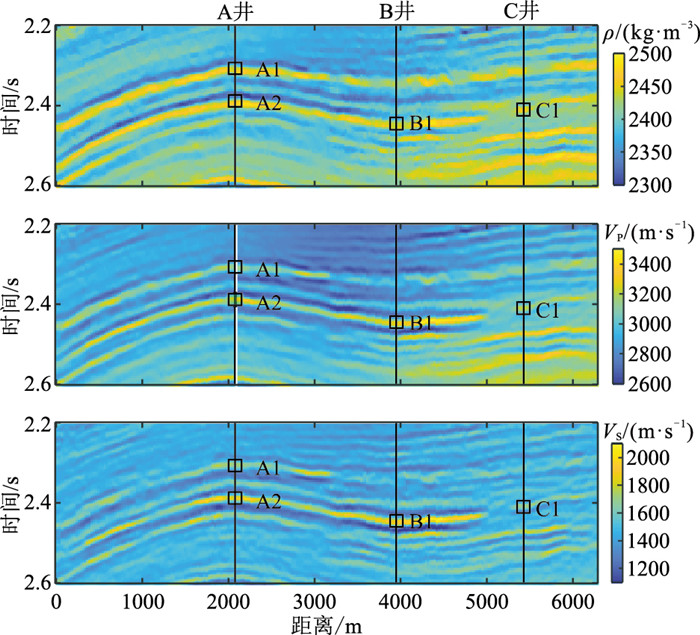
3 实际应用

实际数据来自中国东部A油田，图 1为A井、B井及C井测井数据。由图可见，A1、A2和C1主要为含油层，B1主要为含水层。采用叠前AVO反演^[24]得到ρ、V_P和V_S(图 2)。首先采用本文提出的贝叶斯反演方法初步反演ϕ，再联合反演储层区域($ \phi > 0.1 $)的ϕ和s_w。

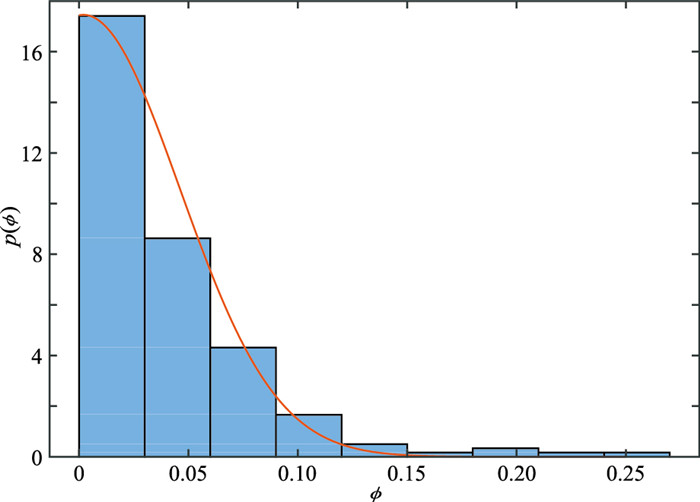
在初步反演ϕ的过程中，ϕ的先验分布为正态分布N(0，2×10^-3)。图 3为C井ϕ测井数据直方图和先验分布。在对储层区域的反演过程中，根据物性参数测井数据得到ϕ > 0.1时的ϕ和s_w的期望和协方差矩阵

$\begin{aligned} \boldsymbol{\mu}_0 & =\left(\begin{array}{ll} 15 & 90 \end{array}\right)^{\mathrm{T}} \\ \boldsymbol{\varSigma}_0 & =\left(\begin{array}{ll} 2.7 \times 10^{-3} & 5.0 \times 10^{-3} \\ 5.0 \times 10^{-3} & 1.5 \times 10^{-2} \end{array}\right) \end{aligned} $

图 4为ϕ和s_w的先验分布。由图可见，先验分布呈截断的高斯分布，其中ϕ的变化范围为[0，0.3]，s_w的变化范围为[0, 1]。

在两步反演过程中，各组分密度和体积模量数据见表 1。根据文献[8, 19, 25]选取其他辅助参数，并根据C井物性参数和井旁道弹性参数(图 5)进行了校准：$ \eta /\kappa =1\mathrm{ }\mathrm{P}\mathrm{a}\cdot \mathrm{s}\cdot \mathrm{\mu }{\mathrm{m}}^{-2} $，$ f=30\mathrm{ }\mathrm{H}\mathrm{z} $，$ {\rho }_{\mathrm{a}}=400\mathrm{ }\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} $，$ R=2\mathrm{ }\mathrm{m}\mathrm{m} $。选择C井为校准井，给出固体骨架模量的计算公式

$ \left\{\begin{array}{l}K=233.3{\phi }^{2}-53.06\phi +16.54\\ G=84.45{\phi }^{2}-9.558\phi +5.315\end{array}\right. $

(21)

将C井的物性参数数据代入式(13)获得观测误差样本。根据观测误差样本关于正态分布的分位数—分位数图(图 6)分析样本的正态性。可见，若样本数据点(蓝色)整体越接近参考值(红色)，则表示样本分布越接近正态分布。由于$ \rho $样本整体不满足正态分布假设，所以在反演中仅使用储层区域(ϕ > 0.1)的密度数据。根据观测误差样本，得到$ \rho $平均偏差为0，I_P平均偏差为$ -0.6\times {10}^{6}\mathrm{k}\mathrm{g}\cdot {\mathrm{s}}^{-1}\cdot {\mathrm{m}}^{-2} $，I_S平均偏差为$ -0.2\times {10}^{6}\mathrm{k}\mathrm{g}\cdot {\mathrm{s}}^{-1}\cdot {\mathrm{m}}^{-2} $，并给定$ \rho $权重为$ 3\times {10}^{-2}(\mathrm{k}{\mathrm{g}}^{-1}\cdot {\mathrm{m}}^{-3}{)}^{-1}\mathrm{、} $ I_P权重为$ 2\times {10}^{-6}(\mathrm{k}\mathrm{g}\cdot {\mathrm{s}}^{-1}\cdot {\mathrm{m}}^{-2}{)}^{-1} $，I_S权重为$ 3\times {10}^{-6}(\mathrm{k}\mathrm{g}\cdot {\mathrm{s}}^{-1}\cdot {\mathrm{m}}^{-2}{)}^{-1} $。在遗传算法方面，选取迭代次数为20，种群个体数为20，交叉概率为0.9，变异概率为0.1。

图 7为ϕ和s_w反演结果。由图可见：①含油区域(A1、A2和C1)呈高ϕ、低s_w特征，含水区域(B1)呈高ϕ、高s_w特征。②与图 2相比，图 7的储层和非储层的ϕ差别更明显，储层位置和形态更清晰；与图 2相比，图 7的含油区域和含水区域的s_w差异更明显，能有效识别流体类别。

4 结束语

本文基于BISQ模型提出了一种新的物性参数贝叶斯反演方法，其中BISQ模型描述了储层物性参数和弹性参数之间的确定性物理关系。在贝叶斯统计理论框架下，采用观测误差和先验概率模型刻画实际问题存在的随机性，并为基于BISQ模型的反演问题引入正则化约束，从而提高了反演精度。此外，引入的杂交遗传算法可以有效改善基于复杂岩石物理模型的物性参数反演的多解性。实际应用结果表明，所提反演方法具有广阔的应用前景。