0 引言

地震反演作为解释技术的重要组成部分，广泛应用于储层预测与评价、油气特征描述等方面^[1-5]。通过地震反演，可以将振幅、波形、频率等信息转化为地下岩石的弹性参数。波阻抗反演^[6-7]作为地震反演的主要内容，各种技术层出不穷，经历了从最开始的直接递推反演到如今的基于模型的迭代反演。波阻抗反演作为储层预测的核心技术，反演算法不断完善和成熟。

传统波阻抗反演是利用叠后反射波资料和声波测井数据，经反演得到地层的声阻抗(acoustic impe‑ dance，AI)信息，并以此预测储层。与其他反演结果相比，AI能得到丰富、稳定和可靠的地层弹性参数，是探测岩性、地层等隐蔽油气藏的核心技术，在实际应用中取得了显著效果^[8]。李庆忠^[9]指出，“波阻抗反演是高分辨率地震资料处理的最终表达形式”，说明波阻抗反演在地震数据处理中有着重要且特殊的地位。

地震勘探理论和技术在发展，地震勘探仪器的性能和地震资料质量也在提高，尤其是覆盖次数的提高极大地加强了叠前反演的适应性。基于叠后数据的反演技术迅速在AVO分析^[10-13]的基础上拓展到基于叠前数据的弹性阻抗(Elastic Impedance，EI)反演。Connolly^[14]于1999年提出EI的概念，考虑到地震反射振幅随炮检距或入射角的变化(即AVO效应)，利用不同炮检距的地震资料，在地震波非垂直入射的情况下，同时利用部分叠加技术提高数据的信噪比，由此打开了阻抗反演领域的一扇新大门^[15-19]。基于此，Whitcombe^[20]提出了扩展EI(EEI)的概念，建立了介质弹性参数和EI的联系，扩大了EI的适用范围。马劲风^[21]提出利用简化纵横波阻抗反射系数的方法简化波阻抗计算公式，以此得到的波阻抗称为广义EI。

EI及其衍生概念，显著地扩大了用于阻抗反演的地震资料的范围。但是，EI也有自身缺陷。首先，EI的提出是基于Zoeppritz方程^[22]有关近似于垂直入射的P-P波反射系数近似表达式，对地层性质和观测系统有特定的假设条件，如阻抗界面两侧的弹性参数差异小、入射角较小等，在实际应用中具有一定的局限性。其次，EI不同于AI，它没有确定的量纲，不是一个物理量，无法直接解释其物理含义。为此，本文从阻抗本身的物理定义入手，利用地震波引起的应力作用与介质振动速度得到一个阻抗表达式，构建阻抗张量，该阻抗张量有明确的量纲。利用阻抗张量的法向分量近似表达反射系数，并发展了相应的反演方法。通过模型测试所提反演方法的精度，并对比不同反演方法的反演效果，以验证所提方法的适用性。

1 阻抗张量的构成及其分量

如图 1所示，设x和z分别表示水平方向和垂直方向。地下水平界面上、下两种介质的纵波速度、横波速度、密度分别为$ {\alpha }_{1}、{\beta }_{1}、{\rho }_{1} $和$ {\alpha }_{2}、{\beta }_{2}、{\rho }_{2} $，拉梅常数分别为$ {\lambda }_{1}、{\mu }_{1} $和$ {\lambda }_{2}、{\mu }_{2} $。设一列平面入射P波以入射角$ \theta $入射到界面上，会产生反射P₁波、S₁波和透射P₂波、S₂波。

显然，入射P波会引起介质质点的振动，使介质局部产生应变，从而在介质中产生相应的应力作用^[23]。设入射P波的位移函数为

$ \left(\begin{array}{l}{u}_{z}\\ {u}_{x}\end{array}\right) =\left(\begin{array}{l}\mathrm{c}\mathrm{o}\mathrm{s}\theta \\ \mathrm{s}\mathrm{i}\mathrm{n}\theta \end{array}\right){A}_{1}{\mathrm{e}}^{\mathrm{j}\omega \left(t-\frac{x\mathrm{s}\mathrm{i}\mathrm{n}\theta +z\mathrm{c}\mathrm{o}\mathrm{s}\theta }{{\alpha }_{1}}\right)} $

(1)

式中：A₁为入射波振幅；u_z、u_x分别为z、x方向的位移函数；ω为角频率；t为时间。z、x方向的质点振动速度v_z、v_x和应力σ_z、σ_x分别为

$ \left(\begin{array}{l}{v}_{z}\\ {v}_{x}\end{array}\right)=\left(\begin{array}{l}\frac{\partial {u}_{z}}{\partial t}\\ \frac{\partial {u}_{x}}{\partial t}\end{array}\right)=\left(\begin{array}{l}\mathrm{c}\mathrm{o}\mathrm{s}\theta \\ \mathrm{s}\mathrm{i}\mathrm{n}\theta \end{array}\right)\mathrm{j}\omega {A}_{1}{\mathrm{e}}^{\mathrm{j}\omega \left(t-\frac{x\mathrm{s}\mathrm{i}\mathrm{n}\theta +z\mathrm{c}\mathrm{o}\mathrm{s}\theta }{{\alpha }_{1}}\right)} $

(2)

$\begin{aligned} \left(\begin{array}{c} \sigma_z \\ \sigma_x \end{array}\right) & =\left(\begin{array}{c} \left(\lambda_1+2 \mu_1\right) \frac{\partial u_z}{\partial z}+\lambda_1 \frac{\partial u_x}{\partial x} \\ \mu_1\left(\frac{\partial u_z}{\partial x}+\frac{\partial u_x}{\partial z}\right) \end{array}\right) \\ & =-\left(\begin{array}{c} \lambda_1+2 \mu_1 \cos ^2 \theta \\ 2 \mu_1 \sin \theta \cos \theta \end{array}\right) \mathrm{j} \frac{\omega}{\alpha_1} A_1 \mathrm{e}^{\mathrm{j} \omega\left(t-\frac{x \sin \theta+z \cos \theta}{\alpha_1}\right)} \end{aligned} $

(3)

在物理学中，阻抗描述了某一介质对质点运动的“阻碍”作用，可以理解为弹性介质的阻抗反映了质点应力与质点速度的比值。将σ_z、σ_x和v_z、v_x分别相除取反，构成阻抗张量T(tensor impedance)^[24]，即

$ \left(\begin{array}{cc}{T}_{zz}& {T}_{zx}\\ {T}_{xz}& {T}_{xx}\end{array}\right)=- \left(\begin{array}{cc}\frac{{\sigma }_{z}}{{v}_{z}}& \frac{{\sigma }_{z}}{{v}_{x}}\\ \frac{{\sigma }_{x}}{{v}_{z}}& \frac{{\sigma }_{x}}{{v}_{x}}\end{array}\right) $

(4)

四个分量T_zz、T_zx、T_xz和T_xx分别为垂直作用的法向阻抗、垂直作用的切向阻抗、水平作用的法向阻抗和水平作用的切向阻抗。对于反射P₁波、S₁波和透射P₂波、S₂波，也可以按照类似的做法，给出波传播时介质中的阻抗张量及其分量。

当θ < 45°时，入射P波和反射P波作用于界面时以法向应力为主，介质质点的v_z > v_x，T_zz是阻抗张量的主元素。为此，重点研究该分量，简记为T，简称“法向阻抗分量”。将式(2)和式(3)代入式(4)得

$ T=\frac{{\rho }_{1}{\alpha }_{1}^{2}-2{\rho }_{1}{\beta }_{1}^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{{\alpha }_{1}\mathrm{c}\mathrm{o}\mathrm{s}\theta }=\frac{A}{\mathrm{c}\mathrm{o}\mathrm{s}\theta }(1-2{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta ) $

(5)

式中$ :A={\rho }_{1}{\alpha }_{1} $为AI；$ \gamma ={\beta }_{1}/{\alpha }_{1} $。可见：当垂直入射时，$ \theta =0 $，$ T={\rho }_{1}{\alpha }_{1} $，退化为AI；当介质为流体时，$ \gamma =0 $，$ T={\rho }_{1}{\alpha }_{1}/\mathrm{c}\mathrm{o}\mathrm{s}\theta $，退化为流体中的声阻抗；当$ \theta \ne 0 $，$ \gamma \ne 0 $时，T是$ {\alpha }_{1}、{\beta }_{1}、{\rho }_{1} $的函数，且随θ变化。因此，T是AI和声阻抗的拓展，且与AI的量纲相同。

图 2为T、T_zx、T_xz和T_xx随θ的变化。由图可见：T在θ=0°时与AI相等，随$ \theta $的增加而增加；T_zx则相反，在θ=0°时趋于无穷，随θ的增加而减小；T_xz和T_xx呈一定的对称性，T_xz在θ=90°时取极大值，T_xx在θ=0°时取极大值。

2 基于T的P-P波反射系数精度分析

AI是速度和密度的乘积，与入射角无关，只适用于地震波垂直入射情况。EI引入入射角为变量，但是EI的提出需要基于一系列假设条件，如入射角小、相邻界面阻抗差小等。Zoeppritz方程^[22]虽然能准确地计算不同入射角的反射系数，但其计算复杂，计算量大，大大降低了反演效率。

考虑到垂直入射时P-P波反射系数等于界面两侧声阻抗的差与其和之比，流体介质中非垂直入射时P-P波反射系数等于界面两侧声阻抗的差与其和之比。作为该结论的拓展，提出使用T作为AI和声阻抗的拓展量，以近似表达弹性介质中非垂直入射的P-P波反射系数，即

$ r=\frac{{T}_{2}-{T}_{1}}{{T}_{2}+{T}_{1}} $

(6)

并通过数值算例的正演和反演验证式(6)的精度。式中T₁和T₂分别为入射波和透射波所在介质的T。

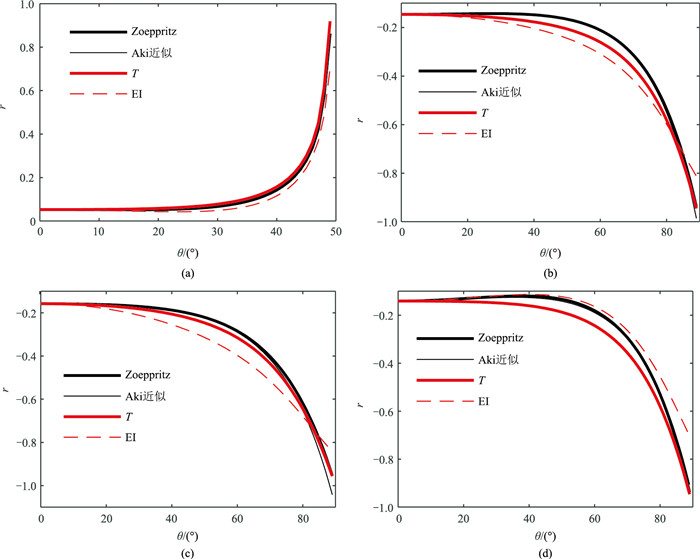
为了检验T的适用性，根据经典的四类AVO响应构造双气层模型，模型参数如表 1所示。同时以Zoeppritz方程求得的反射系数为标准，对比基于T、Aki近似式^[25]和EI求取的反射系数随入射角的变化(图 3)。可见：在第Ⅱ类(图 3b)和第Ⅲ类(图 3c)AVO响应中，利用T计算的反射系数误差明显小于EI；另外两类AVO响应的反射系数计算误差基本相当(图 3a、图 3d)。因此，T具有波阻抗反演的理论基础。同时，利用T计算的反射系数的入射角适用范围更广，相较于EI，T拥有明确的物理意义，且更具有实用价值。

3 基于T的纵横波阻抗反演 3.1 T反演算法

EI反演要利用3个角度道，同时反演纵、横波速度及密度共3个参数。与此不同的是，T反演只需要2个角度道，也只能反演2个参数。根据式(5)，T是声阻抗A、$ \mathrm{横}\mathrm{纵}\mathrm{波}\mathrm{速}\mathrm{度}\mathrm{比}\gamma $和$ \mathrm{入}\mathrm{射}\mathrm{角}\theta $的函数，即$ T=f(A, \gamma , \theta ) $。为此，使用两个角度道(角道集的叠加)，基于T反演可以求得A和$ \gamma $，当然也可以进一步求取泊松比。

使用与EI反演相似的做法，分别利用两个角度道反演

$ \left\{\begin{array}{l}f(A, B, {\theta }_{1})=\frac{A}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}}(1-2{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{1})=T\left({\theta }_{1}\right)\\ f(A, B, {\theta }_{2})=\frac{A}{\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{2}}(1-2{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{2})=T\left({\theta }_{2}\right)\end{array}\right. $

(7)

得到两个角度的法向阻抗$ T\left({\theta }_{1}\right) $和$ T\left({\theta }_{2}\right) $，联立求解，可以得到$ A $和$ \gamma $。由于$ \gamma =\frac{{\beta }_{1}}{{\alpha }_{1}}=\frac{{\rho }_{1}{\beta }_{1}}{{\rho }_{1}{\alpha }_{1}}=\frac{B}{A} $，其中$ B={\rho }_{1}{\beta }_{1} $为横波阻抗，于是就可以求得B，即可以同时反演纵横波阻抗。

3.2 数值算例

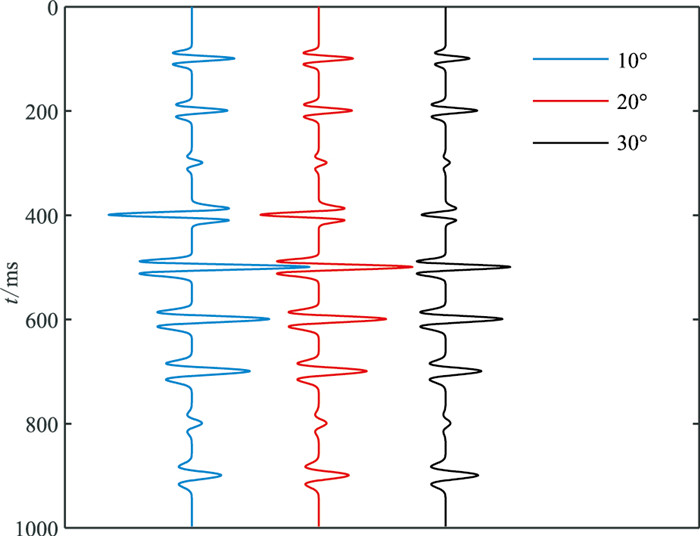
为了检验基于T反演的实际效果，以某测井曲线深时转换分层结果(图 4)为基础，选取其中一段建立地层模型。设密度为2.0 g/cm³，采用主频为40 Hz的雷克子波，通过精确求解Zoeppritz方程，分别合成入射角为10°、20°和30°的地震记录(图 5)。

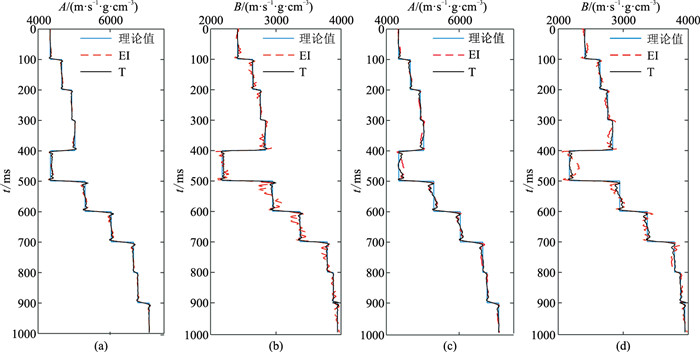
参照常规叠后波阻抗反演方法，分别对3个角度道进行T反演，得到T(10°)、T(20°)和T(30°)(图 6)。根据式(7)，分别利用三个角度道的其中两个进行EI反演，得到纵、横波阻抗(图 7)。可见：T反演、EI反演的结果基本一致，且均与理论值吻合较好，但在低速层处，T反演的横波阻抗(图 7b、图 7d)相对较平稳，振荡较小；EI反演结果振荡更大，这与EI表达式中含有幂函数是一致的。

3.3 抗噪性测试

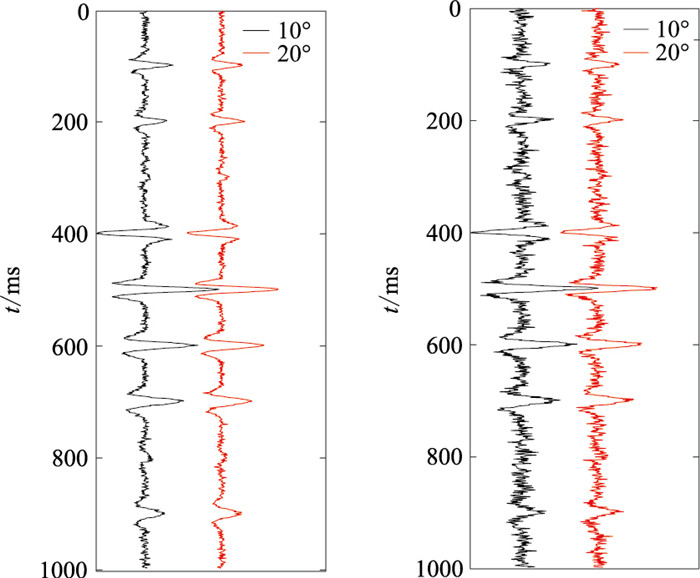
无论何种阻抗反演，均使用反射波各时刻的振幅信息。与走时信息不同，振幅信息易受噪声污染而产生误差^[26]。因此，对于含噪数据，反演方法的稳定性是衡量方法优劣的重要指标，且抗噪性决定了方法可行性。为此，需测试反演方法的抗噪性。对图 5数据加入随机噪声(图 8)进行测试，得到反演结果(图 9)。可见：①信噪比为5时反演结果(图 9a、图 9b)与无噪反演结果(图 7a、图 7b)基本一致，且与实际值吻合很好，几乎未受随机噪声影响。②信噪比为2时反演结果(图 9c、图 9d)呈剧烈的锯齿状振荡，但是振荡始终维持在真实值周围，尚能分辨地层分界面；T反演的抗噪性很强，反演效果较好，稳定性很高。上述结果表明，相对于EI而言，由于T的定义式中没有指数运算，因此反演结果对速度、密度和角度的敏感度降低，反演结果相对稳定。

4 实际数据测试

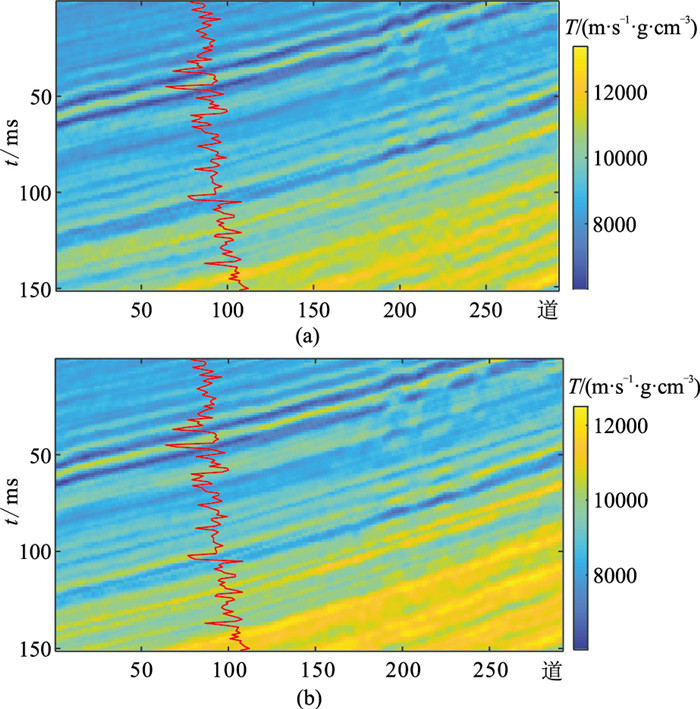
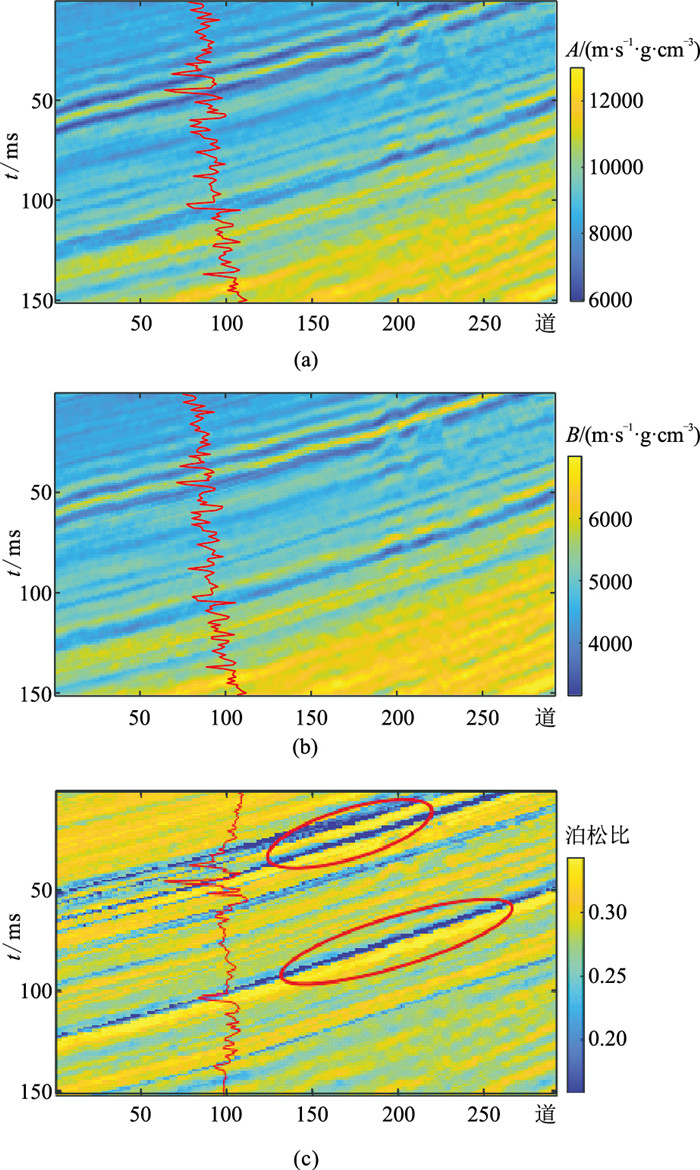
使用M区的0°~9°和9°~17°的角度叠加道集(图 10)验证T反演方法的适用性，后续反演时选取相应道集的角度平均值5°(角度1)和13°(角度2)为入射角。在测井约束下利用T反演得到角度1、角度2的T反演剖面(图 11)及纵、横波阻抗与泊松比反演剖面(图 12)。对比图 10~图 12可见：反演结果与实际钻井资料吻合较好，同相轴振幅强弱(图 10)在反演结果上呈明显的阻抗差异(图 11)；两套薄储层呈清晰的低泊松比异常(图 12c红圈处)。上述结果表明本文所提的法向阻抗反演方法的实际应用效果较好。

5 结论

本文基于阻抗的物理定义构建阻抗张量，通过建立四种AVO响应模型近似计算法向阻抗分量反射系数并反演纵横波阻抗。与常规弹性阻抗反演结果对比结果表明：

(1) 法向阻抗分量物理意义明确，基于法向阻抗分量的P-P波反射系数近似表达式的精度较高、入射角适用范围更广；

(2) 基于法向阻抗分量的纵横波阻抗反演效果较好，且具有较强的抗噪性；

(3) 法向阻抗反演丰富了波阻抗反演的内涵，只需两个角度道可以求得声阻抗和横纵波速度比，故对于入射角范围较窄的地震数据尤为适用；

(4) 实际数据反演结果在井旁道与测井曲线吻合度高，同时较好地反演了地层阻抗的相对差异，并清晰地指示了泊松比变化，说明法向阻抗反演方法的实际应用效果较好。