0 引言

根据烃源岩弹性特征和地震响应特征，可以利用地震资料识别烃源岩、预测总有机碳(TOC)含量。Løseth等^[1]分析了TOC含量与弹性阻抗的关系，认为在烃源岩层顶、底存在两个极性相反的强反射同相轴，仅依据地震数据就可以识别烃源岩层，并根据弹性阻抗与TOC含量的对应关系预测了烃源岩的空间展布特征。Carcione^[2]构建了烃源岩的地震岩石物理模型，分析烃源岩的AVO特征，发现烃源岩层顶部呈第Ⅳ类AVO特征。在此基础上，其他学者^[3-5]利用AVO或地震属性分析和反演方法在不同地区开展了烃源岩预测。另外，众多学者^[6-12]建立了TOC含量与岩石弹性参数之间的映射关系，利用地震资料，通过弹性参数反演实现了烃源岩的预测。随着人工智能技术的发展，部分学者^[13-21]利用神经网络或深度学习技术成功开展了烃源岩和页岩的TOC含量预测。

然而，上述方法多是基于有机质含量与弹性参数之间的对应关系，需要依赖大量的测井数据以获取烃源岩的弹性参数与物性参数的响应规律及对应关系。面对海上钻井难度大、成本较高、烃源岩勘探区多为少井或无井的低勘探程度区等，如何开展精细的井震标定提取准确子波，以及怎样构建精细的低频模型以获取烃源岩弹性参数与物性参数之间的定量关系等，已成为制约烃源岩预测的关键。

常规的叠前地震反演方法大多依靠井震标定从测井数据中获取地震子波，然而无井或少井区难以依据井资料提取确定性子波，使叠前地震反演方法在应用中受到较大限制。为此，部分学者依靠叠前地震资料获取符合工区特点的盲子波。地震子波盲提取的方法最先是由Robinson^[22]提出，即在一系列的假设条件下，只依赖地震数据本身，不需要测井数据参与就可得到估计子波。依据地震数据高阶累积量和它与子波高阶矩的关系，可将高阶累积量方法用于子波提取^[23-24]。相对于二阶累积量，高阶累积量的方法中包含相位信息，可以应用地震数据的四阶累积量对混合相位子波进行提取^[25-26]。之后，Misra等^[27]、Lazear^[28]联合全通子波与最小相位子波估计混合相位子波。遗传算法具备进行全局寻优且不需要对目标函数求导等诸多优点。因此，本文采用遗传算法，结合高阶统计量理论提取混合相位子波^[29]；依据地震数据高阶累积量与子波高阶矩之间的关系推导目标泛函，并加入初始约束项，得到包含约束项的新的目标函数；约束项的加入可提高子波盲提取的稳定性^[30-31]，从而为少井区烃源岩地震反演预测奠定了子波基础。

初始低频模型可以补偿地震数据中缺失的低频分量，从而解决了叠前地震反演中的带限问题，因此选择一个可靠的初始模型将提高地震反演方法的收敛精度和可靠性。然而，可靠的低频参数信息在无井或少井的低勘探程度区中经常难以获取。

为了解决地震反演中模型精度过度依赖低频的问题，专家们试图利用带限的地震数据和模糊的参数模型预测模型参数蕴含的超低频信息。若将地震衰减效应引入纯频率域地震反演中，即将产生复频域地震反演方法，将有助于缓解“带限反演”带来的不确定性。Shin等^[32]利用复频率反演中衰减地震波场的零频率分量，在全波形反演框架下恢复地下模型的长波长速度背景。复频域Laplace反演和低频包络反演^[33-36]是不同变换域低频反演的代表，两者均旨在深度挖掘原始数据中的超低频响应，进而解决不确定性中的低频先验构建问题，提高预测结果的可靠性。依据复Laplace域低频反演的思想，本文改进了复频域反演方法以构建低频模型策略，恢复少井区地震数据中更加丰富的低频信息。

岩石物理模型是岩石弹性参数与物性参数之间的桥梁。准确的岩石物理模型是物性参数反演结果的保障。通过对目标区烃源岩的特征分析，本文选用Yu等^[37]提出的适用于富泥质烃源岩岩石物理模型，建立了弹性阻抗与泥质含量、TOC含量等烃源岩主要参数之间的定量关系，据此利用弹性阻抗反演实现了烃源岩泥质含量、TOC含量等参数的直接预测。不同于依据测井资料所获取的统计关系而开展的弹性参数反演预测TOC含量的间接预测方法，该方法具有明确的物理意义、正演成因，可以定性地预测烃源岩分布范围。

1 方法原理 1.1 根据盲信号理论提取地震子波

在地震子波提取的传统方法中，将地震子波假设为一个确定的子波，但在实际中地震子波是不确定的。在少井区缺乏钻井资料的情况下，不能做统计性假设，因此需要进行盲子波提取。

根据高阶统计量理论，假设噪声为高斯白噪声或者高斯有色噪声，且与地层反射系数独立统计时，噪声的高阶统计量为零，则褶积模型可去掉噪声项，表示为

$ \boldsymbol{s}\left(t\right)=\boldsymbol{w}\left(t\right)\mathrm{*}\boldsymbol{r}\left(t\right) $

(1)

式中：t为时间；$ \boldsymbol{s}\left(t\right) $是不考虑噪声情况下的地震记录；$ \boldsymbol{w}\left(t\right) $是地震子波；$ \boldsymbol{r}\left(t\right) $是地层反射系数。

地震数据与反射系数的$ k $阶累积量关系为

$\begin{gathered} \boldsymbol{c}_s{ }^{(k)}\left(\tau_1, \tau_2, \cdots, \tau_{k-1}\right)=\boldsymbol{c}_r{ }^{(k)}\left(\tau_1, \tau_2, \cdots, \tau_{k-1}\right) * \\ \boldsymbol{c}_w{ }^{(k)}\left(\tau_1, \tau_2, \cdots, \tau_{k-1}\right) \end{gathered}$

(2)

式中：$ {{\boldsymbol{c}}_{{}^{{}_{\boldsymbol{s}}}}}^{\left(k\right)} $、$ {{\boldsymbol{c}}_{\boldsymbol{r}}}^{\left(k\right)} $分别为地震数据、反射系数的$ k $阶累积量；$ {\tau }_{k} $为第k阶时间步长；$ {{\boldsymbol{c}}_{\boldsymbol{w}}}^{\left(k\right)} $为子波的k阶矩阵。

当反射系数个数趋近无穷时，反射系数的$ k $阶累积量表示为

$ {{\boldsymbol{c}}_{\boldsymbol{r}}}^{\left(k\right)}({\tau }_{1}, {\tau }_{2}, \dots , {\tau }_{k-1})={{\boldsymbol{\beta }}_{\boldsymbol{r}}}^{\left(k\right)} $

(3)

式中$ {\boldsymbol{\beta }}_{\boldsymbol{r}} $为反射系数序列$ \boldsymbol{r}\left(t\right) $序列峰度值。此时，地震数据与反射系数的$ k $阶累积量之间的关系变为

$ {{\boldsymbol{c}}_{\boldsymbol{s}}}^{\left(k\right)}({\tau }_{1}, {\tau }_{2}, \dots , {\tau }_{k-1})={{\boldsymbol{\beta }}_{\boldsymbol{r}}}^{\left(k\right)}{{\boldsymbol{c}}_{\boldsymbol{w}}}^{\left(k\right)}({\tau }_{1}, {\tau }_{2}, \dots , {\tau }_{k-1}) $

(4)

$ {{\boldsymbol{c}}_{\boldsymbol{w}}}^{\left(k\right)}({\tau }_{1}, {\tau }_{2}, \dots , {\tau }_{k-1})=\sum\limits _{i=1}^{n}{\boldsymbol{w}}_{i}·{{\boldsymbol{w}}_{i}}_{+{\tau }_{1}}·\dots ·{{\boldsymbol{w}}_{i}}_{+{\tau }_{k-1}} $

(5)

式中n为地震子波脉冲响应样值的总数。

当地层反射系数为超高斯白噪声时，地震数据高阶累积量与子波高阶矩仅相差一个常数，可以构建如下目标函数求取子波高阶累积量。

$ \begin{array}{l}{{\boldsymbol{c}}_{\boldsymbol{w}}}^{\left(4\right)}=\sum\limits _{{\tau }_{1}, {\tau }_{2}, {\tau }_{3}}\left[a\right({\tau }_{1}, {\tau }_{2}, {\tau }_{3})\cdot {{\boldsymbol{c}}_{{}_{\boldsymbol{s}}}}^{\left(4\right)}({\tau }_{1}, {\tau }_{2}, {\tau }_{3})-{{\boldsymbol{\beta }}_{\boldsymbol{r}}}^{\left(4\right)}{{\boldsymbol{c}}_{\boldsymbol{w}}}^{\left(4\right)}({\tau }_{1}, {\tau }_{2}, {\tau }_{3}{\left)\right]}^{2}\mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}{\nu }_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\le w\le {\nu }_{\mathrm{u}\mathrm{p}}\\ \sum w=0\end{array}\right\}\\ \end{array} $

(6)

式中：$ {{\boldsymbol{c}}_{\boldsymbol{s}}}^{\left(4\right)}({\tau }_{1}, {\tau }_{2}, {\tau }_{3}) $是地震数据$ \boldsymbol{s}\left(t\right) $的四阶累积量；$ {{\boldsymbol{c}}_{\boldsymbol{w}}}^{\left(4\right)}({\tau }_{1}, {\tau }_{2}, {\tau }_{3}) $为子波$ \boldsymbol{w}\left(t\right) $的四阶矩阵；$ w $为子波的振幅；$ {\nu }_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\mathrm{、}{\nu }_{\mathrm{u}\mathrm{p}} $分别为子波取值范围的最小值、最大值；$ a({\tau }_{1}, {\tau }_{2}, {\tau }_{3}) $为三维窗函数，选用合适的窗函数可以得到更好的预期效果，即

$ \begin{aligned} a\left(\tau_1, \tau_2, \tau_3\right)= & d\left(\tau_1\right) d\left(\tau_2\right) d\left(\tau_3\right) d\left(\tau_2-\tau_1\right) \times \\ & d\left(\tau_3-\tau_2\right) d\left(\tau_3-\tau_1\right) \end{aligned}$

(7)

式中$ d\left(\tau \right) $为窗函数，本文选用了$ \mathrm{P}\mathrm{a}\mathrm{r}\mathrm{z}\mathrm{e}\mathrm{n} $窗，即

$ d(\tau)= \begin{cases}1-6\left(\frac{|\tau|}{L}\right)^2+6\left(\frac{|\tau|}{L}\right)^3 & |\tau| \leqslant \frac{L}{2} \\ 2\left(1-\frac{|\tau|}{L}\right)^3 & \frac{L}{2}<|\tau| \leqslant L \\ 0 & |\tau|>L\end{cases}$

(8)

式中L为下降时间步长。

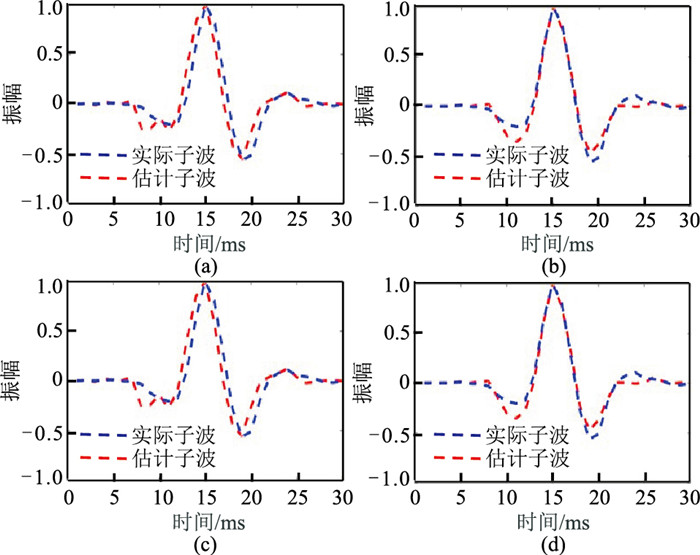
为验证该方法提取地震子波的准确性，本文采用一个已知的混合相位子波与反射系数模型褶积得到合成地震记录，然后利用该合成地震记录进行子波估计。图 1为合成地震记录迭代20~100次的子波提取结果。由图可见，估计子波与实际子波基本吻合，表明该方法在子波盲提取过程中的应用效果较好，能够为少井区烃源岩反演预测提供良好的子波基础。

1.2 基于复频域反演的低频模型/弹性阻抗预测方法

传统叠前地震反演方法中的低频分量通常是从测井资料获得，然而在少井甚至无井的情况下该方法难以获得较为准确的低频模型。本文方法是从地震数据中补充低频分量，基于复频域反演思想，建立符合实际情况的初始模型，然后通过复频域反演实现精细低频模型的预测，为少井区烃源岩反演提供可靠的低频先验约束。

在复频域反演过程中，首先根据复频域Laplace正演算子建立模型参数映射方程，该方程是构建无井反演目标函数的重要基础。

时间域褶积模型(式(1))经过变换可以获得频率域的褶积模型，即

$ \boldsymbol{S}\left(\omega \right)=\boldsymbol{W}\left(\omega \right)\mathrm{*}\boldsymbol{R}\left(\omega \right) $

(9)

式中$ \boldsymbol{S}\left(\omega \right) $、$ \boldsymbol{W}\left(\omega \right) $、$ \boldsymbol{R}\left(\omega \right) $分别表示频率域的地震合成记录、子波和反射系数，其中$ \omega $为频率。将褶积模型的平稳形式加入式(9)，得到一个新的方程

$ F\left(\omega \right)={\int }_{0}^{\mathrm{\infty }}\left[{\int }_{0}^{\mathrm{\infty }}\boldsymbol{W}(\mathrm{t}-\tau )\boldsymbol{R}\left(\tau \right)\mathrm{d}\tau \right]{\mathrm{e}}^{-\boldsymbol{\sigma }t}{\mathrm{e}}^{-\mathrm{j}\omega t}\mathrm{d}t $

(10)

式中：$ F\left(\omega \right) $为地震信号的Laplace谱；$ \boldsymbol{\sigma } $为衰减系数序列；$ \boldsymbol{R}\left(\tau \right)\mathrm{、}\boldsymbol{W}(t-\tau ) $分别表示时间域内的反射序列和带限子波；$ {\mathrm{e}}^{-\boldsymbol{\sigma }\tau }{\mathrm{e}}^{-\mathrm{j}\omega \tau } $为Laplace变换算子。将积分顺序加以变换，则方程变为

$ F\left(\omega \right)={\int }_{0}^{\mathrm{\infty }}\left[{\int }_{0}^{\mathrm{\infty }}\boldsymbol{W}(\mathrm{t}-\tau ){\mathrm{e}}^{-\boldsymbol{\sigma }t}{\mathrm{e}}^{-\mathrm{j}\omega t}\mathrm{d}t\right]\boldsymbol{R}\left(\tau \right)\mathrm{d}\tau $

(11)

根据Laplace变换时移性质，式(10)可以写成

$ F\left(\omega \right)=\boldsymbol{W}\left(\omega \right){\int }_{0}^{\infty }\boldsymbol{R}\left(\tau \right){\mathrm{e}}^{-\boldsymbol{\sigma }\tau }{\mathrm{e}}^{-\mathrm{j}\omega \tau }\mathrm{d}\tau $

(12)

将式(11)简写为

$ {\boldsymbol{F}}_{\boldsymbol{\omega }}={\boldsymbol{W}}_{\boldsymbol{\omega }}·\boldsymbol{C}·{\boldsymbol{E}}_{\boldsymbol{\omega }}·\boldsymbol{m} $

(13)

式中：$ {\boldsymbol{W}}_{\boldsymbol{\omega }} $、$ \boldsymbol{C} $、$ {\boldsymbol{E}}_{\boldsymbol{\omega }} $分别表示地震子波的Laplace谱、Laplace变换的时间域衰减矩阵、Fourier正演算子；$ \boldsymbol{m} $为待反演模型参数。

$ {\boldsymbol{W}}_{\boldsymbol{\omega }} $可表示为对角矩阵形式，即

$ \begin{array}{c}\\ {\boldsymbol{W}}_{{\omega }_{}}=\left[\begin{array}{cccc}W({\sigma }_{1}+\mathrm{i}\boldsymbol{\omega })& 0& & 0\\ 0& W({\sigma }_{2}+\mathrm{i}\boldsymbol{\omega })& & 0\\ & & \ddots & \\ 0& 0& & W({\sigma }_{x}+\mathrm{i}\boldsymbol{\omega })\end{array}\right]\end{array} $

(14)

式中下标x为衰减系数的个数。

衰减矩阵为

$ \boldsymbol{C}={\left[\begin{array}{cccc}{\mathrm{e}}^{-{\tau }_{1}{\sigma }_{1}}& {\mathrm{e}}^{-{\tau }_{2}{\sigma }_{1}}& \dots & {\mathrm{e}}^{-{\tau }_{\mathrm{y}}{\sigma }_{1}}\\ {\mathrm{e}}^{-{\tau }_{1}{\sigma }_{2}}& {\mathrm{e}}^{-{\tau }_{2}{\sigma }_{2}}& \dots & {\mathrm{e}}^{-{\tau }_{\mathrm{y}}{\sigma }_{2}}\\ & & ⋮& \\ {\mathrm{e}}^{-{\tau }_{1}{\sigma }_{k}}& {\mathrm{e}}^{-{\tau }_{2}{\sigma }_{x}}& \dots & {\mathrm{e}}^{-{\tau }_{\mathrm{y}}{\sigma }_{x}}\end{array}\right]}_{x\times y} $

(15)

式中：y为时间采样点数；$ C $中衰减系数将会影响复Laplace域反演中低频分量的扰动。

离散Fourier正演算子为

$ {\boldsymbol{E}}_{\boldsymbol{\omega }}={\left[\begin{array}{cccc}{\mathrm{e}}^{-\mathrm{i}{\tau }_{1}\omega }& 0& & 0\\ 0& {\mathrm{e}}^{-\mathrm{i}{\tau }_{2}\omega }& & 0\\ & & \ddots & \\ 0& 0& & {\mathrm{e}}^{-i{\tau }_{y}{\omega }_{}}\end{array}\right]}_{y\times y} $

(16)

假定频率的个数为$ \lambda $，将式(14)~式(16)代入式(13)，可得到

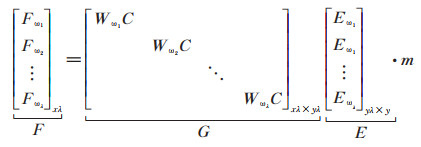
(17)

为更容易构建地震反问题目标泛函，式(17)可以改写成虚部与实部结合的形式，即

$ \left[\begin{array}{l}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}\left(\boldsymbol{F}\right)\\ \mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\left(\boldsymbol{F}\right)\end{array}\right]=\left[\begin{array}{l}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}(\boldsymbol{G}\cdot \boldsymbol{E})\\ \mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}(\boldsymbol{G}\cdot \boldsymbol{E})\end{array}\right] \cdot \boldsymbol{m} $

(18)

令$ \boldsymbol{S}\mathrm{\text{'}}=\left[\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}\right(\boldsymbol{Y}\left)\mathrm{ }\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\right(\boldsymbol{Y}\left)\right] $、$$ \boldsymbol{G}\mathrm{\text{'}}\boldsymbol{L}\mathrm{\text{'}}=\left[\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}\right(\boldsymbol{G}\cdot \boldsymbol{E}\left)\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\right(\boldsymbol{G}\cdot \boldsymbol{E}\left)\right] $，则式(18)可简化为

$ {\boldsymbol{S}}^{\text{'}}={\boldsymbol{G}}^{\text{'}}·{\boldsymbol{L}}^{\text{'}}·\boldsymbol{m} $

(19)

式中：$ \boldsymbol{G}\mathrm{\text{'}} $为子波效应；$ \boldsymbol{L}\mathrm{\text{'}} $为Laplace变换效应。

以式(19)为先验方程，模型参数的后验概率密度函数为

$ p\left(\boldsymbol{m}\left|\boldsymbol{S}\mathrm{\text{'}}\right.\right)=\frac{p\left(\boldsymbol{m}\right)p\left(\boldsymbol{S}\mathrm{\text{'}}\left|\boldsymbol{m}\right.\right)}{\int p\left(\boldsymbol{m}\right)p\left(\boldsymbol{S}\mathrm{\text{'}}\left|\boldsymbol{m}\right.\right)\mathrm{d}\left(\boldsymbol{m}\right)}\propto p\left(\boldsymbol{m}\right)p\left(\boldsymbol{S}\mathrm{\text{'}}\left|\boldsymbol{m}\right.\right) $

(20)

式中：$ p\left(\boldsymbol{m}\right) $为先验概率函数的模型参数；$ p\left(\boldsymbol{S}\boldsymbol{\text{'}}\left|\boldsymbol{m}\right.\right) $为似然函数。它们分别为

$\begin{aligned} & p\left(\boldsymbol{S}^{\prime} \mid \boldsymbol{m}\right)=\frac{1}{2 \pi \sigma_{\mathrm{n}}^2} \times \\ & \quad \exp \left[\frac{-\left(\boldsymbol{S}^{\prime}-G^{\prime} L^{\prime} \boldsymbol{m}\right)^{\mathrm{T}}\left(\boldsymbol{S}^{\prime}-G^{\prime} L^{\prime} \boldsymbol{m}\right)}{2 \sigma_{\mathrm{n}}^2}\right] \end{aligned}$

(21)

$ p\left(\boldsymbol{m}\right)=\frac{1}{(\mathrm{\pi }{\sigma }_{\mathrm{m}}{)}^{n}}\prod \limits_{i=1}^{n}{\left[\frac{1+{R}_{i}^{2}}{{\sigma }_{\mathrm{m}}^{2}}\right]}^{-1} $

(22)

式中：$ {{\sigma }_{\mathrm{m}}}^{2} $和$ {{\sigma }_{\mathrm{n}}}^{2} $分别为模型参数的方差和地震数据噪声的方差；$ {R}_{i} $为离散的反射系数；m、n分别为待反演参数的个数和反射系数的个数。

将式(21)、式(22)代入式(20)，可以得到

$\begin{array}{r} p\left(\boldsymbol{m}, \sigma_{\mathrm{n}} \mid \boldsymbol{S}^{\prime}\right) \propto \exp \left[-\sum\limits_{i=1}^n \ln \left(1+\frac{R_i^2}{\sigma_{\mathrm{m}}^2}\right)\right] \times \\ \exp \left[\frac{-\left(\boldsymbol{S}^{\prime}-\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime} \boldsymbol{m}\right)^{\mathrm{T}}\left(\boldsymbol{S}^{\prime}-\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime} \boldsymbol{m}\right)}{2 \sigma_{\mathrm{m}}^2}\right] \end{array}$

(23)

式(23)中e的指数函数是单调递增的，故可将其改写成另一种形式，即

$\begin{gathered} \ln \left[p\left(\boldsymbol{m}, \sigma_{\mathrm{n}} \mid \boldsymbol{S}^{\prime}\right)\right] \propto-\left(\boldsymbol{S}^{\prime}-\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime} \boldsymbol{m}\right)^{\mathrm{T}}\left(\boldsymbol{S}^{\prime}-\right. \\ \left.\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime} \boldsymbol{m}\right)-2 \sigma_{\mathrm{n}}^2 \sum\limits_{i=1}^n \ln \left(1+\frac{R_i^2}{\sigma_{\mathrm{m}}^2}\right) \end{gathered}$

(24)

对式(24)求偏导，求取$ p(\boldsymbol{m}, {\sigma }_{\mathrm{n}}\left|\boldsymbol{S}\mathrm{\text{'}}\right.) $的极值

$ \begin{array}{c} & \frac{\partial \ln p}{\partial \boldsymbol{m}}=\left[\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime}\right]^{\mathrm{T}}\left[\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime}\right] \boldsymbol{m}-\left[\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime}\right]^{\mathrm{T}} \boldsymbol{S}^{\prime}+ \\ & 4 \frac{\sigma_{\mathrm{n}}^2}{\sigma_{\mathrm{m}}^2} \operatorname{diag}\left[\left(1+\frac{R_i^2}{\sigma_{\mathrm{m}}^2}\right)^{-1}\right] \boldsymbol{m} \\ & \end{array}$

(25)

得到如下目标泛函

$ \begin{aligned} \boldsymbol{m}= & \left(\boldsymbol{S}^{\prime}-\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime} \boldsymbol{m}\right)^{\mathrm{T}}\left(\boldsymbol{S}^{\prime}-\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime} \boldsymbol{m}\right)+ \\ & 2 \sigma_{\mathrm{n}}^2 \sum\limits_{i=1}^n \ln \left(1+\frac{R_i^2}{\sigma_{\mathrm{m}}^2}\right) \end{aligned} $

(26)

为增加无井条件下反演结果的稳定性，加入线性模型约束，得到新的目标函数

$ \begin{aligned} \boldsymbol{m}= & \left(\boldsymbol{S}^{\prime}-\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime} \boldsymbol{m}\right)^{\mathrm{T}}\left(\boldsymbol{S}^{\prime}-\boldsymbol{G}^{\prime} \boldsymbol{L}^{\prime} \boldsymbol{m}\right)+ \\ & 2 \sigma_{\mathrm{n}}^2 \sum\limits_{i=1}^n \ln \left(1+\frac{R_i^2}{\sigma_{\mathrm{m}}^2}\right)+\boldsymbol{\varGamma} \end{aligned}$

(27)

$ \boldsymbol{\varGamma }=\xi {(\boldsymbol{\eta }-P\boldsymbol{m})}^{\mathrm{T}}{(\boldsymbol{\eta }-P\boldsymbol{m})}^{\mathrm{T}} $

(28)

式中：$ \xi $为模型参数的加权系数；$ \boldsymbol{\varGamma } $为线性趋势模型约束；$ \boldsymbol{\eta } $为线性背景参数模型；$ P={\int }_{{t}_{0}}^{t}\mathrm{d}\tau $，t₀为起始时间。

利用式(27)的反演目标函数，即可在复频域内基于贝叶斯理论实现低勘探程度区烃源岩的低频模型和弹性阻抗的反演预测。

2 算例分析

选用A区进行本文方法验证。该区地震资料品质较好且具有丰富的测井资料。通过依次减少参与反演的井数，对比不同井数参与反演的结果，分析复频域低频模型/弹性阻抗反演方法的适用性及准确性。

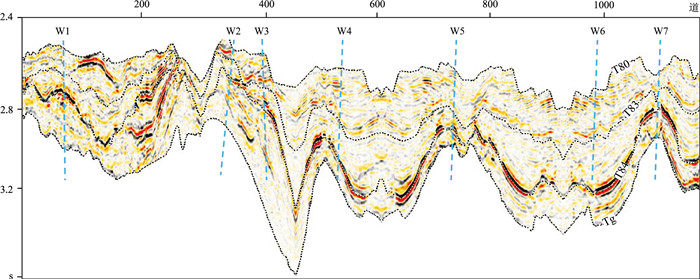
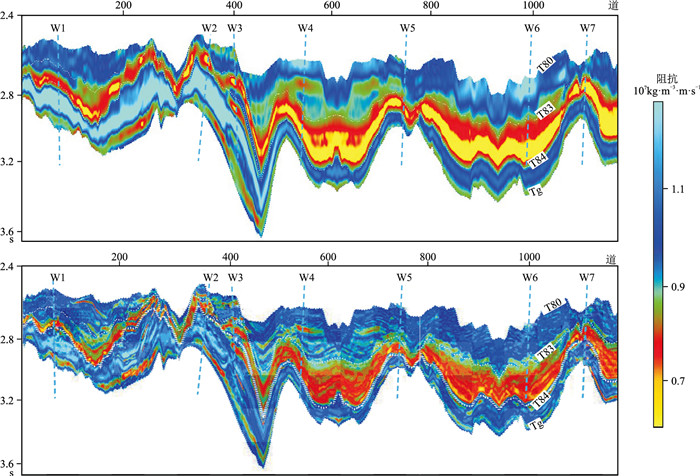
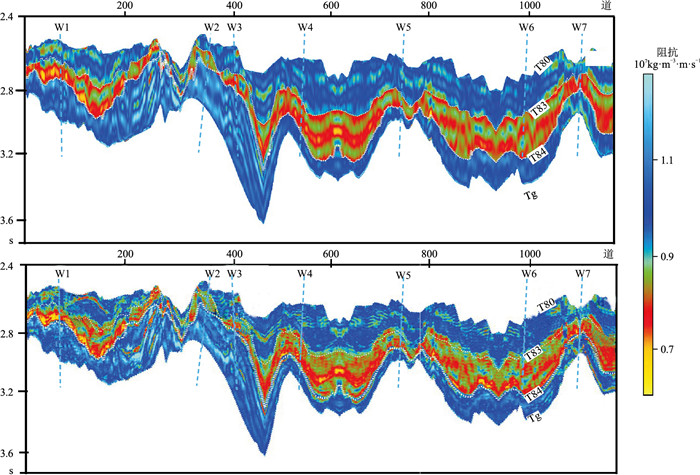
图 2为过A区7口井的连井测线的小角度地震剖面。分别对比7口井(图 3)、1口井(图 4)、无井参与(图 5)反演的弹性阻抗结果，可见随着参与反演井数的减少，反演结果与井的吻合程度存在一定程度下降。但从整体反演效果看，通过复频域无井/少井参与反演得到的弹性阻抗结果与多井趋势一致，且两者预测低阻抗烃源岩层段(T80~Tg)的位置和形态基本相似，这说明复频域的低频模型与弹性阻抗的预测结果较为可信，验证了该方法适用于无井/少井区烃源岩分布范围的预测。

为进一步分析复频域反演方法的准确性，提取反演结果的伪井波阻抗曲线与实际井进行对比，得到二者之间的误差分布直方图(图 6)。由图可见，无井/少井参与反演得到的弹性阻抗反演结果与7口井参与的结果的误差相当，误差均为正态分布，且主要在10%以内，证明复频域反演得到的低频模型可靠，该方法在无井/少井区可行。

3 实际资料应用

选用Yu等^[37]提出的适用于富泥质烃源岩的地震岩石物理模型，建立弹性阻抗与烃源岩参数泥质含量、烃源岩指示因子、孔隙度之间的关系(具体的推导过程见附录A)，分别为

$ {K}_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}=f\left({V}_{\mathrm{s}\mathrm{h}}, \mathrm{T}\mathrm{O}\mathrm{C}, \phi \right) $

(29)

$ {\mu }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}=g\left({V}_{\mathrm{s}\mathrm{h}}, \mathrm{T}\mathrm{O}\mathrm{C}, \phi \right) $

(30)

$ {\rho }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}=h\left({V}_{\mathrm{s}\mathrm{h}}, \mathrm{T}\mathrm{O}\mathrm{C}, \phi \right) $

(31)

上述式中：$ {K}_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}} $为烃源岩的等效体积模量；$ {\mu }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}} $为烃源岩的等效剪切模量；$ {\rho }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}} $为烃源岩的密度；$ {V}_{\mathrm{s}\mathrm{h}} $为泥质含量；$ \phi $为孔隙度；根据f、g、h函数即可建立烃源岩的弹性参数与关键物性参数之间的联系。

已知岩石的弹性模量及密度，即可计算岩石的纵波(V_P)、横波(V_S)速度分别为

$ {V}_{\mathrm{P}}=\sqrt{\frac{{K}_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}+\frac{4}{3}{\mu }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}}{{\rho }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}}} $

(32)

$ {V}_{\mathrm{s}}=\sqrt{\frac{{\mu }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}}{{\rho }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}}} $

(33)

Connolly^[38]推导的经典弹性阻抗方程为

$ \mathrm{E}\mathrm{I}\left(\theta \right)={{V}_{\mathrm{P}}}^{1+\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta }{{V}_{\mathrm{S}}}^{-8K\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{\rho }^{1-4K\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta } $

(34)

式中：$ \rho $为岩石的密度；$ \theta $为部分叠加的角度道集的入射角；$ K $是一个常量，一般根据工区特征通过计算横波平均速度($ {V}_{\mathrm{S}0} $)与纵波平均速度($ {V}_{\mathrm{P}0} $)的比值的平方获取。

综合式(29)~式(34)，即可得到烃源岩弹性阻抗与泥质含量、TOC含量、孔隙度等物性参数之间的定量表达关系，即

$ [\mathrm{E}{\mathrm{I}}_{1}, \mathrm{E}{\mathrm{I}}_{2}, \mathrm{E}{\mathrm{I}}_{3}]={f}_{\mathrm{R}\mathrm{P}\mathrm{M}}\left({V}_{\mathrm{s}\mathrm{h}}, \mathrm{T}\mathrm{O}\mathrm{C}, \phi \right) $

(35)

式中$ \mathrm{E}{\mathrm{I}}_{1} $、$ \mathrm{E}{\mathrm{I}}_{2} $、$ \mathrm{E}{\mathrm{I}}_{3} $分别对应小、中、大三个角度的弹性阻抗。

在实际建模过程中，引入随机误差项$ \varepsilon $，则表达式为

$ [\mathrm{E}{\mathrm{I}}_{1}, \mathrm{E}{\mathrm{I}}_{2}, \mathrm{E}{\mathrm{I}}_{3}]={f}_{\mathrm{R}\mathrm{P}\mathrm{M}}\left({V}_{\mathrm{s}\mathrm{h}}, \mathrm{T}\mathrm{O}\mathrm{C}, \phi \right)+\varepsilon $

(36)

利用贝叶斯理论，构建基于弹性阻抗反演烃源岩重要物性参数的目标函数，并通过最大化期望算法求取最终的反演结果，即

$ \left[{V}_{\mathrm{s}\mathrm{h}}, T, \phi \right]=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}P\left(\left[{V}_{\mathrm{s}\mathrm{h}}, T, \phi \right]\left|\left[\mathrm{E}{\mathrm{I}}_{1}, \mathrm{E}{\mathrm{I}}_{2}, \mathrm{E}{\mathrm{I}}_{3}\right]\right.\right) $

(37)

式中：$ P\left( \cdot \right) $为概率密度函数；$ T $表示烃源岩指示因子。通过反演并不能准确预测TOC含量，得到的是表征烃源岩TOC含量和其他有机质性质的组合，因此本文将T定义为烃源岩指示因子，用于评价烃源岩的有机质丰度。

选择B区实际资料验证本文方法的应用效果。首先，结合目标区先验地质认识，通过复频域低频模型/弹性阻抗反演方法得到目标区的弹性阻抗反演结果；然后，基于构建的弹性阻抗与烃源岩关键物性参数之间的定量表征关系，利用弹性阻抗反演结果进一步预测泥质含量、T的分布特征，从而预测优质烃源岩的空间分布范围及评价其丰度等级。

图 7a和图 7b分别为无井反演预测的$ {V}_{\mathrm{s}\mathrm{h}} $和T。由图可见，反演结果整体上符合地质认识：根据区域地质背景认为在目的层段T73~Tg段为泥质沉积，因此发育优质烃源岩的可能性较大；反演结果显示，该层段$ {V}_{\mathrm{s}\mathrm{h}} $较高，T也较大。

为了获得更明确的烃源岩平面分布特征，利用T预测数据体可对工区内烃源岩丰度进行分级刻画(图 8)。由图可见，T > 1.5时，T73~T80及T80~Tg的优质烃源岩范围均较大；T > 2时，T80~Tg的优质烃源岩范围相对更广，这与区域地质认识相符。

4 结束语

针对少井区难以进行井震标定提取准确子波、构建精细低频模型等问题，本文根据盲井理论，提出了提取地震盲子波和复频域反演地震低频模型的方法。在测井、地震资料丰富的地区，通过盲井测试验证了该方法能够在少井/无井条件下获得可靠的弹性阻抗。为获取烃源岩弹性参数与物性参数之间的定量表征，本文根据研究区的烃源岩岩石物理特征，基于岩石物理模型，建立了弹性阻抗与泥质含量、烃源岩指示因子之间的关系，并基于贝叶斯理论，通过弹性阻抗直接反演预测了泥质含量、烃源岩指示因子等关键参数，实现了少井区烃源岩空间分布的定性及定量预测，预测结果符合地质认识。

附录A 富泥质烃源岩岩石物理模型表达式

根据Yu等^[37]提出的适用于富泥质烃源岩岩石物理模型，可以直接写出烃源岩体积模量、剪切模量、密度与泥质含量、干酪根含量、孔隙度等关键物性参数之间的关系式，即

$ \begin{array}{l}{K}_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}=\left[{K}_{\mathrm{m}}+{V}_{\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}}({K}_{\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}}-{K}_{\mathrm{m}}){P}^{\mathrm{*}}\right]{(1-\phi )}^{P}+\\ \quad\quad\quad\quad\quad\quad\frac{{\alpha }^{2}{K}_{\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{i}\mathrm{d}}}{\phi +\left(\alpha -\phi \right)\frac{{K}_{\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{i}\mathrm{d}}}{{K}_{\mathrm{m}}}}\end{array} $

(A-1)

$ \begin{array}{l}{K}_{\mathrm{m}}=\frac{1}{2}\left({V}_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{y}}{K}_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{y}}+{V}_{\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{z}}{K}_{\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{z}}+{V}_{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}}{K}_{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}}\right)+\\ \quad\quad\quad\frac{1}{2\left(\frac{{V}_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{y}}}{{K}_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{y}}}+\frac{{V}_{\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{z}}}{{K}_{\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{z}}}+\frac{{V}_{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}}}{{K}_{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}}}\right)}\end{array} $

(A-2)

$ \begin{array}{l}{\mu }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}=\left[{\mu }_{\mathrm{m}}+{V}_{\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}}({\mu }_{\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}}-{\mu }_{\mathrm{m}}){Q}^{\mathrm{*}}\right]\times \\ \quad\quad\quad\quad\quad\quad{(1-\phi )}^{Q}\end{array} $

(A-3)

$ \begin{array}{l}{\mu }_{\mathrm{m}}=\frac{1}{2}\left({V}_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{y}}{\mu }_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{y}}+{V}_{\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{z}}{\mu }_{\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{z}}+{V}_{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}}{\mu }_{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}}\right)+\\ \quad\quad\quad\frac{1}{2\left(\frac{{V}_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{y}}}{{\mu }_{\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{y}}}+\frac{{V}_{\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{z}}}{{\mu }_{\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{z}}}+\frac{{V}_{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}}}{{\mu }_{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}}}\right)}\end{array} $

(A-4)

$ \begin{aligned} & \rho_{\text {source-rock }}=\left(1-V_{\text {kerogen }}-\phi\right)\left[V_{\text {clay }} \rho_{\text {clay }}+\right. \\ & \left.\quad\left(1-V_{\text {clay }}\right) \rho_{\text {quartz }}\right]+V_{\text {kerogen }} \rho_{\text {kerogen }}+\phi \rho_{\text {fluid }} \end{aligned}$

(A-5)

上述式中：$ K $、$ \mu $、$ \rho $、V分别为体积模量、剪切模量、密度、体积含量；下标kerogen、clay、quartz、other、f分别代表干酪根、黏土矿物、石英矿物、其他基质矿物、混合流体；下标m是指由黏土矿物、石英矿物等其他基质矿物组成的岩石基质；$ {P}^{\mathrm{*}} $、$ {Q}^{\mathrm{*}} $均是与干酪根纵横比有关的几何因子；$ P $、$ Q $均表示与基质孔隙纵横比有关的几何因子；$ \alpha =1-{\left(1-\phi \right)}^{P} $，$ \phi $是岩石的孔隙度。其中，干酪根含量$ {V}_{\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}} $与TOC含量的关系为

$ {V}_{\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}}=\frac{{\rho }_{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{-}\mathrm{r}\mathrm{o}\mathrm{c}\mathrm{k}}}{0.75{\rho }_{\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}}}\mathrm{T}\mathrm{O}\mathrm{C} $

(A-6)