2. 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
2. Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
含流体裂缝孔隙岩石的地震各向异性及地震波频散、衰减特性对储层渗流特征提取及流体识别具有指导意义。当地震波穿过饱含流体的裂缝介质时,流体流动会影响地震各向异性特征,同时伴随着地震波的能量耗散。在裂缝介质中,孔隙单元之间的流体流动是引起地震频带内地震波频散、衰减的主要原因[1],而流体的流动依赖于介质渗透率。因此,研究裂缝孔隙岩石渗透率的各向异性与地震各向异性间的影响机理具有重要意义。
为了研究中尺度裂缝引起的地震频带内的强衰减特性,Chapman[2]建立了包含一组定向排列的中尺度裂缝的局部喷射流模型,综合考虑流体性质、裂缝尺度等因素,分析并解释了裂缝介质中地震波的频散、衰减现象,结果表明裂缝尺度是影响地震各向异性的关键因素;Brajanovski等[3]类比线性滑动理论[4],通过周期性排列的高孔隙度薄层等效裂缝介质,分析裂缝与孔隙之间流体交换引起的弹性波频散和衰减;2009年,Chapman[5]将一组定向排列裂缝扩展到两组裂缝,通过控制裂缝闭合情况,分析了裂缝方位角对地震波频散、衰减和地震各向异性的影响。
在上述研究中,岩石物理模型中的渗透率均为标量(各向同性),储层流体饱和仅考虑单一流体和均匀饱和的情况,而实际储层中多相流体及非均饱和情况普遍存在,裂缝介质的渗透率多表现为各向异性,并且可通过等效渗透率进行描述[6-8]。为了进一步了解裂缝储层中地震波的频散、衰减特性,学者们对多相流体等效黏滞度[9]及流体饱和情况[10-13]开展了广泛研究。
Snow[14-15]采用平行平板对裂缝进行等效建模,提出了包含任意数量、方向及孔径的裂缝介质等效模型,将裂缝与基质的渗透率线性叠加获得裂缝介质的等效渗透率张量;Long等[16-17]提出的离散裂缝网(DFN)模型,利用统计数据模拟裂缝系统,但该模型忽略了基质固有渗透率,无法描述裂缝与基质间流体交换过程中的地震波能量耗散;Vu等[18]假设裂缝受到无限远处的均匀压力梯度,基于Darcy定律和Eshelby等效夹杂理论[19-21]推导包含多组裂缝的裂缝介质等效渗透率表达式;Xiong等[22]建立三维孔隙网络模型,探讨了流体性质和孔隙连通性对岩石渗透率的影响;熊繁升等[23]提出三维裂缝网络模型,定量分析了岩石渗透率随裂缝参数(发育密度、纵横比)、孔隙流体类型和围压等因素的变化规律。上述研究表明,裂缝的半径、相对位置及发育密度等因素会使裂缝介质的渗透率表现出各向异性。
诸多学者还研究了不同渗流条件下地震波频散、衰减特性。Pride等[24]研究表明地震数据中的振幅可能包含与渗透率相关的信息;Kozlov[25]通过地震数据频谱分析,明确了地震频谱中包含渗透率信息;Rubino等[26]通过改变储层渗透率的大小,分析渗透率对气水饱和储层中地震波频散、衰减的影响,结果表明随着储层渗透率增加地震波速度从高频极限不断下降到低频极限;Ren等[27]建立周期性裂缝储层模型,模型的渗透率表现为纵向各向异性,分析了渗透率对含气储层地震反射振幅的影响;Müller等[28]通过推导动态等效渗透率模型分析渗透率的空间变化规律,并且探讨了渗透率对地震波频散、衰减的影响,发现渗透率的变化会引起弛豫峰值沿频率轴移动;Rubino等[29-30]通过分析裂缝的连通性及其控制裂缝介质的各向异性渗流情况,研究了渗透率对地震波频散、衰减的影响,结果表明裂缝介质渗透率的变化会引起弛豫时间的差异。王丁等[31]在非均匀裂隙孔隙介质中建立各向异性渗流模型,研究各向异性渗流条件下弹性波传播规律,结果表明渗透率的变化使地震波衰减曲线产生第二个弛豫峰。
上述研究缺乏合适的介观尺度裂缝模型探讨裂缝参数变化导致的渗透率各向异性,同时,缺乏对渗透率各向异性条件下地震各向异性变化特征的研究。为此,本文首先通过裂缝参数表征裂缝介质的等效渗透率,分析裂缝参数变化引起的裂缝介质中渗透率的各向异性;然后基于Chapman多组裂缝岩石物理模型[5],研究各向异性渗流条件下,不同类型流体饱和的正交介质中地震波频散、衰减与地震各向异性的变化规律,探讨渗透率各向异性与地震各向异性间的响应机理,为由地震各向异性提取实际储层渗流特征及流体识别提供理论依据。
1 方法原理 1.1 裂缝介质渗透率表征基于Vu等[18]提出的裂缝介质等效渗透率半解析表征方法,综合考虑背景介质的渗透率、裂缝方向及半径等裂缝参数,对裂缝介质渗透率进行表征。假设含多组椭圆形裂缝的裂缝介质受到远场均匀压力,则第m个裂缝组的等效渗透率
| $\boldsymbol{\kappa}_m^{\mathrm{f}}=\rho^m \frac{16 \kappa c^m R_m^3}{3 c^m+\frac{16}{3} \kappa R_m}\left(\boldsymbol{E}-\boldsymbol{n}_m \otimes \boldsymbol{n}_m^{\mathrm{T}}\right) \cdot \boldsymbol{A}$ | (1) |
式中:
|
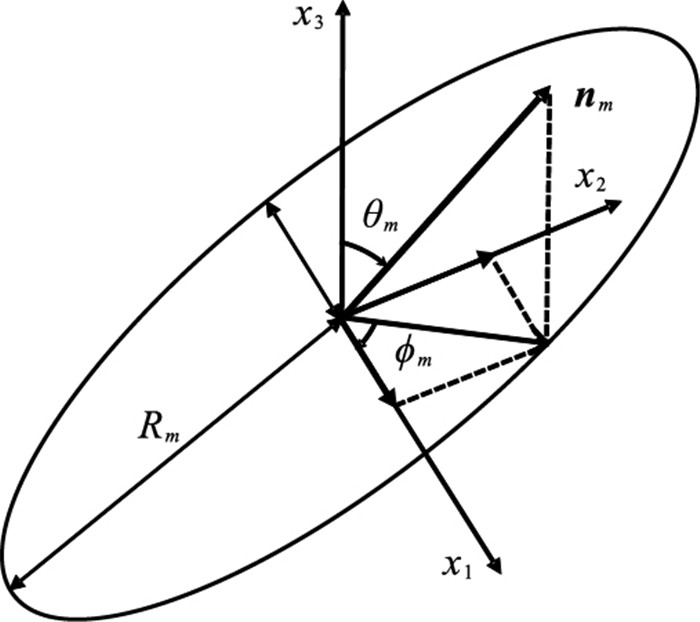
图 1 椭圆形裂缝平面法向量投影示意图 |
如图 1所示,假设第m个裂缝组的法向量
| $\boldsymbol{n}_m=\left(\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{m}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{m}, \mathrm{s}\mathrm{i}\mathrm{n}{\phi }_{m}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{m}, \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{m}\right) $ | (2) |
由此,包含N个裂缝组的裂缝介质的等效渗透率可表示为
| $\boldsymbol{\kappa}^{\mathrm{eff}}=\kappa \boldsymbol{E}+\sum\limits_{m=1}^N \boldsymbol{\kappa}_m^{\mathrm{f}} $ | (3) |
假设裂缝介质的主渗透方向与观测坐标系
| $ \boldsymbol{\kappa}^{\mathrm{e}\mathrm{f}\mathrm{f}}=\left[\begin{array}{ccc}{\kappa }_{11}& {\kappa }_{12}& {\kappa }_{13}\\ {\kappa }_{12}& {\kappa }_{22}& {\kappa }_{23}\\ {\kappa }_{13}& {\kappa }_{23}& {\kappa }_{33}\end{array}\right] $ | (4) |
由此,裂缝介质不同平面内的渗透率各向异性可通过三个主渗透方向的渗透率比值来评估,即
| $ {\alpha }_{ij}=\left|\frac{{\kappa }_{jj}}{{\kappa }_{ii}}-1\right| $ | (5) |
式中:
Chapman[5]将含有一组对齐裂缝的等效介质模型拓展到两组裂缝的情况,正交介质频率依赖的等效刚度矩阵由背景介质刚度矩阵、球形孔隙校正量和两个裂缝组校正量的总和给出,即
| $\boldsymbol{C}_{i j}(\omega)=\boldsymbol{C}_{i j}^0-\boldsymbol{C}_{i j}^{\mathrm{p}}(\omega)-\sum\limits_{m=1}^2 \boldsymbol{C}_{i j}^m(\omega) $ | (6) |
式中:
考虑裂缝介质渗透率各向异性情况下,第m个裂缝组与孔隙间流体交换的弛豫时间
| $ {\tau }_{m}=\frac{8l\left(1-\upsilon \right)\left(1+{K}_{c}\right)}{3\mu }\frac{\eta }{{\kappa }_{m}^{\mathrm{\text{'}}}}{R}_{m} $ | (7) |
其中
| $ {\kappa }_{m}^{\mathrm{\text{'}}} = \sqrt{\frac{{\kappa }_{11}^{2}+{\kappa }_{22}^{2}+{\kappa }_{33}^{2}}{3}} {}^{} $ |
式中:
通过弛豫时间可计算出不同裂缝组中的流体压力,考虑裂缝孔隙间流体质量守恒并运用Eshelby等效夹杂理论[21],获得了各向异性渗流条件下正交介质频率依赖的等效刚度矩阵,即
| $ \left[\begin{array}{cccccc} C_{11} & C_{12} & C_{13} & 0 & 0 & 0 \\ C_{12} & C_{22} & C_{23} & 0 & 0 & 0 \\ C_{13} & C_{23} & C_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{array}\right]$ | (8) |
根据上述等效刚度矩阵,垂直入射的地震波纵波复速度计算公式[32]为
| $ v\left(\omega \right)=\sqrt{\frac{{C}_{33}\left(\omega \right)}{\rho }} $ | (9) |
式中ρ为裂缝介质密度。
由此,根据复速度v计算频率依赖的纵波速度
| $ \left\{\begin{array}{l}{V}_{\mathrm{P}}\left(\omega \right)=\frac{1}{\mathrm{R}\mathrm{e}\left[\frac{1}{v\left(\omega \right)}\right]}\\ \frac{1}{{Q}_{\mathrm{P}}\left(\omega \right)}=\frac{\mathrm{I}\mathrm{m}\left[{v}^{2}\left(\omega \right)\right]}{\mathrm{R}\mathrm{e}\left[{v}^{2}\left(\omega \right)\right]}\end{array}\right. $ | (10) |
式中Re[·]和Im[·]分别表示对复数求实部和虚部。
Thomsen[32]通过等效刚度矩阵计算各向异性系数以刻画各向异性介质的地震各向异性特征,Tsvankin[33]在此基础上推导了正交介质的各向异性系数。据此,得到由等效刚度矩阵元素表示的正交介质各个平面内描述流体流动的地震各向异性系数。
(1) 在[x1,x3]平面内
| $ \left\{\begin{array}{l}{\varepsilon }_{1}=\frac{{C}_{11}-{C}_{33}}{2{C}_{33}}\\ {\delta }_{1}=\frac{{\left({C}_{13}+{C}_{55}\right)}^{2}-{\left({C}_{33}-{C}_{55}\right)}^{2}}{2{C}_{33}\left({C}_{33}-{C}_{55}\right)}\end{array}\right. $ | (11) |
(2) 在[x2,x3]平面内
| $ \left\{\begin{array}{l}{\varepsilon }_{2}=\frac{{C}_{22}-{C}_{33}}{2{C}_{33}}\\ {\delta }_{2}=\frac{{\left({C}_{23}+{C}_{44}\right)}^{2}-{\left({C}_{33}-{C}_{44}\right)}^{2}}{2{C}_{33}\left({C}_{33}-{C}_{44}\right)}\end{array}\right. $ | (12) |
(3) 在[x1,x2]平面内
| $ {\delta }_{3}=\frac{{\left({C}_{12}+{C}_{66}\right)}^{2}-{\left({C}_{11}-{C}_{66}\right)}^{2}}{2{C}_{11}\left({C}_{11}-{C}_{66}\right)} $ | (13) |
式中
以下基于不同裂缝参数进行裂缝介质的渗透率表征及渗透率各向异性特征分析。假设远场均匀压力梯度与裂缝介质渗透率的主渗透方向重合,各向同性介质渗透率为20 mD,两组裂缝的基本参数如表 1所示。
|
|
表 1 裂缝参数 |
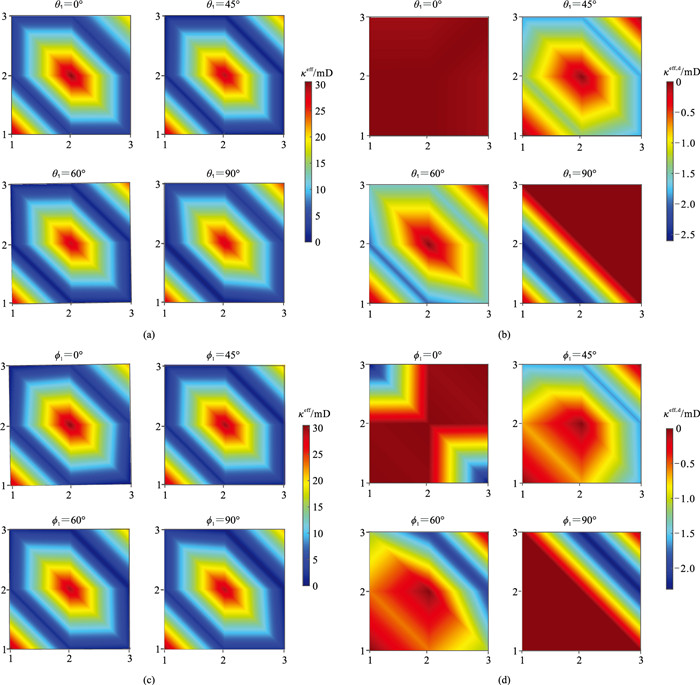
为了研究裂缝参数变化对裂缝介质渗透率张量的影响,参照表 1调整裂缝组1的参数变化范围,并展示了当裂缝半径R1=R2=0.50 m时,不同倾角和方位角对应的等效渗透率张量(图 2),边框数值代表等效渗透率的元素下标。图 2a、图 2b分别为
|
图 2 不同裂缝方位角、裂缝倾角对应的不同渗透率张量 (a) |
由图 2a、图 2c可见,不同裂缝倾角和方位角对应的等效渗透率张量几乎一致;由图 2b、图 2d可见,不同裂缝倾角和方位角对应的
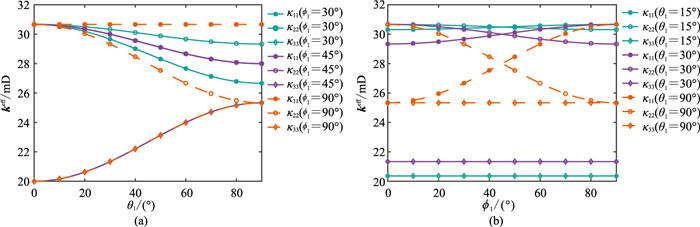
图 3显示了主渗透方向渗透率随θ1和
|
图 3 裂缝介质主渗透方向渗透率随 |
为了探究其他裂缝参数对裂缝介质渗透率的影响,绘制了θ1=45°时,主渗透方向渗透率随R1及

|
图 4 θ1=45°裂缝介质主渗透方向渗透率随 |
图 5显示由于θ1和

|
图 5 裂缝倾角、方位角变化引起不同平面内渗透率各向异性平面图 (a)[x1,x3]平面;(b)[x2,x3]平面;(c)[x1,x2]平面 |
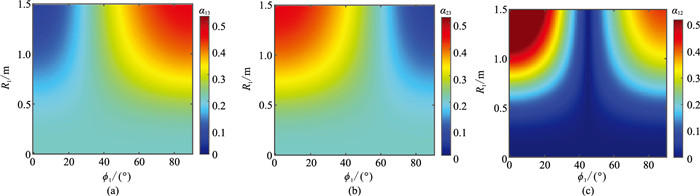
图 6展示了θ1=45°时,
|
图 6 裂缝半径、方位角变化引起不同平面内渗透率各向异性平面图 (a)[x1,x3]平面;(b)[x2,x3]平面;(c)[x1,x2]平面 |
为了研究渗透率各向异性情况下,裂缝介质的地震各向异性变化规律和地震波的频散衰减特征,本文基于Chapman多组裂缝等效介质模型[5]设计了双相流体饱和的正交介质模型进行数值模拟。设置裂缝组1的θ=0°、
|
|
表 2 背景介质参数 |
对于裂缝介质的流体饱和情况,本文基于Jin等[12]提出的各向异性介质的双相流体饱和模型,分别考虑裂缝介质为气水饱和及油水饱和两种情况(流体物理参数见表 3)。此外,岩石中填充流体的基本参数由Batzle等[34]的方程在压力为25MPa、温度为50℃条件下计算得到。
|
|
表 3 流体参数 |
图 7为岩石在不混溶双相流体饱和情况下,地震波速度及衰减系数随频率、含气(油)饱和度变化平面图。由图可见,无论气水饱和岩石还是油水饱和岩石,地震波衰减平面图中(图 7b)均出现了两个弛豫峰,但因饱含流体类型的不同,地震波速度频散、衰减的特征频率(地震波速度变化速率最高点或衰减系数的极值对应的频率)变化趋势不同,衰减系数的强弱也有区别。

|
图 7 双相流体饱和岩石随含气(油)饱和度和频率变化的速度(a)、衰减(b)平面图 |
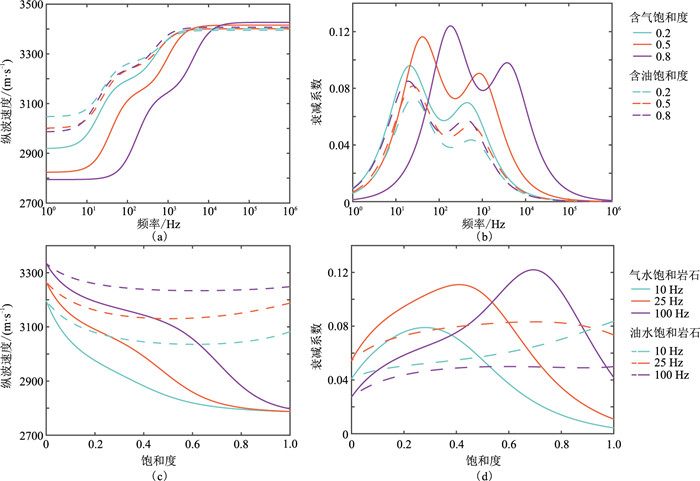
图 8更清晰地分析了地震波速度和衰减系数随饱和度和频率的变化。由图 8可见:①地震波速度出现两个频段内速度剧烈变化的情况,且衰减系数曲线相应出现两个弛豫峰,对应的特征频率为ω1和ω2,这是由于岩石渗透率的各向异性而引起的。地震波经过岩石会引起孔隙流体诱导压力,岩石中流体运移能力强的位置平衡该诱导压力所需时间短、特征频率高;反之,则时间长、特征频率低,故地震波衰减曲线有低频段特征频率ω1和高频段特征频率ω2。②由于气体与油的黏滞度存在差异,随着饱和度增加,气水饱和岩石对应衰减系数曲线的弛豫峰值增加且向高频方向移动;油水饱和岩石对应衰减系数曲线弛豫峰值增加且向低频方向移动。此外,由于水相与气相间湿润性的差异远大于水相与油相间的差异,在含气饱和度与含油饱和度相等情况下,气水饱和岩石中的地震波频散范围更宽、衰减更强,这是因为地震波经过气水饱和岩石时会产生更强的流体诱导压力,引起更多的流体流动,故气水饱和岩石中地震波衰减更强(图 8a、图 8b)。③不同频率的地震波速度对含气(油)饱和度的敏感性不同。随着饱和度的增加,不同频率的地震波速度均呈非线性降低趋势,降低的速率与饱和度相关;气水饱和岩石的衰减系数曲线呈现先增加后减小的趋势,油水饱和岩石的衰减系数曲线呈现单调增加趋势,不同频率的衰减系数随饱和度的变化速率各不相同,这种差异是岩石渗透率各向异性与流体饱和度共同作用的结果(图 8c、图 8d)。
|
图 8 双相流体饱和岩石中纵波速度和衰减系数随频率、饱和度的变化曲线 (a)纵波速度与频率;(b)衰减系数与频率;(c)纵波速度与饱和度;(d)衰减系数与饱和度 |
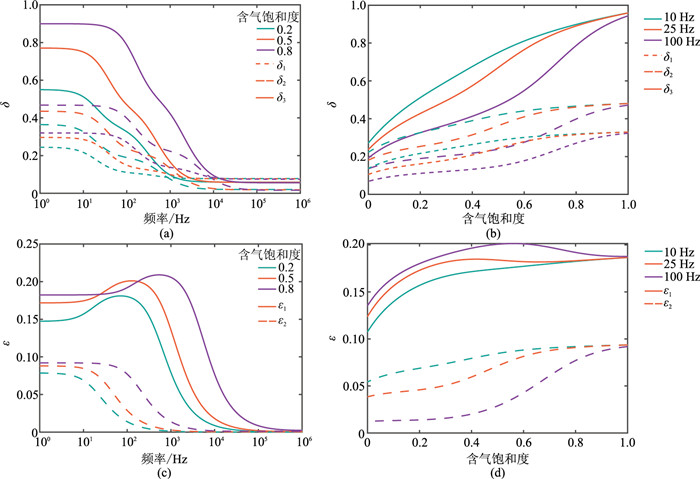
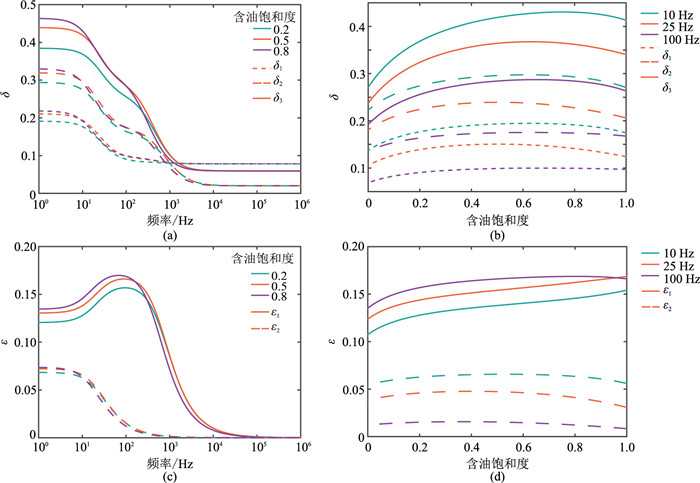
通过各向异性系数随频率和含气(油)饱和度的变化曲线(图 9、图 10)分析各向异性渗流条件下,正交介质中不同平面内的地震各向异性变化规律。从图 9、图 10可见:①受渗透率各向异性与流体饱和度的共同影响,裂缝介质不同平面内地震各向异性变化特征存在差异。随着频率增加,各向异性系数δ非线性单调减小,不同频带内减小速率不同;各向异性系数
|
图 9 气水饱和岩石中δ和 |
|
图 10 油水饱和岩石中δ和 |
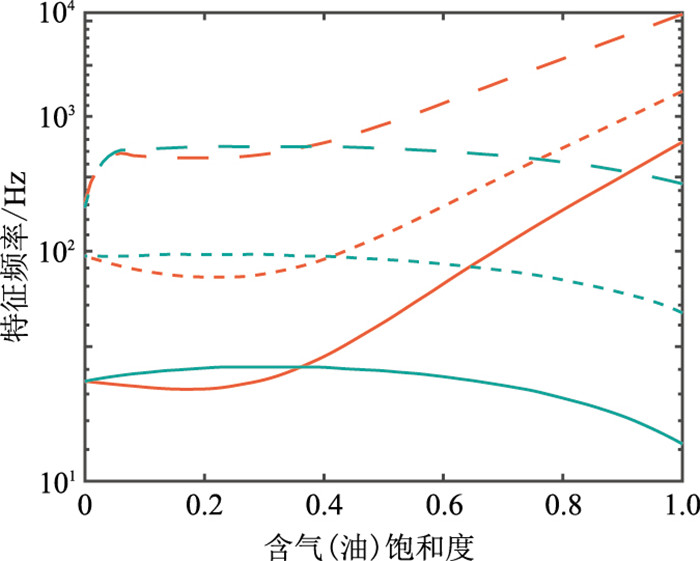
结合图 8~图 10中δ3、δ2随频率变化的曲线可知,δ3、δ2在两个频段内剧烈减小,并且这两个频带将特征频率ω1和ω2包含在内。此外,还可见
|
图 11 双相流体饱和岩石随饱和度变化的特征频率曲线 红色曲线代表气水饱和岩石,绿色曲线代表油水饱和岩石;实线代表ω1,虚线表示ω2,点线代表ω3。 |
本文分析了裂缝参数变化引起的裂缝介质渗透率各向异性变化规律,探讨了各向异性渗流条件下,双相不混溶流体饱和的裂缝介质地震波频散、衰减和地震各向异性特征以及渗透率各向异性与地震各向异性的相关性,得到如下结论。
(1) 渗透率随裂缝参数(半径、倾向及方位)的变化规律各不相同,进而导致裂缝介质渗透率表现出各向异性。裂缝方位角引起的渗透率各向异性变化具有对称性;裂缝半径和倾角主要引起渗透率各向异性的强弱变化,其中裂缝半径的影响尤为显著。
(2) 渗透率各向异性条件下,地震波速度频散、衰减曲线呈现两个弛豫峰。同时,随饱和度增加,地震波速度的衰减增强,其中衰减系数对含气饱和度的变化极为敏感。
(3) 裂缝介质渗透率各向异性的强弱与地震各向异性系数相关,同时地震波速度频散、衰减的特征频率与各向异性系数极值或各向异性系数变化率的极值所对应的频率密切相关,这种相关性依赖于渗透率的各向异性情况、流体类型及流体饱和度。
| [1] |
MÜLLER T M, GUREVICH B, LEBEDEV M. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks: A review[J]. Geophysics, 2010, 75(5): 75A147-75A164. DOI:10.1190/1.3463417 |
| [2] |
CHAPMAN M. Frequency-dependent anisotropy due to mesoscale fractures in the presence of equant poro-sity[J]. Geophysical Prospecting, 2003, 51(5): 369-379. DOI:10.1046/j.1365-2478.2003.00384.x |
| [3] |
BRAJANOVSKI M, GUREVICH B, SCHOENBERG M. A model for P-wave attenuation and dispersion in a porous medium permeated by aligned fractures[J]. Geophysical Journal International, 2005, 163(1): 372-384. DOI:10.1111/j.1365-246X.2005.02722.x |
| [4] |
SCHOENBERG M. Elastic wave behavior across linear slip interfaces[J]. The Journal of the Acoustical Society of America, 1980, 68(5): 1516-1521. DOI:10.1121/1.385077 |
| [5] |
CHAPMAN M. Modeling the effect of multiple sets of mesoscale fractures in porous rock on frequency-dependent anisotropy[J]. Geophysics, 2009, 74(6): D97-D103. DOI:10.1190/1.3204779 |
| [6] |
ODA M. Permeability tensor for discontinuous rock masses[J]. Géotechnique, 1985, 35(4): 483-495. DOI:10.1680/geot.1985.35.4.483 |
| [7] |
KACHANOV M. Continuum model of medium with cracks[J]. Journal of the Engineering Mechanics Divi-sion, 1980, 106(5): 1039-1051. DOI:10.1061/JMCEA3.0002642 |
| [8] |
JAKOBSEN M. Effective hydraulic properties of frac-tured reservoirs and composite porous media[J]. Journal of Seismic Exploration, 2007, 16(2): 199-224. |
| [9] |
CHEN X H, ZHONG W L, HE Z H, et al. Frequencydependent attenuation of compressional wave and seismic effects in porous reservoirs saturated with multi-phase fluids[J]. Journal of Petroleum Science and Engineering, 2016, 147: 371-380. DOI:10.1016/j.petrol.2016.08.031 |
| [10] |
PAPAGEORGIOU G, AMALOKWU K, CHAPMAN M. Theoretical derivation of a Brie-like fluid mixing law[J]. Geophysical Prospecting, 2016, 64(4): 1048-1053. DOI:10.1111/1365-2478.12380 |
| [11] |
PAPAGEORGIOU G, CHAPMAN M. Wave-propa-gation in rocks saturated by two immiscible fluids[J]. Geophysical Journal International, 2017, 209(3): 1761-1767. DOI:10.1093/gji/ggx128 |
| [12] |
JIN Z Y, CHAPMAN M, PAPAGEORGIOU G. Frequency-dependent anisotropy in a partially saturated fractured rock[J]. Geophysical Journal International, 2018, 215(3): 1985-1998. DOI:10.1093/gji/ggy399 |
| [13] |
刘芸菲, 陈学华, 罗鑫, 等. 双相不混溶流体饱和裂缝-孔隙岩石依赖频率的地震响应数值分析[J]. 石油地球物理勘探, 2020, 55(4): 821-830. LIU Yunfei, CHEN Xuehua, LUO Xin, et al. Numerical analysis of frequency-dependent seismic responses from fractured-porous rock saturated with two-phase immiscible fluids[J]. Oil Geophysical Prospecting, 2020, 55(4): 821-830. |
| [14] |
SNOW D T. Anisotropie permeability of fractured media[J]. Water Resources Research, 1969, 5(6): 1273-1289. DOI:10.1029/WR005i006p01273 |
| [15] |
SNOW D T. The frequency and apertures of fractures in rock[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1970, 7(1): 23-40. |
| [16] |
LONG J C, REMER J S, WILSON C R, et al. Porous media equivalents for networks of discontinuous fractures[J]. Water Resources Research, 1982, 18(3): 645-658. DOI:10.1029/WR018i003p00645 |
| [17] |
LONG J C, GILMOUR P, WITHERSPOON P A. A model for steady fluid flow in random three-dimensional networks of disc-shaped fractures[J]. Water Resources Research, 1985, 21(8): 1105-1115. DOI:10.1029/WR021i008p01105 |
| [18] |
VU M N, POUYA A, SEYEDI D M. Modelling of steady-state fluid flow in 3D fractured isotropic porous media: application to effective permeability calculation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(14): 2257-2277. DOI:10.1002/nag.2134 |
| [19] |
SHAFIRO B, KACHANOV M. Anisotropic effective conductivity of materials with nonrandomly oriented inclusions of diverse ellipsoidal shapes[J]. Journal of Applied Physics, 2000, 87(12): 8561-8569. DOI:10.1063/1.373579 |
| [20] |
BARTHÉLÉMY J F. Effective permeability of media with a dense network of long and micro fractures[J]. Transport in Porous Media, 2009, 76(1): 153-178. DOI:10.1007/s11242-008-9241-9 |
| [21] |
ESHELBY J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems[J]. Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences, 1957, 241(1226): 376-396. |
| [22] |
XIONG F S, SUN W T, BA J, et al. Effects of fluid rheology and pore connectivity on rock permeability based on a network model[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(3): e2019JB018857. |
| [23] |
熊繁升, 甘利灯, 孙卫涛, 等. 裂缝-孔隙介质储层渗透率表征及其影响因素分析[J]. 地球物理学报, 2021, 64(1): 279-288. XIONG Fansheng, GAN Lideng, SUN Weitao, et al. Characterization of reservoir permeability and analysis of influencing factors in fracture-pore media[J]. Chinese Journal of Geophysics, 2021, 64(1): 279-288. |
| [24] |
PRIDE S R, HARRIS J M, JOHNSON D L, et al. Permeability dependence of seismic amplitudes[J]. The Leading Edge, 2003, 22(6): 518-525. DOI:10.1190/1.1587671 |
| [25] |
KOZLOV E. Seismic signature of a permeable, dualporosity layer[J]. Geophysics, 2007, 72(5): SM281-SM291. DOI:10.1190/1.2763954 |
| [26] |
RUBINO J G, VELIS D R, HOLLIGER K. Permea-bility effects on the seismic response of gas reservoirs[J]. Geophysical Journal International, 2012, 189(1): 448-468. DOI:10.1111/j.1365-246X.2011.05322.x |
| [27] |
REN H T, GOLOSHUBIN G, HILTERMAN F J. Poro-elastic analysis of permeability effects in thinly layered porous media[J]. Geophysics, 2009, 74(6): N49-N54. DOI:10.1190/1.3223185 |
| [28] |
MÜLLER T M, LAMBERT G, GUREVICH B. Dynamic permeability of porous rocks and its seismic signatures[J]. Geophysics, 2007, 72(5): E149-E158. DOI:10.1190/1.2749571 |
| [29] |
RUBINO J G, MÜLLER T M, GUARRACINO L, et al. Seismoacoustic signatures of fracture connectivity[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(3): 2252-2271. DOI:10.1002/2013JB010567 |
| [30] |
RUBINO J G, GUARRACINO L, MÜLLER T M, et al. Do seismic waves sense fracture connectivity?[J]. Geophysical Research Letters, 2013, 40(4): 692-696. DOI:10.1002/grl.50127 |
| [31] |
王丁, 张美根. 各向异性渗流条件下弹性波的传播特征[J]. 物理学报, 2014, 63(6): 069101. WANG Ding, ZHANG Meigen. Elastic wave propagation characteristics under anisotropic squirt-flow con-dition[J]. Acta Physica Sinica, 2014, 63(6): 069101. |
| [32] |
THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [33] |
TSVANKIN I. Anisotropic parameters and P-wave velocity for orthorhombic media[J]. Geophysics, 1997, 62(4): 1292-1309. DOI:10.1190/1.1444231 |
| [34] |
BATZLE M, WANG Z. Seismic properties of pore fluids[J]. Geophysics, 1992, 57(11): 1396-1408. DOI:10.1190/1.1443207 |



 陈学华,四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室,610059。Email:
陈学华,四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室,610059。Email: