中国深部页岩储层具有埋藏深、压力大且裂缝发育等特点,油气资源潜力巨大[1-4]。页岩储层为典型的横向各向同性(Vertical Transverse Isotropy,VTI)介质[5],除了黏土等矿物的优选排列之外,水平裂缝也是影响页岩储层VTI的一个重要因素[6-7]。因此,深部页岩储层弹性参数的预测不仅需要考虑黏土等矿物的优选排列,还需要考虑压力对水平裂缝的影响。
地震岩石物理模型是搭建岩石微观物性参数与弹性参数的桥梁[8-9]。Vernik等[10]发现页岩各向异性源于矿物定向排列,并最早利用Bcakus平均理论构建了VTI介质岩石物理模型;Hornby等[11]将各向异性SCA-DEM模型用于页岩储层岩石物理建模,利用高斯分布模拟黏土矿物与干酪根的定向排列,效果更接近实际,因而成为在页岩各向异性地震岩石物理建模中最常用的方法之一;Xu等[12]将页岩岩石物理模型框架划分为岩石基质、骨架和流体三个部分;Jiang等[13]利用Chapman模型耦合水平裂缝,以构建岩石物理模型;Guo等[14]将指示黏土矿物定向排列的压实指数(CL)用于岩石物理模型,并通过井资料反演研究CL对页岩各向异性的影响。
上述模型主要是针对浅层页岩储层,压力对浅层页岩储层影响较小,因此建模时仅重点考虑了黏土等矿物的影响,而未考虑压力作用。
可以利用实验数据构建地震波速度与围压、孔隙压力、有效压力等之间的经验关系[15-17],也可以通过地震岩石物理模型预测深部页岩储层的压力。Dinh等[18]利用储层孔隙结构与压力之间的关系,提出了孔隙刚度空间各向同性岩石物理模型;Li等[19]根据Digby接触模型,利用纵波约束求取配位数(Cp)方法,在建模中考虑压力的影响,构建了基于干岩石模量预测横波速度的方法;Zong等[20]建立了基于孔隙空间刚度理论的页岩岩石物理模型以及耦合有效压力的各向同性致密砂岩岩石物理模型。
上述考虑压力作用的岩石物理建模方法,大多针对各向同性介质,未考虑裂缝对压力的影响。
裂缝是诱导储层各向异性的主要原因之一。Hudson模型[21]假设裂缝为薄硬币形状的椭球,从而提出了含裂缝的弹性固体平均波场散射理论,但Hudson模型适用于裂缝稀疏排列且裂缝纵横比较小的情况;Schoenberg线性滑动模型[22]认为裂缝是没有厚度的平面且裂缝面两侧位移不连续,从而指出了定向排列裂缝组对背景介质弹性性质的影响,但Schoenberg线性滑动模型忽略了裂缝结构;裂缝纵横比是描述裂缝信息的重要参数,因此提出了Eshelby-Cheng模型[23-24],该模型适用于任意裂缝纵横比,并可用于含单一裂缝组的横向各向同性介质。
因此,本文开展了考虑压力的深部页岩储层地震岩石物理建模方法研究。首先,根据Toksöz包体理论推导有效压力与水平裂缝纵横比的关系,选择对裂缝纵横比更敏感的Eshelby-Cheng模型进行压力修正,并利用各向异性SCA-DEM模型耦合黏土颗粒与干酪根,构建了考虑压力的深部页岩储层地震岩石物理模型;然后,通过构建的地震岩石物理模型讨论了有效压力对裂缝纵横比、Thomsen各向异性参数以及储层纵、横波速度的影响;最后,将该模型应用于实际工区,并对比非压力修正的Eshelby-Cheng模型对储层纵波速度(VP)、横波速度(VS)预测的精度,验证了本文方法的可行性和准确性。
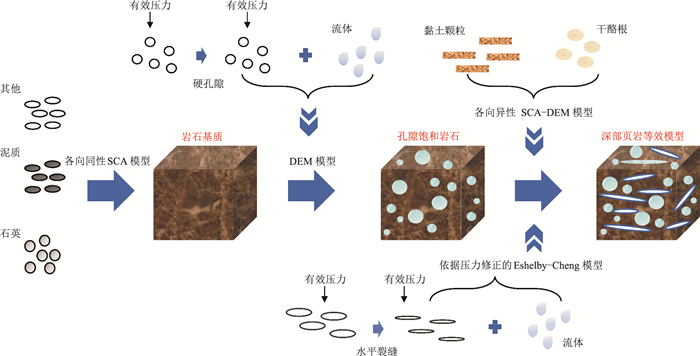
1 方法原理 1.1 岩石物理建模考虑压力的深部页岩储层岩石物理模型的构建过程包括混合背景基质、添加硬孔隙、耦合黏土颗粒与干酪根和耦合水平裂缝等四个部分(图 1)。
|
图 1 考虑压力的深部页岩储层地震岩石物理建模流程 |
通常由石英石、方解石、黄铁矿、白云石、长石等构成页岩储层背景基质。在实际建模中,需要根据研究区的实际情况选取矿物组分。这些矿物随机、均匀排列,表现为宏观各向同性特征,因此可以应用各向同性的SCA模型计算页岩储层混合固体基质的等效弹性模量,即
| $ \begin{align}{V}_{\mathrm{Q}\mathrm{u}\mathrm{a}} & \left({K}_{\mathrm{Q}\mathrm{u}\mathrm{a}}-{K}_{\mathrm{m}1}^{\mathrm{*}}\right){P}_{\mathrm{Q}\mathrm{u}\mathrm{a}}^{\mathrm{*}}+{V}_{\mathrm{F}\mathrm{e}\mathrm{l}}\left({K}_{\mathrm{F}\mathrm{e}\mathrm{l}}-{K}_{\mathrm{m}1}^{\mathrm{*}}\right){P}_{\mathrm{F}\mathrm{e}\mathrm{l}}^{\mathrm{*}}+\\ &{V}_{\mathrm{C}\mathrm{a}\mathrm{l}}\left({K}_{\mathrm{C}\mathrm{a}\mathrm{l}}-{K}_{\mathrm{m}1}^{\mathrm{*}}\right){P}_{\mathrm{C}\mathrm{a}\mathrm{l}}^{\mathrm{*}}+{V}_{\mathrm{D}\mathrm{o}\mathrm{l}}\left({K}_{\mathrm{D}\mathrm{o}\mathrm{l}}-{K}_{\mathrm{m}1}^{\mathrm{*}}\right){P}_{\mathrm{D}\mathrm{o}\mathrm{l}}^{\mathrm{*}}+\\ &{V}_{\mathrm{P}\mathrm{y}\mathrm{r}}\left({K}_{\mathrm{P}\mathrm{y}\mathrm{r}}-{K}_{\mathrm{m}1}^{\mathrm{*}}\right){P}_{\mathrm{P}\mathrm{y}\mathrm{r}}^{\mathrm{*}}=0\end{align} $ | (1) |
| $ \begin{align}{V}_{\mathrm{Q}\mathrm{u}\mathrm{a}}& \left({\mu }_{\mathrm{Q}\mathrm{u}\mathrm{a}}-{\mu }_{\mathrm{m}1}^{\mathrm{*}}\right){Q}_{\mathrm{Q}\mathrm{u}\mathrm{a}}^{\mathrm{*}}+{V}_{\mathrm{F}\mathrm{e}\mathrm{l}}\left({\mu }_{\mathrm{F}\mathrm{e}\mathrm{l}}-{\mu }_{\mathrm{m}1}^{\mathrm{*}}\right){Q}_{\mathrm{F}\mathrm{e}\mathrm{l}}^{\mathrm{*}}+\\ &{V}_{\mathrm{C}\mathrm{a}\mathrm{l}}\left({\mu }_{\mathrm{C}\mathrm{a}\mathrm{l}}-{\mu }_{\mathrm{m}1}^{\mathrm{*}}\right){Q}_{\mathrm{C}\mathrm{a}\mathrm{l}}^{\mathrm{*}}+{V}_{\mathrm{D}\mathrm{o}\mathrm{l}}\left({\mu }_{\mathrm{D}\mathrm{o}\mathrm{l}}-{\mu }_{\mathrm{m}1}^{\mathrm{*}}\right){Q}_{\mathrm{D}\mathrm{o}\mathrm{l}}^{\mathrm{*}}+\\ &{V}_{\mathrm{P}\mathrm{y}\mathrm{r}}\left({\mu }_{\mathrm{P}\mathrm{y}\mathrm{r}}-{\mu }_{\mathrm{m}1}^{\mathrm{*}}\right){Q}_{\mathrm{P}\mathrm{y}\mathrm{r}}^{\mathrm{*}}=0\end{align} $ | (2) |
上述式中:V为体积含量;
页岩储层裂缝中所含流体一般具有部分饱和、不均匀分布的特点,因此在本文的建模中,利用Domenico公式[25]对储层气体、液体体积模量进行加权平均,即
| $ {K}_{\mathrm{f}}={S}_{\mathrm{w}}{K}_{\mathrm{w}}+\left(1-{S}_{\mathrm{w}}\right){K}_{\mathrm{g}} $ | (3) |
式中:
分布在页岩储层背景介质中的硬孔隙抗压缩能力强,在受到压力时其纵横比基本不变,通常可假设为1。由于这些硬孔隙均匀分布在背景基质中,填充着气、水混合流体,因此可以利用DEM模型向混合背景基质中添加包含混合流体的硬孔隙,其表达式为
| $ \frac{\mathrm{d}{K}_{\mathrm{m}2}^{\mathrm{*}}}{\mathrm{d}{\phi }_{\mathrm{p}}}=\frac{\left({K}_{1}-{K}_{\mathrm{m}2}^{\mathrm{*}}\right){P}_{{}_{{\phi }_{\mathrm{p}}}}^{\mathrm{*}}}{1-{\phi }_{\mathrm{p}}} $ | (4) |
| $ \frac{\mathrm{d}{\mu }_{\mathrm{m}2}^{\mathrm{*}}}{\mathrm{d}{\phi }_{\mathrm{p}}}=\frac{\left({\mu }_{1}-{\mu }_{\mathrm{m}2}^{\mathrm{*}}\right)Q{P}_{{}_{{\phi }_{\mathrm{p}}}}^{\mathrm{*}}}{1-{\phi }_{\mathrm{p}}} $ | (5) |
上述式中:
定向排列分布的黏土颗粒和干酪根是导致页岩储层表现VTI特征的主要原因之一,因此基于已构建含硬孔隙的背景介质,采用各向异性SCA-DEM模型模拟黏土颗粒与干酪根混合物以构建横向各向同性等效岩石,即
| $ \begin{align}\underset{\_}{\tilde{\boldsymbol{C}}}=&\sum _{n=1}^{N}{v}_{n}{\underset{\_}{\boldsymbol{C}}}^{n}{\left[\boldsymbol{I}+\underset{\_}{\widehat{\boldsymbol{G}}}\left({\underset{\_}{\boldsymbol{C}}}^{n}-\underset{\_}{\tilde{\boldsymbol{C}}}\right)\right]}^{-1}\times \\ &\begin{array}{cc}& \end{array}{\left\{{\sum _{n=1}^{N}{v}_{n}\left[\boldsymbol{I}+\underset{\_}{\widehat{\boldsymbol{G}}}\left({\underset{\_}{\boldsymbol{C}}}^{n}-\underset{\_}{\tilde{\boldsymbol{C}}}\right)\right]}^{-1}\right\}}^{-1}\end{align} $ | (6) |
式中:
有效压力是上覆地层压力与孔隙压力的函数,即
| $ {\sigma }_{\mathrm{e}}={\sigma }_{\mathrm{c}}-{\sigma }_{\mathrm{p}} $ | (7) |
式中:
Toksöz包体理论[26]给出有效压力与裂缝体积变化率的关系,即
| $ \frac{\mathrm{d}V}{V}=\frac{-\frac{{\sigma }_{\mathrm{e}}}{{K}_{\mathrm{m}2}^{\mathrm{*}}}}{\frac{{E}_{1}-{E}_{2}{E}_{3}}{{E}_{3}+{E}_{4}}} $ | (8) |
式中:
根据裂缝纵横比与裂缝体积的关系[21],可推导出有效压力与裂缝纵横比关系为
| $ {\alpha }_{\mathrm{m}}={\alpha }_{0}\left[1+\frac{\mathrm{d}V}{V}\left({\alpha }_{0}, {\sigma }_{\mathrm{e}}\right)\right] $ | (9) |
式中:
基于Eshelby模型,Cheng[24]构建了含有裂缝的岩石储层的等效介质模型,即Eshelby-Cheng模型。相比于其他经典裂缝模型,Eshelby-Cheng模型适用的裂缝纵横比变化范围更大,对裂缝纵横比变化更敏感。鉴于本文重点研究有效压力对水平裂缝纵横比的影响,因此根据Toksöz包体理论对Eshelby-Cheng模型进行压力修正。
Eshelby-Cheng模型表达式[24]为
| $ {C}_{ij}^{\mathrm{e}\mathrm{f}\mathrm{f}}={C}_{ij}^{0}-{\phi }^{\mathrm{\text{'}}}{C}_{ij}^{1} $ | (10) |
式中:
将
| $ {\stackrel{-}{C}}_{ij}^{\mathrm{e}\mathrm{f}\mathrm{f}}={C}_{ij}^{0}-{\phi }_{\mathrm{m}}{\stackrel{-}{C}}_{ij}^{1} $ | (11) |
式中:
深部页岩储层具有VTI各向异性特征,VTI各向异性刚度矩阵一般可以通过5个独立参数进行表达,其表达式为
| $ {\boldsymbol{C}}_{\mathrm{V}\mathrm{T}\mathrm{I}}=\left[\begin{array}{cccccc}{c}_{11}& {c}_{12}& {c}_{13}& 0& 0& 0\\ {c}_{12}& {c}_{11}& {c}_{13}& 0& 0& 0\\ {c}_{13}& {c}_{13}& {c}_{33}& 0& 0& 0\\ 0& 0& 0& {c}_{44}& 0& 0\\ 0& 0& 0& 0& {c}_{44}& 0\\ 0& 0& 0& 0& 0& {c}_{66}\end{array}\right] $ | (12) |
其中
| $ {c}_{66}=\frac{1}{2}\left({c}_{11}-{c}_{12}\right) $ |
Thomsen将各向异性的影响从各向同性背景中分离出来,将弹性参数组成无量纲各向异性参数[27],其表达式为
| $ \left\{\begin{array}{l}{V}_{\mathrm{P}0}=\sqrt{\frac{{c}_{33}}{\rho }}\\ {V}_{\mathrm{S}0}=\sqrt{\frac{{c}_{44}}{\rho }}\\ \varepsilon=\frac{{c}_{11}-{c}_{33}}{2{c}_{33}}\\ \gamma =\frac{{c}_{66}-{c}_{44}}{2{c}_{44}}\\ \delta =\frac{{\left({c}_{13}+{c}_{44}\right)}^{2}-{\left({c}_{33}-{c}_{44}\right)}^{2}}{2{c}_{33}\left({c}_{33}-{c}_{44}\right)}\end{array}\right. $ | (13) |
式中:
为了分析有效压力对储层微观物性的弹性响应规律,建立参数如表 1所示模型,分别模拟不同
|
|
表 1 矿物成分及弹性参数 |
可以根据
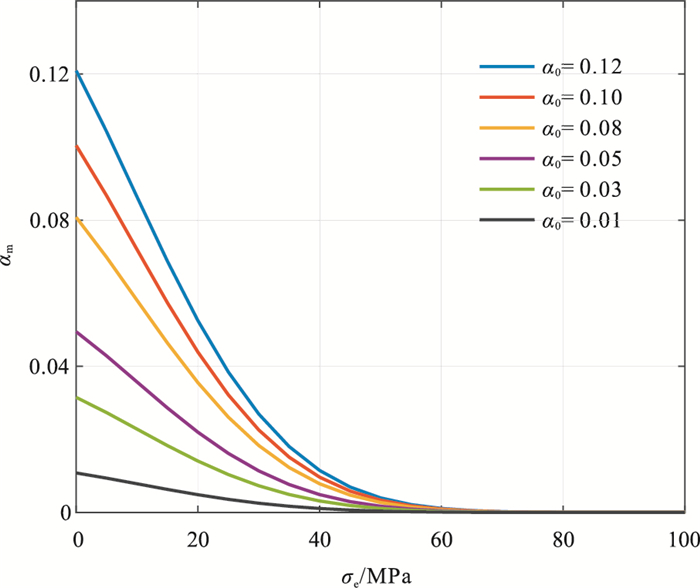
|
图 2 不同 |
本文构建的地震岩石物理模型考虑了影响深部页岩储层VTI各向异性特征的主要因素,即黏土矿物优选排列和受压力影响的水平裂缝。通过模型分析有效压力与Thomsen各向异性参数的关系,可获取有效压力对深部页岩储层各向异性特征的影响规律。
Thomsen各向异性参数中,
从图 3可以看出,
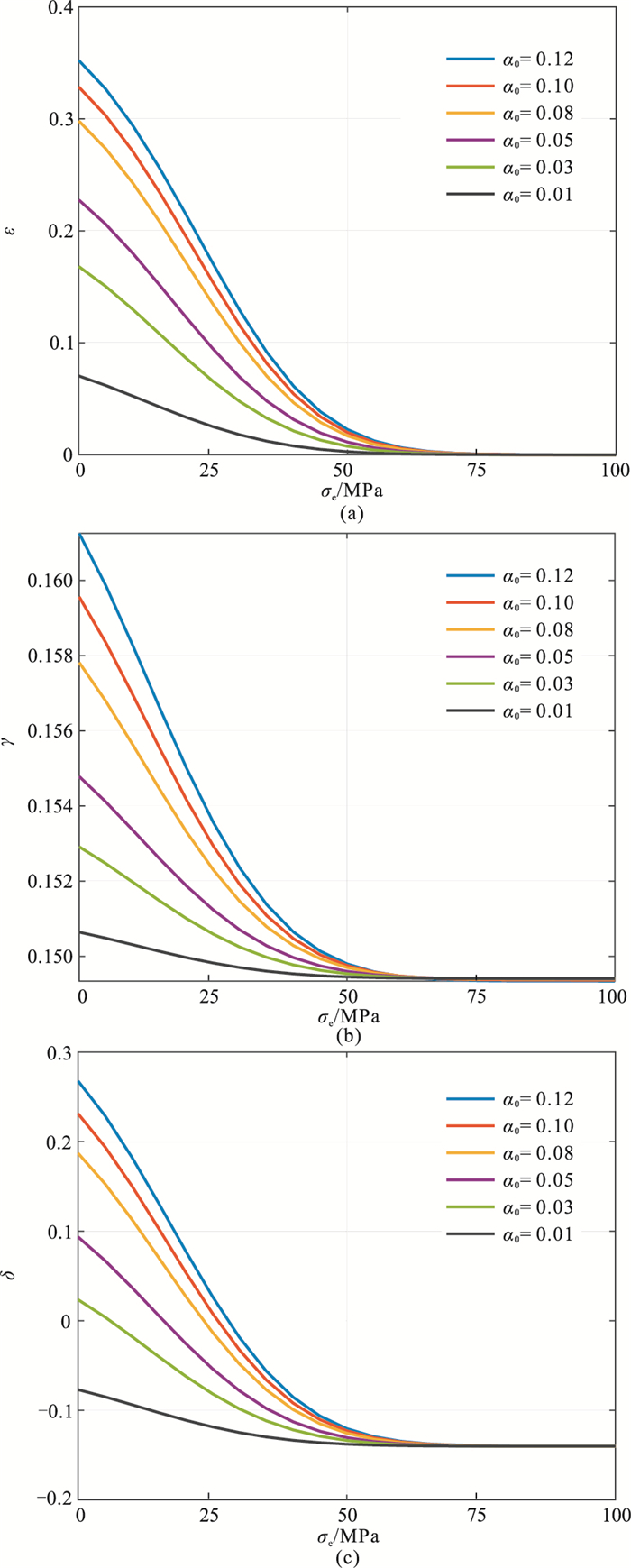
|
图 3 不同 |
深部页岩储层中多发育裂缝纵横比较小的微裂缝,选择合适的初始裂缝纵横比(α0=0.08)[28]可以模拟
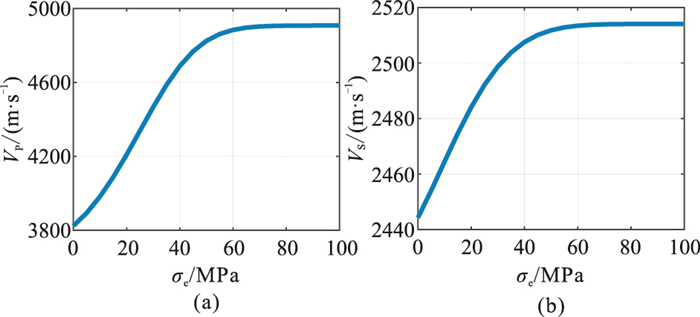
|
图 4 α0=0.08时纵、横波速度随 |
由图 4可见,随着
由图 3、图 4可以看出,当
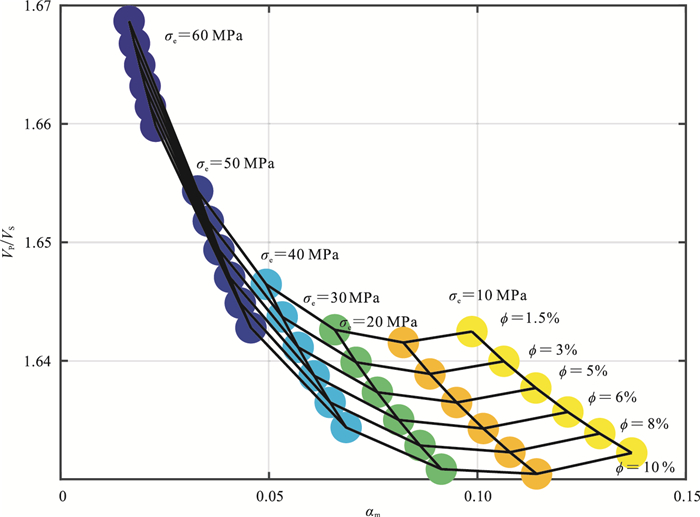
根据本文方法构建的深部页岩储层岩石物理模板如图 5所示。由图可见,
|
图 5 深部页岩储层岩石物理模板 |
为了验证考虑压力的深部页岩储层地震岩石物理模型(本文方法)的有效性,选取四川A井实际资料预测纵、横波速度。A井所含流体主要为地层水和天然气,基质矿物主要为石英、黏土颗粒及干酪根。建模所用的各矿物组分体积模量、剪切模量及密度如表 2所示。
|
|
表 2 矿物成分及弹性参数 |
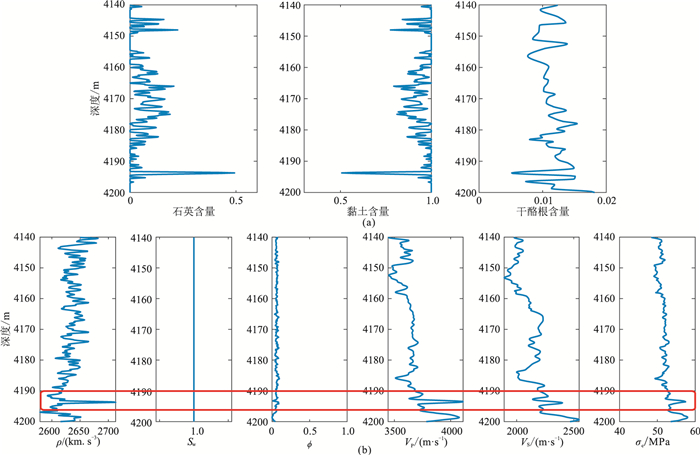
A井的矿物组分含量及物性参数(
|
图 6 A井深层各矿物组分体积含量与物性曲线 (a)各矿物组分体积含量;(b)物性曲线 |
利用本文方法建立的深部页岩储层岩石物理模型计算A井深层的VP、VS,并分别与实际测井数据进行对比;然后与未考虑压力影响的页岩岩石物理模型计算的VP、VS进行对比。未考虑压力影响的页岩岩石物理模型利用非压力修正的Eshelby-Cheng模型[23-24](式(9))耦合水平裂缝,其余建模流程与本文方法相同。为了方便表述,将未考虑压力影响的页岩岩石物理模型称为非压力修正的Eshelby-Cheng模型。储层VP、VS估算与相对误差分析如图 7所示。

|
图 7 A井不同模型计算VP、VS结果与相对误差 (a)VP;(b)VS |
从图 7可以看出,通过非压力修正Eshelby-Cheng模型得到的VP、VS与实测VP、VS差别较大,尤其在有效压力激增段(黑色箭头处),非压力修正Eshelby-Cheng模型得到的VP、VS对有效压力变化均不敏感。而据图 6b可知,在有效压力激增层段,储层有效孔隙度减小,实测地震波速度随有效压力增大而增大。通过本文岩石物理模型得到的VP、VP与实测VP、VP变化趋势大致相同,尤其在有效压力激增段(黑色箭头处)。对比两种岩石物理模型计算所得VP、VS的相对误差,可以看出本文建模方法误差明显降低,验证了本文岩石物理模型的有效性。
4 结论页岩储层的VTI各向异性特征主要由黏土矿物的优选排列和水平裂缝引起。随着埋藏深度的加大,压力对储层性质的影响不可忽略。深部页岩储层虽含有的裂缝纵横比较小,但裂缝对岩石弹性性质具有明显的影响。本文针对深部页岩储层裂缝发育、压力大的特点,从有效压力影响水平裂缝结构的角度出发,推导了有效压力与裂缝纵横比的关系,选择对裂缝纵横比更敏感且适用范围更广的Eshelby-Cheng模型进行压力修正,构建了考虑压力的深部页岩储层岩石物理模型。
依据本文方法分析了有效压力对储层弹性参数、物性参数及各向异性参数等的影响。在有效压力增大初期,对储层性质影响较显著,但当增大到一定限度时,储层性质趋于稳定且不再随有效压力增大而改变。
将本文建模方法应用于实际工区,与非压力修正Eshelby-Cheng模型的VP、VS估算结果进行对比,可见在有效压力较大层段,本文建模方法预测结果与实际数据吻合度更高,因而本文方法具备有效性和实用性。
| [1] |
邹才能, 陶士振, 杨智, 等. 中国非常规油气勘探与研究新进展[J]. 矿物岩石地球化学通报, 2012, 31(4): 312-322. ZOU Caineng, TAO Shizhen, YANG Zhi, et al. New advance in unconventional petroleum exploration and research in China[J]. Bulletin of Mineralogy, Petrology and Geochemistry, 2012, 31(4): 312-322. DOI:10.3969/j.issn.1007-2802.2012.04.002 |
| [2] |
王濡岳, 胡宗全, 周彤, 等. 四川盆地及其周缘五峰组—龙马溪组页岩裂缝发育特征及其控储意义[J]. 石油与天然气地质, 2021, 42(6): 1295-1306. WANG Ruyue, HU Zongquan, ZHOU Tong, et al. Characteristics of fractures and their significance for reservoirs in Wufeng-Longmaxi shale, Sichuan Basin and its periphery[J]. Oil & Gas Geology, 2021, 42(6): 1295-1306. |
| [3] |
张金川, 陶佳, 李振, 等. 中国深层页岩气资源前景和勘探潜力[J]. 天然气工业, 2021, 41(1): 15-28. ZHANG Jinchuan, TAO Jia, LI Zhen, et al. Prospect of deep shale gas resources in China[J]. Natural Gas Industry, 2021, 41(1): 15-28. |
| [4] |
张少龙, 闫建平, 郭伟, 等. 基于岩石物理相的深层页岩气地质—工程甜点参数测井评价方法——以四川盆地LZ区块五峰组—龙马溪组为例[J]. 石油地球物理勘探, 2023, 58(1): 214-227. ZHANG Shaolong, YAN Jianping, GUO Wei, et al. Logging evaluation method of geological-engineering sweet spot parameters for deep shale gas based on petrophysical facies: a case study of the Wufeng-Longmaxi Formation in LZ block of Sichuan Basin[J]. Oil Geophysical Prospecting, 2023, 58(1): 214-227. |
| [5] |
VERNIK L, NUR A. Ultrasonic velocity and anisotropy of hydrocarbon source rocks[J]. Geophysics, 1992, 57(5): 727-735. DOI:10.1190/1.1443286 |
| [6] |
VERNIK L, LIU X. Velocity anisotropy in shales: a petrophysical study[J]. Geophysics, 1997, 62(2): 521-532. DOI:10.1190/1.1444162 |
| [7] |
刘财, 邓馨卉, 郭智奇, 等. 基于岩石物理的页岩储层各向异性表征[J]. 石油地球物理勘探, 2018, 53(2): 339-346. LIU Cai, DENG Xinhui, GUO Zhiqi, et al. Shale reservoir anisotropic characterization based on rock physics[J]. Oil Geophysical Prospecting, 2018, 53(2): 339-346. |
| [8] |
周琦, 印兴耀, 李坤. 煤系地层地震岩石物理建模及横波预测方法[J]. 石油地球物理勘探, 2022, 57(2): 357-366. ZHOU Qi, YIN Xingyao, LI Kun. Seismic rock physics modeling and shear wave velocity prediction method of coal measure strata[J]. Oil Geophysical Prospecting, 2022, 57(2): 357-366. |
| [9] |
陈超, 印兴耀, 陈祖庆, 等. 基于页岩岩石物理等效模型的地层压力系数预测方法[J]. 石油地球物理勘探, 2022, 57(2): 367-376, 394. CHEN Chao, YIN Xingyao, CHEN Zuqing, et al. Prediction for formation pressure coefficients based on an equivalent petrophysical model of shale[J]. Oil Geophysical Prospecting, 2022, 57(2): 367-376, 394. |
| [10] |
VERNIK L, LANDIS C. Elastic anisotropy of source rocks: implications for hydrocarbon generation and primary migration[J]. AAPG Bulletin, 1996, 80(4): 531-544. |
| [11] |
HORNBY B E, SCHWARTZ L M, HUDSON J A. Anisotropic effective-medium modeling of the elastic properties of shales[J]. Geophysics, 1994, 59(10): 1570-1583. |
| [12] |
XU S, WHITE R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. |
| [13] |
JIANG M, SPIKES K T. Estimation of reservoir properties of the Haynesville Shale by using rock-physics modelling and grid searching[J]. Geophysical Journal International, 2013, 195(1): 315-329. |
| [14] |
GUO Z, LIU C, LIU X, et al. Research on anisotropy of shale oil reservoir based on rock physics model[J]. Applied Geophysics, 2016, 13(2): 382-392. |
| [15] |
WYLLIE M R J, GREGORY A R, GARDNER G H F. An experimental investigation of factors affecting elastic wave velocities in porous media[J]. Geophysics, 1958, 23(3): 459-493. |
| [16] |
钱丽萍, 王霞, 李丰, 等. Fillippone公式结合等效介质理论预测地层压力[J]. 石油地球物理勘探, 2018, 53(增刊2): 224-229. QIAN Liping, WANG Xia, LI Feng, et al. Formation pore pressure prediction using Fillipone formula combined with equivalent medium theory[J]. Oil Geophysical Prospecting, 2018, 53(S2): 224-229. |
| [17] |
马中高, 伍向阳, 王中海. 有效压力对岩石纵横波速度的影响[J]. 勘探地球物理进展, 2006, 29(3): 183-186. MA Zhonggao, WU Xiangyang, WANG Zhonghai. Effect of effective pressure on compressional and shear wave velocities[J]. Progress in Exploration Geophysics, 2006, 29(3): 183-186. |
| [18] |
DINH H, VAN DER BAAN M, RUSSELL B. Pore space stiffness approach for a pressure-dependent rock-physics model[C]. SEG Technical Program Expanded Abstracts, 2016, 35: 3226-3230.
|
| [19] |
LI L, MA J. The influence of pore system change during CO2 storage on 4D seismic interpretation[J]. Oil & Gas Science and Technology, 2019, 74: 81. |
| [20] |
ZONG Z, JIANG M, XU M. Influencing factor analysis of the elastic properties of shale with rock-physical model including pressure effects[J]. Interpretation, 2020, 8(3): T515-T524. |
| [21] |
HUDSON J A. Overall properties of a cracked solid[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1980, 88(2): 371-384. |
| [22] |
SCHOENBERG M. Elastic wave behavior across linear slip interfaces[J]. The Journal of the Acoustical Society of America, 1980, 68(5): 1516-1521. |
| [23] |
ESHELBY J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1957, 241(1226): 376-396. |
| [24] |
CHENG C. Seismic Velocities in Porous Rocks: Direct and Inverse Problems[D]. Massachusetts Institute of Technology, Cambridge, 1978.
|
| [25] |
DOMENICO S N. Elastic properties of unconsolidated porous sand reservoirs[J]. Geophysics, 1977, 42(7): 1339-1368. |
| [26] |
KUSTER G T, TOKSOZ M N. Velocity and attenuation of seismic waves in two-phase media; part Ⅰ, theoretical formulations[J]. Geophysics, 1974, 39(5): 587-606. |
| [27] |
THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. |
| [28] |
YAN J, LI X, ENRU L. Effects of pore aspect ratios on velocity prediction from well-log data[J]. Geophysical Prospecting, 2002, 50(3): 289-300. |



 印兴耀,山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
印兴耀,山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email: