2. 中国石化胜利油田 物探研究院, 山东东营 257022;
3. 中山大学地球科学与工程学院, 广东珠海 519080
2. Geophysical Research Institute, Shengli Oilfield Branch Co., SINOPEC, Dongying, Shandong 257022;
3. School of Earth Sciencesand Engineering, Sun Yat-Sen University, Zhuhai, Guangdong 519080
随着勘探对象日益复杂且成像精度要求不断提高,叠前深度偏移已成为目前地震勘探数据处理的重要技术。偏移可使绕射波收敛、反射波归位,得到真实地反映地下构造的结果。相比于时间域,叠前深度偏移对于复杂构造具有更强适应性,但深度域模型对于速度模型的准确度依赖性较高且运算量巨大。近年来,随着计算机技术的飞速发展,计算能力不足已不再是深度偏移技术的瓶颈,该方法得以推广应用。为了提高计算效率,Micikevicius[1]在2009年利用GPU实现了有限差分的快速算法;李博等[2]、刘守伟等[3]及Foltinek等[4]相继利用GPU加速的有限差分算法实现了叠前逆时偏移成像,取得了一些成果。尽管如此,传统的叠前深度偏移方法仍然存在正演应用频率高且运行周期长、叠前炮记录偏移流程长等诸多问题。即便是模拟研究,仍需先正演后偏移的一系列繁杂流程。因此,对相关的应用和研究极为不利。
成像算子在光学领域被定义为成像系统对点光源的脉冲响应。理想的光学系统是物体上一个点发出的光,不经历任何散射、折射等作用,直接成像在一个点上。关于成像算子,最早可追溯到20世纪90年代,即Gelius等[5-7]提出的广义散射层析方法。随后,Hamran等[8]实现了基于局部平面波的散射层析成像,Sethian[9]提出基于波前扩展的快速推进法射线追踪方法。至此,基于成像算子的成像方法已初具雏形。
进入21世纪,张雪建等[10]提出在深度域合成地震记录的方法;Lecomet等[11-14]综合前人研究成果,提出了模拟叠前局部成像方法;张金陵等[15]利用地震子波取得一维点扩散函数;吴涵等[16]提出基于成像算子的模拟叠前深度成像方法;段伟国等[17]提出基于密度扰动的两步正演法计算点扩散函数(光学上表示一点产生的光源)。至此,该方法已臻于成熟,但尚存一些不足。如基于成像算子的模拟成像方法目前主要采用分区重构和近似代替方法,在子波形态、能量归位等方面难如人意;同时,不可避免地出现突变界面,这些问题亟待解决。
针对深度域子波及地震资料,张雪建等[10]讨论了地震子波时深转换问题;何惺华[18]对深度域子波、褶积和傅里叶变换等基本问题进行了充分讨论和分析;林柏香等[19]将时间域计算方法引入深度域,得到深度域合成地震记录;樊中海等[20]分类介绍了地震反演方法,阐述了子波提取的重要性;邵广周等[21]使用加窗自适应子波提取方法从观测记录中提取与实际数据匹配较好的震源子波。
在此基础上,本文发展了一种基于照明补偿的变“子波”模拟叠前深度成像方法。该方法仅需速度模型、观测系统及震源即可得到成像结果,简化了先正演后偏移的传统流程,提高了计算效率,且能适用于地下复杂构造,对于观测系统优化及传统成像结果分析具有重要指导意义。
1 模拟成像方法原理常速介质中,地震波频率与波数的对应关系为
| $ k=\frac{2f}{v} $ | (1) |
式中:f为子波主频;k为波数;v为介质速度。
一维情况下,点扩散函数的波长与周期满足
| $ {\int }_{0}^{\lambda }\frac{\mathrm{d}x}{v\left(x\right)}=T $ | (2) |
式中:T为时域子波的周期;λ为深度域点扩散函数的波长;v(x)为x处地层的速度。
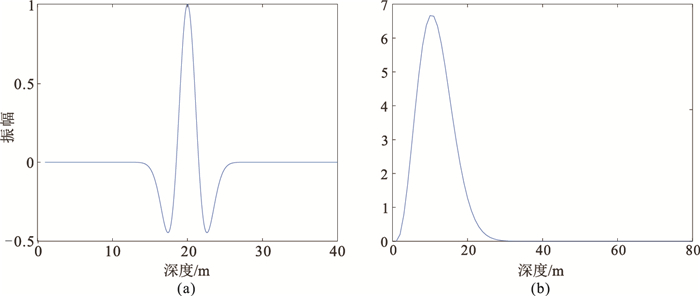
给定时间域子波和速度,可得深度域点扩散函数(图 1a);将深度域点扩散函数变换到波数域,即可得波数域点扩散函数(图 1b)。
|
图 1 深度域点扩散函数(a)和波数域扩散函数(b) |
分别用正演算子F和反演算子I表示地下介质速度模型
| $ S\left(\boldsymbol{r}\right)=F\left(\boldsymbol{r}\right)V\left(\boldsymbol{r}\right) $ | (3) |
| $ R\left(\boldsymbol{r}\right)=S\left(\boldsymbol{r}\right)I\left(\boldsymbol{r}\right) $ | (4) |
式中:F(r)为正演算子;I(r)为成像算子;S(r)为正演结果;R(r)为成像结果;V(r)为速度场;r为地下模型散射点位置。
如果将二者结合,最终成像结果可表示为
| $ R\left(\boldsymbol{r}\right)=F\left(\boldsymbol{r}\right)I\left(\boldsymbol{r}\right)V\left(\boldsymbol{r}\right)=D\left(\boldsymbol{r}\right)V\left(\boldsymbol{r}\right) $ | (5) |
式中D(r)为直接成像算子。
已知标量声波方程
| $ {\nabla }^{2}P(\boldsymbol{r}, t)=\frac{1}{{V}^{2}\left(\boldsymbol{r}\right)}\frac{{\partial }^{2}P(\boldsymbol{r}, t)}{\partial {t}^{2}} $ | (6) |
式中:
| $ {P}_{\mathrm{s}\mathrm{c}}({\boldsymbol{r}}_{\mathrm{g}}, {\boldsymbol{r}}_{\mathrm{s}})=-{\int }_{V}{P}_{\rm{in}}(\boldsymbol{r}, {\boldsymbol{r}}_{\rm{s}}){k}_{0}^{2}O\left(\boldsymbol{r}\right)G({\boldsymbol{r}}_{\mathrm{g}}, \boldsymbol{r})\mathrm{d}\boldsymbol{r} $ | (7) |
式中:O(r)为地下速度扰动(可近似看作反射率);V0(r)为背景速度场;Psc为散射波场;Pin为入射波场;rg为检波点位置;rs为炮点位置。由于该背景场是不均匀且无衰减的,所以其格林函数可由射线追踪得到[9],同时结合Stamnes给出的格林函数近似解[22],引入偏移算子
| $ R\left(\boldsymbol{r}\right)={\int }_{{}_{V}}O\left(\boldsymbol{r}\right)\left(\iint \frac{\alpha ({\boldsymbol{r}}_{\mathrm{g}}, {\boldsymbol{r}}_{\mathrm{s}}, \boldsymbol{r})}{\alpha ({\boldsymbol{r}}_{\mathrm{g}}, {\boldsymbol{r}}_{\mathrm{s}}, {\boldsymbol{r}}^{\mathrm{\text{'}}})}l({\boldsymbol{r}}_{\rm{g}}, {\boldsymbol{r}}_{\rm{s}}, {\boldsymbol{r}}^{\text{'}}){\mathrm{e}}^{\text{i}\omega \left[\tau \right({\boldsymbol{r}}_{\rm{g}}, {\boldsymbol{r}}_{\rm{s}}, \boldsymbol{r})-\tau ({\boldsymbol{r}}_{\rm{g}}, {\boldsymbol{r}}_{\rm{s}}, {\boldsymbol{r}}^{\text{'}}\left)\right]}\mathrm{d}{\boldsymbol{r}}_{\rm{g}}\mathrm{d}{\boldsymbol{r}}_{\rm{s}}\right)\mathrm{d}\boldsymbol{r}={\int }_{{}_{V}}O\left(\boldsymbol{r}\right)D(\boldsymbol{r}, {\boldsymbol{r}}^{\mathrm{\text{'}}})\mathrm{d}\boldsymbol{r} $ | (8) |
式中:
| $ D(\boldsymbol{r}, {\boldsymbol{r}}^{\mathrm{\text{'}}})\approx \iint \frac{l({\boldsymbol{r}}_{\mathrm{g}}, {\boldsymbol{r}}_{\mathrm{s}}, {\boldsymbol{r}}^{\mathrm{\text{'}}}){\mathrm{e}}^{\mathrm{i}\boldsymbol{K}(\boldsymbol{r}-{\boldsymbol{r}}^{\mathrm{\text{'}}})}}{\left|J\left(\boldsymbol{K}\right|{\boldsymbol{r}}_{\mathrm{g}}, {\boldsymbol{r}}_{\mathrm{s}})\right|}{\mathrm{d}}^{2}K $ | (9) |
式中K=
| $ R\left(\boldsymbol{r}\right)={\int }_{v}O\left(\boldsymbol{r}\right)D(\boldsymbol{r}, {\boldsymbol{r}}^{\text{'}})\text{d}\boldsymbol{r}=O\left(\boldsymbol{r}\right) $ | (10) |
此时,只需将地震子波作用于直接成像算子,就可得到带有子波响应的模拟叠前深度剖面
| $ D(\boldsymbol{r}, {\boldsymbol{r}}^{\mathrm{\text{'}}})=\iint s\left(\omega \right){\mathrm{e}}^{\mathrm{i}\boldsymbol{K}(\boldsymbol{r}-{\boldsymbol{r}}^{\mathrm{\text{'}}})}{\mathrm{d}}^{2}\boldsymbol{K} $ | (11) |
式中:
|
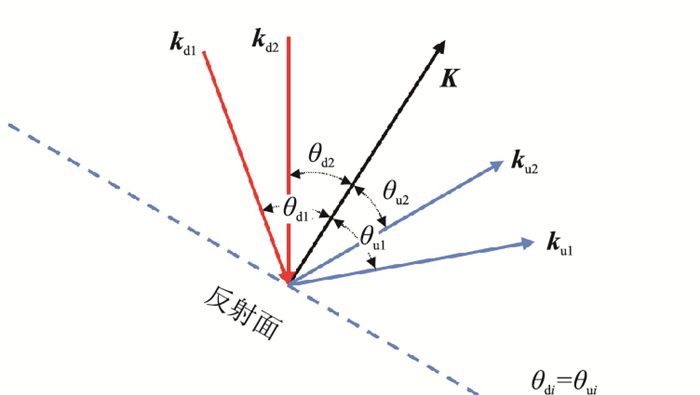
图 2 散射向量示意图 |
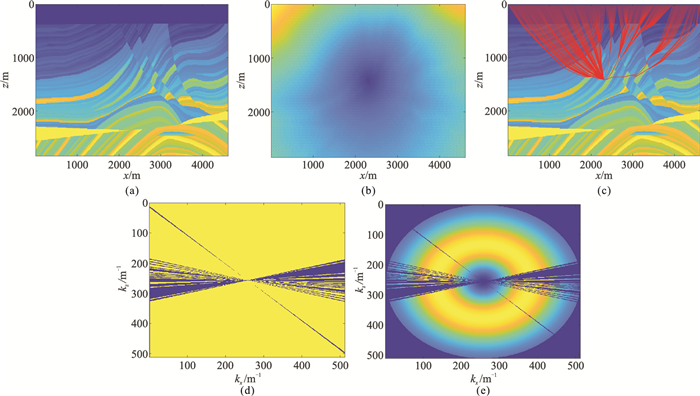
直接成像算子可在波数域由点扩散函数与上传波数向量和下传波数向量构建,通过计算下传波数向量与上传波数向量在成像点处的差值,可得到模拟成像所需的波传向量K,因此波传向量的构建首先需计算成像点到各检波点及震源点的射线路径。以Marmousi模型(图 3a)为例,计算成像算子位于(2300 m,1420 m)的走时场(图 3b),得到该点射线路径(图 3c),进而得到该点处的波传向量(图 3d),最终与该点的点扩散函数在波数域构建成像算子(图 3e)。
|
图 3 Marmousi模型的成像算子求取过程 (a)速度模型;(b)(2300 m,1420 m)点处走时场;(c)射线路径;(d)波数向量场;(e)成像算子 |
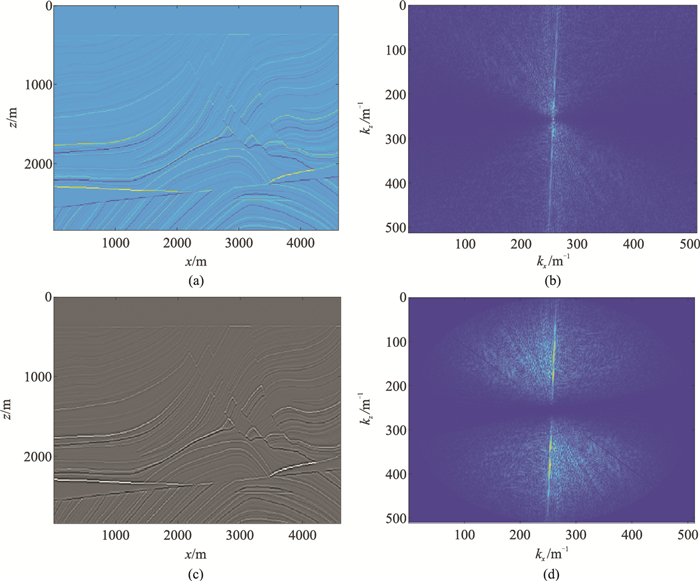
将地下速度模型的速度扰动信息与成像算子相互作用,即可得到模拟成像结果,因此只需将成像算子与反射系数模型做褶积即可。而空间域的褶积运算相当于波数域的乘积运算,所以需将反射系数模型(图 4a)变换到波数域(图 4b),与成像算子(图 3e)相乘,即可得到波数域成像结果(图 4d);再将波数域成像结果进行傅里叶反变换,即可得到模拟成像结果(图 4c)。
|
图 4 Marmousi模型空间域反射系数模型(a)及其成像结果(c)、波数域反射系数模型(b)及其成像结果(d) |
图 4所示的Marmousi模型试算,共461×294个网格,采用正方形网格,网格大小为10 m。雷克子波主频为30 Hz,采用地面放炮地面接收,共20炮,每炮230道接收,道间距20 m。可见该方法适用性良好,模拟成像结果能较准确地反映地下构造信息。但该方法所得成像结果在子波形态及能量分配等方面尚有待后续改善。
2 模拟成像法存在问题及解决方案 2.1 存在的问题相较于传统成像方法,模拟成像方法虽具有计算速度快、成像清晰的优势,但该方法主要利用成像算子与反射系数模型作褶积得到成像结果,无法达到子波随地层速度而变化的效果,而成像算子的构建若仅采用一点的子波信息,当算子位置不同时,由于所用子波不同,成像结果也会有所偏差。
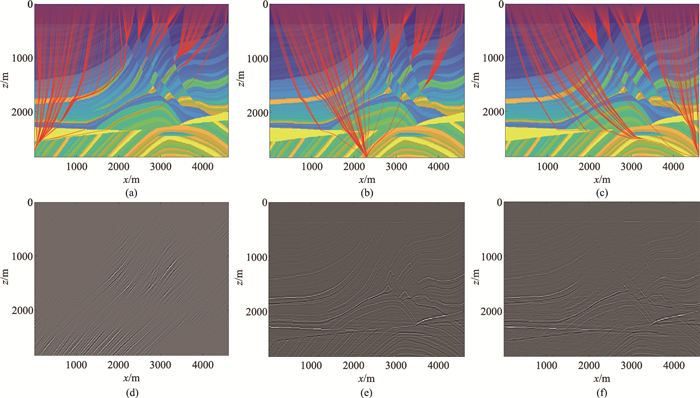
同时,成像算子的构建离不开波传向量的计算。波传向量提供的主要信息是潜在照明点反射面对应的倾角,只有当该位置存在垂直于波传向量的反射面,才能照明出该反射面。当算子位置不同或观测系统改变时,波传向量改变会导致照明情况不同,模拟成像结果也会存在差异。图 5展示了成像算子位置不同时的射线路径及模拟成像结果。
|
图 5 不同位置处的射线路径(上)及其模拟成像结果(下) (a)、(d)对应(100 m,2840 m)处;(b)、(e)对应(2310 m,2840 m)处;(c)、(f)对应(4610 m,2840 m)处 |
当成像算子在(100 m,2840 m)时(图 5d),仅有左下方一小部分能够成像;当成像算子位于(2310 m,2840 m)处时(图 5e),模拟成像结果大致反映了地下构造的基本形态,但在中部高陡倾角构造处出现许多虚假构造;当成像算子位于(4610 m,2840 m)处时(图 5f),深部的低速区成像结果不理想,出现缺失。这是因为成像算子位置不同时,射线路径不同,通过射线路径所构造的波传向量无法将地下构造面照出,也就无法成像。
2.2 基于可变子波和照明补偿的模拟成像方法获取准确的深度域点扩散函数是模拟叠前成像方法的基础。一个波动过程,既可表示为时间的函数,即时间域子波,表示某一质点的各时刻振幅形成的曲线;也可表示为空间的函数——深度域点扩散函数,即一系列质点的振动形成的曲线。一维情况下,点扩散函数的波长与周期关系由式(2)给出,给定时域子波和速度,通过式(2)即可得到深度域点扩散函数,常速介质中频率与波数的关系由式(1)给出。选择时域内主频为30 Hz的雷克子波,得到对应的时间域子波(图 6a),假设介质速度均匀,分别给定介质速度为3000 m/s和1000 m/s,可得到对应速度为3000 m/s(图 6b)和1000 m/s(图 6c)的深度域点扩散函数。

|
图 6 时间域子波(a)、介质速度为3000 m/s(b)及介质速度为1000 m/s(c)的深度域点扩散函数 |
由图 6b和图 6c可见,地下介质速度越大,深度域点扩散函数的波形更“胖”一些;地下介质速度越小,波形更“瘦”一些。深度域点扩散函数与地下介质有关,是关于速度的函数,其形态、波数和相位都随着速度的变化而改变;由于“线性时不变”条件在深度域中并不成立,即在不同介质分界面处波形并不对称,因此使用单一的深度域点扩散函数是不合适的。
考虑使用多个点扩散函数,就须改变褶积方式。时间域褶积模型的实质是时间域子波与对应点的反射系数相乘相加的过程。而在深度域中,由于点扩散函数是速度的函数,褶积的过程可转换为一种非稳态的运算过程
| $ \boldsymbol{s}=\boldsymbol{W}\boldsymbol{R}=\left[\begin{array}{c}{\boldsymbol{w}}_{1}\\ \begin{array}{l}{\boldsymbol{w}}_{2}\\ ⋮\end{array}\\ {\boldsymbol{w}}_{n}\end{array}\right]\boldsymbol{R} $ | (12) |
式中:s为深度域合成记录;
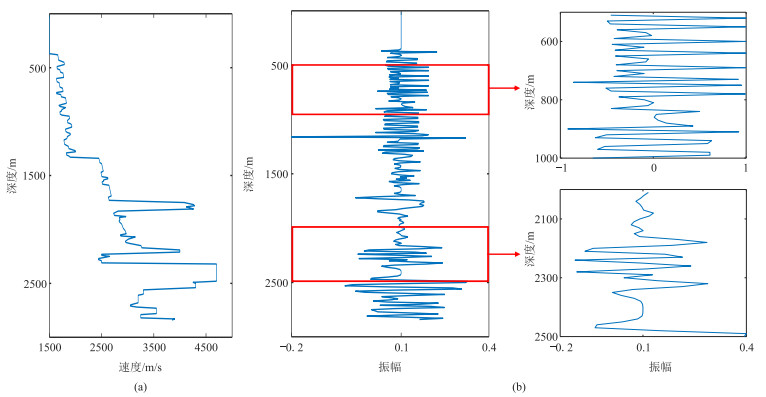
图 7为采用主频为30 Hz的雷克子波,在Marmousi速度模型中抽取第80道(图 7a),按照时域子波以不同速度求取深度域点扩散函数,并与深度域的反射系数进行非稳态褶积,得到模拟深度域的合成记录(图 7b)。对比不同深度处的波形,可见其间的差距十分明显。
|
图 7 Marmousi模型第80道的速度曲线(a)、非稳态褶积结果(b)及其局部放大显示(c) |
考虑到成像算子的构建需要波数域点扩散函数与波传向量,而使用一点的点扩散函数会导致成像结果不准确,故采用单位脉冲替代波数域点扩散函数与波传向量,构建成像算子;同时,在深度域中,反射系数模型与深度域点扩散函数作非稳态褶积,得到深度域的模拟地震记录,将深度域模拟记录转化到波数域并施加成像算子的作用,最后变换到深度域即可得到成像结果。具体计算流程如图 8所示。

|
图 8 模拟成像算法流程图 |
同时,由于构建成像算子时并未使用该点的子波而是用单位脉冲做替代,那么可将多个点的模拟成像结果叠加以解决常规模拟成像结果中能量不匹配或个别区域无法照明的问题。首先,需在深度域进行非稳态褶积,得到模拟的地震记录,然后将深度域模拟地震记录变换到波数域,将其与成像算子相乘即可得到波数域成像结果,将波数域成像结果反变换,可得到变“子波”深度域模拟成像结果。
又因为傅里叶变换遵循线性性质,所以模拟成像结果叠加运算可以转换为成像算子叠加运算,也就是在波数域将成像算子叠加,然后将叠加后的成像算子作用在波数域模拟地震记录上,即可得到波数域成像结果,进而将波数域成像结果反变换回深度域,得到最终的模拟成像结果。整个过程可表述为
| $ \begin{array}{l}R\left(\boldsymbol{r}\right)=\sum {R}_{i}\left(\boldsymbol{r}\right)=\sum \left[V\left(\boldsymbol{r}\right){D}_{i}\left(\boldsymbol{r}\right)\right]\\ \;\;\;\;\;\;=\left[\sum {D}_{i}\left(\boldsymbol{r}\right)\right]V\left(\boldsymbol{r}\right)\end{array} $ | (13) |
式中:
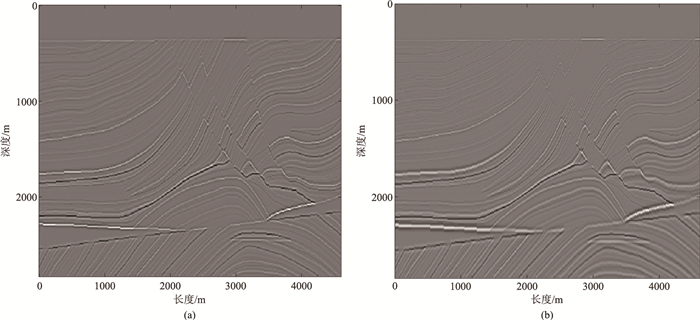
按照本文提出的方法,采用主频为30 Hz的雷克子波,地面放30炮,共230道接收,以道间距20 m进行计算,选用(100 m,2840 m)、(2310 m,2840 m)和(2310 m,2840 m)三点的成像算子叠加。得到照明补偿后的模拟成像结果(图 9b)。与照明补偿前模拟成像(图 9a)结果对比,两种方法都可以较为准确地刻画地下构造形态,只有在一些细微的地方存在差异。
|
图 9 照明补偿前(a)、后(b)的模拟成像结果 |
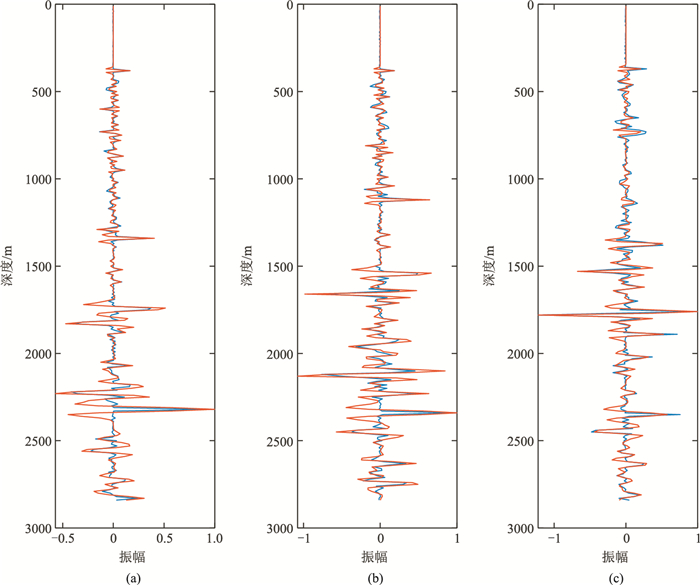
抽取单一成像算子模拟成像结果第80道与深度域非稳态褶积波形对比(图 10a),同时抽取照明补偿后的变“子波”模拟成像结果第80道波形与深度域非稳态褶积波形对比(图 10b),可见改进后的模拟成像方法得到的成像振幅更接近理论振幅,成像结果中也包含了更多的细节,该方法不论在浅层还是深层成像振幅都与理论振幅吻合较好,相比单一成像算子模拟成像效果具有显著提升。
|
图 10 使用单一算子(a)、叠加算子(b)的Marmousi模型模拟成像结果波形与非稳态褶积结果对比 |
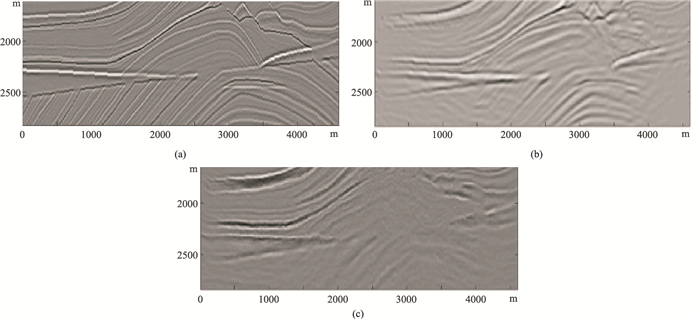
在相同观测参数下,采用不同方法分别得到Marmousi模型成像结果(图 11)。逆时偏移成像结果中振幅随着深度增加显著降低,导致深层一些构造无法显示,Kirchhoff偏移在复杂构造或深部地区成像结果较差,对比发现改进的模拟成像方法能真实地反映地下构造,为不同方法成像结果的评判提供参考。
|
图 11 不同成像方法结果对比 (a)改进的模拟成像方法(b)逆时偏移(c)Kirchhoff偏移 |
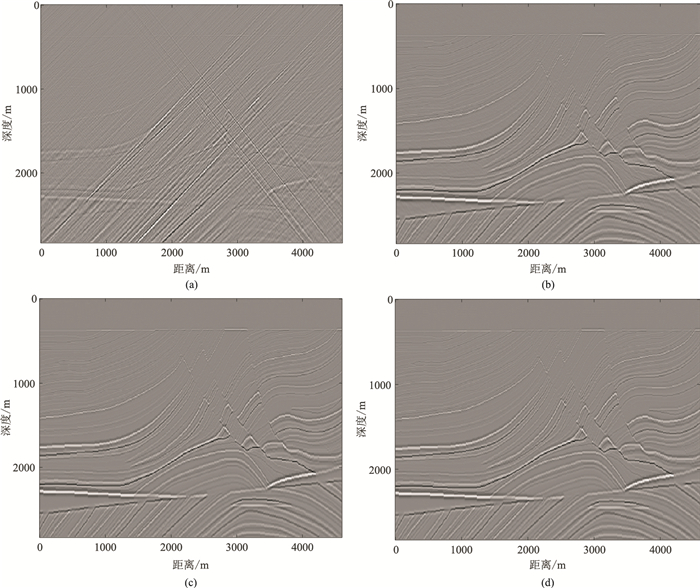
由于成像算子的构建离不开射线路径计算,所以,模拟成像结果的好坏可以间接反映观测系统的选择是否恰当。图 12为地面230道接收、道间距为20 m、炮数不同时的模拟成像结果。
|
图 12 Marmousi模型不同炮点距时的模拟成像结果 (a)10炮;(b)20炮;(c)30炮;(d)40炮 |
对比图 12,地面启爆30~40炮,即炮间距为100~150 m时模拟成像结果良好,模拟成像结果可作为传统成像结果的参考,同时对于现场观测系统的优化具有指导意义。
4 结束语本文改进了一种基于照明补偿的变“子波”模拟叠前深度偏移成像方法。该方法可在已知速度模型的基础下,根据观测系统的布置,直接得到深度域模拟成像结果;相较于传统方式大大节省计算时间,计算效率高;同时,它在成像精度、振幅保持及子波形态方面有明显优势,能精细地刻画地下构造形态,成像结果波形符合实际情况。因此,该方法对于指导观测系统的优化、成像结果评判及储层预测等方面,均具有重要意义。
| [1] |
MICIKEVICIUS P. 3D finite difference computation on GPUs using CUDA[C]. Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units, Association for Computing Machinery, Washington D C, 2009, 79-84.
|
| [2] |
李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策[J]. 地球物理学报, 2010, 53(12): 2938-2943. LI Bo, LIU Hongwei, LIU Guofeng, et al. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU[J]. Chinese Journal of Geophysics, 2010, 53(12): 2938-2943. DOI:10.3969/j.issn.0001-5733.2010.12.017 |
| [3] |
刘守伟, 王华忠, 陈生昌, 等. 三维逆时偏移GPU/CPU机群实现方案研究[J]. 地球物理学报, 2013, 56(10): 3487-3496. LIU Shouwei, WANG Huazhong, CHEN Shengchang, et al. Implementation strategy of 3D reverse time migration on GPU/CPU clusters[J]. Chinese Journal of Geophysics, 2013, 56(10): 3487-3496. DOI:10.6038/cjg20131023 |
| [4] |
FOLTINEK D, EATON D, MAHOVSKY J, et al. Industrial scale reverse time migration on GPU hardware[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2789-2793.
|
| [5] |
GELIUS L J and STAMNES J J. Diffraction Tomagraphy imaging: Potentials and problems//Scattering in Volumes and Surfaces[M]. Elsevier, Amsterdam, 1990.
|
| [6] |
GELIUS L J, JOHANSEN I, SPONHEIM N, et al. A generalized diffraction tomography algorithm[J]. The Journal of the Acoustical Society of America, 1991, 89(2): 523-528. DOI:10.1121/1.400376 |
| [7] |
GELIUS L J, LECOMTE I, TABTI H. Analysis of the resolution function in seismic prestack depth imaging[J]. Geophysical Prospecting, 2002, 50(5): 505-515. DOI:10.1046/j.1365-2478.2002.00331.x |
| [8] |
HAMRAN S E, LECOMTE I. Local plane-wavenumber diffraction tomography in heterogeneous back-grounds, Part I: Theory[J]. Journal of Seismic Exploration, 1993, 2(2): 133-146. |
| [9] |
SETHIAN J A. A fast marching level set method for monotonically advancing fronts[J]. Proceedings of the National Academy of Sciences, 1996, 93(4): 1591-1595. DOI:10.1073/pnas.93.4.1591 |
| [10] |
张雪建, 梁锋, 王桂玲. 深度域合成地震记录的制作方法研究[J]. 石油地球物理勘探, 2000, 35(3): 377-380, 385. ZHANG Xuejian, LIANG Feng, WANG Guiling. A method for synthesizing seismorgram in depth domain[J]. Oil Geophysical Prospecting, 2000, 35(3): 377-380, 385. DOI:10.3321/j.issn:1000-7210.2000.03.015 |
| [11] |
LECOMTE I, GELIUS L J. Have a look at the resolution of prestack migration for any model, survey and wavefields[C]. SEG Technical Program Expanded Abstrcats, 1998, 17: 1112-1115.
|
| [12] |
LECOMTE I, HAMRAN S E, TABTI H, et al. New insights in migration through analogies between generalized diffraction tomography and synthetic aperture radar[C]. SEG Technical Program Expanded Abstracts, 2001, 20: 1111-1114.
|
| [13] |
LECOMTE I. Resolution and illumination analyses in PSDM: A ray-based approach[J]. The Leading Edge, 2008, 27(5): 650-663. DOI:10.1190/1.2919584 |
| [14] |
LECOMTE I, HAMRAN S E, GELIUS L J. Improving Lirchhoff migration with repeated local planewave imaging?A SAR-inspired signal-processing approach in prestack depth imaging[J]. Geophysical Prospecting, 2005, 53(6): 767-785. DOI:10.1111/j.1365-2478.2005.00501.x |
| [15] |
张金陵, 徐美茹, 叶月明, 等. 利用点扩散函数的深度域地震记录合成方法[J]. 石油地球物理勘探, 2019, 54(4): 875-881. ZHANG Jinling, XU Meiru, YE Yueming, et al. Seismogram synthetizing in the depth-domain with point spread function[J]. Oil Geophysical Prospecting, 2019, 54(4): 875-881. |
| [16] |
吴涵, 廉西猛, 孙成禹, 等. 叠前深度偏移地震记录直接模拟方法[J]. 石油地球物理勘探, 2020, 55(4): 747-753. WU Han, LIAN Ximeng, SUN Chengyu, et al. Research on direct simulation to seismic record of prestack depth migration[J]. Oil Geophysical Prospecting, 2020, 55(4): 747-753. |
| [17] |
段伟国, 毛伟建, 张庆臣, 等. 基于密度扰动的点扩散函数计算与三维深度域模拟成像[J]. 地球物理学报, 2022, 65(4): 1402-1415. DUAN Weiguo, MAO Weijian, ZHANG Qingchen, et al. Computation of denisty perturbation based point spread function and simulation of migration image in 3D depth domain[J]. Chinese Journal of Geophysics, 2022, 65(4): 1402-1415. |
| [18] |
何惺华. 深度域地震资料若干问题初探[J]. 石油物探, 2004, 43(4): 353-358. HE Xinghua. Discussion on seismic data of depth domain[J]. Geophysical Prospecting for Petroleum, 2004, 43(4): 353-358. DOI:10.3969/j.issn.1000-1441.2004.04.011 |
| [19] |
林伯香, 胡中平, 薛诗桂. 利用变换深度域速度函数制作深度域合成地震记录[J]. 石油地球物理勘探, 2006, 41(6): 640-643. LIN Boxiang, HU Zhongping, XUE Shigui. Using velocity function in transformed depth domain to make synthetic seismograph in depth domain[J]. Oil Geophysical Prospecting, 2006, 41(6): 640-643. |
| [20] |
樊中海, 胡渤, 宋吉杰, 等. 地震反演储层描述精度影响因素分析[J]. 石油地球物理勘探, 2022, 57(2): 441-451. FAN Zhonghai, HU Bo, SONG Jijie, et al. Analysis of influencing factors in reservoir description accuracy by seismic inversion[J]. Oil Geophysical Prospecting, 2022, 57(2): 441-451. |
| [21] |
邵广周, 独婷, 吴华. 基于自适应震源子波提取与校正的瑞利波波形反演[J]. 石油地球物理勘探, 2022, 57(4): 838-846. SHAO Guangzhou, DU Ting, WU Hua. Waveform inversion based on adaptive source wavelet extraction and correction for Rayleigh waves[J]. Oil Geophysical Prospecting, 2022, 57(4): 838-846. |
| [22] |
STAMNES J J. Waves in Focal Regions: Propagation, Diffraction and Focusing of Light, Sound and Water Waves[M]. Routledge, New York, 1986.
|
| [23] |
BEYLKIN G, ORISTAGLIO M, MILLER D. Spatial resolution of migration algorithms[C]. Proceedings of the 14th International Symposium on Acoustical Image, 1985, 155-167.
|
| [24] |
BEYLKIN G. Imaging of discontinuities in the inverse scattering problem by inversion of a causal generalized Radon transform[J]. Journal of Mathematical Physics, 1985, 26(1): 99-108. |



 孙成禹,山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院地球物理系,266580。Email:
孙成禹,山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院地球物理系,266580。Email: