2. 大地测量与地球动力学国家重点实验室, 湖北武汉 430077;
3. 中国科学院大学, 北京 100049
2. State Key Laboratory of Geodesy and Earth s Dynamics, Wuhan, Hubei 430077, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
近年来,基于双程波的逆时偏移成像技术突破了成像角度的限制,对陡倾构造成像具有显著优势[1-2]。但地震波在传播过程中,由于地下介质通常具有黏滞性,导致其能量衰减及相位畸变,尤其当勘探目标区域存在气云等强衰减构造时,对其做偏移成像会导致分辨率降低和照明不足[3]。为此,学者们进行了大量的研究,模拟地震波在地下介质传播过程中的衰减效应。
起初,对黏性逆时偏移的研究是基于近似常Q模型[4]波动方程展开的,通过单个或多个力学元件的串、并联或叠加(如标准线性体、Maxwell体等)描述地下介质的衰减效应[5-8],但基于该模型推导的波动方程中包含记忆变量,需较多表征参数,这些参数还需要计算优化选择,额外增加计算量[9]。此外,在这类波动方程中,振幅衰减与相位频散相耦合,在逆时偏移成像过程中不能准确地校正相位,会导致深部目标层成像的位置误差。基于常Q模型[4]推导的波动方程中含有分数阶时间导数,对波动方程计算当前时刻波场值时,需依赖该时刻以前所有时刻的波场,因此其计算成本高、效率低且内存消耗巨大。
Chen等[10]采用分数阶拉普拉斯算子代替分数阶时间导数,将时间导数转换为空间导数,运用伪谱法在波数域求解黏声波动方程,提高了计算效率。Treeby等[11]基于幂律衰减模型,推导了解耦的分数阶拉普拉斯算子黏滞声波波动方程,实现了振幅衰减与相位频散的分离。刘文卿等[12]基于GPU/CPU协同系统,通过GPU实现波场逆时外推,并采用随机速度边界提高算法的并行性,解决了逆时偏移中大规模存储的I/O问题。Zhu等[13]基于常Q频散关系,推导了含解耦的分数阶拉普拉斯算子时域黏声波动方程,在波传播过程中具有近似常Q的衰减和频散特征,实现了振幅衰减与相位频散的分离,在逆时偏移过程中对能量补偿、相位校正十分便利,只需在波场外推过程中,反转振幅衰减算子的符号且保持相位频散算子符号不变,就可较准确地校正由地下介质黏滞性引起的振幅衰减与相位频散效应,并基于此方程实现了Q补偿逆时偏移(Q-compensated reverse-time migration,Q-RTM)[14]。
然而,采用Q-RTM在对地震波振幅进行衰减补偿时,也会增强数据中的高频噪声,在波场外推过程中出现数值不稳定现象。此前,高频噪声通常采用低通Tukey滤波器压制[14-15]。但该方法是时不变的,不能适应在空间变化的Q值和深度。
Treeby[16]提出一种频域时变Tukey滤波器以稳定衰减补偿过程,但采用低通滤波法会损失地震数据中部分有用高频信号。Wang[17]通过引入稳定因子,提出一种反Q偏移方法稳定补偿过程,并认为某深度处的地震波吸收衰减效应应是从地表到当前深度吸收衰减的累积;Wang等[18]在此基础上提出一种新的Q补偿逆时偏移自适应稳定方法,并通过推导分数阶拉普拉斯算子黏滞声波波动方程及其补偿方程和衰减方程的波数域格林函数,从理论上解释了波场外推在高频端不稳定的原因。与传统基于低通滤波的方法相比,该方法具有更强的时间不一致性和Q依赖性,提高了衰减补偿稳定性和抗噪性。陈汉明等[19]应用最小二乘反演理论,推导了分数阶拉普拉斯算子黏滞声波方程对应的Born正演模拟算子和伴随方程,利用反演思路补偿地震波的吸收衰减,解决了补偿不稳定问题。Chen等[20]提出一种隐式稳定策略,将时变滤波器隐式地纳入振幅增强波场外推步骤,并在频谱中加入一个稳定因子,避免了Q-RTM中任何显式的滤波操作,且该方法不增加额外计算量。
对于逆时偏移成像产生的低频噪声,目前主要采用如角度衰减因子成像条件[21-22]、对成像结果进行滤波(最小二乘滤波器、拉普拉斯滤波等)[23-24]、波场方向分解[25-26]等方法压制。杜启振等[27]总结了各类成像方法,认为采用波场分解的成像方法在复杂构造区能更好地消除低频噪声。Liu等[25-26]提出上下行波场分解的方法,构造新的偏移成像条件,实现不同向的震源波场和检波点波场的互相关成像,从而消除低频噪声。Fei等[28]指出速度模型中存在强速度梯度或反射界面时,震源下行波场和检波点上行波场在逆时偏移成像过程中可能产生假象,成像时需略去这两项。
此外,常规波场分解是在f-k域实现,这需将震源波场和检波点波场进行存储,然后再进行时空域的傅里叶变换,因此会产生巨大的计算量和I/O量。针对该问题,胡江涛等[29]提出一种基于声波波动方程的解析时间波场外推方法,并将其运用于VSP(Vertical Seismic Profile)数据的逆时偏移成像。该方法在时间外推过程中实现了波传播方向的显式分解,避免了巨大的I/O量和计算量,实现了低频噪声与有效信号的分离,并能有效地消除图像中由复杂介质引起的假像。Zhou等[30]采用一步法波场外推实现了Q补偿逆时偏移波场外推,并基于该方法波场为解析信号的性质实现了波场的分离,运用Q补偿逆时偏移和分解的波场成像极大程度提高了偏移成像的质量,但该方法采用的是传统低通滤波器稳定化衰减补偿过程,且一步法外推的计算速度较慢。
目前,Q-RTM主要采用成像后滤波的方式压制低频噪声,但该方法会改变成像剖面中同相轴振幅大小和波数成分。基于波场分解的成像方法能更有效地压制双程波逆时偏移成像中的低频噪声和速度模型中存在较强速度梯度时产生的假象。
综上所述,本文采用基于常Q模型解耦的分数阶拉普拉斯算子黏声波动方程对震源波场和检波点波场进行外推,避免由于时间历史记忆变量而需存储每个时刻的波场,实现衰减算子和频散算子的分离,可通过反转衰减算子符号和保持频散算子符号不变达到补偿能量和校正频散的目的,并基于该方程实现Q补偿逆时偏移算法。
采用自适应稳定因子方案稳定化衰减补偿过程中数值不稳定问题。对于逆时偏移产生的低频噪声和假象,采用解析时间波场外推方法,在时间外推过程中实现波传播方向的显式分解,选取分解后的震源下行波场和检波点上行波场进行互相关成像,减少由复杂介质及强速度梯度引起的偏移成像中的低频噪声和假象。
1 方法原理 1.1 常Q模型应力—应变关系在一维线性非弹性介质中,应力与应变的关系[31]为
| $ \sigma ={\psi }_{1-2\gamma }\left(t\right)\mathrm{*}\frac{\mathrm{d}\varepsilon }{\mathrm{d}t}=\frac{{M}_{0}}{{t}_{0}^{-2\gamma }}\frac{{\partial }^{2\gamma }\varepsilon }{\partial {t}^{2\gamma }} $ | (1) |
式中:
弛豫函数定义[9]为
| $ {\psi }_{1-2\gamma }=\frac{{M}_{0}}{\varGamma (1-2\gamma )}{\left(\frac{t}{{t}_{0}}\right)}^{-2\gamma }H\left(t\right) $ | (2) |
式中:
对于均匀声波介质,一阶线性动量守恒方程为
| $ \frac{\partial }{\partial t}\boldsymbol{v}=\frac{1}{{\rho }_{0}}\nabla \sigma $ | (3) |
应变速度方程为
| $ \frac{\partial }{\partial t}\varepsilon =\nabla \cdot \boldsymbol{v} $ | (4) |
两式中:
结合式(3),可得时间分数阶波动方程
| $ \frac{{\partial }^{2-2\gamma }\sigma }{\partial {t}^{2-2\gamma }}={c}^{2}{\omega }_{0}^{-2\gamma }{\nabla }^{2}\sigma $ | (5) |
式中:
将平面波解
| $ \frac{{\omega }^{2}}{{c}^{2}}={\left(\mathrm{i}\right)}^{2\gamma }{\omega }_{0}^{-2\gamma }{\omega }^{2\gamma }{\boldsymbol{k}}^{2} $ | (6) |
式中:
由
| $ \begin{array}{l}\frac{{\omega }^{2}}{{c}^{2}}={\omega }_{0}^{-2\gamma }{\omega }^{2\gamma }{\boldsymbol{k}}^{2}\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{\pi }\gamma \right)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{i}{\omega }_{0}^{-2\gamma }{\omega }^{2\gamma }{\boldsymbol{k}}^{2}\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{\pi }\gamma \right)\end{array} $ | (7) |
分数阶拉普拉斯算子的傅里叶变换为
| $ (-{\nabla }^{2}{)}^{\alpha /2}\varphi (r, t)\stackrel{\mathrm{F}}{\to }{k}^{\alpha }\varPhi (k, \omega ) $ | (8) |
式中:
对式(7)进行时空二维反傅里叶变换,可得
| $ \frac{1}{{c}^{2}}\frac{{\partial }^{2}\sigma }{\partial {t}^{2}}=\eta (-{\nabla }^{2}{)}^{\gamma +1}+\tau \frac{\partial }{\partial t}(-{\nabla }^{2}{)}^{\gamma +1/2}\sigma $ | (9) |
式中:
逆时偏移有三个主要步骤:①震源波场外推;②检波点波场外推;③采用适当的成像条件对外推的震源和检波点波场进行成像,如互相关成像条件[32]
| $ I\left(x\right)={\int }_{0}^{{T}_{\max}}S(t, x)R(t, x)\mathrm{d}t $ | (10) |
式中:
Zhu等[14]基于式(9)实现Q补偿逆时偏移,并给出统一的震源及检波点波场外推的黏声波动方程
| $ \frac{1}{{c}_{0}^{2}}\frac{{\partial }^{2}p}{\partial {t}^{2}}={\nabla }^{2}p+{\beta }_{1}\left\{\eta \boldsymbol{L}-{\nabla }^{2}\right\}p+{\beta }_{2}\tau \frac{\partial }{\partial t}\boldsymbol{H}p $ | (11) |
式中:
| $ \frac{1}{{c}_{0}^{2}}\frac{{\partial }^{2}p}{\partial {t}^{2}}={\nabla }^{2}p+\left\{\eta \boldsymbol{L}-{\nabla }^{2}\right\}p-\tau \frac{\partial }{\partial t}\boldsymbol{H}p $ | (12) |
本文通过式(12)对震源波场和检波点波场进行外推,校正地下介质对地震波造成的能量衰减和频散效应,并采用规则网格有限差分法计算时间导数、伪谱法计算拉普拉斯算子。
1.4 自适应稳定因子Wang等[18]提出一种新的Q补偿逆时偏移自适应稳定补偿策略,推导过程如下。
Q-RTM的衰减时间传播算子可表示为
| $ {\varGamma }_{\mathrm{a}\mathrm{t}\mathrm{t}}\left(\boldsymbol{k}, t\right)=\frac{\mathrm{s}\mathrm{i}\mathrm{n}\left[{\xi }_{1}\left(\boldsymbol{k}\right)t\right]{\mathrm{e}}^{-{\xi }_{2}\left(\boldsymbol{k}\right)t}}{{\xi }_{1}\left(\boldsymbol{k}\right)} $ | (13) |
补偿时间传播算子可表示为
| $ {\varGamma }_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}}\left(\boldsymbol{k}, t\right)=\frac{\mathrm{s}\mathrm{i}\mathrm{n}\left[{\xi }_{1}\left(\boldsymbol{k}\right)t\right]{\mathrm{e}}^{{\xi }_{2}\left(\boldsymbol{k}\right)t}}{{\xi }_{1}\left(\boldsymbol{k}\right)} $ | (14) |
上两式中:
根据上两式,振幅衰减算子定义为
| $ \beta (\boldsymbol{k}, t)={\mathrm{e}}^{-{\xi }_{2}\left(\boldsymbol{k}\right)t}={\mathrm{e}}^{\frac{1}{2}{c}_{0}^{2\gamma -1}{\omega }_{0}^{-2\gamma }\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{\pi }\gamma \right){\left|\boldsymbol{k}\right|}^{2\gamma +1}t} $ | (15) |
振幅补偿算子定义为
| $ \varLambda (\boldsymbol{k}, t)={\beta }^{-1}(\boldsymbol{k}, t)={\mathrm{e}}^{{\xi }_{2}\left(\boldsymbol{k}\right)t} $ | (16) |
式(16)由于指数项的存在,它在时间上是发散的,因此定义如下稳定化的振幅补偿算子
| $ \varLambda (\boldsymbol{k}, t)=\frac{\beta (\boldsymbol{k}, t)}{{\beta }^{2}(\boldsymbol{k}, t)+{\sigma }^{2}}=\frac{{\mathrm{e}}^{{\xi }_{2}\left(\boldsymbol{k}\right)t}}{1+{\sigma }^{2}{\mathrm{e}}^{2{\xi }_{2}\left(\boldsymbol{k}\right)t}} $ | (17) |
式中
由于振幅补偿算子已体现在波场外推过程中,则稳定因子可表示为
| $ S(\boldsymbol{k}, t)=\frac{1}{1+{\sigma }^{2}{\mathrm{e}}^{2{\xi }_{2}\left(\boldsymbol{k}\right)t}} $ | (18) |
考虑当前时刻的衰减效应为零时刻到当前时刻衰减效应的累积,则每个时间步长稳定因子系数定义为
| $ \prod\limits _{n=1}^{m}s(\boldsymbol{k}, n\Delta t)=S(\boldsymbol{k}, m\mathrm{\Delta }t) $ | (19) |
第n个时间步稳定因子系数为
| $ \begin{array}{l}s(\boldsymbol{k}, l\mathrm{\Delta }t)=\frac{S(\boldsymbol{k}, n\mathrm{\Delta }t)}{S\left[\boldsymbol{k}, (n-1)\mathrm{\Delta }t\right]}=\frac{1+{\sigma }^{2}{\mathrm{e}}^{2{\xi }_{2}\left(\boldsymbol{k}\right)(n-1)\mathrm{\Delta }t}}{1+{\sigma }^{2}{\mathrm{e}}^{2{\xi }_{2}\left(\boldsymbol{k}\right)n\mathrm{\Delta }t}}\\ \;\;\;\;\;\;\;n=\mathrm{2, 3}, \dots , m\end{array} $ | (20) |
由于采用双程波动方程,震源波场和检波点波场中同时包含上行波和下行波,运用成像条件使波路径上不必要的震源波场和检波点波场(震源上行波场与检波点上行波场,震源下行波场与检波点下行波场)互相关会在成像结果上产生低频噪声。此外,Fei等[28]指出当速度模型精度不高,存在较强速度梯度时,在特殊地质构造区,震源上行波场和检波点下行波场成像时可能会产生假象。
为避免上述情况,本文采用的成像条件为
| $ I\left(x\right)={\int }_{0}^{{T}_{\max}}{S}_{d}(t, x){R}_{u}(t, x)\mathrm{d}t $ | (21) |
式中:下标u(upgoing)表示上行波;d(downgoing)表示下行波,如
在f-k域通过简单的计算很容易分离上行波与下行波分量[33]
| $ \left\{\begin{array}{l}{S}_{\mathrm{d}}(\omega , {k}_{z})=\left\{\begin{array}{l}S(\omega , {k}_{z})\;\;\;\;\;\;\omega {k}_{z}\ge 0\;\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\omega {k}_{z} < 0\;\;\;\;\;\;\end{array}\right.\\ {S}_{\mathrm{u}}(\omega , {k}_{z})=\left\{\begin{array}{l}S(\omega , {k}_{z})\;\;\;\omega {k}_{z} < 0\;\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\omega {k}_{z}\ge 0\;\;\;\;\;\;\end{array}\right.\end{array}\right. $ | (22) |
式中:
Liu等[26]通过固定波数符号,将震源和检波点波场分为波数大于零和小于零的四个分量,使波数符号相反的震源波场与检波点波场相乘,再将相乘后的两个分量相加,最后使用互相关成像条件成像(如震源波场波数符号为正,则与之相乘的检波点波场波数符号为负。若频率为正,则分别为震源上行波场及检波点下行波场;若频率为负,则分别为震源下行波场和检波点上行波场),实现传播方向相反的震源和检波点波场的互相关成像。但该方法中上行波场与下行波场互相耦合,不能将波场进行显式地分解。
为了实现波场的显式分解,需尽量使用一个变量(频率或波数)的符号来确定波场传播的方向。由于在时间域波场外推中,时间步长上波数信息较易获取,若能获取一个其频谱仅为正或负的波场,则波场的方向分解就可通过波数的正、负号确定。为此,胡江涛等[29]提出一种解析时间波场外推方法。解析波场频谱只包含正频率,可仅依靠空间波数的符号实现波场方向的分解。解析波场包括实部和虚部两部分,实部由信号本身构成,虚部由经希尔伯特变换后的原信号构成。
震源的时间解析波场可表示为
| $ \overline{S}(t, z)=S(t, z)+\mathrm{i}{S}_{\mathrm{H}}(t, z) $ | (23) |
式中;
| $ \overline{R}(t, z)=R(t, z)+\mathrm{i}{R}_{\mathrm{H}}(t, z) $ | (24) |
式中:
基于式(22)和解析波场仅包含正频率的性质,只需根据波数的符号就可达到对波场进行方向分解的目的。震源的上、下行波场表示为
| $ \left\{\begin{array}{l}{S}_{\mathrm{u}}(x, t)=\mathrm{R}\mathrm{e}\left\{{\mathrm{F}}^{-1}\left[{\tilde{S}}^{+}(x, {k}_{z})\right]\right\}\\ {\tilde{S}}^{+}(x, {k}_{z})=\left\{\begin{array}{l}\tilde{S}(x, {k}_{z})\;\;\;\;\;\;\;\;\;\;\;\;{k}_{z}\ge 0\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{k}_{z} < 0\;\;\end{array}\right.\\ {S}_{\mathrm{d}}(x, t)=\mathrm{R}\mathrm{e}\left\{{\mathrm{F}}^{-1}\left[{\tilde{S}}^{-}(x, {k}_{z})\right]\right\}\\ {\tilde{S}}^{-}(x, {k}_{z})=\left\{\begin{array}{l}\tilde{S}(x, {k}_{z})\;\;\;\;\;\;\;\;\;\;\;\;{k}_{z} < 0\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{ }\;\;\;{k}_{z}\ge 0\;\;\end{array}\right.\end{array}\right. $ | (25) |
式中:Re表示实部;
| $ \left\{\begin{array}{l}{R}_{\mathrm{u}}(x, t)=\mathrm{R}\mathrm{e}\left\{{\mathrm{F}}^{-1}\left[{\tilde{R}}^{+}(x, {k}_{z})\right]\right\}\\ {\tilde{R}}^{+}(x, {k}_{z})=\left\{\begin{array}{l}\tilde{R}(x, {k}_{z})\;\;\;\;\;\;\;\;\;\;\;{k}_{z}\ge 0\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{ }\;{k}_{z} < 0\;\;\end{array}\right.\\ {R}_{\mathrm{d}}(x, t)=\mathrm{R}\mathrm{e}\left\{{\mathrm{F}}^{-1}\left[{\tilde{R}}^{-}(x, {k}_{z})\right]\right\}\\ {\tilde{R}}^{-}(x, {k}_{z})=\left\{\begin{array}{l}\tilde{R}(x, {k}_{z})\;\;\;\;\;\;\;\;\;\;\;\mathrm{ }\;{k}_{z} < 0\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{k}_{z}\ge 0\;\;\end{array}\right.\end{array}\right. $ | (26) |
式中
值得注意的是,由于采用解析波场外推分离上下行波场,与传统逆时偏移成像方法相比多了震源波场外推、检波点波场外推及时间切片上的波场傅里叶变换,因此该方法计算时间会高于传统Q补偿逆时偏移成像。实验表明,本文方法的计算时间约为采用拉普拉斯滤波Q-RTM方法的1.3倍。但与传统的波场分解相比,该方法规避了I/O量过大的弊端,解决了波场存储问题,且提高了计算效率。
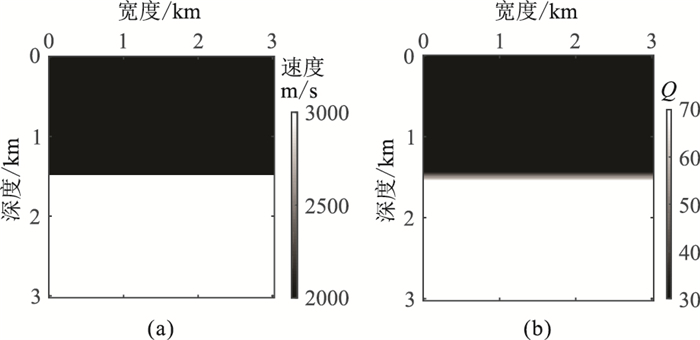
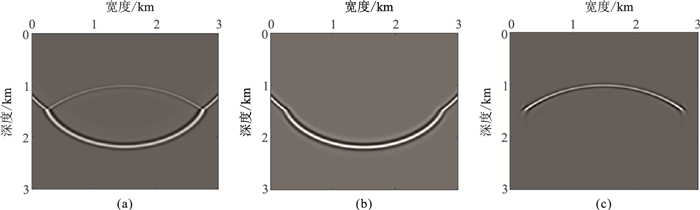
2 数值算例 2.1 两层模型为了测试本文方法的有效性,首先采用水平层状模型对解析波场分离上下行波的有效性进行测试。图 1a所示速度模型中,第一、第二层层速度分别为2000、3000 m/s,模型网格尺寸为300×300,x和z方向的网格间距为dx=dz=10 m,得到该层状模型对应的Q模型(图 1b)。图 2a为1.0 s时刻未分离的波场快照,用解析波场分解方法得到该时刻经波场分离后的下行波场(图 2b)和上行波场(图 2c)。可见本文方法能有效分离上下行波场。
|
图 1 两水平层速度模型(a)及其Q模型(b) |
|
图 2 1.0 s时刻波场快照 (a)原始波场;(b)下行波场;(c)上行波场 |
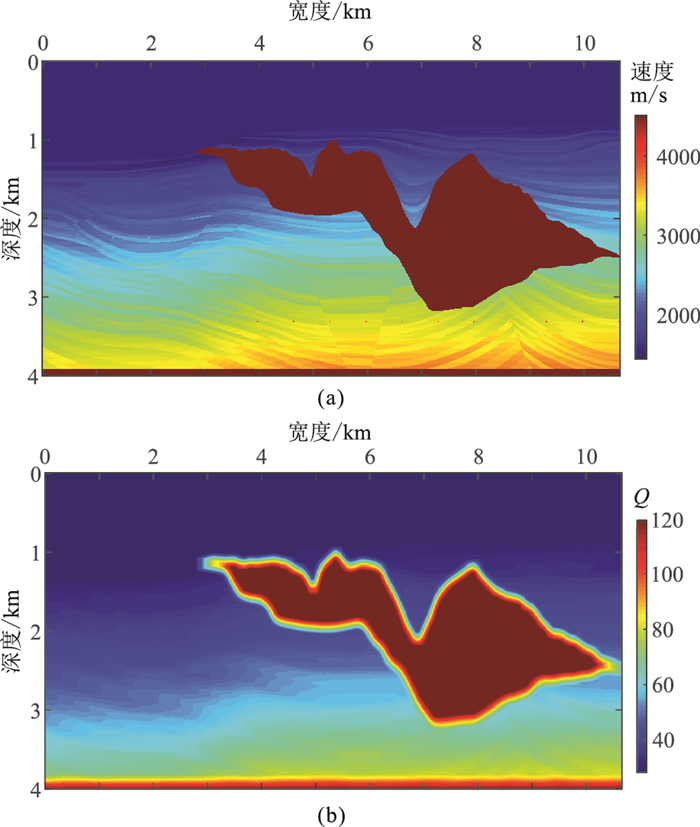
为验证采用的新成像方法与Q补偿逆时偏移对振幅补偿和相位校正的有效性及对复杂模型的适应性,采用抽稀后的Sigsbee模型做数值模拟测试。速度模型(图 3a)及对应的Q模型(图 3b,由经验公式得出)的大小为1067×401,网格间距为dx=dz=10 m,时间采样间隔为1 ms,采样点数为4001,震源采用主频为30 Hz的Ricker子波,总共104炮,均匀分布在深度50 m处,炮间距为100 m。
|
图 3 Sigsbee速度模型(a)及其Q模型(b) |
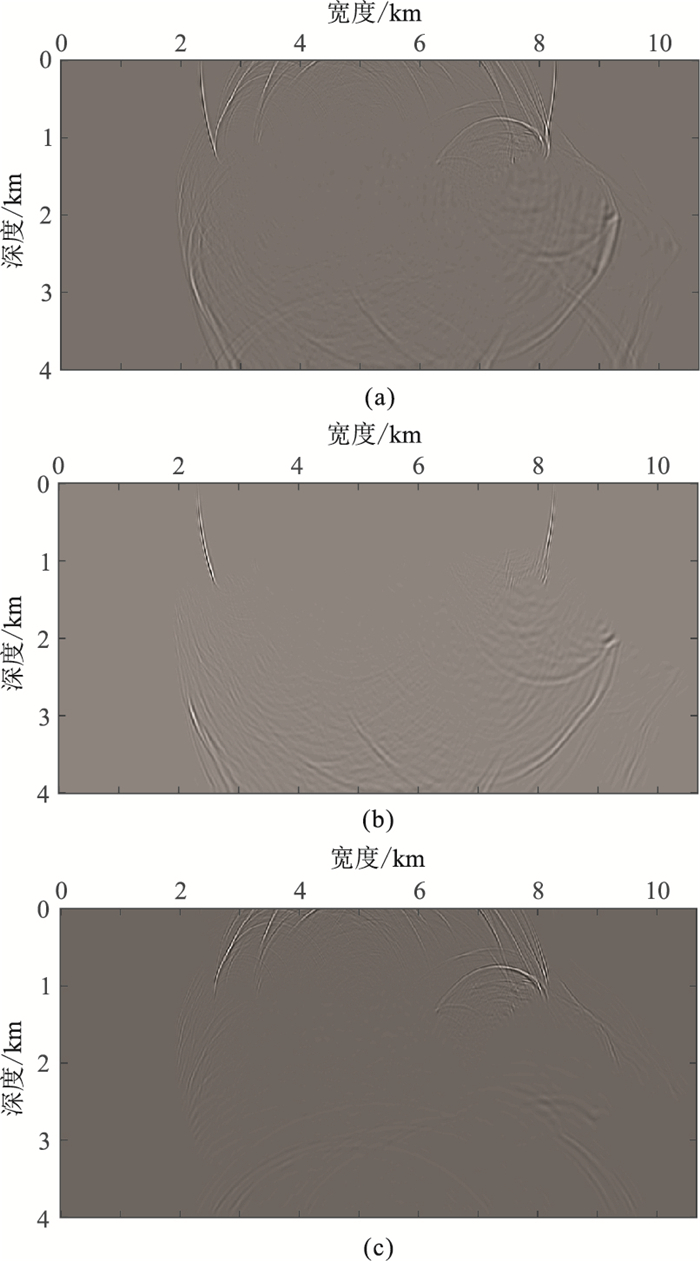
图 4a为2.0 s时刻未分离的波场快照,用解析波场分解方法分别得到该时刻经波场分离后的下行波场(图 4b)和上行波场(图 4c)。
|
图 4 2.0 s时刻波场快照 (a)原始波场;(b)下行波场;(c)上行波场 |
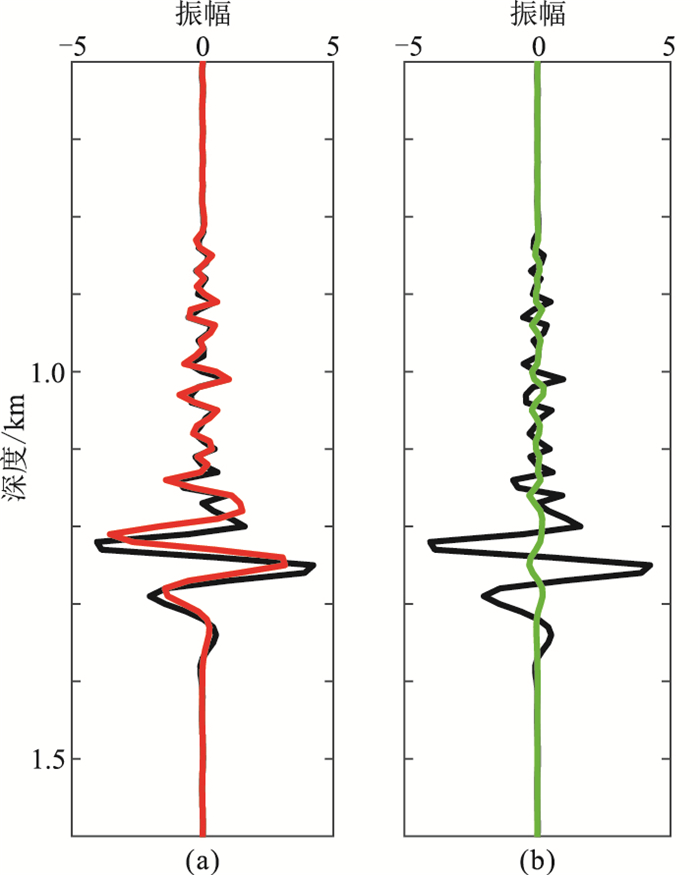
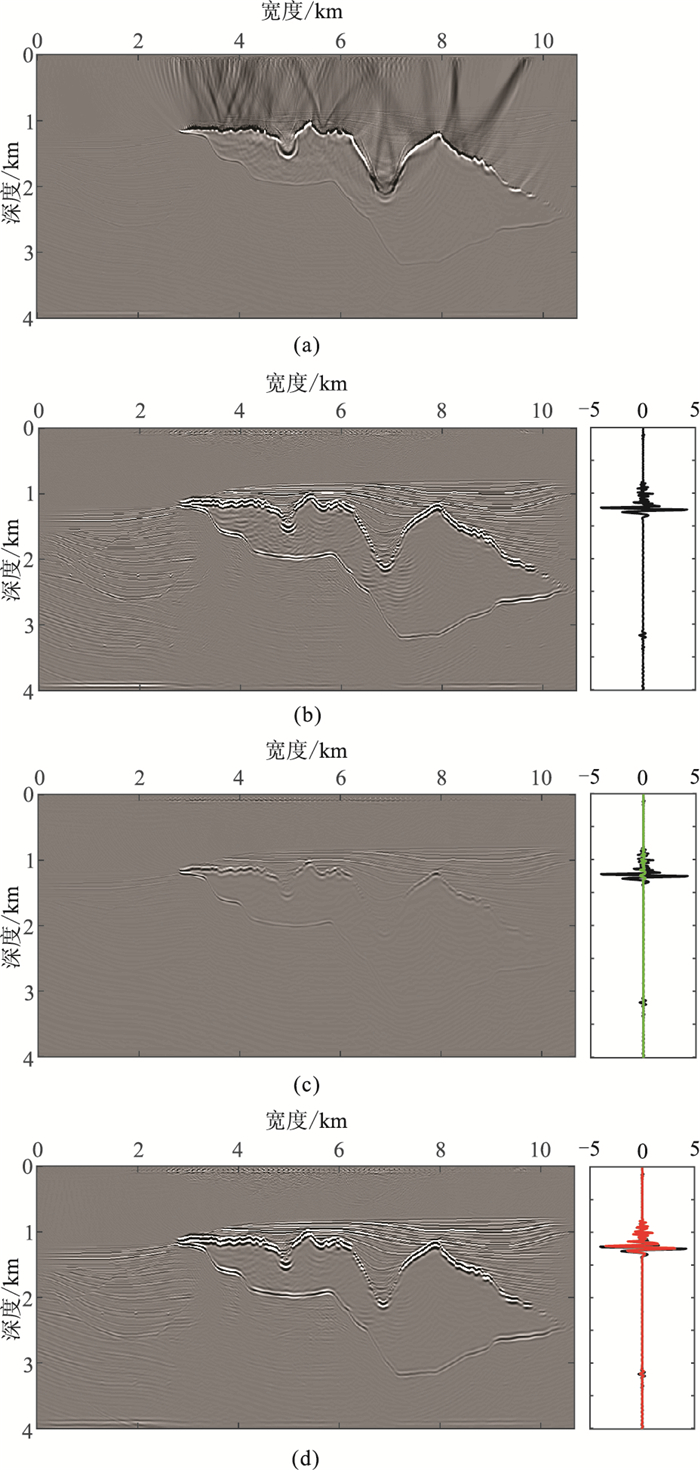
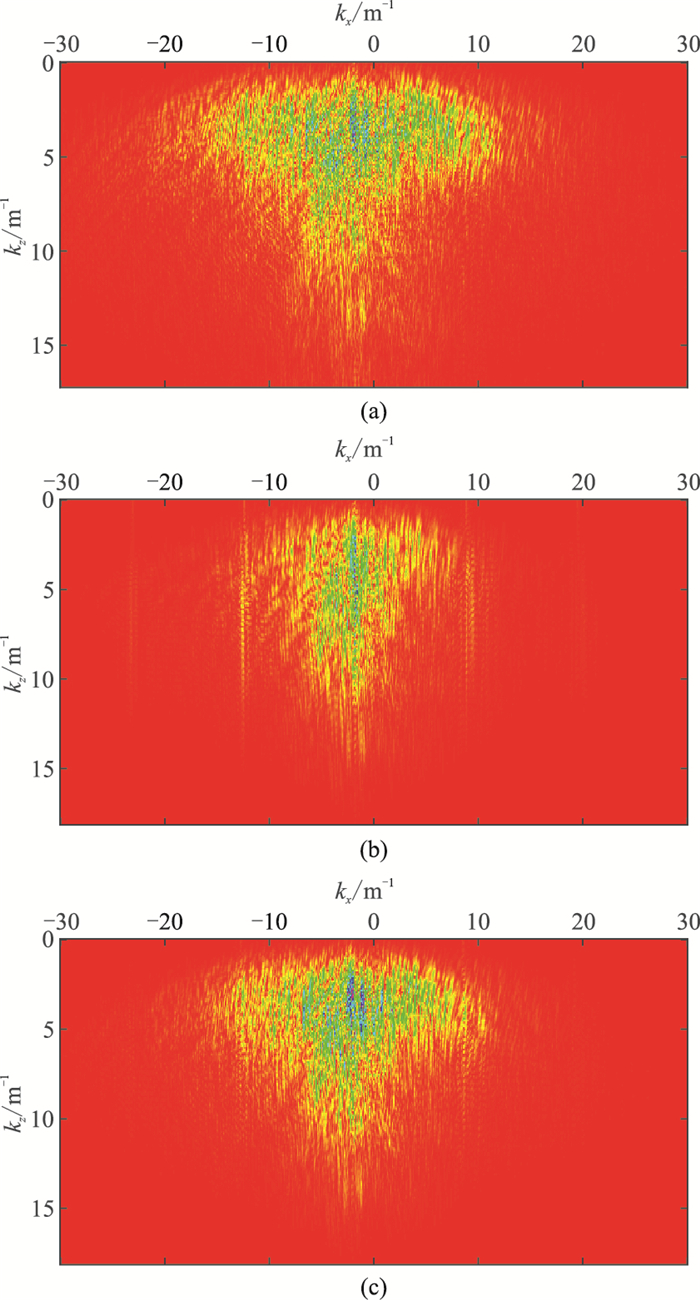
图 5a为未经波场分离的传统声波逆时偏移成像结果,分别得到波场分离后的声波逆时偏移成像结果(图 5b,参考)、波场分离后的未补偿衰减数据逆时偏移成像结果(图 5c)及Q补偿逆时偏移成像结果(图 5d)。图 5b右侧子图为选取水平距离8000 m处作为参考的单道信息(黑色实线),图 5c、图 5d右侧子图则分别为水平距离8000 m处(图 5c虚线位置)相应的单道信息和参考单道信息(黑色实线)。图 6为从上述子图中截取的0.6~1.6 km层段单道信息。其对应的图 5b~图 5d的振幅谱如图 7a~图 7c所示。
|
图 5 偏移成像结果 (a)未波场分离的声波逆时偏移;(b)波场分离后的声波逆时偏移成像;(c)波场分离后的衰减数据偏移;(d)波场分离后的Q补偿黏声逆时偏移 |
|
图 7 不同逆时偏移的振幅谱 (a)声波逆时偏移;(b)衰减数据逆时偏移;(c)Q补偿逆时偏移 |
与图 5b(声波)相比,图 5c(衰减)偏移成像层位及盐丘下边界能量减弱;通过对应的单道信息子图与振幅谱对比,与作为参考的声波数据相比,衰减数据的振幅减小,相位发生畸变,频带变窄。而图 5d(Q补偿逆时偏移)中层位及盐丘下边界更清晰;通过与参考图像(5b)截取的子图及振幅谱对比,可见其损失的振幅与产生的相移都得到一定程度校正,与参考图像吻合度较高,频带得到拓宽。从图 5a与图 5b可知,采用传统的逆时偏移成像方法在成像剖面上存在严重的噪声及假象,降低成像精度,而采用上、下行波场分离成像的偏移结果则避免了这种影响,提高了分辨率。
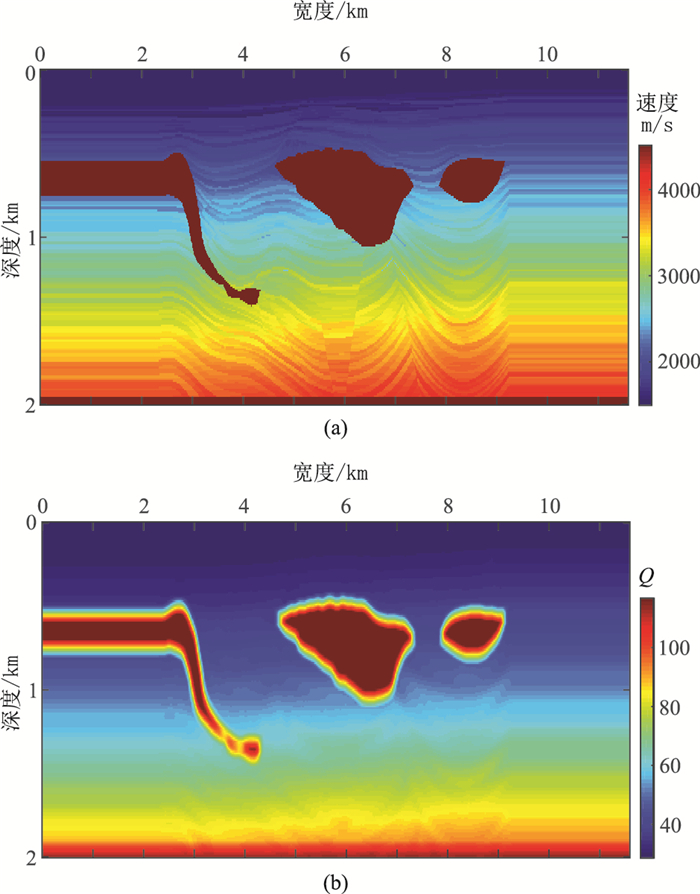
2.3 抽稀的Pluto模型为进一步验证Q补偿逆时偏移对深层能量补偿的效果及与传统的拉普拉斯滤波方法对偏移成像噪声压制的效果,采用抽稀后的Pluto模型进行数值模拟测试。其速度模型(图 8a)及对应的Q模型(图 8b,由经验公式得出)的大小为1160×201,网格间距为dx=dz=10 m,时间采样间隔为0.5 ms,采样点数为4002,震源采用主频为30 Hz的Ricker子波,总共114炮,炮间距为100 m,均匀分布在深度50 m处。
|
图 8 Pluto速度模型(a)及其Q模型(b) |
图 9a为1.0 s时刻未分离的波场快照,用上述方法分别得到该时刻经波场分离后的下行波场(图 9b)和上行波场(图 9c)波场快照。

|
图 9 1.0s时刻波场快照 (a)原始波场;(b)下行波场;(c)上行波场 |
图 10a为未经波场分离的传统声波逆时偏移成像结果,分别得到声波逆时偏移经拉普拉斯滤波后成像结果(图 10c)、Q补偿逆时偏移经拉普拉斯滤波后成像结果(图 10e)、波场分离后的声波逆时偏移成像结果(图 10b,参考)、波场分离后的衰减数据逆时偏移成像结果(图 10d)及波场分离后的Q补偿逆时偏移成像结果(图 10f)。图 10b右侧子图为水平距离6000 m处作为参考的单道信息(黑色实线),图 10d、图 10f右侧子图则分别为水平距离6000 m处相应的单道信息(红色虚线)和参考单道信息(黑色实线)。图 11a~图 11c对应为10b、图 10d、图 10f中水平距离5~8 km、深度1.3~1.8 km范围的振幅谱。
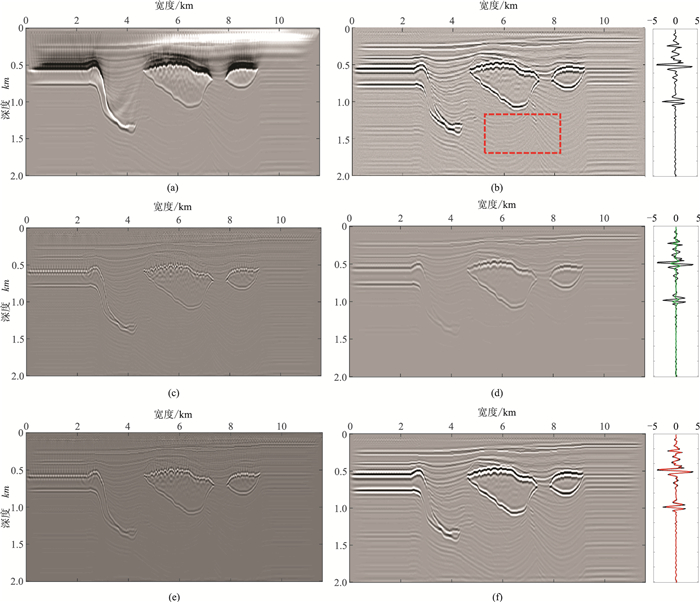
|
图 10 不同的逆时偏移成像结果 (a)未波场分离的声波逆时偏移;(b)波场分离后声波逆时偏移;(c)采用拉普拉斯滤波的声波逆时偏移;(d)波场分离后未补偿黏声逆时偏移;(e)采用拉普拉斯滤波的Q补偿逆时偏移;(f)波场分离后Q补偿黏声逆时偏移 |
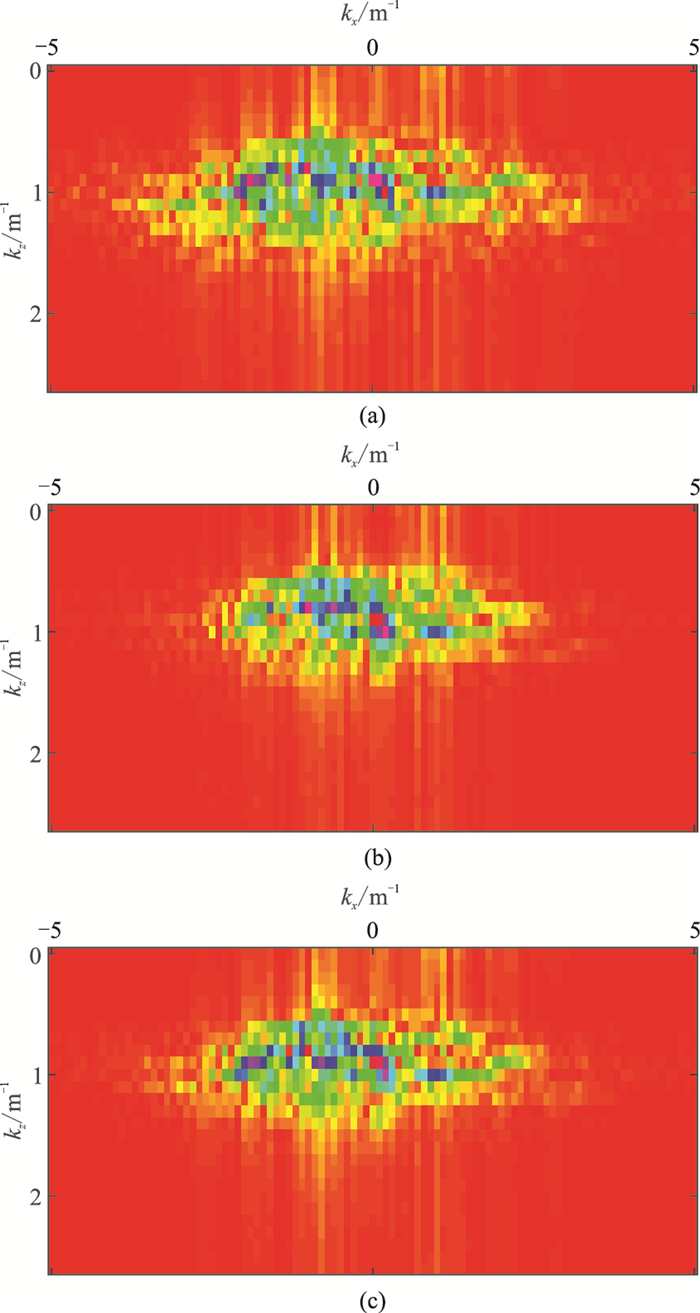
|
图 11 图 10d中红框对应位置振幅谱 (a)声波逆时偏移;(b)衰减数据逆时偏移;(c)Q补偿逆时偏移 |
与图 10b(参考)相比,图 10d(衰减未补偿)因地层的衰减效应,其能量减弱,偏移成像层位不清晰,尤其是盐下边界以下;图 10f由于采用Q补偿逆时偏移,其能量得到补偿。对比10b、图 10d、图 10f的单道信息与图 11a~图 11c的振幅谱,可见缘于地层的非完全弹性效应,对成像结果造成振幅衰减及相位畸变,而采用Q补偿逆时偏移(图 11c)能在一定程度上减缓这种效应的影响,拓宽其振幅谱,补偿衰减的能量,并对畸变的相位进行校正,提高了成像质量。由图 10a可知,采用传统的互相关偏移方法,成像结果中浅层的有效信息完全湮没在噪声中,严重干扰成像精度;而采用拉普拉斯滤波后的成像结果(图 10c、图 10e)中低频噪声受到一定程度压制,但对浅层信息仍有较明显的干扰。
综上所述,本文采用的Q补偿逆时偏移方法能有效补偿由地下介质非弹性特性造成的振幅损失和相移,采用该成像方法所得偏移成像结果(图 10d~图 10f)中,有效地压制由传统成像条件所引起的低频噪声及假象。
值得注意的是,该方法是在进行两次震源波场和检波点波场外推的情况下,还要在时间切片上对波场进行傅里叶变换,所以计算时间稍长于采用拉普拉斯滤波的Q-RTM,测试结果(表 1)显示约为其1.3倍。但该方法不用对波场进行存储,避免了巨大的I/O量。
|
|
表 1 不同方案下的计算时间 |
本文提出一种上、下行波分解的解耦分数阶拉普拉斯算子黏滞声波逆时偏移成像方法:采用解耦的分数阶拉普拉斯算子黏滞声波方程对震源波场和检波点波场进行外推,能显著减缓由于地下介质的黏滞性所引起的振幅衰减和频散效应,提高了偏移成像的照明能量;采用分数阶拉普拉斯算子代替分数阶时间导数,不需在求解波动方程计算当前时刻波场值时依赖该时刻以前所有时段的波场。采用解析时间波场能显式地分解上下行波场。新的成像条件能避免同向传播的震源波场和检波点波场在应用互相关成像条件时所产生的低频噪声,消除由于偏移速度模型存在较强速度梯度时由震源上行波场和检波点下行波场互相关产生的假象,从而提高偏移成像的分辨率和质量。
| [1] |
陈生昌, 刘亚楠, 李代光. 基于波动方程偏移的地震数据地层成像[J]. 石油地球物理勘探, 2022, 57(5): 1105-1113. CHEN Shengchang, LIU Yanan, LI Daiguang. Stratigraphic imaging with seismic data based on wave equation migration[J]. Oil Geophysical Prospecting, 2022, 57(5): 1105-1113. DOI:10.13810/j.cnki.issn.1000-7210.2022.05.011 |
| [2] |
吴丹, 吴海莉, 李群, 等. 应用自适应矩估计的快速最小二乘逆时偏移[J]. 石油地球物理勘探, 2022, 57(2): 386-394. WU Dan, WU Haili, LI Qun, et al. Fast least-squares reverse time migration with adaptive moment estimation[J]. Oil Geophysical Prospecting, 2022, 57(2): 386-394. |
| [3] |
ZHOU J, BIRDUS S, HUNG B, et al. Compensating attenuation due to shallow gas through Q tomography and Q-PSDM, a case study in Brazil[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 3332-3336.
|
| [4] |
KJARTANSSON E. Constant Q-wave propagation and attenuation[J]. Journal of Geophysical Research: Solid Earth, 1979, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737 |
| [5] |
LIU H P, ANDERSON D L, KANAMORI H. Velocity dispersion due to anelasticity; implications for seismology and mantle composition[J]. Geophysical Journal International, 1976, 47(1): 41-58. DOI:10.1111/j.1365-246X.1976.tb01261.x |
| [6] |
EMMERICH H, KORN M. Incorporation of attenuation into time-domain computations of seismic wave fields[J]. Geophysics, 1987, 52(9): 1252-1264. DOI:10.1190/1.1442386 |
| [7] |
PAPOULIA K D, PANOSKALTSIS V P, KURUP N V, et al. Rheological representation of fractional order viscoelastic material models[J]. Rheologica Acta, 2010, 49(4): 381-400. DOI:10.1007/s00397-010-0436-y |
| [8] |
MOCZO P, KRISTEK J. On the rheological models used for time‐domain methods of seismic wave propagation[J]. Geophysical Research Letters, 2005, 32(1): L01306. |
| [9] |
BLANCH J O, ROBERTSSON J O A, SYMES W W. Modeling of a constant Q: Methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique[J]. Geophysics, 1995, 60(1): 176-184. DOI:10.1190/1.1443744 |
| [10] |
CHEN W, HOLM S. Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency[J]. The Journal of the Acoustical Society of America, 2004, 115(4): 1424-1430. DOI:10.1121/1.1646399 |
| [11] |
TREEBY B E, COX B T. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian[J]. The Journal of the Acoustical Society of America, 2010, 127(5): 2741-2748. DOI:10.1121/1.3377056 |
| [12] |
刘文卿, 王宇超, 雍学善, 等. 基于GPU/CPU叠前逆时偏移研究及应用[J]. 石油地球物理勘探, 2012, 47(5): 712-716. LIU Wenqing, WANG Yuchao, YONG Xueshan, et al. Prestack reverse time migration on GPU/CPU co-parallel computation[J]. Oil Geophysical Prospecting, 2012, 47(5): 712-716. |
| [13] |
ZHU T, HARRIS J M. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians[J]. Geophysics, 2014, 79(3): T105-T116. DOI:10.1190/geo2013-0245.1 |
| [14] |
ZHU T, HARRIS J M, BIONDI B. Q-compensated reverse-time migration[J]. Geophysics, 2014, 79(3): S77-S87. DOI:10.1190/geo2013-0344.1 |
| [15] |
LI Q, ZHOU H, ZHANG Q, et al. Efficient reverse time migration based on fractional Laplacian viscoacoustic wave equation[J]. Geophysical Journal International, 2015, 204(1): 488-504. |
| [16] |
TREEBY B E. Acoustic attenuation compensation in photoacoustic tomography using time-variant filtering[J]. Journal of Biomedical Optics, 2013, 18(3): 036008. DOI:10.1117/1.JBO.18.3.036008 |
| [17] |
WANG Y. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 2006, 71(3): V51-V60. DOI:10.1190/1.2192912 |
| [18] |
WANG Y, ZHOU H, CHEN H, et al. Adaptive stabilization for Q-compensated reverse time migration[J]. Geophysics, 2018, 83(1): S15-S32. DOI:10.1190/geo2017-0244.1 |
| [19] |
陈汉明, 周辉, 田玉昆. 分数阶拉普拉斯算子黏滞声波方程的最小二乘逆时偏移[J]. 石油地球物理勘探, 2020, 55(3): 616-626. CHEN Hanming, ZHOU Hui, TIAN Yukun. Least-squares reverse-time migration based on a fractional Laplacian viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2020, 55(3): 616-626. |
| [20] |
CHEN H, ZHOU H, RAO Y. An implicit stabilization strategy for Q-compensated reverse time migration[J]. Geophysics, 2020, 85(3): S169-S183. DOI:10.1190/geo2019-0235.1 |
| [21] |
YOON K, MARFURT K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 2006, 37(1): 102-107. DOI:10.1071/EG06102 |
| [22] |
康玮, 程玖兵. 叠前逆时偏移假象去除方法[J]. 地球物理学进展, 2012, 27(3): 1163-1172. KANG Wei, CHENG Jiubing. Methods of suppressing artifacts in prestack reverse time migration[J]. Progress in Geophysics, 2012, 27(3): 1163-1172. |
| [23] |
GUITTON A, KAELIN B, BIONDI B. Least-squares attenuation of reverse-time-migration artifacts[J]. Geophysics, 2007, 72(1): S19-S23. |
| [24] |
ZHANG Y, SUN J. Practical issues in reverse time migration: true amplitude gathers, noise removal and harmonic source encoding[J]. First Break, 2009, 27(1): 53-60. |
| [25] |
LIU F, ZHANG G, MORTON S A, et al. Reverse-time migration using one-way wavefield imaging condition[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 2170-2174.
|
| [26] |
LIU F, ZHANG G, MORTON S A, et al. An effective imaging condition for reverse-time migration using wavefield decomposition[J]. Geophysics, 2011, 76(1): S29-S39. |
| [27] |
杜启振, 朱钇同, 张明强, 等. 叠前逆时深度偏移低频噪声压制策略研究[J]. 地球物理学报, 2013, 56(7): 2391-2401. DU Qizhen, ZHU Yitong, ZHANG Mingqiang, et al. A study on the strategy of low wavenumber noise suppression for prestack reverse-time depth migration[J]. Chinese Journal of Geophysics, 2013, 56(7): 2391-2401. |
| [28] |
FEI T W, LUO Y, YANG J, et al. Removing false images in reverse time migration: The concept of deprimary[J]. Geophysics, 2015, 80(6): S237-S244. |
| [29] |
胡江涛, 王华忠. 基于解析时间波场外推与波场分解的逆时偏移方法研究[J]. 地球物理学报, 2015, 58(8): 2886-2895. HU Jiangtao, WANG Huazhong. Reverse time migration using analytical time wavefield extrapolation and separation[J]. Chinese Journal of Geophysics, 2015, 58(8): 2886-2895. |
| [30] |
ZHOU H, LIU Y, WANG J. Viscoacoustic reverse time migration by attenuation compensation and wavefield decomposition[C]//SEG 2018 Workshop: SEG Seismic Imaging Workshop, Beijing, China, 2019, 90-93.
|
| [31] |
BLAND D R. The Theory of Linear Viscoelasticity[M]. Dover Publications Inc., Mineola, 2016.
|
| [32] |
CLAERBOUT J F. Toward a unified theory of reflector mapping[J]. Geophysics, 1971, 36(3): 467-481. |
| [33] |
HU L Z, MCMECHAN G A. Wave-field transformations of vertical seismic profiles[J]. Geophysics, 1987, 52(3): 307-321. |



 毛伟建,湖北省武汉市洪山区徐东大街340号中国科学院精密测量科学与技术创新研究院计算与勘探地球物理研究中心,430077。Email:
毛伟建,湖北省武汉市洪山区徐东大街340号中国科学院精密测量科学与技术创新研究院计算与勘探地球物理研究中心,430077。Email: