2. 长安大学地质工程与测绘学院地球物理系, 陕西西安 710054;
3. 长安大学计算地球物理研究所, 陕西西安 710054
2. Department of Geophysics, College of Geological Engineering and Geomatics, Chang'an University, Xi'an, Shaanxi 710054, China;
3. Institute of Computational Geophysics, Chang'an University, Xi'an, Shaanxi 710054, China
基于几何地震学的地震波走时计算技术具有算法便捷、计算效率高等优点而被广泛应用于地震层析成像[1-4]、地震定位[5-7]等领域。地震波走时计算方法主要可分为三种:一是基于运动学方程的射线追踪类方法[8-9],但当遇到复杂介质时,这类方法容易陷入局域解,存在阴影区问题;二是基于费马原理的最短路径算法(Shorest Path Method,SPM)[10-11],这类方法通过采用大量的网格线段近似逼近地震波射线,为保证结果精度,需用比其他方法更庞大数量的网络节点,这也导致了更高的计算空间要求;三是基于有限差分求解程函方程类方法,它有效避免了运动学方程类方法的不足,且在计算精度与计算效率方面具有显著优势,自提出以来即发展迅速,作为正演算法多次解决地震波走时反演问题[12-14],近年有不少学者将其推广至各向异性介质[15-20]。
快速行进法(Fast Marching Method,FMM)[21]与快速扫描法(Fast Sweeping Method,FSM)[22]均是通过有限差分求解程函方程,从而得到全局地震波走时的计算方法。FMM采用窄带技术近似波前扩展,即隐含了这样一个假设:群速度给出的能量传播方向与相速度给出的波前传播方向相同。然而,该假设仅对各向同性介质是成立的,对于各向异性介质则不成立。虽然近年来也有不少学者通过加入其他约束性条件将其推广至各向异性介质[23-25],但过多的约束条件也使得算法变得复杂且低效。因此,对于各向异性介质而言,人们更愿意采用FSM。FSM由Zhao[22]率先提出,通过沿交替方向扫描计算域求解程函方程,在有限次数的迭代中收敛得到数值解,比FMM更灵活且稳健性更高。有关FMM与FSM的详细比较,可参考文献[26]。尽管FSM在各向异性介质及稳健性上明显优于FMM,但研究表明[27-28],对于复杂模型或网格节点较多的模型而言,FSM计算效率低于FMM。主要原因是对于较复杂模型FSM需更多的迭代次数才能收敛,对于具有大量网格节点的复杂模型,此问题更严重。如Li等[29]为保证反演效率,选择FMM作为正演算法以解决反演算法的效率问题;Benaichouche等[30]则选用FSM作为正演地震波走时计算方法,然而在反演计算雅可比矩阵时,选用FMM求解原始程函方程,这样虽然提高了效率,但在一定程度上牺牲了计算精度。
FMM是通过有限差分求解程函方程,采用窄带近似波前而扩展起来的一种方法,Rawlinson等[31]将FMM与分区多步计算技术(Multistage Computational Technique)相结合,实现了2D复杂地质结构下的多震相地震波走时计算(Multistage FMM)。随后,de Kool等[32]考虑地球曲率影响,又将该算法推广至球坐标系下进行多震相地震波走时计算。孙章庆等[33]基于FMM,提出不等距迎风差分格式(Uneven Grid Upwind Finite-Difference Formula)计算3D起伏地表条件的直达波走时,随后又引入群行进法(Group Marching Method)[34]以提高FMM计算效率[35]。然而,震源点奇异性问题一直伴随着FMM的发展。为解决此问题,Rawlinson等[31]采用源点网格加密技术,分析表明,经过对震源附近网格细化后的FMM可明显降低源点附近的计算误差,但相对于整个计算区域,源点附近的计算误差仍然较大,因此震源区网格细化并不能根本解决震源点的奇异性问题。此外,震源区网格细化的同时也意味着额外增加了计算量。Alkhalifah等[36]则在球坐标系下求解程函方程,但这种算法复杂,实际应用中难以推广。Fomel等[37]提出将地震波走时因式分解,用FSM求解因式分解程函方程以解决震源奇异性问题,数值模拟表明,求解因式分解程函方程数值解的准确性高于直接计算原始程函方程,且震源附近改善效果更明显。周小乐等[38]推导建立了曲线坐标系因式分解程函方程,结合FSM,在解决震源奇异性问题的同时,可得到起伏地表条件的地震波走时。
鉴于FMM对复杂模型计算效率的优势及求解因式分解程函方程可解决震源奇异性问题,本文提出了一种起伏地表条件下基于FMM求解因式分解程函方程的数值算法,同样可从根源上解决震源奇异性问题。与传统FMM相同,本文所提算法可在保证O(NlgN,N为网络节点数)计算成本内使用一阶或二阶有限差分公式求解因式分解程函方程。同时,考虑到加入后续震相约束可显著提高反演分辨率,本文又结合分区多步计算技术实现了多震相地震波走时的计算。
文中首先阐释如何建立因式分解程函方程;然后介绍利用FMM求解因式分解程函方程;最后通过2D/3D均匀模型、速度线性增加模型和起伏界面模型验证了所提算法的有效性与鲁棒性。为表述方便,将本文所提算法称为基于因式分解程函方程FMM,简称FMM-F。
1 因式分解程函方程的导出限于篇幅,在推导因式分解程函方程过程中,仅展示2D直角坐标系情形。对于3D,只需进行类似的扩展即可。首先引入2D直角坐标系程函方程
| $ {\left|\nabla T(x, z)\right|}^{2}={S}^{2}(x, z) $ | (1) |
式中T(x,z)和S(x,z)均为空间位置坐标(x,z)的函数,分别表示震源点O到空间点(x,z)的地震波走时与该点的波慢度。将T(x,z)分解为一个关于点(x,z)到震源点O的距离函数
| $ T={T}_{0}\cdot {T}_{1} $ | (2) |
这样,根据链式求导法则,标准程函方程式(1)便可写成
| $ {\left|{T}_{0}\cdot \nabla {T}_{1}+{T}_{1}\cdot \nabla {T}_{0}\right|}^{2}={S}^{2}(x, z) $ | (3) |
式中
| $ {T}_{0}(x, z)=\sqrt[]{(x-{x}_{0}{)}^{2}+(z-{z}_{0}{)}^{2}} $ | (4) |
则对于震源点
| $ {T}_{0}({x}_{0}, {z}_{0})=0 $ | (5) |
对于任意一点,有
| $ (\nabla \cdot {T}_{0}{)}^{2}=1 $ | (6) |
则对于震源点
| $ {T}_{1}({x}_{0}, {z}_{0})=S({x}_{0}, {z}_{0}) $ | (7) |
上述
传统FMM采用有限差分近似走时梯度,利用窄带模拟波前扩展,采用堆排序算法寻找波前中走时最小点作为次级震源。本文算法同样基于以上技术,这些技术已在许多FMM算法相关文献[21, 31-32]中有详细阐述,此处不再赘述。本文算法的关键在于如何利用FMM求解因式分解程函方程,下面分别阐述两种方法求解T1。
2.1 规则网格求解首先,对因式分解程函方程进行离散,则有(为表述方便,用点(x,z)的编号(i,j)表示其位置)
| $ \mathrm{m}\mathrm{a}\mathrm{x}{\left[{D}_{n}^{-x}T\left(i, j\right), {D}_{n}^{+x}T\left(i, j\right), 0\right]}^{2}+\\ \;\;\;\;\mathrm{m}\mathrm{a}\mathrm{x}{\left[{D}_{n}^{-z}T\left(i, j\right), {D}_{n}^{+z}T\left(i, j\right), 0\right]}^{2}={S}^{2}(x, z) $ | (8) |
式中:max(A,B,C)表示求取A、B、C中最大值;
规则网格(图 1)中,假定此时(i,j)点的走时为待求点走时,引入符号Tknow表示T值已知、Tunknow表示T值未知。对于一阶差分,可得到式(9);根据链式求导法,则有式(10)
| $ \mathrm{m}\mathrm{a}\mathrm{x}\left(x\right)=\left\{\begin{array}{l}{D}_{1}^{-x}T(i, j)\left\{\begin{array}{l}\mathrm{当}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j)\\ \mathrm{或}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j)\mathrm{且}\\ {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j) < {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j)\end{array}\right.\\ {D}_{1}^{+x}T(i, j)\left\{\begin{array}{l}\mathrm{当}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j)\\ \mathrm{或}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j)\mathrm{且}\\ {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j)\mathrm{ } < {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j)\end{array}\right.\\ 0\mathrm{当}{T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j)\end{array}\right. $ | (9) |
| $ \left\{\begin{array}{c}{D}_{1}^{-x}T(i, j)={T}_{0}(i, j)\cdot \frac{{T}_{1}(i, j)-{T}_{1}(i-1, j)}{h}+P(i, j)\cdot {T}_{1}(i, j)\\ {D}_{1}^{+x}T(i, j)={T}_{0}(i, j)\cdot \frac{{T}_{1}(i+1, j)-{T}_{1}(i, j)}{h}+P(i, j)\cdot {T}_{1}(i, j)\end{array}\right. $ | (10) |
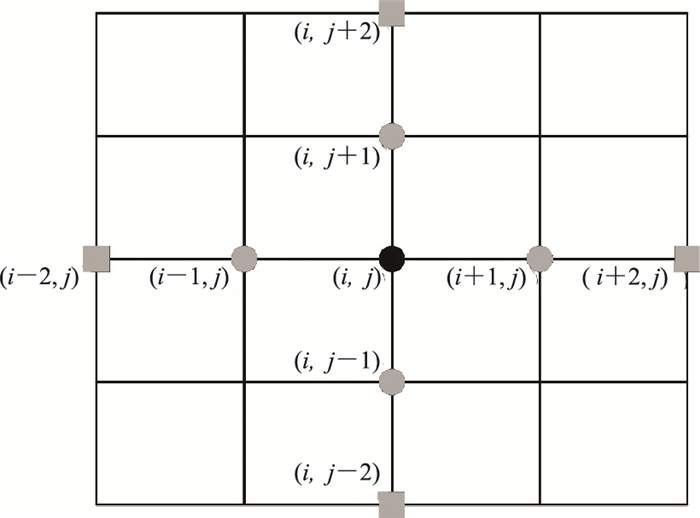
|
图 1 规则网格走时扰动因子T1求解示意图 黑圆点为待求点,灰圆点为一阶差分,小方块为二阶差分。 |
式中:
对于二阶差分,实际为混合阶数差分(当不满足二阶差分条件时,即运用一阶差分)。与一阶差分相似,仍需先判断待求点
| $ \mathrm{m}\mathrm{a}\mathrm{x}\left(x\right)= \\ \left\{\begin{array}{l}{D}_{1}^{-x}T(i, j)\left\{\begin{array}{l}\mathrm{当}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-2, j)\\ \mathrm{或}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-2, j), \mathrm{且}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j) < {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j)\end{array}\right.\\ {D}_{1}^{+x}T(i, j)\left\{\begin{array}{l}\mathrm{当}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+2, j)\\ \mathrm{或}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j), {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+2, j), \mathrm{且}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j) < {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j)\end{array}\right.\\ {D}_{2}^{-x}T(i, j)\left\{\begin{array}{l}\mathrm{当}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j){T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-2, j), \mathrm{且}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j) > {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-2, j)\\ \mathrm{或}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j), {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-2, j), \mathrm{且}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j) > {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j) > {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-2, j)\end{array}\right.\\ {D}_{2}^{+x}T(i, j)\left\{\begin{array}{l}\mathrm{当}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j){T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+2, j), \mathrm{且}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j) > {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+2, j)\\ \mathrm{或}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j), {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j), {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+2, j), \mathrm{且}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j) > {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j) > {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+2, j)\end{array}\right.\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{当}{T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i+1, j), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}(i-1, j)\end{array}\right. $ | (11) |
式中:
| $ \left\{\begin{array}{l}{D}_{2}^{-x}T(i, j)={T}_{0}(i, j)\cdot \frac{3\times {T}_{1}(i, j)-4\times {T}_{1}(i-1, j)+{T}_{1}(i-2, j)}{h}+P(i, j)\cdot {T}_{1}(i, j)\\ {D}_{2}^{+x}T(i, j)={T}_{0}(i, j)\cdot \frac{-3\times {T}_{1}(i, j)+4\times {T}_{1}(i+1, j)-{T}_{1}(i+2, j)}{h}+P(i, j)\cdot {T}_{1}(i, j)\end{array}\right. $ | (12) |
式中各变量物理意义与一阶差分(式(9))类似。
z方向差分算子的推导,与x方向类似。至此,再结合窄带技术[21],便可实现直达波走时计算。
2.2 不规则网格求解为提高走时反演成像的分辨率,采用多震相走时联合反演是一个不错的选择,这就要求正演算法具有计算多震相地震波走时的能力。分区多步计算技术自提出以来,就与多种网格类地震波走时计算方法相结合,用于模拟多震相地震波传播。本算法同样作为网格单元类算法,也可结合分区多步计算技术实现多震相地震波走时的计算。
然而实际地表(或地下界面)多呈不规则性,若用规则网格剖分,则地下界面(或地表)附近会产生不规则网格(图 2b中M1M2界面)。这样,上述规则网格的迎风差分公式显然已不适用,因此需要针对界面附近不规则网格,推导建立新的局部走时计算公式。图 2不规则网格中的点可划分为两类:一类是界面附近点(C点);另一类是界面点(M点)。下面分别针对这两类点建立局部走时计算公式。
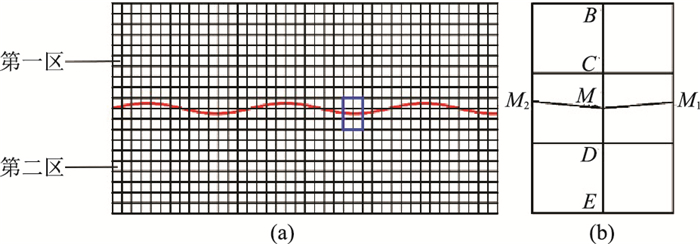
|
图 2 模型界面及网格剖分示意图(a)及其局部放大图(b) 红色实线为界面,蓝色矩形块对应放大区域。 |
(1)C点为当前待计算点
此时以C点为中心的z方向出现
| $ \left\{\begin{array}{l}{D}_{1}^{-z}T\left(C\right)={T}_{0}\left(C\right)\cdot \frac{{T}_{1}\left(C\right)-{T}_{1}\left(M\right)}{{h}_{1}}+P\left(C\right)\cdot {T}_{1}\left(C\right)\\ {D}_{2}^{-z}T\left(C\right)={T}_{0}\left(C\right)\cdot \frac{{h}_{1}^{2}\times {T}_{1}\left(D\right)-{h}^{2}\times {T}_{1}\left(M\right)+({h}^{2}-{h}_{1}^{2})\times {T}_{1}\left(C\right)}{{h}^{2}\times {h}_{1}-{h}_{1}^{2}\times h}+P\left(C\right)\cdot {T}_{1}\left(C\right)\end{array}\right. $ | (13) |
而二阶差分算子的推导过程如下,利用泰勒函数将
| $ \left\{\begin{array}{l}{T}_{1}\left(M\right)={T}_{1}\left(C\right)-{h}_{1}\cdot {T}_{1}^{\text{'}}\left(C\right)+{h}_{1}^{2}\cdot {T}_{1}^{\text{'}\text{'}}\left(C\right)+O\left(C\right)\\ {T}_{1}\left(D\right)={T}_{1}\left(C\right)-h\cdot {T}_{1}^{\text{'}}\left(C\right)+{h}^{2}\cdot {T}_{1}^{\text{'}\text{'}}\left(C\right)+O\left(C\right)\end{array}\right. $ | (14) |
式中:
| $ {T}_{1}^{\text{'}}\left(C\right)=\\ \;\;\;\;\frac{{h}_{1}^{2}\times {T}_{1}\left(D\right)-{h}^{2}\times {T}_{1}\left(M\right)+({h}^{2}-{h}_{1}^{2})\times {T}_{1}\left(C\right)}{{h}^{2}\times {h}_{1}-{h}_{1}^{2}\times h} $ | (15) |
将式(15)代入式(14),可得不等距二阶迎风差分公式。
此外,由于
| $ T\left(C\right)=\left\{\begin{array}{l}\mathrm{m}\mathrm{i}\mathrm{n}\left[{T}_{0}\left(C\right)\times {T}_{1}^{\mathrm{u}\mathrm{p}}\left(C\right), {T}_{0}\left(C\right)\times {T}_{1}^{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\left(C\right)\right]\mathrm{当}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}\left(B\right), {T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}\left(M\right)\\ {T}_{0}\left(C\right)\times {T}_{1}^{\mathrm{u}\mathrm{p}}\left(C\right)\mathrm{当}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}\left(B\right), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}\left(M\right)\\ {T}_{0}\left(C\right)\times {T}_{1}^{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}\left(C\right)\mathrm{当}{T}_{\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}\left(M\right), {T}_{\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{n}\mathrm{o}\mathrm{w}}\left(B\right)\end{array}\right. $ | (16) |
式中
(2)M点为当前待计算点
此时M点周围的四个网格均为非正交,导致程函方程不成立。Rawlinsnon等[31]采用三角网格缝合界面,而后在三角网格中求解程函方程,但实现较为困难。本文综合不等距迎风差分公式、费马原理与惠更斯原理,求解界面走时。对于M点的z轴下方向,同样有不等距一阶、二阶差分公式
| $ \begin{array}{l}\\ \left\{\begin{array}{l}{D}_{1}^{-z}T\left(M\right)={T}_{0}\left(M\right)\cdot \frac{{T}_{1}\left(M\right)-{T}_{1}\left(D\right)}{{h}_{2}}+P\left(M\right)\cdot {T}_{1}\left(M\right)\\ {D}_{2}^{-z}T\left(M\right)={T}_{0}\left(M\right)\cdot \frac{\left[{h}_{2}^{2}-{\left({h}_{2}+h\right)}^{2}\right]\cdot {T}_{1}\left(M\right)-{\left({h}_{2}+h\right)}^{2}\cdot {T}_{1}\left(D\right)+{h}_{2}^{2}\cdot {T}_{1}\left(E\right)}{{h}_{2}^{2}\cdot \left({h}_{2}+h\right)-{\left({h}_{2}+h\right)}^{2}\cdot {h}_{2}}+P\left(M\right)\cdot {T}_{1}\left(M\right)\end{array}\right.\end{array} $ | (17) |
式中
此外对于M点x方向,由于界面起伏,x方向常规差分公式已不再适用。本文采用惠更斯原理,即将M1、M2视为子波源,就有
| $ T\left(M\right)=T\left({M}_{i}\right)+{l}_{i}\cdot {\stackrel{-}{s}}_{{M}_{i}M}(i=\mathrm{1, 2}) $ | (18) |
式中:li为Mi与M之间的距离;
最后,再利用费马原理,得到
| $ \begin{array}{l}T\left(M\right)=\mathrm{m}\mathrm{i}\mathrm{n}\left[T\left({M}_{i}\right)+\right.\\ \;\;\;\;\;\;\;\;\;\left.{T}_{1}^{\rm{up}}\left(M\right), {T}_{0}\left(M\right)\cdot {T}_{1}^{\rm{down}}\left(M\right)\right]\end{array} $ | (19) |
式中
综上所述,由于起伏界面的存在,可将界面上的点分为三类:第一类为规则网格中节点,采用常规迎风差分公式(式(8)~式(10))计算修正因子
基于前面构建的起伏地表模型下规则网格与不规则网格的迎风差分格式,再结合分区多步技术与窄带技术,便可实现多震相地震波走时计算。所谓分区多步计算技术即指按照地下起伏界面的具体情况,将模型分成独立的层状(或起伏层状)区域,相邻区域由地下界面相连接[18](图 2a)。窄带技术根据模型中网格节点所处状态将所有节点分为三种:“完成点”、“窄带点”及“远离点”。其中“完成点”表示走时计算已结束的网格点;“窄带点”表示当前波前上的网格节点,其走时大小还可更新;“远离点”表示走时计算还未实施的网格节点。
表 1给出了本文所提FMM-F算法计算直达波走时的实现框图,当要计算其他震相的地震波走时时,只需将界面上走时最小的点作为新的子震源,而后与计算直达波相同,计算当前所需震相的地震波走时即可。
|
|
表 1 FMM-F算法实施过程 |
现以图 2a所示模型计算上界面反射波为例,说明反射波走时计算原理(震源所在位置为第一分区),其他震相的走时计算也可类推。
(1)首先设定算法初始化条件,给定
(2)判断当前震源点所在网格是否包含界面或起伏地表:若是,则采用非规则网格迎风差分格式(式(13)~式(19))计算震源周围点走时扰动因子T1;若否,则采用规则网格迎风差分格式(式(8)~式(12))计算T1,通过式(2)和式(4)得到震源周围点地震波走时,这些点构成的面即为当前波前所在位置,其状态记为“窄带点”;
(3)在“窄带点”中搜寻走时最小点,将此点作为次级震源并将其状态更新为“完成点”继续循环第(2)步计算,直到得到震源所在分区的全局走时;
(4)读取界面离散点地震波走时并将其状态均赋为“窄带点”,返回第(3)步,要注意的是由于是计算反射波,所以在第(2)步时只需考虑界面以上的网格节点即可。
若要追踪透射波,则在第(4)步返回第(3)步时,自界面上走时最小的点向透射区域进行波前扩展即可;若要追踪转换波,则自离散界面上走时最小的点开始向转换波所在区域进行波前扩展扫描时时,采用不同的速度模型即可。简而言之,分区多步计算的原理就是根据所要计算地震波的类型,设计要调用的独立区域的先后顺序及对应的速度模型,达到运用简单组合完成复杂模型中多震相地震波走时计算之目的。
4 数值模拟及结果分析采用几组模型进行数值模型计算,通过本算法与Multistage FMM算法[31]详尽(主要是计算精度与计算效率)对比,验证本文算法的优越性。当选用模型存在解析解时,将以解析解作为参考解;当选用模型不存在解析解时,将以发展较成熟的不规则最短路径算法(ISMP)[37]作为参考解,且通过加密ISMP算法网格间距,确保该算法计算结果的精度。计算所用处理器配置为:Intel(R)Core(TM)i7-10750H CPU @ 2.60 GHz。另外,在分析算法所用CPU时间时,均是设置程序循环执行100次后取均值得到每次所用CPU时间,以避免偶然性。
4.1 模型1(均匀模型)2D均匀模型大小为4 km×4 km,地震波传播速度为1 km/s,震源位于(2 km,2 km);3D均匀模型大小为10 km×10 km×10 km,地震波传播速度为2 km/s,震源位于(5 km,5 km,5 km)。对于FMM,采用震源网格加密方式保证精度,加密区域范围为
表 2(2D)和表 3(3D)分别给出均匀模型不同网格间距剖分下FMM与FMM-F的计算结果对比。从该表可见,对于均匀模型,本文所提FMM-F计算结果误差为零(注意:误差分析结果已消除因计算机自身小数保留位数而导致的计算误差);同时,可看到随着网格间距的减小,两种算法的计算效率都降低了,但在相同的网格剖分间距下,FMM-F计算效率明显高于FMM,考虑是由于FMM采用震源网格加密方式保证精度,从而使得FMM计算效率降低。另外,当采用二阶差分时,两种算法计算效率都降低了,但降低并不明显。
|
|
表 2 2D均匀模型中FMM与FMM-F计算地震波走时误差及CPU时间对比 |
|
|
表 3 3D均匀模型中FMM与FMM-F计算地震波走时误差及CPU时间对比 |
再采用速度线性增加模型(图 3)进行试算。2D模型(图 3a)大小为
| $ {T}_{\mathrm{e}\mathrm{x}\mathrm{a}\mathrm{c}\mathrm{t}}=\frac{1}{\alpha }\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left[1+\frac{1}{2{v}_{0}}{\alpha }^{2}v\left(\boldsymbol{x}\right)‖\boldsymbol{x}-{\boldsymbol{x}}_{0}‖\right] $ | (20) |
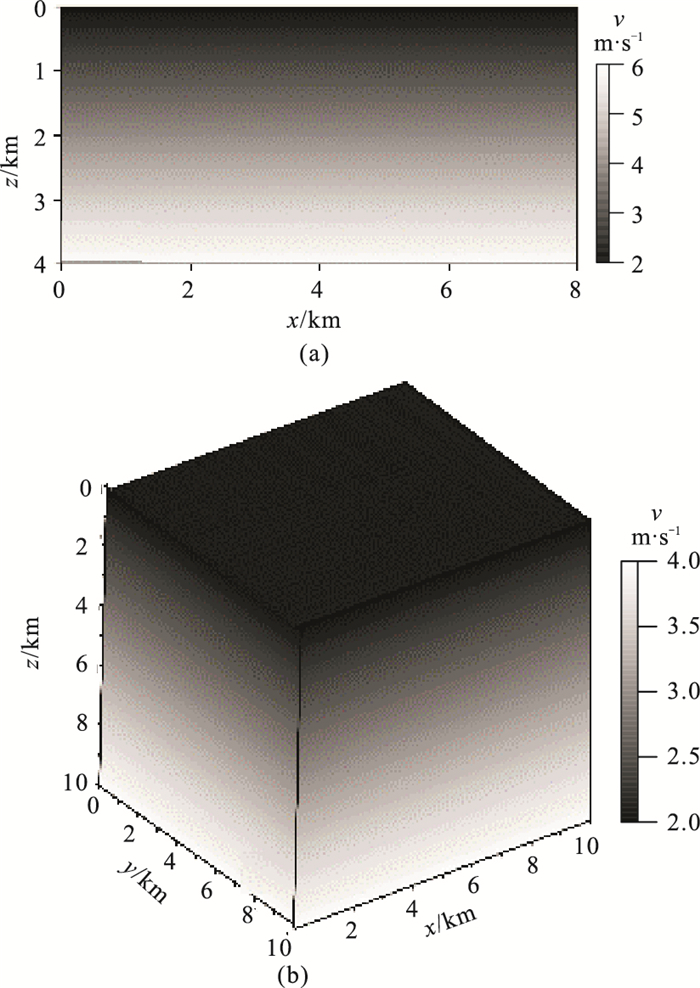
|
图 3 速度线性增加的2D(a)和3D(b)模型 |
式中:
表 4和表 5分别给出不同网格间距剖分计算2D和3D线性模型时FMM与FMM-F的计算结果对比。同样采用震源网格加密方式保证FMM计算精度。水平轴加密区域范围为
|
|
表 4 图 3a模型中FMM与FMM-F计算地震波走时误差及CPU时间对比 |
|
|
表 5 图 3b模型中FMM与FMM-F计算地震波走时误差及CPU时间对比 |
从表 4和表 5可见,随着网格间距的不断减小,不论是FMM还是FMM-F,其平均绝对误差与平均相对误差都不断减小,计算精度不断提高。但同时,网格间距的减小,导致网格节点数变多,计算效率也随之下降。另外还发现,当采用二阶差分时,两种算法的计算精度都有大幅度提高,且与均匀模型相同,计算效率降低并不明显,因此建议实际应用中采用二阶差分格式。重要的是在两种算法对比中发现,网格间距相同时,2D或3D情形下,无论是计算精度还是CPU计算时间,FMM-F优于FMM。这是因为计算精度方面,FMM-F成功地避免了震源点的奇异性问题;而计算效率方面则是传统FMM为了克服震源点的奇异性需对震源附近网格细化,导致计算量增加。
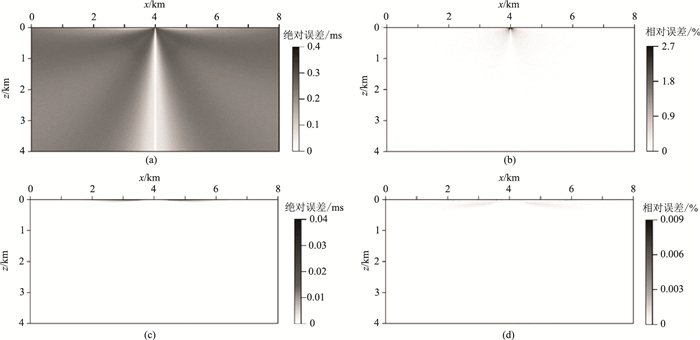
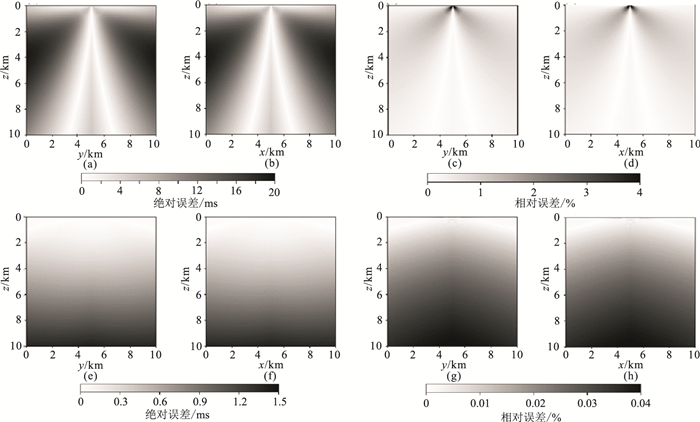
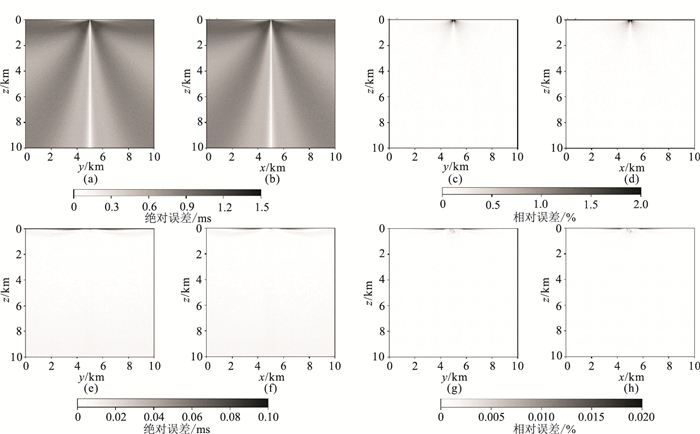
为进一步分析误差分布情况,又给出当h= 0.05 m时两种算法分别采用一阶(图 4(2D)、图 6(3D))、二阶(图 5(2D)、图 7(3D))差分所得的绝对误差和相对误差分布图。可发现传统FMM计算所得地震波走时在震源对角线附近区域误差较大,当采用一阶差分格式时,其最大绝对误差分别可达4.80 ms(2D)和20 ms(3D),最大相对误差则分别高达7%(2D)和4%(3D);而FMM-F最大绝对误差仅分别为0.16 ms(2D)和1.5 ms(3D),而最大相对误差也分别仅为0.016%(2D)和0.04%(3D)。当采用二阶差分格式时,两种算法的计算精度都得到了很大提高,FMM最大绝对误差分别降至0.4 ms(2D)和1.5 ms(3D),同样最大相对误差也分别减小到2.7%(2D和2%(3D);而FMM-F最大绝对误差则分别进一步减至0.04 ms(2D)和0.1 ms(3D),最大相对误差则分别减至0.009%(2D)和0.02%(3D)。可见,本文的FMM-F不论采用一阶还是二阶差分格式,其计算精度高于传统FMM;同时,通过误差分布图可发现FMM-F完全解决了震源点的奇异性问题。
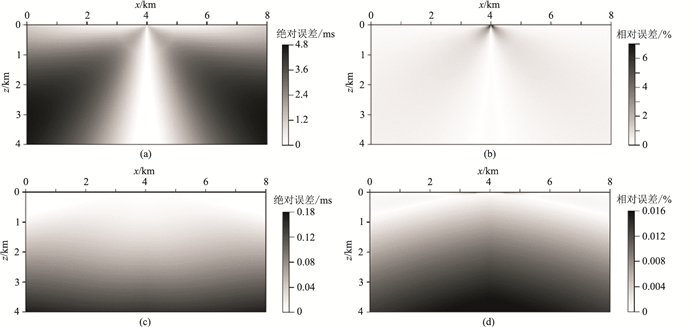
|
图 4 2D模型FMM(a、b)、FMM-F(c、d)算法一阶差分计算的绝对误差(a、c)和相对误差(b、d) |
|
图 5 对应图 4的二阶差分计算结果 |
|
图 6 3D模型中FMM(上)和FMM-F(下)算法采用一阶差分格式计算误差分布 (a)、(c)、(e)、(g)对应x=5 km剖面;(b)、(d)、(f)、(h)对应y=5 km剖面;(a)、(b)、(e)、(f)为绝对误差分布;(c)、(d)、(g)、(h)为相对误差分布。 |
|
图 7 对应图 6采用二阶差分格式计算结果 |
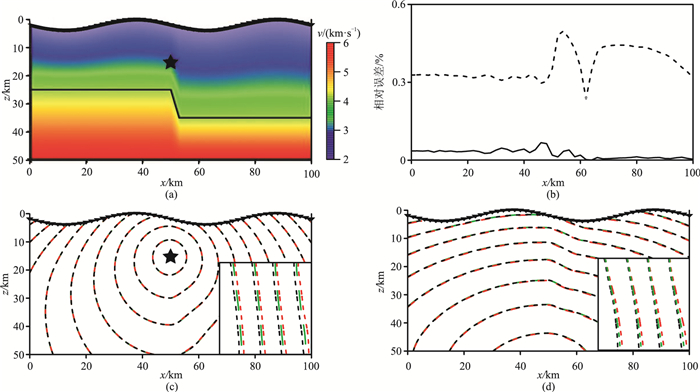
在上文分析了直达波的走时计算精度的基础上,通过一个数值例子验证本文算法的多震相走时计算精度。因没有解析解,故将Multistage ISPM算法[39]的计算结果作为参考值。为了保证Multistage ISPM算法较高的计算精度,网格主节点间距设置为0.25 km,且在主节点间加入19个次级节点,这样通过Multistage ISPM算法求取结果的精度较高,可作为参考值。所用模型如图 8a(2D)、图 9a(3D)所示,其大小分别为
|
图 8 2D起伏模型计算精度分析 (a)起伏界面速度模型,其中黑线为断层界面,五角星为震源,倒三角形为检波器;(b)地表检波器走时相对误差,其中虚线为一阶差分计算结果,实线为二阶差分计算结果;(c)直达下行波走时等值线,其中黑色虚线为ISPM计算结果,红色、绿色虚线分别为本文算法采用一阶、二阶差分计算结果,右下角为局部放大图:(d)经底界面反射后的上行波走时等值线,图例同图c。 |
|
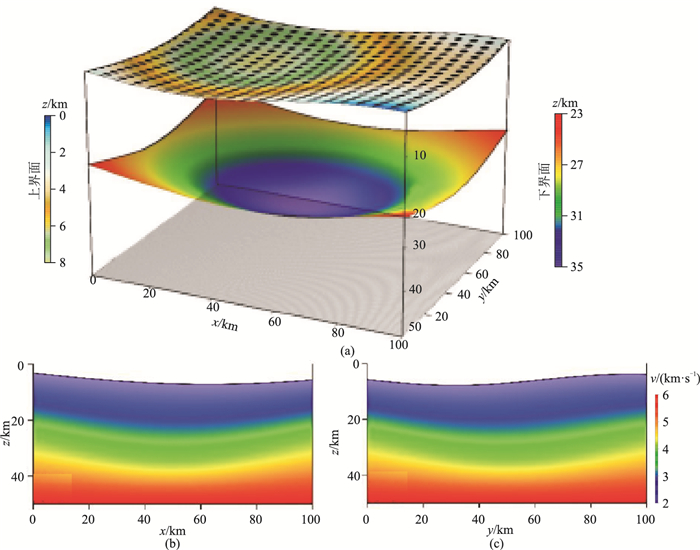
图 9 3D起伏模型及不同剖面的速度分布 (a)3D起伏界面模型,其起伏地表包含一个孔洞形界面,并将底界面作为计算时的反射界面,圆点为检波器;(b) |
2D模型地表的起伏函数设置为:
3D模型地表起伏函数设置为:
由于常规Multistage FMM[31]采用三角网格离散界面,为满足迎风差分条件,需对钝角三角网格进行剖分,导致常规Multistage FMM对界面的离散与Multistage ISPM算法和本文算法不一致,且无可比性,故此部分不再将Multistage FMM作为对比的算法,而仅将Multistage ISPM算法作为参照,以验证本文算法的有效性。
图 8c、图 8d分别为采用图 8a的炮检排列与速度结构模型时,自震源激发后的直达波和自底界面反射上行波的走时等值线图,可见Multistage ISPM算法计算结果对应的黑色虚线、本文算法采用一阶差分计算结果对应的红色虚线及采用二阶差分对应的绿色虚线三种等值线的重合度较高,表明本文算法在计算直达波与反射波时精度较高。为进一步突显对比效果,还对等值线图做了局部放大显示(图 8c、图 8d右下角)及与地面检波器观测反射波到时的相对误差(图 8b,计算公式为
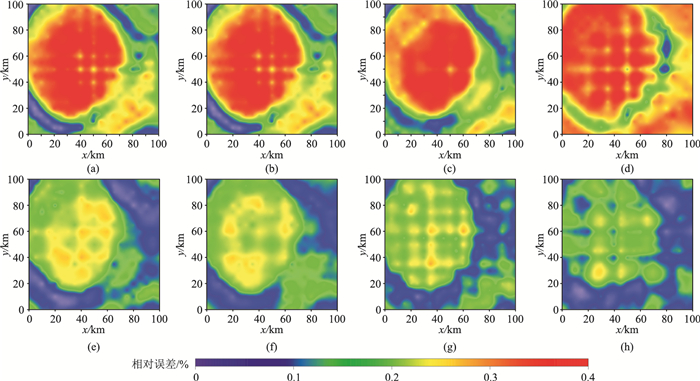
针对3D模型,模拟计算了8种震相地震波的走时,并以Multistage ISPM算法作为标准计算了相对误差(误差计算公式与2D相同,图 10)。它们分别为经上界面反射后的纯反射波P1P(图 10a)、S1S(图 10b)与反射转换波P1S(图 10c)、S1P(图 10d),经底界面反射后的纯反射波P2P(图 10e)与反射转换波S2P(图 10f),以及经上界面与下界面多次透射、反射的转换波P2S1P2S、S2S1P2P。对比图 10上图与下图可见,经上界面反射后的地震波走时的相对误差明显大于经底界面反射的地震波走时,这是缘于上界面存在一个较大孔洞,而底界面仅为一平面;同时,8种地震波震相的走时相对误差均在0.4%以内,可见本文算法对复杂起伏地表(含地下孔穴等剧烈起伏地质异常体)模型中多震相地震波走时的计算精度也较高,可作为一种高效、计算精度高的多震相地震波走时场计算的有效方法。
|
图 10 3D起伏模型地表检波器接收的多震相走时的相对误差分布 上图为经上界面反射后传回检波器的走时相对误差:(a)P1P波;(b)S1S波;(c)P1S波;(d)S1P波;(e)P2P波、(f)S2P波为经下界面反射后传回检波器的走时相对误差;(g)P2S1P2S波、(h)S2S1P2P波为经下界面反射、又经上界面反射后,再次经底界面反射后传回检波器的走时相对误差。 |
由于原始程函方程的FMM采用平面波近似波前,其波前曲率较大,导致震源奇异性问题,且利用三角形(2D)或四面体(3D)缝合界面,实现较为困难。为此,本文发展了一种利用快速行进法求解因式分解程函方程的多震相地震波走时计算算法。该方法采用因式分解求解程函方程解决震源奇异性问题,以不等距差分格式精确定位地表位置,通过迎风混合网格差分公式计算地震波走时,并用窄带技术作为算法的整体波前扩展技术。数值模拟实例表明,以解析解、Multistage ISPM算法[31]作为参考解,与Multistage FMM算法[18]对比分析,得到以下认识:
(1)所提算法计算精度较高,不论是平均绝对误差还是平均相对误差都显著降低;
(2)通过弃用震源网格细化以保证计算精度,且该算法计算效率较高;
(3)利用该算法可灵活、稳定地计算复杂地表条件下的走时。
| [1] |
RAWLINSON N, KENNETT B L. Teleseismic tomography of the upper mantle beneath the southern Lachlan Orogen, Australia[J]. Physics of the Earth and Planetary Interiors, 2008, 167(1-2): 84-97. DOI:10.1016/j.pepi.2008.02.007 |
| [2] |
张风雪, 李永华, 吴庆举, 等. FMTT方法研究华北及邻区上地幔P波速度结构[J]. 地球物理学报, 2011, 54(5): 1233-1242. ZHANG Fengxue, LI Yonghua, WU Qingju, et al. The P wave velocity structure of upper mantle beneath the North China and surrounding regions from FMTT[J]. Chinese Journal of Geophysics, 2011, 54(5): 1233-1242. DOI:10.3969/j.issn.0001-5733.2011.05.012 |
| [3] |
左建军, 林松辉, 孔庆丰, 等. 井间地震直达波和反射波联合层析成像及应用[J]. 石油地球物理勘探, 2011, 46(2): 226-231. ZUO Jianjun, LIN Songhui, KONG Qingfeng, et al. Imaging by a joint tomography of direct wave traveltime and reflection wave traveltime in crosswell seismic and its application[J]. Oil Geophysical Prospecting, 2011, 46(2): 226-231. DOI:10.13810/j.cnki.issn.1000-7210.2011.02.012 |
| [4] |
李忠, 赵锐锐, 周强, 等. 起伏地表TTI各向异性速度建模技术在柯东复杂山地的应用[J]. 石油地球物理勘探, 2022, 57(增刊1): 70-77. LI Zhong, ZHAO Ruirui, ZHOU Qiang, et al. Application of irregular surface TTI anisotropic velocity modeling technology in Kedong complex mountains[J]. Oil Geophysical Prospecting, 2022, 57(S1): 70-77. |
| [5] |
BAI C, GREENHALGH S. 3D local earthquake hypocenter determination with an irregular shortest-path method[J]. Bulletin of the Seismological Society of America, 2006, 96(6): 2257-2268. DOI:10.1785/0120040178 |
| [6] |
赵爱华, 丁志峰, 白志明. 基于射线追踪技术计算地震定位中震源轨迹的改进方法[J]. 地球物理学报, 2015, 58(9): 3272-3285. ZHAO Aihua, DING Zhifeng, BAI Zhiming. Improvement of the ray-tracing based method calculating hypocentralloci for earthquake location[J]. Chinese Journal of Geophysics, 2015, 58(9): 3272-3285. |
| [7] |
刘磊, 宋维琪, 杨小慧, 等. 剪张源约束下的单井微地震震源机制反演[J]. 石油地球物理勘探, 2021, 56(5): 1093-1104. LIU Lei, SONG Weiqi, YANG Xiaohui, et al. Single-well microseismic focal mechanism inversion under shear-tensile source constraint[J]. Oil Geophysical Prospecting, 2021, 56(5): 1093-1104. DOI:10.13810/j.cnki.issn.1000-7210.2021.05.016 |
| [8] |
JULIAN B R, GUBBINS D. Three dimensional seismic ray tracing[J]. Journal of Geophysics, 1977, 43(1): 95-113. |
| [9] |
UM J, THURBER C. A fast algorithm for two-point seismic ray tracing[J]. Bulletin of the Seismological Society of America, 1987, 77(3): 972-986. DOI:10.1785/BSSA0770030972 |
| [10] |
MOSER T J. Shortest path calculation of seismic rays[J]. Geophysics, 1991, 56(1): 59-67. DOI:10.1190/1.1442958 |
| [11] |
BAI C, GREENHALGH S, ZHOU B. 3D ray tracing with a modified shortest path method[J]. Geophysics, 2007, 72(4): T27-T36. DOI:10.1190/1.2732549 |
| [12] |
LEUNG S, QIAN J. An adjoint state method for three-dimensional transmission traveltime tomography using first-arrivals[J]. Communications in Mathematical Sciences, 2006, 4(1): 249-266. DOI:10.4310/CMS.2006.v4.n1.a10 |
| [13] |
TONG P. Adjoint-state traveltime tomography: eikonal equation-based methods and application to the Anza Area in Southern California[J]. Journal of Geophysics Research: Solid Earth, 2021, 126(5): e2021JB021818. DOI:10.1029/2021JB021818 |
| [14] |
谢春, 刘玉柱, 董良国, 等. 伴随状态法初至波走时层析[J]. 石油地球物理勘探, 2014, 49(5): 877-883. XIE Chun, LIU Yuzhu, DONG Liangguo, et al. First arrival tomography based on the adjoint state method[J]. Oil Geophysical Prospecting, 2014, 49(5): 877-883. |
| [15] |
LUO S, QIAN J. Fast sweeping methods for factored anisotropic eikonal equations: multiplicative and additive factors[J]. Journal of Scientific Computing, 2012, 52(2): 360-382. DOI:10.1007/s10915-011-9550-y |
| [16] |
HAN S, ZHANG W, ZHANG J. Calculating qP-wave traveltimes in 2-D TTI media by high-order fast sweeping methods with a numerical quartic equation solver[J]. Geophysical Journal International, 2017, 210(3): 1560-1569. DOI:10.1093/gji/ggx236 |
| [17] |
崔宁城, 黄光南, 李红星, 等. 求解椭圆各向异性介质程函方程的源点快速扫描算法[J]. 石油地球物理勘探, 2019, 54(4): 796-804. CUI Ningcheng, HUANG Guangnan, LI Hongxing, et al. A source fast sweeping method for solving elliptically anisotropic eikonal equation[J]. Oil Geophysical Prospecting, 2019, 54(4): 796-804. |
| [18] |
HUANG G, LUO S, DENG J, et al. Traveltime calculations for qP, qSV, and qSH waves in two‐dimensional tilted transversely isotropic media[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(8): e2019 JB018868. |
| [19] |
HUANG G, LUO S. Hybrid fast sweeping methods for anisotropic eikonal equation in two-dimensional tilted transversely isotropic media[J]. Journal of Scientific Computing, 2020, 84(2): 32. DOI:10.1007/s10915-020-01280-3 |
| [20] |
芦永明, 张伟. 求解二次方程的二维VTI介质qSV波和qSH波走时快速扫描算法[J]. 地球物理学报, 2022, 65(1): 244-255. LU Yongming, ZHANG Wei. Calculating the traveltimes of qSV and qSH waves using fast sweeping method for 2D VTI media by solving quadratic equation[J]. Chinese Journal of Geophysics, 2022, 65(1): 244-255. |
| [21] |
SETHIAN J A, POPOVICI A M. 3-D traveltime computation using the fast marching method[J]. Geophysics, 1999, 64(2): 516-523. DOI:10.1190/1.1444558 |
| [22] |
ZHAO H. A fast sweeping method for Eikonal equations[J]. Mathematics of Computation, 2005, 74(250): 603-627. |
| [23] |
SETHIAN J A, VLADIMIRSKY A. Ordered upwind methods for static Hamilton-Jacobi equations: theory and algorithms[J]. SIAM Journal on Numerical Analysis, 2003, 41(1): 325-363. |
| [24] |
QIAO B, PAN Z, HUANG W, et al. An adaptive finite-difference method for accurate simulation of first-arrival traveltimes in heterogeneous media[J]. Applied Mathematics and Computation, 2021, 394: 125792. |
| [25] |
WAHEED U B. A fast marching eikonal solver for tilted transversely isotropic media[J]. Geophysics, 2020, 85(6): S385-S393. |
| [26] |
兰海强, 张智, 徐涛, 等. 地震波走时场模拟的快速推进法和快速扫描法比较研究[J]. 地球物理学进展, 2012, 27(5): 1863-1870. LAN Haiqiang, ZHANG Zhi, XU Tao, et al. A comparative study on the fast marching and fast sweeping methods in the calculation of first-arrival traveltime field[J]. Progress in Geophysics, 2012, 27(5): 1863-1870. |
| [27] |
GREMAUD P A, KUSTER C M. Computational study of fast methods for the eikonal equation[J]. SIAM Journal on Scientific Computing, 2006, 27(6): 1803-1816. |
| [28] |
CHACON A, VLADIMIRSKY A. Fast two-scale methods for eikonal equations[J]. SIAM Journal on Scientific Computing, 2012, 34(2): A547-A578. |
| [29] |
LI S, VLADIMIRSKY A, FOMEL S. First-break traveltime tomography with the double-square-root eikonal equation[J]. Geophysics, 2013, 78(6): U89-U101. |
| [30] |
BENAICHOUCHE A, NOBEL M. GESRET A. First arrival traveltime tomography using the fast marching method and the adjoint state technique[C]. Extended Abstracts of 77th EAGE Conference and Exhibition, 2015, 1-5.
|
| [31] |
RAWLINSON N, SAMBRIDGE M. Multiple reflection and transmission phases in complex layered media using multistage fast marching method[J]. Geophysics, 2004, 69(5): 1338-1350. |
| [32] |
DE KOOL M, RAWLINSON N, SAMBRIDGE M. A practical grid-based method for tracking multiple refraction and reflection phases in three-dimensional heterogeneous media[J]. Geophysical Journal International, 2006, 167(1): 253-270. |
| [33] |
孙章庆, 孙建国, 韩复兴. 三维起伏地表条件下地震波走时计算的不等距迎风差分法[J]. 地球物理学报, 2012, 55(7): 2441-2449. SUN Zhanqing, SUN Jianguo, HAN Fuxing. Traveltime computation using the upwind finite difference method with nonuniform grid spacing in a 3D undulating surface condition[J]. Chinese Journal of Geophysics, 2012, 55(7): 2441-2449. |
| [34] |
KIM S, FOLIE D. The group marching method: An O(N) level set eikonal solver[C]. SEG Technical Program Expanded Abstracts, 2000, 19: 2297-2300.
|
| [35] |
孙章庆, 孙建国, 王雪秋, 等. 三维复杂山地多级次群推进迎风混合法多波型走时计算[J]. 地球物理学报, 2017, 60(5): 1861-1873. SUN Zhangqing, SUN Jianguo, WANG Xueqiu, et al. Computation of multiple seismic traveltime in mountainous areas with complex 3D conditions using the multistage group marching upwind hybrid method[J]. Chinese Journal of Geophysics, 2017, 60(5): 1861-1873. |
| [36] |
ALKHALIFAH T, FOMEL S. Implementing the fast marching eikonal solver: Spherical versus Cartesian coordinates[J]. Geophysical Prospecting, 2001, 49(2): 165-178. |
| [37] |
FOMEL S, LUO S, ZHAO H. Fast sweeping method for the factored eikonal equation[J]. Journal of Computational Physics, 2009, 228(17): 6440-6455. |
| [38] |
周小乐, 兰海强, 陈凌, 等. 曲线坐标系因式分解程函方程及其走时计算[J]. 地球物理学报, 2020, 63(2): 638-651. ZHOU Xiaole, LAN Haiqiang, CHEN Ling, et al. The factored eikonal equation in curvilinear coordinate system and its numerical solution[J]. Chinese Journal of Geophysics, 2020, 63(2): 638-651. |
| [39] |
BAI C, HUANG G, ZHAO R. 2-D/3-D irregular shortest-path ray tracing for multiple arrivals and its applications[J]. Geophysical Journal International, 2010, 183(3): 1596-1612. |



 李夕海,陕西省西安市灞桥区同心路2号火箭军工程大学,710025。Email:
李夕海,陕西省西安市灞桥区同心路2号火箭军工程大学,710025。Email: