2. 长安大学理学院, 陕西西安 710054
2. School of Science, Chang'an University, Xi'an, Shaanxi 710064, China
传统的瑞雷面波勘探技术常以人工激发方式产生的振动作为震源,通过对地面记录的信号进行分析,提取面波频散曲线并反演探区横波速度,以实现对探区的浅地表结构成像。但因该技术探测深度较小,故在城市环境等外界噪声干扰大的地区施工受到诸多条件限制。而以人类生产活动引起的振动与自然界海啸、地震、火山喷发等天然振动作为震源的被动源面波勘探技术,能够探测到更深的地层,且具有野外施工方式灵活、数据采集成本低等优点,所受关注越来越多。
被动源成像技术的研究和应用主要集中在数据采集方式、频散曲线提取方法和频散曲线反演成像等方面[1-3]。随着研究的不断深入,被动源波场模拟研究逐渐得到充分重视。刘军[4]利用射线追踪方法进行了二维微地震多波场正演模拟研究,但只考虑了震源随位置的变化,而未考虑震源随时间的变化;容娇君等[5]采用延时爆炸反射点代替微地震震源,采用单程波动方程相移结合插值的波场延拓方法对设计的地质模型进行了数值模拟,但只考虑了二维情况下单分量接收和震源随时间的变化;Zhao等[6]对流体注入储层引发的微地震进行了数值模拟,得到了与实际观测数据一致的结果;朱恒等[7]基于地震波有限差分数值模拟得到虚炮集记录的叠加剖面,同时验证了虚炮集记录的准确性,证明了地震干涉技术的可行性;张唤兰[8]根据水力裂缝特征建立微地震震源分布的数学模型,利用三维高阶交错网格有限差分法对微地震波场进行了数值模拟,实现了微地震的定位,但模拟过程中压力震源需满足正态分布;唐杰等[9]通过有限差分正演模拟探讨了微地震波场的传播特性,结果表明微地震震源特性对波形有显著影响;徐宗博[10]采用面波理论公式模拟背景噪声,实现了背景噪声波场模拟,并将该方法的模拟结果与有限差分模拟结果对比,发现有限差分模拟结果细节信息更丰富,更符合实际情况;Wang等[11]对地下储气库进行微震检测过程中进行了微地震波传播的数值模拟,并根据模拟的结果对微震事件进行了分析;雷朝阳等[12]在被动源成像研究中,分别将震源均匀分布在地下某一深度和随机分布在400~500 m范围内,采用声波有限差分进行波场数值模拟,同时利用随机时间序列与Ricker子波褶积构造噪声源合成噪声记录,证实了从透射响应中提取反射响应的有效性;张晟瑞[13]采用两种不同的震源加载方式,同时依据水力压裂诱发微地震的震源激发方式不同,引入三种不同震源机制进行微地震数值模拟,对正演地震记录和不同时刻波场快照进行对比分析,得到了不同震源机制情况下的波场特征。
总体而言,无论是基于已知模型对背景噪声成像方法以及频散曲线提取方法的有效性进行验证,还是对背景噪声数据采集方式进行参数优化,实现背景噪声波场模拟均显得尤为重要。本文通过将随机震源加载于不同地质模型上,模拟计算检波器的叠加响应,从合成记录中提取频散曲线,并与Schwab-Knopoff快速计算方法[14]得出的理论频散曲线进行对比、研究,验证了本文三维背景噪声模拟方法的可行性和有效性。
1 随机震源的产生与加载 1.1 随机震源的产生三维背景噪声波场模拟过程中,随机震源子波类型的产生和震源的加载都是必不可少的。常见子波类型有Ricker子波、Fuchs-Muller子波、正弦衰减子波和Gaussian导数子波等,四种子波表达式分别为
| $ w\left(t\right)=\left\{1-2{\left[\mathrm{{\rm{ \mathsf{π} }} }{f}_{0}\left(t-{t}_{\mathrm{d}}\right)\right]}^{2}\right\}{\mathrm{e}}^{-{\left[\mathrm{{\rm{ \mathsf{π} }} }{f}_{0}\left(t-{t}_{\mathrm{d}}\right)\right]}^{2}} $ | (1) |
| $ w\left(t\right)=\mathrm{s}\mathrm{i}\mathrm{n}\left[2\mathrm{{\rm{ \mathsf{π} }} }{f}_{0}\left(t-{t}_{\mathrm{d}}\right)\right]-0.5\mathrm{s}\mathrm{i}\mathrm{n}\left[4\mathrm{{\rm{ \mathsf{π} }} }{f}_{0}\left(t-{t}_{\mathrm{d}}\right)\right] $ | (2) |
| $ w\left(t\right)=0.75\mathrm{{\rm{ \mathsf{π} }} }{f}_{0}\mathrm{s}\mathrm{i}\mathrm{n}{\left[\mathrm{{\rm{ \mathsf{π} }} }\left(t+{t}_{\mathrm{d}}\right){f}_{0}\right]}^{3} $ | (3) |
| $ w\left(t\right)=-0.01{\left(\mathrm{{\rm{ \mathsf{π} }} }{f}_{0}\right)}^{2}\left(\frac{t-1.2}{2{f}_{0}}\right){\mathrm{e}}^{-{\left(\mathrm{{\rm{ \mathsf{π} }} }{f}_{0}\right)}^{2}{\left(\frac{t-1.2}{2{f}_{0}}\right)}^{2}} $ | (4) |
式中:
|
|
表 1 随机震源参数 |
随机震源的产生是波场模拟的前提,同时,随机震源的加载在整个背景噪声模拟过程中亦是至关重要的,只有在模拟的过程中有效加载了震源才能得到地震波在介质中的传播情况。本文采用的三维均匀介质弹性波应力—速度方程为
| $ \left\{\begin{array}{l}\rho \frac{\partial {V}_{x}}{\partial t}=\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}+{f}_{x}\\ \rho \frac{\partial {V}_{y}}{\partial t}=\frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}+{f}_{y}\\ \rho \frac{\partial {V}_{z}}{\partial t}=\frac{\partial {\tau }_{zx}}{\partial x}+\frac{\partial {\tau }_{zy}}{\partial y}+\frac{\partial {\tau }_{zz}}{\partial z}+{f}_{z}\\ \frac{\partial {\tau }_{xx}}{\partial t}=\left(\lambda +2\mu \right)\frac{\partial {V}_{x}}{\partial x}+\lambda \left(\frac{\partial {V}_{y}}{\partial y}+\frac{\partial {V}_{z}}{\partial z}\right)\\ \frac{\partial {\tau }_{yy}}{\partial t}=\left(\lambda +2\mu \right)\frac{\partial {V}_{y}}{\partial y}+\lambda \left(\frac{\partial {V}_{z}}{\partial z}+\frac{\partial {V}_{x}}{\partial x}\right)\\ \frac{\partial {\tau }_{zz}}{\partial t}=\left(\lambda +2\mu \right)\frac{\partial {V}_{z}}{\partial z}+\lambda \left(\frac{\partial {V}_{x}}{\partial x}+\frac{\partial {V}_{y}}{\partial y}\right)\\ \frac{\partial {\tau }_{xy}}{\partial t}=\mu \left(\frac{\partial {V}_{y}}{\partial x}+\frac{\partial {V}_{x}}{\partial y}\right)\\ \frac{\partial {\tau }_{xz}}{\partial t}=\mu \left(\frac{\partial {V}_{z}}{\partial x}+\frac{\partial {V}_{x}}{\partial z}\right)\\ \frac{\partial {\tau }_{yz}}{\partial t}=\mu \left(\frac{\partial {V}_{z}}{\partial y}+\frac{\partial {V}_{y}}{\partial z}\right)\end{array}\right. $ | (5) |
式中:
对三维均匀介质弹性波速度—应力方程采用交错网格有限差分[16-18]进行模拟。首先将密度、速度和应力分量等参数交错布置与模型网格点或半网格点上;其次,将式(4)所有一阶偏导数进行差分近似,根据计算需要得到相应阶数的差分方程;最后,将时间变量离散,随着时间的步进,根据差分方程循环交替地计算各网格点的应力或速度,最终得到各网格点不同时刻的变量值。本文所采用的交错网格有限差分的优点之一就是分开计算速度和应力,从而可根据不同数据集以不同方式便利地加载震源。
在地震勘探中,常见震源有集中、爆炸和剪切震源[19]。本文采用的差分算法可将震源加载到应力和速度分量中,通过这两种方法的组合能够构建各种震源。将震源加载到应力
| $ \begin{array}{l}{\tau }_{xxi, j, k}^{t+1}= & {\tau }_{xxi, j, k}^{t}+\frac{\mathrm{\Delta }t}{\mathrm{\Delta }h}\{{s}^{t+1}+(\lambda +2\mu \left)\right[{c}_{1}({V}_{xi+1/2, j, k}^{t+1/2}-{V}_{xi-1/2, j, k}^{t+1/2})-{c}_{2}({V}_{xi+3/2, j, k}^{t+1/2}-{V}_{xi-3/2, j, k}^{t+1/2})]+\lambda [{c}_{1}({V}_{yi, j+1/2, k}^{t+1/2}-\\ &{V}_{yi, j-1/2, k}^{t+1/2})-{c}_{2}({V}_{yi, j+3/2, k}^{t+1/2}-{V}_{xi, j-3/2, k}^{t+1/2})+{c}_{1}({V}_{zi, j, k+1/2}^{t+1/2}-{V}_{zi, j, k-1/2}^{t+1/2})-{c}_{2}({V}_{zi, j, k+3/2}^{t+1/2}-{V}_{zi, j, k-3/2}^{t+1/2}\left)\right]\}\end{array} $ | (6) |
| $ \begin{array}{l}{\tau }_{xyi+1/2, j+1/2, k}^{t+1}= & {\tau }_{xyi+1/2, j+1/2, k}^{t}+\frac{\mathrm{\Delta }t}{\mathrm{\Delta }h}\mu [{s}^{t+1}+{c}_{1}({V}_{yi, j+1/2, k}^{t+1/2}-{V}_{yi, j-1/2, k}^{t+1/2})-{c}_{2}({V}_{yi, j+3/2, k}^{t+1/2}-{V}_{yi, j-3/2, k}^{t+1/2}\left)\right]+\\ & \frac{\mathrm{\Delta }t}{\mathrm{\Delta }h}\mu [{s}^{t+1}+{c}_{1}({V}_{xi+1/2, j, k}^{t+1/2}-{V}_{xi-1/2, j, k}^{t+1/2})-{c}_{2}({V}_{xi+3/2, j, k}^{t+1/2}-{V}_{xi-3/2, j, k}^{t+1/2}\left)\right]\end{array} $ | (7) |
式中:空间步长为
将震源代入不同速度网格点可实现不同方向集中力源的加载过程,将震源加载到速度分量
| $ \begin{array}{l}{V}_{xi+1/2, j, k}^{t+1/2}= & {V}_{xi+1/2, j, k}^{t-1/2}+\frac{\mathrm{\Delta }t}{\rho \mathrm{\Delta }h}[{s}^{t+1/2}+{c}_{1}({\tau }_{xxi+1, j, k}^{t}-{\tau }_{xxi, j, k}^{t})+{c}_{2}({\tau }_{xxi+2, j, k}^{t}-{\tau }_{xxi-1, j, k}^{t}\left)\right]+\\ & \frac{\mathrm{\Delta }t}{\rho \mathrm{\Delta }h}[{s}^{t+1/2}+{c}_{1}({\tau }_{xyi+1/2, j+1/2, k}^{t}-{\tau }_{xxi+1/2, j-1/2, k}^{t})+{c}_{2}({\tau }_{xyi+1/2, j+3/2, k}^{t}-{\tau }_{xxi+1/2, j-3/2, k}^{t}\left)\right]+\\ & \frac{\mathrm{\Delta }t}{\rho \mathrm{\Delta }h}[{s}^{t+1/2}+{c}_{1}({\tau }_{xzi+1/2, j, k+1/2}^{t}-{\tau }_{xxi+1/2, j, k-1/2}^{t})+{c}_{2}({\tau }_{xzi+1/2, j, k+3/2}^{t}-{\tau }_{xxi+1/2, j, k-3/2}^{t}\left)\right]\end{array} $ | (8) |
同理,可得到震源加载到正应力(
| $ \mathrm{\Delta }h\le \frac{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{n}=\frac{{V}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{n{f}_{\mathrm{m}\mathrm{a}\mathrm{x}}} $ | (9) |
式中:
同时,为避免数值模拟过程中发生不稳定,需进行稳定性判别,判别条件[20]采用
| $ \left\{\begin{array}{l}\mathrm{\Delta }t\le \frac{\mathrm{\Delta }h}{q\sqrt{3}{V}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\\ q=\sum\limits_{o}\left|{\beta }_{o}\right|\end{array}\right. $ | (10) |
式中:
本文背景噪声波场模拟在已知模型介质结构和参数的前提下实现。首先将产生的随机震源加载于模型的交错网格系统之上,利用交错差分计算并研究地震波在地下介质中的传播规律;然后提取各检波器的叠加响应得到频散曲线。模拟得到的信号为无道头微机格式,能够作为二进制文件直接进行读取,跳过文件卷头和道头,即为信号存储的数据文件。通常在提取频散曲线前需对模拟数据进行如滤波、台站道间距计算、时间域数据标准化和频谱白化等预处理。整个随机震源数值模拟及频散曲线提取过程如图 1所示。

|
图 1 随机震源数值模拟及频散曲线提取流程 |
本文通过三组理论模型的被动源数值模拟数据提取频散曲线与理论频散曲线或频散能量图进行对比,以验证本文随机震源的产生与加载在被动源噪声波场模拟中的可行性和有效性。
2.1 高速双层模型高速双层模型尺寸为3120 m×3120 m×3120 m,具体参数如表 2所示。
|
|
表 2 高速双层模型参数 |
模型网格间距
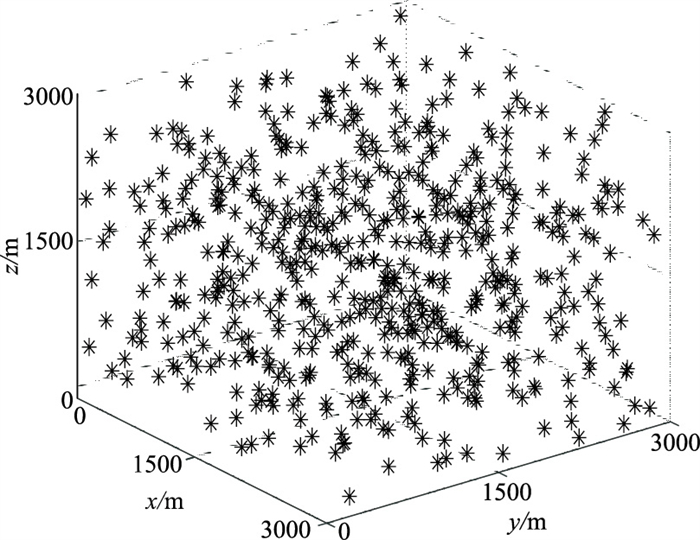
|
图 2 高速双层模型随机震源空间分布图 |
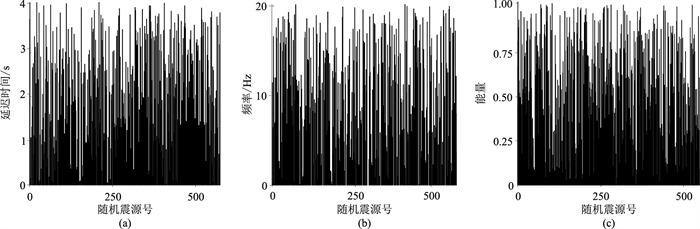
|
图 3 高速双层模型随机震源的相关参数柱状图 (a)震源延迟时间柱状图;(b)震源主频柱状图;(c)震源能量柱状图 |
沿地表x方向布设221个线性排列的检波器,间距为12 m。采样率为0.2 ms,采样时间为4.0 s。模型四周采用吸收层厚度为20个网格点的CPML吸收边界,地表采用镜像法处理的自由边界[19],正演得到有效的合成地震记录(图 4)。
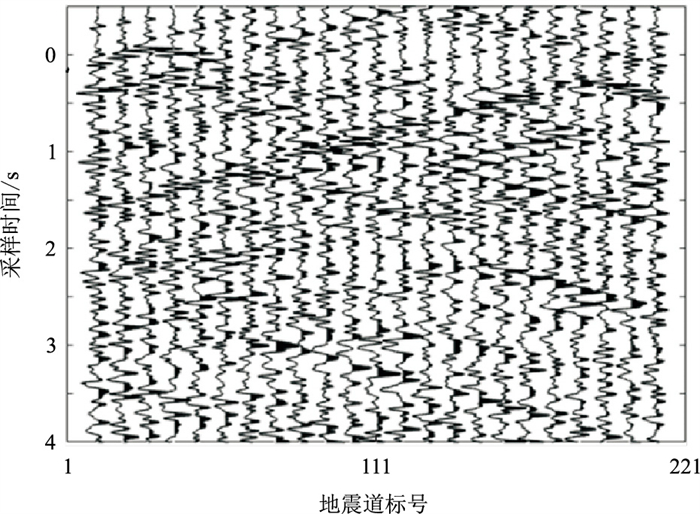
|
图 4 高速双层模型噪声合成记录(每10道显示1道) |
模型尺寸为200 m×100 m×100 m,具体参数如表 3所示。
|
|
表 3 三层含低速层模型参数 |
模型网格间距
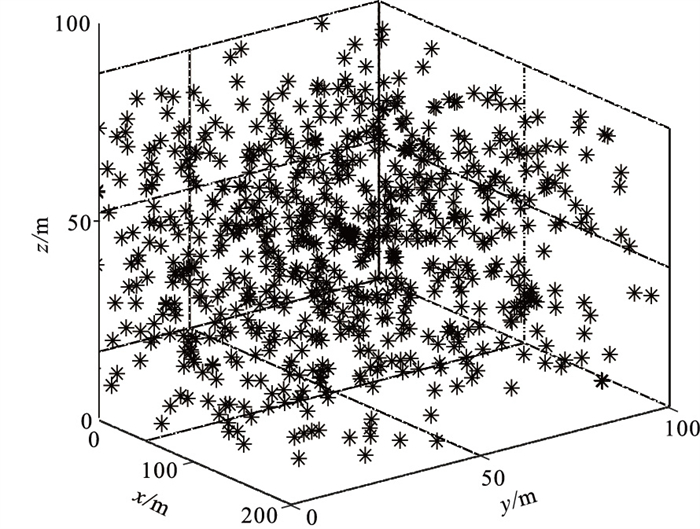
|
图 5 三层含低速层模型随机震源空间分布图 |

|
图 6 三层含低速层模型随机震源的相关参数柱状图 (a)震源延迟时间柱状图;(b)震源主频柱状图;(c)震源能量柱状图 |
沿地表
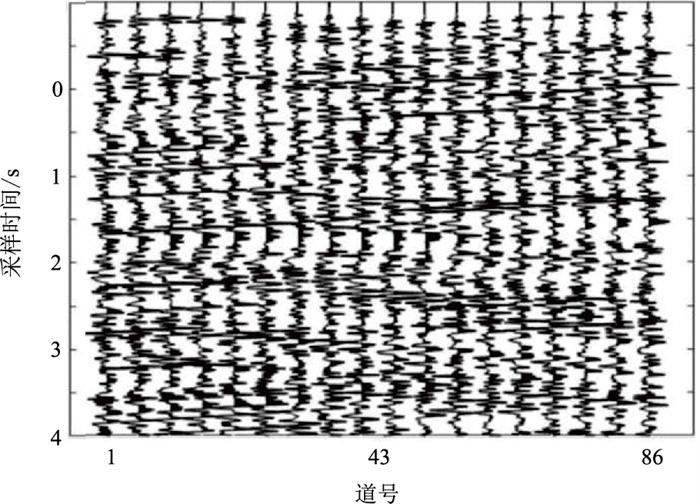
|
图 7 三层含低速层模型噪声合成记录(每5道显示1道) |
模型尺寸为200 m×100 m×100 m,具体参数如表 4所示。
|
|
表 4 垂直断层模型参数 |
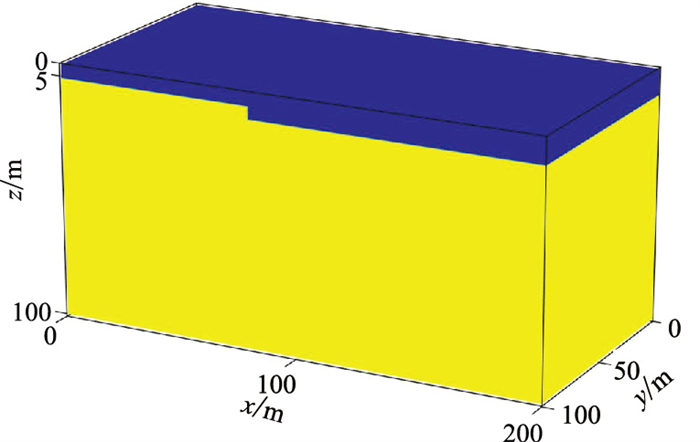
垂直断层断面位于x方向80 m处,模型结构如图 8所示。模型网格间距
|
图 8 垂直断层模型 |
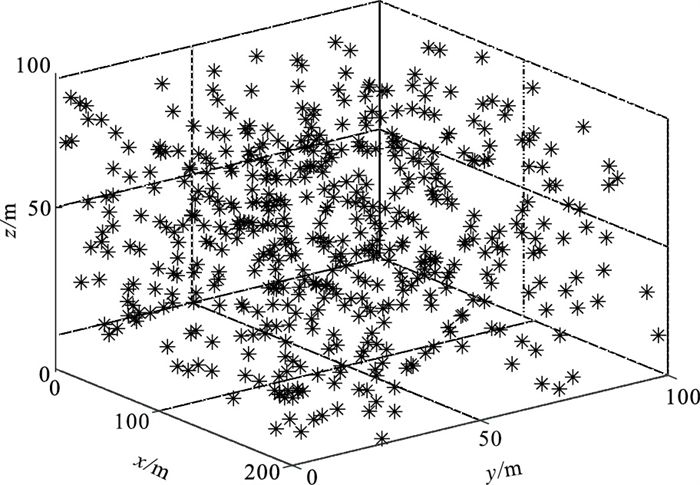
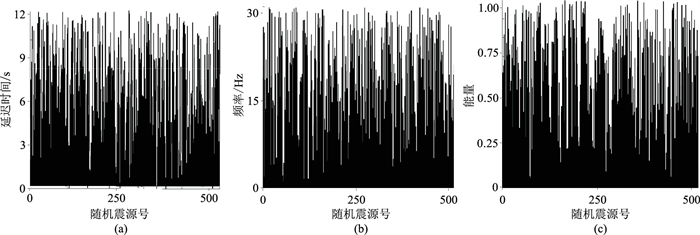
图 9和图 10分别为垂直断层模型随机震源空间分布图和随机震源的相关参数柱状图。
|
图 9 断层模型随机震源空间分布图 |
|
图 10 垂直断层模型随机震源相关参数柱状图 (a)震源延迟时间柱状图;(b)震源主频柱状图;(c)震源能量柱状图 |
沿地表x方向线性排列的检波器有86个,道间距为2 m,采样率为0.2 ms,采样时间为1.0 s。模型四周采用吸收层厚度为20个网格点的CPML吸收边界,地表采用镜像法处理的自由边界[21]。正演得到有效的合成地震记录见图 11。

|
图 11 断层模型噪声合成记录(每3道显示1道) |
为验证三维背景噪声模拟的可行性和有效性,本文通过理论合成噪声记录提取面波频散曲线,并与频散方程得到的理论频散曲线进行对比、研究。
3.1 预处理在提取面波频散曲线之前,需要对数值模拟生成的被动源地震记录进行预处理。首先,计算各道之间的距离,为随后的互相关计算提供参数。然后,依据不同设计地质模型采用不同通带、阻带频段进行带通滤波,并对滤波后的地震记录采用滑动绝对平均法进行时间域标准化,以消除采集台站周围异常信号的影响。经多次试验,发现时间窗口长度为40 s时得到的数据结果最佳。再次,经过傅里叶变换将信号从时间域转换到频率域,对时间域标准化后的数据进行频谱白化。频谱白化的目的是使频谱曲线更均匀,避免之后计算出现“谱孔现象”。最后,利用傅里叶逆变换将频谱白化后的数据再次转换到时间域。
3.2 互相关处理本文提取频散曲线采用基于Aki公式的两道法[22],该方法基于互相关理论,利用互相关谱和第一类零阶贝塞尔函数进行拟合。而互相关处理是对预处理的频率域的实部进行负半轴的反序和正半轴的叠加,再进行对称化处理的过程。
在高速双层模型的互相关处理过程中,选取第1道与第10道的随机震源合成噪声记录进行相关处理和傅里叶变换,得到互相关结果和频率域互相关谱。同时,为了验证三维背景噪声波场模拟在频散曲线提取效果上的优势,在相关参数保持不变的前提下,本文基于二维和三维波动方程模拟背景噪声,并选取第1道与第55道的二维和三维随机震源合成噪声记录进行相关处理。为验证三维背景噪声波场模拟方法在复杂模型的适用性,使用垂直断层模型并选取其第1道与第78道的三维随机震源合成噪声记录进行相关处理。
3.3 提取频散曲线两道法[22]提取频散曲线的基本原理是对数值模拟数据经预处理和互相关处理后,得到的互相关谱实部,进行三次多项式插值获得相应零点
在高速双层模型频散曲线提取时,发现
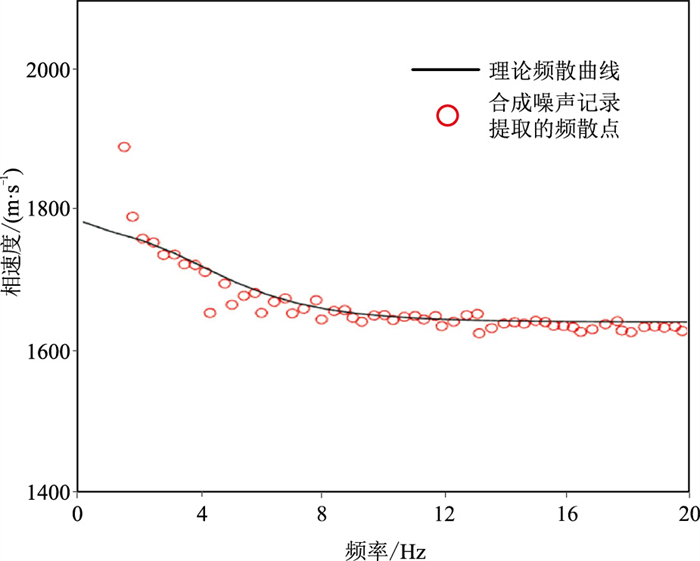
|
图 12 理论频散曲线与合成噪声记录提取频散曲线对比 |
三层含低速层模型频散曲线提取过程中,发现
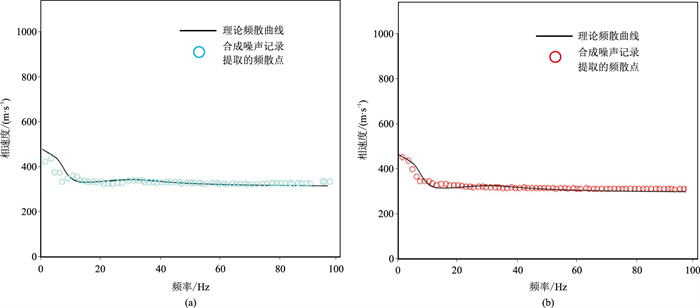
|
图 13 理论频散曲线与二维(a)、三维(b)波动方程合成噪声记录提取的频散曲线对比 |
由于理论频散曲线的计算模型局限于层状介质,无法计算断层模型的理论频散曲线,故设置一个相同断层模型使用主动源方法作为对照,主动源方法炮检距为0,震源子波采用主频为20 Hz的Ricker子波。
将主动源提取的频散能量图和背景噪声提取的频散曲线进行对比。在提取垂直断层模型频散曲线时,发现m=0时频散曲线提取效果最佳,图 14即为m=0时,对背景噪声模拟数据利用两道法提取的频散曲线与主动源方法频散能量图。由图可见,利用两道法计算的频散曲线(离散点)与主动源方法模拟频散能量图拟合较好,只有少量的离散点偏离理论频散曲线。
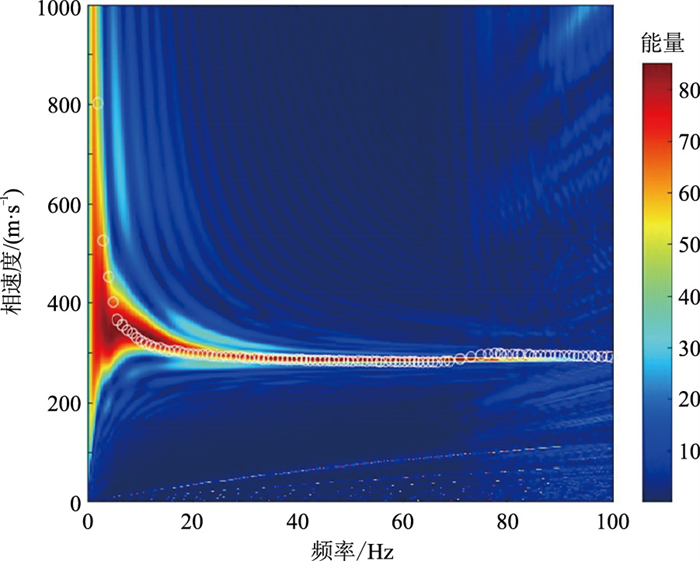
|
图 14 背景噪声频散曲线与主动源方法频散能量图 |
本文以三维波动方程和二维波动方程为理论基础,用随机震源产生的振动叠加模拟背景噪声,实现了不同地质模型的背景噪声波场模拟。对比、分析模拟数据提取的频散曲线与理论频散曲线表明,当震源参数处于合理范围时,模拟数据提取的频散曲线与理论频散曲线拟合程度较为理想。在无法得到理论频散曲线的模型中,将背景噪声提取的频散曲线与相同模型使用主动源方法得到的频散能量图进行对比,也可得到较理想结果,从而验证了背景噪声模拟对较复杂模型的适用性。此外,三维模拟数据频散曲线提取精度在低频段比二维模拟数据更高,且高频段的频散曲线更光滑。
| [1] |
OKADA H. Estimates of an S wave velocity distribution using long-period microtremors[J]. Geophysical Bulletin of Hokkaido University, 1983, 42: 119-143. |
| [2] |
TSAI V C, MOSCHETTI M P. An explicit relationship between time-domain noise correlation and spatial autocorrelation (SPAC) results[J]. Geophysical Journal International, 2010, 182(1): 454-460. |
| [3] |
EKSTRÖM G, ABERS G A, WEBB S C. Determination of surface-wave phase velocities across US array from noise and Aki's spectral formulation[J]. Geophysical Research Letters, 2009, 36(18): L18301. DOI:10.1029/2009GL039131 |
| [4] |
刘军. 基于射线追踪的微地震模型多波场正演模拟[D]. 山东青岛: 中国石油大学(华东), 2009. LIU Jun. Research on Multi-Wave Field Forward Simulation of Micro-Seismic Model Based on Ray Tracing[D]. China University of Petroleum (East China), Qingdao, Shandong, 2009. |
| [5] |
容娇君, 张固澜, 郭晓玲, 等. 压裂/微地震事件地面响应信号模拟[J]. 石油天然气学报, 2010, 32(4): 247-250, 432. RONG Jiaojun, ZHANG Gulan, GUO Xiaoling, et al. Surface response signal simulation of fracturing and microseismic events[J]. Journal of Oil and Gas Technology, 2010, 32(4): 247-250, 432. |
| [6] |
ZHAO X, YOUNG R P. Numerical modeling of seismicity induced by fluid injection in naturally fractured reservoirs[J]. Geophysics, 2011, 76(6): WC167-WC180. DOI:10.1190/geo2011-0025.1 |
| [7] |
朱恒, 王德利, 时志安, 等. 地震干涉技术被动源地震成像[J]. 地球物理学进展, 2012, 27(2): 496-502. ZHU Heng, WANG Deli, SHI Zhian, et al. Passive seismic imaging of seismic interferometry[J]. Progress in Geophysics, 2012, 27(2): 496-502. DOI:10.6038/j.issn.1004-2903.2012.02.012 |
| [8] |
张唤兰. 微地震数值模拟及震源定位方法研究[D]. 陕西西安: 西安科技大学, 2014. ZHANG Huanlan. Numerical Simulation of Microseismic and Study on Source Location Method[D]. Xi'an University of Science and Technology, Xi'an, Shaanxi, 2014. |
| [9] |
唐杰, 方兵, 蓝阳, 等. 压裂诱发的微地震震源机制及信号传播特性[J]. 石油地球物理勘探, 2015, 50(4): 643-649. TANG Jie, FANG Bing, LAN Yang, et al. Focal mechanism of micro-seismic induced by hydrofracture and its signal propagation characteristics[J]. Oil Geophysical Prospecting, 2015, 50(4): 643-649. |
| [10] |
徐宗博. 高频背景噪声波场模拟与面波成像[D]. 湖北武汉: 中国地质大学(武汉), 2016. XU Zongbo. High-Frequency Ambient Seismic Noise Simulation and Surface-Wave Imaging[D]. China University of Geosciences(Wuhan), Wuhan, Hubei, 2016. |
| [11] |
WANG F, XU G, QU X, et al. Numerical simulation of microseismic wave propagation for underground gas storage[C]. International Geophysical Conference, 2017, 827-830.
|
| [12] |
雷朝阳, 刘怀山. 被动源成像中透射与反射响应关系研究[J]. 中国海洋大学学报(自然科学版), 2017, 47(6): 112-118. LEI Chaoyang, LIU Huaishan. Study on relation between transmission and reflection responses of passive seismic imaging[J]. Periodical of Ocean University of China(Nature Science), 2017, 47(6): 112-118. |
| [13] |
张晟瑞. 水力压裂微地震正演模拟分析及应用研究[D]. 黑龙江大庆: 东北石油大学, 2018. ZHANG Shengrui. A Study on Analysis and Application of Hydraulic Fracturing Microseismic Forward Modeling[D]. Northeast Petroleum University, Daqing, Heilongjiang, 2018. |
| [14] |
KNOPOFF L. A matrix method for elastic wave problems[J]. Bulletin of the Seismological Society of America, 1964, 54(1): 431-438. DOI:10.1785/BSSA0540010431 |
| [15] |
李远林. 被动源面波法在渭河盆地地层结构分层中的应用研究[D]. 陕西西安: 长安大学, 2020. LI Yuanlin. Application of Passive Surface Wave Method in Stratigraphic Classification of Weihe Basin[D]. Chang'an University, Xi'an, Shaanxi, 2020. |
| [16] |
MADARIAGA R. Dynamics of an expanding circular fault[J]. Bulletin of the Seismological Society of America, 1976, 66(3): 639-666. DOI:10.1785/BSSA0660030639 |
| [17] |
彭更新, 刘威, 郭念民, 等. 基于时空域交错网格有限差分法的应力速度声波方程数值模拟[J]. 石油物探, 2022, 61(1): 156-165, 173. PENG Gengxin, LIU Wei, GUO Nianmin, et al. A time-space domain dispersion-relationship-based staggered-grid finite-difference scheme for modeling the stress-velocity acoustic wave equation[J]. Geophysical Prospecting for Petroleum, 2022, 61(1): 156-165, 173. DOI:10.3969/j.issn.1000-1441.2022.01.016 |
| [18] |
唐超, 文晓涛, 王文化. 基于最小范数优化交错网格有限差分系数的波动方程数值模拟[J]. 石油地球物理勘探, 2021, 56(5): 1039-1047. TANG Chao, WEN Xiaotao, WANG Wenhua. Numerical simulation of wave equations based on minimum-norm optimization of staggered-grid finite-difference coefficients[J]. Oil Geophysical Prospecting, 2021, 56(5): 1039-1047. |
| [19] |
全红娟, 朱光明, 王晋国, 等. 地震波震源加载方式对波场特征的影响[J]. 西北大学学报(自然科学版), 2012, 42(6): 902-906. QUAN Hongjuan, ZHU Guangming, WANG Jinguo, et al. The influence of loading method of seismic source on wave field characteristic[J]. Journal of Northwest University (Natural Science Edition), 2012, 42(6): 902-906. DOI:10.3969/j.issn.1000-274X.2012.06.006 |
| [20] |
COURANT R, FRIEDRICHS K, LEWY H. On the partial difference equations of mathematical physics[J]. IBM Journal of Research and Development, 1967, 11(2): 215-234. DOI:10.1147/rd.112.0215 |
| [21] |
GRAVES R W. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences[J]. Bulletin of the Seismological Society of America, 1996, 86(4): 1091-1106. |
| [22] |
邵广周, 岳亮, 李远林, 等. 被动源瑞利波两道法提取频散曲线的质量控制方法[J]. 物探与化探, 2019, 43(6): 1297-1308. SHAO Guangzhou, YUE Liang, LI Yuanlin, et al. A study of quality control of extracting dispersion curves by two-channel method of passive Rayleigh waves[J]. Geophysical and Geochemical Exploration, 2019, 43(6): 1297-1308. |
| [23] |
李欣欣. 主动源与被动源瑞利波联合成像方法研究[D]. 陕西西安: 长安大学, 2017. LI Xinxin. Study on the Joint Tomographic Method for Active and Passive Source Rayleigh Wave Data[D]. Chang'an University, Xi'an, Shaanxi, 2017. |
| [24] |
BENSEN G D, RITZWOLLER M H, BARMIN M P, et al. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements[J]. Geophysical Journal International, 2007, 169(3): 1239-1260. |
| [25] |
BOSCHI L, WEEMSTRA C, VERBEKE J, et al. On measuring surface wave phase velocity from station-station cross-correlation of ambient signal[J]. Geophysical Journal International, 2013, 192(1): 346-358. |



 邵广周, 陕西省西安市雁塔区雁塔路126号长安大学雁塔校区,710054。Email:
邵广周, 陕西省西安市雁塔区雁塔路126号长安大学雁塔校区,710054。Email: