2. 内蒙古有色地质矿业(集团)物探勘查公司, 内蒙古呼和浩特 010010
2. Inner Mongolia Nonferrous Geology and Mining (Group) Geophysical Exploration Co., Ltd, Hohhot, Inner Mongolia 010010, China
受到地层黏滞性的影响,地震波在地下介质中传播时能量会衰减,这种衰减在地表附近尤为严重。若用完全弹性模型模拟地下真实介质,结果与实际差别较大。研究表明,黏弹模型可以较精确地反映地层的吸收作用,近似代替实际地下介质更为合理。很多学者对黏弹介质中的地震波场进行了数值模拟。Robertsson等[1]设计了二维速度—应力交错网格模拟方法,并推广至三维黏弹模型[2];Xu等[3-4]实现了三维起伏地表黏弹模型的数值模拟,并通过定义新的复合记忆变量有效节省了计算机内存;Štekl等[5]在频率域用旋转有限差分算子对黏弹模型进行了精确的数值模拟。在中国,宋常瑜等[6]利用有限差分法进行了井间数值黏弹模拟,并分析了地震波在井间的传播特征;唐启军等[7]利用有限差分法模拟了黏弹单斜各向异性介质中的地震波场;陈玉玺等[8]研究了三维黏弹介质地震波场数值模拟技术;陈豪等[9]利用交错网格有限差分法模拟了三维黏弹性介质中的地震波场,并分析了品质因子对波场特征的影响。
常用的数值模拟方法包括有限差分法[10-12]、伪谱法[13-14]、有限元法[15-16]、普元法[17-18]等。其中有限差分法因具有原理简单、易编程实现、计算效率高、对内存需求相对较小等特点,在地震波数值模拟中使用最广泛。常规有限差分法采用笛卡尔坐标系下的规则网格,在模拟起伏地表时必然会出现阶梯状的边界,从而引起虚假散射波。为减弱这种虚假散射波,需采用精细网格,这会导致存储量的增加和计算量的增大。因此,发展了可变网格和不规则网格地震波数值模拟方法。Hayashi等[19]采用空间变网格法加密起伏地表附近的网格,从而尽量消除阶梯状网格带来的误差,同时能减小计算量。董良国[20]和Tarrass等[21]利用纵向坐标变换思路,将起伏边界变换为水平边界,然后在变换后的矩形网格中采用有限差分法求解地震波方程。但是他们的方法只适用于地形起伏较缓的情况,在起伏较大时容易出现不稳定现象。Lan等[22]、Sun等[23]在贴体网格下使用同位网格有限差分法求解波动方程,能够适应任意起伏地表,计算精度较高,但为了满足自由边界条件需要做繁杂的坐标旋转和插值运算。为此,蒋丽丽[24]、丘磊[25]、李庆洋等[26]提出采用正交贴体网格对起伏地表模型进行网格剖分。
在对现有各种起伏地表地震波数值模拟方法进行研究的基础上,本文将Zhang等[27]提出的改进RL(Ryskin & Leal)正交贴体网格生成技术[28]引入起伏地表下黏弹介质的网格剖分,采用牵引力镜像法实现起伏地表处的自由边界条件。由于采用了正交贴体网格,可以直接实施笛卡尔坐标系下的自由边界条件,从而避免了繁杂的坐标旋转或插值运算。在曲线坐标系中,通常情况下变量并非严格定义在半网格点上[29],因而必须进行复杂的插值运算求取没有定义在交错位置上的变量值,这不仅会降低计算效率,还极大地影响了差分算法的精度。因此,本文采用Boegy等[30]提出的选择性滤波同位网格有限差分法计算曲线坐标系下的一阶速度—应力方程。最后通过数值算例验证本文方法的精度和适用性。
1 网格剖分方法正交贴体网格生成实际上是一个数学变换过程,即由任意形状的物理域
| $ \left\{\begin{array}{l}\xi =\xi \left(x, z\right)\\ \eta =\eta \left(x, z\right)\end{array}\right. $ | (1) |
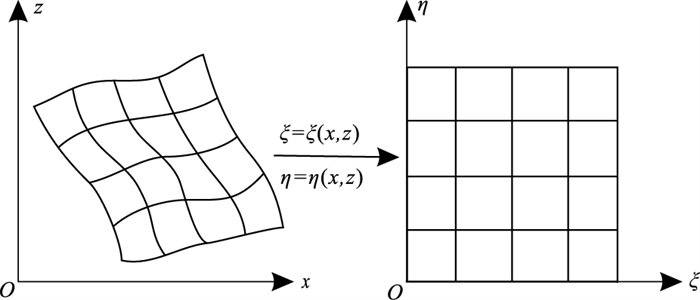
|
图 1 网格映射示意图 |
RL正交贴体网格可由(x,z)平面上的一对Laplace方程生成[28]
| $ \left\{\begin{array}{l}\frac{\partial }{\partial \xi }\left(f{x}_{, \xi }\right)+\frac{\partial }{\partial \eta }\left(\frac{1}{f}{z}_{, \eta }\right)=0\\ \frac{\partial }{\partial \xi }\left(f{z}_{, \xi }\right)+\frac{\partial }{\partial \eta }\left(\frac{1}{f}{x}_{, \eta }\right)=0\end{array}\right. $ | (2) |
式中:
| $ f=\frac{{h}_{\eta }}{{h}_{\xi }}=\sqrt{\frac{({x}_{, \eta }{)}^{2}+({z}_{, \eta }{)}^{2}}{({x}_{, \xi }{)}^{2}+({z}_{, \xi }{)}^{2}}} $ | (3) |
| $ \left\{\begin{array}{l}{h}_{\xi }=\sqrt{{g}_{\xi \xi }}\\ {h}_{\eta }=\sqrt{{g}_{\eta \eta }}\end{array}\right. $ | (4) |
式中:
| $ \left\{\begin{array}{l}{g}_{\xi \xi }=({x}_{, \xi }{)}^{2}+({z}_{, \xi }{)}^{2}\\ {g}_{\eta \eta }=({x}_{, \eta }{)}^{2}+({z}_{, \eta }{)}^{2}\end{array}\right. $ | (5) |
如果
| $ {\stackrel{-}{f}}_{i, j}=\frac{{\left({\stackrel{-}{h}}_{\eta }\right)}_{j}\cdot {r}_{\eta }+{\left({h}_{\eta }\right)}_{i, j}\cdot \left(1-{r}_{\eta }\right)}{{\left({\stackrel{-}{h}}_{\xi }\right)}_{i}\cdot {r}_{\xi }+{\left({h}_{\xi }\right)}_{i, j}\cdot \left(1-{r}_{\xi }\right)} $ | (6) |
| $ {\left({\stackrel{-}{h}}_{\xi }\right)}_{i}=\frac{1}{{N}_{\eta }-2}\sum\limits_{j=2}^{{N}_{\eta }-1}{\left({h}_{\xi }\right)}_{i, j} $ | (7) |
| $ {\left({\stackrel{-}{h}}_{\eta }\right)}_{j}=\frac{1}{{N}_{\xi }-2}\sum\limits_{i=2}^{{N}_{\xi }-1}{\left({h}_{\eta }\right)}_{i, j} $ | (8) |

|
图 2 内部网格点严重畸变的网格剖分示意图 |
式中:i和j分别为
| $ {\left({r}_{\xi }\right)}_{i, j} =\frac{\left|{\left({h}_{\xi }\right)}_{i, j}-{\left({\stackrel{-}{h}}_{\xi }\right)}_{i}\right|}{{\left({h}_{\xi }\right)}_{i, j}+{\left({\stackrel{-}{h}}_{\xi }\right)}_{i}} $ | (9) |
| $ {\left({r}_{\eta }\right)}_{i, j}=\frac{\left|{\left({h}_{\eta }\right)}_{i, j}-{\left({\stackrel{-}{h}}_{\eta }\right)}_{j}\right|}{{\left({h}_{\eta }\right)}_{i, j}+{\left({\stackrel{-}{h}}_{\eta }\right)}_{j}} $ | (10) |
利用改进的RL算法兼顾了网格剖分的正交性和光滑性,避免了起伏地表附近网格点的畸变(图 3)。
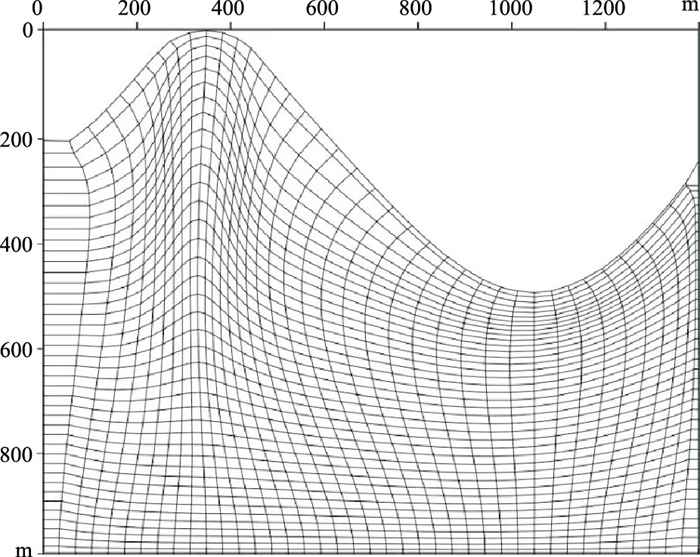
|
图 3 改进后的RL正交贴体网格剖分示意图 |
利用链式法则和笛卡尔坐标系下的Kelvin黏弹介质一阶速度—应力方程,可以推导出曲线坐标系下的二维黏弹介质一阶速度—应力波动方程。矩阵形式的波动方程可表示为
| $ \dot{{\boldsymbol{U}}}={\boldsymbol{A}}{{\boldsymbol{U}}}_{, \xi }+{\boldsymbol{B}}{{\boldsymbol{U}}}_{, \eta }+{\boldsymbol{C}}{\dot{{\boldsymbol{U}}}}_{, \xi }+{\boldsymbol{D}}{\dot{{\boldsymbol{U}}}}_{, \eta } $ | (11) |
式中:U为由速度和应力组成的列矩阵;
| $ {\boldsymbol{U}}={\left[{v}_{x}, {v}_{z}, {\tau }_{xx}, {\tau }_{zz}, {\tau }_{xz}\right]}^{\mathrm{T}} $ | (12) |
| $ \begin{array}{l}\\ {\boldsymbol{A}}=\left[\begin{array}{ccccc}0& 0& {\xi }_{, x}/\rho & 0& {\xi }_{, z}/\rho \\ 0& 0& 0& {\xi }_{, z}/\rho & {\xi }_{, x}/\rho \\ \left(\lambda +2\mu \right){\xi }_{, x}& \lambda {\xi }_{, z}& 0& 0& 0\\ \lambda {\xi }_{, x}& \left(\lambda +2\mu \right){\xi }_{, z}& 0& 0& 0\\ \mu {\xi }_{, z}& \mu {\xi }_{, x}& 0& 0& 0\end{array}\right]\end{array} $ | (13) |
| $ {\boldsymbol{B}}=\left[\begin{array}{ccccc}0& 0& {\eta }_{, x}/\rho & 0& {\eta }_{, z}/\rho \\ 0& 0& 0& {\eta }_{, z}/\rho & {\eta }_{, x}/\rho \\ \left(\lambda +2\mu \right){\eta }_{, x}& \lambda {\eta }_{, z}& 0& 0& 0\\ \lambda {\eta }_{, x}& \left(\lambda +2\mu \right){\eta }_{, z}& 0& 0& 0\\ \mu {\eta }_{, z}& \mu {\eta }_{, x}& 0& 0& 0\end{array}\right] $ | (14) |
| $ {\boldsymbol{C}}=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ \left({\lambda }^{\text{'}}+2{\mu }^{\text{'}}\right){\xi }_{, x}& {\lambda }^{\text{'}}{\xi }_{, z}& 0& 0& 0\\ {\lambda }^{\text{'}}{\xi }_{, x}& \left({\lambda }^{\text{'}}+2{\mu }^{\text{'}}\right){\xi }_{, z}& 0& 0& 0\\ {\mu }^{\text{'}}{\xi }_{, z}& {\mu }^{\text{'}}{\xi }_{, x}& 0& 0& 0\end{array}\right] $ | (15) |
| $ {\boldsymbol{D}}=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ \left({\lambda }^{\text{'}}+2{\mu }^{\text{'}}\right){\eta }_{, x}& {\lambda }^{\text{'}}{\eta }_{, z}& 0& 0& 0\\ {\lambda }^{\text{'}}{\eta }_{, x}& \left({\lambda }^{\text{'}}+2{\mu }^{\text{'}}\right){\eta }_{, z}& 0& 0& 0\\ {\mu }^{\text{'}}{\eta }_{, z}& {\mu }^{\text{'}}{\eta }_{, x}& 0& 0& 0\end{array}\right] $ | (16) |
其中:
| $ \left\{\begin{array}{l}\lambda +2\mu =\rho {v}_{\mathrm{P}}^{2}\\ \mu =\rho {v}_{\mathrm{S}}^{2}\\ {\lambda }^{\text{'}}+2{\mu }^{\text{'}}=\frac{\rho {v}_{\mathrm{P}}^{2}}{{Q}_{\mathrm{P}}\omega }\\ {\mu }^{\text{'}}=\frac{\rho {v}_{\mathrm{S}}^{2}}{{Q}_{\mathrm{S}}\omega }\end{array}\right. $ | (17) |
式中ω为圆频率。
2.2 空间离散算法对式(11)的空间导数,本文用优化的7点同位网格中心差分格式[31]求解。该格式中所有变量和模型介质参数都定义在同一个网格点上(图 4)。对于一维问题的差分格式为
| $ \frac{\partial u}{\partial \xi }\approx \frac{1}{\mathrm{\Delta }\xi }\sum\limits_{j=-3}^{3}{a}_{j}u\left(\xi +j\mathrm{\Delta }\xi \right) $ | (18) |
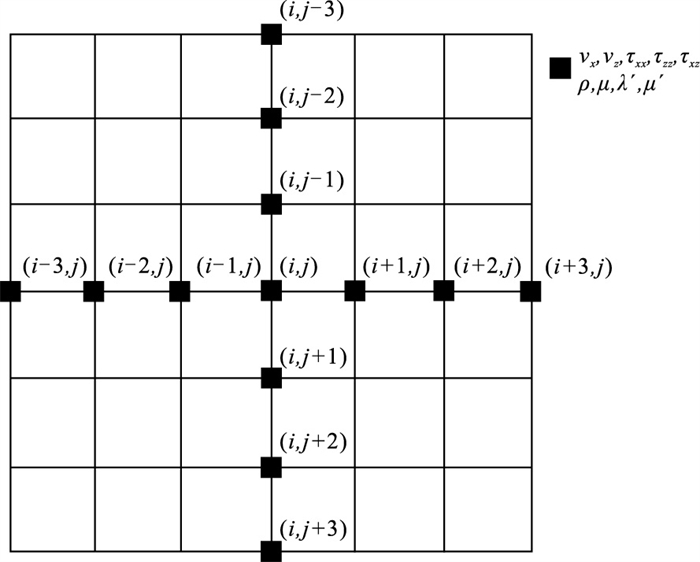
|
图 4 优化的7点同位网格有限差分示意图 |
式中:
中心差分格式只能用于内部网格点上变量偏导数的离散求解,对于模型边界附近的网格点,由于缺少模型外网格点上的变量值,因此必须使用非中心差分格式求解。本文釆用Berland等[32]提出的7点非中心差分格式计算边界网格点上的偏导数
| $ \frac{\partial u}{\partial \xi }\approx \frac{1}{\mathrm{\Delta }\xi }\sum\limits_{j=-P}^{Q}{b}_{j}u\left(\xi +j\mathrm{\Delta }\xi \right) $ | (19) |
式中:P=1或2,Q=5或4;
同位网格差分格式在求解一阶速度—应力波动方程时会产生高频的格点振荡现象。为了消除格点振荡带来的影响,对式(18)和式(19)的计算结果做选择性滤波处理
| $ \left\{\begin{array}{l}{u}^{\mathrm{d}}\left(\xi \right)=u\left(\xi \right)-\sigma F\left(\xi \right)\\ F\left(\xi \right)=\sum\limits_{j=-P}^{Q}{d}_{j}u\left(\xi +j\mathrm{\Delta }\xi \right)\end{array}\right. $ | (20) |
式中:
图 5是自由界面附近垂直方向导数的离散求解示意图。设
| $ \left\{\begin{array}{l}{\left.{\tau }_{zz}\right|}_{j=n}=0\\ {\left.{\tau }_{xz}\right|}_{j=n}=0\end{array}\right. $ | (21) |
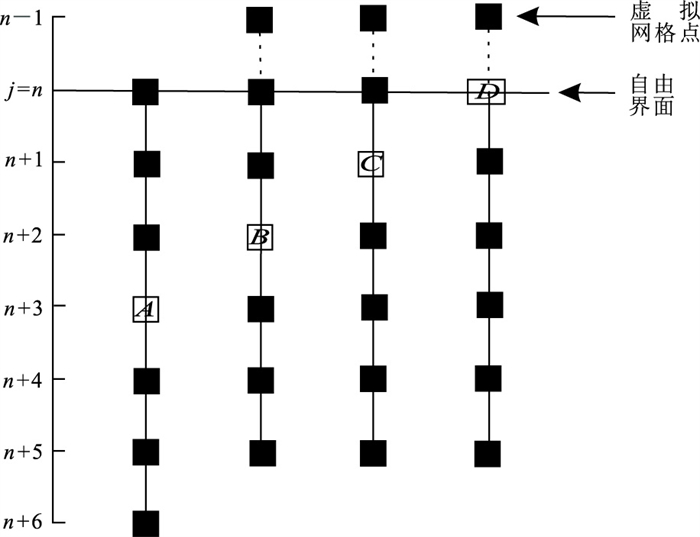
|
图 5 自由边界处有限差分格式示意图 |
自由地表以上虚拟网格点上的应力则可以根据应力镜像法求得,即
| $ \left\{\begin{array}{l}{\left.{\tau }_{zz}\right|}_{j=n-1}=-{\left.{\tau }_{zz}\right|}_{j=n+1}\\ {\left.{\tau }_{xz}\right|}_{j=n-1}={\left.-{\tau }_{xz}\right|}_{j=n+1}\end{array}\right. $ | (22) |
在自由地表处对式(11)中的应力水平分量进行求解时,需要用到速度分量在
| $ \left\{\begin{array}{l}{\dot{v}}_{x}=\frac{1}{\rho }\left({\xi }_{, x}{\tau }_{xx, \xi }+{\eta }_{, x}{\tau }_{xx, \eta }\right)\\ \lambda \left({\xi }_{, x}{v}_{x, \xi }+{\eta }_{, x}{v}_{x, \eta }\right)+\left(\lambda +2\mu \right)\times \\ \begin{array}{cc}\begin{array}{l}\left({\xi }_{, z}{v}_{z, \xi }+{\eta }_{, z}{v}_{z, \eta }\right)+\\ {\lambda }^{\text{'}}\left({\xi }_{, x}{\dot{v}}_{x, \xi }+{\eta }_{, x}{\dot{v}}_{x, \eta }\right)=0\end{array}& \end{array}\\ \mu \left({\xi }_{, z}{v}_{x, \xi }+{\eta }_{, z}{v}_{x, \eta }\right)+\mu \left({\xi }_{, x}{v}_{z, \xi }+{\eta }_{, z}{v}_{z, \eta }\right)+\\ \begin{array}{cc}& {\mu }^{\text{'}}\left({\xi }_{, z}{\dot{v}}_{x, \xi }+{\eta }_{, z}{\dot{v}}_{x, \eta }\right)=0\end{array}\end{array}\right. $ | (23) |
利用式(23)可求出
其他边界采用基于辅助微分方程的完美匹配层(ADE-PML)吸收边界条件[33]消除人工边界反射。
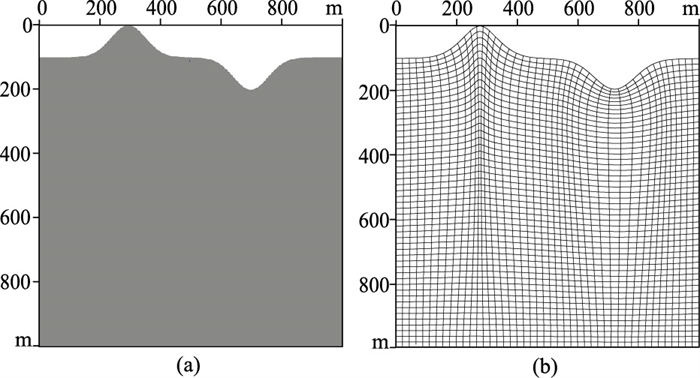
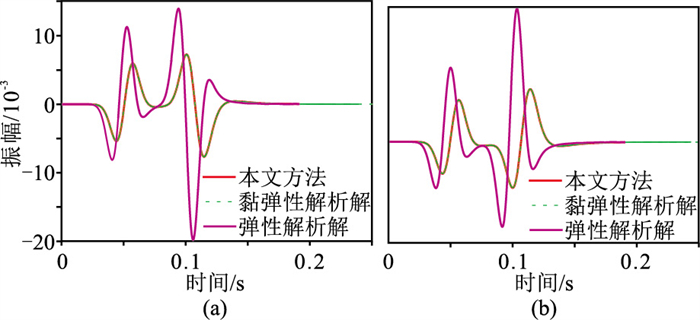
3 数值算例分析 3.1 起伏地表均匀介质模型为了测试本文方法对起伏地表模型的有效性和精度,设计如图 6a所示的起伏地表均匀介质模型,参数为:vP=3.3 km/s,vS=2.2 km/s,ρ=2.0 g/cm3,QP=25,QS=20。图 6b为利用本文方法得到的正交贴体网格,其计算域中两个方向的空间网格步长都为5 m。可以看出,本文提出的网格剖分法不仅能够精确描述起伏地表,而且在边界上具有精确的正交性。主频为75 Hz的Ricker子波作为震源,位于(500 m,5 m)处,分别采用本文方法和规则网格有限差分法进行模拟。图 7为利用两种方法模拟的0.15 s时刻的波场快照,可以看出,本文方法能够有效压制边界处阶梯状网格引起的虚假散射波。图 8为利用本文方法模拟的直达波在(500 m,600 m)处的单道地震记录与黏弹解析解及弹性波解析解的对比,可以看出,本文方法的数值解与黏弹解析解完全吻合,且与弹性波解相比振幅明显衰减。
|
图 6 起伏地表均匀介质模型(a)和网格剖分示意图(b) |

|
图 7 起伏地表均匀模型本文方法(左)与规则网格有限差分法(右)模拟的0.15s时刻波场快照对比 (a)水平分量;(b)垂直分量 |
|
图 8 本文方法模拟的直达波与黏弹解析解及弹性解析解的对比 (a)水平分量;(b)垂直分量 |
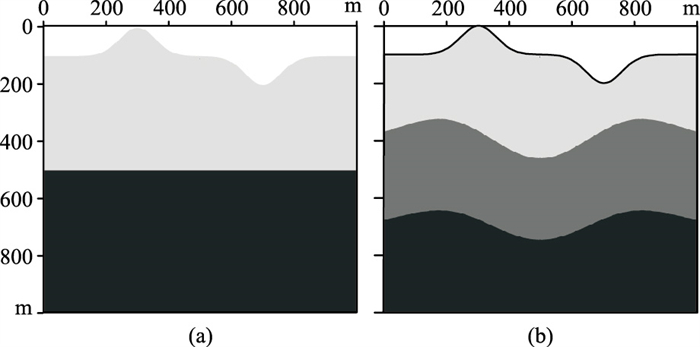
为了测试本文方法对起伏地表模型的适用性,建立了起伏地表两层和三层黏弹介质模型(图 9),各层参数如表 1所示。采用与起伏地表均匀模型相同的方法对起伏地表两层和三层模型进行网格剖分(图 6b,地形相同,网格剖分相同)。
|
图 9 起伏地表两层(a)和三层(b)黏弹介质模型 |
|
|
表 1 起伏地表多层介质模型参数 |
以主频为75 Hz的Ricker子波作为震源,位于(500 m,5 m),图 10和图 11分别为两层模型本文方法模拟的0.20和0.25 s时刻的波场快照。由图可见,地震波在传播到山峰和山谷的拐点时都会产生强烈的散射波和绕射波,且发生面波和体波之间的相互转换,散射面波的能量要强于散射体波;当地震波传播到界面时会产生反射波、透射波和转换波。图 12为三层模型本文方法模拟的两分量单炮记录。从图中可以观察到起伏地表拐点处产生的强烈散射波和两个介质分界面上的反射波、转换波。由于地层界面是崎岖的,因此反射波同相轴发生了畸变,不再是以炮点为中心的双曲线。起伏地表两层和三层黏弹介质模型计算结果表明本文方法对复杂模型同样有较强的适用性。

|
图 10 两层模型本文方法模拟的0.20 s时刻的波场快照 (a)水平分量;(b)垂直分量 |

|
图 11 两层模型本文方法模拟的0.25 s时刻的波场快照 (a)水平分量;(b)垂直分量 |

|
图 12 三层模型本文方法模拟的单炮记录 (a)水平分量;(b)垂直分量 |
地震波数值模拟是研究地层中地震波传播规律的有效方法。本文采用改进的RL正交贴体网格生成方法对起伏地表下的黏弹性介质进行网格剖分,并利用优化的选择性滤波同位网格有限差分法模拟曲线坐标系下的一阶速度—应力方程。数值算例表明:
(1)改进的RL算法能够对起伏地表模型进行精确的正交贴体网格剖分,从而有效消除阶梯状网格引起的虚假散射波;
(2)网格的正交性使得在实施自由边界条件时无需做复杂的坐标转换和插值运算,从而有效提高了模拟精度;
(3)因为二维和三维使用的是相同的差分格式,所以本文算法很容易向三维推广。
| [1] |
ROBERTSSON J O, BLANCH J O, SYMES W W. Viscoelastic finite-difference modeling[J]. Geophysics, 1994, 59(9): 1444-1456. DOI:10.1190/1.1443701 |
| [2] |
BLANCH J O, ROBERTSSON J O A, SYMES W W. Modeling of a constant Q: Methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique[J]. Geophysics, 1995, 60(1): 176-184. DOI:10.1190/1.1443744 |
| [3] |
XU T, MCMECHAN G A. Efficient 3-D viscoelastic modeling with application to near-surface land seismic data[J]. Geophysics, 1998, 63(2): 601-612. DOI:10.1190/1.1444359 |
| [4] |
XU T, MCMECHAN G A. Composite memory variables for viscoelastic synthetic seismograms[J]. Geophysical Journal International, 1995, 121(2): 634-639. DOI:10.1111/j.1365-246X.1995.tb05738.x |
| [5] |
ŠTEKL I, Pratt R G. Accurate viscoelastic modeling by frequency-domain finite differences using rotated operators[J]. Geophysics, 1998, 63(5): 1779-1794. DOI:10.1190/1.1444472 |
| [6] |
宋常瑜, 裴正林. 井间地震粘弹性波场特征的数值模拟研究[J]. 石油物探, 2006, 45(5): 508-513. SONG Changyu, PEI Zhenglin. Numerical simulation of viscoelastic wavefield for crosshole seismic exploration[J]. Geophysical Prospecting for Petroleum, 2006, 45(5): 508-513. DOI:10.3969/j.issn.1000-1441.2006.05.014 |
| [7] |
唐启军, 韩立国, 王恩利, 等. 基于随机各向同性背景的粘弹性单斜介质二维三分量正演模拟[J]. 西北地震学报, 2009, 31(1): 35-39. TANG Qijun, HAN Liguo, WANG Enli, et al. 2-D three-component seismic modeling for viscoelastic monoclinic media based on background of random isotropic media[J]. Northwestern Seismological Journal, 2009, 31(1): 35-39. |
| [8] |
陈玉玺, 王璐, 章阳. 三维黏弹性介质地震波场数值模拟技术研究[J]. 西部探矿工程, 2016, 28(12): 26-29. CHEN Yuxi, WANG Lu, ZHANG Yang. Numerical simulation of seismic wave field in 3D viscoelastic media[J]. West-China Exploration Engineering, 2016, 28(12): 26-29. DOI:10.3969/j.issn.1004-5716.2016.12.009 |
| [9] |
陈豪, 李春香, 魏艳敏. 粘弹性介质三维地震波场数值模拟研究——基于交错网格高阶有限差分法[J]. 贵州工程应用技术学院学报, 2022, 40(3): 47-53. CHEN Hao, LI Chunxiang, WEI Yanmin. Research on forward modeling of 3D seismic wave field in viscoelastic media based on finite difference method[J]. Journal of Guizhou University of Engineering Science, 2022, 40(3): 47-53. |
| [10] |
杨尚倍, 白超英, ZHOU Bing. 时间域广义2.5D一阶波动方程曲网格有限差分法数值模拟[J]. 石油地球物理勘探, 2021, 56(6): 1262-1278. YANG Shangbei, BAI Chaoying, ZHOU Bing. Curvilinear-grid finite-difference numerical simulation method for generalized first-order 2.5D time-domain wave equation[J]. Oil Geophysical Prospecting, 2021, 56(6): 1262-1278. |
| [11] |
李灿苹, 刘学伟, 勾丽敏, 等. 冷泉活动区天然气水合物上覆水体中气泡羽状流的数值模拟[J]. 中国科学: 地球科学, 2013, 43(3): 391-399. LI Canping, LIU Xuewei, GOU Limin, et al. Numerical simulation of bubble plumes in overlying water of gas hydrate in the cold seepage active region[J]. Scientia Sinica (Terrae), 2013, 43(3): 391-399. |
| [12] |
孙楠, 孙耀充, 庾汕. 含有限水体介质中地震波场数值模拟[J]. 地震研究, 2017, 40(4): 557-564. SUN Nan, SUN Yaochong, YU Shan. Numerical simulation of seismic wave field in medium with limited water[J]. Journal of Seismological Research, 2017, 40(4): 557-564. DOI:10.3969/j.issn.1000-0666.2017.04.007 |
| [13] |
罗文山, 陈汉明, 王成祥, 等. 时间域黏滞波动方程及其数值模拟新方法[J]. 石油地球物理勘探, 2016, 51(4): 707-713. LUO Wenshan, CHEN Hanming, WANG Chengxiang, et al. A novel time-domain viscoacoustic wave equation and its numerical simulation[J]. Oil Geophysical Prospecting, 2016, 51(4): 707-713. |
| [14] |
谭文卓, 吴帮玉, 李博, 等. 梯形网格伪谱法地震波场模拟[J]. 石油地球物理勘探, 2020, 55(6): 1282-1291. TAN Wenzhuo, WU Bangyu, LI Bo, et al. Seismic wave simulation using a trapezoid grid pseudo-spectral method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1282-1291. |
| [15] |
刘瑞合, 周建科, 周学锋, 等. 基于紧凑存储的任意四边形网格有限元法地震波场数值模拟[J]. CT理论与应用研究, 2015, 24(5): 667-680. LIU Ruihe, ZHOU Jianke, ZHOU Xuefeng, et al. Finite element method with arbitrary quadrilateral meshes for numerical modeling of seismic wave based on compact storage[J]. CT Theory and Applications, 2015, 24(5): 667-680. |
| [16] |
刘少林, 李小凡, 汪文帅, 等. Lax-Wendroff集中质量有限元法地震波场模拟[J]. 石油地球物理勘探, 2015, 50(5): 905-911, 924. LIU Shaolin, LI Xiaofan, WANG Wenshuai, et al. A Lax-Wendroff lumped mass finite element method for seismic simulations[J]. Oil Geophysical Prospecting, 2015, 50(5): 905-911, 924. |
| [17] |
刘少林, 杨顶辉, 徐锡伟, 等. 模拟地震波传播的三维逐元并行谱元法[J]. 地球物理学报, 2021, 64(3): 993-1005. LIU Shaolin, YANG Dinghui, XU Xiwei, et al. Threedimensional element-by-element parallel spectral-element method for seismic wave modeling[J]. Chinese Journal of Geophysics, 2021, 64(3): 993-1005. |
| [18] |
孟雪莉, 刘少林, 杨顶辉, 等. 基于优化数值积分的谱元法模拟地震波传播[J]. 石油地球物理勘探, 2022, 57(3): 602-612. MENG Xueli, LIU Shaolin, YANG Dinghui, et al. Spectral-element method based on optimal numerical integration for seismic waveform modeling[J]. Oil Geophysical Prospecting, 2022, 57(3): 602-612. |
| [19] |
HAYASHI K, BURNS D R, TOKSÖZ M N. Discontinuous-grid finite-difference seismic modeling including surface topography[J]. Bulletin of the Seismological Society of America, 2001, 91(6): 1750-1764. |
| [20] |
董良国. 复杂地表条件下地震波传播数值模拟[J]. 勘探地球物理进展, 2005, 28(3): 187-194. DONG Liangguo. Numerical simulation of seismic wave propagation under complex near surface conditions[J]. Progress in Exploration Geophysics, 2005, 28(3): 187-194. |
| [21] |
TARRASS I, GIRAUD L, THORE P. New curvilinear scheme for elastic wave propagation in presence of curved topography[J]. Geophysical Prospecting, 2011, 59(5): 889-906. |
| [22] |
LAN H, ZHANG Z. Comparative study of the free-surface boundary condition in two-dimensional finite-difference elastic wave field simulation[J]. Journal of Geophysics and Engineering, 2011, 8(2): 275-286. |
| [23] |
SUN Y, ZHANG W, CHEN X. Seismic-wave modeling in the presence of surface topography in 2D general anisotropic media by a curvilinear grid finite difference method[J]. Bulletin of the Seismological Society of America, 2016, 106(3): 1036-1054. |
| [24] |
蒋丽丽. 面向地质条件的贴体网格生成技术[D]. 吉林长春: 吉林大学, 2010.
|
| [25] |
丘磊. 正交曲线坐标系下的地震波数值模拟技术研究[D]. 浙江杭州: 浙江大学, 2011.
|
| [26] |
李庆洋, 黄建平, 李振春, 等. 起伏地表贴体全交错网格仿真型有限差分正演模拟[J]. 石油地球物理勘探, 2015, 50(4): 633-642. LI Qingyang, HUANG Jianping, LI Zhenchun, et al. Undulating surface body-fitted grid seismic modeling based on fully staggered-grid mimetic finite difference[J]. Oil Geophysical Prospecting, 2015, 50(4): 633-642. |
| [27] |
ZHANG Y, JIA Y, WANG S S Y. 2D nearly orthogonal mesh generation with controls on distortion function[J]. Journal of Computational Physics, 2006, 218(2): 549-571. |
| [28] |
AKCELIK V, JARAMAZ B, GHATTAS O. Nearly orthogonal two-dimensional grid generation with aspect ratio control[J]. Journal of Computational Physics, 2001, 171(2): 805-821. |
| [29] |
MAGNIER S A, MORA P, TARANTOLA A. Finite differences on minimal grids[J]. Geophysics, 1994, 59(9): 1435-1443. |
| [30] |
BOGEY C, BAILLY C. A family of low dispersive and low dissipative explicit schemes for flow and noise computations[J]. Journal of Computational Physics, 2004, 194(1): 194-214. |
| [31] |
TAM C K W. Computational aeroacoustics: issues and methods[J]. AIAA Journal, 1995, 33(10): 1788-1796. |
| [32] |
BERLAND J, BOGEY C, MARSDEN O, et al. High order, low dispersive and low dissipative explicit schemes for multiple-scale and boundary problems[J]. Journal of Computational Physics, 2007, 224(2): 637-662. |
| [33] |
MARTIN R, KOMATITSCH D. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation[J]. Geophysical Journal International, 2009, 179(1): 333-344. |



 刘志强, 内蒙古自治区呼和浩特市赛罕区昭乌达路306号内蒙古农业大学水利与土木建筑工程学院,010018。Email:
刘志强, 内蒙古自治区呼和浩特市赛罕区昭乌达路306号内蒙古农业大学水利与土木建筑工程学院,010018。Email: