2. 东华理工大学地球物理与测控技术学院, 江西南昌 330013
2. School of Geophysics and Measurement-control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China
瑞雷波是纵波和横波相互干涉叠加形成的一种沿着地表或介质分界面传播的波。起初,瑞雷波只被当作噪声,研究人员主要是根据瑞雷波的特点减小其在地震中带来的危害或压制其在石油地震勘探中对有效信息的影响。随着研究的深入,人们发现瑞雷波在层状介质中传播会出现频散现象,于是便开始将瑞雷波应用于地下地层结构的研究[1]。与反射地震等常规勘探方法相比,瑞雷波勘探具有无损、施工便捷、浅层分辨率高、检测速度快等优点[2],在土层划分[3]、工程无损检测[4]、地质灾害勘察[5]等领域应用广泛。
瑞雷波勘探可分为三个步骤:野外面波数据采集、频散曲线拾取和频散曲线反演。频散曲线的反演作为瑞雷波勘探的关键步骤,直接决定了所求地层信息的可靠性。目前,频散曲线的反演算法主要有两种:局部优化算法和全局优化算法。
局部优化算法包括最小二乘法、Levenberg-Marquardt(L-M)算法、奥卡姆算法等。Dorman等[6]首次利用阻尼最小二乘法反演频散曲线,得到的横波速度与折射波法一致,证实了瑞雷波勘探的有效性。Xia等[7]将L-M算法与奇异值分解技术相结合反演瑞雷波相速度,加速了解的收敛,提高了反演的计算效率和稳定性。艾东海等[8]在Constable等[9]研究的基础上,将奥卡姆算法用于瑞雷波频散曲线反演,并且还在反演中引入自适应修改拉格朗日乘子光滑系数协调了模型分辨率与解的精度。局部优化算法因计算速度快而被广泛应用,但反演效果过度依赖初始模型[10]。另外,局部优化算法易陷入局部极值,且涉及偏导数计算,反演结果受雅可比矩阵精度的制约,因此应用受到限制。
全局优化算法能避免初始模型选取和偏导数计算,也被应用于频散曲线反演,如遗传算法(GA)、模拟退火算法等。石耀霖等[11]将GA用于频散曲线反演,通过分析初始搜索结果修改搜索范围,从而提高了搜索效率;Yamanaka等[12]在应用GA对瑞雷波频散曲线进行反演时,加入精英筛选策略,加快了解的收敛;Dal Moro等[13]将GA与后验概率密度估计相结合反演瑞雷波频散曲线,提高了解的精度。Martínez等[14]利用模拟退火算法对瑞雷波的群速度和相速度进行反演,降低了对初始模型的依赖,但需经验控制退火过程的一些参数;Beaty等[15]采用快速模拟退火算法反演了多阶频散曲线,并与基阶频散曲线反演结果进行了对比,结果表明多阶频散曲线反演的横波速度分辨率更高、不确定性更小、更可靠;Lu等[16]基于模拟退火算法提出了热浴模拟退火算法,并与L-M算法进行对比,结果表明热浴模拟退火算法更适于频散曲线反演。与局部优化算法相比,全局优化算法有不依赖初始模型、不易陷入局部最优解等优势,但运算时间长、收敛速度慢。
为解决全局优化算法反演频散曲线存在的问题,有学者引入了其他全局优化算法,如洗牌蛙跳算法[17]、自适应混沌遗传粒子群算法[18]、蚱蜢算法[19]、自适应蜻蜓算法[20]等,也有学者结合多种算法的优势进行反演,如遗传算法与L-M算法的结合[21]、模拟退火算法与阻尼最小二乘法结合[22]等。
闪电连接过程优化(Lightning Attachment Procedure Optimization,LAPO)算法模拟雷云向地放电过程,是一种全局优化算法,本文将其用于瑞雷波频散曲线的反演。为详尽评价LAPO算法反演频散曲线的能力,首先利用不含噪声的模型数据验证了LAPO算法用于频散曲线反演的可行性;其次,往模型数据中加入10%的随机噪声测试了LAPO算法的稳定性;同时应用含噪和不含噪理论模型数据,对比分析了LAPO算法与粒子群(PSO)算法的反演性能;再次,利用理论模型数据测试了LAPO算法的多阶频散曲线反演能力;最后用美国怀俄明地区实际数据检验了LAPO算法实用能力。
1 LAPO算法原理 1.1 原理描述LAPO算法是Nematollahi等[23]根据闪电连接这一物理现象提出的一种自然启发式算法,模拟了雷云对地放电过程。雷云对地放电时,雷云先发展出下行先导,下行先导向下延伸,接近地面目标(高建筑物、高树木等)后,在目标上激发向上发展的上迎先导,当上迎先导与下行先导距离足够小,出现完全击穿,雷击就会产生。下行先导是指从雷云开始发展、向下延伸的先导通道;上迎先导是指从地面(高建筑物、高树木等)开始发展、向上延伸的先导通道[24]。描述该过程的数学模型可表示为以下五步。
(1)初始化。LAPO算法首先需要通过随机方式在定义域中产生一个初始种群。种群的每个个体代表优化问题中的一个解,可以看作云与地面之间的候选点。候选点的产生可以描述为
| $ {{\boldsymbol{X}}}_{i}^{\left(0\right)}={{\boldsymbol{X}}}_{i}^{\mathrm{l}\mathrm{b}}+({{\boldsymbol{X}}}_{i}^{\mathrm{u}\mathrm{b}}-{{\boldsymbol{X}}}_{i}^{\mathrm{l}\mathrm{b}})\times r $ | (1) |
式中:
| $ {F}_{i}^{\left(0\right)}=\varPhi \left[{{\boldsymbol{X}}}_{i}^{\left(0\right)}\right] $ | (2) |
式中Φ为目标函数。
(2)确定闪电的下一跳。闪电下一跳的移动需要用到所有候选点的均值Xave和均值点的适应度值Fave,即
| $ \left\{\begin{array}{l}{{\boldsymbol{X}}}_{\mathrm{a}\mathrm{v}\mathrm{e}}=\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left[{{\boldsymbol{X}}}_{1}^{\left(t\right)}, {{\boldsymbol{X}}}_{2}^{\left(t\right)}, \cdots \right]\\ {F}_{\mathrm{a}\mathrm{v}\mathrm{e}}=\varPhi \left({{\boldsymbol{X}}}_{\mathrm{a}\mathrm{v}\mathrm{e}}\right)\end{array}\right. $ | (3) |
式中t为迭代次数。闪电在传播过程中需在多个点移动,其移动时存在多个选择点。在LAPO算法中对该过程进行数学描述时,对种群中的某一点,考虑了所有其他点都可能成为下一个跳跃点。由于闪电是一个随机行为,对于候选点i,在种群中随机选择一个点j(i≠j),若点j的电场值高于均值点的电场值(电场值越大,适应度值越小),则闪电向j点跳跃,即
| $ {{\boldsymbol{X}}}_{i, \mathrm{n}\mathrm{e}\mathrm{w}}^{\left(t\right)}={{\boldsymbol{X}}}_{i}^{\left(t\right)}+{r}_{1}\times \left[{{\boldsymbol{X}}}_{\mathrm{a}\mathrm{v}\mathrm{e}}+{r}_{2}{{\boldsymbol{X}}}_{j}^{\left(t\right)}\right] $ | (4) |
否则,闪电向另一方向移动,即
| $ {{\boldsymbol{X}}}_{i, \mathrm{n}\mathrm{e}\mathrm{w}}^{\left(t\right)}={{\boldsymbol{X}}}_{i}^{\left(t\right)}-{r}_{1}\times \left[{{\boldsymbol{X}}}_{\mathrm{a}\mathrm{v}\mathrm{e}}+{r}_{2}{{\boldsymbol{X}}}_{j}^{\left(t\right)}\right] $ | (5) |
式中:
(3)闪电分支消失。在该阶段,如果新的候选点的电场值高于旧的电场值,则新候选点所在的分支保留,反之,该分支消失。这一过程可以表示为
| $ \left\{\begin{array}{l}{{\boldsymbol{X}}}_{i}^{\left(t\right)}={{\boldsymbol{X}}}_{i, \mathrm{n}\mathrm{e}\mathrm{w}}^{\left(t\right)}\\ {{\boldsymbol{X}}}_{i, \mathrm{n}\mathrm{e}\mathrm{w}}^{\left(t\right)}={{\boldsymbol{X}}}_{i}^{\left(t\right)}\end{array}\right. $ | (6) |
以上三步模拟了闪电连接过程的下行先导向地面移动的阶段。
(4)上迎先导的移动。在这一阶段,所有的候选点都被认为是上迎先导,并向上移动。上迎先导的移动受到下行先导电荷分布的影响,下行先导的电荷呈指数分布。指数因子定义为
| $ S=1-\frac{t}{{t}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\times \mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{t}{{t}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right) $ | (7) |
式中tmax为最大迭代次数。上迎先导的下一候选点的选择过程可以描述为
| $ {{\boldsymbol{X}}}_{i}^{(t+1)}={{\boldsymbol{X}}}_{i, \mathrm{n}\mathrm{e}\mathrm{w}}^{\left(t\right)}+r\times S\times \left[{{\boldsymbol{X}}}_{min}^{\left(t\right)}-{{\boldsymbol{X}}}_{max}^{\left(t\right)}\right] $ | (8) |
式中
(5)连接点的确定。当上迎先导和下行先导相遇时,连接点确定,闪电过程停止。上迎先导和下行先导相遇这一过程可表达为算法满足收敛条件。
1.2 算法测试对于全局优化算法性能评估,人们一般采用各种标准函数进行测试。这些测试函数可分为单峰函数、多峰函数和复合函数。本文引用参考文献[23]中Rastrigrin和Ackley两个多峰函数测试LAPO和PSO算法的性能,评价算法探索特性和跳出局部最优能力。Rastrigin函数的表达式为
| $ {F}_{1}\left({\boldsymbol{x}}\right)=\sum\limits_{j=1}^{n}\left[{x}_{j}^{2}-10\mathrm{c}\mathrm{o}\mathrm{s}\left(2\mathrm{{\rm{ \mathsf{π} }} }{x}_{j}\right)+10\right] $ | (9) |
式中n 为函数维度。测试时设置n=30,搜索区间为[-5.12,5.12],最优解位于0。Ackley 函数表达式为
| $ \begin{array}{l}{F}_{2}\left({\boldsymbol{x}}\right)=-20\mathrm{e}\mathrm{x}\mathrm{p}\left(-0.2\sqrt{\frac{1}{n}\sum\limits_{j=1}^{n}{x}_{j}^{2}}\right)-\\ \begin{array}{cc}& \end{array}\mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{1}{n}\sum\limits_{j=1}^{n}\mathrm{c}\mathrm{o}\mathrm{s}\left(2\mathrm{{\rm{ \mathsf{π} }} }{x}_{j}\right)\right]+20+e\end{array} $ | (10) |
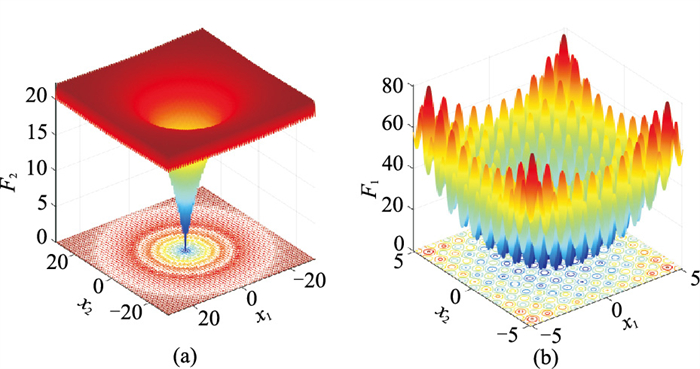
式中e为自然常数,取值为2.7182。测试时同样设置n=30,搜索区间为[-32, 32],最优解位于0。二维情况下,两个函数形状如图1所示。
|
图 1 二维 Ackley(a)和Rastrigin(b)函数形状 |
在算法对比时,需控制参数变量以合理对算法进行评估。在寻优时,LAPO算法迭代一次需求取两次目标函数,PSO算法迭代一次只求取一次目标函数,因此前者的种群数设置为40,是后者种群数80的一半。迭代次数都设为200次。PSO算法的其他参数见参考文献[25]。由于两种算法都是基于粒子的随机运动寻优,需要对多次反演结果进行统计分析。参照文献[23],本文对两种方法进行了30次试验。30次测试结果中所求得的最优函数值、平均值及标准差统计如表1所示(表中数据均保留两位小数),可以看出,对于Rastrigin和Ackley两个多峰函数,LAPO算法优于PSO算法,说明LAPO算法具有更强的全局探索能力。由参考文献[23]中其他测试结果可知,LAPO算法的局部开发能力和收敛性能也强于PSO算法。
|
|
表 1 两种方法的标准函数测试结果统计 |
在面波数据中,基阶面波能量强、易观测,在工程中应用最为广泛,因此,本文首先测试了LAPO算法反演基阶频散曲线的能力。Xia等[7]的研究表明,对瑞雷波频散曲线特征变化影响最大的是地层的横波速度和厚度,其余参数影响较小。为节省计算量,本文仅对横波速度和层厚进行反演,其他参数根据先验信息确定。理论模型测试搜索区域的上、下限设定为与真实值相差50%。反演参数中LAPO算法的种群数设置为10,PSO算法的种群数设置为20,迭代次数都设置为50。为避免算法中随机因子对反演结果的影响,每个理论模型测试都进行20次独立反演,且每次反演时初始模型都随机生成。最后将20次的均值作为反演结果,将20次反演数据的标准差作为衡量算法稳定性的指标。
瑞雷波频散曲线反演的本质就是通过算法搜索到一个最佳横波速度模型,使反演频散曲线与实测频散曲线的拟合误差达到最小。本文使用均方根误差作为目标函数,以评价二者的拟合程度。对于基阶频散曲线反演,目标函数为
| $ {\varPhi }_{1}=\sqrt{\sum\limits_{k=1}^{N}\frac{{\left({v}_{k}^{\mathrm{o}\mathrm{b}\mathrm{s}}-{v}_{k}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right)}^{2}}{N}} $ | (11) |
式中:N为基阶频散曲线的频点数;vobs和vcal分别为观测和反演的瑞雷波相速度。对于多阶频散曲线反演,目标函数为
| $ {\varPhi }_{2}=\frac{1}{L}\sum\limits_{l=1}^{L}\sqrt{\frac{\sum\limits_{k=1}^{{N}_{l}}{\left({v}_{l, k}^{\mathrm{o}\mathrm{b}\mathrm{s}}-{v}_{l, k}^{\mathrm{c}\mathrm{a}\mathrm{l}}\right)}^{2}}{{N}_{l}}} $ | (12) |
式中:L为频散曲线条数;Nl为第l条频散曲线频点数。频散曲线的正演模拟采用的是快速标量传递算法[26]。
2.1 无噪基阶频散曲线反演首先使用模型A的无噪声理论曲线对LAPO和PSO算法进行反演测试。模型A为含软夹层的四层模型,各层的纵波速度(VP)、横波速度(VS)、密度(ρ)和厚度(h)参数如表2所示。当频率大于70 Hz后,该模型观测不到基阶频散曲线,因此频率范围设为5~68 Hz,间隔为3 Hz。
|
|
表 2 模型A参数及反演搜索范围 |
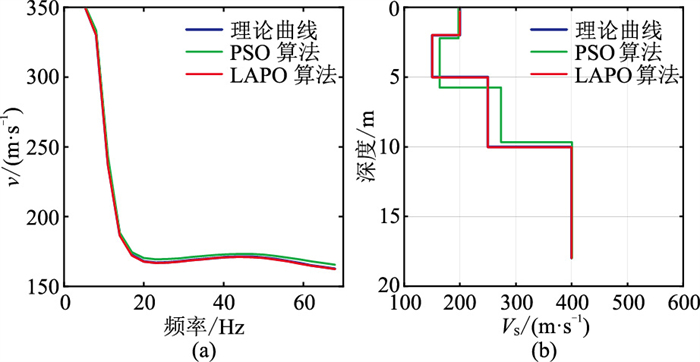
两种方法反演结果如图2与表3所示(表中数据均保留两位小数)。由图2a可知,LAPO算法反演的频散曲线几乎和理论模型频散曲线完全重合,PSO算法反演的频散曲线与理论模型频散曲线也拟合得很好。但图2b中LAPO算法反演的地层横波速度曲线与真实模型基本吻合,PSO算法反演的横波速度曲线与真实模型却存在一定偏差。另外,LAPO算法反演结果的最大相对误差为1.38%和最大标准差为6.16,显著低于PSO算法反演结果的11.75%和62.94。因此,与PSO算法相比,LAPO算法的寻优能力更强,能搜索到适应度值更小的结果。
|
图 2 模型A无噪声理论数据两种算法反演结果对比 (a)频散曲线;(b)横波速度曲线 |
|
|
表 3 模型A无噪声理论数据两种算法反演结果统计 |
实际地震数据不可避免地会包含噪声[27],会降低反演结果的准确性,因此有必要检验算法的抗噪能力。在模型A的频散曲线中加入10%的随机噪声[28],然后使用LAPO和PSO算法对加噪后的频散曲线进行反演(图3和表4)。本文使用的加噪方式为
| $ {v}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}=v\left[1+2(0.5-r)p\right] $ | (13) |

|
图 3 模型A含噪理论频散曲线两种方法反演结果对比 (a)频散曲线;(b)横波速度曲线 |
|
|
表 4 模型A含噪理论曲线两种算法反演结果统计 |
式中:vnoise表示加入噪声后的频散数据;v为加噪前的频散数据;p为加入噪声的程度。
由图3a可以看出,在频散曲线中加入噪声后,LAPO算法反演的频散曲线依然能很好地拟合理论频散曲线,PSO算法的拟合效果稍差。在图3b中,与PSO算法相比,LAPO反演的横波速度曲线更接近真实模型。与不含噪声理论频散曲线的反演结果相比,含噪频散曲线反演结果的相对误差和标准差大多有所增大,可见噪声会影响反演结果的准确性。与不含噪理论曲线的反演结果相比,LAPO算法含噪频散曲线反演的最大相对误差从1.38%变为5.44%,最大标准差从6.16变为9.51,增幅较小,整体变化也不大,可见LAPO算法具有良好的稳定性。PSO算法在反演含噪声理论曲线时,与不含噪声时相比,反演结果的相对误差和标准差整体上有所增加,大于LAPO反演含噪声数据和不含噪声数据结果间的变化幅度。由此可知,LAPO比PSO算法的抗噪能力更强、更稳定。
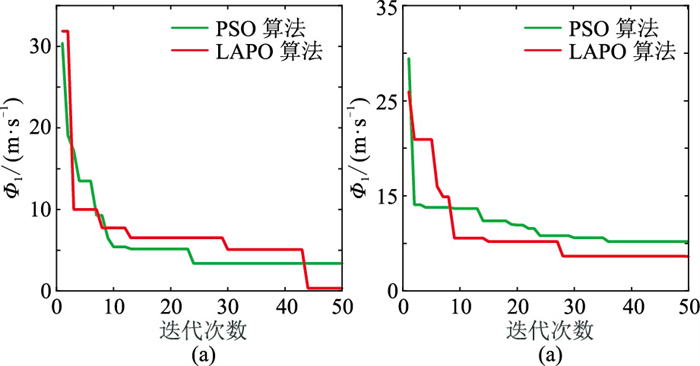
从无噪和含噪理论曲线的LAPO和PSO算法各20次反演结果中,选取精度最高的一次进行收敛曲线对比(图4)。对于无噪理论频散曲线,在迭代的前、中期,两种算法收敛精度和速度相差不大;在中、后期PSO算法早熟,LAPO算法还在继续收敛;迭代结束后LAPO算法的收敛精度更高(图4a)。对于含噪理论频散曲线,多数情况下,LAPO算法的收敛速度和收敛精度高于优于PSO算法。可见,与PSO算法相比,LAPO算法具有更高的收敛速度和精度。
|
图 4 模型A无噪(a)和含噪(b)理论曲线的 两种方法反演迭代收敛曲线对比 |
面波在一些特殊地层中传播时,可能出现高阶模式占主导的情况[29]。若联合反演基阶和高阶频散曲线,能增加对反演结果的约束,提升反演结果的精度。模型B(表5)为含硬夹层的四层模型,理论频散曲线的频率范围为5~98 Hz,频率间隔为3 Hz。
|
|
表 5 模型B参数及反演搜索范围 |
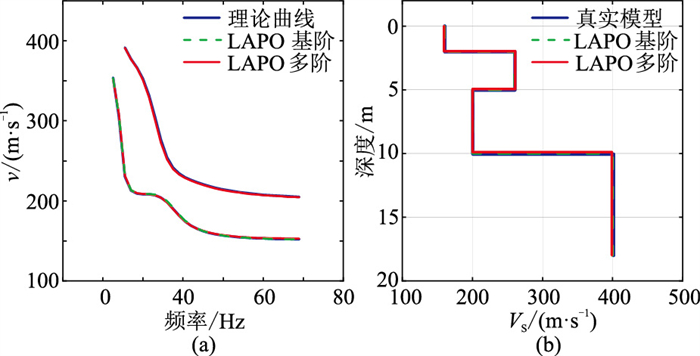
模型B的基阶和一阶频散曲线联合LAPO算法反演结果如图5和表6所示。在图5a中,反演的基阶和一阶频散曲线与理论频散曲线均拟合较好。由图5b可以看出,反演的横波速度曲线与真实模型曲线非常接近。对比基阶模式频散曲线的反演结果与多阶频散曲线的联合反演结果(表6)可以明显看出,多阶频散曲线联合反演的模型参数相对误差和标准差整体上都有所降低。可见,利用多阶频散曲线联合反演的结果确实更准确、更可靠,也说明LAPO算法不仅可用于基阶频散曲线的反演,也适用于多阶频散曲线的反演。
|
图 5 模型B无噪声多阶理论频散曲线反演结果 (a)频散曲线;( b)横波速度曲线 |
|
|
表 6 模型B基阶与多阶无噪声频散曲线LAPO算法反演结果统计对比 |
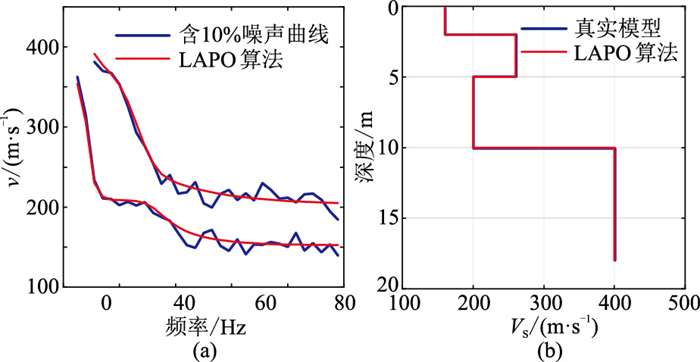
向模型B的多阶频散曲线中加入10%的随机噪声,对LAPO算法进行测试,结果如图6和表7所示。由图6可知,无论是反演的频散曲线还是横波速度曲线都与真实曲线拟合得很好。与表6相比,表7中统计数据变化较小,表明LAPO算法用于含噪多阶频散曲线反演表现不错。
|
图 6 模型B含噪多阶理论频散曲线反演结果 (a)频散曲线;(b)横波速度曲线 |
|
|
表 7 模型B含噪多阶理论频散曲线反演结果统计 |
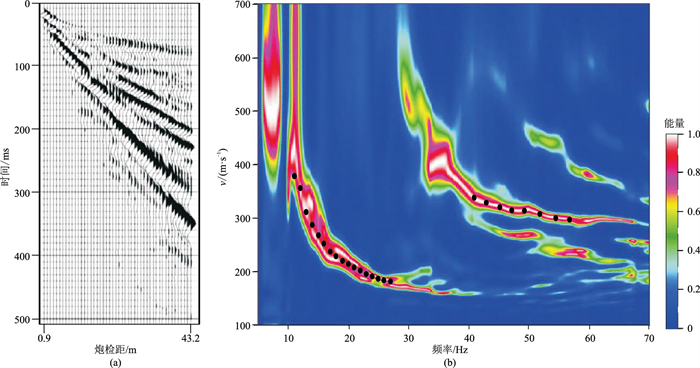
实际瑞雷面波数据采集自美国怀俄明地区[30]。由锤击震源激发,48个8 Hz 垂直检波器接收,最小炮检距和道间距都为0.9 m。原始地震记录如图7a所示。图7b为频散能量谱,从中提取基阶和二阶频散曲线用于反演。实际数据反演参数与理论模型测试保持一致。根据测井资料岩性解释将模型划分为5层,估计的横波速度等其他物性参数如表8所示。
|
图 7 美国怀俄明地区实际面波地震记录(a)和频散能量谱(b)[31] |
|
|
表 8 怀俄明地区面波反演搜索范围及模型参数设置[31] |
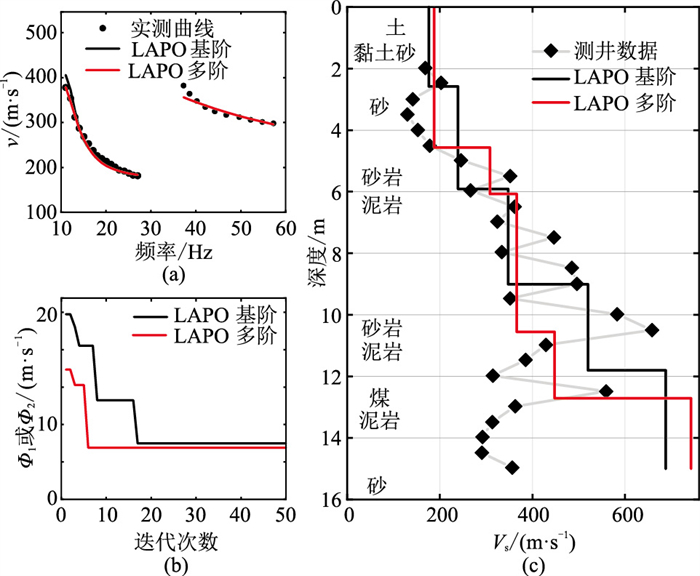
图8a为实际数据LAPO算法的基阶和多阶反演的频散曲线与实测曲线对比,三者很吻合。图8b为LAPO算法反演过程中目标函数随迭代次数的变化曲线,可以看出,使用多阶数据比只使用基阶数据的反演精度更高。多阶数据反演的横波速度模型 (图8c中红色实线)比基阶数据反演得到的横波速度模型(图8c中黑色实线)更接近测井数据(图8c中带菱形的灰色折线),尤其是在浅层,说明LAPO算法对于多阶瑞雷面波频散曲线反演具有良好的实用性。
|
图 8 怀俄明地区基阶和多阶瑞雷波相速度反演结果对比 (a)频散曲线;(b)收敛曲线;(c)横波速度曲线 |
本文将一种新颖的全局优化算法——LAPO算法用于瑞雷波频散曲线反演。在反演时,通过设置较大的模型参数搜索范围以模拟无先验信息或者仅有少量已知信息的情况。利用两个理论模型对LAPO算法的性能进行了测试,最后再应用美国怀俄明地区的实测数据检验了LAPO的实用性。测试结果表明:LAPO算法能有效用于频散曲线反演,该算法在获得高精度地层模型参数的同时,还保证了反演过程收敛速度以及较强的稳定性,具有良好的发展潜力。对于瑞雷波频散曲线反演,LAPO算法比传统的粒子群算法,精度更高、收敛更快、稳定性更强。
| [1] |
邱新明, 王赟, 韦永祥, 等. 多分量面波研究进展[J]. 石油物探, 2021, 60(1): 46-56. QIU Xinming, WANG Yun, WEI Yongxiang, et al. Advancements in multi-component surface waves:A review[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 46-56. DOI:10.3969/j.issn.1000-1441.2021.01.005 |
| [2] |
伍敦仕, 孙成禹, 林美言. 基于互相关相移的主动源地震面波频散成像方法[J]. 地球物理学进展, 2017, 32(4): 1693-1700. WU Dunshi, SUN Chengyu, LIN Meiyan. Active seismic surface wave dispersion imaging method based on cross-correlation and phase-shifting[J]. Progress in Geophysics, 2017, 32(4): 1693-1700. |
| [3] |
宫胜家. 瞬态面波的勘探及应用[J]. 中国煤炭地质, 2008, 20(增刊1): 84-86. GONG Shengjia. Prospecting and application of transient ground roll[J]. Coal Geology of China, 2008, 20(S1): 84-86. |
| [4] |
赵硕九, 金钢燮, 汪利民. 瑞雷面波在多尺度勘探上的研究现状与展望[J]. 勘探地球物理进展, 2010, 33(1): 1-10. ZHAO Shuojiu, JIN Gangxie, WANG Limin. Review of Rayleigh wave techniques in survey of different scales and its future prospects[J]. Progress in Exploration Geophysics, 2010, 33(1): 1-10. |
| [5] |
许新刚, 岳建华, 李娟娟, 等. 面波勘查技术及在滑坡地质调查中的应用研究[J]. 地球物理学进展, 2016, 31(3): 1367-1372. XU Xingang, YUE Jianhua, LI Juanjuan, et al. Surface wave exploration technique and its application in landslide geology survey[J]. Progress in Geophysics, 2016, 31(3): 1367-1372. |
| [6] |
DORMAN J, EWING M. Numerical inversion of seismic surface wave dispersion data and crust-mantle structure in the New York-Pennsylvania area[J]. Journal of Geophysical Research, 1962, 67(13): 5227-5241. DOI:10.1029/JZ067i013p05227 |
| [7] |
XIA J, MILLER R D, PARK C B. Estimation of nearsurface shear-wave velocity by inversion of Rayleigh waves[J]. Geophysics, 1999, 64(3): 691-700. DOI:10.1190/1.1444578 |
| [8] |
艾东海, 程庆群. 低速软弱夹层二维横波速度结构的OCCAM反演[J]. 工程勘察, 2009, 37(4): 87-90. AI Donghai, CHENG Qingqun. Estimation of 2D S-wave velocity section with low velocity layers by OCCAM algorithm[J]. Geotechnical Investigation & Surveying, 2009, 37(4): 87-90. |
| [9] |
CONSTABLE S C, PARKER R L, CONSTABLE C G. Occam's inversion:A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [10] |
王一鸣, 宋先海, 张学强. 瑞雷面波频散曲线的粒子群蚁群混合优化反演[J]. 石油地球物理勘探, 2022, 57(2): 303-310, 356. WANG Yiming, SONG Xiahai, ZHANG Xueqiang. Inversion of Rayleigh wave dispersion curves based on particle swarm and ant colony hybrid optimization[J]. Oil Geophysical Prospecting, 2022, 57(2): 303-310, 356. |
| [11] |
石耀霖, 金文. 面波频散反演地球内部构造的遗传算法[J]. 地球物理学报, 1995, 38(2): 189-198. SHI Yaolin, JIN Wen. Genetic algorithms inversion of lithospheric structure from surface wave dispersion[J]. Chinese Journal of Geophysics, 1995, 38(2): 189-198. |
| [12] |
YAMANAKA H, ISHIDA H. Application of genetic algorithms to an inversion of surface-wave dispersion data[J]. Bulletin of the Seismological Society of America, 1996, 86(2): 436-444. DOI:10.1785/BSSA0860020436 |
| [13] |
DAL MORO G, PIPAN M, GABRIELLI P. Rayleigh wave dispersion curve inversion via genetic algorithms and marginal posterior probability density estimation[J]. Journal of Applied Geophysics, 2007, 61(1): 39-55. DOI:10.1016/j.jappgeo.2006.04.002 |
| [14] |
MARTÍNEZ M D, LANA X, OLARTE J, et al. Inversion of Rayleigh wave phase and group velocities by simulated annealing[J]. Physics of the Earth and Planetary Interiors, 2000, 122(1-2): 3-17. |
| [15] |
BEATY K S, SCHMITT D R, SACCHI M. Simulated annealing inversion of multimode Rayleigh wave dispersion curves for geological structure[J]. Geophysical Journal International, 2002, 151(2): 622-631. |
| [16] |
LU Y, PENG S, DU W, et al. Rayleigh wave inversion using heat-bath simulated annealing algorithm[J]. Journal of Applied Geophysics, 2016, 134: 267-280. |
| [17] |
SUN C, WANG Y, WU D, et al. Nonlinear Rayleigh wave inversion based on the shuffled frog-leaping algorithm[J]. Applied Geophysics, 2017, 14(4): 551-558. |
| [18] |
杨博, 熊章强, 张大洲, 等. 利用自适应混沌遗传粒子群算法反演瑞雷面波频散曲线[J]. 石油地球物理勘探, 2019, 54(6): 1217-1227. YANG Bo, XIONG Zhangqiang, ZHANG Dazhou, et al. Rayleigh surface-wave dispersion curve inversion based on adaptive chaos genetic particle swarm optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(6): 1217-1227. |
| [19] |
于东凯, 宋先海, 张学强, 等. 蚱蜢算法在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2019, 54(2): 288-301. YU Dongkai, SONG Xianhai, ZHANG Xueqiang, et al. Rayleigh wave dispersion inversion based on grasshopper optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(2): 288-301. |
| [20] |
高旭, 于静, 李学良, 等. 自适应权重蜻蜓算法及其在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2021, 56(4): 745-757. GAO Xu, YU Jing, LI Xueliang, et al. Rayleigh wave dispersion curve inversion based on adaptive weight dragonfly algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4): 745-757. |
| [21] |
文成哲, 刘财, 郭智奇, 等. 遗传算法和LM算法联合反演瑞雷波相速度[J]. 地球物理学进展, 2010, 25(1): 303-309. WEN Chengzhe, LIU Cai, GUO Zhiqi, et al. Joint inversion of Rayleigh wave phase velocity by GA and Levenberg-Marquardt(LM) algorithm[J]. Progress in Geophysics, 2010, 25(1): 303-309. |
| [22] |
LU J, LI S, LI W, et al. A hybrid inversion method of damped least squares with simulated annealing used for Rayleigh wave dispersion curve inversion[J]. Earthquake Engineering and Engineering Vibration, 2014, 13(1): 13-21. |
| [23] |
NEMATOLLAHI A F, RAHIMINEJAD A, VAHIDI B. A novel physical based meta-heuristic optimization method known as lightning attachment procedure optimization[J]. Applied Soft Computing, 2017, 59: 596-621. |
| [24] |
陈渭明. 雷电学原理[M]. 北京: 气象学出版社, 2003: 289-292.
|
| [25] |
HU X, EBERHART R. Solving constrained nonlinear optimization problems with particle swarm optimization[C]. Proceedings of the Sixth World Multiconference on Systemics, Cybernetics and Informatics, Citeseer, 2002, 203-206.
|
| [26] |
凡友华, 刘家琦, 肖柏勋. 计算瑞利波频散曲线的快速矢量传递算法[J]. 湖南大学学报(自然科学版), 2002, 29(5): 25-30. FAN Youhua, LIU Jiaqi, XIAO Baixun. Fast vectortransfer algorithm for computation of Rayleigh wave dispersion curves[J]. Journal of Hunan University (Natural Sciences), 2002, 29(5): 25-30. |
| [27] |
ZHANG S, CHAN L. Possible effects of misidentified mode number on Rayleigh wave inversion[J]. Journal of Applied Geophysics, 2003, 53(1): 17-29. |
| [28] |
王一鸣, 宋先海, 张学强. 应用人工神经网络算法的地震面波非线性反演[J]. 石油地球物理勘探, 2021, 56(5): 979-991. WANG Yiming, Song Xianhai, ZHANG Xueqiang. Research on nonlinear inversion of seismic surface waves based on artificial neural network algorithm[J]. Oil Geophysical Prospecting, 2021, 56(5): 979-991. |
| [29] |
GAROFALO F, FOTI S, HOLLENDER F, et al. InterPACIFIC project:Comparison of invasive and non-invasive methods for seismic site characterization, Part Ⅰ:Intra-comparison of surface wave methods[J]. Soil Dynamics and Earthquake Engineering, 2016, 82: 222-240. |
| [30] |
XIA J. Estimation of near-surface shear-wave velocities and quality factors using multichannel analysis of surface-wave methods[J]. Journal of Applied Geophysics, 2014, 103: 140-151. |
| [31] |
蔡伟, 宋先海, 袁士川, 等. 基于萤火虫和蝙蝠群智能算法的瑞雷波频散曲线反演[J]. 地球物理学报, 2018, 61(6): 2409-2420. CAI Wei, SONG Xianhai, YUAN Shichuan, et al. Inversion of Rayleigh wave dispersion curves based on firefly and bat algorithms[J]. Chinese Journal of Geophysics, 2018, 61(6): 2409-2420. |



 姚振岸, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email:
姚振岸, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email: