旅行时近似是时差校正、速度分析、反演等地学领域的重要研究课题之一[1-3]。炮检距函数应用于具有垂直对称轴的横向各向同性(Transverse Isotropy Medium with Vertical Symmetry Axis,VTI)介质时,常使用非双曲线形式。
在早期研究中,学者们提出了多种适用于VTI介质的P波旅行时近似方程。Taner等[4]建议在旅行时公式中加入泰勒级数项得到非双曲线型公式;May等[5]提出一种基于正交多项式的非双曲线近似方法计算四阶时差谱。由于VTI介质的影响,这些方法计算的旅行时会随炮检距的变大而出现偏差。随后,学者们提出了其他基于泰勒级数的方法提高远炮检距旅行时的计算精度。Alkhalifah等[6]利用声学近似理论提出了基于泰勒级数的4阶旅行时近似方程;胡中平[7]提出一种优化炮检距6阶项的计算方法;Stovas等[8]在泰勒展开式的基础上提出了三种旅行时近似公式;之后,Ursin等[9]利用泰勒级数高阶项进行系数匹配得到了4阶旅行时计算方程。以上几种方法使用的均是高阶泰勒级数的截断形式,远炮检距处旅行时的计算精度并不理想[10]。通过进一步分析旅行时公式在各向异性介质中的表现,学者们提出了基于泰勒级数与其他理论相结合的P波旅行时计算方程。邓怀群等[11]研究了适用于弱各向异性VTI介质中的旅行时计算方法;之后,Song等[12]利用基于高阶泰勒级数系数的Padé近似方法估计远炮检距时差;Sripanich等[13]通过特定参数选择提出了简化的旅行时近似方程;Xu等[14]基于泰勒级数的炮检距扩展和弹性正交介质中的声学近似优化了P波旅行时计算公式;另外,Abedi等[15]与Blias[16]提出了基于广义时差近似的旅行时计算方法;随后,Abedi等[17]利用微扰理论推导出新的旅行时近似方程;2020年Abedi[18]提出了P波运动学有理近似方法;之后,Farra等[19]推导了基于弱各向异性参数的非双曲线型P波时差方程;2021年Abedi等[20]又提出了一种基于声学假设的六参数旅行时计算方程;之后,一种利用降阶补偿的处理方法开始用于计算介质中的旅行时[21]。随着旅行时公式的进一步完善,能够提高旅行时计算精度的方法的种类也随之增加。
针对常用的基于泰勒级数的P波旅行时近似方程在水平层状VTI介质中的计算有待提高的问题,本文先利用平方处理将其转换为旅行时平方近似方程,再结合系数匹配方法依次处理炮检距的高阶项,由此得到一种含有与各向异性相关的新系数y的P波旅行时计算方法。经数据测试与方法对比表明,该方法可以改善远炮检距处旅行时的计算且误差较小。
1 理论方法 1.1 基于泰勒级数的炮检距4阶旅行时公式Ursin等[9]在常规基于泰勒级数的旅行时公式基础上,提出一种基于系数匹配方法的P波旅行时计算方程
| $ t\left(x\right)={t}_{0}+\frac{{x}^{2}}{2{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}}+\frac{d{x}^{4}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{4}{t}_{0}^{3}\left(1+\frac{D{x}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}^{2}}\right)} $ | (1) |
其中
| $ d=-\frac{{S}_{2}}{8} $ | (2) |
| $ D=\frac{2{S}_{2}^{2}-{S}_{3}}{2{S}_{2}} $ | (3) |
式中:t0为垂直双程旅行时;x为炮检距;vNMO为正常时差速度;S2、S3为非均质性参数,其中S2与各向异性参数η的关系为[9, 22-23]
| $ {S}_{2}=1+8\eta $ | (4) |
通过推导出的S2与S3的近似关系可进一号简化式(3)。首先写出基于泰勒级数定义的垂直慢度的系数
| $ \left\{\begin{array}{l}{a}_{0}=2\delta \\ {a}_{1}=\frac{2(\varepsilon -\delta )}{1-{\gamma }_{0}^{2}}(1-{\gamma }_{0}^{2}+2\delta )\\ {a}_{2}=\frac{4(\varepsilon -\delta )}{(1-{\gamma }_{0}^{2}{)}^{2}}(1-{\gamma }_{0}^{2}+2\delta )\left[\varepsilon -\delta (1+{\gamma }_{0}^{2})\right]\\ \;\;\;\;\;\;\;\;\;\; \vdots\end{array}\right. $ | (5) |
式中:
S2、S3与系数
| $ \left\{\begin{array}{l}{S}_{2}=1+\frac{4{a}_{1}}{(1+{a}_{0}{)}^{2}}\\ {S}_{3}=1+\frac{4{a}_{1}}{(1+{a}_{0}{)}^{2}}+\frac{8{a}_{2}}{(1+{a}_{0}{)}^{3}}\end{array}\right. $ | (6) |
结合声学近似理论[22],即
| $ {S}_{3}=1+8\eta +32{\eta }^{2}=\frac{1+{S}_{2}^{2}}{2} $ | (7) |
再将式(7)代入式(3),即可得到参数D的近似形式
| $ D=\frac{3{S}_{2}^{2}-1}{4{S}_{2}}=\frac{3{(1+8\eta )}^{2}-1}{4(1+8\eta )} $ | (8) |
与旅行时平方公式相比,式(1)是一种不常作为研究对象的旅行时方程。
首先,通过将式(1)两边平方将其转换为平方形式。然后,按炮检距阶数从小到大排列
| $ {t}^{2}={t}_{0}^{2}+\frac{{x}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}}+A{x}^{4}+B{x}^{6}+C{x}^{8} $ | (9) |
其中
| $ \left\{\begin{array}{l}A=\frac{1+8d}{4{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{4}{t}_{0}^{2}\left(1+\frac{D{x}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}^{2}}\right)}\\ B=\frac{D+4d}{4{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{6}{t}_{0}^{4}\left(1+\frac{D{x}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}^{2}}\right)}\\ C=\frac{{d}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{8}{t}_{0}^{6}{\left(1+\frac{D{x}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}^{2}}\right)}^{2}}\end{array}\right. $ | (10) |
由式(9)和式(10)可见,三个高阶项系数A、B和C均包含相对复杂的结构。为了保持相对简洁的结构以及体现高阶泰勒级数的意义,根据式(1)的组成形式,可使式(9)中炮检距的最高阶数仍为常规形式的四阶。
在推导基于泰勒级数的旅行时公式过程中,常对高阶项采用近似处理来简化方程形式。常用的处理方式有:①省略高阶项的截断近似;②利用高阶项进行系数匹配[10]的近似。分析式(9)可知,截断近似并不能使其满足应用要求,而系数匹配近似是更适合的处理方法。
首先,将系数匹配方法用于处理式(9)的8阶项,即利用B和C可以得到
| $ {t}^{2}={t}_{0}^{2}+\frac{{x}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}}+A{x}^{4}+\frac{(D+4d){x}^{6}}{4{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{6}{t}_{0}^{4}\left(1+\frac{\mu D{x}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}^{2}}\right)} $ | (11) |
式中
| $ \mu =\frac{C}{B}{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}^{2}\left(1+\frac{D{x}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}^{2}}\right)=\frac{4{d}^{2}}{D+4d}=\frac{{S}_{2}^{3}}{4({S}_{2}^{2}-1)} $ | (12) |
在式(11)的基础上,继续利用系数匹配方法处理6次方项。为了简化旅行时公式的参数结构,可先得到中间参数λ,即
| $ \lambda =-\frac{B}{A}{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}^{2}=\frac{{S}_{2}^{2}-1}{4{S}_{2}({S}_{2}-1)}=\frac{1+{S}_{2}}{4{S}_{2}} $ | (13) |
结合式(13)即可得到最终形式的计算方程,即基于新系数y的炮检距四阶旅行时公式
| $ {t}^{2}={t}_{0}^{2}+\frac{{x}^{2}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}}-\frac{8\eta {x}^{4}}{{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}\left(4{v}_{\mathrm{N}\mathrm{M}\mathrm{O}}^{2}{t}_{0}^{2}+yD{x}^{2}\right)} $ | (14) |
其中
| $ y=\lambda {\mu }^{-1}=\frac{(1+{S}_{2})({S}_{2}^{2}-1)}{{S}_{2}^{4}} $ | (15) |
基于平方处理与系数匹配方法得到的旅行时平方方程(式(14)),可定义为SCM(Squaring and Coefficient Matching)法。
2 实验结果从实验角度分析SCM与有理近似法(TR)[18]、三射线广义时差近似法(TG)[24]和扩展广义时差近似法(TE)[1, 20]等4种方法与精确时间的计算误差,实验使用水平层状VTI介质模型,参数如表 1所示。
|
|
表 1 层状模型参数 |
介质中P波的准确时间可由
| $ \left\{\begin{array}{c}x\left(p\right)=\sum\limits_{i}{u}_{x, i}{w}_{i}\\ t\left(p\right)=\sum\limits_{i}{u}_{t, i}{w}_{i}\end{array}\right. $ | (16) |
| $ \left\{\begin{array}{l}{u}_{x, i}=p{v}_{\mathrm{N}\mathrm{M}\mathrm{O}, i}^{2}\\ {u}_{t, i}=(1-2{\eta }_{i}{p}^{2}{v}_{\mathrm{N}\mathrm{M}\mathrm{O}, i}^{2}{)}^{2}+2{\eta }_{i}{p}^{4}{v}_{\mathrm{N}\mathrm{M}\mathrm{O}, i}^{4}\\ {w}_{i}=\frac{{t}_{0\left(i\right)}}{\sqrt{(1-2{\eta }_{i}{p}^{2}{v}_{\mathrm{N}\mathrm{M}\mathrm{O}, i}^{2}{)}^{3}(1-{p}^{2}{v}_{h, i}^{2})}}\end{array}\right. $ | (17) |
x(p)、t(p)分别表示通过射线参数p计算出的炮检距与旅行时;t0,i、vNMO,i、vh,i、ηi分别表示第i层的双程旅行时、正常时差速度、水平速度、各向异性参数。
定义实验误差为
| $ \mathrm{T}\mathrm{M}\mathrm{O}=\left|\frac{{T}_{\mathrm{a}}-{T}_{\mathrm{x}}}{{T}_{\mathrm{a}}}\right| $ | (18) |
式中:Ta表示准确时间;Tx表示通过TR、TG、TE和SCM法所得计算值。
2.1 模型一模型一为椭圆各向异性介质模型。图 1是本文方法(SCM)、TR、TG、TE法的旅行时计算误差曲线。由图可见,当炮检距与深度的比值为0~2.5时,SCM法的计算精度高于其他3种方法。在图 2中,TR、TG、TE与SCM法的TMO之差均为正值,可知SCM法的计算误差最小。TE法作为公认的一种较准确的计算方法,其误差仅小于SCM法。虽然TG与TR法的TMO差值非常小,实际上TR法仍具有更小的误差。从数值上分析表明,当炮检距与深度的比值等于2.5时,即远炮检距处,SCM、TE、TR、TG法的误差分别为4.00%、4.48%、5.30%、5.30%。

|
图 1 模型一旅行时计算误差 |

|
图 2 模型一4种方法的TMO差值 (a)TG分别与TR、TE、SCM方法的对比;(b)TR、TE、SCM方法间的对比 |
模型一的实验结果表明,SCM法在炮检距与深度的比值在0~2.5的范围内具有更小的计算误差,最大比值2.5处的误差同样较小,但方法间的TMO差值相对较小。
2.2 模型二针对模型二,上述4种方法的误差曲线与各方法间的TMO差值分别如图 3、图 4所示。当炮检距与深度的比值为0~2.5时,SCM法的计算误差最小,TE法的表现优于TG和TR法,TG法仍然具有较大的误差。这与图 1、图 2中的曲线趋势一致。当炮检距与深度的比值为2.5时,SCM、TE、TR、TG法的误差分别为:0.55%、1.65%、2.27%和2.27%。
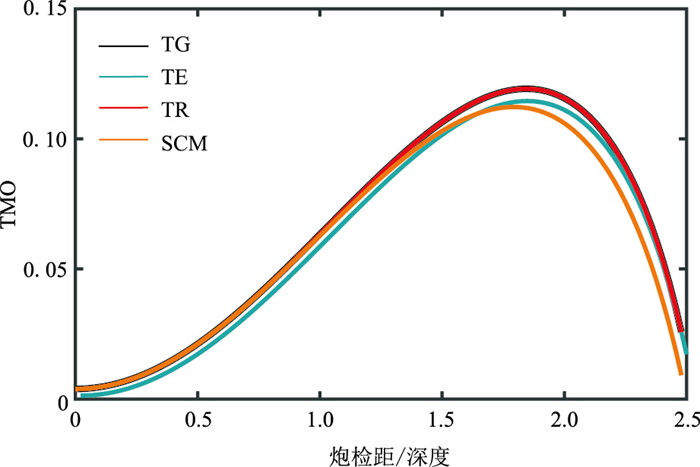
|
图 3 模型二旅行时计算误差 |
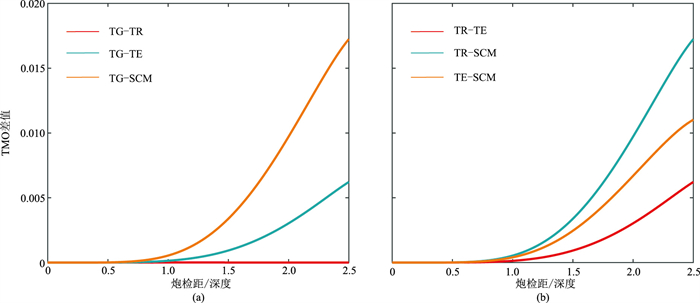
|
图 4 模型二4种方法的TMO差值 (a)TG分别与TR、TE、SCM方法的对比;(b)TR、TE、SCM方法间的对比 |
模型二的实验结果表明,SCM法在整体与远炮检距处的误差同样较小。对比模型一,此时各方法间的TMO差值变大。
3 讨论根据常用的基于泰勒级数的P波旅行时近似方程的组成结构,本文提出一种基于平方处理和系数匹配方法的P波旅行时计算方法,即SCM方法。该方法具有与常规基于泰勒级数的计算方程类似的结构,不同之处在于参数组成以及近似处理。本文讨论了将SCM方法中炮检距的最高阶数保持为4阶形式的方法,若改变处理8阶项和6阶项的次序,是否能够得到具有类似计算表现的方程是值得思考的。另外,本文使用的实验模型的类型有限,对于其他模型以及实际地震数据而言,这种参数组合形式是否仍具有类似的结果以及稳定性,需要继续测试来验证并加以优化。
与反射波旅行时快速算法[24]相比,旅行时近似方程在计算速度上并没有优势,推导旅行时近似方程的主要目的是进行各向异性速度分析、求取各向异性参数以及时差校正等处理[1-3, 25]。在实际工程中,选择何种旅行时近似方程同样需要考虑该方程在实际地震数据中的计算表现。若研究区的介质性质不完全受到VTI介质的影响,在利用旅行时方程进行处理时应特别注意。在此基础上,如何使基于旅行时近似方程的分析方式更好地为叠加成像[26]、偏移成像[27-28]提供有力支撑值得进一步探讨。
4 结论本文首先使用垂直慢度方程和声学近似理论得出了近似系数D的新形式;然后,利用平方处理和两次系数匹配方法对非平方形式的偏移距4阶旅行时方程进行近似处理,由此推导出了新参数μ与中间参数λ;最后,得到了更加直观的P波旅行时平方方程,即SCM法。
对两个水平层状VTI介质模型的测试结果表明,SCM法的误差比有理近似法、三射线广义时差近似法和扩展广义时差近似法更小。当炮检距与深度的比值达到最大值2.5时,SCM法的计算优于其他方法。因此,该方法能够提高VTI介质中P波旅行时的计算精度。
| [1] |
ABEDI M M, STOVAS A. Extended generalized nonhyperbolic moveout approximation[J]. Geophysical Journal International, 2019, 216(2): 1428-1440. DOI:10.1093/gji/ggy504 |
| [2] |
樊中海, 胡渤, 宋吉杰, 等. 地震反演储层描述精度影响因素分析[J]. 石油地球物理勘探, 2022, 57(2): 441-451. FAN Zhonghai, HU Bo, SONG Jijie, et al. Analysis of influencing factors in reservoir description accuracy by seismic inversion[J]. Oil Geophysical Prospecting, 2022, 57(2): 441-451. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.024 |
| [3] |
蔡志东, 王世成, 韦永祥, 等. VSP波场研究与应用现状[J]. 石油物探, 2021, 60(1): 81-91. CAI Zhidong, WANG Shicheng, WEI Yongxiang, et al. Research and application status of VSP wavefields[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 81-91. DOI:10.3969/j.issn.1000-1441.2021.01.008 |
| [4] |
TANER M T, KOEHLER F. Velocity spectra-digital computer derivation and applications of velocity functions[J]. Geophysics, 1969, 34(6): 859-881. DOI:10.1190/1.1440058 |
| [5] |
MAY B T, STRALEY D K. Higher-order moveout spectra[J]. Geophysics, 1979, 44(7): 1193-1207. DOI:10.1190/1.1441002 |
| [6] |
ALKHALIFAH T, TSVANKIN I. Velocity analysis for transversely isotropic media[J]. Geophysics, 1995, 60(5): 1550-1566. DOI:10.1190/1.1443888 |
| [7] |
胡中平. 优化6次项NMO校正方法研究[J]. 石油地球物理勘探, 2003, 38(6): 603-607. HU Zhongping. Study of NMO correction method by optimized sixth-order term[J]. Oil Geophysical Prospecting, 2003, 38(6): 603-607. DOI:10.3321/j.issn:1000-7210.2003.06.004 |
| [8] |
STOVAS A, URSIN B. New travel-time approximations for a transversely isotropic medium[J]. Journal of Geophysics and Engineering, 2004, 1(2): 128-133. DOI:10.1088/1742-2132/1/2/004 |
| [9] |
URSIN B, STOVAS A. Traveltime approximations for a layered transversely isotropic medium[J]. Geophysics, 2006, 71(2): D23-D33. DOI:10.1190/1.2187716 |
| [10] |
SONG H, ZHANG J, YAO Z. Normal moveout for long offset in isotropic media using the Padé approximation[J]. Applied Geophysics, 2016, 13(4): 658-666. DOI:10.1007/s11770-016-0587-4 |
| [11] |
邓怀群, 刘雯林. 横向各向同性介质中地震波旅行时的计算[J]. 石油地球物理勘探, 2000, 35(4): 508-516. DENG Huaiqun, LIU Wenlin. Computation of seismic travel times in transversely isotropic medium[J]. Oil Geophysical Prospecting, 2000, 35(4): 508-516. DOI:10.3321/j.issn:1000-7210.2000.04.013 |
| [12] |
SONG H, GAO Y, ZHANG J, et al. Long-offset moveout for VTI using Padé approximation[J]. Geophysics, 2016, 81(5): C219-C227. DOI:10.1190/geo2015-0094.1 |
| [13] |
SRIPANICH Y, FOMEL S, STOVAS A, et al. 3D generalized nonhyperboloidal moveout approximation[J]. Geophysics, 2017, 82(2): C49-C59. DOI:10.1190/geo2016-0180.1 |
| [14] |
XU S, STOVAS A, MIKADA H. Traveltime and relative geometric spreading approximation in elastic orthorhombic medium[J]. Geophysics, 2020, 85(5): C153-C162. DOI:10.1190/geo2019-0811.1 |
| [15] |
ABEDI M M, STOVAS A. A new parameterization for generalized moveout approximation, based on three rays[J]. Geophysical Prospecting, 2019, 67(5): 1243-1255. DOI:10.1111/1365-2478.12770 |
| [16] |
BLIAS E. VSP extension of the generalized FomelStovas approximation[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [17] |
ABEDI M M, RIAHI M A, STOVAS A. Threeparameter normal moveout correction in layered anisotropic media: a stretch-free approach[J]. Geophysics, 2019, 84(3): C129-C142. DOI:10.1190/geo2017-0855.1 |
| [18] |
ABEDI M M. Rational approximation of P-wave kinematics-part 1:transversely isotropic media[J]. Geophysics, 2020, 85(5): C163-C173. DOI:10.1190/geo2020-0005.1 |
| [19] |
FARRA V, PŠENČÍK I. P-wave reflection-moveout approximation for horizontally layered media of arbitrary moderate anisotropy[J]. Geophysics, 2020, 85(2): C61-C70. DOI:10.1190/geo2019-0232.1 |
| [20] |
ABEDI M M, PARDO D. Large-offset P-wave traveltime in layered transversely isotropic media[J]. Geophysics, 2021, 86(3): C65-C74. DOI:10.1190/geo2020-0415.1 |
| [21] |
魏建, 孙祥娥. VTI介质中基于降阶补偿处理的旅行时计算方法[J]. 山东科技大学学报(自然科学版), 2022, 41(1): 86-91. WEI Jian, SUN Xiang'e. A method of traveltime calculation based on descending order compensation processing in VTI medium[J]. Journal of Shandong University of Science and Technology (Natural Science), 2022, 41(1): 86-91. |
| [22] |
STOVAS A, URSIN B. Improved geometricspreading approximation in layered transversely isotropic media[J]. Geophysics, 2009, 74(5): D85-D95. DOI:10.1190/1.3158051 |
| [23] |
BANIK N C. An effective anisotropy parameter in transversely isotropic media[J]. Geophysics, 1987, 52(12): 1654-1664. DOI:10.1190/1.1442282 |
| [24] |
张建中, 安全, 于建明, 等. 倾斜层状TI介质反射波旅行时快速计算[J]. 石油地球物理勘探, 2022, 57(1): 111-117. ZHANG Jianzhong, AN Quan, YU Jianming, et al. Rapid calculation of reflected wave travel time in layered TI media with dipping interfaces[J]. Oil Geophysical Prospecting, 2022, 57(1): 111-117. |
| [25] |
陈占国, 曾昭翰, 杨心超. 基于VSP数据的任意弱各向异性参数反演方法[J]. 石油地球物理勘探, 2022, 57(2): 311-319. CHEN Zhanguo, ZENG Zhaohan, YANG Xinchao. An inversion method for arbitrary weak anisotropy parameters based on VSP data[J]. Oil Geophysical Prospecting, 2022, 57(2): 311-319. |
| [26] |
杨飞龙, 任广莹, 姚凤鸣, 等. 井间地震逆菲涅尔束叠加成像及其应用[C]. 2022年中国石油物探学术年会论文集(下册), 2022, 207-210. YANG Feilong, REN Guangying, YAO Fengming, et al. Inverse fresnel beam stack imaging of cross-well seismic and its application[C]. Proceedings of the 2022 China Petroleum Geophysical Exploration Academic Annual Conference (Volume 2), 2022, 207-210. |
| [27] |
秦宁. 弹性波各向异性高斯束逆时偏移[J]. 石油物探, 2022, 61(2): 321-328. QIN Ning. Elastic reverse time migration with Gaussian beams in anisotropic media[J]. Geophysical Prospecting for Petroleum, 2022, 61(2): 321-328. DOI:10.3969/j.issn.1000-1441.2022.02.013 |
| [28] |
秦宁, 王常波, 梁鸿贤, 等. 一次波和层间多次波联合成像方法[J]. 石油地球物理勘探, 2022, 57(6): 1375-1383. QIN Ning, WANG Changbo, LIANG Hongxian, et al. Joint imaging method of primaries and internal multiples[J]. Oil Geophysical Prospecting, 2022, 57(6): 1375-1383. |



 孙祥娥, 湖北省荆州市南环路1号长江大学电子信息学院,434023。Email:
孙祥娥, 湖北省荆州市南环路1号长江大学电子信息学院,434023。Email: