0 引言

地震波在传播过程中会发生衰减，有球面波的几何扩散，有透射损失、折射、散射等造成的视衰减，还有在非完全弹性介质中传播时由介质的吸收效应引起的吸收衰减，又称固有衰减或本征衰减。吸收衰减使地震波的振幅减小、相位畸变、频带变窄、主频降低，这严重影响了地震资料分辨率的提高^[1-2]。为估算这一项损耗，可以用地震波在一个波长内的能量损失描述吸收衰减，并用品质因子Q值定量计算^[3]。在地震资料处理中，品质因子是补偿高频能量、拓宽有效频带、提高分辨率等的关键参数。有效的品质因子估计方法对提高地震资料成像精度、合理解释AVO效应和正确地反演介质物理属性十分重要。

目前，估计地层Q值的方法主要有两类：一是基于信号分析的Q值估计方法^[4-10]；二是基于层析反演的Q值估计方法^[11-14]。层析反演类方法精度较高，但计算量很大，且依赖初始模型参数。基于信号分析的Q值估计方法相对容易实现，计算量低，结果稳定，大多是对地震资料预处理后的道集和单道进行分析，利用时间域、频率域、时频域等估计平均或等效Q值，可以为层析反演提供初始模型。赵宪生等^[15]利用叠前地震资料相邻层间地震子波相似系数的相关性确定Q值。Dasgupta等^[16]根据Q值随炮检距变化（QVO）的关系，用谱比法对叠前CMP道集进行Q值估算。Hackert等^[17]改进了QVO方法，结合测井资料消除了薄层对振幅谱的影响，在对振幅谱进行校正后再提取Q值。Zhang等^[18]推导出Q值和子波振幅谱峰值频率随炮检距和旅行时变化的关系，即基于水平层状介质模型的CMP道集反射波衰减方程，并利用这个方程进行Q值反演和反Q滤波。任浩然等^[19]用非递归波场代替递归波场进行延拓，用等效Q值代替地层Q值，在平面波假设条件下实现了对叠前数据沿波传播路径的吸收衰减补偿。吕喜滨^[20]对Q扫描方法开展了较详细的研究，认为该方法需要选取浅层强反射界面作为标准层。王小杰等^[21]利用S变换分析时频谱并将炮检距归零处理，从叠前地震资料中得到零炮检距的地层Q值。赵静等^[22]改进了适用于常相位子波的EPIFVO（子波包络峰值处瞬时频率随炮检距变化）方法，用不同炮检距的值线性回归，但这只适用于层状均匀介质。Ma等^[23]使用基于贝叶斯学习的评判准则扫描求取较准确的Q值。张瑾等^[24]提出一种基于泰勒级数展开的振幅谱积分差值（ASID）方法。杨登锋等^[25]用高斯加权谱比法拟合对数谱比的斜率，提高了谱比法估计Q值的稳定性。

为了快速得到地层背景Q模型用于层析反演，本文采用基于相对熵准则的背景Q值扫描方法。首先，基于CMP道集对子波振幅谱做Q扫描补偿，只考虑吸收衰减对子波振幅谱的影响，当吸收衰减被正确补偿时，不同炮检距的振幅谱一致性最佳，据此得到背景Q值估计结果；然后，对比了度量Q补偿振幅谱一致性的几种准则，理论实验证明相对熵准则和JS散度准则对扫描Q值变化最敏感，抗噪性也较强。在实际数据应用中，采用JS散度准则Q扫描获得的地层背景Q模型用于Q补偿偏移，获得了较好的效果。

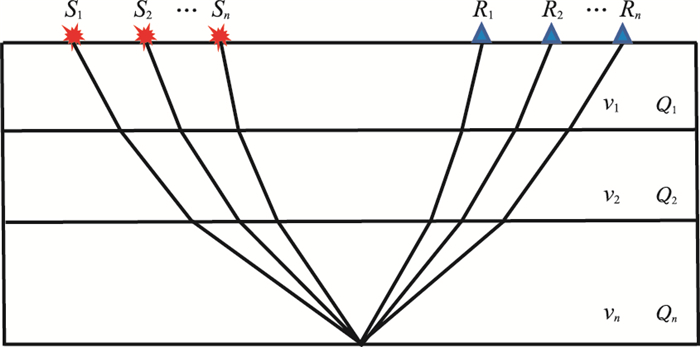
1 CMP道集Q值扫描估计方法原理

目前常用的地层吸收衰减参数计算方法主要是基于零炮检距的垂直地震剖面（VSP）或叠后地震资料。VSP地震记录通常难以获得，而叠加又会扭曲原始地震数据的频率信息^[26-27]。虽然叠前地震资料有更丰富的振幅、旅行时信息，包含更多细微的地层特征信息，但是叠前数据也可能受到传播路径变化、NMO拉伸、反射—透射效应以及噪声和多次波的影响，使频谱的幅度、形态与炮检距之间的变化关系复杂。基于叠前CMP道集，假设地层为水平层状，速度和Q值均是横向不变的，反射波满足双曲时距关系，其传播路径如图 1所示。

假设震源为任意源谱$ U\left(\omega , 0\right) $，其中$ \omega $为角频率，地层为常Q介质，不考虑几何扩散、散射等能量衰减项，只讨论吸收衰减的影响。基于平面波假设，地震子波沿路径的传播结果可以表示为

$ \begin{array}{l}U\left(f, t\right)={A}_{\mathrm{s}}\left(f\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{i}2\mathrm{\pi }ft\right)\times \\ \qquad \;\; \qquad \mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{\mathrm{\pi }ft}{Q}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{i}\frac{2ft}{Q}\mathrm{l}\mathrm{n}\frac{f}{{f}_{\mathrm{m}}}\right)\end{array} $

(1)

式中：$ U\left(f, t\right) $是地震波传播时间$ t $后的频谱，其中$ f $是频谱的频率；$ {f}_{\mathrm{m}} $是震源子波主频；$ {A}_{\mathrm{s}}\left(f\right) $是$ t=0 $时刻的震源子波振幅谱。旅行时满足双曲时距关系$ {t}^{2}={t}_{0}^{2}+{x}^{2}/{v}_{rms}^{2} $，其中$ {v}_{\mathrm{r}\mathrm{m}\mathrm{s}} $为均方根速度；i表示虚数单位。

对于图 1所示的多层水平介质，反射波振幅$ {A}_{\mathrm{r}}\left(f, t\right)={A}_{\mathrm{s}}\left(f\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-\sum\limits_{i=1}^{n}\frac{\mathrm{\pi }f\mathrm{\Delta }{t}_{i}}{{Q}_{i}}\right) $，其中，$ {Q}_{i} $和$ \mathrm{\Delta }{t}_{i} $分别表示地下第i层的品质因子和地震波在该层内的传播时间，n为地层总层数。

用等效Q值表征多层介质内吸收衰减的累积，反射波振幅可写为

$ {A}_{\mathrm{r}}\left(f, t\right)={A}_{\mathrm{s}}\left(f\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\pi }f\frac{\sum\limits_{i=1}^{n}\mathrm{\Delta }{t}_{i}}{{Q}_{\mathrm{e}\mathrm{f}\mathrm{f}}}\right) $

(2)

$ {Q}_{\mathrm{e}\mathrm{f}\mathrm{f}} $即为n层介质的等效Q值，有

$ {Q}_{\mathrm{e}\mathrm{f}\mathrm{f}}=\frac{\sum\limits_{i=1}^{n}\mathrm{\Delta }{t}_{i}}{\sum\limits_{i=1}^{n}\frac{\mathrm{\Delta }{t}_{i}}{{Q}_{i}}} $

(3)

在直射线假设下，可认为射线在每层的入射角相等。根据相似三角形原理，等效Q值可近似为

$ {Q}_{\mathrm{e}\mathrm{f}\mathrm{f}}\approx \frac{\sum\limits_{i=1}^{n}\mathrm{\Delta }{t}_{0, i}}{\sum\limits_{i=1}^{n}\frac{\mathrm{\Delta }{t}_{0, i}}{{Q}_{i}}} $

(4)

式中$ \mathrm{\Delta }{t}_{0, i} $为第i层内的双程垂直传播时间。对前i层的等效Q值与前i-1层的等效Q值求差，可得第i层的层Q值

$ {Q}_{i}=\frac{{t}_{0\left(i\right)}-{t}_{0\left(i-1\right)}}{\frac{{t}_{0\left(i\right)}}{{Q}_{\mathrm{e}\mathrm{f}\mathrm{f}, i}}-\frac{{t}_{0\left(i-1\right)}}{{Q}_{\mathrm{e}\mathrm{f}\mathrm{f}, i-1}}} $

(5)

式中：$ {t}_{0\left(i\right)} $为前i层的双程垂直传播时间之和；$ {Q}_{\mathrm{e}\mathrm{f}\mathrm{f}, i} $为前i层的等效Q值。只要获取等效Q值，即可由式（5）逐层得到时间域层Q值。

在地震资料处理过程中，常规的均方根速度通过采用最高能量估算法得到，即在速度扫描能量谱上拾取速度，通过CMP道集的实时动校正进行单点速度的质量控制。类比速度扫描，建立Q值扫描自动化流程。具体而言，Q扫描法是以反Q滤波补偿作为基础^[28]，对预处理后的CMP道集按照一定间隔给出一组Q值；然后用它们对CMP道集各道做反Q滤波补偿；再依据不同炮检距地震道的反Q滤波补偿效果，在各个时间段上选择最佳Q值，把获取的最佳Q值作为地层等效Q值。

在CMP道集中，可以根据Q补偿后子波振幅谱的形态差异判断Q补偿效果。选用不同的Q值补偿CMP道集中不同炮检距处的地震子波，在一定度量原则下，若各道子波Q补偿后振幅谱的一致性最佳，此时的Q值即为对应地层等效Q值。

在正常沉积、水平层状地层条件下，地层从浅到深，Q值一般表现为逐渐增大的趋势。但也有例外，如存在油气、含水饱和度较高的区域，使得深层局部Q值不增反减；还有裂隙、断层、岩石类型、晶体排列方式等都有可能造成局部地层Q值减小。

在时间域制作Q值谱时，横坐标为地层等效Q值；纵坐标为地震波双程旅行时。一般要求Q值谱能量团聚焦良好，Q值谱点的等效Q值尽可能接近理论上的真实值，其余地方则受噪声等干扰小。那么，度量子波补偿振幅谱一致性的准则就成了制作高精度Q值谱的关键，该准则需要对两个含吸收衰减效应的地震子波振幅谱的差异很敏感，且拥有一定的抗噪性能。如果找到一个合适的度量准则，利用该准则可以快速制作出高分辨率的Q值谱，以用于实际地震数据处理，建立合理的背景Q值模型。

2 振幅谱一致性度量的相对熵准则

制作高精度Q值谱依赖于敏感的振幅谱一致性度量参数，一般可用各道频谱的峰值频移量或质心频移量作为度量参数。当子波振幅谱的吸收衰减效应得到正确补偿，在不考虑几何扩散和噪声影响的条件下，不同炮检距处的子波振幅谱形态趋于一致，则道与道之间的峰值频率偏移量为零，质心频率偏移量也为零。然而，受傅里叶变换时窗、截断误差、高频噪声等影响，振幅谱的高频部分会出现微小的波动，振幅补偿的e指数项会极大地放大高频误差，出现数值不稳定现象。因此，有必要进行增益截频，选取合适的频带范围度量子波Q补偿振幅谱的一致性。在实际数据中，CMP道集的道数较少，存在缺道、坏道等现象，此时仅利用峰值频率或质心频率随炮检距的变化估计Q值容易出现统计误差，因此应尽可能利用整个振幅谱的形态信息。

从信息论中发展了度量随机分布函数距离的参数，例如定义在概率密度函数$ {p}_{X}\left(\boldsymbol{x}\right) $与$ {g}_{X}\left(\boldsymbol{x}\right) $之间的相对熵（X为离散型随机变量，x为离散型随机变量具体取值组成的向量），即KL散度（Kullback–Leibler Divergence）^[29-30]

$ \begin{array} {l}\mathrm{K}\mathrm{L}\left({p}_{X}\left|\right|{g}_{X}\right)={\int }_{-\infty }^{\infty }{p}_{X}\left(\boldsymbol{x}\right)ln\frac{{p}_{X}\left(\boldsymbol{x}\right)}{{g}_{X}\left(\boldsymbol{x}\right)}d\boldsymbol{x} \\ \qquad \qquad \quad\;\;\; ={E}_{p}\left[\mathrm{l}\mathrm{n}\frac{{p}_{X}\left(\boldsymbol{x}\right)}{{g}_{X}\left(\boldsymbol{x}\right)}\right] \end{array} $

(6)

式中$ {E}_{p} $[·]表示求期望，下标$ p $指以$ {p}_{X}\left(\boldsymbol{x}\right) $为权系数求期望。

在统计学中，相对熵对应似然比的对数期望。相对熵$ \mathrm{K}\mathrm{L}\left({p}_{X}\left|\right|{g}_{X}\right) $用来度量当真实分布为$ {p}_{X} $而假定分布为$ {g}_{X} $时的无效性，也被用来衡量两个概率密度分布函数之间的相似性。相对熵具有非负性但并不对称，不满足三角不等式，因此在严格意义上不能表示两个分布之间的距离。然而，将相对熵视为分布之间的距离往往会很有用^[31]。相对熵越小，真实分布与近似分布之间的匹配程度越高。当相对熵等于零时，代表两个概率密度函数完全相同。振幅谱与概率密度函数有共同之处，即都是一维非负实信号。概率密度函数满足规范性，即累积分布函数积分值为1。在合适的频带内，对Q补偿后的子波振幅谱进行规范化处理，即区间内每一点的振幅谱值除以区间所有振幅谱值之和，这样得到的规范化振幅谱满足规范性，可以近似用相对熵度量不同炮检距处规范化后的子波振幅谱一致性。相对熵越小，代表不同炮检距处Q补偿子波振幅谱一致性越好。

为解决KL散度的不对称性问题，在KL散度的基础上定义了JS散度（Jensen-Shannon Divergence）

$ \begin{array}{l}\mathrm{J}\mathrm{S}\left({P}_{1}‖{P}_{2}\right)=\frac{1}{2}\mathrm{K}\mathrm{L}\left({P}_{1}‖\frac{{P}_{1}+ {P}_{2}}{2}\right)+\\ \qquad \qquad \qquad \frac{1}{2}\mathrm{K}\mathrm{L}\left({P}_{2}‖\frac{{P}_{1}+{P}_{2}}{2}\right) \end{array}$

(7)

式中$ {P}_{1} $和$ {P}_{2} $分别为不同的分布函数。一般而言，JS散度是对称的，值为0~1。需要说明的是，如果$ {P}_{1} $与$ {P}_{2} $完全没有重叠部分，那么KL散度值可能没有意义，而JS散度值是一个常数。Wessertein距离（EMD）可以有效解决这个问题，即使两个分布的支撑集没有交集，Wessertein距离仍然能反映两个分布的远近^[32]。对于不同炮检距的地震子波振幅谱做规范化处理后，在有限频带范围内是有重叠部分的，可以用KL散度或JS散度度量规范化后的振幅谱的一致性。

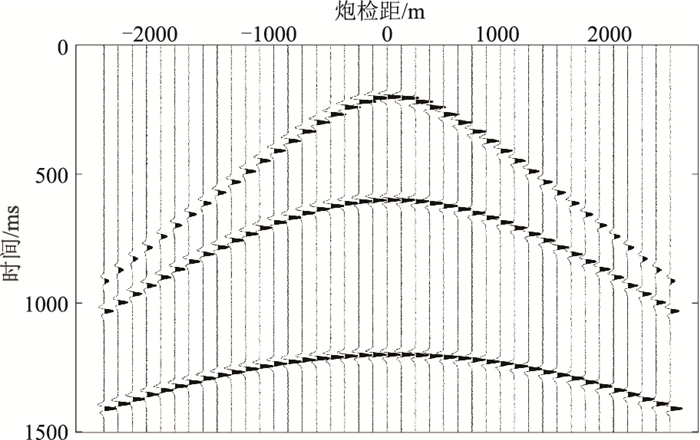
给定均方根速度模型和对应的品质因子Q模型，采样时间、Q值分别为0~200 ms、50，200~600 ms、100，600~1200 ms、200，1200~1500 ms、1000。共401道，道间距为12.5 m，最大炮检距为5000 m。地层反射系数均为0.2，与主频为30 Hz的Ricker子波褶积生成吸收衰减CMP道集（图 2），每隔10道显示1道子波波形。由图 2可见，随着炮检距的增大，同相轴上的子波衰减效应愈明显。

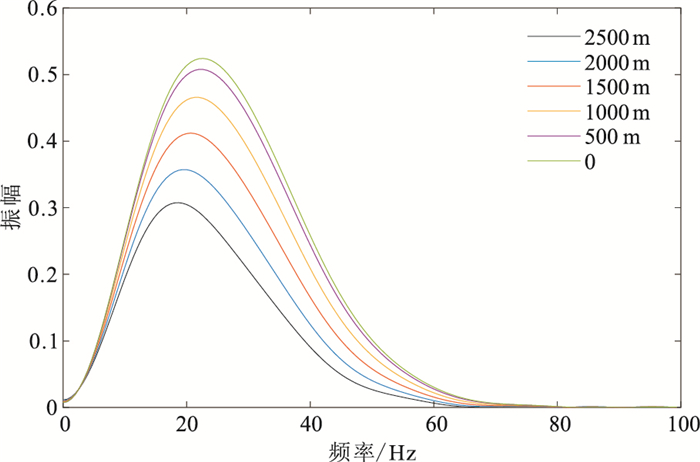
在该吸收衰减CMP道集上，沿中间的双曲线轨迹开时窗，窗长大于一个子波长度，经傅里叶变换后可以得到不同炮检距处衰减子波振幅谱（图 3）。由图可见，随着炮检距的增大，振幅谱的主频降低，频带变窄，高频部分衰减程度相对比低频部分更大。对有效频带范围（0~60 Hz）的衰减子波振幅谱做Q补偿处理，当补偿Q值为所在层位的等效Q值时，有效频带范围内不同炮检距的子波振幅谱一致性应达到最佳。

选取七种准则用于吸收衰减CMP道集中不同炮检距处子波的Q补偿振幅谱一致性的度量，分别为Pearson相关系数、Spearman相关系数、相似系数（Sc）、峰值频率随炮检距的变化（PFVO）、质心频率随炮检距的变化（CFVO）、KL散度的倒数和JS散度的倒数。截止频率统一为$ {f}_{\mathrm{T}}=60 $ Hz。各度量准则定义如下。

以子波Q补偿振幅谱的Pearson相关系数为参考量，当Q补偿后不同炮检距子波振幅谱的Pearson相关系数为1或最大时，可认为该Q值最接近地层等效Q值。Pearson相关系数扫描Q值谱的公式为

$ r\left(i, j\right)=\frac{\sum\limits_{f=0}^{{f}_{\mathrm{T}}}\left({A}_{i, f}-\overline{{A}_{i, f}}\right)\left({A}_{j, f}-\overline{{A}_{j, f}}\right)}{{\left[\sum\limits_{f=0}^{{f}_{\mathrm{T}}}{\left({A}_{i, f}-\overline{{A}_{i, f}}\right)}^{2}\sum\limits_{f=0}^{{f}_{\mathrm{T}}}{\left({A}_{j, f}-\overline{{A}_{j, f}}\right)}^{2}\right]}^{1/2}} $

(8)

$ \stackrel{-}{r}=\frac{1}{N}\sum\limits_{i=1}^{N}r\left(i, m\right) $

(9)

上述式中：$ r\left(i, j\right) $为第$ i $道与第$ j $道的Pearson相关系数；$ \overline{{A}_{i, f}}=\frac{1}{{f}_{\mathrm{T}}}\sum\limits_{f=0}^{{f}_{\mathrm{T}}}{A}_{i, f} $，$ \overline{{A}_{j, f}}=\frac{1}{{f}_{\mathrm{T}}}\sum\limits_{f=0}^{{f}_{\mathrm{T}}}{A}_{j, f} $，其中$ \overline{{A}_{i, f}} $、$ \overline{{A}_{j, f}} $分别为第$ i $、$ j $道的截止频率$ {f}_{\mathrm{T}} $内振幅谱$ {A}_{i, f} $、$ {A}_{j, f} $的均值；$ m $为CMP道集零炮检距道号；$ N $为总道数；$ \stackrel{-}{r} $为各道与零炮检距道的Pearson相关系数的均值。

Pearson相关系数只能反映线性关系，且变量之间相互独立，总体呈正态分布或接近正态的单峰分布。相比之下，Spearman相关系数对数据分布没有要求^[33-35]。在实际应用中，变量间的连接是无关紧要的，Spearman相关系数可简化为

$ R\left(i, j\right)=1-\frac{6\sum\limits_{f=0}^{{f}_{\mathrm{T}}}{d}_{i, j}^{2}}{k\left({k}^{2}-1\right)} $

(10)

$ \stackrel{-}{R}=\frac{1}{N}\sum\limits_{i=1}^{N}R\left(i, m\right) $

(11)

上述式中：$ R\left(i, j\right) $为第$ i $道与第$ j $道之间的Spearman相关系数；$ {d}_{i, j} $为第$ i $道与第$ j $道信号的等级差（某个数的等级是指将它所在的一列数据按照从小到大排序后该数所在的位置）；$ k $为截止频率$ {f}_{\mathrm{T}} $内的频率采样个数；$ \stackrel{-}{R} $为各道与零炮检距道的Spearman相关系数的均值。

以上两种相关系数在统计学中常用，但不适用于不同炮检距地震子波振幅谱一致性的度量。在速度分析的速度谱制作中，常用相似系数Sc作为子波波形相似性的度量。将Sc用于不同炮检距子波Q补偿振幅谱一致性的度量时，若Sc达到1或最大时，则可认为该Q值最接近地层等效Q值。相似系数扫描Q值谱的公式为

$ \mathrm{S}\mathrm{c}=\frac{\sum\limits_{f=0}^{{f}_{\mathrm{T}}}{\left(\sum\limits_{i=1}^{N}{A}_{i, f}\right)}^{2}}{N\sum\limits_{f=0}^{{f}_{\mathrm{T}}}\sum\limits_{i=1}^{N}{A}_{i, f}^{2}} $

(12)

用相似系数度量子波波形相似性是可行的，但未考虑衰减子波振幅谱的特征。因此，选择与衰减子波振幅谱相关的特征量（如峰值频率、质心频率等），以子波Q补偿振幅谱的PFVO为参考量，当Q补偿后不同炮检距子波振幅谱的峰值频率的方差为零或最小时，可认为该Q值最接近地层等效Q值。PFVO扫描Q值谱的公式为

$ \mathrm{P}\mathrm{F}\mathrm{V}\mathrm{O}=\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{N}\sum\limits_{i=1}^{N}{\left({f}_{p, i}-{\stackrel{-}{f}}_{p}\right)}^{2}\right] $

(13)

式中：$ {f}_{p, i} $为CMP道集中第$ i $道振幅谱0~60 Hz内的峰值频率；$ \overline{{f}_{p}} $为N道振幅谱峰值频率的均值。

以子波Q补偿振幅谱的质心频率偏移量为参考量，当Q补偿后不同炮检距子波振幅谱的质心频率的方差为零或最小时，可认为该Q值最接近地层等效Q值。CFVO扫描Q值谱的公式为

$ \mathrm{C}\mathrm{F}\mathrm{V}\mathrm{O}=\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{N}\sum\limits_{i=1}^{N}{\left({f}_{c, i}-{\stackrel{-}{f}}_{c}\right)}^{2}\right] $

(14)

$ {f}_{c}=\frac{{\int }_{0}^{{f}_{\mathrm{T}}}f\left|A\left(f\right)\right|\mathrm{d}f}{{\int }_{0}^{{f}_{\mathrm{T}}}\left|A\left(f\right)\right|\mathrm{d}f} $

(15)

上述式中：$ {f}_{c, i} $为CMP道集中第$ i $道子波振幅谱0~60 Hz内的质心频率；$ \overline{{f}_{c}} $为N道子波振幅谱质心频率的均值。常相位子波频谱的质心频率为包络峰值处的瞬时频率。

为降低统计误差，尽可能利用振幅谱的形态信息，如选择相对熵参数。以规范化后子波Q补偿振幅谱的相对熵（KL散度）的倒数IKLD为参考量，当IKLD为最大时，表示不同炮检距处的子波Q补偿振幅谱一致性最佳，可认为该Q值最接近地层等效Q值。IKLD扫描Q值谱的公式为

$ \mathrm{I}\mathrm{K}\mathrm{L}\mathrm{D}=\frac{1}{\sum\limits_{i=1}^{N}\sum\limits_{f=0}^{{f}_{\mathrm{T}}}\left[{A}_{\mathrm{m}\mathrm{i}\mathrm{d}}\left(f\right)\times \mathrm{l}\mathrm{n}\frac{{A}_{\mathrm{m}\mathrm{i}\mathrm{d}}\left(f\right)}{{A}_{i}\left(f\right)}\right]} $

(16)

式中：$ {A}_{\mathrm{m}\mathrm{i}\mathrm{d}} $为规范化后的CMP道集中零炮检距处子波的Q补偿振幅谱；$ {A}_{i} $为规范化后的第$ i $道子波Q补偿振幅谱。

类似地，以规范化后子波Q补偿振幅谱的JS散度的倒数IJSD为参考量，当IJSD为最大时，表示不同炮检距处子波的Q补偿振幅谱一致性最佳，可认为该Q值最接近地层等效Q值。IJSD扫描Q值谱的公式为

$ \mathrm{I}\mathrm{J}\mathrm{S}\mathrm{D}=\frac{1}{\sum\limits_{i=1}^{N}\sum\limits_{f=0}^{{f}_{\mathrm{T}}}\left\{\begin{array}{l}0.5{A}_{\mathrm{m}\mathrm{i}\mathrm{d}}\left(f\right)\mathrm{l}\mathrm{n}\frac{{A}_{\mathrm{m}\mathrm{i}\mathrm{d}}\left(f\right)}{0.5\left[{A}_{i}\left(f\right)+{A}_{mid}\left(f\right)\right]}+0.5{A}_{i}\left(f\right)\mathrm{l}\mathrm{n}\frac{{A}_{i}\left(f\right)}{0.5\left[{A}_{i}\left(f\right)+{A}_{mid}\left(f\right)\right]}\\ \end{array}\right\}} $

(17)

JS散度克服了相对熵的不对称性缺陷，在一定程度上削弱了参考道的影响。

以上是七种度量准则的设计。好的度量参数不仅对Q值变化敏感，还应具有一定的抗噪性。用信噪比SNR表征噪声强弱程度，即

$ \mathrm{S}\mathrm{N}\mathrm{R}=10\mathrm{l}{\mathrm{g}}_{}\frac{{P}_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}}{{P}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}}=20\mathrm{l}{\mathrm{g}}_{}\frac{{A}_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}}{{A}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}} $

(18)

式中：$ {P}_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}} $和$ {P}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}} $分别表示信号功率和噪声功率；$ {A}_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}} $和$ {A}_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}} $分别表示信号振幅和噪声振幅。

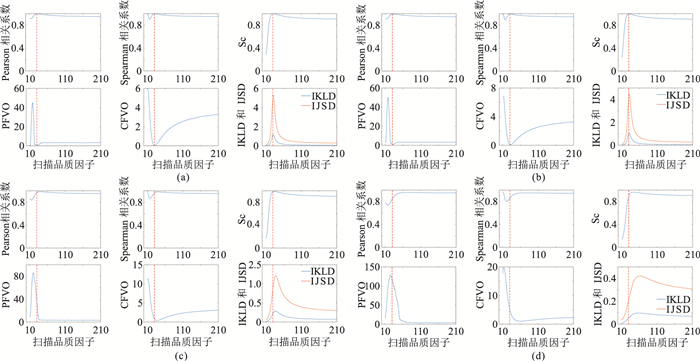
合成两个不同程度吸收衰减（Q=30和100）的CMP道集，扫描间隔为1，Q值扫描范围则为10~210，针对不同炮检距子波的振幅谱做衰减补偿，并按照以上七种准则度量一致性。当频带范围为0~60 Hz时，不同程度吸收衰减、信噪比条件下七种度量准则的Q扫描结果对比分别如图 4、图 5所示，其中红色虚线的横坐标为正确的Q值。

从对扫描Q值的敏感程度和信噪比（图 4、图 5）来看，七种准则中IJSD对Q值变化最为敏感，抗噪能力最强，稳定性最好，并且当衰减较弱即Q值较大时，利用IJSD准则做Q扫描也是可行的；然后是IKLD和CFVO，其余准则不适合作为Q扫描检测振幅谱一致性的度量。

3 扫描制作Q值谱及地层Q值建模

在存在较强噪声干扰情况下，子波振幅谱的形态发生较大变化，很难用扫描的方法给出等效Q值估计。下面采用前文定义的CFVO、IKLD、IJSD三种度量准则分别对理论数据和实际数据做Q扫描，得到Q值谱，进而拾取能量最强的谱点以获得等效Q模型，最后转化为层Q模型。

3.1 扫描制作Q值谱

采用理论合成的吸收衰减CMP道集及速度模型、真Q模型（图 2），比较CMP道集扫描Q值方法的优劣。

地层反射系数均设为0.2，即不考虑反射系数大小对估计地层Q值的影响。考虑到高频补偿的数值不稳定现象，实验中均选取0~60 Hz频带范围度量各道子波的Q补偿振幅谱一致性。Q值谱具体扫描流程如图 6所示。

图 7为无噪时用CFVO、IKLD、IJSD准则做Q扫描的对比效果。由图可见，在无噪情况下，CFVO准则制作的Q值谱聚焦较差，纵、横向分辨率都较低；而IKLD、IJSD准则制作的Q值谱聚焦良好，方便快速、准确地拾取等效Q值。此外，IJSD准则制作的Q谱对深部Q值较大处聚焦更好。

为了对比不同方法的抗噪能力，对吸收衰减CMP道集添加一定程度的高斯白噪声，道集信噪比分别为20 dB和10 dB的扫描Q值谱对应如图 8和图 9所示。由图 8、图 9可见，在较强噪声干扰情况下，以上几种准则扫描制作的Q值谱均不聚焦，难以从Q值谱上获取地层等效Q值。

3.2 建立Q值模型

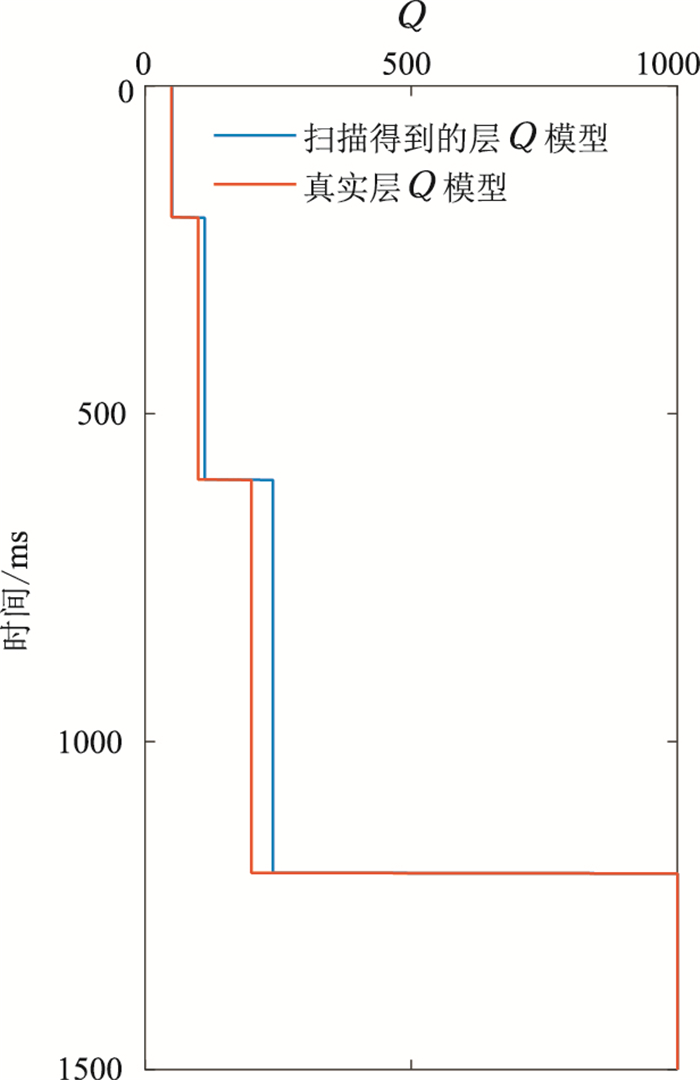
由扫描制作的Q值谱拾取等效Q值，根据式（5）可以得到时间域层Q模型。对图 7c用IJSD准则扫描制作的Q谱拾取获得等效Q值模型，进而转化为时间域层Q模型，它与真实的时间域层Q模型（抽道）对比如图 10所示。由图可见，扫描Q谱得到的层Q值与真实Q值吻合良好，仅在深层出现了一定的累积误差。由此可见，IKLD准则下的Q扫描可以快速、准确地建立层Q模型。

为进一步验证该准则下的Q扫描方法的适用性，采用胜利油田一条二维CDP剖面（图 11）进行测试。该剖面共207道，最大炮检距为3487 m，时间采样点数为2901，时间采样间隔为2 ms。

选取1.0~2.6 s内的数据体，速度模型采用常规速度分析得到的NMO速度，Q值从10起，每间隔2扫描至410，在IJSD准则下的扫描Q值谱及转化后的层Q模型抽道显示如图 12所示。由图可见，扫描得到的Q值谱在浅、中层聚焦良好，由时间域层Q模型可知浅、中层吸收衰减较为严重。而叠前CDP道集的中深层有效信号被噪声掩盖，无法直接用扫描的方式完成地层Q值建模，因此需要先对叠前数据进行去噪等预处理，提高道集资料的信噪比，同时尽量不伤害有效信号的吸收衰减特征。

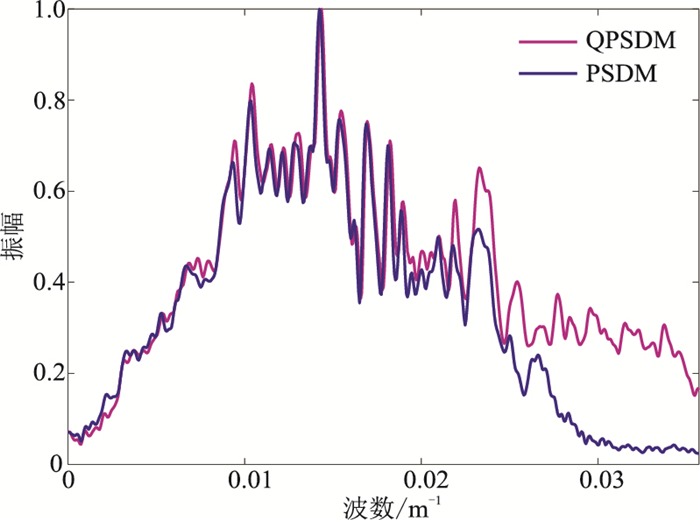
对另一条测线的CDP道集做Q扫描，输入的速度模型由速度分析得到，可以快速得到一个时间域地层Q模型。按照速度模型的时深转换关系，得到深度域地层Q模型（图 13）。用该Q模型分别做Q补偿的Kirchhoff叠前深度偏移（QPSDM）和未做Q补偿的Kirchhoff叠前深度偏移（PSDM）处理，并对两个偏移后产生的CIG道集叠加得到叠加剖面（图 14）。选择叠加剖面中浅层小块范围（红色方框内）做频谱分析（图 15），可以看到Q补偿后地震资料的频谱频带拓宽，高频抬升明显，主频有一定提高。

4 结论

对于中等以上信噪比CMP道集而言，基于相对熵准则的CMP道集Q扫描法估算水平层状地层等效Q值是一种简单、有效的背景Q值建模方法。速度模型精度、信噪比、度量准则、频带范围、时窗参数等会影响扫描Q谱的结果。

Q值补偿后CMP道集上相同$ {t}_{0} $时间、不同炮检距反射子波振幅谱一致性测量准则是该方法的关键技术。

（1）KL散度和JS散度对振幅谱一致性度量准则最敏感，抗噪性比质心频率和峰值频率更强。

（2）在弱噪声情况下，利用KL散度或JS散度度量准则进行等效Q扫描分析能够快速、有效地得到地层Q值的背景模型，可用于层析Q值反演的初始模型。