2. 南方科技大学地球与空间科学系, 广东深圳 518055;
3. 广东省地球物理高精度成像技术重点实验室(南方科技大学), 广东深圳 518055;
4. 东方地球物理公司综合物化探处, 河北涿州 072751
2. Department of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China;
3. Guangdong Provincial Key Laboratory of Geophysical High-resolution Imaging Technology (Southern University of Science and Technology), Shenzhen, Guangdong 518055, China;
4. GME and Geochemical Surveys, BGP Inc., Zhuozhou, Hebei 072751, China
地球表层即使在未发生可感知的天然地震期间也经常存在轻微的颤动,这种由人类活动(如常见的工厂机器、道路交通等)、风雨波动、火山活动等现象引起的地面的不停的颤动称之为微动。根据可利用的有效波的不同种类,微动探测可分为面波成像法和体波成像法及H/V谱比法等。其中利用面波的方法又可称为被动源面波法,或天然源面波法,在国外也被称为背景噪声成像[1]。
背景噪声的研究始于二十世纪中期,基于背景噪声是时间和空间上的稳态随机过程的前提,Aki[2]提出空间自相关(SPAC)算法,并进行了理论推导。在此基础上,Cho等[3]提出圆形台阵CCA方法;Ling等[4]和Okada等[5]提出扩展空间自相关ESAC(Extensible spatial autocorrelation)方法;Asten等[6]提出多模式台阵空间自相关法MMSPAC。随后,国内学者基于SPAC方法也进行了类似应用研究[7-8]。近年来研究发现在层状介质中Rayleigh波不但会发生频散现象,而且在某一频率范围内高阶模态有时会比基阶模态具有更大能量[9-10],这就意味着只利用基阶面波反演具有很大的不确定性,必须将基阶面波与高阶面波联合反演以降低这种不确定性[11-12]。SPAC方法并不能对高阶模式面波进行有效成像,为此陈晓非院士团队提出频率—贝塞尔(F-J)方法[13],并在实际应用中取得了不错的高阶模式成像效果[14]。
现行的静校正方法主要有折射波法和微测井等[15-16],虽然上世纪末主动源面波已用于石油地震勘探的静校正中,但因受限于震源而并未得到普及[17]。但随着人类活动范围的不断扩大,常规静校正方法常会受到道路、村庄等场地限制而无法实施,而利用被动源面波方法无需震源、且观测系统不受场地限制的特点,可解决静校正速度获取问题。
由于利用微动做静校正的方法在油气勘探领域的应用刚刚开始,且F-J方法自提出后并无在该领域的成功应用案例,因此本文就F-J方法在表层调查中的适用性进行了应用研究。
1 F-J方法原理F-J变换基于半空间各向同性水平层状介质、柱面坐标系及格林函数的频散特性[18-19],通过贝塞尔函数的正交性得出[13]。
水平层状均匀介质中的格林函数
| $ {G}_{zz}(r, \omega )={\int }_{0}^{+\mathrm{\infty }}{g}_{z}(k, \omega ){J}_{0}\left(kr\right)k\mathrm{d}k $ | (1) |
式中:
| $ {g}_{z}(k, \omega )=\frac{H(k, \omega )}{D(k, \omega )} $ | (2) |
式中:
空间任意两点
| $ {\tilde{C}}_{zz}(r, \omega )\approx A\cdot \mathrm{I}\mathrm{m}\left[{\tilde{G}}_{zz}(r, \omega )\right] $ | (3) |
式中:A是常数;
| $ {\tilde{C}}_{zz}(r, \omega )=\left[{\tilde{u}}_{z}\right({x}_{1}{, \omega \left)\right]}^{*}\left[{\tilde{u}}_{z}\right({x}_{2}, \omega \left)\right] $ | (4) |
式中:
经F-J变换,可得
| $ I(\omega , k)={\int }_{0}^{+\mathrm{\infty }}{\tilde{C}}_{zz}(r, \omega ){J}_{0}\left(kr\right)r\mathrm{d}r $ | (5) |
式中
首先采用合成噪声数据测试不同观测系统对F-J成像方法的影响。地层模型(表 1)采用含有低速层的四层模型,本文合成地震数据均由该模型合成。选用1000个随机分布于地表、半径为500~1500 m的圆环内的点震源,采用雷克子波作为震源时间函数,主频在6~10 Hz范围内随机产生,震源强度随机处于0.001~1(图 1)。
|
|
表 1 四层地层模型参数[10] |

|
图 1 噪声源分布(a,蓝点为震源)和随机分布噪声震源中心频率柱状图(b) |
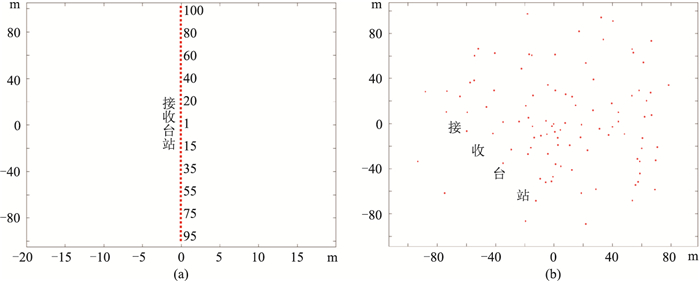
实际微动探测中最常用、最易实施的观测系统为线性和随机分布台站,为了更接近实情,采用合成数据测试两者对F-J成像的影响。采用100个台站分布于图 1圆环内100*100区域(图 2),并对100个台站1 min数据做F-J频散成像(图 3)。从图 3可见,随机分布的100个台站1 min成像数据F-J频散成像(图 3b)质量明显好于线性等间距。
|
图 2 100台观测台站线性2 m等间距分布(a)和随机分布(b)对比图 |

|
图 3 100台站2 m等间距直线排列(a)和随机分布(b)合成噪声1 min数据频散谱对比 白色点线为理论频散曲线 |
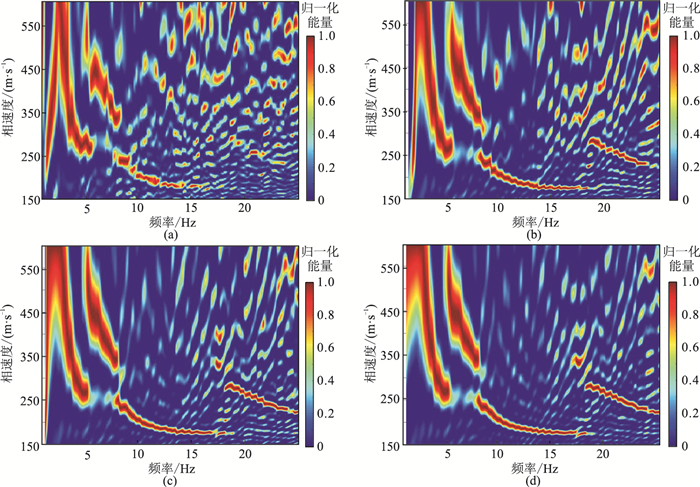
基于上述随机分布的台站数据,改变参与成像台站的数目,随机选取10、15、20、50个台站进行F-J频散成像(图 4)。从图 4a可看到10个台站的频散谱成像干扰严重;当增至15个台站(图 4b)时,频散谱中基阶和高阶模式频散已可明显识别;随着台站数目的增加,频散谱成像质量不断提高,图像中干扰明显减少,20个台站时频散谱中基阶与高阶面波成像已可分辨(图 4c);当台站为50个时频散谱成像已较清晰、连续(图 4d);当台站为100个时,从图 3b可看到频散谱已无明显干扰,尤其是高频部分成像质量得到大幅度提升。

|
图 4 不同数量随机分布台站频散谱对比 (a)10个;(b)15个;(c)20个;(d)50个 |
从图 4的对比分析可知,当台站数仅为15时,1 min噪声数据的F-J频散成像仍具有一定的分辨率。这样基于15个随机分布台站,将参与成像的数据时间增至20 min,并把20 min的连续数据分割为20个1 min的短时噪声数据,分别成像叠加,对比分析时间长度对成像质量的影响。
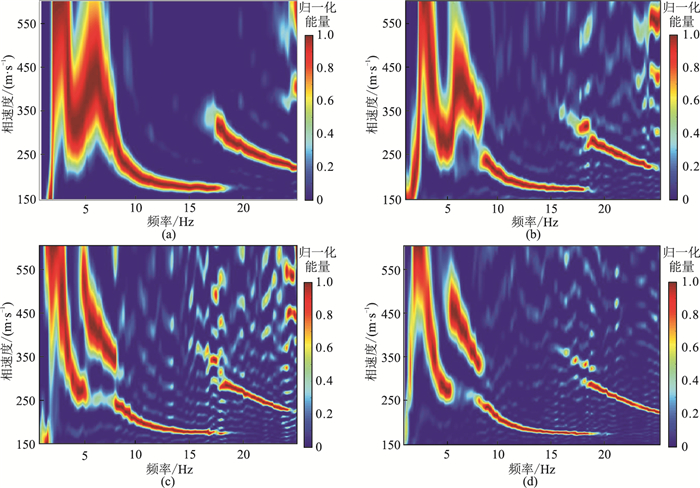
从图 5可见,随着数据时间的增长、叠加次数的增加,频散谱成像质量不断提高。其中1 min数据到5 min的频散谱成像质量提高得最显著(图 5a、图 5b);5、10、20 min数据的频散谱(图 5b~图 5d)质量虽不断提高,但随着时间的不断增加,成像质量的提升越来越不明显。说明一味地增长采集数据的长度并不能无限提高成像质量,需在效率与质量间找到一个平衡点。从图 5可见20 min后数据成像质量最佳,满足提取频散曲线反演的要求。
|
图 5 随机分布15个台站不同时长频散谱对比 (a)1 min;(b)5 min;(c)10 min;(d)20 min |
为了研究台站展布(台站间的最大距离)对频散谱成像的影响,选用100个台站,随机分布在不同展布半径的圆内,展布半径分别为30、50、70、100 m,采样时长为1 min。从图 6a可见频散谱中4~8 Hz频率范围内,高阶模式和基阶并不能有效分离成像;随着展布半径的增加,在4~8 Hz区域的高阶模式和基阶模式成像质量不断提高,当展布为50 m时(大于低速层40 m埋深),高阶模式已能与基阶模式有效分离成像。这样,说明了实际探测中经常遇到的频散曲线“Z”字型[25],即是观测系统空间展布不够,高阶模式、基阶模式无法分离成像所致。
|
图 6 相同台站数量(100台站随机分布)不同最大展布半径频散谱对比 (a)30 m;(b)50 m;(c)70 m;(d)100 m |
为了测试F-J在实际勘探中的成像能力,在四川北部进行微动采集。该区在早白垩世主要为陆相河流—湖相沉积环境。自底部苍溪组至顶部七曲寺组表现为一个整体粒度变细、向上水体变深的沉积旋回。七曲寺组以砖红、紫红色泥岩、黏土岩为主,夹粉砂岩、细—中粒砂岩,构成向上变细的韵律互层,偶夹钙质砾岩条带及透镜体,含丰富介形类化石。
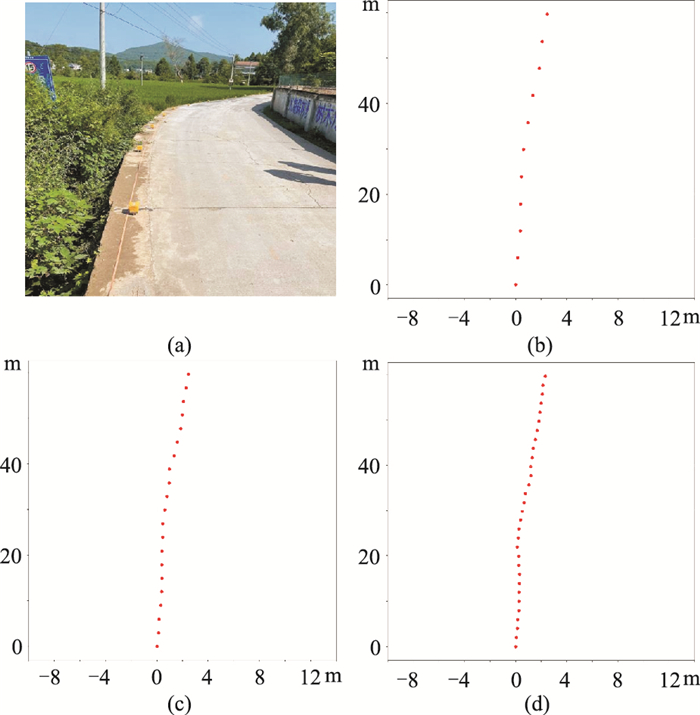
3.1 不同道间距对F-J成像的影响在实际微动数据采集中,常受到实验场地限制,最易实施的观测系统为沿道路近似直线型等间距布设台站。因此,本次分别以5、3、2 m道间距沿道路布设台站,最大台间距为60 m,采集20 min数据,采样率为200 Hz。采用RTK测量台站坐标,台站分布见图 7。当观测系统展布一定时,采用上述不同道间距,参与成像的台站数量分别为11、21、31。
|
图 7 四川北部实验场地现场和台站分布 (a)微动采集现场照片;(b)5 m道间距11个台站;(c)3 m道间距21个台站;(d)2 m道间距31个台站 |
图 8a显示11个台站的频散谱在高频(> 20 Hz)区域,基阶与高阶模式无法有效分离。从图 8b可见21个台站高频区域基阶与高阶模式已分离,但低频区域成像无改进。图 8c显示高频区域基阶与高阶模式已分离,低频区域成像质量也得到一定提高,且干扰受到明显压制。这样从图 8可看到展布60 m直线观测系统,随着台站间距减小,参与成像的台站增加,成像质量不断增加,尤其是高频区域高阶模式成像质量提高显著;同时,随着台站数量的增加,干扰也受到明显压制。在实际探测中,当观测系统展布固定时,台站数量不宜低于20个。

|
图 8 展布60 m直线观测系统不同道间距频散谱对比 (a)5 m道间距11个台站;(b)3 m道间距21个台站;(c)2 m道间距31个台站 |
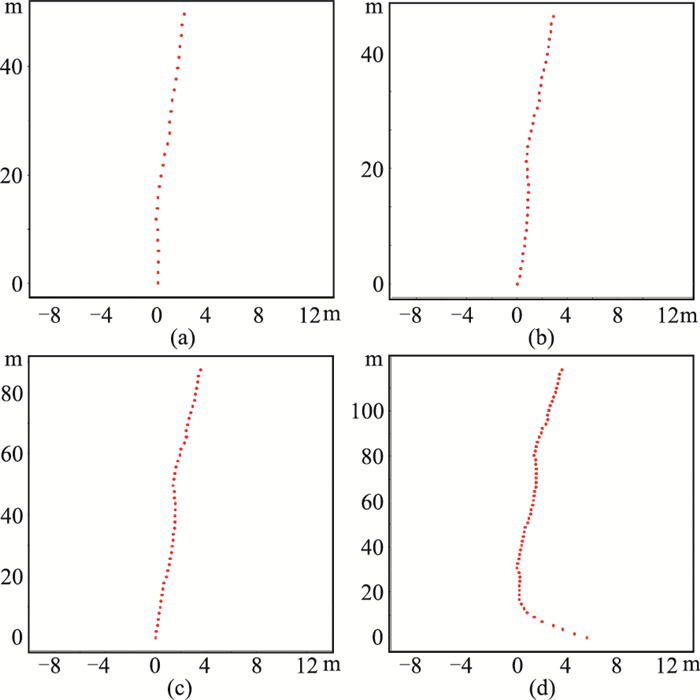
上文已述及,当观测系统的展布一定时,随着台间距减少、台站增加,可有效压制干扰,提高高阶模式的成像质量。但在实际数据采集中,不可能无限制地减小台间距以提高成像质量。本文选择采用2 m台间距,在同一区域开展不同观测系统展布对比实验。台站沿道路布设(图 9),展布长度分别为50、70、90、120 m,台站数量分别为26、36、45、61台,采集时间为20 min。
|
图 9 2 m间距不同展布台站分布 (a)50 m、26台站;(b)70 m、36台站;(c)90 m、45台站;(d)120 m、61台站 |
图 10中各频散谱分别对应图 9中的台站分布。可见随着展布长度的增加,6~20 Hz区域内的高阶模式成像质量提高显著,但120 m时的高阶成像质量反而下降,且干扰明显增强。分析原因主要是因为F-J是基于水平层状一维结构对台站下方地层进行频散成像,而实际地下结构通常并非均匀水平层状一维结构,而是变化复杂的三维结构。因此,若观测系统展布持续变大,所覆盖区域地层起伏的可能越大,近似为水平层状的地层带来的误差越大,则在浅层高频区域的干扰反而增强;尤其是在风化壳、岩石界面对应的4~6 Hz区域,成像反而变得不连续,说明台站区域下方起伏较大。

|
图 10 2 m间距不同展布频散谱对比 (a)50 m、26个台站;(b)70 m、36个台站;(c)90 m、45个台站;(d)120 m、61个台站 |
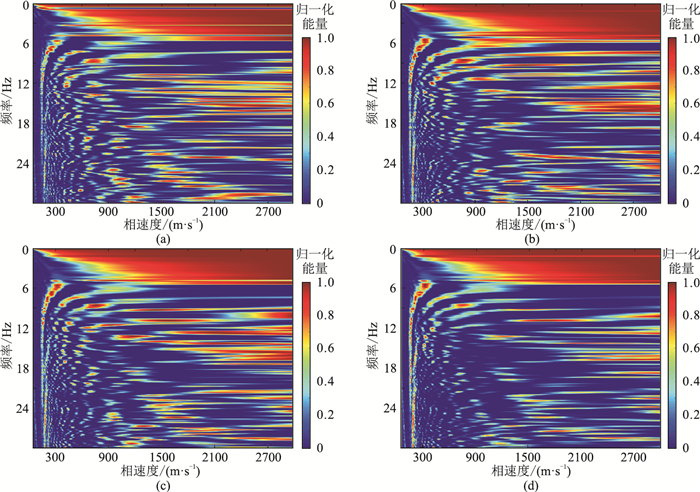
在上述实验区域,以2 m台间距沿直线布设51台地震仪,展布100 m。噪声数据按1 min长度分别成像,最后进行叠加。对比5、10、15、20 min数据叠加后对成像质量的影响。从图 11可见,实际数据的长度对F-J频散的成像的影响与合成数据测试的结果一致;当数据小于10 min时,成像质量随时间增加提高明显,当数据大于10 min时,成像质量随时间增加改善的幅度明显下降。
|
图 11 2 m间距、100 m直线展布不同时长频散谱对比 (a)5 min;(b)10 min;(c)15 min;(d)20 min |
通过合成数据和实际资料测试F-J频散成像,发现基于水平层状模型的F-J在合成数据测试中,面状随机分布观测系统成像质量优于直线型观测系统(图 3b),而实际数据测试中地层并非严格的水层层状,所以面状观测系统(图 9d)并非优于线型观测系统。在台站数量、展布及时间长度的测试中,合成数据和实际数据取得了一致结果,台站数量不宜低于20个,时间长度不宜短于15 min。
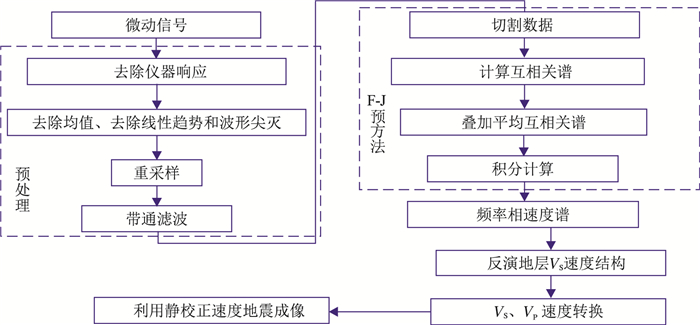
4 实际应用在实验区选择有钻孔位置进行数据采集,按上述实验结果和探测目标深度,使用34台地震仪,测线展布约为100 m,采样时长为20 min,采样频率为200 Hz。微动数据采集和处理流程(图 12)如下。
|
图 12 利用F-J微动信号进行静校正的流程 |
(1)预处理:去坏道、去均值、去趋势等预处理。
(2)分段择优叠加:将20 min数据分为20段,对每段1 min数据分别进行成像,生成20张频散谱图(图 13),选择成像质量好的频散谱做叠加成像。

|
图 13 每60 s分段数据频散谱对比 |
(3)多模式联合反演:从频散谱中拾取基阶、高阶模式频散曲线,建立初始模式,进行多模式联合反演。本次采用粒子群算法做多模式联合反演[26]。因粒子群反演算法不是本文研究重点,不再赘述。
(4)利用微动反演结果Vs波速,结合泊松比数据,获得P波波速作为约束,进行静校正。
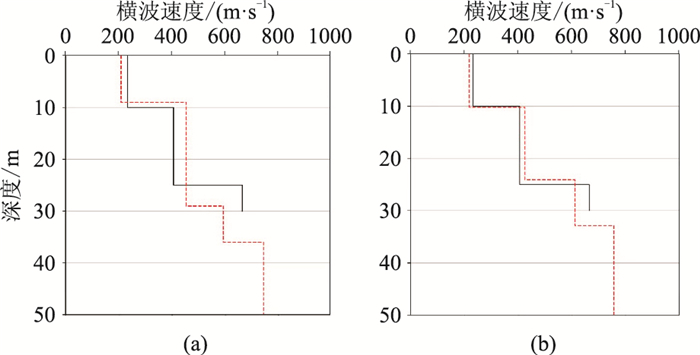
从图 13可知并不是每一分段数据都具有较高成像质量,若将所有分段成像直接叠加不然会存在大量干扰。因此,择优叠加策略是仅选择成像质量好的数据开展叠加成像,并取得了较好的应用效果(图 14)。从频散谱(图 14b)提取基阶、高阶模式频散曲线进行基阶模式和多模式联合反演[11]。从图 15可见,多模式联合反演结果中风化壳和岩层的界面深度(30 m处)的成像明显比仅用基阶模式的反演结果更准确,且与测井数据基本一致。随后将所得地层速度参数与测井数据对比黑线为测井所得横波速度,红线为面波反演所得横波速度。该区域反演结果用于静校正,在三维地震成像中也取得了不错效果(图 16)。

|
图 14 所有分段直接叠加(a)与择优分段叠加(b)所得频散谱的对比 |
|
图 15 仅基阶模式(a)与多模式联合(b)面波反演 |
|
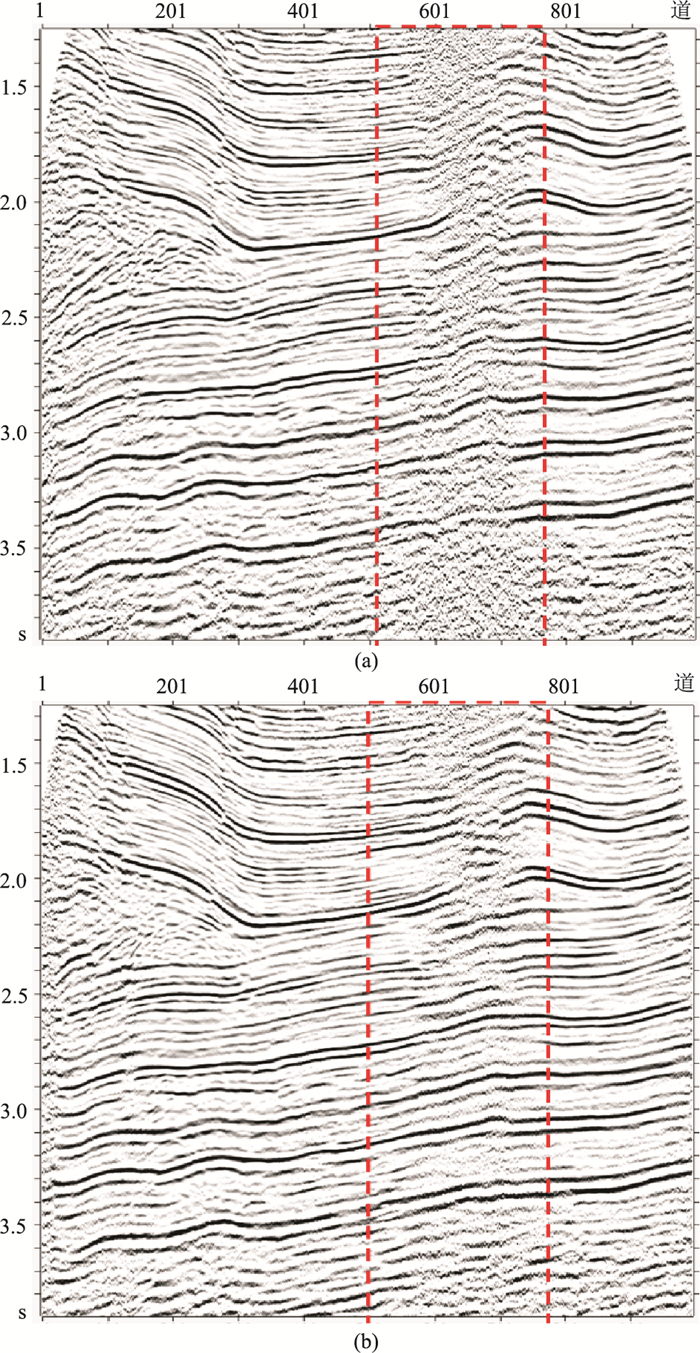
图 16 采用被动源面波反演结果做静校正的三维地震成像对比 (a)未采用微动反演结果;(b)采用微动反演结果红色方框指示成像改进区域。 |
从微动勘探最关切的实际问题出发,本文对最新提出的F-J方法进行了适用性分析,以指导实际勘探应用。通过合成数据和实际资料,文中分析了观测系统形状、台站数量、展布和采集时间长度对F-J频散成像的影响。研究发现基于水平层状模型的F-J方法在合成数据测试中,面状随机分布观测系统成像优于直线型观测系统;但实际数据测试中并未得到与合成数据一样的结果,而是线状观测系统的效果好于面状观测系统。分析认为,由于实际地层并非严格的水平层状,面状观测系统覆盖区域更趋于三维地层,线性观测系统下方地层更接近一维水平地层;在实际探测中沿道路近似线性的观测系统是现场最常用和最易实施的观测系统,且发现F-J方法十分契合该观测系统;当探测目标深度约50 m时线性观测系统台站数量不应少于20台,数据采集时间不宜短于20 min;采用分段择优叠加技术可大幅度地压制干扰,在兼顾效率、探测成本条件下最大程度地提高阶模式面波成像质量。
考察F-J方法的适用性,发现该方法可有效地从微动数据里提取高阶模式频散信息,使利用多模式联合反演精确反演地层速度结构成为可能,为油气三维地震勘探无法实施折射法及微测井区域的静校正提供实用的解决方案。
| [1] |
赵东. 被动源面波勘探方法与应用[J]. 物探与化探, 2010, 34(6): 759-764. ZHAO Dong. Passive surface waves: methods and applications[J]. Geophysical and Geochemical Exploration, 2010, 34(6): 759-764. |
| [2] |
AKI K. Space and time spectra of stationary stochastic waves, with special reference to microtremors[J]. Bulletin of the Earthquake Research Institute, 1957, 35(3): 415-456. |
| [3] |
CHO I, TADA T, SHINOZAKI Y. A new method of microtremor exploration using miniature seismic arrays: quick estimation of average shear velocities of the shallow soil[J]. BUTSURI-TANSA, 2008, 61(6): 457-468. |
| [4] |
LING S, OKADA H. An extended use of the spatial autocorrelation method for the estimation of geological structure using microtremors[C]. Proceedings of the 89th SEGJ Conference, Japanese, 1993, 44-48.
|
| [5] |
OKADA H, SUTO K, ASTEN M W. The microtremor survey method[J]. Geophysical Monograph Series No 12, SEG, Tulsa, 2003, https://doi.org/10.1190/1.9781560801740.
|
| [6] |
ASTEN M, ROBERTS J. Analysis of esg2006 blind-trial microtremor data using the MMSPAC method[J]. Journal of Telemedicine & Telecare, 2006, 13(1): 7-14. |
| [7] |
徐佩芬, 李传金, 凌甦群, 等. 利用微动勘察方法探测煤矿陷落柱[J]. 地球物理学报, 2009, 52(7): 1923-1930. XU Peifen, LI Chuanjin, LING Suqun, et al. Mapping collapsed columns in coal mines utilizing microtremor survey methods[J]. Chinese Journal of Geophysics, 2009, 52(7): 1923-1930. |
| [8] |
徐佩芬, 李世豪, 凌甦群, 等. 利用SPAC法估算地壳S波速度结构[J]. 地球物理学报, 2013, 52(11): 3846-3854. XU Peifen, LI Shihao, LING Suqun, et al. Application of SPAC method to estimate the crustal S-wave velocity structure[J]. Chinese Journal of Geophysics, 2013, 52(7): 1923-1930. |
| [9] |
苏悦, 杨振涛, 杨博, 等. 基于矢量波数变换法的主动源瑞雷波多模式提取方法在近地表地层结构探测中的应用研究[J]. 北京大学学报(自然科学版), 2020, 56(3): 427-435. SU Yue, YANG Zhentao, YANG Bo, et al. Application research of active source Rayleigh wave multi-mode extraction method based on vector wavenumber transformation method in near surface stratigraphic structure detection[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2020, 56(3): 427-435. |
| [10] |
杨振涛, 陈晓非, 潘磊, 等. 基于矢量波数变换法(VWTM)的多道Rayleigh波分析方法[J]. 地球物理学报, 2019, 62(1): 298-305. YANG Zhentao, CHEN Xiaofei, PAN Lei, et al. Multichannel analysis of Rayleigh waves based on the vector wavenumber transformation method (VWTM)[J]. Chinese Journal of Geophysics, 2019, 62(1): 298-305. |
| [11] |
罗银河, 夏江海, 刘江平, 等. 基阶与高阶瑞利波联合反演研究[J]. 地球物理学报, 2008, 51(1): 242-249. LUO Yinhe, XIA Jianghai, LIU Jiangping, et al. Joint inversion of fundamental and higher mode Rayleigh waves[J]. Chinese Journal of Geophysics, 2008, 51(1): 242-249. |
| [12] |
夏江海, 高玲利, 潘雨迪, 等. 高频面波方法的若干新进展[J]. 地球物理学报, 2015, 58(8): 2591-2605. XIA Jianghai, GAO Lingli, PAN Yudi, et al. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics, 2015, 58(8): 2591-2605. |
| [13] |
WANG J, WU G, CHEN X. Frequency-Bessel transform method for effective imaging of higher-mode Rayleigh dispersion curves from ambient seismic noise data[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(4): 3708-3723. |
| [14] |
李雪燕, 陈晓非, 杨振涛, 等. 城市微动高阶面波在浅层勘探中的应用: 以苏州河地区为例[J]. 地球物理学报, 2020, 63(1): 247-255. LI Xueyan, CHEN Xiaofei, YANG Zhentao, et al. Application of high-order surface waves in shallow exploration: An example of the Suzhou river, Shanghai[J]. Chinese Journal of Geophysics, 2020, 63(1): 247-255. |
| [15] |
林伯香, 孙晶梅, 刘清林. 层析成像低速带速度反演和静校正方法[J]. 石油物探, 2002, 41(2): 136-140. LIN Boxiang, SUN Jingmei, LIU Qinglin. Tomography for LVZ velocity inversion and statics[J]. Geophysical Prospecting for Petroleum, 2002, 41(2): 136-140. |
| [16] |
林伯香, 孙晶梅, 徐颖, 等. 几种常用静校正方法的讨论[J]. 石油物探, 2006, 45(4): 367-372. LIN Boxiang, SUN Jingmei, XU Ying, et al. Static correction approaches being frequently applied[J]. Geophysical Prospecting for Petroleum, 2006, 45(4): 367-372. |
| [17] |
李庆春, 邵广周, 刘金兰, 等. 瑞雷面波勘探的过去、现在和未来[J]. 地球科学与环境学报, 2006, 28(3): 74-77. LI Qingchun, SHAO Guangzhou, LIU Jinglan, et al. Past, present and future of Rayleigh surface wave exploration[J]. Journal of Earth Sciences and Environment, 2006, 28(3): 74-77. |
| [18] |
CHEN X. Seismogram synthesis in multi-layered half-space part Ⅰ.Theoretical formulations[J]. Earthquake Research in China, 1999, 13(2): 149-174. |
| [19] |
CHEN X. A systematic and efficient method of computing normal modes for multilayered half-space[J]. Geophysical Journal International, 1993, 115(2): 391-409. |
| [20] |
LUCO J E, APSEL R J. On the green's functions for a layered half-space.Part Ⅰ[J]. Bulletin of the Seismological Society of America, 1983, 73(4): 909-929. |
| [21] |
KENNETT B. Seismic wave propagation in stratified media[J]. Geophysical Journal of the Royal Astronomical Society, 1986, 86(1): 219-220. |
| [22] |
HISADA Y. An efficient method for computing green's functions for a layered half-space with sources and receivers at close depths[J]. Bulletin of the Seismological Society of America, 1994, 84(5): 1456-1472. |
| [23] |
SÁNCHEZ-SESMA F J, CAMPILLO M. Retrieval of the Green's function from cross correlation: the canonical elastic problem[J]. Bulletin of the Seismological Society of America, 2006, 96(3): 1182-1191. |
| [24] |
SATO H, FEHLER M C, MAEDA T. Green's Function retrieval from the cross-correlation function of Random waves//SATO H, FEHLER M C, MAEDA T. Seismic Wave Propagation and Scattering in the Heterogeneous Earth(2nd ed)[M]. Springer, Berlin, Heidelberg, 2012, 401-450.
|
| [25] |
张碧星, 肖柏勋, 杨文杰, 等. 瑞利波勘探中"之"形频散曲线的形成机理及反演研究[J]. 地球物理学报, 2000, 43(4): 557-567. ZHANG Bixing, XIAO Baixun, YANG Wenjie, et al. Mechanism of zigzag dispersion curves in Rayleigh exploration and its inversion study[J]. Chinese Journal of Geophysics, 2000, 43(4): 557-567. |
| [26] |
杨博, 熊章强, 张大洲, 等. 利用自适应混沌遗传粒子群算法反演瑞雷面波频散曲线[J]. 石油地球物理勘探, 2019, 54(6): 1217-1227. YANG Bo, XIONG Zhangqiang, ZHANG Dazhou, et al. Rayleigh surface-wave dispersion curve inversion based on adaptive chaos genetic particle swarm optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(6): 1217-1227. |



 杨振涛, 广东省深圳市南山区学苑大道1088号南方科技大学地球与空间科学系(理学楼E4147), 518055。Email:
杨振涛, 广东省深圳市南山区学苑大道1088号南方科技大学地球与空间科学系(理学楼E4147), 518055。Email: 