2. 兰州市体育运动学校, 甘肃兰州 730207
2. Lanzhou Sports School, Lanzhou, Gansu 730207, China
受人类活动、仪器、天气等周围环境诸多因素影响,野外采集的地震数据不可避免地含有各类噪声。这些噪声会降低所采集数据的质量,并对之后的处理和解释产生不利影响,应在地震数据处理的早期进行压制。消除噪声以获取高信噪比地震数据一直是地震勘探领域面临的难题[1]。20世纪以来,众多地球物理学者致力于探究地震数据的去噪方法,主要分为模型驱动类和数据驱动类方法。
经过多年发展,模型驱动类去噪方法已得到广泛而深入的研究与应用,如基于预测的方法[2-4]、基于稀疏变换的方法[5-8]、基于分解的方法[9-12]等。
随着深度学习的蓬勃发展,已在图像识别、目标检测、图像分割、图像复原等领域取得了显著效果。常见的网络包括卷积神经网络(CNN)、残差神经网络(ResNet)和生成对抗网络(GAN)等,其中CNN因局部感知和权重共享的优势而得到了广泛应用。与此同时,经过多年的发展,积累了大量的数据以及人工处理或解释的成果,为数据驱动类深度学习方法的应用创造了良好的条件[13]。深度学习几乎渗透到地震勘探领域的各个方向,如阻抗反演[14-16]、速度反演[17]、插值[18-20]、倾角估计[21]、断层解释[22-23]等。深度学习可克服传统方法对数据先验信息的依赖,越来越多的学者将其应用到地震数据去噪中,并取得了较好的效果[24-32]。杨翠倩等[33]针对CNN大多关注局部特征以及在特征提取方面的局限性,提出了一种结合全局上下文和注意力机制的深度卷积神经网络(GC-ADNet),并采用残差学习压制地震数据随机噪声,保留了更多局部细节信息。董新桐等[34]针对低信噪比、有效信号和噪声频谱混叠严重的沙漠地震资料,提出了一种基于对抗思想的深度学习网络(DSCA-Net)。该网络以GAN的对抗博弈思想为基础,利用降噪器代替生成器,将降噪器本身的均方误差损失与降噪器、判别器之间的对抗损失相结合。买皓[35]提出了一种地震资料噪声压制神经网络模型(Seis-ResNet),可以自适应地识别地震数据中的随机噪声。该模型采用41层深度残差神经网络结构,输入地震数据进行训练,并输出随机噪声。高好天等[36]将用于地震随机噪声压制的两种CNN网络——U型卷积神经网络(U-Net)和去噪卷积神经网络(DnCNN)进行了对比,结果表明前者的效果优于后者,且噪声学习相较于信号学习更具优势。罗任泽等[37]为提升泛化性能,在U-Net基础上加入残差模块,以增强网络对随机噪声的捕获能力。
监督学习在去噪方面的良好效果,得益于通过在大量带标签数据集中学习含噪数据与无噪数据的相关性获得它们之间的非线性映射,从而削弱数据中的噪声。然而在地震勘探领域,收集大量带标签的无噪数据耗时较大,甚至无法实现。此外,经过合成数据训练的监督去噪网络,由于与实际噪声分布的差异在应用中往往表现不佳。相比之下,无监督学习只使用原始的含噪数据便可有效压制随机噪声。由于其便捷性和良好的效果,近年来得到深入研究。在图像处理领域,Lempitsky等[38]提出了深度图像先验(DIP)的无监督学习方法,只需一张退化图像便可训练模型,从而进行多种图像处理任务,如去噪、超分辨率和修复。Lehtinen等[39]引入了Noise2Noise,以同一场景的成对含噪图像作为训练图像对,几乎达到了与有监督学习相同的去噪效果。但由于需要相同场景的不同含噪观测,限制了进一步应用。Krull等[40]证明Noise2Void可以直接对含噪数据进行训练,以自监督的方式有效地压制随机噪声,同时引入盲点网络防止学习到恒等映射。Moran等[41]提出利用Noisier2Noise在含噪图像上添加噪声作为输入,以含噪图像自身作为标签,构造训练图像对。Huang等[42]提出Neighbor2Neighbor方法,从一幅含噪图像中采样两幅含噪子图,进行Noise2Noise方式的训练。
本文基于DIP的思想对二维地震数据随机噪声进行压制。首先探讨跳跃连接对网络去噪性能的影响,确定了网络架构;其次,在损失函数中加入加权全变分(WTV)正则项,其权重系数不再是人为设定的超参数,而是与数据空间结构有关的可学习参数,使网络对于权重参数的选取更灵活;最后通过交替方向乘子法(ADMM)求解该优化问题。合成和实际数据实验表明,结合WTV正则与ADMM的DIP方法在压制地震数据随机噪声的同时可减少有效信号损失,并且相较于原始ADAM求解的DIP方法,相邻迭代拟合信号峰值信噪比波动小,网络稳定性得到提高。
1 基本理论 1.1 深度图像先验DIP使用CNN作为生成网络,网络输入不再是含噪图像y,而是随机化的初始输入z。它经过参数初始化的网络,通过对比拟合信号与含噪图像得到损失值,将其反向传播以更新参数。网络的优化目标为
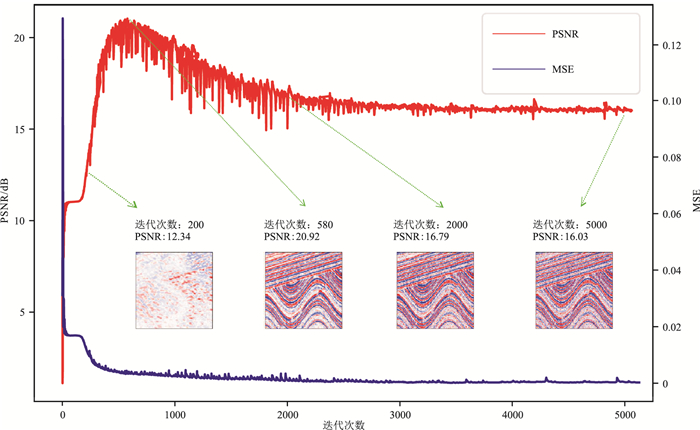
由于地震信号本身具有一定连续性和冗余性,CNN具有对地震信号的低阻抗性和对随机噪声的高阻抗性,即在拟合过程中,模型先、后学习地震信号和噪声。网络完成地震信号(去噪结果)拟合后再对其中的噪声拟合,即发生过拟合。图 1中迭代次数为2000和5000时发生了严重的过拟合,即去噪结果中包含有大量的噪声。由图可见:峰值信噪比(PSNR)曲线为一个倾斜的钟形曲线,峰值之前主要是信号恢复阶段,峰值之后大量噪声也被恢复;当PSNR曲线达到峰值时,均方误差(MSE)损失曲线并没有达到最低,而是随迭代次数的增加呈下降趋势,因而无法直接通过MSE曲线给出停止迭代准则。对于实际数据,无法获得PSNR曲线。因此,DIP的实用性取决于使用早停机制得到最优去噪结果,否则网络最终输出为含噪数据。之后也有学者在DIP的基础上不断改善网络性能,一种常见的方法是添加合适的正则项进行约束以满足信号的先验信息,这也是本文采取的策略。
|
图 1 DIP+ADAM(无跳跃连接)去噪的过拟合现象 |
图像恢复是从模糊且含有噪声的观测结果中恢复清晰的图像,可以表示为如下的反问题[43]
| $ \boldsymbol{Hx}+\boldsymbol{m}=\boldsymbol{y} $ | (1) |
式中:
| $ \boldsymbol{x}+\boldsymbol{m}=\boldsymbol{y} $ | (2) |
式(2)的反问题是不适定问题,即得到的解缺乏稳定性或唯一性,通常根据一些先验知识对解进行约束。比较常见的是基于正则化重构的方法,正则项的加入可以使原来的不适定问题转化为适定问题,即将式(2)的问题转化成如下优化问题
| $\boldsymbol{x}^*=\underset{\boldsymbol{x}}{\arg \min }\left\{\frac{1}{2}\|\boldsymbol{x}-\boldsymbol{y}\|_2^2+R(\boldsymbol{x})\right\}$ | (3) |
其中等号右侧第一项和第二项分别是数据保真项和正则化项。
经典的TV正则化为
| $ u\mathrm{T}\mathrm{V}\left(\boldsymbol{x}\right)=u{\sum\limits_{i=1}^{n}{‖{\left(D\boldsymbol{x}\right)}_{i}‖}_{2}}_{} $ | (4) |
式中:
| $ \mathrm{W}\mathrm{T}\mathrm{V}\left(\boldsymbol{x}\right)=\sum\limits_{i=1}^{n}{u}_{i}{‖{\left(D\boldsymbol{x}\right)}_{i}‖}_{2} $ | (5) |
其中权重系数
ADMM是一种求解可分离凸优化问题的重要方法,在机器学习领域有着广泛的应用,可应用于非凸图像恢复问题[45]。ADMM将大问题分解为多个较小且易求解的局部子问题,并通过协调子问题的解得到大问题的解[46]。利用ADMM对DIP添加WTV正则后的优化问题求解。考虑最小化问题
| $\underset{\boldsymbol{\theta}}{\arg \min }\left\{\frac{1}{2}\left\|f_{\boldsymbol{\theta}}(\boldsymbol{z})-\boldsymbol{y}\right\|_2^2+\sum\limits_{i=1}^n u_i\left\|\left[D f_{\boldsymbol{\theta}}(\boldsymbol{z})\right]_i\right\|_2\right\}$ | (6) |
为了更方便地求解上述问题,将其转化为以下带约束的优化问题
| $\left\{\begin{array}{l}\underset{\boldsymbol{\theta}, \boldsymbol{t}}{\arg \min }\left\{\frac{1}{2}\left\|f_{\boldsymbol{\theta}}(\boldsymbol{z})-\boldsymbol{y}\right\|_2^2+\sum\limits_{i=1}^n u_i\left\|\boldsymbol{t}_i\right\|_2\right\} \\ D f_{\boldsymbol{\theta}}(\boldsymbol{z})=\boldsymbol{t}\end{array}\right.$ | (7) |
式中:t为
| $\begin{aligned} & L(\boldsymbol{\theta}, \boldsymbol{t}, \boldsymbol{\lambda})=\frac{1}{2}\left\|f_{\boldsymbol{\theta}}(\boldsymbol{z})-\boldsymbol{y}\right\|_2^2+\sum\limits_{i=1}^n u_i\left\|\boldsymbol{t}_i\right\|_2+ \\ & \frac{\beta}{2}\left\|D f_{\boldsymbol{\theta}}(\boldsymbol{z})-\boldsymbol{t}\right\|_2^2+\left\langle\boldsymbol{\lambda}, D f_{\boldsymbol{\theta}}(\boldsymbol{z})-\boldsymbol{t}\right\rangle\end{aligned}$ | (8) |
式中
| $ \left\{\begin{array}{l}{\boldsymbol{\theta} }^{(k+1)}=\underset{\boldsymbol{\theta}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\frac{1}{2}{‖{f}_{\boldsymbol{\theta}}\left(\boldsymbol{z}\right)-\boldsymbol{y}‖}_{2}^{2}+\\ \frac{\beta }{2}{‖D{f}_{\boldsymbol{\theta}}\left(\boldsymbol{z}\right)-{\boldsymbol{t}}^{\left(k\right)}+\frac{{\boldsymbol{\lambda} }^{\left(k\right)}}{\beta }‖}_{2}^{2}\\ {\boldsymbol{t}}^{(k+1)}=\underset{\boldsymbol{t}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\sum\limits_{i=1}^{n}{u}_{i}^{\left(k\right)}{‖{\boldsymbol{t}}_{i}‖}_{2}+\\ \frac{\beta }{2}{‖\boldsymbol{t}-\left[D{f}_{{\boldsymbol{\theta}}^{(k+1)}}\left(\boldsymbol{z}\right)+\frac{{\boldsymbol{\lambda} }^{\left(k\right)}}{\beta }\right]‖}_{2}^{2}\\ \\ {\boldsymbol{\lambda} }^{(k+1)}={\boldsymbol{\lambda} }^{\left(k\right)}+\beta \left[D{f}_{{\theta}^{(k+1)}}\right(\boldsymbol{z})-{\boldsymbol{\boldsymbol{t}}}^{(k+1)}]\end{array}\right. $ | (9) |
其中
| $u_i^{(k+1)}=\frac{1}{2 n} \frac{\left\|f_{\boldsymbol{\theta}^{(k+1)}}(\boldsymbol{z})-\boldsymbol{y}\right\|_2^2}{\left\|\left[D f_{\boldsymbol{\theta}^{(k+1)}}(z)\right]_i\right\|_2}$ | (10) |
由式(10)可见,
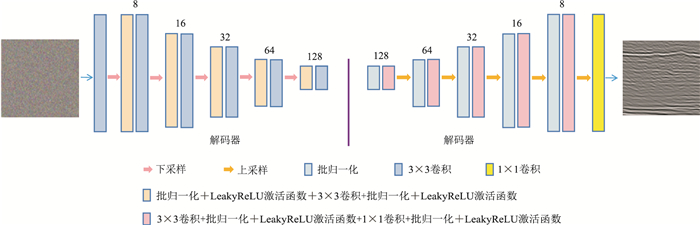
由于地震数据与图像之间的差异,必须采用合适的网络结构以适应地震数据特征。Qiu等[48]探索了适用于地震数据去噪的网络架构(网络深度为5,各层滤波器数量分别为8、16、32、64、128),网络结构如图 2所示。采用上述网络对二维合成地震数据进行去噪实验,结合PSNR曲线获得最优去噪结果。
|
图 2 DIP地震数据随机噪声压制网络架构[48] 图中8、16、32、64、128表示滤波器数量。 |
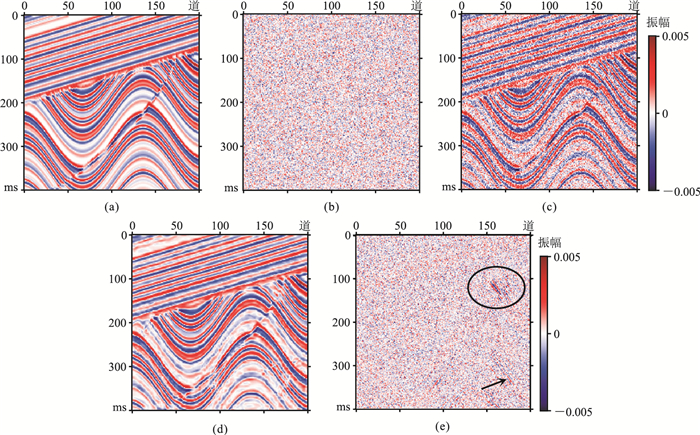
无噪和含噪合成地震数据如图 3a和图 3c所示,图 3b为噪声,去噪结果如图 3d所示。能否最大程度地保护有效信号幅度也是衡量去噪表现的重要指标。如果去噪残差图中包含有效信号成分,则说明在压制噪声的同时造成了有效信号损失;反之,能够较好地保护有效信号[34]。去噪残差图(图 3e)中圆圈和箭头指向的地方均有明显的有效信号,因此DIP结合上述结构的CNN在去噪时损失了部分有效信号。
|
图 3 DIP +ADAM合成数据去噪效果(无跳跃连接) (a)无噪地震数据;(b)均值为0、方差为1的高斯白噪声;(c)加噪地震数据(峰值信噪比为16 dB);(d)DIP +ADAM去噪结果;(e)DIP +ADAM去噪残差 |
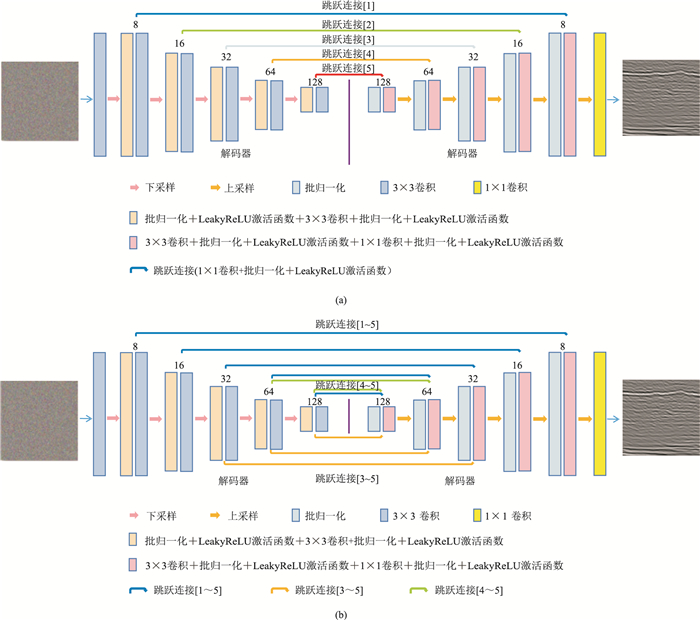
U-Net结构的关键在于编码部分和解码部分之间的跳跃连接,实现浅层信息与深层信息的融合,为解码过程提供更多语义信息。受其启发,本文探究不同的跳跃连接方式对网络去噪性能的影响,以期克服网络训练中损失部分有效信号的缺点,从而得到适用于地震数据去噪的网络结构。本文跳跃连接包含一个卷积层、一个批归一化层和一个激活函数。测试实验分为以下两种:①单个网络层添加跳跃连接,即每次实验仅在一个网络层添加跳跃连接,网络有5层,则一共有5个测试实验,连接方式如图 4a所示;②多个网络层添加跳跃连接,即每次实验在多个层同时添加跳跃连接,测试又分为三种,即1~5层(图 4b中蓝线)、3~5层(图 4b中橙线)、4~5层(图 4b中绿线)同时添加。
|
图 4 单层(a)及多层(b)网络添加跳跃连接方式示意图 图中跳跃连接[j]表示在网络第j层添加跳跃连接,如跳跃连接[1]表示在网络第1层添加跳跃连接,跳跃连接[1~5]表示在网络第1~第5层均添加跳跃连接。 |
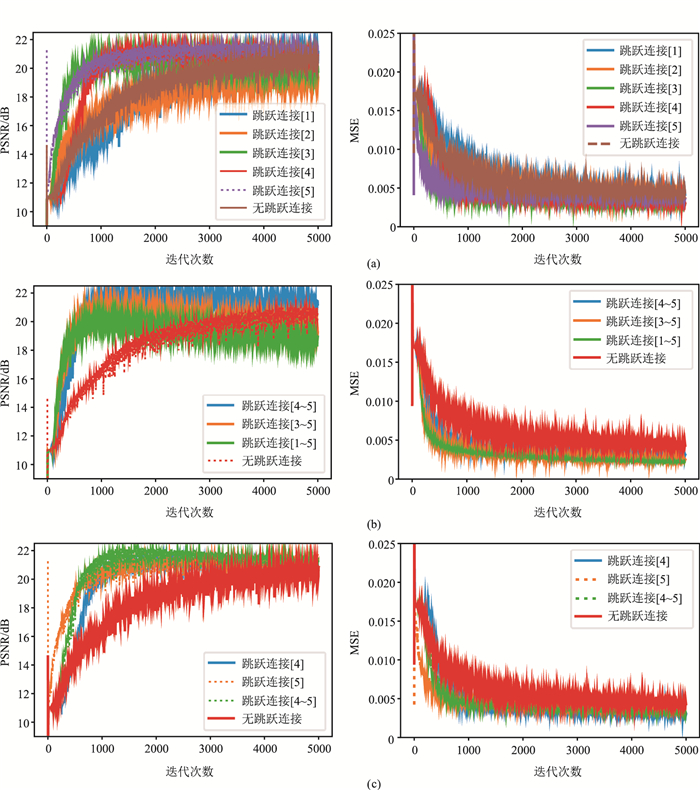
本文在二维合成数据上进行测试,通过对比采用不同跳跃连接方式的网络去噪的PSNR和MSE变化趋势(图 5),确定去噪效果最优的连接方式,同时表 1列出了迭代过程中的最大PSNR和最小损失。PSNR的计算公式为
| $\mathrm{PSNR}=10 \lg \frac{[\max (|\boldsymbol{x}|)]^2}{\left\|\boldsymbol{x}-\boldsymbol{x}^*\right\|_2^2}$ | (11) |
|
图 5 合成数据DIP+ADAM采用不同跳跃连接方式去噪的PSNR(左)与收敛趋势(右)对比 (a)单个网络层添加跳跃连接;(b)多个网络层添加跳跃连接;(c)单个网络层与多个网络层添加跳跃连接 |
|
|
表 1 合成数据去噪时不同跳跃连接方式的最大PSNR及对应迭代次数和MSE |
PSNR的值越大,去噪效果越好。
由图 5a可见,在单个网络层添加跳跃连接中效果最优的是第5层,其收敛速度虽然不是最快,但是去噪性能最好;其次是第4层。虽然图 5a左迭代后期蓝色曲线(第1层)要高于红色曲线(第4层),但结合表 1可知在第4层添加跳跃连接的去噪性能更好,且收敛速度较快。由图 5b可见,在多个网络层添加跳跃连接中效果最优的是第4~第5层,这是因为深层网络富含语义信息,但特征分辨率较低,所以在深处添加跳跃连接可以帮助网络捕获更丰富的全局信息。最后,对比图 5a与图 5b去噪效果较好的跳跃连接方式,结果如图 5c所示,可以看出总体去噪效果最好的是在网络第4~第5层同时添加跳跃连接。基于此,本文选择在网络第4~第5层同时添加跳跃连接的CNN作为地震数据去噪的网络结构。
2 数值实验为验证DIP结合WTV正则与ADMM方法在地震数据去噪方面的有效性,将DIP+ADAM、DIP+TV+ADMM和DIP+WTV+ADMM、非局部均值(NLM)、三维块匹配滤波(BM3D)等5种方法对二维合成数据和实际数据去噪测试。本文设置DIP+ADAM的迭代次数为5000,使用ADMM求解时包括两层迭代,内部迭代次数为200,外部迭代次数为300。对于合成数据,为了定量地衡量去噪结果的质量,本文使用了两个性能指标:PSNR和结构相似性(SSIM)。SSIM用于衡量两幅图像的相似度,计算公式如下
| $\operatorname{SSIM}(\boldsymbol{x}, \boldsymbol{y})=\frac{\left(2 u_x u_y+c_1\right)\left(2 \sigma_{x y}+c_2\right)}{\left(u_x^2+u_y^2+c_1\right)\left(\sigma_x^2+\sigma_y^2+c_2\right)}$ | (12) |
式中:
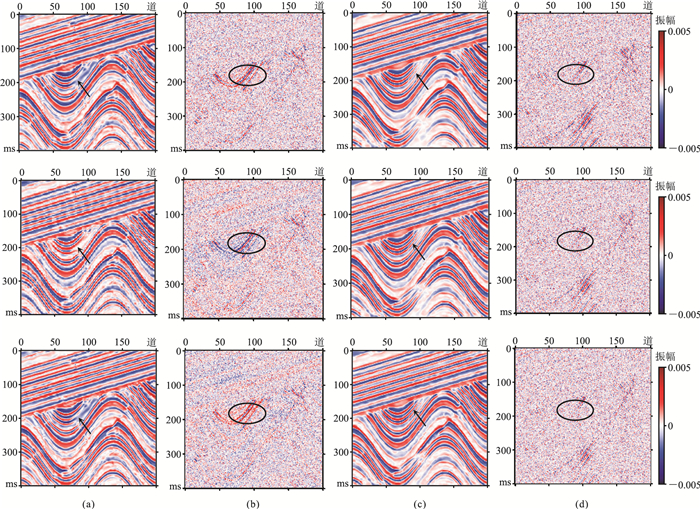
为方便观察DIP+ADAM和DIP+WTV+ADMM两种方法的去噪过程,本文输出了这两种方法在合成数据上的去噪过程图(图 6)。图 6a展示了DIP+ADAM迭代800、900、1000次的去噪结果,观察图 6a中箭头指向的地方,可以看出迭代800次时学到的信号在迭代900次后丢失了,在迭代到第1000次后又重新被学习,这从图 6b的去噪残差图中也可以观察到。图 6c展示了DIP+WTV+ADMM迭代15、20、25次的去噪结果,观察箭头指向的同一位置,随着迭代次数的增加,之前学到的信号依然存在,即DIP+WTV+ADMM的迭代过程比DIP+ADAM更加稳定。
|
图 6 DIP+ADAM与DIP+WTV+ADMM的去噪迭代过程部分结果输出(合成数据) (a)DIP+ADAM去噪结果,从上至下分别为迭代800、900、1000次;(b)DIP+ADAM去噪残差;(c)DIP+WTV+ADMM去噪结果,从上至下分别为迭代15、20、25次;(d)DIP+WTV+ADMM去噪残差 |
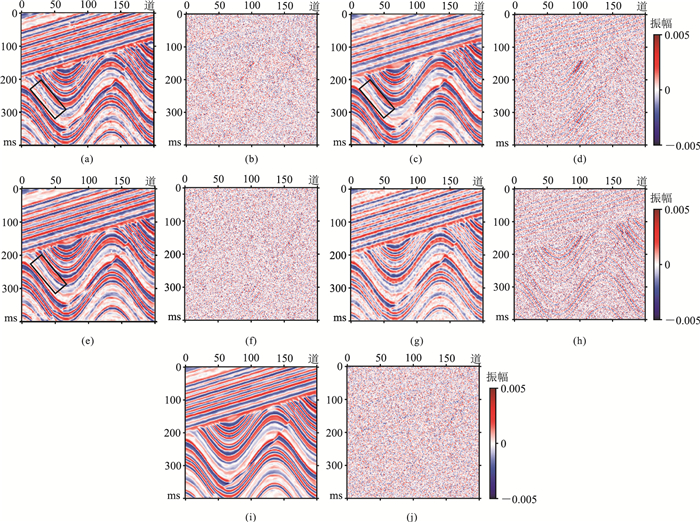
图 7展示了不同方法的去噪效果。由图 7a、图 7c和图 7e中的矩形区域可见,DIP+WTV+ADMM恢复的有效信号更清晰、连续,残差(图 7f)中几乎不包含有效信号。以上两方面都说明DIP+WTV+ADMM方法的去噪效果优于DIP+ADAM方法,并且能够有效减少信号损失。另外,注意到DIP+TV+ADMM的去噪结果没有达到减少信息损失、提升PSNR的效果,但并不能直接断定TV正则对网络性能提升没有作用。必须强调,TV正则项的权重系数是人为设定的超参数,通过多次测试可能会有优于本文的展示效果。此外,图 7还展示了NLM与BM3D的去噪结果与去噪残差,NLM去噪结果(图 7g)中仍包含大量噪声,从去噪残差(图 7h)中可以观察到信号损失。BM3D的去噪结果(图 7i)最佳,几乎接近无噪数据。
|
图 7 不同方法去噪结果与去噪残差(合成数据) (a)DIP+ADAM去噪结果;(b)DIP+ADAM去噪残差;(c)DIP+TV+ADMM去噪结果;(d)DIP+TV+ADMM去噪残差;(e)DIP+WTV+ADMM去噪结果;(f)DIP+WTV+ADMM去噪残差;(g)NLM去噪结果;(h)NLM去噪残差;(i)BM3D去噪结果;(j)BM3D去噪残差 |
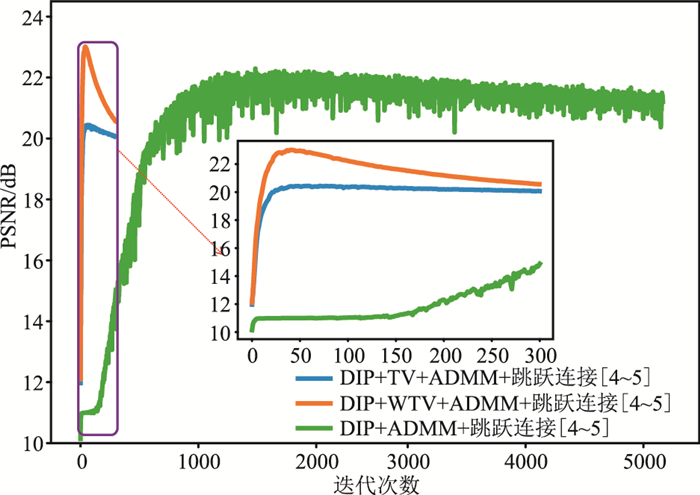
由图 8所示的PSNR变化趋势图可见,DIP+ADAM方法曲线波动大,DIP结合正则项与ADMM算法的曲线更光滑,网络学习过程更稳定。若迭代次数过多,仍然会发生过拟合现象,但相邻迭代拟合信号PSNR波动小,较易制定早停准则,更实用。同时,DIP+TV+ADMM相比于其他两种方法,其PSNR更低。相比之下,WTV正则可以自适应地学习适合于地震数据去噪的参数,并且去噪效果优于其余两种方法。
|
图 8 不同方法去噪的峰值信噪比变化趋势对比 |
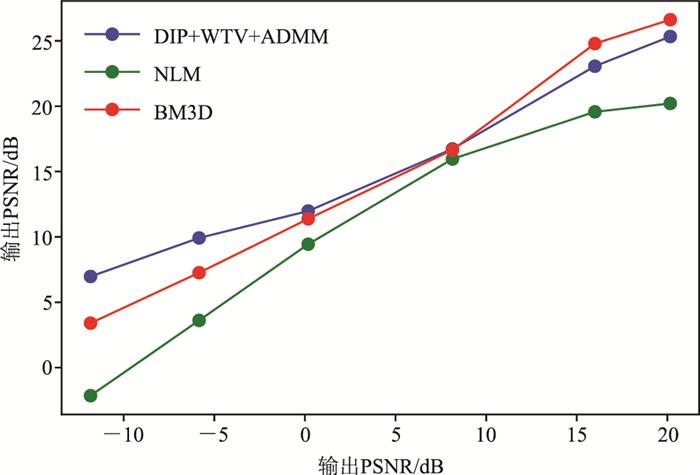
表 2列出了不同方法在二维合成数据上测试的定量指标计算结果。尽管DIP在超分辨率和修复这些反问题中表现出显著的性能,但对合成数据中的高斯噪声,PSNR往往低于BM3D[49]。由表 2可见,在高信噪比时,BM3D方法的去噪效果略好于DIP+WTV+ADMM方法。经测试,在低信噪比时,DIP+WTV+ADMM具有一定优势(图 9)。DIP+WTV+ADMM的PSNR值较DIP+ADAM提升了0.77 dB,SSIM值也有提升,证明DIP+WTV+ADMM的去噪效果更好。
|
|
表 2 合成含噪数据(PSNR为16dB)不同方法去噪PSNR、SSIM对比 |
|
图 9 三种方法在不同噪声水平下的去噪性能(合成数据) |
此外,在二维合成数据中加入6个不同水平的高斯噪声,然后使用DIP+WTV+ADMM、NLM、和BM3D压制随机噪声,以分析不同方法的去噪性能。如图 9所示,在弱噪声环境下,BM3D方法的去噪效果最佳;但当输入数据的峰值信噪比为-11.83 dB时,DIP+WTV+ADMM具有更强的有效信号提取能力。与其他两种基准测试方法相比,DIP+WTV+ADMM能够在强噪声环境下有效地分离弱信号,即随机噪声衰减能力更强。
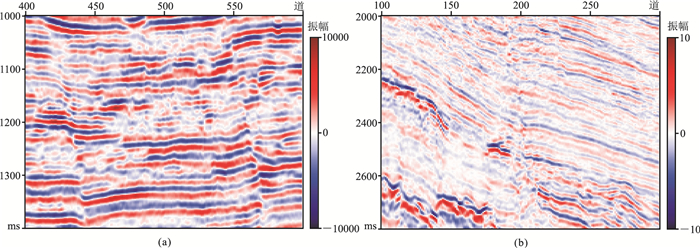
2.2 实际数据去噪选取两个实际数据进行去噪测试,其中一个为X油田西部三维数据体的一个二维剖面(图 10a);另外一个是Kerry3D数据体中的一个二维剖面(图 10b)。从图 10可以看出,一些有效的信号被噪声污染。
|
图 10 实际地震数据 (a)X油田西部某二维剖面;(b)Kerry3D二维剖面 |
为了验证DIP+WTV+ADMM去噪的有效性,本节采用不同方法对两个实际数据进行去噪实验,其结果如图 11和图 12所示。
|
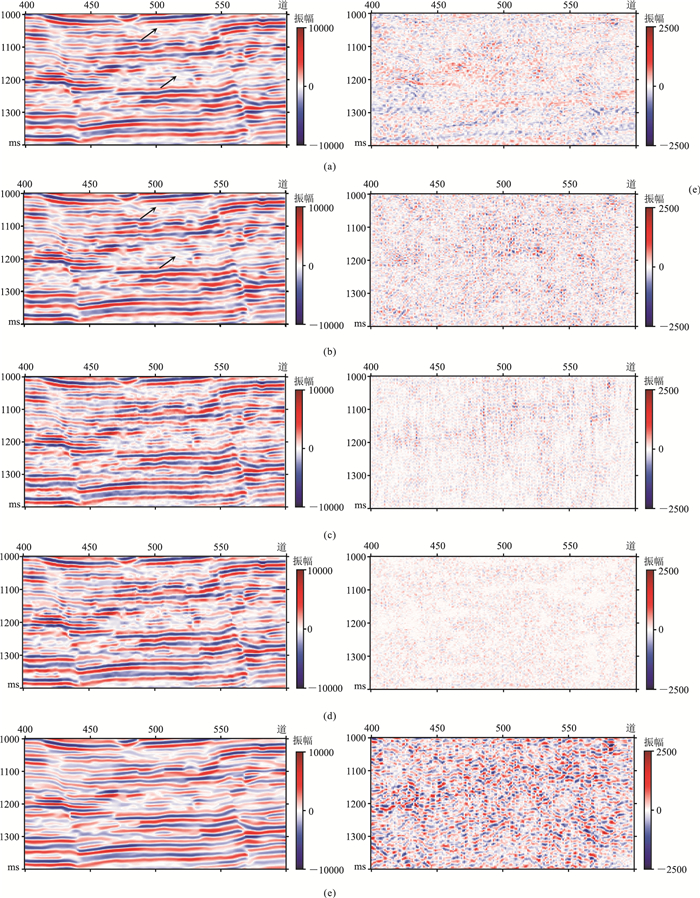
图 11 不同方法对图 10a的去噪结果(左)及残差(右) (a)DIP+ADAM;(b)DIP+WTV+ADMM;(c)某商业软件;(d)NLM(e)BM3D |
|
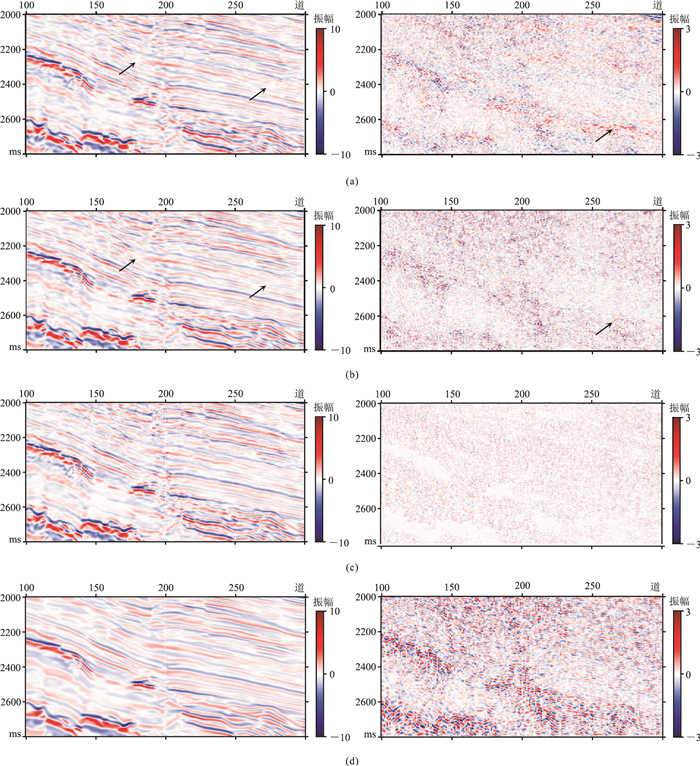
图 12 不同方法对图 10b的去噪结果(左)及残差(右) (a)DIP+ADAM(b)DIP+WTV+ADMM;(c)NLM;(d)BM3D |
图 11展示了不同方法对图 10a的去噪效果,从中可以看出,DIP压制了大部分随机噪声,但从去噪结果(图 11a左)中箭头所指的地方可以看出有效信号连续性较差。从去噪残差图(图 11a右)看,噪声在一定程度上得以消除,但存在明显的信号泄漏。而DIP+WTV+ADMM噪声压制较好,信号也得到了保护(图 11b)。某商业软件的去噪结果(图 11c)与NLM(图 11d)相近,只有少部分噪声被消除。BM3D的去噪结果(图 11e左)与DIP+WTV+ADMM相近,但残差图(图 11e右)包含的有效信号较多。
图 12展示了不同方法对图 10b去噪效果。图 12a展示了DIP+ADAM的去噪效果,可以清楚地观察到,在去除噪声时一些有效信号被损坏了。DIP+WTV+ADMM去噪后的数据质量明显得到改善(图 12b左)。此外,受噪声影响相对较弱的有效信号变得连续和清晰。相应地,在去除的噪声部分中信号泄漏较少(图 12b右)。NLM的去噪结果(图 12c)中只有少部分随机噪声被去除,去噪效果较差。BM3D的去噪结果(图 12d左)损失了较多的地震信号细节,这一点从残差图(图 12d右)中也可看到。结果表明,DIP结合WTV正则与ADMM的方法在有效去除随机噪声的同时,能够减少信号损失。
3 结论本文基于无监督的深度图像先验(DIP)框架压制二维地震数据随机噪声。首先基于合成数据,测试具有不同跳跃连接网络的去噪效果,以此确定了地震数据随机噪声压制最优网络架构;其次在损失函数中加入加权全变分正则(WTV正则);最后通过ADMM求解优化问题。通过合成数据与实际数据实验,可以得出如下结论:
(1)DIP结合CNN去噪会造成一定程度的有效地震信号损失,而在CNN中添加合适的跳跃连接可有效提升去噪效果;
(2)传统TV正则项前的权重系数需要人为设置,较难确定最佳值,而本文所采用的WTV正则项可以自适应选择权重系数,即算法会将正则项的权重系数视作需要迭代更新的参数,这样会避免人工设置的主观性,而且去噪效果也更好;
(3)DIP与ADAM相结合的方法稳定性较差,即网络在拟合地震数据过程中,会丢失之前已经学好的信号。DIP结合WTV正则与ADMM后,网络稳定性得到了极大改善,而且能够在噪声压制和有效信号保存之间实现更好的平衡,是一种更加有效的地震数据随机噪声压制方法。
| [1] |
朱跃飞, 曹静杰, 殷晗钧. 一种自动判定保留的奇异值个数的地震随机噪声压制算法[J]. 石油地球物理勘探, 2022, 57(3): 570-581. ZHU Yuefei, CAO Jingjie, YIN Hanjun. Seismic random noise suppression algorithm with automatic determination of the number of retained singular values[J]. Oil Geophysical Prospecting, 2022, 57(3): 570-581. DOI:10.13810/j.cnki.issn.1000-7210.2022.03.008 |
| [2] |
GÜLÜNAY N. Signal leakage in f-x deconvolution algorithms[J]. Geophysics, 2017, 82(5): W31-W45. DOI:10.1190/geo2017-0007.1 |
| [3] |
ABMA R, CLAERBOUT J. Lateral prediction for noise attenuation by t-x and f-x techniques[J]. Geophysics, 1997, 60(6): 1887-1896. |
| [4] |
李志娜, 李振春, 王鹏, 等. 地震资料F-K滤波去除相干噪声综合性实验[J]. 实验技术与管理, 2022, 39(1): 66-71. LI Zhina, LI Zhenchun, WANG Peng, et al. Comprehensive experiment on coherent noise removal by F-K filtering in seismic data[J]. Experimental Technology and Management, 2022, 39(1): 66-71. |
| [5] |
TAO R, DENG B, WANG Y. Research progress of the fractional Fourier transform in signal processing[J]. Science in China, Series F, 2006, 49(1): 1-25. |
| [6] |
CHEN Y, LIU T, CHEN X, et al. Time-frequency analysis of seismic data using synchrosqueezing wavelet transform[J]. Journal of Seismic Exploration, 2014, 23(4): 303-312. |
| [7] |
HENNENFENT G, HERRMANN F J. Seismic denoising with nonuniformly sampled curvelets[J]. Computing in Science & Engineering, 2006, 8(3): 16-25. |
| [8] |
TRAD D, ULRYCH T, SACCHI M. Latest views of the sparse Radon transform[J]. Geophysics, 2003, 68(1): 386-399. DOI:10.1190/1.1543224 |
| [9] |
OROPEZA V, SACCHI M. Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis[J]. Geophysics, 2011, 76(3): V25-V32. DOI:10.1190/1.3552706 |
| [10] |
KENDALL R, JIN S, RONEN S, et al. An SVD-polarization filter for ground roll attenuation on multicomponent data[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 928-931.
|
| [11] |
GÓMEZ J L, VELIS D R. A simple method inspired by empirical mode decomposition for denoising seismic data[J]. Geophysics, 2016, 81(6): 403-413. DOI:10.1190/geo2015-0566.1 |
| [12] |
MA H, YAN J, LI Y. Low-frequency noise suppression of desert seismic data based on variational mode decomposition and low-rank component extraction[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 17(2): 337-341. |
| [13] |
MOUSAVI S M, BEROZA G C. Deep-learning seismology[J]. Science, 2022, 377(6607): EABM4470. DOI:10.1126/science.abm4470 |
| [14] |
WU B, MENG D, WANG L, et al. Seismic impedance inversion using fully convolutional residual network and transfer learning[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(12): 2140-2144. DOI:10.1109/LGRS.2019.2963106 |
| [15] |
ZHENG X, WU B, ZHU X. Multi-task deep learning seismic impedance inversion optimization based on homoscedastic uncertainty[J]. Applied Sciences, 2022, 12(3): 1200. DOI:10.3390/app12031200 |
| [16] |
WU B, MENG D, ZHAO H. Semi-supervised learning for seismic impedance inversion using generative adversarial networks[J]. Remote Sensing, 2021, 13(5): 909. DOI:10.3390/rs13050909 |
| [17] |
WANG L, MENG D, WU B. Seismic inversion via closed-loop fully convolutional residual network and transfer learning[J]. Geophysics, 2021, 86(5): R671-R683. DOI:10.1190/geo2020-0297.1 |
| [18] |
YU J, WU B. Attention and hybrid loss guided deep learning for consecutively missing seismic data reconstruction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-8. |
| [19] |
LI X, WU B, ZHU X, et al. Consecutively missing seismic data interpolation based on coordinate attention attention UNET[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [20] |
HE T, WU B, ZHU X. Seismic data consecutively missing trace interpolation based on multistage neural network training process[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [21] |
HUANG W, GAO F, LIAO J, et al. A deep learning network for estimation of seismic local slopes[J]. Petroleum Science, 2021, 18(1): 92-105. DOI:10.1007/s12182-020-00530-1 |
| [22] |
WANG Z, LI B, LIU N, et al. Distilling knowledge from an ensemble of convolutional neural networks for seismic fault detection[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [23] |
LIU N, HE T, TIAN Y, et al. Common-azimuth seismic data fault analysis using residual UNet[J]. Interpretation, 2020, 8(3): SM25-SM37. DOI:10.1190/INT-2019-0173.1 |
| [24] |
宋辉, 高洋, 陈伟, 等. 基于卷积降噪自编码器的地震数据去噪[J]. 石油地球物理勘探, 2020, 55(6): 1210-1219. SONG Hui, GAO Yang, CHEN Wei, et al. Seismic noise suppression based on convolutional denoising autoencoders[J]. Oil Geophysical Prospecting, 2020, 55(6): 1210-1219. |
| [25] |
WANG F, CHEN S. Residual learning of deep convolutional neural network for seismic random noise attenuation[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(8): 1314-1318. DOI:10.1109/LGRS.2019.2895702 |
| [26] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869, 877. HAN Weixue, ZHOU Yatong, CHI Yue. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869, 877. DOI:10.3969/j.issn.1000-1441.2018.06.008 |
| [27] |
王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 421-433. WANG Yuqing, LU Wenkai, LIU Jinlin, et al. Random seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 421-433. |
| [28] |
方文倩, 李志明. 基于双重残差网络的地震数据随机噪声压制[J]. 工程地球物理学报, 2021, 18(1): 44-50. FANG Wenqian, LI Zhiming. Random noise attenuation in seismic data based on dual residual networks[J]. Chinese Journal of Engineering Geophysics, 2021, 18(1): 44-50. |
| [29] |
刘小舟, 胡天跃, 刘韬, 等. 数据增广的编解码卷积网络地震层间多次波压制方法[J]. 石油地球物理勘探, 2022, 57(4): 757-767. LIU Xiaozhou, HU Tianyue, LIU Tao, et al. Seismic internal multiple suppression method with encoder-decoder convolutional network based on data augmentation[J]. Oil Geophysical Prospecting, 2022, 57(4): 757-767. |
| [30] |
张猛. 基于自注意力机制的卷积自编码器多次波压制方法[J]. 石油物探, 2022, 61(3): 454-462. ZHANG Meng. A multiple suppression method based on self-attention convolutional auto-encoder[J]. Geophysical Prospecting for Petroleum, 2022, 61(3): 454-462. |
| [31] |
张岩, 李新月, 王斌, 等. 基于深度学习的鲁棒地震数据去噪[J]. 石油地球物理勘探, 2022, 57(1): 12-25. ZHANG Yan, LI Xinyue, WANG Bin, et al. Robust seismic data denoising based on deep learning[J]. Oil Geophysical Prospecting, 2022, 57(1): 12-25. |
| [32] |
徐彦凯, 刘曾梅, 薛亚茹, 等. 应用双通道卷积神经网络的地震随机噪声压制方法[J]. 石油地球物理勘探, 2022, 57(4): 747-756. XU Yankai, LIU Zengmei, XUE Yaru, et al. Suppression of seismic random noise using dual‑channel convolutional neural network[J]. Oil Geophysical Prospecting, 2022, 57(4): 747-756. |
| [33] |
杨翠倩, 周亚同, 何昊, 等. 基于全局上下文和注意力机制深度卷积神经网络的地震数据去噪[J]. 石油物探, 2021, 60(5): 751-762, 855. YANG Cuiqian, ZHOU Yatong, HE Hao, et al. Global context and attention-based deep convolutional neural network for seismic data denoising[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 751-762, 855. |
| [34] |
董新桐, 钟铁, 王洪洲, 等. 基于卷积对抗降噪网络的塔里木盆地沙漠地震资料消噪方法研究[J]. 地球物理学报, 2022, 65(7): 2661-2672. DONG Xintong, ZHONG Tie, WANG Hongzhou, et al. The denoising of desert seismic data acquired from Tarim Basin based on convolutional adversarial denoising network[J]. Chinese Journal of Geophysics, 2022, 65(7): 2661-2672. |
| [35] |
买皓. 基于深度残差网络的地震数据去噪研究[D]. 北京: 中国石油大学(北京), 2019. MAI Hao. Seismic Data Noise Attenuation Based on Deep Residual Network[D]. China University of Petroleum (Beijing), Beijing, 2019. |
| [36] |
高好天, 孙宁娜, 孙可奕, 等. DnCNN和U-Net对地震随机噪声压制的对比分析[J]. 地球物理学进展, 2021, 36(6): 2441-2453. GAO Haotian, SUN Ningna, SUN Keyi, et al. Comparative analysis of DnCNN and U-Net on suppression of seismic random noise[J]. Progress in Geophysics, 2021, 36(6): 2441-2453. |
| [37] |
罗仁泽, 李阳阳. 一种基于RUnet卷积神经网络的地震资料随机噪声压制方法[J]. 石油物探, 2020, 59(1): 51-59. LUO Renze, LI Yangyang. Random seismic noise attenuation based on RUnet convolutional neural network[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 51-59. |
| [38] |
LEMPITSKY V, VEDALDI A, ULYANOV D. Deep image prior[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, 9446-9454.
|
| [39] |
LEHTINEN J, MUNKBERG J, HASSELGREN J, et al. Noise2Noise: learning image restoration without clean data[C]. Proceedings of the 35th International Conference on Machine Learning, 2018, 2965-2974.
|
| [40] |
KRULL A, BUCHHOLZ T O, JUG F. Noise2Void - learning denoising from single noisy images[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019, 2124-2132.
|
| [41] |
MORAN N, SCHMIDT D, ZHONG Y, et al. Noisier2Noise: learning to denoise from unpaired noisy data[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020, 12061-12069.
|
| [42] |
HUANG T, LI S, JIA X, et al. Neighbor2neighbor: self-supervised denoising from single noisy images[C]. 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2021, 14776-14785.
|
| [43] |
LIU J, SUN Y, XU X, et al. Image restoration using total variation regularized deep image prior[C]. 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2019, 7715-7719.
|
| [44] |
CALATRONI L, LANZA A, PRAGLIOLA M, et al. Adaptive parameter selection for weighted-TV image reconstruction problems[J]. Journal of Physics: Conference Series, 2020, 1476: 012003. |
| [45] |
WANG Y, YIN W, ZENG J. Global convergence of ADMM in nonconvex nonsmooth optimization[J]. Journal of Scientific Computing, 2019, 78(1): 29-63. |
| [46] |
宋洁, 陈平, 潘晋孝. 实现稀疏角度下的精确CT重建: 利用ADMM-LP算法求解非凸模型[J]. 中国组织工程研究, 2018, 22(31): 4998-5002. SONG Jie, CHEN Ping, PAN Jinxiao. Reconstruction accuracy of sparse angle CT imaging: ADMM-CT algorithm based on LP-norm[J]. Chinese Journal of Tissue Engineering Research, 2018, 22(31): 4998-5002. |
| [47] |
CASCARANO P, SEBASTIANI A, COMES M C, et al. Combining weighted total variation and deep image prior for natural and medical image restoration via ADMM[C]. 2021 21st International Conference on Computational Science and Its Applications (ICCSA), 2021, 39-46.
|
| [48] |
QIU C, WU B, LIU N, et al. Deep learning prior model for unsupervised seismic data random noise attenuation[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [49] |
JO Y, CHUN S Y, CHOI J. Rethinking deep image prior for denoising[C]. 2021 IEEE/CVF International Conference on Computer Vision (ICCV), 2021, 5067-5076.
|



 吴帮玉, 陕西省西安市碑林区咸宁西路28号西安交通大学数学与统计学院, 710049。Email:
吴帮玉, 陕西省西安市碑林区咸宁西路28号西安交通大学数学与统计学院, 710049。Email: 