2. 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580
2. School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China
地震子波的精确提取是反演和成像的重要前提。然而地震子波的主频和相位不仅随时间而且随空间变化,难以精确提取。
近年来,对单道地震子波的时变特性的研究已较为成熟,并提出了一系列提取方法,如使用自适应分段技术的时变子波提取方法。戴永寿等[1]根据自适应分段法对非平稳地震记录进行时窗划分,有效提高了时窗寻优精度,从而实现了时变子波估计;王蓉蓉等[2]采用改进的广义S变换将地震记录变换至时频域,采用两次傅里叶变换得到子波的振幅谱,并使用自适应分段法逐段提取子波相位,实现了对非平稳单地震道的时变子波提取。张鹏等[3]基于经验模态分解(Empirical Mode Decomposition,EMD)法,利用子波振幅谱与相位谱关系分别提取子波的振幅谱和相位谱,实现了时变子波的估计;并结合CEEMD(Complementary Ensemble Empirical Mode Decomposition)与递推最小二乘法改进了该方法[4]。
另外,Jiang等[5-6]提出了一种基于FWE(Frequency Weighted Exponential)函数的时变子波提取方法,实现了不考虑Q值和震源子波的非平稳反褶积。该方法从非平稳地震资料中得到时变子波的解析式,从而实现时变子波的提取。然而该方法提取的子波往往需满足地震记录分段平稳等假设,且将子波的提取范围局限于单一地震道,忽略了地震子波形态的横向变化,在实际应用中受限。
针对空变子波提取方法的研究仍处于发展阶段,现有方法大多依赖于测井信息与传统的信号处理技术。内插法[7]通过展开井旁道子波,在不同井之间对子波做线性内插,经内插估算其余道子波,实现了多道空变子波的提取,然而实际的地震道并不完全符合该内插关系,因此应用范围受限。同时,使用测井数据可直接计算反射系数序列,基于褶积模型利用井旁地震道反演[8]得到实际子波,同时使用近似时段子波的相位谱估算不同道的子波,得到空变子波剖面。
深度学习类算法在地震勘探领域得到了广泛应用,如地震反演[9]、地震数据低频补偿[10]和震源子波提取[11]等。卷积神经网络(CNN)作为一类具有代表性的深度学习图像处理模型,已应用于全波形反演[12]、储层预测[13]、断层识别[14]、微地震事件检测[15]和地震数据去噪[16]等,证明CNN可有效提取地震信号的分布特征。生成对抗网络(GAN)为一类结合双CNN架构的人工神经网络模型,其改进型——循环一致性生成对抗网络(CycleGAN)在压制地震随机噪声方面取得了较好的效果[17]。韩浩宇等[18]使用GAN实现了叠前地震数据的深层震源子波提取,验证了其子波提取的可行性与准确性,但忽略了地震子波的空变特征。近年来,以长短时记忆(LSTM)网络为代表的循环神经网络(RNN)适用于时间序列的相关分析与处理,已用于地震前兆数据的异常诊断[19],取得了一定的应用效果。然而,单层LSTM网络内部加入的多个门控结构后计算较为复杂,对于长时间信号易出现过拟合现象,Cho等[20]提出了一种内部结构更为精简的门控循环单元(Gated Recurrent Unit,GRU)神经网络模型,该方法简化了网络计算,提升了网络的训练效率。
为进一步深入拓展数据处理范围,深度学习领域众多新网络被陆续提出。深层神经网络(DNN)在语音识别和视觉物体识别等方面均展现了较优异的性能,具备将数据进行任意维度的尺寸变换和特征提取能力[21],为自编码—解码架构中编码和解码计算奠定了基础。自编码—解码架构由Vincent等[22]提出,探索了一种新的构建DNN方案,在图像去噪领域取得了一定的效果。然而DNN的深层网络结构加大了训练难度,对于完备训练数据的依赖程度较高。自编码—解码架构与CNN的结合,即卷积自编码器可实现对图像数据的特征提取与计算,能有效压制地震随机噪声[23]。Sutskever等[24]提出了一种输入和输出端均为序列数据的自编码—解码网络架构,成功将自编码—解码架构的优势与LSTM网络相结合。该方法用一个多层LSTM网络将输入序列映射为固定维度的向量,再用另一个深层LSTM网络将向量解码为目标序列,相比于传统排列形式的LSTM网络,该方法在语言翻译方面的精准度更高。Shi等[25]将CNN与LSTM网络相结合,提出了一种针对时空域序列预测类问题的卷积长短时记忆单元(ConvLSTM)网络架构,该方法将不同时刻的二维雷达气象图划分为不重叠的数据块,通过将数据块内部像素值作为输入,将LSTM网络处理的数据由时间序列拓展为高维时空域序列,实现了短期气象图的时空预测。而Ballas等[26]针对ConvLSTM网络存在的计算复杂度过高问题,提出了将CNN与GRU网络结合的卷积门控循环单元(ConvGRU)网络,该方法在保证网络性能的同时更加易于训练。
以上研究证明,将RNN与先进的深度学习架构结合,相较于使用CNN的传统自编码—解码器,虽然固定了处理数据的维度与尺寸,但进一步发掘了RNN在处理时序数据的潜力,为解决多地震道的子波提取问题提供了新思路。为此,本文提出了一种应用自编码—解码架构的ConvGRU的神经网络用于提取空变地震子波。本文方法结合卷积运算与门控运算,实现了地震信号时序特征和空间分布特征的同时提取。对中国西部实际地震数据提取了二维空变子波,通过反褶积提高了地震资料分辨率。
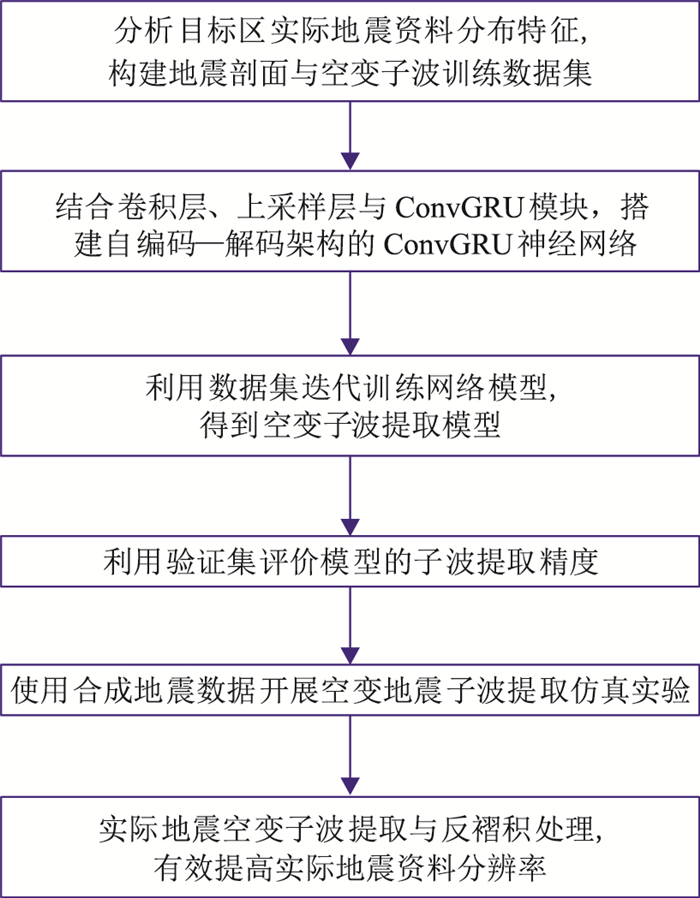
1 原理本文构建的空变子波提取网络模型结合了GRU网络与CNN中的卷积运算,并采用自编码—解码器架构的排列方式搭建网络模型。本文方法可分为训练数据集的构建、搭建与训练网络模型、子波提取三个阶段(图 1)。首先,对待处理工区地震数据开展特征分析,构建了符合实际工区的大规模复杂训练数据集;其次,搭建自编码—解码网络模型,输入数据经编码网络模块计算得到空变子波特征变量,特征变量经解码网络模块拓展为空变子波的数据尺寸,使用训练数据集对搭建的网络模型进行迭代训练,得到具备空变子波提取能力的网络模型;最后,使用仿真数据和实际地震数据验证该模型的子波提取效果。
|
图 1 结合自编码—解码架构与ConvGRU网络的空变子波提取流程 |
GRU为ConvGRU网络的基本计算模块,是RNN的变体[20]。与LSTM网络相比,GRU将门控计算结构精简为更新门和重置门,有效缓解了梯度消失和梯度爆炸问题。而由于GRU各个门控单元与输入数据之间仅使用全连接计算进行链接,无法处理二维地震剖面,仅具有处理一维时间序列数据的能力,因此只能提取单道地震子波。
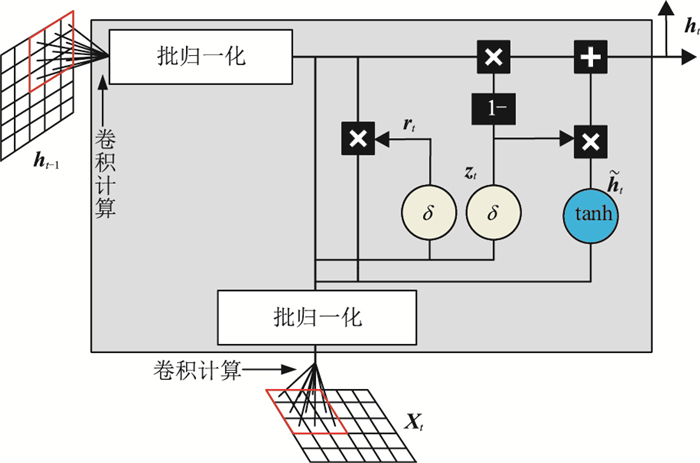
为实现对地震数据的空变子波剖面提取,本文将GRU内部门控的全连接计算替换为二维卷积运算[26],将对单道地震信号的计算拓展为地震剖面的处理。ConvGRU的内部结构如图 2所示。
|
图 2 ConvGRU内部结构 |
图 2中Xt为输入数据,即经分割后的多个地震道,t为输入数据的序号;δ表示激活函数sigmoid;tanh为激活函数tanh,为输入数据添加非线性特征;
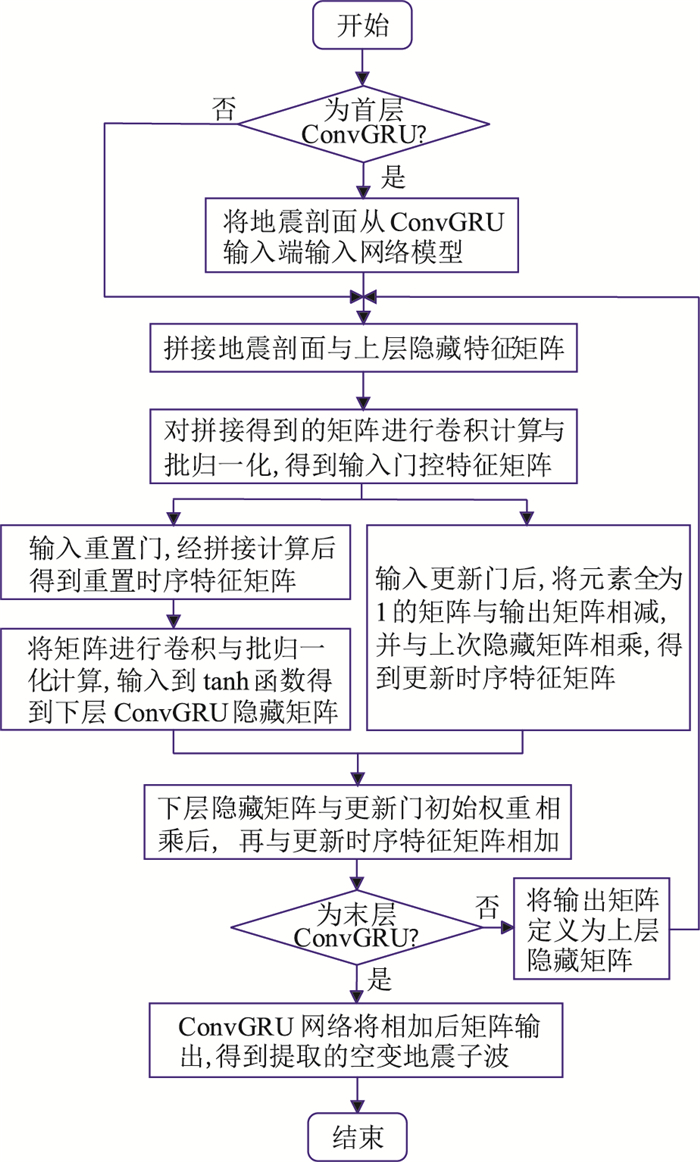
|
图 3 ConvGRU处理地震数据计算流程 |
ConvGRU内部门控权重参数与隐藏矩阵的计算过程如下
| $ {z}_{t}=\delta ({\boldsymbol{W}}_{\boldsymbol{X}z}{\boldsymbol{X}}_{t}+{\boldsymbol{W}}_{\boldsymbol{h}z}{\boldsymbol{h}}_{t-1}) $ | (1) |
| $ {\boldsymbol{r}}_{t}=\delta ({\boldsymbol{W}}_{\boldsymbol{X}\boldsymbol{r}}{\boldsymbol{X}}_{t}+{\boldsymbol{W}}_{\boldsymbol{h}\boldsymbol{r}}{\boldsymbol{h}}_{t-1}) $ | (2) |
| $ {\tilde{\boldsymbol{h}}}_{t}=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left[{\boldsymbol{W}}_{\boldsymbol{X}\boldsymbol{h}}{\boldsymbol{X}}_{t}+{\boldsymbol{r}}_{t}\circ \left({\boldsymbol{W}}_{\boldsymbol{h}\boldsymbol{h}}{\boldsymbol{h}}_{t-1}\right)\right] $ | (3) |
| $ {\boldsymbol{h}}_{t}=(1-{z}_{t})\circ {\tilde{\boldsymbol{h}}}_{t}+{z}_{t}\circ {\boldsymbol{h}}_{t-1} $ | (4) |
式中:WXz、WXr、WXh分别为网络输入数据经更新门、重置门、隐藏矩阵计算后的权重参数;Whz、Whr、Whh分别为网络隐藏矩阵经更新门、重置门与上层ConvGRU隐藏矩阵计算后的权重参数;“
自编码—解码架构将网络区分为编码器模块和解码器模块。输入端经编码器映射至固定维数的特征向量,特征向量经解码器解码后拓展为对应的空变子波剖面。
1.2.1 编码器ConvGRU网络输入端为地震道集或剖面。将输入数据裁剪成尺寸为64×500的数据块,并进行归一化处理。不同的输入块隐含了信号沿时间方向的变化特征。为充分提取每个数据块包含的时间和空间特征,本文将网络的编码器设定为二维卷积(Conv2D)层与ConvGRU层交错堆叠的形式。Conv2D模块使用卷积核在输入的二维地震剖面上滑动进行卷积计算,将地震剖面映射为固定维度的特征图;ConvGRU模块用于提取不同块之间的时序隐藏特征。经编码器编码后,将地震剖面映射成尺寸为16×125的特征变量,该特征变量包含输入剖面所对应空变子波的时间与空间分布特征。
1.2.2 解码器为了将提取的特征变量准确拓展为空变地震子波的数据尺寸,本文将上采样计算(Transpose Conv2D)模块加入解码器的解码过程。上采样计算模块可视作Conv2D模块的逆计算,将输入解码器的特征变量拓展尺寸并进一步提取特征。上采样模块融合卷积和ConvGRU层后,将解码得到的特征变量拓展映射为空变地震子波。
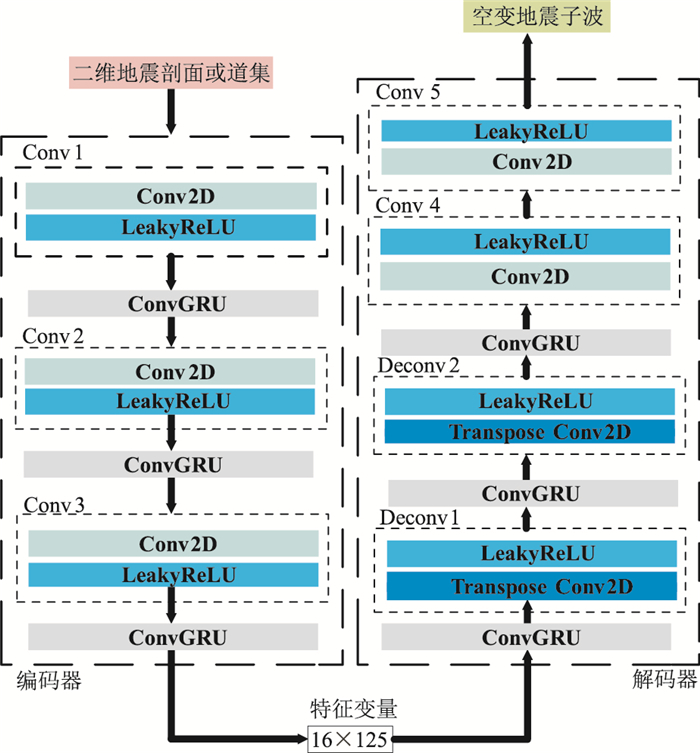
本文提出的应用自编码—解码架构的ConvGRU网络模型如图 4所示。编码器中的Conv1~Conv3模块用于提取输入地震剖面的特征。为将输入剖面编码为16×125的特征变量,依据卷积计算的基本原理,每个Conv模块的卷积核大小、通道数等参数均可进行适用性调整,以高效提取地震剖面中的有效信号特征。解码器中的Deconv1与Deconv2模块将空变子波特征变量进行特征拓展,特征变量经Deconv1模块后数据尺寸被拓展为32×250,经Deconv2模块后数据尺寸被拓展为64×500。Conv4、Conv5被用于进一步提取Deconv输出数据中的有效特征信息,经两模块计算后数据将趋近于目标子波剖面,最终输出空变地震子波。
|
图 4 应用自编码—解码架构的ConvGRU网络模型 |
图 4中LeakyReLU为激活函数,该函数将非线性元素特征引入网络计算。
1.3 训练数据集完备的训练数据集是深度学习解决问题的重要前提。为了网络模型能适用于实际工区地震资料的空变子波提取,首先要对实际地震数据进行频谱和衰减分析。依照实际地震资料的频谱结果,使训练数据集中地震子波的主频均在实际地震资料的优势频带范围之内。
本文结合复杂地下构造特征与地震子波空变特性,应用有限差分正演法和非平稳褶积模型[27]建立了大规模的训练数据集。使用有限差分正演,可得到符合地下复杂构造特征的叠前炮记录;使用非平稳褶积模型,可得到有效反射信号变化明显的叠后地震数据。使用两种方法生成训练集数据,在较大程度上保证了训练数据的差异性,增强了网络的泛化能力。
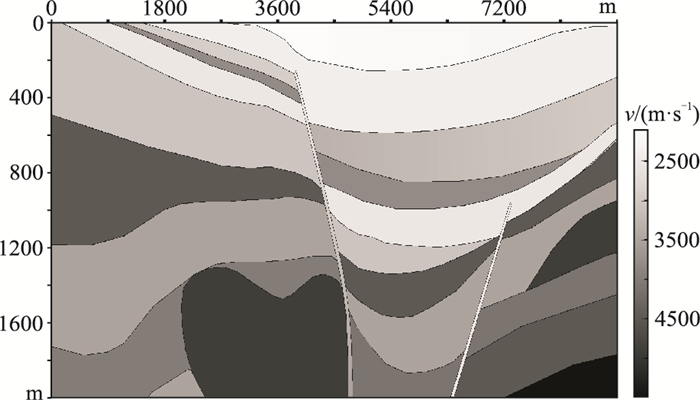
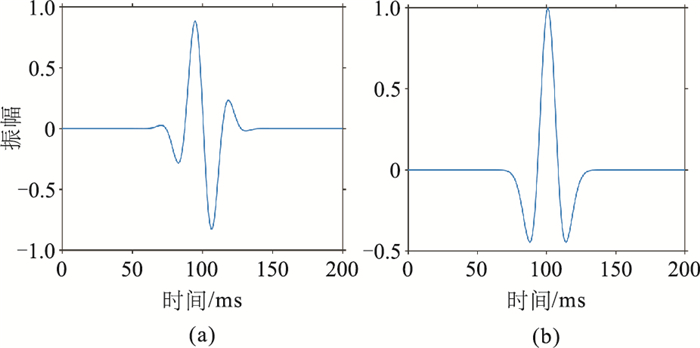
有限差分正演使用了十个速度模型,其中一个如图 5所示。使用Puzirov和Ricker两种子波(图 6)作为震源,主频随机在10~30 Hz间变化,各1250个。共获得2500个炮集数据,每炮100道,每道2000个样点,采样间隔为1ms。每个道集对应的空变地震子波标签则通过多次布置VSP、提取下行直达波记录获得。
|
图 5 有限差分正演使用的Migdemo模型 |
|
图 6 Puzirov(a)和Ricker(b)子波 |
本文将非平稳褶积模型拓展至多道,使用不同反射系数序列模拟得到了2500类随机分布的地下反射界面,并利用随机参数生成不同形态的子波构造对应的非平稳地震剖面。非平稳子波由平稳子波构建
| $ w(t, \tau , i)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\widehat{w}\left({f}_{i}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left[-\mathrm{j}2\mathrm{\pi }{f}_{i}(t-\tau )+\frac{\mathrm{j}2{f}_{i}\tau }{Q}\mathrm{l}\mathrm{n}\left|\frac{{f}_{i}}{{f}_{\mathrm{r}}}\right|-\frac{\mathrm{\pi }{f}_{i}\tau }{Q}\right]\mathrm{d}f $ | (5) |
褶积模型为
| $ x(t, i)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}w(t, \tau , i)\mathrm{*}R\left(\tau \right)\mathrm{d}\tau $ | (6) |
式中:
本文选择Ricker和ARMA(Autoregressive Moving Average Model)子波作为非平稳褶积模型的平稳子波,其中Ricker子波的主频范围为10~30 Hz,共1250道,ARMA子波采用了最小相位与混合相位两类假设,也为1250道。
图 7展示了两种方法构建的地震道集或剖面及其对应的空变子波。训练数据集中包含5000对使用两种方法构造的数据。为增加网络模型的鲁棒性,在地震数据剖面中添加了强度随机分布的高斯噪声,信噪比(SNR)范围为3~12 dB。

|
图 7 两种方法构建的正演数据(a)及其对应的空变子波(b) 左为图 5速度模型的有限差分正演结果;右为非平稳褶积模型合成的结果。 |
本文使用均方误差(MSE)损失函数衡量网络模型训练过程中的提取误差,其计算公式为
| $ L\left(w\right)\mathrm{ }=\frac{1}{N}\sum\limits_{i=1}^{N}{‖{\boldsymbol{w}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}, i}-{\boldsymbol{w}}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}, i}‖}_{2}^{2} $ | (7) |
式中:N为道数;
为优化网络的训练效果,本文选择Adam优化器进行训练的优化操作。网络的迭代训练次数设定为1000,并设定动态学习率,即网络的每轮训练结束后都将自行检验误差相比上一轮是否有效下降,一旦连续四轮训练的提取误差均为有效下降,网络将自行调整学习率。具体的网络训练流程如图 8所示。

|
图 8 应用自编码—解码架构的ConvGRU网络训练流程 |
为了验证方法的准确性,使用训练后的网络模型开展合成数据仿真实验,并使用量化评价指标对比了基于EMD子波提取方法、传统ConvGRU网络与本文方法的提取精度。
2.1 空变子波提取仿真实验 2.1.1 测试数据集测试数据集包含128对使用有限差分正演和与非平稳褶积模型生成的数据,并添加了信噪比为3~12 dB变化的随机噪声。测试数据使用了Ricker子波、Puzirov子波和混合相位或最小相位的ARMA模型子波,主频分布于10~30 Hz。部分二维测试数据块如图 9所示。

|
图 9 有限差分正演(a)和非平稳褶积模型(b)生成的部分测试数据块 |
使用测试集数据开展空变子波剖面的提取测试,与理论子波进行对比以验证所提方法的准确性和抗噪能力。
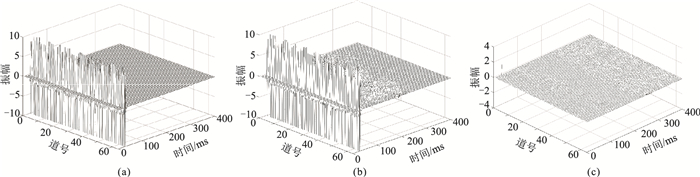
图 10为从使用Puzirov子波进行有限差分正演的地震数据中提取空变地震子波的仿真实验结果,其中Puzirov子波的主频在为10~30 Hz,正演数据加入随机噪声的信噪比(SNR)为4.71 dB,干扰较强。与理论子波(图 10a)相比,虽然采用自编码—解码架构的ConvGRU网络在较强随机噪声情况下的提取结果出现了小幅度干扰(图 10b、图 10c),但地震子波主体误差较小,说明网络具备一定的抗强噪能力。
|
图 10 Puzirov子波有限差分正演数据空变子波提取仿真实验结果 (a)理论子波;(b)提取结果;(c)提取结果与理论子波的差 |
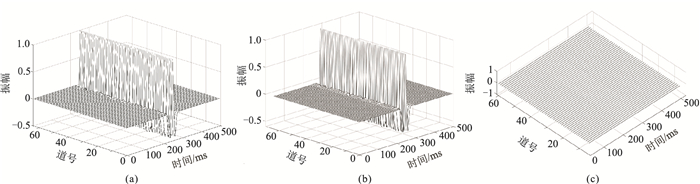
图 11为从使用Ricker子波进行有限差分正演的地震数据中提取空变子波的仿真实验结果,其中子波主频同样为10~30 Hz,加入随机噪声后SNR为9.11 dB,噪声强度中等。结果表明,在该强度的噪声干扰下,本文建立的网络模型对不同主频的子波均达到了较高的提取精度。
|
图 11 Ricker子波有限差分正演数据空变子波提取仿真实验结果 (a)理论子波;(b)提取结果;(c)提取结果与理论子波的差 |
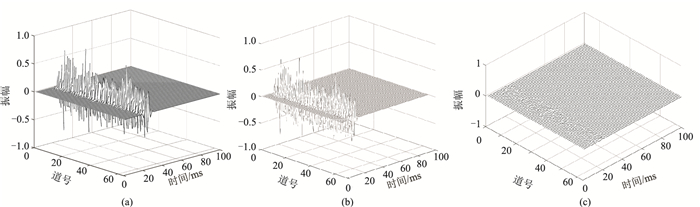
图 12为使用非平稳褶积模型合成的数据中提取空变子波的仿真实验结果,其中理论空变子波为ARMA模型子波,既有混合相位,也有最小相位。合成数据中各道的Q值不同,分布于100~150,子波衰减程度多变。加入的噪声较弱,SNR为11.82 dB。由图 12可见,在衰减多变且子波相位不同的条件下,应用自编码—解码架构的ConvGRU网络提取的空变子波与理论子波较为一致。
|
图 12 ARMA空变子波非平稳褶积数据的空变子波提取仿真实验结果 (a)理论子波;(b)提取结果;(c)提取结果与理论子波的差 |
为体现本文提出的应用自编码—解码架构的ConvGRU网络优越性,将本文方法的空变子波提取结果与常规堆叠式ConvGRU网络的提取结果进行对比。常规ConvGRU网络由6层ConvGRU与全连接层组成。
使用本文建立的训练数据对两种网络模型分别训练1000轮,在测试数据集上测试空变子波提取结果。本文网络模型提取结果的MSE为1.41×10-7,常规ConvGRU网络模型提取结果的MSE为7.90×10-4,可见本文提出的网络提取精度更高、更优越。
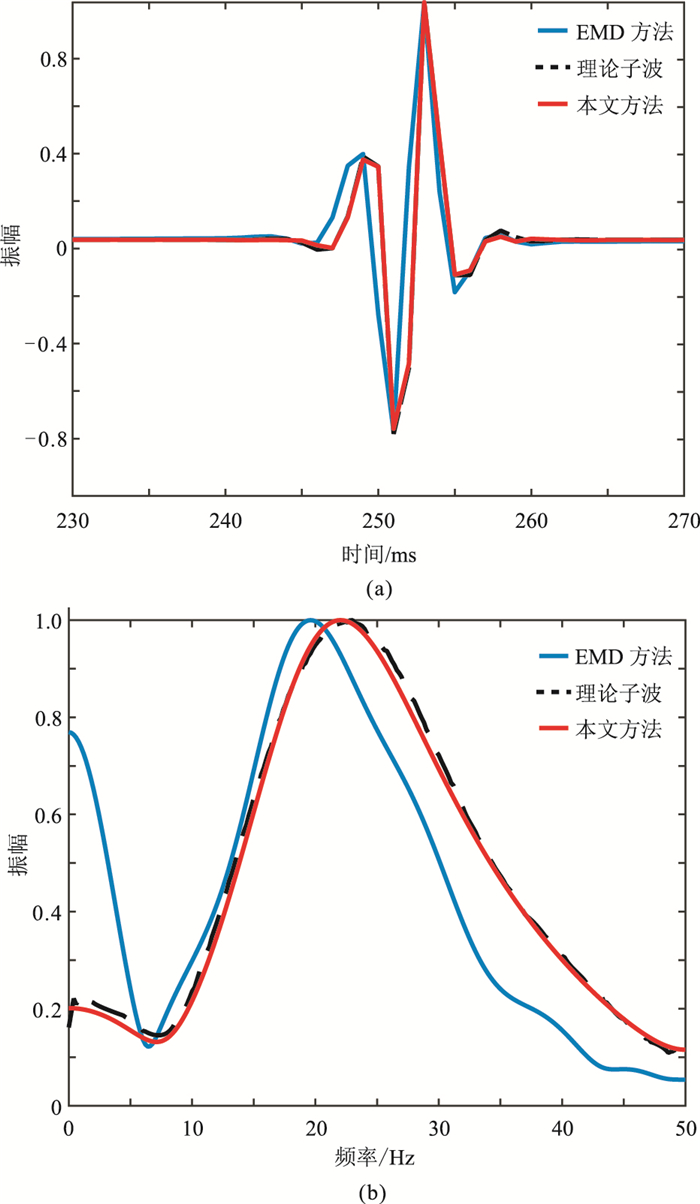
基于EMD及振幅谱和相位谱关系的子波提取方法(EMD方法)仅具备单道处理能力,因此效率较低。对非平稳褶积模型数据应用EMD方法和本文方法提取子波,其中图 9b右第27道的子波波形和振幅谱如图 13所示。对比两种方法提取子波的波形(图 13a)可见,EMD方法提取的子波有较明显的误差,出现了时移现象,精度明显比本文方法低。对比两种方法提取子波的频谱(图 13b)可见,EMD方法提取的子波主频有1~2 Hz的误差,子波低频分量(时域中子波旁瓣部分)出现了不同程度的干扰,而本文方法提取的子波频谱与理论子波频谱吻合程度依然很高。
|
图 13 本文方法与EMD方法提取ARMA空变子波的单道波形(a)与振幅谱(b)对比 |
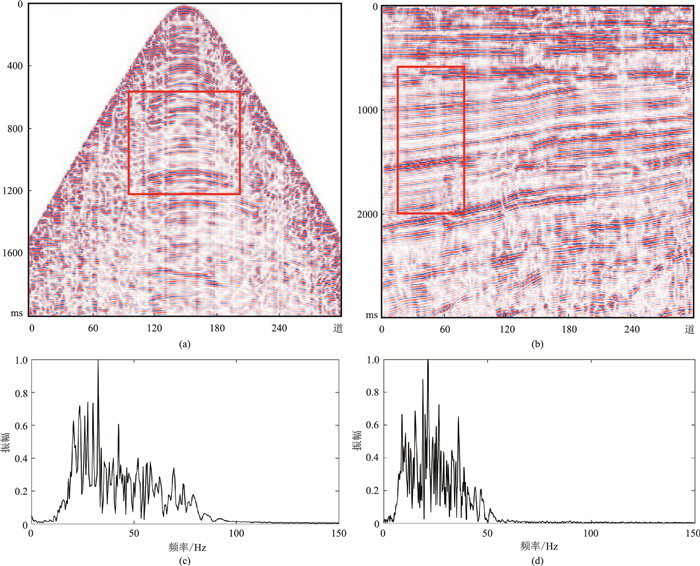
使用中国西部地区的实际地震数据开展空变子波提取,并进行反褶积试验,验证所提方法的效果。实际叠前、叠后数据如图 14a、图 14b所示,红框标注区为试验数据块。叠前数据块低频成分出现了一定程度缺失(图 14c)的现象,而叠后地震数据有效频带较窄,高频成分有待补充(图 14d),具备开展反褶积试验的条件。
|
图 14 实际地震数据及红框块的频谱曲线 (a)叠前数据;(b)叠后数据;(c)局部叠前数据频谱;(d)局部叠后数据频谱 |
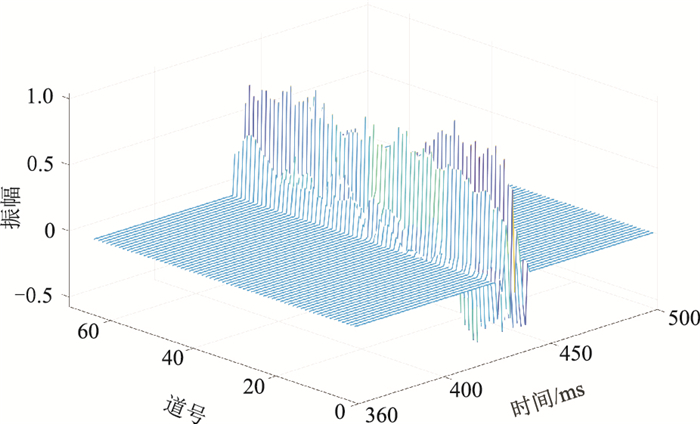
将该实际地震数据划分尺寸为64×500的块输入至训练完成的应用自编码—解码构架的ConvGRU网络,提取空变子波(图 15、图 16)。

|
图 15 实际叠前数据本文方法提取的空变子波 |
|
图 16 实际叠后数据本文方法提取的空变子波 |
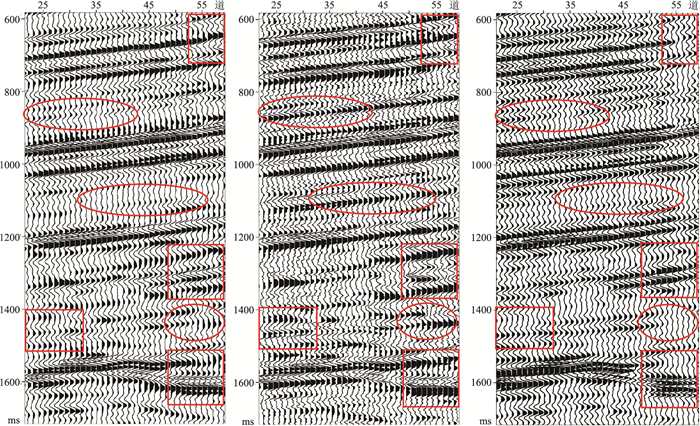
采用本文方法提取的空变子波,对实际数据进行反褶积处理,并与EMD方法提取的单道地震子波的反褶积结果进行对比(图 17、图 18)。与原始叠前道集相比(图 17a),应用本文方法提取的子波进行反褶积处理后,叠前弱反射信号得到了一定程度上的恢复,同相轴更连续,形态更加清晰,提高了分辨率(图 17b方框所示)。而使用EMD方法提取的单道子波进行反褶积处理后,有效信号能量未得到增强,部分同相轴能量消失或减弱,未能有效提高实际叠前道集的分辨率(图 17c方框所示)。与反褶积前叠加剖面(图 18a)相比,使用本文方法提取的空变子波进行反褶积处理后,剖面整体能量得到增强,同相轴更清晰、更连续,分辨率得到提高(图 18b方框所示),恢复了更多的细节信息(图 18b椭圆所示)。而使用EMD方法提取的单道子波进行反褶积后,虽在一定程度上增强了部分反射波能量(图 18c椭圆所示),但同时部分同相轴能量减弱,出现了末端断裂或缺失的现象(图 18c方框所示)。

|
图 17 实际叠前地震数据两种方法子波的反褶积处理结果对比(a)原始道集;(b)本文方法;(c)EMD方法 |
|
图 18 实际叠后地震数据两种方法反褶积处理结果对比(a)原始剖面;(b)本文方法;(c)EMD方法 |
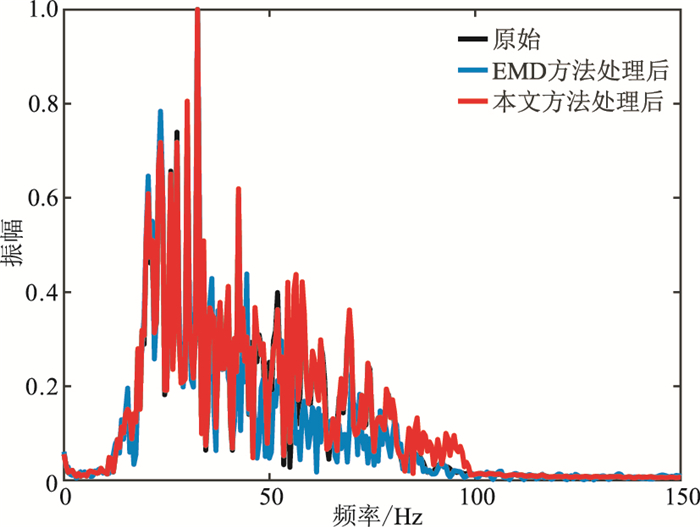
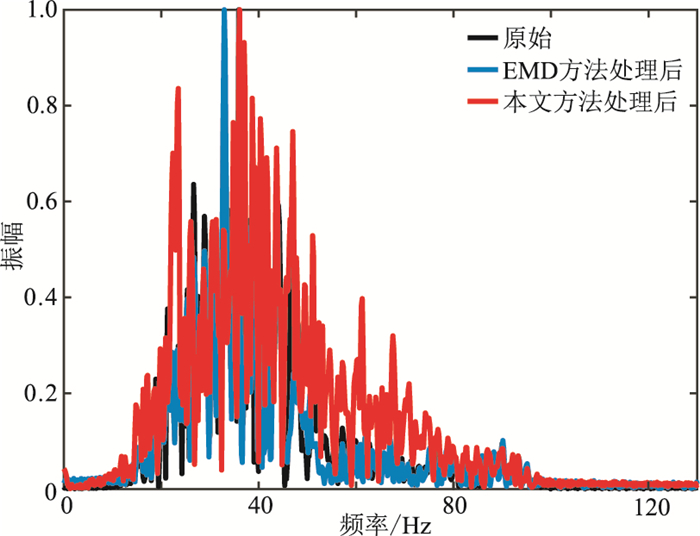
图 19、图 20分别为图 17和图 18数据的频谱对比。与叠前原始数据的频谱曲线相比,使用EMD方法提取的单道地震子波进行反褶积后,叠前道集中低频部分能量虽得到一定程度增强,但损失了部分中、高频段反射信号能量。使用本文方法提取的空变子波进行反褶积后的叠前数据频谱在较高程度保持了低频能量的同时,地震数据频带有效拓宽,高频能量增强效果较为突出。与叠后原始剖面的频谱曲线相比,经本文方法提取子波反褶积后,低中高频段反射信号能量均得到一定程度的增强,其中高低频段能量增强效果明显,峰值频率没有变化。而使用EMD方法提取的单道子波进行反褶积后,地震剖面能量增强效果较为有限,峰值频率反褶积后出现偏移(约38 Hz处),存有一定的提取误差,分辨率提升效果有限。
|
图 19 实际叠前地震道集反褶积处理前、后频谱对比 |
|
图 20 实际叠后地震剖面反褶积处理前、后频谱对比 |
应用峰度从定量的角度反映反褶积的有效性。峰度计算公式为
| $ V=\frac{1}{N}\sum\limits_{n=1}^{N}\frac{\sum\limits_{m=1}^{M}{x}^{4}\left(m\right)}{{\left[\sum\limits_{m=1}^{M}{x}^{2}\left(m\right)\right]}^{2}} $ | (8) |
式中:x为地震信号振幅;M为信号长度。
两种方法反褶积前、后的峰度统计结果如表 1所示。由表 1可见,无论是叠前地震数据还是叠后地震数据,两种方法反褶积后的峰度均有提高,但本文方法的效果更加明显,且该波正常子距叠后优于叠前,因为叠后数据的信噪比较高。
|
|
表 1 实际数据两种方法反褶积前、后的峰度统计 |
本文提出了一种应用自编码—解码架构的ConvGRU网络的空变子波提取方法。利用有限差分正演与非平稳褶积模型构建适用于中国西部实际工区的大规模训练数据集对网络模型进行训练,实现了地震数据的空变子波剖面提取。由理论分析、数值仿真实验验证、实际数据的处理结果,可以得到如下结论:
(1)本文构建的应用自编码—解码架构的ConvGRU网络模型能有效提取地震数据中有效信号的空间和时间方向特征,实现了空变子波的直接提取,突破了传统方法对于地震子波先验信息的依赖性;
(2)本文方法在不同随机噪声强度下均具备可行性,对衰减多变、主频不同的地震信号均可实现空变地震子波的准确提取,且方法具备一定普适性,与未经改进的深度学习方法和EMD子波提取方法相比,子波提取精度更高;
(3)应用本文的自编码—解码架构的ConvGRU网络能提取中国西部实际地震数据的炮记录或叠后剖面的空变子波,经反褶积后能提升弱信号能量,提高了分辨率,说明本文方法具备一定的实际应用价值。
本文方法对于数据尺寸仍有固定的要求,且需做噪声压制预处理。
| [1] |
戴永寿, 王晓波, 丁进杰, 等. 自适应分段的时变子波估计方法[J]. 石油地球物理勘探, 2015, 50(4): 607-612. DAI Yongshou, WANG Xiaobo, DING Jinjie, et al. Time-variant wavelet estimation based on adaptive segmentation[J]. Oil Geophysical Prospecting, 2015, 50(4): 607-612. |
| [2] |
王蓉蓉, 戴永寿, 李闯, 等. 时频分析和自适应分段相结合的时变子波提取方法[J]. 石油地球物理勘探, 2016, 51(5): 850-862. WANG Rongrong, DAI Yongshou, LI Chuang, et al. Time-varying wavelet extraction based on time-frequency analysis and adaptive segmentation[J]. Oil Geophysical Prospecting, 2016, 51(5): 850-862. |
| [3] |
张鹏, 戴永寿, 谭永成, 等. 利用EMD和子波振幅谱与相位谱关系的时变子波提取方法[J]. 地球物理学报, 2019, 62(2): 680-696. ZHANG Peng, DAI Yongshou, TAN Yongcheng, et al. A time-varying wavelet extraction method using EMD and the relationship between wavelet amplitude and phase spectra[J]. Chinese Journal of Geophysics, 2019, 62(2): 680-696. |
| [4] |
ZHANG P, DAI Y, ZHANG H, et al. Combining CEEMD and recursive least square for the extraction of time-varying seismic wavelets[J]. Journal of Applied Geophysics, 2019, 170(11): 103854. |
| [5] |
JIANG Y, CAO S, CHEN S, et al. Time-varying wavelet estimation and deconvolution for nonstationary data based on a FWE function[J]. Journal of Applied Geophysics, 2020, 183(1): 104198. |
| [6] |
JIANG Y, CAO S, CHEN S, et al. A data driven method for time-varying wavelet extraction based on the local frequency spectrum[J]. Studia Geophysica et Geodaetica, 2021, 65(1): 70-85. DOI:10.1007/s11200-020-1251-2 |
| [7] |
孙成禹. 空变子波提取方法研究[J]. 石油大学学报(自然科学版), 2000, 24(1): 77-80, 84. SUN Chenyu. Study on the extraction of spatial varied seismic wavelets[J]. Journal of the University of Petroleum, China(Edition of Natural Science), 2000, 24(1): 77-80, 84. |
| [8] |
高少武, 赵波, 贺振华, 等. 地震子波提取方法研究进展[J]. 地球物理学进展, 2009, 24(4): 1384-1391. GAO Shaowu, ZHAO Bo, HE Zhenhua, et al. Research progress of seismic wavelet extraction[J]. Progress in Geophysics, 2009, 24(4): 1384-1391. |
| [9] |
DAS V, POLLACK A, WOLLNER U, et al. Convolutional neural network for seismic impedance inversion[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2071-2075.
|
| [10] |
CHOI Y, JO Y, SEOL S J, et al. Deep learning spectral enhancement considering features of seismic field data[J]. Geophysics, 2021, 86(5). |
| [11] |
CHEN D, GAO J, HOU Y, et al. High resolution inversion of seismic wavelet and reflectivity using iterative deep neural networks[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2538-2542.
|
| [12] |
SIAHKOOHI A, LOUBOUTIN M, KUMAR R, et al. Deep convolutional neural networks in prestack seismic: two exploratory examples[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2196-2200.
|
| [13] |
林年添, 张栋, 张凯, 等. 地震油气储层的小样本卷积神经网络学习与预测[J]. 地球物理学报, 2018, 61(10): 4110-4125. LIN Niantian, ZHANG Dong, ZHANG Kai, et al. Predicting distribution of hydrocarbon reservoirs with seismic data based on learning of the small-sample convolution neural network[J]. Chinese Journal of Geophysics, 2018, 61(10): 4110-4125. |
| [14] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [15] |
王维波, 徐西龙, 盛立, 等. 卷积神经网络微地震事件检测[J]. 石油地球物理勘探, 2020, 55(5): 939-949. WANG Weibo, XU Xilong, Sheng Li, et al. Detection of microseismic events based on convolutional neural network[J]. Oil Geophysical Prespecting, 2020, 55(5): 939-949. |
| [16] |
吕尧, 单小彩, 霍守东, 等. 基于深度卷积神经网络的地震数据局部信噪比估计[J]. 地球物理学报, 2020, 63(1): 320-328. LYU Yiao, SHAN Xiaocai, HUO Shoudong, et al. Local SNR estimation of seismic data based on deep convolutional neural network[J]. Chinese Journal of Geophysics, 2020, 63(1): 320-328. |
| [17] |
吴学锋, 张会星. 基于循环一致性生成对抗网络的地震数据随机噪声压制方法[J]. 石油地球物理勘探, 2021, 56(5): 958-968. WU Xuefeng, ZHANG Huixing. Random noise suppression method of seismic data based on CycleGAN[J]. Oil Geophysical Prospecting, 2021, 56(5): 958-968. |
| [18] |
韩浩宇, 戴永寿, 宋建国, 等. 基于生成对抗网络的塔里木深层超深层叠前地震子波提取[J]. 地球物理学报, 2022, 65(2): 763-772. HAN Haoyu, DAI Yongshou, SONG Jianguo, et al. Deep prestack seismic wavelets extraction in Tarim based on generative adversarial network[J]. Chinese Journal of Geophysics, 2022, 65(2): 763-772. |
| [19] |
CAI Y, SHYU M L, TU Y, et al. Anomaly detection of earthquake precursor data using long short-term memory networks[J]. Applied Geophysics, 2019, 16(3): 257-266. |
| [20] |
CHO K, VAN MERRIËNBOER B, BAHDANAU D, et al. On the properties of neural machine translation: encoder-decoder approaches[C]. Proceedings of SSST-8 Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, 2014, 103-111.
|
| [21] |
DAHL G E, YU D, DENG L, et al. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition[J]. IEEE Transactions on Audio, Speech and Language Processing, 2012, 20(1): 30-42. |
| [22] |
VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denosing autoencoders: Learning useful representations in a deep network with a local denoising criterion[J]. The Journal of Machine Learning Research, 2010, 11(6): 3371-3408. |
| [23] |
宋辉, 高洋, 陈伟, 等. 基于卷积降噪自编码器的地震数据去噪[J]. 石油地球物理勘探, 2020, 55(6): 1210-1219. SONG Hui, GAO Yang, CHEN Wei, et al. Seismic noise suppression based on convolutional denoising autoencoders[J]. Oil Geophysical Prospecting, 2020, 55(6): 1210-1219. |
| [24] |
SUTSKEVER I, VINYALS O, LE Q V. Sequence to sequence learning with neural networks[C]. Proceedings of the 27th International Conference on Neural Information Processing Systems, 2014, 3104-3112.
|
| [25] |
SHI X, CHEN Z, WANG H, et al. Convolutional LSTM network: A machine learning approach for precipitation nowcasting[C]. Proceedings of the 28th International Conference on Neural Information Processing Systems, 2015, 802-810.
|
| [26] |
BALLAS N, LI Y, PAL, et al. Delving deeper into convolutional networks for learning video representations[C]. International Conference on Learning Representations 2016, 2016, 1-11.
|
| [27] |
MARGRAVE G F. Theory of nonstationary linear filtering in the Fourier domain with application to time-variant filtering[J]. Geophysics, 1998, 63(1): 244-259. |



 李泓浩, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)海洋与空间信息学院, 266580。Email:
李泓浩, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)海洋与空间信息学院, 266580。Email: 