2. 江西省防震减灾与工程地质灾害探测工程研究中心, 江西南昌 330013;
3. 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 湖南长沙 410083
2. Engineering Research Center for Seismic Disaster Prevention and Engineering Geological Disaster Detection of Jiangxi Province, Nanchang, Jiangxi 330013, China;
3. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring (Central South University), Ministry of Education, Changsha, Hunan 410083, China
广域电磁法是由何继善院士及其团队潜心研究多年提出的一种频率域有源电磁方法[1-4]。相比可控源音频大地电磁法(CSAMT),广域电磁法仅需单分量电磁场即可定义视参数,而无需正交电场和磁场,野外工作效率较高[5-8]。另外,由于CSAMT沿用了卡尼亚视电阻率计算公式,需要利用正交电场和磁场计算阻抗,导致过渡区和近区的数据不满足平面波的假设,因而这部分数据不能参与资料解译工作,这在一定程度上影响了CSAMT勘探效果。相反,广域电磁法摒弃了远区的限制,扩展了频率域可控场源观测区范围,具有勘探深度大、观测范围广、工作效率高等优点,对地下地质结构的探测效果明显。近年来,广域电磁法已经在油气、页岩气等矿产资源、地下水资源以及环境工程等领域得到了广泛应用,取得了较好的应用效果[1, 9-10]。
现阶段广域电磁法资料解译工作主要集中在一维、二维[6, 11],迫切需要开展三维广域电磁法资料解译技术研究。三维正演模拟是资料解译的重要环节,同时又是认识复杂地质结构响应特征的必要途径。因此,研究高效率、高精度的三维广域电磁法正演方法成为目前研究的热点。
三维数值模拟方法主要包含积分方程法[12-16]、有限差分法[17-19]、有限体积法[20-22]、谱元法[23-24]以及有限单元法[25-29]。每一种数值模拟方法都具有不同的应用特点,如:积分方程(IE)法是一种纯二次场算法,只需要对异常体进行剖分,具有较高的计算精度,但该方法形成的系统矩阵是密实矩阵,求解效率低,需要开展相应的加速算法(快速FFT)[14, 30];有限差分法数值模拟方法理论简单,网格拓扑关系简洁[17],但刻画复杂地形及模型较困难;有限单元法[31-32]是目前应用最广的数值模拟方法之一,随着非结构网格离散技术的发展,对起伏地形和复杂地质结构模型的剖分更加精细[33]。随着自适应技术的发展,基于后验误差估计策略的自适应有限元技术得到飞速发展[34-35]。自适应加密技术主要采用两类策略:一类基于全局误差估计的自适应加密策略;另一类是面向目标的自适应加密策略。前者主要关注整体数值误差;后者重点考虑的则是观测点的数值误差,对非重点区域不做过多的考虑,避免了不必要的网格离散。当前,自适应有限元正演技术已在频率域电磁法数值模拟中得到较广泛的应用[36-38]。但是,关于广域电磁法的自适应正演算法鲜有报道。此外,基于有限体积法的电磁法数值模拟近年来得到了更多关注,尤其是与非结构网格相结合的应用发展较快。谱元法是有限元和谱方法相结合而发展起来的一种数值模拟方法,兼顾了谱方法的高精度和有限元的灵活性[23-24],近年来在电磁法数值模拟方面得到了广泛关注。目前,该方法网格离散大多采用结构化网格,而关于非结构化的谱方法数值模拟技术报道较少[39-40]。
综上所述,为了更好地模拟复杂地电模型及提高广域电磁法正演精度,本文采用自适应有限元技术并结合非结构四面体单元实现三维广域电磁法的高精度、高效率正演计算。首先,从广域电磁法满足的微分方程出发,推导出三维广域电磁法满足的电场方程,并采用矢量有限元对电场方程进行离散,形成线性方程组;其次,开展以电流密度法向连续后验误差估计策略为依据的自适应有限元算法进行高精度电磁场分量计算,并采用一种稳健的Brent-Dekker算法计算广域视电阻率;最后,设计地电模型验证自适应算法的正确性,并对广域视电阻率响应特征进行分析。
1 方法理论 1.1 广域电磁法边值问题假定负谐时间因子为
| $ \nabla \times \mathit{E}=\mathrm{i}\omega \mu \mathit{H} $ | (1) |
| $ \nabla \times \mathit{H}=\left(\sigma -\mathrm{i}\omega \epsilon \right)\mathit{E}+{\mathit{J}}_{\mathrm{s}} $ | (2) |
| $ \nabla \cdot \mu \mathit{H}=0 $ | (3) |
| $ \nabla \cdot \left[\left(\sigma -\mathrm{i}\omega \epsilon \right)\mathit{E}\right]=-\nabla \cdot {\mathit{J}}_{\mathrm{s}} $ | (4) |
式中:
| $ \nabla \times \frac{1}{\mu }\nabla \times \mathit{E}-\mathrm{i}\omega \left(\sigma -\mathrm{i}\omega \epsilon \right)\mathit{E}=\mathrm{i}\omega {\mathit{J}}_{\mathrm{s}} $ | (5) |
以式(5)为控制方程,利用Galerkin有限元推导有限元方程。设余量
| $ \mathit{r}=\nabla \times \frac{1}{\mu }\nabla \times \mathit{E}-\mathrm{i}\omega \left(\sigma -\mathrm{i}\omega \epsilon \right)\mathit{E}-\mathrm{i}\omega {\mathit{J}}_{\mathrm{s}} $ | (6) |
令
| $ {\int }_{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} }_{\mathrm{e}}}{N}^{\mathrm{e}}\cdot r\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} =0 $ | (7) |
式中
| $ \begin{array}{l}{\int }_{{\mathit{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} }}_{e}}\frac{1}{\mu }\nabla \times {\mathit{N}}^{e}\cdot \nabla \times \mathit{E}\mathrm{d}\mathit{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} }-{\int }_{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} }_{\mathrm{e}}}{N}^{\mathrm{e}}\cdot \mathrm{i}\omega \left(\sigma -\mathrm{i}\omega \epsilon \right)E\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \\ ={\int }_{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} }_{\mathrm{e}}}{N}^{\mathrm{e}}\cdot \mathrm{i}\omega {J}_{\mathrm{s}}\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \end{array} $ | (8) |
采用非结构四面体单元离散整个求解区域,引入矢量基函数
| $ \mathit{E}\left(\mathit{r}\right)=\sum _\limits{j=1}^\limits{6}\left[{\mathit{N}}_{j}^{\mathrm{e}}\left(\mathit{r}\right)\cdot {E}_{j}^{\mathrm{e}}\right] $ | (9) |
式中:
| $ \begin{aligned} & \sum\limits_{j=1}^6\left[\int_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\mathrm{e}}} \frac{1}{\mu} \nabla \times \boldsymbol{N}_i^{\mathrm{e}} \cdot \nabla \times \boldsymbol{N}_j^{\mathrm{e}} \mathrm{d} \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}-\right. \\ & \left.\int_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\mathrm{e}}} \boldsymbol{N}_i^{\mathrm{e}} \cdot \mathrm{i} \omega(\sigma-\mathrm{i} \omega \varepsilon) \boldsymbol{N}_j^{\mathrm{e}} \mathrm{d} \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\right] E_j^{\mathrm{e}} \\ = & \int_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\mathrm{e}}} \boldsymbol{N}_i^{\mathrm{e}} \cdot \mathrm{i} \omega \boldsymbol{J}_{\mathrm{s}} \mathrm{d} \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \end{aligned} $ | (10) |
式中
| $ \mathit{K}\mathit{E}=\mathit{S} $ | (11) |
式中:
| $ {\mathit{J}}_{\mathrm{s}}=\mathit{I}\delta (x-{x}_{0})\delta (y-{y}_{0})\delta (z-{z}_{0}) $ | (12) |
式中:
为保证有限元数值解的精度,需人为对网格单元进行优化,这一过程耗时且费力。近年来,基于后验误差估计的自适应有限元技术逐步应用于地球物理数值模拟,提高了正演计算的精度。为了实现三维多场源广域电磁法自适应正演模拟,需要构建三维广域电磁法问题对应的对偶问题
| $ \begin{array}{l}\nabla \times \frac{1}{\mathrm{i}\omega \mu }\nabla \times \mathit{W}-\left(\sigma -\mathrm{i}\omega \epsilon \right)\mathit{W}\\ =\sum _\limits{k=0}^\limits{T}\kappa \frac{{\boldsymbol{{ I}}}_{0}}{{V}_{k}}\end{array} $ | (13) |
式中:T表示测点所涉及四面体单元个数;
| $ \mathit{K}\mathit{W}={\mathit{S}}_{1} $ | (14) |
式中
后验误差分析是自适应网格加密的核心引擎[33-35]。为此,本文采用以电流密度法向连续为后验估计的网格自适应细化方案[33, 36-37],单元的后验误差e可根据下式求得
| $ {e}^{2}=\sum _\limits{i=1}^\limits{4}{‖\boldsymbol{n}\cdot \left({\mathit{J}}_{1}-{\mathit{J}}_{2}\right)‖}_{2, \partial {\mathrm{\Delta }}_{i}} $ | (15) |
式中:
| $ {w}^{2}=\sum _\limits{i=1}^\limits{4}{‖\mathit{n}\cdot \left({\sigma }_{1}{\boldsymbol{W}}_{1}-{\sigma }_{2}{\boldsymbol{W}}_{2}\right)‖}_{{L}^{2}, \partial {\mathrm{\Delta }}_{i}} $ | (16) |
式中:
| $ \beta =ew $ | (17) |
通过上述过程可以标记每个单元的加权误差,然后按照一定比例对四面体进行细化处理,从而得到新的网格单元;然后,重复上述过程,直到有限元解的精度满足要求或达到最大网格细化迭代次数为止;最后,通过得到的电场或磁场分量计算广域视电阻率。需要指出,可控源电磁法在场源位置不满足电流密度法向连续的条件,因而包含场源的单位误差会很大。为此,本文利用局部加密技术细化场源,在计算单元误差时将源所在单元剔除,以降低源的影响,保证细化过程朝预设目标进行。
1.3 广域视电阻率的计算广域电磁法的特点是采用电磁场单分量进行计算,利用均匀半空间条件下电磁场分量关于电阻率的非线性方程定义广域电磁视电阻率,克服了卡尼亚电阻率定义中对远区的要求,拓展了人工场源的观测范围,简化了野外观测装备,可显著提高工作效率。为了阐述广域视电阻率的优势,以x方向布设的电偶源为例,均匀半空间的视电阻率为
| $ {\rho }_{\mathrm{a}}^{E-{E}_{x}}={K}_{E-{E}_{x}}\frac{\mathrm{\Delta }{U}_{\mathrm{M}\mathrm{N}}}{I}\frac{1}{{F}_{E-{E}_{x}}\left(\mathrm{i}kr\right)} $ | (18) |
式中:r表示收发距;k表示波数;I表示电流强度;
假设一个电阻率为
首先,假设在区间
然后,对每一步迭代进行逆二次插值
| $ \begin{array}{l}{s}_{k}=\frac{f\left({a}_{k-1}\right)f\left({b}_{k-1}\right)}{\left[f\left({b}_{k-2}\right)-f\left({a}_{k-1}\right)\right]\left[f\left({b}_{k-2}\right)-f\left({b}_{k-1}\right)\right]}{b}_{k-2}+\\ \ \ \ \ \ \ \ \ \ \ \frac{f\left({b}_{k-2}\right)f\left({b}_{k-1}\right)}{\left[f\left({a}_{k-1}\right)-f\left({b}_{k-2}\right)\right]\left[f\left({a}_{k-1}\right)-f\left({b}_{k-1}\right)\right]}{a}_{k-1}+\\ \ \ \ \ \ \ \ \ \ \ \frac{f\left({b}_{k-2}\right)f\left({a}_{k-1}\right)}{\left[f\left({b}_{k-1}\right)-f\left({b}_{k-1}\right)\right]\left[f\left({b}_{k-1}\right)-f\left({a}_{k-1}\right)\right]}{b}_{k-1}\end{array} $ | (19) |
如果
| $ {s}_{k}={b}_{k-1}-\frac{{b}_{k-1}-{b}_{k-2}}{f\left({b}_{k-1}\right)-f\left({b}_{k-2}\right)}f\left({b}_{k-1}\right) $ | (20) |
式中
|
|
表 1 均匀半空间模型不同算法广域视电阻率计算结果 |
从表 1可知,Brent-Dekker算法相较于直接迭代法,在全区迭代次数相对稳定、相同精度条件下,在过渡带(8 Hz)和近区(1 Hz)的迭代次数明显少于二分法。因此,为稳定求解三维模型视电阻率,本文采用Brent-Dekker算法。
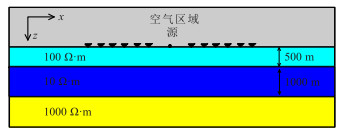
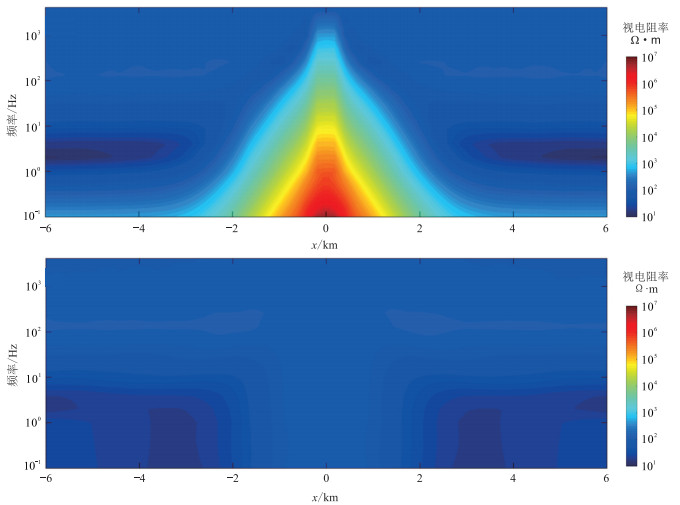
2 算例分析 2.1 层状模型为了验证算法的正确性,设计图 1所示的三层层状介质模型。场源沿x方向布设,长度为10 m,中心坐标为(0,0,0),发射电流为1 A,设置14个发射频率,范围为0.1~4096 Hz。沿x轴-6000~6000 m范围布设了一条观测剖面,测点间距为200 m。求解区域为[-40 km,40 km]3。该模型的卡尼亚视电阻率和广域视电阻率剖面见图 2,0.1 Hz和8 Hz所对应的视电阻率和相对误差error曲线见图 3和图 4。
|
图 1 层状模型示意图 |
|
图 2 层状模型卡尼亚视电阻率(上)和广域视电阻率(下)剖面 |
|
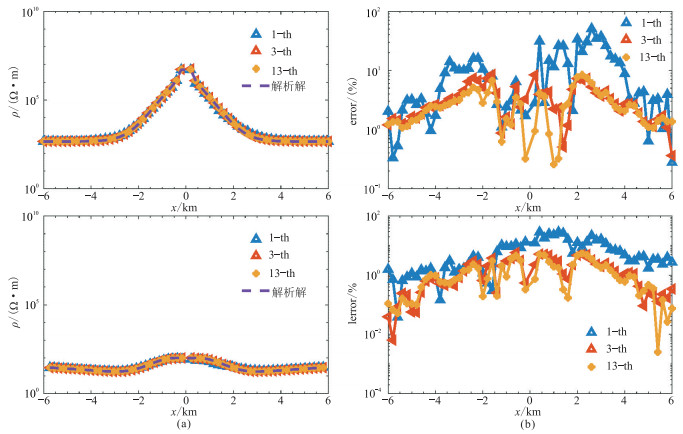
图 3 层状模型0.1 Hz时1-th、3-th以及13-th网格下的卡尼亚(上)和广域电磁(下)视电阻率(a)和相对误差(b)曲线 |
|
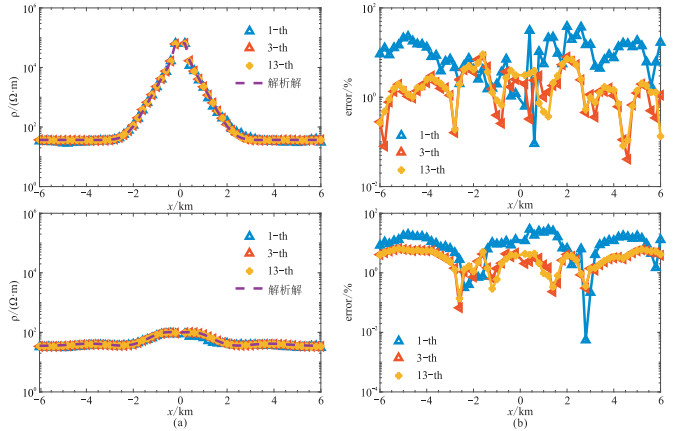
图 4 层状模型8 Hz时1-th、3-th以及13-th网格下的卡尼亚(上)和广域电磁(下)视电阻率(a)和相对误差(b)曲线 |
图 3和图 4分别展示了不同层次(1‑th,3‑th,13‑th)网格下得到的卡尼亚和广域电磁视电阻率曲线及误差分布。由图可见,随着网格密度的增加,计算精度明显提升,相对误差在4%以内。13‑th网格条件下得到视电阻率与解析解吻合最好,误差相对较小。还可以看出,卡尼亚视电阻率相对广域电磁视电阻率受非平面波的影响更大。图 5为以电流密度法向连续的自适应有限技术细化三种层次网格(1‑th、3‑th、13‑th)后的加权误差β,可见随着网格密度增加,误差整体出现降低趋势,符合预期。
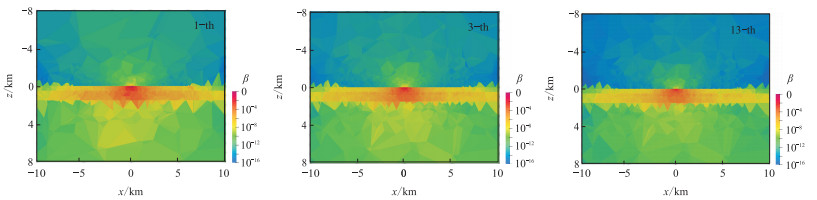
|
图 5 层状模型不同网格剖分下的加权误差β 左:1‑th网格;中:3‑th加密网格;右:13‑th加密网格 |
为了分析广域视电阻率受地形影响的特征,设计图 6所示的梯形山模型。地下半空间的电阻率为100
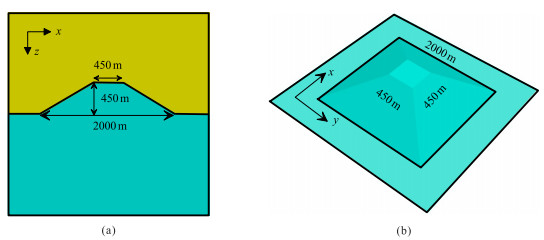
|
图 6 梯形山地形模型示意图 (a)x-z剖面;(b)x-y剖面 |
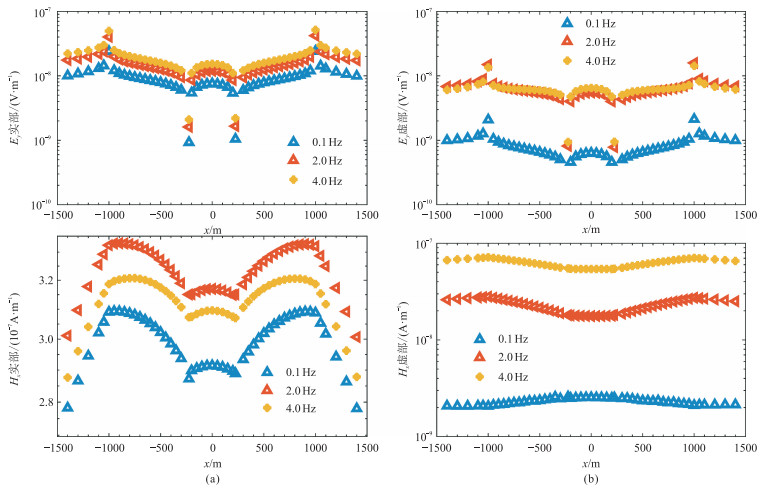
|
图 7 梯形山地形模型电场分量Ey(上)和磁场分量Hx(下)的实部(a)和虚部(b)曲线 |
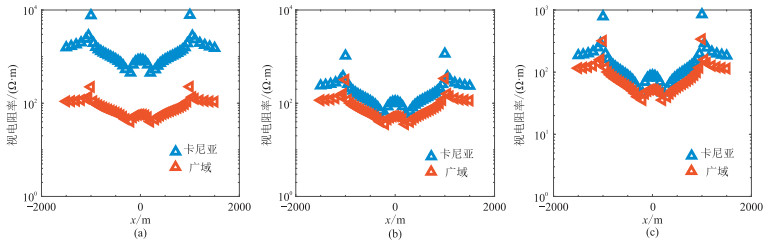
|
图 8 梯形山地形模型卡尼亚和广域视电阻率曲线 (a)0.1 Hz;(b)2.0 Hz; (c)4.0 Hz |
图 7为不同频率下电场分量
图 8是不同频率卡尼亚视电阻率和广域视电阻率曲线,可见随着频率增高,卡尼亚视电阻率曲线出现抬升特征,数据进入了近区,无法真实客观地反映地下介质电阻率信息。然而,整个频率段的广域视电阻率值受场源影响较小,一定程度上能够避免卡尼亚视电阻率因场源影响而被抬升的情况。频率为0.1 Hz时此现象最明显,几乎在每一个观测点上这两种视电阻率的差值均达到一个数量级。与卡尼亚视电阻率曲线相比,广域视电阻率值更接近真实情况,说明了后者具有更大勘探深度,具备近区勘探能力。
2.3 球状异常体模型设计图 9所示的球状异常体模型。计算区域为
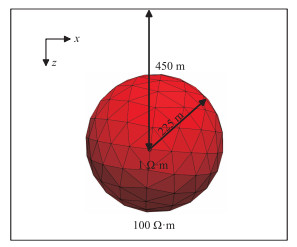
|
图 9 球状异常体模型示意图 |
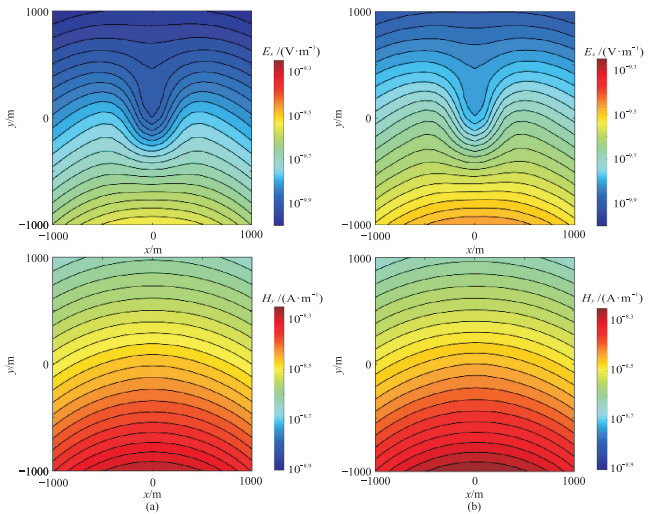
|
图 10 球状异常体模型1 Hz(a)和2 Hz(b)电场Ex(上)和磁场HY(下)分布 |
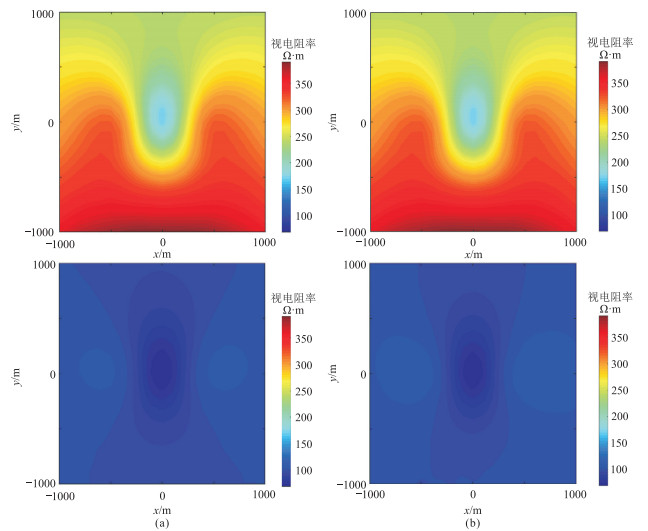
|
图 11 球状异常体模型1 Hz(a)和2 Hz(b)卡尼亚视电阻率(上)和广域视电阻率(下)分布 |

|
图 12 球状异常体模型8 Hz(a)和16 Hz(b)电场分量Ex(上)和磁场分量Hy(下)分布 |
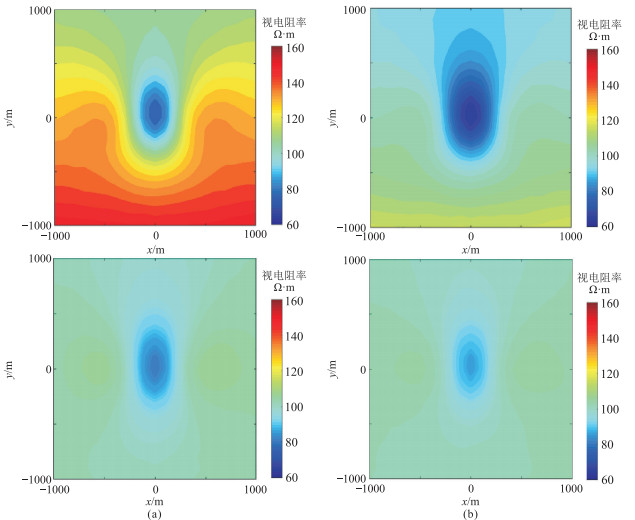
|
图 13 球状异常体模型8 Hz(a)和16 Hz(b)卡尼亚视电阻率(上)和广域视电阻率(下)分布 |
由图 10和图 11可见,越靠近场源,电磁场越强,符合物理规律。磁场对地下异常体的敏感度弱于电场,因而电场
图 12展示了球状异常体模型在8、16 Hz时的电场分量
总之,在同等收发距的前提下,广域电磁法摒弃了“远区”的限制,不受非平面波的影响,与CSAMT相比具有更大的勘探范围和深度,得到视电阻率能够较真实地反映地下介质的电性分布,适用性更强,准确度更高。
3 结论本文采用基于电流密度法向连续为后验策略的自适应有限元算法,实现了三维广域电磁法正演计算。通过模型测试得出以下几点认识:
(1)针对广域视电阻率的计算,采用了一种稳健的Brent-Dekker求根算法,该算法结合二分法、割线法等算法的优势,使求根过程更稳健,迭代次数相对适中,确保了计算结果的正确性。
(2)将电流密度法向连续的后验误差估计策略的自适应有限元算法引入三维广域电磁法正演模拟,提高了广域视电阻率的计算精度。通过与解析解对比,验证了算法的正确性。该算法测试发现,场源附近单元受场源影响较大,会造成场源附近单元的过度细化,影响了场源积分的求解效率。
(3)对球状异常体和梯形山地形等典型模型进行正演计算,分析了广域电磁法的探测深度与范围。在同等情况下,CSAMT因受到非平面波的影响,视电阻率曲线发生抬升现象,不能很好地反映真实的地下介质信息,而广域视电阻率摒弃了近区的限制,得到的视电阻率更真实可靠,拓展了有源电磁法的观测范围,同时增加了勘探深度。模型计算结果表明,地形对广域电磁法和CSAMT都有影响,尤其在地形拐点,畸变尤为明显。因此,在进行资料解释时需要考虑地形的影响,尽量降低地形影响带来的解释误差。
| [1] |
何继善, 李帝铨, 戴世坤. 广域电磁法在湘西北页岩气探测中的应用[J]. 石油地球物理勘探, 2014, 49(5): 1006-1012. HE Jishan, LI Diquan, DAI Shikun. Shale gas detection with wide field electromagnetic method in North western Hunan[J]. Oil Geophysical Prospecting, 2014, 49(5): 1006-1012. DOI:10.13810/j.cnki.issn.1000-7210.2014.05.052 |
| [2] |
何继善, 薛国强. 短偏移距电磁探测技术概述[J]. 地球物理学报, 2018, 61(1): 1-8. HE Jishan, XUE Guoqiang. Review of the key techniques on short-offset electromagnetic detection[J]. Chinese Journal of Geophysics, 2018, 61(1): 1-8. DOI:10.3969/j.issn.1672-7940.2018.01.001 |
| [3] |
HE J. Combined application of wide-field electromagnetic method and flow field fitting method for highresolution exploration: a case study of the Anjialing No. 1 Coal Mine[J]. Engineering, 2018, 4(5): 667-675. DOI:10.1016/j.eng.2018.09.006 |
| [4] |
何继善. 大深度高精度广域电磁勘探理论与技术[J]. 中国有色金属学报, 2019, 29(9): 1809-1816. HE Jishan. Theory and technology of wide field electromagnetic method[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(9): 1809-1816. DOI:10.19476/j.ysxb.1004.0609.2019.09.02 |
| [5] |
周印明, 王金海, 胡晓颖, 等. 基于矢量位和标量位的广域电磁法三维有限元数值模拟[J]. 石油地球物理勘探, 2021, 56(1): 181-189. ZHOU Yinming, WANG Jinhai, HU Xiaoying, et al. WFEM 3D finite element numerical simulation based on vector potential and scalar potential[J]. Oil Geophysical Prospecting, 2021, 56(1): 181-189. DOI:10.13810/j.cnki.issn.1000-7210.2021.01.021 |
| [6] |
柳建新, 佟铁钢, 刘春明, 等. E-E φ 广域视电阻率定义的改进方法及场特性识别[J]. 中国有色金属学报, 2013, 23(9): 2359-2364. LIU Jianxin, TONG Tiegang, LIU Chunming, et al. Recognition of electromagnetic field asymptotic properties and improved definition of wide field apparent resistivity on E-Eφ array[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2359-2364. |
| [7] |
张志勇. 基于正反演统一程序框架的广域电磁正反演研究[D]. 湖南长沙: 中南大学, 2015. ZHANG Zhiyong. Numerical Simulation and Inversion for Wide Field Electromagnetic Method Based on the Code Frame Work of Geophysics Modeling and Inversion[D]. Central South University, Changsha, Hunan, 2015. |
| [8] |
李帝铨. E-Ex和E-Eφ 广域电磁法测量范围[J]. 石油地球物理勘探, 2017, 52(6): 1315-1323. LI Diquan. Measurement range of E-Ex and E-Eφ wide field electromagnetic methods[J]. Oil Geophysical Prospecting, 2017, 52(6): 1315-1323. |
| [9] |
张乔勋, 李帝铨, 田茂军. 广域电磁法在赣南某盆地油气勘探中的应用[J]. 石油地球物理勘探, 2017, 52(5): 1085-1092. ZHANG Qiaoxun, LI Diquan, TIAN Maojun. Application of wide field electromagnetic method to the hydrocarbon exploration in a basin of South Jiangxi[J]. Oil Geophysical Prospecting, 2017, 52(5): 1085-1092. DOI:10.13810/j.cnki.issn.1000-7210.2017.05.023 |
| [10] |
陈后扬, 李帝铨, 凌帆, 等. 朱溪钨铜矿的广域电磁法深部探测[J]. 中国有色金属学报, 2022, 32(10): 3227-3243. CHEN Houyang, LI Diquan, LING Fan, et al. Deep exploration of wide field electromagnetic method in Zhuxi W-Cu deposit[J]. The Chinese Journal of Nonferrous Metals, 2022, 32(10): 3227-3243. |
| [11] |
周峰, 张志勇, 汤井田, 等. 频率域2.5维广域电磁法正反演研究[J]. 中南大学学报(自然科学版), 2021, 52(9): 3273-3283. ZHOU Feng, ZHANG Zhiyong, TANG Jingtian, et al. 2.5-dimension forward and inversion of WFEM in frequency domain[J]. Journal of Central South University (Science and Technology), 2021, 52(9): 3273-3283. |
| [12] |
汤井田, 周峰, 任政勇, 等. 复杂地下异常体的可控源电磁法积分方程正演[J]. 地球物理学报, 2018, 61(4): 1549-1562. TANG Jingtian, ZHOU Feng, REN Zhengyong, et al. Three-dimensional forward modeling of the controlled-source electromagnetic problem based on the integral equation method with an unstructured grid[J]. Chinese Journal of Geophysics, 2018, 61(4): 1549-1562. |
| [13] |
HOHMANN G W. Three-dimensional induced polarization and electromagnetic modeling[J]. Geophysics, 1975, 40(2): 309-324. DOI:10.1190/1.1440527 |
| [14] |
ZHDANOV M S, DMITRIEV V I, FANG S, et al. Quasi-analytical approximations and series in electromagnetic modeling[J]. Geophysics, 2000, 65(6): 1746-1757. DOI:10.1190/1.1444859 |
| [15] |
王若, 底青云, 王妙月, 等. 用积分方程法研究源与勘探区之间的三维体对CSAMT观测曲线的影响[J]. 地球物理学报, 2009, 52(6): 1573-1582. WANG Ruo, DI Qingyun, WANG Miaoyue, et al. Research on the effect of 3D body between transmitter and receivers on CSAMT response using integral equation method[J]. Chinese Journal of Geophysics, 2009, 52(6): 1573-1582. DOI:10.3969/j.issn.0001-5733.2009.06.019 |
| [16] |
陈桂波, 汪宏年, 姚敬金, 等. 利用积分方程法的各向异性地层频率测深三维模拟[J]. 计算物理, 2010, 27(2): 274-280. CHEN Guibo, WANG Hongnian, YAO Jingjin, et al. Three-dimensional modeling of frequency sounding in layered anisotropic earth using integral equation method[J]. Chinese Journal of Computational Physics, 2010, 27(2): 274-280. |
| [17] |
谭捍东, 余钦范, BOOKER J, 等. 大地电磁法三维交错采样有限差分数值模拟[J]. 地球物理学报, 2003, 46(5): 705-711. TAN Handong, YU Qinfan, BOOKER J, et al. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 2003, 46(5): 705-711. DOI:10.3321/j.issn:0001-5733.2003.05.019 |
| [18] |
陈辉, 殷长春, 邓居智. 基于Lorenz规范条件下磁矢势和标势耦合方程的频率域电磁法三维正演[J]. 地球物理学报, 2016, 59(8): 3087-3097. CHEN Hui, YIN Changchun, DENG Juzhi. A finitevolume solution to 3D frequency-domain electromagnetic modelling using Lorenz-gauged magnetic vector and scalar potentials[J]. Chinese Journal of Geophysics, 2016, 59(8): 3087-3097. |
| [19] |
WEISS C J. Project APhiD: A Lorenz-gauged A-Φ decomposition for parallelized computation of ultrabroadband electromagnetic induction in a fully heterogeneous Earth[J]. Computers & Geosciences, 2013, 58: 40-52. |
| [20] |
杨波, 徐义贤, 何展翔, 等. 考虑海底地形的三维频率域可控源电磁响应有限体积法模拟[J]. 地球物理学报, 2012, 55(4): 1390-1399. YANG Bo, XU Yixian, HE Zhanxiang, et al. 3D frequency-domain modeling of marine controlled source electromagnetic responses with topography using finite volume method[J]. Chinese Journal of Geophysics, 2012, 55(4): 1390-1399. |
| [21] |
彭荣华, 胡祥云, 李建慧, 等. 基于二次耦合势的广域电磁法有限体积三维正演计算[J]. 地球物理学报, 2018, 61(10): 4160-4170. PENG Ronghua, HU Xiangyun, LI Jianhui, et al. 3D finite-volume forward modeling of wide-field EM using scattered potentials[J]. Chinese Journal of Geophysics, 2018, 61(10): 4160-4170. DOI:10.6038/cjg2018L0363 |
| [22] |
JAHANDARI H, FARQUHARSON C G. Finite-volume modelling of geophysical electromagnetic data on unstructured grids using potentials[J]. Geophysical Journal International, 2015, 202(3): 1859-1876. |
| [23] |
徐锦通, 汤井田. 基于谱元法的广域电磁法三维正演模拟[J]. 地球物理学报, 2022, 65(4): 1461-1471. XU Jintong, TANG Jingtian. Spectral element method for 3D wide field electromagnetic method forward modeling[J]. Chinese Journal of Geophysics, 2022, 65(4): 1461-1471. |
| [24] |
刘玲, 殷长春, 刘云鹤, 等. 基于谱元法的频率域三维海洋可控源电磁正演模拟[J]. 地球物理学报, 2018, 61(2): 756-766. LIU Ling, YIN Changchun, LIU Yunhe, et al. Spectral element method for 3D frequency-domain marine controlled-source electromagnetic forward modeling[J]. Chinese Journal of Geophysics, 2018, 61(2): 756-766. |
| [25] |
BADEA E A, EVERETT M E, NEWMAN G A, et al. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials[J]. Geophysics, 2001, 66(3): 786-799. |
| [26] |
ANSARI S, FARQUHARSON C G. 3D finite-element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids[J]. Geophysics, 2014, 79(4): E149-E165. |
| [27] |
REN Z, KALSCHEUER T, GREENHALGH S, et al. A finite-element-based domain-decomposition approach for plane wave 3D electromagnetic modeling[J]. Geophysics, 2014, 79(6): E255-E268. |
| [28] |
杨军, 刘颖, 吴小平. 海洋可控源电磁三维非结构矢量有限元数值模拟[J]. 地球物理学报, 2015, 58(8): 2827-2838. YANG Jun, LIU Ying, WU Xiaoping. 3D simulation of marine CSEM using vector finite element method on unstructured grids[J]. Chinese Journal of Geophysics, 2015, 58(8): 2827-2838. |
| [29] |
周峰, 张志勇, 陈煌, 等. 基于非结构网格的三种CSEM有限元三维正演系统分析[J]. 石油地球物理勘探, 2021, 56(5): 1190-1202. ZHOU Feng, ZHANG Zhiyong, CHEN Huang, et al. Analysis of 3D finite-element forward modeling of CSEM data using three different formulas and unstructured grids[J]. Oil Geophysical Prospecting, 2021, 56(5): 1190-1202. |
| [30] |
XIONG X. Symmetry properties of the scattering matrix in 3-D electromagnetic modeling using the integral equation method[J]. Geophysics, 1992, 57(9): 1199-1202. |
| [31] |
PUZYREV V, KOLDAN J, DE LA PUENTE J, et al. A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling[J]. Geophysical Journal International, 2013, 193(2): 678-693. |
| [32] |
汤井田, 任政勇, 周聪, 等. 浅部频率域电磁勘探方法综述[J]. 地球物理学报, 2015, 58(8): 2681-2705. TANG Jingtian, REN Zhengyong, ZHOU Cong, et al. Frequency-domain electromagnetic methods for exploration of the shallow subsurface: A review[J]. Chinese Journal of Geophysics, 2015, 58(8): 2681-2705. |
| [33] |
RULFF P, BUNTIN L M, KALSCHEUER T. Efficient goal-oriented mesh refinement in 3-D finite-element modelling adapted for controlled source electromagnetic surveys[J]. Geophysical Journal International, 2021, 227(3): 1624-1645. |
| [34] |
LI Y, CONSTABLE S. 2D marine controlled-source electromagnetic modeling: Part 2-the effect of bathymetry[J]. Geophysics, 2007, 72(2): WA63-WA71. |
| [35] |
LI Y, KEY K. 2D marine controlled-source electromagnetic modeling: Part 1-an adaptive finite-element algorithm[J]. Geophysics, 2007, 72(2): WA51-WA62. |
| [36] |
REN Z, KALSCHEUER T, GREENHALGH S, et al. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling[J]. Geophysical Journal International, 2013, 194(2): 700-718. |
| [37] |
殷长春, 张博, 刘云鹤, 等. 面向目标自适应三维大地电磁正演模拟[J]. 地球物理学报, 2017, 60(1): 327-336. YIN Changchun, ZHANG Bo, LIU Yunhe, et al. A goal-oriented adaptive algorithm for 3D magnetotelluric forward modeling[J]. Chinese Journal of Geophysics, 2017, 60(1): 327-336. |
| [38] |
赵宁, 王绪本, 余刚, 等. 面向目标自适应海洋可控源电磁三维矢量有限元正演[J]. 地球物理学报, 2019, 62(2): 779-788. ZHAO Ning, WANG Xuben, YU Gang, et al. 3D MCSEM parallel goal-oriented adaptive vector finite element modeling[J]. Chinese Journal of Geophysics, 2019, 62(2): 779-788. |
| [39] |
LU X, FARQUHARSON C G. 3D finite-volume time-domain modeling of geophysical electromagnetic data on unstructured grids using potentials[J]. Geophysics, 2020, 85(6): E221-E240. |
| [40] |
LU X, FARQUHARSON C G, MIEHÉ J M, et al. 3D electromagnetic modeling of graphitic faults in the Athabasca Basin using a finite-volume time-domain approach with unstructured grids[J]. Geophysics, 2021, 86(6): B349-B367. |
| [41] |
NEDELEC J C. Mixed finite element in 3D in H(div) and H(curl)[C]. Equadiff 6, 1986, 321-325.
|
| [42] |
BRENT R P. Algorithms for Minimization Without Derivatives[M]. Courier Corporation, Mineola, 2013.
|
| [43] |
邓敬亚, 张小苗, 尹应增, 等. 一种快速综合基站天线赋形方向图的迭代方法[J]. 西安电子科技大学学报, 2011, 38(5): 142-146. DENG Jingya, ZHANG Xiaomiao, YIN Yingzeng, et al. Fast iterative method for the synthesis of the base-station antenna's shaped beam[J]. Journal of Xidian University, 2011, 38(5): 142-146. |
| [44] |
汤井田, 何继善. 可控源音频大地电磁法及其应用[M]. 湖南长沙: 中南大学出版社, 2005. TANG Jingtian, HE Jishan. Controllable Source Audio Magnetotelluric Method and Its Application[M]. Changsha, Hunan: Central South University Press, 2005. |



 张志勇, 江西省南昌市经开区广兰大道418号东华理工大学,330013。Email:
张志勇, 江西省南昌市经开区广兰大道418号东华理工大学,330013。Email: