2. 中南大学有色金属成矿预测与 地质环境监测教育部重点实验室, 湖南长沙 410083;
3. 东华理工大学地球物理与测控技术学院, 江西南昌 330013
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring (Central South University), Ministry of Education, Changsha, Hunan 410083, China;
3. School of Geophysics and Measurement- Control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China
目前直流电阻率法正演模拟主要采用积分方程法、有限差分法和有限单元法(Finite element method,FEM)。相比积分方程法和有限差分法,FEM的优势是适应于任意地形和任意复杂的地质目标的模拟,具有适应性强、精度高、计算效率较高等特点,是目前直流电阻率法和电磁法正演模拟中主要的数值模拟方法[1-10]。近年来,在常规FEM基础上,基于非结构化单元和自适应加密策略的自适应FEM得到了快速发展[11-24]。自适应FEM利用图形几何学相关单元剖分器对任意分布节点进行网格剖分。非结构化单元适用于起伏地形和地下形态复杂目标体的正演模拟,可在局部区域自适应地加密单元,模拟过程更灵活,具有较高的模拟精度。基于非结构化单元的FEM可很好地模拟复杂起伏地形和地下复杂目标体,但不规则单元剖分不可避免。由于使用预定义的、基于节点连接信息的单元进行模拟,不可避免地需要进行网格单元剖分[25-28]。随着计算机硬件的快速发展,以及野外实际生产中待开发区域地质条件日趋复杂,对资料解释及勘探精细化的要求不断提高,尤其对复杂地电模型的模拟灵活性和模拟精度需求更高。发展创新型的精细化、高灵活性和更高模拟精度的地球物理勘探数据解译系统,已成为地球物理勘探领域的研究热点。
相比传统数值模拟方法,基于全局弱式的无单元Galerkin法(Element-Free Galerkin Method,EFGM)无需进行基于节点连接信息的单元剖分[29],可方便地根据实际需求任意布置和加密节点,对任意复杂地电模型及局部加密等问题具有很强的适应性,是一种高灵活性、高精度的正演模拟方法[30-33]。在地球物理领域,无单元Galerkin法在地震波场[34-40]、探地雷达[27, 41-42]、大地电磁[43-47]及重力勘探[48-49]等正演模拟研究中取得了良好的研究成果。在直流电阻率法正演模拟中,麻昌英等[50-51]、Ma等[52]分别利用径向基点插值(RPIM)形函数和移动最小二乘(MLS)形函数开展了2.5维直流电阻率EFGM正演,实现了任意复杂形体、地形起伏、局部节点加密的直流电阻率法的正演模拟。研究成果表明,EFGM能有效地解决传统数值模拟方法受单元约束的局限性,与传统数值模拟方法相辅相成,具有较高的灵活性、适应性和模拟精度,尤其在任意复杂地电模型的正演中效果很好,在地球物理领域具有良好的发展前景。
EFGM是一种基于全局弱式的无单元法,需要借助于全局域剖分背景单元进行积分计算,对单元仍有一定的依赖性,一定程度上损失了无单元的属性。为进一步减小对单元的依赖性,避免使用全局域背景单元积分,基于局部弱式的无单元法得以快速发展。Atluri等[53]在弹性静力学局部边界积分方程的基础上,提出了无网格局部Petrov-Galerkin法(Mesh-Free Local Petrov-Galerkin Method,MLPGM)。该方法利用加权余量法,将全局域积分转化为节点局部域积分。MLPGM应用于大地电磁场的二维正演模拟[28, 54],展现了较强的灵活性和适应性及较高的计算精度。然而,与EFGM引入权函数不同,MLPGM采用加权余量法进行方程离散,使用了更多的模拟参数;同时,离散方程按节点编号进行组装,系数矩阵稀疏但不对称。Melenk等[55]和Babuška等[56]提出了单位分解有限单元法(Partition of Unity Finite Element Method,PUFEM)和单位分解法(Partition of Unity Method,PUM),并进行了严格的数学证明和论述;Carpinteri等[57]将PUM积分应用于EFGM,将全局域积分转化为节点局部域积分,实现了基于局部弱式的无单元法。随后,该方法在各个领域得到深入研究和广泛的应用[58-62]。基于局部弱式的无单元法与EFGM类似,计算过程基本一致,均继承了FEM的一些优点,形成稀疏对称的系数矩阵;但基于局部弱式的无单元法利用了单位分解积分将全局域积分转化为节点局部域积分,摆脱了背景单元的限制,是一种真正的无单元法,具有更高的灵活性和更强的适应性。
本文基于戴前伟等[41]、Feng等[42]、麻昌英等[50]、Ma等[52]提出的探地雷达和直流电阻率EFGM正演方法,将单位分解积分应用于直流电阻率EFGM正演,提出直流电阻率无单元局部弱式法(Local Weak Form Element-Free Method,LWF-EFM),实现了高灵活性、高精度的2.5维直流电阻率正演模拟。将上述方法分别应用于层状模型及二维异常体模型的正演模拟,验证了本文算法的有效性,结果表明本文方法相比于FEM和无单元Galerkin法具有更强的灵活性和更高的模拟精度,可为高精度直流电阻率资料解释提供技术支持。
1 直流电阻率法2.5维边值问题的全局弱式形式当采用第三类边界条件时,2.5维直流电阻率法波数域总电位
| $ \begin{cases}\nabla \cdot(\sigma \nabla U)-\lambda^2 \sigma U=-I_0 \delta(A) & \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \\ \frac{\partial U}{\partial \boldsymbol{n}}=0 & \in \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} _{\mathrm{s}} \\ \frac{\partial U}{\partial \boldsymbol{n}}+\lambda \frac{K_1\left(\lambda r_A\right)}{K_0\left(\lambda r_A\right)} \cos \left(\boldsymbol{r}_A, \boldsymbol{n}\right) U=0 & \in \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\infty}\end{cases} $ | (1) |
| $ \left\{\begin{aligned} F(U) & =\frac{1}{2} \int_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} }\left\{\sigma\left[(\nabla U)^2+\lambda^2 U^2\right]-2 I_0 \delta(A) U\right\} \mathrm{d} \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \\ & +\frac{1}{2} \int_{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\infty}} \sigma \frac{\lambda K_1\left(\lambda r_A\right) \cos \left(\boldsymbol{r}_A, \boldsymbol{n}\right)}{K_0\left(\lambda r_A\right)} U^2 \mathrm{~d} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \\ \delta F(U) & =0 \end{aligned}\right. $ | (2) |
式中:
| $ {\boldsymbol{K}}^{\left(1\right)}={\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}\sigma \left[\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\cdot {\left(\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\right)}^{\mathrm{T}}+{\lambda }^{2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\right]\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $ | (3) |
| $ {\boldsymbol{K}}^{\left(2\right)}={\int }_{{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}_{\mathrm{\infty }}^{}}\sigma \frac{\lambda \mathrm{c}\mathrm{o}\mathrm{s}\left({\boldsymbol{r}}_{A}, \mathit{n}\right){K}_{1}\left(\lambda {r}_{A}\right)}{{K}_{0}\left(\lambda {r}_{A}\right)}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} $ | (4) |
| $ \mathit{F}={\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} }{I}_{0}\delta \left(A\right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $ | (5) |
式中
覆盖和单位分解是单位分解积分[25, 56]的基础。设
| $ {\mathit{Q}}_{N}=\left\{{\mathit{x}}_{1}, {\mathit{x}}_{2}, \cdots , {\mathit{x}}_{N}\right\}{\mathit{x}}_{k}\in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $ | (6) |
基于
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}_{k}=\left\{\mathit{x}\in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}:{‖\mathit{x}-{\mathit{x}}_{k}‖}_{{\mathit{R}}^{d}} < {r}_{k}\right\} $ | (7) |
| $ \overline{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}\subset \underset{k=1}{\overset{N}{\cup }}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}_{k} $ | (8) |
则称

|
图 1 有限覆盖示意图 |
设
| $ \begin{gathered}{\psi }_{k}\left(\mathit{x}\right)\in {C}_{0}^{\mathrm{\infty }}\left({\mathit{R}}^{d}\right)\begin{array}{cc}& \end{array}\\ 0\le {\psi }_{k}\left(\mathit{x}\right)\le 1, \mathit{x}\in {\mathit{R}}^{d}, k=\mathrm{1, 2}, \cdots , N\end{gathered} $ | (9) |
| $ \sum\limits _{k=1}^{N}{\psi }_{k}\left(\mathit{x}\right)=1\begin{array}{cc}& \end{array}\forall \mathit{x}\in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $ | (10) |
| $ \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}{\psi }_{k}\left(\mathit{x}\right)\in {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}_{k}\begin{array}{cc}& \end{array}k=\mathrm{1, 2}, \cdots , N $ | (11) |
则称
假设
| $ {\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}f\left(\mathit{x}\right)\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}=\sum\limits _{k=1}^{N}{\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\bigcap {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}_{k}}{\psi }_{k}\left(\mathit{x}\right)f\left(\mathit{x}\right)\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $ | (12) |
由于式(12)具有单位分解的性质,因此称这种积分方式为单位分解积分(Partition of Unity Quadrature,PUQ)。式(12)是单位分解积分的基础,通过该式可将有界区域Ω(包含边界)上的积分转化成节点子域Ωk上的积分之和。若将单位分解积分应用到式(3)~式(5),则积分式将用到两个函数集:形函数
| $ \sum\limits _{k=1}^{N}{\varphi }_{k}\left(\mathit{x}\right)=1\begin{array}{cc}& \end{array}\forall \mathit{x}\in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} $ | (13) |
即形函数
| $ {\psi }_{k}\left(\mathit{x}\right)={\phi }_{k}\left(\mathit{x}\right)\begin{array}{ccc}& & \end{array}k=\mathrm{1, 2}, \cdots , N $ | (14) |
其中
在LWF-EFM中,首先需要为每一个节点构造节点局部积分域,目的是将全局域积分转化为节点局部域积分;然后,计算域Ω中的集合
对于一个节点,其节点局部积分域的尺寸
| $ {d}_{\mathrm{s}}={\alpha }_{\mathrm{s}}p $ | (15) |
式中:
| $ p=\frac{{D}_{\mathrm{s}}}{{n}_{\mathrm{D}\mathrm{s}}-1} $ | (16) |
式中:
| $ p=\frac{\sqrt{S}}{\sqrt{{n}_{S}}-1} $ | (17) |
式中:
| $ {\boldsymbol{d}}_{\mathrm{s}}={\boldsymbol{\alpha }}_{s}\boldsymbol{p} $ | (18) |
式中:
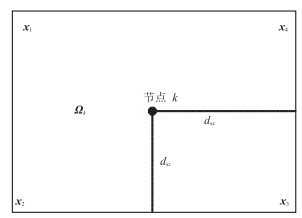
|
图 2 矩形节点局部积分域示意图 x轴向右、z轴向下为正方向。 |
图 2中节点k的坐标为
(
(
(
(
如果该矩形节点局部积分域超出了全局计算域,则应将矩形节点局部积分域划在计算域内,超出计算域Ω的部分应去掉。当域Ω的边界为矩形时,边界上矩形节点局部积分域顶点坐标为
(
(
(
(
其中:
为保证数值积分的计算精度,通常将节点局部积分域进一步划分成

|
图 3 |
第
(
(
(
(
式中:
由于采用节点局部积分域计算,在地形起伏区域内地表上的节点积分域与地形相交,靠近地表的节点局部积分域也可能与地形相交,对地形以外的区域不需要进行积分计算,特别是地形起伏形态复杂时,需要对该部分节点局部积分域进行特殊处理,使得计算区域更加贴合地形。为了更好地模拟计算域Ω的地表边界,当积分域落在计算域Ω地表边界之外时,可省略Ω之外的积分域,仅对Ω内和边界进行积分。根据上述节点局部积分域构造方法,可知节点局部积分域的大小与节点疏密程度成正相关,即在节点密集分布区域对节点局部积分域自适应缩小尺寸,反之则放大尺寸,可自动获得与节点分布相适应的一组节点局部积分域。因此,节点局部积分域越小,越有利于模拟地形形态,因此对节点局部积分域进一步细分有利于LWF-EFM对地形起伏模型的精确模拟。
3.2 局部弱式无单元法正演将单位分解积分式(12)分别代入式(3)和式(4),得到
| $ \begin{array}{l}{\boldsymbol{K}}^{\left(1\right)}={\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}\sigma \left[\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\cdot {\left(\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\right)}^{\mathrm{T}}+{\lambda }^{2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\right]\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\\ ={\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}\sum\limits _{k=1}^{N}{\psi }_{k}\left(\boldsymbol{x}\right)\sigma \left[\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\cdot {\left(\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\right)}^{\mathrm{T}}+{\lambda }^{2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\right]\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\\ =\sum\limits _{k=1}^{N}{\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}{\psi }_{k}\left(\boldsymbol{x}\right)\sigma \left[\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\cdot {\left(\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\right)}^{\mathrm{T}}+{\lambda }^{2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\right]\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \\ =\sum\limits _{k=1}^{N}{\int }_{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}_{k}}{\psi }_{k}\left(\boldsymbol{x}\right)\sigma \left[\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\cdot {\left(\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\right)}^{\mathrm{T}}+{\lambda }^{2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\right]\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \end{array} $ | (19) |
| $ \begin{array}{l}{\boldsymbol{K}}^{\left(2\right)}={\int }_{{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}_{\mathrm{\infty }}}\sigma \frac{\lambda {K}_{1}\left(\lambda {r}_{A}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left({\boldsymbol{r}}_{A}, \mathit{n}\right)}{{K}_{0}\left(\lambda {r}_{A}\right)}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\\ ={\int }_{{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}_{\mathrm{\infty }}}\sum\limits _{k=1}^{N}{\psi }_{k}\left(\boldsymbol{x}\right)\sigma \frac{\lambda {K}_{1}\left(\lambda {r}_{A}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left({\boldsymbol{r}}_{A}, \mathit{n}\right)}{{K}_{0}\left(\lambda {r}_{A}\right)}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\\ =\sum\limits _{k=1}^{N}{\int }_{{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}_{\mathrm{\infty }}}{\psi }_{k}\left(\boldsymbol{x}\right)\sigma \frac{\lambda {K}_{1}\left(\lambda {r}_{A}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left({\boldsymbol{r}}_{A}, \mathit{n}\right)}{{K}_{0}\left(\lambda {r}_{A}\right)}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \\ =\sum\limits _{k=1}^{N}{\int }_{{{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}^{k}}_{\mathrm{\infty }}}{\psi }_{k}\left(\boldsymbol{x}\right)\sigma \frac{\lambda {K}_{1}\left(\lambda {r}_{A}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left({\boldsymbol{r}}_{A}, \mathit{n}\right)}{{K}_{0}\left(\lambda {r}_{A}\right)}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \end{array} $ | (20) |
应用单位分解积分法对原积分进行离散化后,将计算域Ω(包含边界
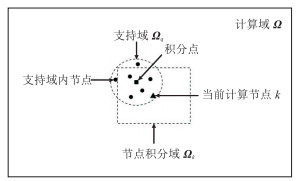
|
图 4 基于单位分解积分的无单元法求解示意图 |
假设节点局部积分域
| $ {\boldsymbol{K}}^{\left(1\right)}=\sum\limits _{k=1}^{N}\sum\limits _{g=1}^{{N}_{\mathrm{g}}}{w}_{g}{\psi }_{k}\left({\mathit{x}}_{g}\right)\left(\mathit{B}+\mathit{C}\right){J}_{g} $ | (21) |
| $ {\boldsymbol{K}}^{\left(2\right)}=\sum\limits _{k=1}^{N}\sum\limits _{g=1}^{{N}_{\mathrm{g}}}{w}_{g}{\psi }_{k}\left({\mathit{x}}_{g}\right)\mathit{D}{J}_{g} $ | (22) |
式中
| $ \mathit{B}=\sigma \nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left({\mathit{x}}_{g}\right)\cdot \nabla {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\left({\mathit{x}}_{g}\right) $ | (23) |
| $ \mathit{C}=\sigma {\lambda }^{2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left({\mathit{x}}_{g}\right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\left({\mathit{x}}_{g}\right) $ | (24) |
| $ \mathit{D}=\sigma \frac{\lambda \mathrm{c}\mathrm{o}\mathrm{s}\left({\boldsymbol{r}}_{A}, \mathit{n}\right){K}_{1}\left(\lambda {r}_{A}\right)}{{K}_{0}\left(\lambda {r}_{A}\right)}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left({\mathit{x}}_{g}\right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}^{\mathrm{T}}\left({\mathit{x}}_{g}\right) $ | (25) |
展开式(23)~式(25),得到
| $ \mathit{B}=\sigma \left(\begin{array}{l}\nabla {\phi }_{1}\nabla {\phi }_{1}\ \ \ \ \nabla {\phi }_{1}\nabla {\phi }_{2}\cdots \mathrm{ }\nabla {\phi }_{1}\nabla {\phi }_{{n}_{\mathrm{q}}}\\ \nabla {\phi }_{2}\nabla {\phi }_{1}\ \ \ \ \nabla {\phi }_{2}\nabla {\phi }_{2}\cdots \mathrm{ }\nabla {\phi }_{2}\nabla {\phi }_{{n}_{\mathrm{q}}}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathrm{︙}\\ \nabla {\phi }_{{n}_{\mathrm{q}}}\nabla {\phi }_{1}\ \ \ \ \nabla {\phi }_{{n}_{\mathrm{q}}}\nabla {\phi }_{2}\cdots \mathrm{ }\nabla {\phi }_{{n}_{\mathrm{q}}}\nabla {\phi }_{{n}_{\mathrm{q}}}\end{array}\right) $ | (26) |
| $ \mathit{C}=\sigma {\lambda }^{2}\left(\begin{array}{l}{\phi }_{1}{\phi }_{1}\ \ \ \ {\phi }_{1}{\phi }_{2}\cdots {\phi }_{1}{\phi }_{{n}_{\mathrm{q}}}\\ {\phi }_{2}{\phi }_{1}\ \ \ \ {\phi }_{2}{\phi }_{2}\cdots {\phi }_{2}{\phi }_{{n}_{\mathrm{q}}}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathrm{︙}\\ {\phi }_{{n}_{\mathrm{q}}}{\phi }_{1}\ \ \ \ {\phi }_{{n}_{\mathrm{q}}}{\phi }_{2}\cdots {\phi }_{{n}_{\mathrm{q}}}{\phi }_{{n}_{\mathrm{q}}}\end{array}\right) $ | (27) |
| $ \mathit{D}=\sigma \frac{\lambda \mathrm{c}\mathrm{o}\mathrm{s}\left({\boldsymbol{r}}_{A}, \mathit{n}\right){K}_{1}\left(\lambda {r}_{A}\right)}{{K}_{0}\left(\lambda {r}_{A}\right)}\left(\begin{array}{l}{\phi }_{1}{\phi }_{1}\ \ \ \ {\phi }_{1}{\phi }_{2}\cdots {\phi }_{1}{\phi }_{{n}_{\mathrm{q}}}\\ {\phi }_{2}{\phi }_{1}\ \ \ \ {\phi }_{2}{\phi }_{2}\cdots {\phi }_{2}{\phi }_{{n}_{\mathrm{q}}}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathrm{︙}\\ {\phi }_{{n}_{\mathrm{q}}}{\phi }_{1}\ \ \ \ {\phi }_{{n}_{\mathrm{q}}}{\phi }_{2}\cdots {\phi }_{{n}_{\mathrm{q}}}{\phi }_{{n}_{\mathrm{q}}}\end{array}\right) $ | (28) |
其中
| $ {\boldsymbol{K}}_{kg}^{\left(1\right)}={\psi }_{k}\left({\mathit{x}}_{g}\right){w}_{g}\left(\mathit{B}+\mathit{C}\right){J}_{g} $ | (29) |
| $ {\boldsymbol{K}}_{kg}^{\left(2\right)}={\psi }_{k}\left({\mathit{x}}_{g}\right){w}_{g}\mathit{D}{J}_{g} $ | (30) |
上式为积分点子系数矩阵,其矩阵元素为
| $ {K}_{kgij}^{\left(1\right)}={\psi }_{k}\left({\mathit{x}}_{g}\right){w}_{g}\sigma \left[\frac{\partial {\phi }_{i}\left({\mathit{x}}_{g}\right)}{\partial x}\frac{\partial {\phi }_{j}\left({\mathit{x}}_{g}\right)}{\partial x}+\frac{\partial {\phi }_{i}\left({\mathit{x}}_{g}\right)}{\partial z}\frac{\partial {\phi }_{j}\left({\mathit{x}}_{g}\right)}{\partial z}+{\lambda }^{2}{\phi }_{i}\left({\mathit{x}}_{g}\right){\phi }_{j}\left({\mathit{x}}_{g}\right)\right]{J}_{g} $ | (31) |
| $ {K}_{kgij}^{\left(2\right)}={\psi }_{k}\left({\mathit{x}}_{g}\right){w}_{g}\sigma \frac{\lambda \mathrm{c}\mathrm{o}\mathrm{s}\left({\boldsymbol{r}}_{A}, \mathit{n}\right){K}_{1}\left(\lambda {r}_{A}\right)}{{K}_{0}\left(\lambda {r}_{A}\right)}{\phi }_{i}\left({\mathit{x}}_{g}\right){\phi }_{j}\left({\mathit{x}}_{g}\right){J}_{g} $ | (32) |
式中
对于式(5),若采用
| $ \mathit{F}={\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} }{I}_{0}\delta \left(A\right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}=\left[\begin{array}{l}{\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}{I}_{0}\delta \left(A\right){\phi }_{1}\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\\ {\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}{I}_{0}\delta \left(A\right){\phi }_{2}\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\\\ \ \ \ \ \ \ \ \ \ ⋮\\ {\int }_{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}{I}_{0}\delta \left(A\right){\phi }_{N}\mathrm{d}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\end{array}\right]=\left[\begin{array}{l}{f}_{1}\\ {f}_{2}\\\ \ \ ⋮\\ {f}_{N}\end{array}\right] $ | (33) |
当无单元法形函数具有Kronecker delta函数性质时,上式右端项为
| $ {f}_{i}=\left\{\begin{array}{l}0\ \ \ \ \ \ \ A\ne i, i=\mathrm{1, 2}, \cdots , {n}_{\mathrm{q}}\\ {I}_{0}/2\ \ \ A=i, i=\mathrm{1, 2}, \cdots , {n}_{\mathrm{q}}\end{array}\right. $ | (34) |
当无单元法形函数不具有Kronecker delta函数性质时,式(33)的右端项为
| $ {f}_{i}=\left\{\begin{array}{l}0\ \ \ \ \ \ \ \ \ \ A\ne i, i=\mathrm{1, 2}, \cdots , {n}_{\mathrm{q}}\\ {\phi }_{i}{I}_{0}/2\ \ \ A=i, i=\mathrm{1, 2}, \cdots , {n}_{\mathrm{q}}\end{array}\right. $ | (35) |
如图 5所示,当节点局部积分域相无不重叠且恰好覆盖计算域时,节点局部积分域内任意一点对应该节点的单位分解函数为1,这种情况即为基于全局弱式积分的数值模拟法,例如EFGM和FEM。在EFGM中节点局部积分域可视为背景积分单元,在FEM中节点局部积分域可视为基于节点拓扑关系剖分的网格单元。相比于基于全局弱式的EFGM,LWF-EFM在求解

|
图 5 节点局部积分域相互不重叠且恰好覆盖计算域示意图 |
采用具有解析解的三层电阻率模型(图 6)验证直流电阻率LWF-EFM算法的有效性。建立水平方向宽380 m(
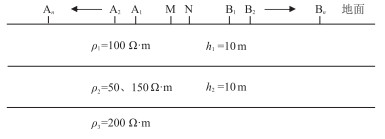
|
图 6 层状模型及对称四极装置观测示意图 A-B表示接收电极对,M-N表示发射电极对;ρ1、ρ2、ρ3分别表示地表以下第一层、第二层和基底电阻率,h1、h2分别表示地表以下第一层、第二层厚度。 |

|
图 7 层状模型节点分布示意图 |
图 8和图 9分别是ρ2为150、50 Ω·m时的视电阻率和相对误差曲线。可以看出:无论中间层为高阻或低阻,LWF-EFM的模拟结果与解析解均吻合较好,相对误差较小。表 1为模拟结果平均相对误差,可见LWF-EFM模拟结果平均相对误差与EFGM相差不大,均小于1%,低于FEM平均相对误差,表明了LWF-EFM的有效性。层状模型不同方法模拟结果分析表明,在计算域较小时,FEM受到边界影响较大,EFGM和LWF-EFM可获得高精度的模拟结果。采用合适的模拟参数时,相比于FEM,LWF-EFM可获得更高的模拟精度,与EFGM模拟精度相当。

|
图 8 层状模型ρ2=150 Ω·m时不同方法模拟视电阻率(左)和相对误差(右)曲线 |
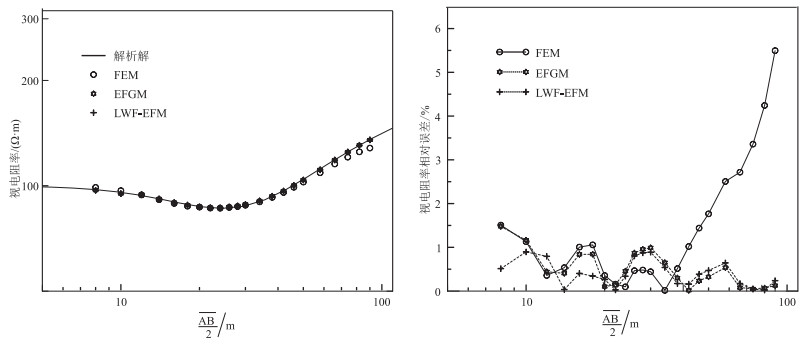
|
图 9 层状模型ρ2=50 Ω·m时不同方法模拟视电阻率(左)和相对误差(右)曲线 |
|
|
表 1 层状模型不同方法视电阻率平均相对误差 |
建立一个均匀半空间模型,介质电阻率ρ1=100Ω·m;在均匀半空间中有一个电阻率ρ2=1000 Ω·m的二维矩形异常体,异常体宽10 m(x方向),高8 m(z方向),中心点坐标(x,z)为(0,15 m)[52]。计算域Ω水平方向宽200 m(
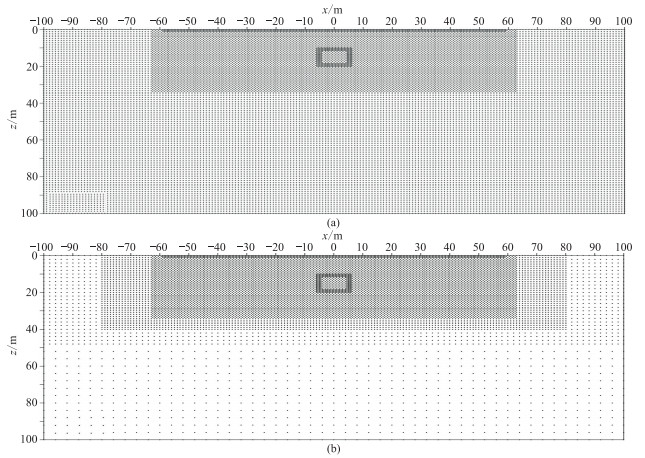
分别采用三种类型节点分布离散计算域:第1种为均匀节点分布,节点间距为1 m,节点总数为20301;第2种节点分布是在第1种节点分布基础上,对靠近场源的浅层区域和异常体区域进行节点加密,节点总数为25150(图 10a);第3种节点分布是在第2种节点分布基础上,对计算域外围区域的节点进行抽稀,节点总数为12878(图 10b)。在地表水平方向-58~58 m范围内以2 m的间隔均匀布置59根电极,进行直流电阻率法温纳装置[64]观测。下文若不加以说明,均采用该电极布置和观测装置。为减小边界影响,采用FEM进行正演模拟时,首先在第2种节点分布基础上对计算域进行扩边,扩边后的范围为2000 m×1000 m;然后,分别使用第1种节点分布和第3种节点分布,采用EFGM和LWF‑ EFM进行正演模拟。EFGM模拟采用1 m
|
图 10 二维模型模拟采用的剖分节点分布示意图[52] (a)第2种节点分布;(b)第3种节点分布。图中黑色矩形表示电阻率异常体。 |
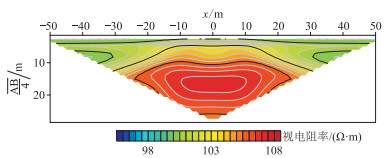
图 11为基于第2种节点分布、采用FEM计算的电阻率拟断面。由于第2种节点分布相比于其他两种节点分布节点数最多,且在靠近场源和异常体周围区域进行了节点加密,因此该节点分布条件下的计算结果更精确,故将图 11所示结果作为标准结果。图 12a和图 12b为采用EFGM获得的模拟结果,图 12c和图 12d为EFGM模拟结果与参考标准结果的相对误差。对比图 12c和图 12d可知,使用第3种节点分布的相对误差较小,大部分区域相对误差接近0,而使用第1种节点分布时,在浅层和异常体周围区域相对误差明显相对较大。
|
图 11 二维模型基于第2种节点的FEM视电阻率拟断面 |

|
图 12 二维模型EFGM视电阻率拟断面(上)及相对误差剖面(下) (a)和(c)对应第1种节点分布;(b)和(d)对应第3种节点分布 |
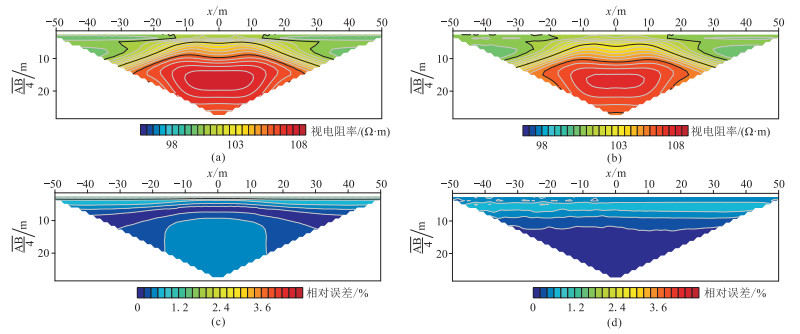
图 13为采用LWF-EFM获得的模拟结果。对比图 13a、图 13b与图 11可知,LWF-EFM的模拟结果与参考结果基本一致,表明LWF-EFM模拟结果是可靠的。对比图 13c和图 13d可知,与EFGM类似,LWF-EFM使用第3种节点分布得到的模拟结果相对误差较小,大部分区域相对误差接近0,而采用第1种节点分布时,在浅层和异常体周围区域相对误差明显相对较大。
|
图 13 二维模型LWF-EFM视电阻率拟断面(上)及相对误差剖面(下) (a)和(c)对应第1种节点分布;(b)和(d)对应第3种节点分布 |
表 2为第1种和第2种节点分布的节点数、模拟结果最大相对误差、平均相对误差和计算时间统计。可知采用第1种节点分布时最大相对误差和平均相对误差均大于第3种节点分布;同时,由于第1种节点分布使用了更多的节点,计算成本显著更高。对比相对误差统计结果可知,与EFGM一样,LWF-EFM也可采用不规则的节点分布,在场源和异常体周围区域加密节点,在计算域外围区域使用稀疏的节点分布,可在使用更少节点的条件下获得与均匀节点分布相同或更高的模拟精度;同时,使用更少的节点也可节省计算成本。相比EFGM,LWF-EFM计算效率较低,主要原因是不同节点分布的节点局部积分域之间通常存在很多重合区域,实际计算积分面积大于计算域Ω,导致计算量增加。但由于采用节点局部积分域进行积分,仅需要设定节点局部积分域参数,不再需要背景单元剖分,相对需要背景单元的EFGM对单元的依赖性更小,是真正的无单元法,正演过程更方便。同时,在计算域内任意区域进行节点加密或者稀释均十分方便,可根据节点分布情况自动构造节点局部积分域,无需其他处理,具有更高的灵活性。
|
|
表 2 二维模型LWF-EFM不同节点分布的节点数、模拟相对误差和计算时间 |
建立图 14a所示水平地形起伏模型,地下空间介质电阻率ρ1=100 Ω·m。计算域Ω覆盖x方向300 m(-150~150 m),垂直方向(z)最大深度为115 m,山脊最高点高度为7.6 m,位于

|
图 14 地形起伏模型节点示意图 (a)未加密;(b)加密 |
基于图 14a所示节点分布,采用不规则节点对场源附近的浅层区域和地形起伏区域进行节点加密,在计算域的外围区域使用稀疏节点分布(图 14b)。分别采用LWF-EFM、EFGM和FEM对模型进行正演,模拟直流电阻率法的视电阻率。采用EFGM模拟时,在地形起伏区域采用任意四边形背景单元模拟地形。为减小边界影响,采用FEM模拟时,在上述计算域的基础上进行扩边,扩边后水平方向宽2000 m,垂直方向高1000 m。
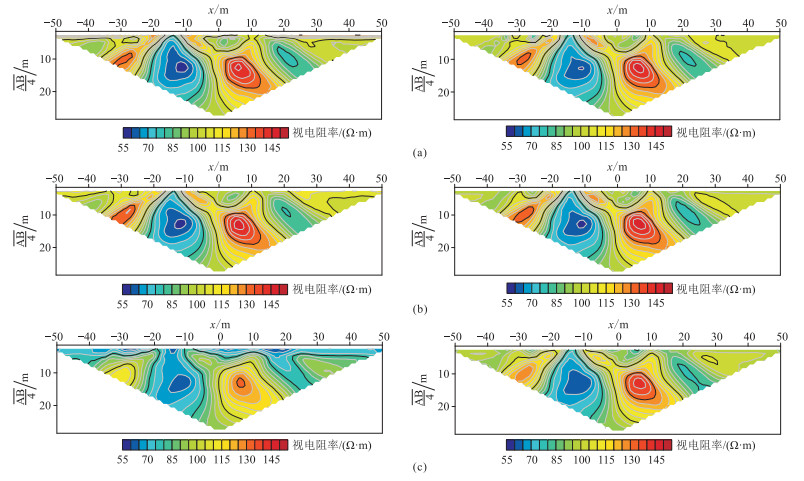
图 15为分别采用地形起伏模型未加密节点分布(图 14a)和地表加密节点分布(图 14b)时,EFGM、FEM和LWF-EFM模拟结果。由图可知,无论采用未加密节点还是加密节点,EFGM和FEM的计算结果基本一致。其中,EFGM通过采用任意四边形背景单元,很好地模拟了地形起伏。对比图 15c(左)与图 15a(左)、图 15b(左)可知,在局部区域LWF-EFM与EFGM和FEM的模拟结果有较明显的差异,表明在地形起伏区域,若采用较稀疏的节点分布,LWF-EFM对地形起伏模型的模拟精度较低。其主要原因是LWF-EFM是基于节点局部积分域进行积分,在地形起伏区域节点局部积分域不可避免地会与地形相交,因而不能准确地模拟地形,导致模拟结果出现偏差。在地形起伏区域,LWF-EFM采用节点局部积分域进行积分,理论上当节点局部积分域与地形相交时,需要将位于地形以外的积分域区域删除。相比于EFGM和基于非结构化三角形的FEM,LWF-EFM处理复杂地形与积分域的难度和工作量会很大,因此需要提高LWF-EFM对地形的模拟精度,
|
图 15 地形起伏模型采用未加密节点(左)和加密节点(右)时不同方法正演视电阻率拟断面 (a)EFGM;(b)FEM;(c)LWF-EFM |
首先,由于LWF-EFM通常根据节点分布构造节点局部积分域,本文对地表起伏段进行合理的节点加密,使得靠近地形起伏区域的节点局部积分域使用较小尺寸的剖分单元,可更精确地描述地形起伏形态,提高对地形的模拟精度;同时,在地表起伏区域和源附近加密节点,也有利于提高模拟精度。其次,当高斯点位于地形以外时,本文采用对高斯点不做计算的处理策略。虽然这可能出现同一子域内部分高斯点进行了计算而另一部分高斯点不做计算的情况,造成一定的积分误差,但这样处理方法简单方便,同时可保证积分区域尽可能地贴合地形。
图 15c(右)为LWF-EFM经上述两种方法处理后的模拟结果。对比图 15c(左)与图 15c(右)可知,在地形起伏区域进行加密节点可明显改善LWF-EFM对地形起伏模型的模拟效果。对比图 15c(右)与图 15a(右)、图 15b(右)可知,若采用加密节点,三种算法对地形起伏模型的正演模拟结果基本一致,表明采用上述两种方法可有效提高LWF-EFM对地形起伏的模拟精度。此外,由于LWF-EFM采用节点局部积分域积分,相对于EFGM需要考虑背景单元分布与节点分布相适应的问题[52],LWF-EFM在节点加密方面更方便,设计任意节点分布具有更高的灵活性和适应性。
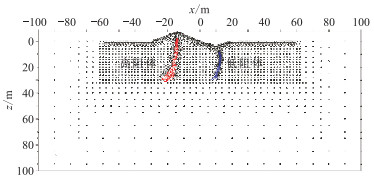
为了模拟地下复杂形态异常体,在地形起伏模型基础上加入具有复杂形态的两个近直立异常体(图 16中蓝色和红色区域)。其中,红色区域为高阻异常体,位于地形起伏模型山脊顶点的下方,电阻率为ρ2;蓝色区域为低阻异常体,位于地形起伏模型山谷低点的下方,电阻率为ρ3。
|
图 16 复杂地电模型节点示意图 |
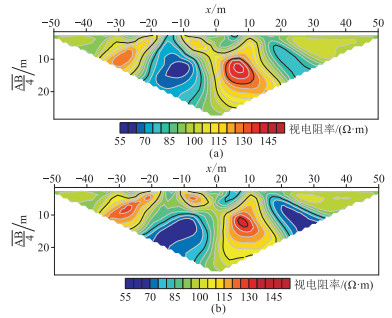
使用本文方法分别对ρ2=200 Ω·m、ρ3=20 Ω·m和ρ2=5000 Ω·m、ρ3=1 Ω·m两种情况下的复杂地电模型进行正演模拟,结果如图 17所示。分析图 17可知,山脊地形可以引起明显的低阻异常,山谷地形可以引起明显的高阻异常。对比分析图 17a和图 17b可知,在山脊和山谷下方分别加入高阻和低阻异常体后,若异常体的电阻率与围岩的电阻率差异不大时,高阻和低阻异常体引起的异常基本被地形引起的异常湮没;随着异常体与围岩之间电阻率差异的增加,异常体引起的异常逐步显现,但未能完全湮没地形的影响。
|
图 17 复杂地电模型LWF-EFM模拟视电阻率拟断面图 (a)ρ2=200 Ω·m,ρ3=20 Ω·m;(b)ρ2=5000 Ω·m,ρ3=1 Ω·m |
因此,对复杂地电模型正演结果综合分析表明,直流电阻率法受地形影响较大,地形之下的异常体(如直立异常体)产生的视电阻率异常很可能被地形引起的异常掩盖。
5 结论本文提出一种灵活、高精度的直流电阻率无单元局部弱式正演方法。该方法将单位分解积分应用于基于全局弱式积分的直流电阻率EFGM正演,将全局域积分转化为节点局部积分域积分。对不同地电模型应用三种方法(EFGM,FEM,LWF-EFM)进行数值模拟,结果验证了本文算法应用于直流电阻率正演模拟的正确性和有效性。与EFGM相比,本文算法无需在全局域内进行背景积分单元剖分;与FEM相比,本文算法不需要进行基于节点拓扑关系的单元剖分,是一种更灵活性、适应性较强的高精度无单元正演模拟算法。模拟结果表明,由于本文算法采用的不同节点局部积分域之间通常存在很多重合区域,导致实际积分面积比计算域Ω大,计算量也随之增加。地形起伏模型模拟结果分析表明,相比于EFGM和FEM,本文算法在地形起伏区域节点局部积分域不可避免地会与地形相交,不利于地形起伏模型的精确模拟,因而本文对地形起伏区域进行节点加密,对地形以外的高斯点不做计算,明显提高了地形起伏模型的模拟精度。
| [1] |
强建科, 罗延钟. 三维地形直流电阻率有限元法模拟[J]. 地球物理学报, 2007, 50(5): 1606-1613. QIANG Jianke, LUO Yanzhong. The resistivity FEM numerical modeling on 3-D undulating topography[J]. Chinese Journal of Geophysics, 2007, 50(5): 1606-1613. DOI:10.3321/j.issn:0001-5733.2007.05.038 |
| [2] |
TANG W, LI Y, SWIDINSKY A, et al. Three-dimensional controlled-source electromagnetic modelling with a well casing as a grounded source: a hybrid method of moments and finite element scheme[J]. Geophysical Prospecting, 2015, 63(6): 1491-1507. DOI:10.1111/1365-2478.12330 |
| [3] |
TANG W, LI Y, LIU J, et al. Three-dimensional controlled-source electromagnetic forward modeling by edge-based finite element with a divergence correction[J]. Geophysics, 2021, 86(6): E367-E382. DOI:10.1190/geo2020-0520.1 |
| [4] |
TANG W, CHEN W, DENG J, et al. Forward calculation of 3D controlled-source electromagnetic responses based on joint application of secondary field and coupled potential formulations[J]. Geophysics, 2022, 87(4): E253-E265. DOI:10.1190/geo2021-0480.1 |
| [5] |
张钱江, 戴世坤, 陈龙伟, 等. 多源条件下直流电阻率法有限元三维数值模拟中一种近似边界条件[J]. 地球物理学报, 2016, 59(9): 3448-3458. ZHANG Qianjiang, DAI Shikun, CHEN Longwei, et al. An approximate boundary condition for FEM-based 3-D numerical simulation with multi-source direct current resistivity method[J]. Chinese Journal of Geophysics, 2016, 59(9): 3448-3458. |
| [6] |
XIONG B, LUO T, CHEN L. Direct solutions of 3-D magnetotelluric fields using edge-based finite element[J]. Journal of Applied Geophysics, 2018, 159: 204-208. DOI:10.1016/j.jappgeo.2018.08.013 |
| [7] |
XIE J, CAI H, HU X, et al. 3-D magnetotelluric inversion and application using the edge-based finite element with hexahedral mesh[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-11. |
| [8] |
戴世坤, 冉应强, 张莹, 等. 空间-波数域二维强磁场及其梯度张量数值模拟研究[J]. 石油地球物理勘探, 2023, 58(1): 228-237. DAI Shikun, RAN Yingqiang, ZHANG Ying, et al. Numerical simulation of two-dimensional strong magnetic field and its gradient tensor in space-wavenumber domain[J]. Oil Geophysical Prospecting, 2023, 58(1): 228-237. |
| [9] |
李静和, 何展翔, 穆桐. 接触式激发极化法油气储层压裂监测有限元模拟[J]. 石油地球物理勘探, 2022, 57(3): 719-727. LI Jinghe, HE Zhanxiang, MU Tong. Finite element simulation for fracturing monitoring of oil and gas reservoirs by using contact induced polarization method[J]. Oil Geophysical Prospecting, 2022, 57(3): 719-727. DOI:10.13810/j.cnki.issn.1000-7210.2022.03.022 |
| [10] |
GUO R, WANG Y, EGBERT G D, et al. An efficient multigrid solver based on a four-color cell-block GaussSeidel smoother for 3D magnetotelluric forward modeling[J]. Geophysics, 2022, 87(3): E121-E133. DOI:10.1190/geo2021-0275.1 |
| [11] |
REN Z, TANG J. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method[J]. Geophysics, 2010, 75(1): H7-H17. DOI:10.1190/1.3298690 |
| [12] |
韩骑, 胡祥云, 程正璞, 等. 自适应非结构有限元MT二维起伏地形正反演研究[J]. 地球物理学报, 2015, 58(12): 4675-4684. HAN Qi, HU Xiangyun, CHENG Zhengpu, et al. A study of two-dimensional MT inversion with steep topography using the adaptive unstructured finite element method[J]. Chinese Journal of Geophysics, 2015, 58(12): 4675-4684. DOI:10.6038/cjg20151228 |
| [13] |
蔡红柱, 熊彬, ZHDANOV Michael. 电导率各向异性的海洋电磁三维有限单元法正演[J]. 地球物理学报, 2015, 58(8): 2839-2850. CAI Hongzhu, XIONG Bin, ZHDANOV M. Three-dimensional marine controlled-source electromagnetic modelling in anisotropic medium using finite element method[J]. Chinese Journal of Geophysics, 2015, 58(8): 2839-2850. |
| [14] |
吴小平, 刘洋, 王威. 基于非结构网格的电阻率三维带地形反演[J]. 地球物理学报, 2015, 58(8): 2706-2717. WU Xiaoping, LIU Yang, WANG Wei. 3D resistivity inversion incorporating topography based on unstructured meshes[J]. Chinese Journal of Geophysics, 2015, 58(8): 2706-2717. |
| [15] |
YAN B, LI Y, LIU Y. Adaptive finite element modeling of direct current resistivity in 2-D generally anisotropic structures[J]. Journal of Applied Geophysics, 2016, 130: 169-176. DOI:10.1016/j.jappgeo.2016.04.018 |
| [16] |
CHOU T K, CHOUTEAU M, DUBÉ J S. Intelligent meshing technique for 2D resistivity inverse problems[J]. Geophysics, 2016, 81(4): IM45-IM56. DOI:10.1190/geo2015-0177.1 |
| [17] |
李勇, 吴小平, 林品荣, 等. 电导率任意各向异性海洋可控源电磁三维矢量有限元数值模拟[J]. 地球物理学报, 2017, 60(5): 1955-1978. LI Yong, WU Xiaoping, LIN Pinrong, et al. Three-dimensional modeling of marine controlled-source electromagnetism using the vector finite element method for arbitrary anisotropic media[J]. Chinese Journal of Geophysics, 2017, 60(5): 1955-1978. |
| [18] |
CAI H, HU X, XIONG B, et al. Finite-element time-domain modeling of electromagnetic data in general dispersive medium using adaptive Pad series[J]. Computers & Geosciences, 2017, 109(C): 194-205. |
| [19] |
曹晓月, 殷长春, 张博, 等. 面向目标自适应有限元法的带地形三维大地电磁各向异性正演模拟[J]. 地球物理学报, 2018, 61(6): 2618-2628. CAO Xiaoyue, YIN Changchun, ZHANG Bo, et al. A goal-oriented adaptive finite-element method for 3D MT anisotropic modeling with topography[J]. Chinese Journal of Geophysics, 2018, 61(6): 2618-2628. |
| [20] |
CAI H, LONG Z, LIN W, et al. 3D multinary inversion of controlled-source electromagnetic data based on the finite-element method with unstructured mesh[J]. Geophysics, 2021, 86(1): E77-E92. DOI:10.1190/geo2020-0164.1 |
| [21] |
周峰, 张志勇, 陈煌, 等. 基于非结构网格的三种CSEM有限元三维正演系统分析[J]. 石油地球物理勘探, 2021, 56(5): 1190-1202. ZHOU Feng, ZHANG Zhiyong, CHEN Huang, et al. Analysis of 3D finite-element forward modeling of CSEM data using three different formulas and unstructured grids[J]. Oil Geophysical Prospecting, 2021, 56(5): 1190-1202. DOI:10.13810/j.cnki.issn.1000-7210.2021.05.025 |
| [22] |
汤文武, 邓居智, 黄清华. 非结构化网格与散度校正技术结合的三维CSEM矢量有限元正演[J]. 石油地球物理勘探, 2021, 56(4): 891-901. TANG Wenwu, DENG Juzhi, HUANG Qinghua. Three-dimensional CSEM forward modeling using edge-based finite element method based on unstructured meshes and divergence correction[J]. Oil Geophysical Prospecting, 2021, 56(4): 891-901. DOI:10.13810/j.cnki.issn.1000-7210.2021.04.022 |
| [23] |
赵宁, 黄明卫, 申亚行, 等. 高阶自适应有限元三维直流电阻率正演方法及其在沁水盆地煤气层压裂监测中的应用[J]. 石油地球物理勘探, 2021, 56(1): 209-216. ZHAO Ning, HUANG Mingwei, SHEN Yahang, et al. Forward modeling of 3D DC resistivity based on high-order adaptive finite element and its application in Qinshui Basin[J]. Oil Geophysical Prospecting, 2021, 56(1): 209-216. |
| [24] |
TANG W, HUANG Q, DENG J, et al. Joint application of secondary field and coupled potential formulations to unstructured meshes for 3-D CSEM forward modeling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-9. |
| [25] |
LIU G R, GU Y T. An Introduction to Meshfree Methods and Their Programming[M]. Springer, Dordrecht, 2005.
|
| [26] |
刘欣. 无网格方法[M]. 北京: 科学出版社, 2011.
|
| [27] |
冯德山, 王洪华, 戴前伟. 基于无单元Galerkin法探地雷达正演模拟[J]. 地球物理学报, 2013, 56(1): 298-308. FENG Deshan, WANG Honghua, DAI Qianwei. Forward simulation of Ground Penetrating Radar based on the element-free Galerkin method[J]. Chinese Journal of Geophysics, 2013, 56(1): 298-308. |
| [28] |
卢杰, 李予国. 无网格局部Petrov-Galerkin法大地电磁场二维正演模拟[J]. 地球物理学报, 2017, 60(3): 1189-1200. LU Jie, LI Yuguo. Two-dimensional magnetotelluric modeling using the Mesh-free Local Petrov-Galerkin method[J]. Chinese Journal of Geophysics, 2017, 60(3): 1189-1200. |
| [29] |
BELYTSCHKO T, LU Y Y, GU L. Element-free Galerkin methods[J]. International Journal for Numerical Methods in Engineering, 1994, 37(2): 229-256. DOI:10.1002/nme.1620370205 |
| [30] |
PANT M, SINGH I V, MISHRA B K. Numerical simulation of thermo-elastic fracture problems using element free Galerkin method[J]. International Journal of Mechanical Sciences, 2010, 52(12): 1745-1755. DOI:10.1016/j.ijmecsci.2010.09.008 |
| [31] |
LIU F, CHENG Y. The improved element-free Galerkin method based on the nonsingular weight functions for inhomogeneous swelling of polymer gels[J]. International Journal of Applied Mechanics, 2018, 10(4): 1850047. DOI:10.1142/S1758825118500473 |
| [32] |
CHEN L, LI X. A complex variable boundary elementfree method for the Helmholtz equation using regularized combined field integral equations[J]. Applied Mathematics Letters, 2020, 101: 106067. |
| [33] |
WU Q, PENG M, CHENG Y. The interpolating dimension splitting element-free Galerkin method for 3D potential problems[J]. Engineering With Computers, 2022, 38(4): 2703-2717. |
| [34] |
JIA X, HU T. Element-free precise integration method and its applications in seismic modelling and imaging[J]. Geophysical Journal International, 2006, 166(1): 349-372. |
| [35] |
王月英. 地震波正演模拟中无单元Galerkin法初探[J]. 地球物理学进展, 2007, 22(5): 1539-1544. WANG Yueying. Study of element-free Galerkin method in the seismic forward modeling[J]. Progress in Geophysics, 2007, 22(5): 1539-1544. |
| [36] |
JIE Y, TANG X, LUAN M, et al. Adaptive element-free Galerkin method applied to analysis of earthquake induced liquefaction[J]. Earthquake Engineering and Engineering Vibration, 2008, 7(2): 217-224. |
| [37] |
ZHOU Z, JIA X, QIANG X. GPU-accelerated elementfree reverse-time migration with Gauss points partition[J]. Journal of Geophysics and Engineering, 2018, 15(3): 718-728. |
| [38] |
JIA X, QIANG X. A frequency-domain element-free method for seismic modeling and reverse-time migration[J]. Journal of Geophysics and Engineering, 2018, 15(4): 1719-1728. |
| [39] |
TAKEKAWA J, MIKADA H. A mesh-free finite-difference method for elastic wave propagation in the frequency-domain[J]. Computers & Geosciences, 2018, 118: 65-78. |
| [40] |
刘立彬, 段沛然, 张云银, 等. 基于无网格的地震波场数值模拟方法综述[J]. 地球物理学进展, 2020, 35(5): 1815-1825. LIU Libin, DUAN Peiran, ZHANG Yunyin, et al. Overview of mesh-free method of seismic forward numerical simulation[J]. Progress in Geophysics, 2020, 35(5): 1815-1825. |
| [41] |
戴前伟, 王洪华. 基于随机介质模型的GPR无单元法正演模拟[J]. 中国有色金属学报, 2013, 23(9): 2436-2443. DAI Qianwei, WANG Honghua. Element free method forward modeling of GPR based on random medium model[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2436-2443. |
| [42] |
FENG D, GUO R, WANG H. An element-free Galerkin method for ground penetrating radar numerical simulation[J]. Journal of Central South University, 2015, 22(1): 261-269. |
| [43] |
苏洲, 胡文宝, 朱毅. 二维大地电磁正演中无网格算法研究[J]. 石油天然气学报, 2012, 34(5): 87-90. SU Zhou, HU Wenbao, ZHU Yi. Meshfree method used in two-dimensional magnetotelluric forwarding[J]. Journal of Oil and Gas Technology, 2012, 34(5): 87-90. |
| [44] |
严家斌, 李俊杰. 无网格法在大地电磁正演计算中的应用[J]. 中南大学学报(自然科学版), 2014, 45(10): 3513-3520. YAN Jiabin, LI Junjie. Magnetotelluric forward calculation by meshless method[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 3513-3520. |
| [45] |
嵇艳鞠, 黄廷哲, 黄婉玉, 等. 起伏地形下各向异性的2D大地电磁无网格法数值模拟[J]. 地球物理学报, 2016, 59(12): 4483-4493. JI Yanju, HUANG Tingzhe, HUANG Wanyu, et al. 2D anisotropic magnetotelluric numerical simulation using meshfree method under undulating terrain[J]. Chinese Journal of Geophysics, 2016, 59(12): 4483-4493. |
| [46] |
闫海涛, 张龙, 张继锋, 等. 全局弱式无网格法在大地电磁二维正演中的应用研究[J]. 地球物理学进展, 2019, 34(2): 658-667. YAN Haitao, ZHANG Long, ZHANG Jifeng, et al. Application of global weak-form mesh-free methods in two-dimensional magnetotelluric forward[J]. Progress in Geophysics, 2019, 34(2): 658-667. |
| [47] |
LONG J, FARQUHARSON C G. On the forward modelling of three-dimensional magnetotelluric data using a radial-basis-function-based mesh-free method[J]. Geophysical Journal International, 2019, 219(1): 394-416. |
| [48] |
李俊杰, 严家斌. 重力异常二维正演中的无网格方法[J]. 煤田地质与勘探, 2018, 46(6): 181-186. LI Junjie, YAN Jiabin. Meshfree method for 2-D forward modeling of gravity anomaly[J]. Coal Geology & Exploration, 2018, 46(6): 181-186. |
| [49] |
LONG J, FARQUHARSON C G. Three-dimensional forward modelling of gravity data using mesh-free methods with radial basis functions and unstructured nodes[J]. Geophysical Journal International, 2019, 217(3): 1577-1601. |
| [50] |
麻昌英, 柳建新, 刘海飞, 等. 基于全局弱式无单元法直流电阻率正演模拟[J]. 地球物理学报, 2017, 60(2): 801-809. MA Changying, LIU Jianxin, LIU Haifei, et al. A global weak form element free method for direct current resistivity forward simulation[J]. Chinese Journal of Geophysics, 2017, 60(2): 801-809. |
| [51] |
麻昌英, 柳建新, 郭荣文, 等. 耦合有限单元法扩边的直流电阻率勘探无单元Galerkin法正演[J]. 地球物理学报, 2018, 61(6): 2578-2588. MA Changying, LIU Jianxin, GUO Rongwen, et al. Element-free Galerkin forward modeling of DC resistivity using a coupled finite element method with extended the boundaries[J]. Chinese Journal of Geophysics, 2018, 61(6): 2578-2588. |
| [52] |
MA C, LIU J, LIU H, et al. 2.5D electric resistivity forward modeling with element-free Galerkin method[J]. Journal of Applied Geophysics, 2019, 162: 47-57. |
| [53] |
ATLURI S N, ZHU T. A new Meshless Local Petrov-Galerkin (MLPG) approach in computational mechanics[J]. Computational Mechanics, 1998, 22(2): 117-127. |
| [54] |
李俊杰, 严家斌. 无网格局部Petrov-Galerkin法大地电磁二维正演[J]. 煤田地质与勘探, 2014, 42(6): 101-104, 109. LI Junjie, YAN iabin. Magnetotelluric two-dimensional forward modeling using meshless local Petrov-Galerkin method[J]. Coal Geology & Exploration, 2014, 42(6): 101-104, 109. |
| [55] |
MELENK J M, BABUŠKA I. The partition of unity finite element method: basic theory and applications[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(1-4): 289-314. |
| [56] |
BABUŠKA I. MELENK J M. The partition of unity method[J]. International Journal for Numerical Methods in Engineering, 1997, 40(4): 727-758. |
| [57] |
CARPINTERI A, FERRO G, VENTURA G. The partition of unity quadrature in meshless methods[J]. International Journal for Numerical Methods in Engineering, 2002, 54(7): 987-1006. |
| [58] |
CARPINTERI A, FERRO G, VENTURA G. The partition of unity quadrature in element-free crack modelling[J]. Computers & Structures, 2003, 81(18-19): 1783-1794. |
| [59] |
RABCZUK T, ZI G. A meshfree method based on the local partition of unity for cohesive cracks[J]. Computational Mechanics, 2007, 39(6): 743-760. |
| [60] |
ZOU W, ZHOU J X, ZHANG Z Q, et al. A truly meshless method based on partition of unity quadrature for shape optimization of continua[J]. Computational Mechanics, 2007, 39(4): 357-365. |
| [61] |
RABCZUK T, BORDAS S, ZI G. On three-dimensional modelling of crack growth using partition of unity methods[J]. Computers & Structures, 2010, 88(23-24): 1391-1411. |
| [62] |
CAI Y, HAN L, TIAN L, et al. Meshless method based on Shepard function and partition of unity for two-dimensional crack problems[J]. Engineering Analysis with Boundary Elements, 2016, 65: 126-135. |
| [63] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [64] |
李金铭. 地电场与电法勘探[M]. 北京: 地质出版社, 2005.
|



 姚振岸, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email:
姚振岸, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email: