2. 长江大学信息与数学学院, 湖北荆州 434023;
3. 长江大学电子信息学院, 湖北荆州 434023
2. School of Information and Mathematics, Yangtze University, Jingzhou, Hubei 434023, China;
3. School of Electronic Information, Yangtze University, Jingzhou, Hubei 434023, China
大地电磁(MT)[1-2]是一种比较成熟的地球物理勘探方法,通过计算地面测量的正交电场分量和磁场分量的扰动值研究地下介质的电性结构。MT在油气和工程勘探领域得到了广泛应用。但是,由于该方法以天然电磁场为场源,存在地面信号弱和源激发随机的缺点,极易受到各类噪声的影响,致使后续反演结果中存在不确定性。因此,在MT方法的发展过程中,消除噪声一直是地球物理勘探研究的重点[3-4]。
学者们提出了许多消除MT噪声的数据处理方法,主要包括频域方法、时—频域方法及时间序列编辑方法。频域处理方法最典型的代表是最小二乘法[5]、鲁棒估计方法[6]和远参考方法[7]。利用最小二乘法进行去噪的过程中会产生“飞点”,导致估计值偏离真值[5]。鲁棒估计方法要求大部分数据是可靠的,当输入数据包含较高水平的噪声时,鲁棒估计反而会加重噪声的影响[6]。对于远参考去噪方法,远参考点的处理效果取决于参考点与本地信号及噪声的相关性,在实际应用中,在信号相关的情况下,很难选择一个合适位置设置参考点以保证测点与噪声源之间的距离足够远[7]。时—频域处理方法的典型代表是小波变换[8-9]和Hilbert-Huang变换[10]。小波变换方法需进行母小波的选取,而对于噪声成分复杂、信号频谱丰富的实测MT数据,去噪小波变换中关于母小波的选取规则尚未有明确的结论[8-9]。基于Hilbert-Huang变换的去噪方法的缺点是会在窗口的两端引入误差[10]。对于时间序列编辑方法,Neukirch等[11]和Wang等[12]都认为在时域进行信噪分离是去除强人文噪声最直接、有效的手段。到目前为止,数学形态学、S变换、同步时间序列依赖、信号子空间增强、压缩感知重构等信号处理方法已经应用于MT数据的噪声压制[13],但这些方法都以一定的先验信息为前提,限制了方法的实际应用。为了克服这一缺点,曹小玲等[14-15]和Cao等[16]将盲源分离(Blind Source Separation, BSS)方法应用于MT信号去噪,取得了较好效果。在此研究基础上,考虑到MT信号通常由多道信号构成,每道信号中的噪声类型和强度可能不完全相同,因而需对每个通道的信号分别进行处理,即分别对单通道信号进行盲源分离。如果对整个MT观测信号进行统一去噪,则会不可避免地改变或破坏未受噪声污染的信号分段,从而影响整个MT信号的去噪效果。因此,需要对有噪声信号段和无噪声信号段进行分段识别,使未受噪声污染的信号段完整地保留下来。因此,本文首先采用改进的端点检测技术对噪声信号段进行分段识别;然后,基于经验模态分解(EMD)中的带自适应噪声的完全集合经验模态分解(Complete EEMD with Adaptive Noise, CEEMDAN)方法、盲源分离中的独立分量分析(Independent Component Analysis, ICA)进行去噪处理;最后,将去噪后的信号与未受噪声污染的信号进行拼接,得到去噪后的完整信号。该方法的优点在于将盲源分离和经验模态分解进行有效结合,能够自适应地消除MT信号中的噪声,且不需要任何先验信息。该方法只对有噪声信号分段进行去噪处理,保留了未被噪声污染的信号分段,去噪处理更有针对性,有利于保留有效低频信息。由于版面限制,且脉冲波噪声均可视为方波噪声的特殊形式,故本文只需讨论方波噪声和三角波噪声的去噪处理。
1 方法原理 1.1 CEEMDAN的基本原理EMD是Huang等[17]于1998年提出的一种处理非线性和非平稳信号的时频分析方法,目前已广泛应用于心音分析领域。为了解决EMD的模态混叠现象,Wu等[18]提出了集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)。EEMD是在EMD算法的基础上加入高斯白噪声,利用其均匀尺度特性改善极值点特征和模态混叠现象。但是EEMD的完备性较差,而且如果参数选择不正确,会产生更多的虚假分量。因此,Torres等[19]提出了CEEMDAN方法,改善了分解效果,同时也提高了分解的完备性。
EEMD和完全集合经验模态分解(CEEMD)算法通过在分解信号中加入一对正、负高斯白噪声以减少EMD的模态混合,但是得到的本征模态分量中均存在一定的白噪声,这会影响后续的信号分析和处理。CEEMDAN分解从两个方面解决了上述问题:①EMD后加入带辅助噪声的固有模态分量(Intrinsic Mode Function, IMF),而不是直接在原始信号中加入高斯白噪声信号;②EEMD和CEEMD是对经验模态分解得到的模态分量进行整体平均,而CEEMDAN则是在得到一阶IMF分量后进行整体平均计算,得到最终的一阶IMF分量,然后对剩余部分重复上述操作,有效解决了白噪声从高频向低频的转移和传递问题。
1.2 独立分量分析方法盲源分离[20]的数学模型如图 1所示,图中s(t)=s1(t),s2(t),…,sN(t)T为N维未知源信号向量,t表示时间;A为未知混合系统;x(t)=x1(t),x2(t),…,xM(t)T为M维观测信号向量,是源信号向量s(t)受到噪声向量n(t)=n1(t),n2(t),…,nM(t)T干扰所形成的。x(t)经分离系统W处理后输出信号y(t),即s(t)的估计。

|
图 1 盲源分离数学模型 符号“+”表示加入。 |
盲源分离的目的是在源信号s(t)和混合系统A及噪声n(t)均未知的情况下,仅由观测信号x(t)通过调整分离系统W(寻求分离矩阵),得到源信号s(t)的估计y(t),即
| $ \boldsymbol{y}(t)=W[\boldsymbol{x}(t)] \cong \boldsymbol{s}(t) $ | (1) |
根据Wang等[21]和王书明等[22]对不同地区实测MT信号的特征分析可知,MT信号符合盲源分离对源信号的统计特征要求。
独立分量分析(ICA)是一种十分有效的盲源分离技术,应用极其广泛[23-24]。从线性变换和线性空间角度分析,若源信号为相互独立的非高斯信号,可以将其看作线性空间的基信号,而观测信号则为源信号的线性组合,ICA就是在源信号和线性变换均未知的情况下,基于观测的混合信号估计数据空间的基本结构或者信源信号[25]。ICA的算法流程见图 2。在信源信号s(k)中各分量相互独立的假设下,观察信号x(k)经解混系统分离出各分量,输出的y(k)即可逼近s(k),这里k表示采样点号。ICA中应用较多的是FastICA算法[20, 24],本文亦采用此方法,其原理见文献[15]。

|
图 2 ICA算法流程 |
MT记录通常由多道电场、磁场信号组成,由于每道信号中的噪声形式和数量可能不同,需要对每道信号分别去噪。盲源分离方法通常要求观测信号的数目不少于源信号的数目,而单通道MT信号的去噪处理属于欠定盲源分离,即观测信号的数目小于源信号的数目。因此,必须构造其他观测信号以增加观测信号的数量,才可以采用盲源分离技术。本文提出了一种基于CEEMDAN和ICA的单通道MT噪声消除方法。该方法利用CEEMDAN技术将信号分解为多个IMF分量,实现信号维数的提升,满足BSS对源信号个数的要求。
另一方面,如果对MT信号进行统一的去噪,会对未受噪声污染的信息施加错误处理,从而使最终的去噪结果出现严重偏差,因此只需对含噪信号段进行去噪处理。为了准确识别含噪数据段和无噪数据段,采用改进的端点检测技术检测含噪信号段的端点。传统的端点检测技术主要应用于语音信号处理,通常是针对复杂的背景噪声环境,选择一些抗噪性能好的特征参数区分语音信号和非语音信号,以确定语音信号的起点和终点。语音信号与MT信号都是一维非线性非平稳信号,从波形识别的角度出发,端点检测技术可应用于MT信号中无噪信号与有噪信号的边界识别[26]。
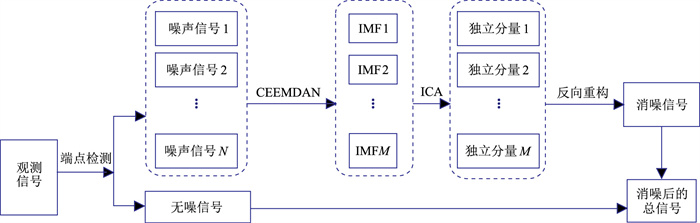
本文对传统端点检测技术进行了改进(包括阈值、能量函数、端点选取规则等方面),使之适用于MT信号的处理,具体过程见图 3。首先,利用改进的端点检测技术识别观测信号中的含噪信号端点,分别提取含噪信号分段和未受噪声污染的信号分段;其次,利用CEEMDAN对含噪声段进行处理,选择起主要作用的IMF分量进行ICA处理;然后,对得到的独立分量进行反向重构,重构结果即为去噪后的信号;最后,将观测信号中未受污染的信号与去噪后的信号进行拼接,即得到最终的去噪信号。
|
图 3 基于CEEMDAN和ICA的MT噪声消除方法流程 |
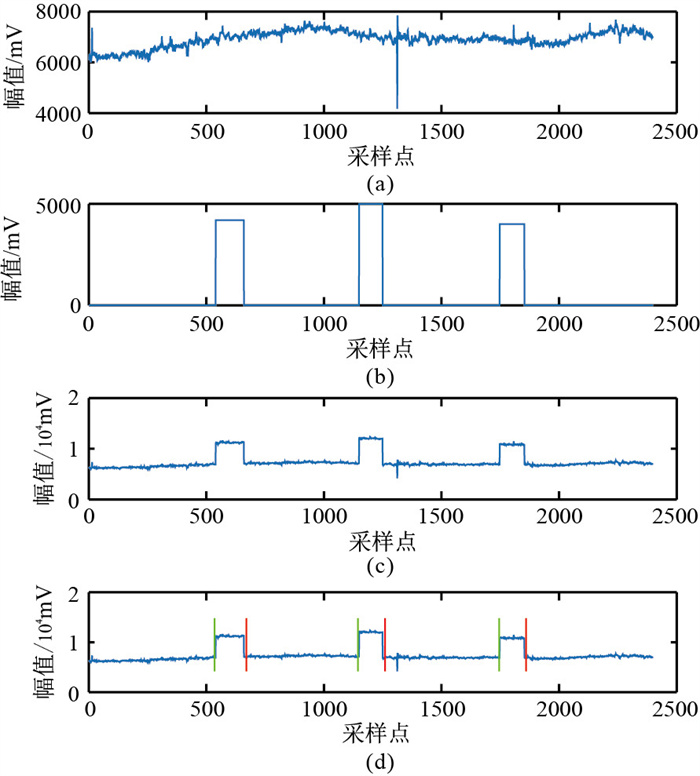
选取中国西部地区的实测数据开展模拟实验,目的是对实测MT数据中的模拟噪声进行算法检测。研究区地广人稀,人文干扰弱,电力线信号、通信信号等干扰也微弱,所以记录的电磁数据可视为无噪信号。在记录的电场Ex信号数据(图 4a)中加入方波噪声(图 4b),得到图 4c所示含噪信号。采用改进端点检测技术识别含噪段,结果如图 4d所示。由于空间限制,这里只显示2400个采样点。可以看出,改进的端点检测技术可以准确识别方波噪声所在的信号段。
|
图 4 实测MT电场分量Ex方波噪声分段识别结果 (a)无噪信号;(b)加入的方波噪声;(c)仿真含噪信号;(d)端点检测结果。绿线和红线分别表示含噪信号段的起点和终点。 |
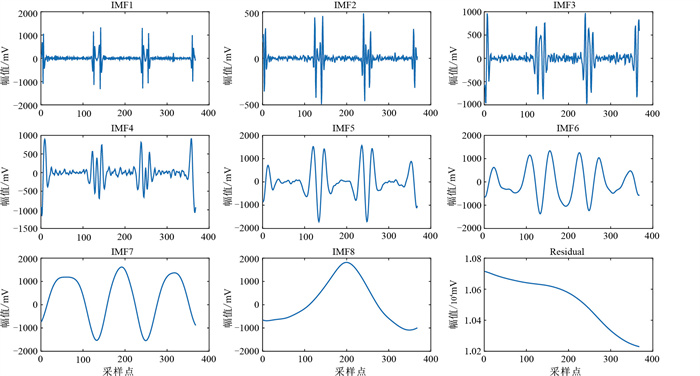
图 5为对识别出的含噪信号段(图 4d)进行CEEMDAN分解,得到的IMF分量IMF1~IMF8及残差分量Residual。由图可见,经CEEMDAN分解后,信号的主要能量集中在IMF1和IMF2中,因此选择IMF1和IMF2开展后续的ICA处理。考虑到Residual代表了信号处理的趋势,故也对其进行ICA处理,结果见图 6。
|
图 5 含噪信号CEEMDAN分解结果 |
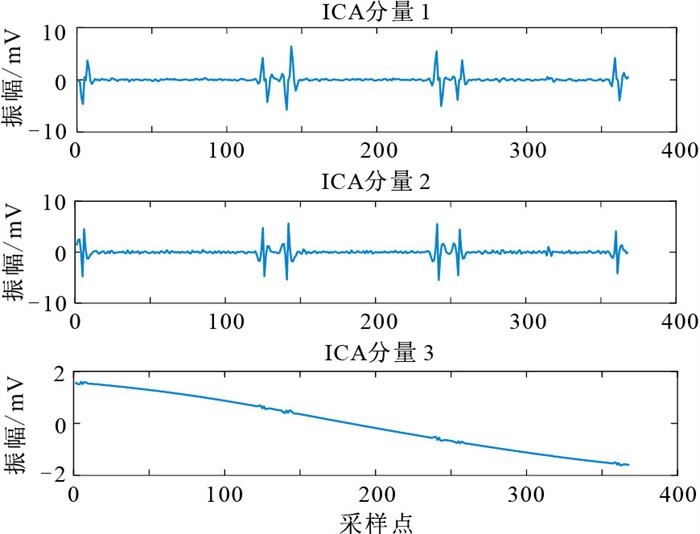
由图 6可见,IMF分量经ICA处理后,可进一步消除噪声信号中的相干噪声。根据动态因子作用方法[16]对得到的三个ICA分量(图 6)进行反方向重构,可得到去噪后的信号,再与未受噪声污染的有用信号进行拼接,可得到去噪后的MT信号。
|
图 6 ICA处理结果 |
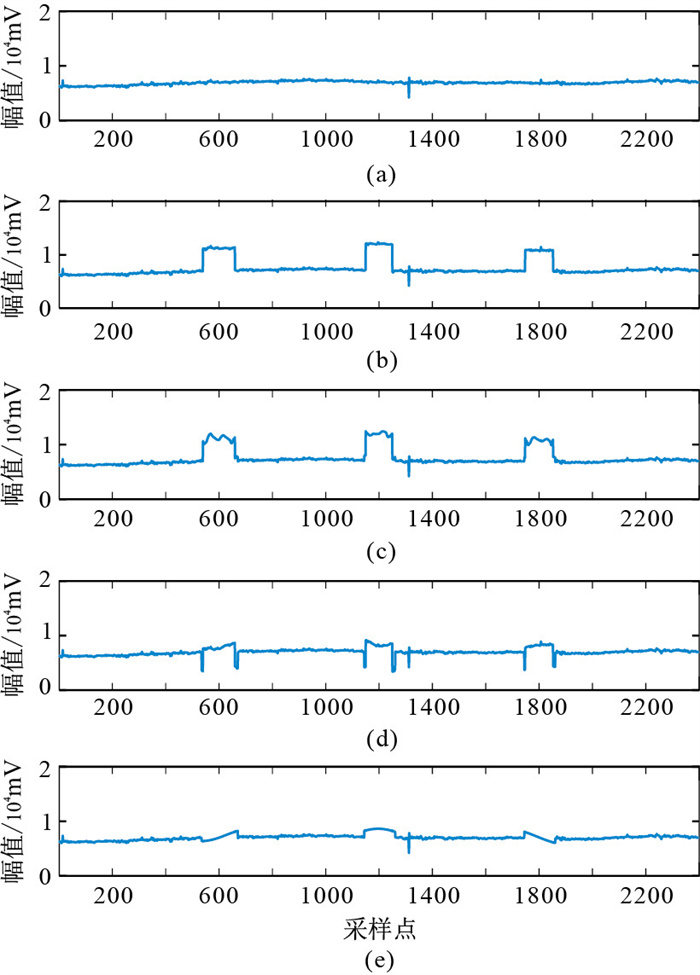
为了更好地评价本文方法处理效果,将本文方法与小波方法(即阈值去噪)和模糊熵方法进行对比。选择图 7a所示原始MT数据,由于噪声水平很低,可视为无噪信号。对该数据加入一定的噪声,得到图 7b所示的仿真含噪信号。分别采用小波方法、模糊熵方法和本文方法进行去噪处理,结果见图 7c~图 7e。分析图 7可知:对于噪声信号,由于没有先验信息,利用小波方法进行去噪处理时无法准确地确定母小波和分解层数,因此去噪效果不理想;模糊熵去噪法以模糊熵作为度量阈值,直接将阈值以下的ICA分量置零,得到去噪信号,因此去噪效果不甚理想,虽然噪声有一定程度的消除,但仍能清晰看到噪声的影响;经本文方法去噪后,信号更接近于原始的无噪声信号,表明本文方法的去噪效果明显优于其他两种方法。
|
图 7 不同方法MT数据去噪效果对比 (a)原始MT信号;(b)仿真含噪信号;(c)小波方法处理结果;(d)模糊熵方法处理结果;(e)本文方法处理结果 |
为了比较恢复信号与原始信号的相似度,采用信噪比(SNR)、斯皮尔曼相关系数(CC1)、皮尔逊相关系数(Pearson Correlation Coefficient, CC2)和均方根误差(Root Mean Square Error, RMSE))定量评价不同方法的去噪效果,其中参数SNR、CC1和CC2的值越大、RMSE的值越小,表明去噪效果越好。选取一组实测电场分量Ex,并加入不同程度的噪声形成4组含噪数据(A、B、C、D),分别对其采用不同的方法进行去噪,去噪数据的SNR、CC1、CC2、RMSE统计结果见表 1。
|
|
表 1 三种方法对不同含噪数据的去噪效果对比 |
由表 1可以看出:小波方法去噪效果不佳,信号恢复不明显;模糊熵方法有一定的去噪能力,特别是SNR较小(D组数据)时,其去噪性能相对较好,但是去噪后的数据较无噪原始信号的相关系数CC1、CC2并没有得到明显提高,说明去噪数据仍然含有大量噪声;利用本文方法去噪后数据的SNR明显提高,参数CC1和CC2也明显更高,同时RMSE始终保持在较低水平。因此,本文方法的去噪性能相对较好,即使信号的SNR较低,仍能获得较好的去噪效果,说明该方法对数据去噪具有鲁棒性。
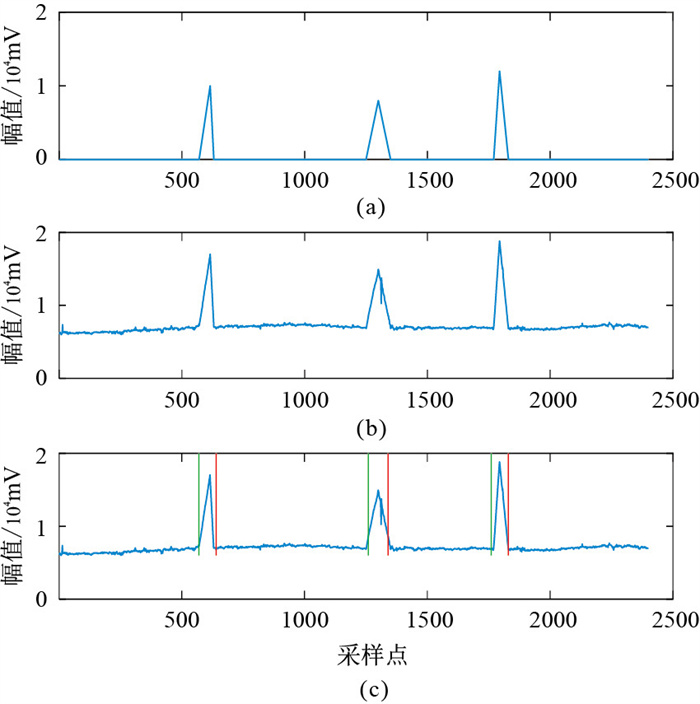
在原始(无噪)MT数据(图 7a)中加入三角波噪声(图 8a),得到含噪信号(图 8b),利用本文方法得到端点检测结果(图 8c)。分别利用小波方法、模糊熵方法及本文方法对噪声信号(图 8b)进行去噪处理,结果见图 9。由图可见,利用本文方法也能对三角波噪声进行准确识别,经本文方法去噪处理后的信号(图 9c)与原始MT信号(图 7a)最接近,说明本文方法对包含三角波噪声信号的识别和去噪也有效。
研究表明,本文方法对含脉冲波噪声数据的去噪也是有效的,由于版面限制及处理结果的相似性,不再赘述。
|
图 8 三角波噪声及识别 (a)三角波干扰噪声;(b)仿真含噪信号;(c)端点检测结果 |

|
图 9 对图 8b数据分别用小波方法(a)、模糊熵方法(b)和本文方法(c)去噪效果对比 |
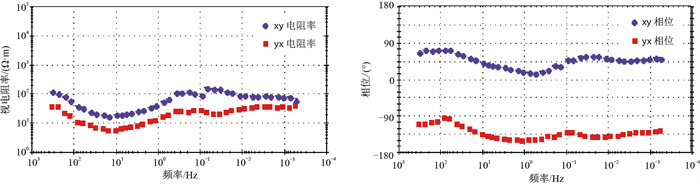
利用图 4a所示无噪MT数据进行消噪处理实验。根据实测数据计算得到测点W的视电阻率曲线和相位曲线如图 10所示,可见曲线平滑稳定,没有跳点,也没有出现45°抬升,证实了该测点基本没有受到噪声的污染。
|
图 10 基于测点W实测数据计算的视电阻率(左)和相位(右)曲线 |
对该测点的5个通道信号(2个电场分量Ex、Ey和3个磁场分量Hx、Hy、Hz)加入方波噪声,得到加噪信号(图 11)。

|
图 11 测点W的加噪电场和磁场信号 |
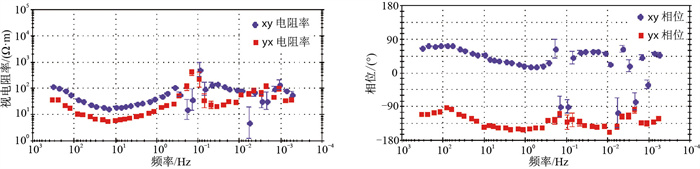
对图 11所示含方波噪声的电磁场数据进行计算,得到测点W的视电阻率和相位(图 12)。对图 11的加噪数据分别采用小波方法、模糊熵方法和本文方法进行去噪处理,并计算得到视电阻率和相位曲线(图 13)。
|
图 12 基于图 11含噪数据得到的视电阻率(左)和相位(右)曲线 |
|
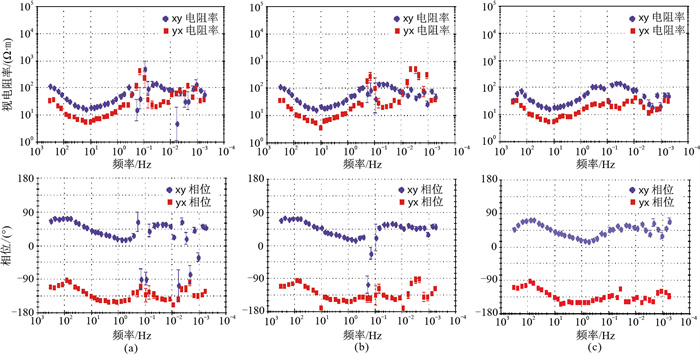
图 13 图 11含噪数据分别经小波法(a)、模糊熵法(b)、本文方法(c)去噪后计算的视电阻率(上)和相位(下)曲线 |
对比图 10、图 12和图 13可以发现,方波噪声对MT信号的视电阻率和相位曲线有很大的影响,尤其是低频部分失真明显。由于小波去噪方法不能准确地确定阈值等关键参数,去噪效果不明显。模糊熵方法和本文方法整体上去噪效果较好。进一步比较图 13b与图 13c,可以发现后者不仅视电阻率和相位曲线的形态明显优于前者,而且曲线也更平滑,说明本文方法的去噪效果优于模糊熵方法。
3.2 含噪MT数据为了验证本文方法对MT数据去噪的优越性,从天津大港工区的实测MT数据中选取两个含噪声数据点A和B进行研究,其中测点A的电磁干扰较强,噪声源主要是强工业干扰;测点B干扰较弱,主要噪声源是高压线。
对于干扰较强的测点A,两个电道信号的噪声之间及三个磁道噪声之间均具有一定的相似性,去噪结果也相似,由于篇幅所限,本文仅展示电道分量Ey和磁道分量Hz的去噪结果。Ey和Hz时间序列及端点识别结果见图 14。分别采用前述三种方法去噪,结果见图 15。
|
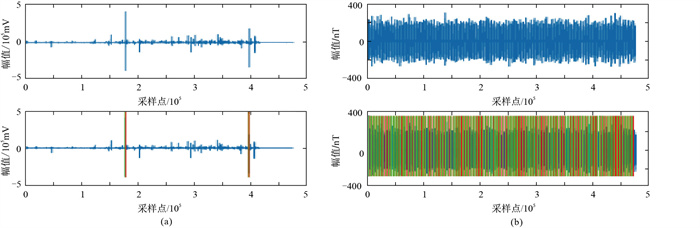
图 14 测点A的实测信号(上)及端点识别结果(下) (a)Ey分量;(b)Hz分量 |

|
图 15 测点A数据分别用小波方法(上)、模糊熵方法(中)和本文方法(下)去噪结果 (a)Ey分量;(b)Hz分量 |
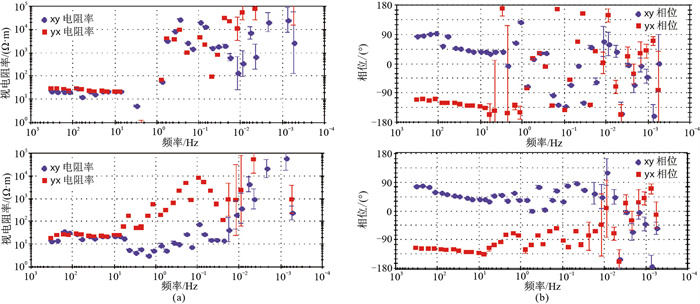
分别利用去噪前和去噪后数据计算测点A的视电阻率和相位,结果见图 16。可以看出,基于本文方法去噪数据得到的视电阻率和相位曲线(图 16下)较去噪前数据的曲线(图 16上)更平滑,特别是0.01~10Hz范围内,视电阻率和相位曲线更光滑,误差棒更短。同时不难看出,去噪后的数据质量仍不能满足后期的处理要求,根本原因在于这类强干扰对MT信号的影响巨大,原始有效信号几乎被噪声湮没,要完全恢复有效信息几乎是不可能的。然而,本文方法的处理效果明显优于其他方法,说明对强工业干扰的去噪效果具有一定的优势,具有鲁棒性。
|
图 16 基于测点A去噪前(上)、去噪后(下)数据计算的视电阻率(a)和相位(b)曲线 |
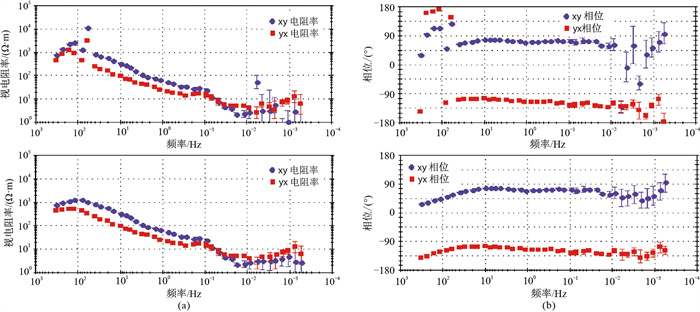
对于测点B实测数据,经本文方法去噪前、后数据计算视电阻率和相位曲线见图 17。可以看出,去噪处理后不仅高频段的“飞点”得到有效遏制,低频段的曲线误差也明显降低,整体上视电阻率和相位曲线都比去噪前更流畅、光滑。与测点A相比,B点处高压线的干扰频率较固定,本文方法对这类干扰的去噪效果较好。
|
图 17 测点B实测数据经本文方法去噪前(上)、去噪后(下)数据计算的视电阻率(a)和相位(b)曲线 |
本文提出了一种基于CEEMDAN和ICA的MT数据去噪方法。首先,利用改进的端点检测技术识别观测信号中的含噪信号分段,并对其进行提取;然后,利用CEEMDAN对含噪信号分段进行分解,实现信号维数的提升,并选择起主要作用的IMF分量进行ICA处理;接着,对得到的独立分量进行反向重构,获得的信号即去噪信号;最后,将观测信号中未受污染的信号与去噪信号进行拼接,得到完整信号。
对MT实测数据进行去噪处理,发现本文方法不仅对弱干扰(如高压线干扰)MT信号的去噪效果十分显著,对强干扰(如强工业干)数据的去噪效果亦优于其他方法。
通过对实测MT数据进行去噪处理,对比不同方法的处理结果,可知本文方法具有如下优势:①利用改进的端点检测技术,可对噪声进行准确识别;②将经验模态分解技术与盲源分离技术进行有效结合,可实现MT数据的自适应去噪;③传统去噪方法仅仅针对不同的噪声形式开展去噪处理,本文方法适用于全部三种主要噪声形式(方波噪声、三角波噪声、脉冲波噪声)的去噪,具有更广泛的实用性。
| [1] |
BERDICHEVSKY M N, DIMITRIEV V I. Basic Principles of Interpretation of Magnetotelluric Soun-ding Curves[M]. Geoelectric & Geothermal Studies, 1976, 163-221.
|
| [2] |
KAUFMAN A A, KELLER G V. The Magnetotelluric Sounding Method[M]. Amsterdam: Elsevier Scientific Pub. Co., 1981.
|
| [3] |
CAI J. A combinatorial filtering method for magnetotelluric data series with strong interference[J]. Arabian Journal of Geosciences, 2016, 9(13): 628. DOI:10.1007/s12517-016-2658-5 |
| [4] |
CHEN R, HE Z, HE L, et al. Random noise and coherent interference estimation of MT instrument [C]. 2008 International Conference on Computer and Electrical Engineering, 2008, 368-372.
|
| [5] |
SIMS W E, BOSTICK F X, SMITH H W. The estimation of magnetotelluric impedance tensor elements from measured data[J]. Geophysics, 1971, 36(5): 938-942. DOI:10.1190/1.1440225 |
| [6] |
EGBERT G D. Robust multiple-station magnetotelluric data processing[J]. Geophysical Journal International, 1997, 130(2): 475-496. DOI:10.1111/j.1365-246X.1997.tb05663.x |
| [7] |
SHALIVAHAN, BHATTACHARYA B B. How remote can the far remote reference site for magnetotelluric measurements be?[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B6): ETG 1-1-ETG 1-7. |
| [8] |
ESCALAS M, QUERALT P, LEDO J, et al. Polarisation analysis of magnetotelluric time series using a wavelet-based scheme: a method for detection and characterisation of cultural noise sources[J]. Physics of the Earth and Planetary Interiors, 2013, 218: 31-50. DOI:10.1016/j.pepi.2013.02.006 |
| [9] |
TARY J B, HERRERA R H, HAN J, et al. Spectral estimation: What is new? What is next?[J]. Reviews of Geophysics, 2014, 52(4): 723-749. DOI:10.1002/2014RG000461 |
| [10] |
CHEN J, HEINCKE B, JEGEN M, et al. Using empirical mode decomposition to process marine magnetotelluric data[J]. Geophysical Journal International, 2012, 190(1): 293-309. DOI:10.1111/j.1365-246X.2012.05470.x |
| [11] |
NEUKIRCH M, GARCIA X. Nonstationary magnetotelluric data processing with instantaneous parameter[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(3): 1634-1654. DOI:10.1002/2013JB010494 |
| [12] |
WANG H, CAMPANYÀ J, CHENG J, et al. Synthesis of natural electric and magnetic time-series using inter-station transfer functions and time-series from a neighboring site (STIN): applications for processing MT data[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(8): 5835-5851. DOI:10.1002/2017JB014190 |
| [13] |
李晋, 燕欢, 汤井田, 等. 基于匹配追踪和遗传算法的大地电磁噪声压制[J]. 地球物理学报, 2018, 61(7): 3086-3101. LI Jin, YAN Huan, TANG Jingtian, et al. Magnetotelluric noise suppression based on matching pursuit and genetic algorithm[J]. Chinese Journal of Geophysics, 2018, 61(7): 3086-3101. |
| [14] |
曹小玲, 严良俊, 陈清礼, 等. 盲源分离算法在大地电磁信号去噪中的应用[J]. 物探化探计算技术, 2017, 39(4): 456-464. CAO Xiaoling, YAN Liangjun, CHEN Qingli, et al. An application of blind source separation algorithm for denoising in magnetotelluric signal[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2017, 39(4): 456-464. DOI:10.3969/j.issn.1001-1749.2017.04.05 |
| [15] |
曹小玲, 刘开元, 严良俊. 大地电磁的小波变换—独立分量分析去噪[J]. 石油地球物理勘探, 2018, 53(1): 206-213. CAO Xiaoling, LIU Kaiyuan, YAN Liangjun. Magnetotelluric data de-noising based on wavelet transform and independent component analysis[J]. Oil Geophy-sical Prospecting, 2018, 53(1): 206-213. |
| [16] |
CAO X, YAN L. Power line interference noise elimination method based on independent component ana-lysis in wavelet domain for magnetotelluric signal[J]. Geosystem Engineering, 2018, 21(5): 251-261. DOI:10.1080/12269328.2017.1394225 |
| [17] |
HUANG N E, SHEN Z, LONG S R, et al. The empiri-cal mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London.Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [18] |
WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [19] |
TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise [C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2011, 4144-4147.
|
| [20] |
JUTTEN C, HERAULT J. Blind separation of sources, part I: an adaptive algorithm based on neuromimetic architecture[J]. Signal Processing, 1991, 24(1): 1-10. DOI:10.1016/0165-1684(91)90079-X |
| [21] |
WANG S, WANG J. Analysis on statistic characteristics of magnetotelluric signal[J]. Acta Seismologica Sinica, 2004, 17(6): 735-740. DOI:10.1007/s11589-004-0013-5 |
| [22] |
王书明, 王家映. 关于大地电磁信号非最小相位性的讨论[J]. 地球物理学进展, 2004, 19(2): 216-221. WANG Shuming, WANG Jiaying. Discussion on the non-minimum phase of magnetotelluric signals[J]. Progress in Geophysics, 2004, 19(2): 216-221. DOI:10.3969/j.issn.1004-2903.2004.02.002 |
| [23] |
周媛媛, 常莹, 陈浩, 等. 基于参考台的盲源分离法在抑制地磁场近场噪音中的应用研究[J]. 地球物理学报, 2019, 62(2): 572-586. ZHOU Yuanyuan, CHANG Ying, CHEN Hao, et al. Application of reference-based blind source separation method in the reduction of near-field noise of geomagnetic measurements[J]. Chinese Journal of Geophy-sics, 2019, 62(2): 572-586. |
| [24] |
COMON P, JUTTEN C. Handbook of Blind Source Separation: Independent Component Analysis and Applications[M]. Oxford: Academic Press, 2010: 208-220.
|
| [25] |
曹小玲, 严良俊, 蒋涛. 基于DWT-EEMD的盲源分离算法在MT工频干扰消除中的应用[J]. 煤田地质与勘探, 2018, 46(2): 164-172. CAO Xiaoling, YAN Liangjun, JIANG Tao. Application of blind source separation algorithm based on DWT-EEMD in removal of power line interference for MT[J]. Coal Geology & Exploration, 2018, 46(2): 164-172. |
| [26] |
李晋, 汤井田, 王玲, 等. 基于信号子空间增强和端点检测的大地电磁噪声压制[J]. 物理学报, 2014, 63(1): 019101. LI Jin, TANG Jingtian, WANG Ling, et al. Noise suppression for magnetotelluric sounding data based on signal subspace enhancement and endpoint detection[J]. Acta Physica Sinica, 2014, 63(1): 019101. |



 曹小玲, 湖北省荆州市荆州区南环路1号长江大学信息与数学学院, 434023。Email:
曹小玲, 湖北省荆州市荆州区南环路1号长江大学信息与数学学院, 434023。Email: 