2. 中国地质大学(武汉)地球内部多尺度成像湖北省重点实验室, 湖北武汉 430074;
3. 中国地质大学(武汉)地质过程与矿产资源国家重点实验室, 湖北武汉 430074
2. Hubei Subsurface Multiscale Imaging Key Laboratory, China University of Geosciences(Wuhan), Wuhan, Hubei 430074, China;
3. State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences(Wuhan), Wuhan, Hubei 430074, China
磁法勘探技术的发展历程按照测量的物理量可以大致分为总磁场强度(标量)测量、磁场三分量(矢量)测量与全张量磁力梯度(张量)测量三个阶段[1]。其中全张量磁力梯度是指二阶磁力梯度张量,即由磁位在三个正交方向的二阶混合导数组成的一个对称矩阵(共9个元素),相比标量和矢量测量,从磁场及其场源角度而言,二阶磁力梯度张量包含更丰富的信息[2-4]。随着磁力梯度张量测量系统的成功研发[5-6],二阶磁力梯度张量探测技术已经广泛应用于军事、环境、工程与资源勘探等诸多领域[6]。在二阶磁力梯度张量概念基础上,Deng等[7]基于引力曲率(gravitational curvature, GC)提出了磁力曲率(magnetic curvature, MC)的概念,即三阶磁力梯度张量,由27个元素组成,每个元素均表示磁位在相应三个正交方向的三阶混合导数。尽管现今还未研制出三阶磁力梯度张量测量仪器,但是根据磁力勘探技术的发展历程以及三阶重力梯度张量勘探的概念[8],可以推测三阶磁力梯度张量探测技术可能是未来磁法勘探、地磁场测量与磁性目标定位的一个重要发展方向。Yin等[9]提出了采用三阶磁力梯度张量部分元素进行磁偶极源定位。
简单规则形体的磁场效应正演计算可为三阶磁力梯度张量的测量技术及其解释与反演方法研究提供重要的仿真模拟工具。Deng等[10]根据重力位四阶导数和泊松方程推导了均匀磁化的球面棱柱体和球壳的三阶磁力梯度张量积分表达式;Sui等[11]给出了磁偶极源的三阶磁力梯度张量解析公式。此外,多数磁力异常转换参量的正演计算也涉及三阶磁力梯度张量的部分元素,例如:Zhang等[12]采用正则化磁源强度(normalized source strength, NSS)的一阶垂向导数估算磁力异常磁化方向,但是仅给出了磁偶极源的正演计算公式;Beiki等[13]、Clark[14-15]推导了磁偶极源与球体等(不包括均匀磁化直立长方体)简单规则形体的正则化磁源强度一阶导数计算公式。但是,作为磁力异常正演模拟[16-18]与三维反演[19]最基本、最常用的一种三度体场源模型,均匀磁化直立长方体的三阶磁力梯度张量解析表达式尚未见相关文献发表。
前人对均匀磁化直立长方体的总磁场强度、磁场三分量与二阶磁力梯度张量等的解析表达式进行了深入的推导与研究[20-27]。郭志宏等[25]首次指出长方体总磁场强度异常(ΔT)及其梯度场理论表达式在上半无源空间存在某些测点场值无法计算的解析奇点问题,并且重新推导了无解析奇点的理论表达式;为了提高计算效率,骆遥等[26]在郭志宏等[25]研究的基础上,采用欧拉方程对长方体磁场理论表达式进行了重新推导,导出了新的长方体ΔT场及其梯度场在上半无源空间的无解析奇点理论表达式;钟炀等[1]再次分别整理与化简了郭志宏等[25]和骆遥等[26]推导的长方体磁力三分量理论表达式,并据此分别推导了两套长方体二阶磁力梯度张量的理论表达式,模型试验分析结果表明基于骆遥等[26]所提方法推导的理论表达式计算效率更高。此外,Kuang等[27]推导了适用于起伏地形的长方体磁力异常无解析奇点正演公式;邰振华等[28]推导了倾斜长方体的二阶磁力梯度张量正演公式。
本文在前人推导的磁力异常三分量和二阶磁力梯度张量解析表达式的基础上推导了均匀磁化直立方长体的三阶磁力梯度张量解析表达式,验证了推导公式的正确性,并将其应用于均匀磁化直立长方体其他磁力异常转换参量(包括总磁场强度异常的一阶垂向导数解析信号、磁力二阶梯度张量不变量的一阶导数及正则化磁源强度的一阶导数)的正演计算,旨在为将来磁力三阶梯度张量测量与勘探方法研究以及基于磁力异常转换参量的解释方法研究[29]提供一种基于均匀磁化直立长方体模型的磁场效应正演计算手段。
1 三阶磁力梯度张量的概念如图 1所示,首先建立直角坐标系xyz,x轴与y轴在水平面内分别指向地理北和地理东,z轴与x、y轴形成右手坐标系。图中,P(x, y, z)为待计算点或观测点,Q(ξ, η, ζ)为长方体内部任意一点,ξ1和ξ2、η1和η2、ζ1和ζ2分别为直立长方体在x轴、y轴、z轴三个方向投影的最小和最大坐标值,

|
图 1 直角坐标系均匀直立长方体几何示意图 |
假设地下场源在测点P(x, y, z)处产生的磁位为V,则磁力矢量B的三个分量[30]为
| $ B_\alpha=\frac{-\partial V}{\partial \alpha} \quad \alpha \in\{x, y, z\} $ | (1) |
二阶磁力梯度张量B为一个3×3的实对称矩阵,其元素为磁力某分量沿三个坐标轴中某方向的一阶导数[28]
| $ B_{\alpha \beta}=\frac{\partial B_a}{\partial \beta}=-\frac{\partial^2 V}{\partial \alpha \partial \beta} \quad \forall\{\alpha, \beta\} \in\{x, y, z\} $ | (2) |
由于该矩阵为对称矩阵,且磁位在无源空间满足拉普拉斯方程(即该矩阵的迹为零),因此二阶磁力梯度张量仅有5个独立元素[2-4]。
三阶磁力梯度张量
| $ \begin{gathered} B_{\alpha \beta \gamma}=\frac{\partial B_{\alpha \beta}}{\partial \gamma}=\frac{\partial^2 B_\alpha}{\partial \beta \partial \gamma}=-\frac{\partial^3 V}{\partial \alpha \partial \beta \partial \gamma} \\ \forall\{\partial, \beta, \gamma\} \in\{x, y, z\} \end{gathered} $ | (3) |
由于该张量具有对称性,且磁力三分量在无源空间依然满足拉普拉斯方程,因此三阶磁力梯度张量仅有7个独立元素[8, 10]。
2 正演计算公式根据骆遥等[26]的公式推导,可以将图 1中均匀磁化直立长方体在无源空间中任一点P(x, y, z)处产生的磁力异常三分量的无解析奇点正演计算公式写为
| $ \begin{gathered} B_\alpha=\left.\left.\left.\frac{\mu_0 M}{4 \pi}\left(l E_\alpha+m F_\alpha+n G_\alpha\right)\right|_{\xi_1-x} ^{\xi_2-x}\right|_{\eta_1-y} ^{\eta_2-y}\right|_{\zeta_1-z} ^{\xi_2-z} \\ \alpha \in\{x, y, z\} \end{gathered} $ | (4) |
式中:l=cosIcosD,m=cosIsinD,n=sinI,其中I为场源磁化倾角,D为场源磁化偏角;μ0=4π×10-7 H/m为真空磁导率;M为磁化强度;Eα、Fα与Gα的表达式见表 1。
|
|
表 1 Eα、Fα与Gα表达式 |
钟炀等[1]基于式(4),保持积分的上、下限不变,对Eα、Fα与Gα分别沿x、y与z方向求偏导数,推导了均匀磁化直立长方体的二阶磁力梯度张量计算公式
| $ B_{\alpha \beta}=-\left.\left.\left.\frac{\mu_0 M}{4 \pi}\left(I E_{\alpha \beta}+m F_{\alpha \beta}+n G_{\alpha \beta}\right)\right|_{\xi_1-x} ^{z_1-x}\right|_{y_1-y} ^{n_2-y}\right|_{b_1-z} ^{\xi_2-z} \quad \forall\{\alpha, \beta\} \in\{x, y, z\} $ | (5) |
式中Eαβ、Fαβ与Gαβ的表达式见表 2。
|
|
表 2 Eαβ、Fαβ与Gαβ的表达式 |
基于式(5)对Eαβ、Fαβ与Gαβ分别沿x、y与z方向求偏导数,经过化简即可推导出均匀磁化直立长方体的三阶磁力梯度张量计算公式为
| $ \begin{gathered} B_{\alpha \beta \gamma}=\left.\left.\left.\frac{\mu_0 M}{4 \pi}\left(l E_{\alpha \beta \gamma}+m F_{\alpha \beta \gamma}+n G_{\alpha \beta \gamma}\right)\right|_{\xi_1-x} ^{\xi_2-x}\right|_{\eta_1-y} ^{\eta_2-y}\right|_{\xi_1-z} ^{\xi_2-z} \\ \forall\{\alpha, \beta, \gamma\} \in\{x, y, z\} \end{gathered} $ | (6) |
其中Eαβγ、Fαβγ与Gαβγ的表达式参见表 3。
|
|
表 3 Eαβγ、Fαβγ与Gαβγ表达式 |
由表 1、表 2和表 3可见,Eα、Fα、Gα之间、Eαβ、Fαβ、Gαβ之间以及Eαβγ、Fαβγ、Gαβγ之间存在一些相同的表达式,例如Fx与Ey、Gx与Ez、Gy与Fz。
3 公式正确性验证下面通过数值计算,分别采用磁力二阶梯度张量空间差分和拉普拉斯方程两种方法验证式(6)的正确性。
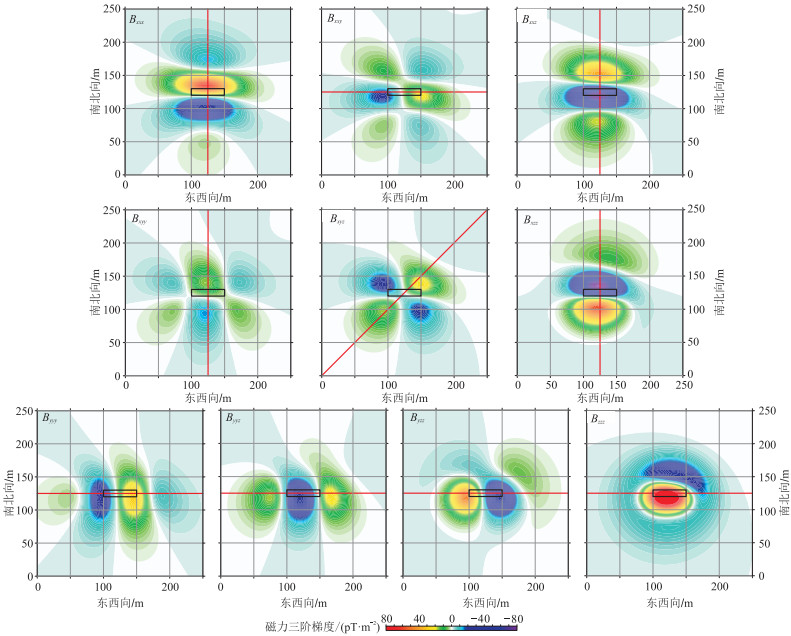
3.1 理论场源模型及正演计算结果对于图 1所示的均匀磁化直立长方体,设置理论模型参数为:I= 50°、D = 30°;M= 10 A/m;地磁场方向与模型磁化方向相同;矩形棱柱体中心坐标为(125 m, 125 m, 50 m),南北向长度为10 m,东西向长度为50 m,垂向长度为6 m;计算高度z= 0;观测测网的大小为250 m×250 m,网格间距为5 m×5 m。利用式(6)计算得到理论模型的磁力三阶梯度张量见图 2。可见,每个元素的空间分布形态各异,这意味着在相同的测点分布情况下,相比于磁力标量测量,梯度张量测量能捕获更多的磁场及其场源信息。
3.2 基于磁力二阶梯度张量差分计算公式的正确性验证为了验证本文推导的计算公式的正确性,首先采用均匀磁化直立长方体的二阶梯度张量公式计算理论模型的磁力二阶梯度张量,然后用中心差分方法计算理论模型的磁力三阶梯度张量,最后与推导的三阶梯度张量公式直接计算结果进行对比。
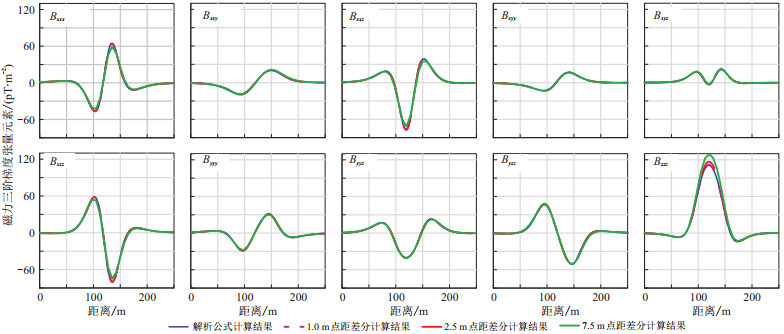
选用3组不同差分点距(1.0、2.5、7.5 m)的计算结果与解析公式直接计算结果进行对比。图 3为图 2中红色实线所示位置的磁力三阶梯度张量曲线以及不同点距的差分计算结果。由图可知,选用的3组点距差分计算结果均逼近磁力三阶梯度张量直接计算结果,并且点距越小差分计算精度越高。表 4为1.0 m点距差分计算结果和解析计算结果的统计,可见两者之间的差异非常微弱,且差异均值均为零,证明了本文推导公式的正确性。
|
图 3 分别采用解析表达式与磁力二阶梯度张量中心差分计算的磁力三阶梯度张量对比 |
|
|
表 4 1.0 m点距差分计算结果与解析计算结果对比 |
磁位在场源外部空间满足拉普拉斯方程,故磁力三阶梯度张量的部分元素应该满足:Bxxx+Bxyy+Bxzz=0,Byxx+Byyy+Byzz=0,Bzxx+Bzyy+Bzzz=0。利用此标准检验图 2计算结果的可靠性。三阶磁力梯度张量拉普拉斯参数计算结果如图 4所示,可见满足上述3个方程,误差几乎为零,从另一方面证明了本文推导公式的正确性。

|
图 4 三阶磁力梯度张量拉普拉斯参数计算结果 (a)Bxxx+Bxyy+Bxzz;(b)Byxx+Byyy+Byzz;(c)Bzxx+Bzyy+Bzzz |
如引言所述,许多磁力异常转换参量的正演计算也涉及三阶磁力梯度张量的部分元素。本节将磁力三阶梯度张量正演计算公式分别应用于直立长方体总磁场强度异常的一阶垂向导数解析信号、磁力二阶梯度张量不变量的一阶导数、正则化磁源强度的一阶导数的正演计算,旨在为基于这些磁力异常转换参量的解释方法与三维反演研究提供一种正演模拟手段。
4.1 总磁场强度异常一阶垂向导数解析信号的正演计算磁异常的解析信号振幅(Analytical Signal Amplitude, ASM)亦称为总梯度模量,利用极大值位置确定地质体的边界或中心位置。Nabighian[31]首次提出二维解析信号的概念,并且证明了二维解析信号振幅不受磁化方向的影响;然后Nabighian[32]将其延伸至三维解析信号;Agarwal等[33]首次证明了三维磁力异常解析信号振幅与磁化方向有关;Li[34]指出三维解析信号振幅弱依赖于磁化方向。为了提高对场源的横向分辨能力,Hsu等[35]提出了三维增强解析信号振幅,即三维n阶垂向导数的解析信号振幅(ASMn),其表达式为
| $ \mathrm{ASM}_n=\sqrt{\left(\frac{\partial}{\partial x} \frac{\partial^n \Delta T}{\partial z^n}\right)^2+\left(\frac{\partial}{\partial y} \frac{\partial^n \Delta T}{\partial z^n}\right)^2+\left(\frac{\partial}{\partial z} \frac{\partial^n \Delta T}{\partial z^n}\right)^2} $ | (7) |
因此,磁异常ΔT的零阶和一阶垂向导数的解析信号计算公式分别为
| $ \mathrm{ASM}_0=\sqrt{\left(\frac{\partial \Delta T}{\partial x}\right)^2+\left(\frac{\partial \Delta T}{\partial y}\right)^2+\left(\frac{\partial \Delta T}{\partial z}\right)^2} $ | (8) |
| $ \mathrm{ASM}_1=\sqrt{\left(\frac{\partial^2 \Delta T}{\partial x \partial z}\right)^2+\left(\frac{\partial^2 \Delta T}{\partial y \partial z}\right)^2+\left(\frac{\partial^2 \Delta T}{\partial z^2}\right)^2} $ | (9) |
其中
| $ \begin{gathered} \frac{\partial \Delta T}{\partial \alpha}=B_{x a} \cos I \cos D+B_{y a} \cos I \sin D+ \\ B_{z a} \sin I \quad \alpha \in\{x, y, z\} \end{gathered} $ | (10) |
| $ \begin{gathered} \frac{\partial^2 \Delta T}{\partial z \partial \alpha}=B_{x z a} \cos I \cos D+B_{y z a} \cos I \sin D+ \\ B_{z z a} \sin I \quad \alpha \in\{x, y, z\} \end{gathered} $ | (11) |
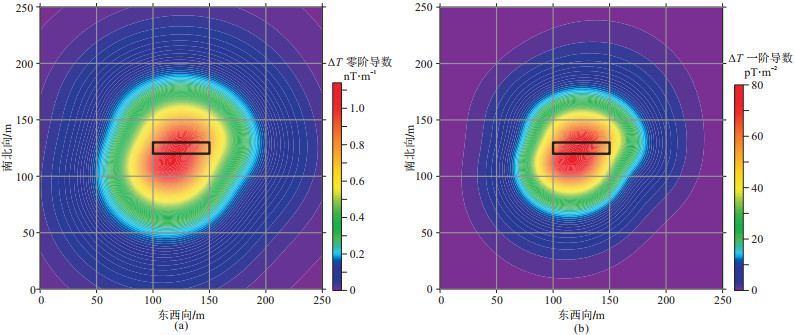
采用与图 1相同的几何参数与物性参数,计算三阶磁力梯度张量部分元素,并将其代入式(10)与式(11),进而根据式(8)与式(9)可获得该均匀磁化直立长方体的总磁场强度异常零阶与一阶垂向导数解析信号分布,如图 5所示。
|
图 5 均匀磁化直立长方体的总磁场强度异常零阶(a)与一阶(b)垂向导数解析信号分布 |
磁力二阶梯度张量B的不变量不随坐标系统旋转而变化且不受地磁场方向的影响[6],因而被广泛应用于磁偶极源定位[9, 11]。二阶磁力梯度张量的本征方程[2]可以表示为
| $ \lambda^3-K_0 \lambda^2+K_1 \lambda-K_2=0 $ | (12) |
式中:λ为张量B的本征值或特征值;K0、K1和K2均为张量B的不变量[2],其表达式分别为
| $ \left\{\begin{array}{l} K_0=B_{x x}+B_{y y}+B_{z z}=0 \\ K_1=B_{x x} B_{y y}+B_{y y} B_{z z}+B_{z z} B_{x x}-B_{x y}^2-B_{y z}^2-B_{z x}^2 \\ K_2=B_{x x}\left(B_{y y} B_{z z}-B_{y z} B_{y z}\right)+B_{x y}\left(B_{y z} B_{x z}-B_{x y} B_{z z}\right)+B_{x z}\left(B_{x y} B_{y z}-B_{x z} B_{y y}\right) \end{array}\right. $ | (13) |
基于Baur等[36]的张量不变量理论,Deng等[37]推导了磁力二阶梯度张量B的另一类张量不变量的J0、J1和J2,其表达式为
| $ \left\{\begin{aligned} J_0= & B_{x x}+B_{y y}+B_{z z}=0 \\ J_1= & B_{x x}^2+B_{y y}^2+B_{z z}^2+2 B_{x y}^2+2 B_{y z}^2+2 B_{z x}^2 \\ J_2= & B_{x x}^3+B_{y y}^3+B_{z z}^3+3 B_{x x}\left(B_{x y}^2+B_{x z}^2\right)+ \\ & 3 B_{y y}\left(B_{x y}^2+B_{y z}^2\right)+3 B_{z z}\left(B_{x z}^2+B_{y z}^2\right)+ \\ & 6 B_{x y} B_{x z} B_{y z} \end{aligned}\right. $ | (14) |
在式(13)与式(14)的基础上,Deng等[37]推导了两类张量不变量的一阶导数Kiα和Jiα(i = 0, 1, 2;α = x, y, z),其计算表达式参见文献[37]。二阶磁力梯度张量B的两类张量不变量的一阶导数之间具有如下关系
| $ \left\{\begin{array}{l} K_{0 a}=J_{0 a} \\ K_{1 a}=J_{0_a} J_0-J_{1 a} / 2 \\ K_{2 a}=J_{2 a} / 3+\left(J_{0_a} J_0^2-J_{0_a} J_0-J_{1 a} J_0\right) / 2 \\ J_{1 a}=2\left(K_{0 a} K_0-K_{1 a}\right) \\ J_{2 a}=3\left(K_{0 a} K_0^2-K_{0 a} K_1-K_{1 a} K_0+K_{2 a}\right) \end{array}\right. $ | (15) |
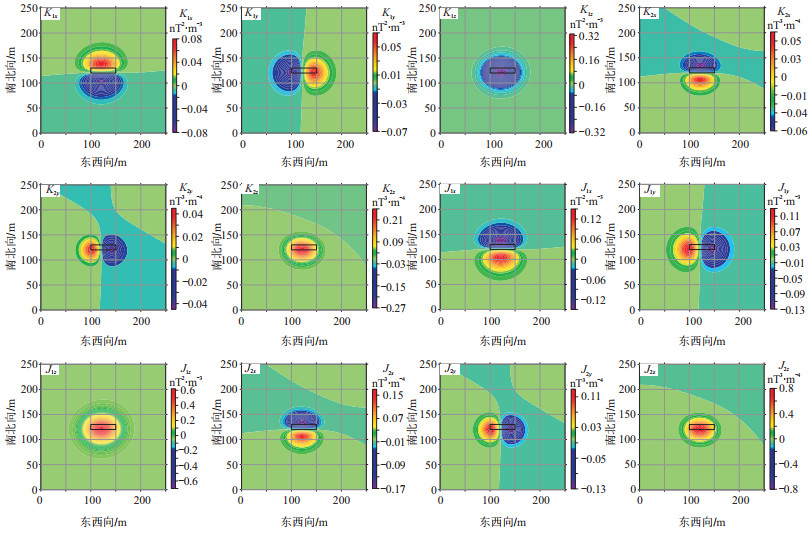
采用与图 1相同的几何与物性参数,计算二阶与三阶磁力梯度张量部分元素,并将其代入Deng等[37]给出的表达式,即可计算得到均匀直立长方体的二阶磁力梯度张量不变量的一阶导数分布,如图 6所示。
|
图 6 均匀直立长方体的二阶磁力梯度张量不变量的一阶导数 |
正则化磁源强度NSS[13]是一个受场源磁化方向影响非常微弱的磁力异常转换参量,广泛应用于磁力异常场源磁化方向估算[38]与三维反演[39]。Zhang等[12]采用NSS的垂向一阶导数进一步降低了场源磁化方向的影响,提升了场源的横向分辨率。
对于磁场二阶梯度张量矩阵B,利用其三个特征值λi(i = 1, 2, 3;λ1 ≥λ2≥ λ3),可以得到正则化磁源强度[2, 13]
| $ \mathrm{NSS}=\sqrt{-\lambda_2^2-\lambda_1 \lambda_3} $ | (16) |
基于式(12),可以求得λi对不同方向的一阶导数
| $ \begin{gathered} \frac{\partial \lambda_i}{\partial \alpha}=\frac{K_{2_\alpha}-K_{1_a \lambda_i}}{3 \lambda_i^2+K_1} \quad \alpha \in\{x, y, z\} \\ 3 \lambda_i^2+K_1 \neq 0 \end{gathered} $ | (17) |
然后,基于
| $ \left\{\begin{array}{l} \mathrm{NSS}_a=\frac{\partial \mathrm{NSS}}{\partial \alpha}=-\frac{\frac{\partial \lambda_1}{\partial \alpha} \lambda_3+2 \frac{\partial \lambda_2}{\partial \alpha} \lambda_2+\frac{\partial \lambda_3}{\partial \alpha} \lambda_1}{2 \mathrm{NSS}} \quad \alpha \in\{x, y, z\} \\ \mathrm{NSS}_{\mathrm{he}}=\sqrt{\mathrm{NSS}_x^2+\mathrm{NSS}_y^2} \\ \mathrm{NSS}_{\mathrm{tg}}=\sqrt{\mathrm{NSS}_x^2+\mathrm{NSS}_y^2+\mathrm{NSS}_z^2} \end{array}\right. $ | (18) |
即可得到NSS的一阶导数(NSSx、NSSy、NSSz)、水平梯度模(NSShg)和总梯度模(NSStg)。
采用与图 1相同的几何与物性参数,计算二阶磁力梯度张量,并将该张量的三个特征值代入式(16)得到NSS,再利用式(17)得到三个特征值在三个方向的一阶导数,最后将其代入式(18),即可计算得到NSS的一阶导数、水平梯度模NSShg和总梯度模NSStg,如图 7所示。

|
图 7 均匀直立长方体的正则化磁源强度NSS(a)及其一阶导数NSSx(b)、NSSy(c)、NSSz(d)、水平梯度模NSShg(e)和总梯度模NSStg(f) |
(1) 基于前人推导的均匀磁化直立长方体磁力三分量和二阶磁力梯度张量无解析奇点正演计算公式,本文推导了均匀磁化直立长方体三阶磁力梯度张量无解析奇点正演计算公式,并且将磁力三分量、二阶与三阶磁力梯度张量正演计算表达式进行了形式上的统一处理。
(2) 将基于磁力二阶梯度张量差分的三阶磁力梯度张量计算结果与本文推导的解析公式的直接计算结果进行对比,验证了本文推导公式的正确性,且计算结果在无源空间满足拉普拉斯方程。
(3) 将本文推导的三阶磁力梯度张量无解析奇点正演计算公式应用于均匀磁化直立长方体其他磁力异常转换参量(包括总磁场强度异常的一阶垂向导数解析信号、磁力二阶梯度张量不变量的一阶导数、正则化磁源强度的一阶导数)的正演计算,可为基于磁力异常转换参量的解释与三维反演方法研究提供一种基于均匀磁化直立长方体的仿真模拟手段和正演计算工具。
| [1] |
钟炀, 管彦武, 石甲强, 等. 长方体全张量磁梯度的两种正演公式对比[J]. 世界地质, 2019, 38(4): 1073-1081, 1090. ZHONG Yang, GUAN Yanwu, SHI Jiaqiang, et al. Comparison of two forward modeling formulas for full tensor magnetic gradient of cuboid[J]. Global Geology, 2019, 38(4): 1073-1081, 1090. DOI:10.3969/j.issn.1004-5589.2019.04.018 |
| [2] |
PEDERSEN L B, RASMUSSEN T M. The gradient tensor of potential field anomalies: some implications on data collection and data processing of maps[J]. Geophysics, 1990, 55(12): 1558-1566. DOI:10.1190/1.1442807 |
| [3] |
SCHMIDT P W, CLARK D A. The magnetic gradient tensor: its properties and uses in source characterization[J]. The Leading Edge, 2006, 25(1): 75-78. DOI:10.1190/1.2164759 |
| [4] |
FOSS C. Improvements in source resolution that can be expected from inversion of magnetic field tensor data[J]. The Leading Edge, 2006, 25(1): 81-84. DOI:10.1190/1.2164761 |
| [5] |
张昌达. 航空磁力梯度张量测量——航空磁测技术的最新进展[J]. 工程地球物理学报, 2006, 3(5): 354-361. ZHANG Changda. Airborne tensor magnetic gradio-metry: the latest progress of airborne magnetometric technology[J]. Chinese Journal of Engineering Geophysics, 2006, 3(5): 354-361. DOI:10.3969/j.issn.1672-7940.2006.05.005 |
| [6] |
吴招才, 刘天佑. 磁力梯度张量测量及应用[J]. 地质科技情报, 2008, 27(3): 107-110. WU Zhaocai, LIU Tianyou. Magnetic gradient tensor: its properties and uses in geophysics[J]. Geological Science and Technology Information, 2008, 27(3): 107-110. DOI:10.3969/j.issn.1000-7849.2008.03.018 |
| [7] |
DENG X, SHEN W. Evaluation of gravitational curvatures of a tesseroid in spherical integral kernels[J]. Journal of Geodesy, 2018, 92(4): 415-429. DOI:10.1007/s00190-017-1073-3 |
| [8] |
杜劲松, 邱峰. 重力位三阶梯度张量及其勘探能力初步分析[J]. 大地测量与地球动力学, 2019, 39(4): 331-338. DU Jinsong, QIU Feng. Third-order gradient tensor of gravitational potential and preliminary analysis of its exploration capacity[J]. Journal of Geodesy and Geodynamics, 2019, 39(4): 331-338. DOI:10.14075/j.jgg.2019.04.001 |
| [9] |
YIN G, ZHANG Y, FAN H, et al. Magnetic dipole localization based on magnetic gradient tensor data at a single point[J]. Journal of Applied Remote Sensing, 2014, 8(1): 083596. DOI:10.1117/1.JRS.8.083596 |
| [10] |
DENG X, SHEN W, KUHN M, et al. Magnetic curvatures of a uniformly magnetized tesseroid using the Cartesian kernels[J]. Surveys in Geophysics, 2020, 41(5): 1075-1099. DOI:10.1007/s10712-020-09595-4 |
| [11] |
SUI Y, LESLIE K, CLARK D. Multiple-order magnetic gradient tensors for localization of a magnetic dipole[J]. IEEE Magnetics Letters, 2017, 8: 1-5. |
| [12] |
ZHANG H, RAVAT D, MARANGONI Y R, et al. Improved total magnetization direction determination by correlation of the normalized source strength derivative and the reduced-to-pole fields[J]. Geophy-sics, 2018, 83(6): J75-J85. |
| [13] |
BEIKI M, CLARK D A, AUSTIN J R, et al. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data[J]. Geophysics, 2012, 77(6): J23-J37. DOI:10.1190/geo2011-0437.1 |
| [14] |
CLARK D A. New methods for interpretation of magnetic vector and gradient tensor data Ⅱ: application to the Mount Leyshon anomaly, Queensland, Australia[J]. Exploration Geophysics, 2013, 43(4): 114-127. |
| [15] |
CLARK D A. New methods for interpretation of magnetic vector and gradient tensor data Ⅰ: eigenvector analysis and the normalised source strength[J]. Exploration Geophysics, 2012, 43(4): 267-282. DOI:10.1071/EG12020 |
| [16] |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005. GUAN Zhining. Geomagnetic Field and Magnetic Exploration[M]. Beijing: Geological Publishing House, 2005. |
| [17] |
马国庆, 杜晓娟, 李丽丽. 优化小子域滤波方法研究及其应用[J]. 石油地球物理勘探, 2013, 48(4): 658-662. MA Guoqing, DU Xiaojuan, LI Lili. An optimized small sub-domain filtering method[J]. Oil Geophysical Prospecting, 2013, 48(4): 658-662. DOI:10.13810/j.cnki.issn.1000-7210.2013.04.022 |
| [18] |
李金朋, 范红波, 刘利, 等. 多参数约束磁性体三维形态反演[J]. 石油地球物理勘探, 2021, 56(2): 407-418. LI Jinpeng, FAN Hongbo, LIU Li, et al. Multi-para-meter constrained three-dimensional shape inversion of magnetic bodies[J]. Oil Geophysical Prospecting, 2021, 56(2): 407-418. DOI:10.13810/j.cnki.issn.1000-7210.2021.02.024 |
| [19] |
LI Y, OLDENBURG D W. 3-D inversion of magnetic data[J]. Geophysics, 1996, 61(2): 394-408. DOI:10.1190/1.1443968 |
| [20] |
BHATTACHARYYA B K. Magnetic anomalies due to prism-shaped bodies with arbitrary polarization[J]. Geophysics, 1964, 29(4): 517-531. DOI:10.1190/1.1439386 |
| [21] |
GOODACRE A K. Some comments on the calculation of the gravitational and magnetic attraction of a homo-geneous rectangular prism[J]. Geophysical Prospecting, 1973, 21(1): 66-69. DOI:10.1111/j.1365-2478.1973.tb00014.x |
| [22] |
PLOUFF D. Gravity and magnetic fields of polygonal prisms and application to magnetic terrain corrections[J]. Geophysics, 1976, 41(4): 727-741. DOI:10.1190/1.1440645 |
| [23] |
KUNARATNAM K. Simplified expressions for the magnetic anomalies due to vertical rectangular prisms[J]. Geophysical Prospecting, 1981, 29(6): 883-890. DOI:10.1111/j.1365-2478.1981.tb01032.x |
| [24] |
RAO D B, BABU N R. A rapid method for three-dimensional modeling of magnetic anomalies[J]. Geophysics, 1991, 56(11): 1729-1737. DOI:10.1190/1.1442985 |
| [25] |
郭志宏, 管志宁, 熊盛青. 长方体ΔT场及其梯度场无解析奇点理论表达式[J]. 地球物理学报, 2004, 47(6): 1131-1138. GUO Zhihong, GUAN Zhining, XIONG Shengqing. Cuboid ΔT and its gradient forward theoretical expressions without analytical odd points[J]. Chinese Journal of Geophysics, 2004, 47(6): 1131-1138. DOI:10.3321/j.issn:0001-5733.2004.06.029 |
| [26] |
骆遥, 姚长利. 长方体磁场及其梯度无解析奇点表达式理论研究[J]. 石油地球物理勘探, 2007, 42(6): 714-719. LUO Yao, YAO Changli. Theoretical study on cuboid magnetic field and its gradient expression without ana-lytic singular point[J]. Oil Geophysical Prospecting, 2007, 42(6): 714-719. DOI:10.3321/j.issn:1000-7210.2007.06.019 |
| [27] |
KUANG X, YANG H, ZHU X, et al. Singularity-free expression of magnetic field of cuboid under undula-ting terrain[J]. Applied Geophysics, 2016, 13(2): 238-248. DOI:10.1007/s11770-016-0565-x |
| [28] |
邰振华, 柴琳, 黄德智, 等. 均匀磁化长方体的磁张量无解析奇点正演方法[J]. 黑龙江科技大学学报, 2022, 32(3): 286-292. TAI Zhenhua, CHAI Lin, HUANG Dezhi, et al. Singularity-free forward calculation method of uniformly magnetized cuboid magnetic tensors[J]. Journal of Heilongjiang University of Science and Technology, 2022, 32(3): 286-292. |
| [29] |
黄远生, 王彦国, 罗潇. 基于归一化磁源强度垂向差分的磁源参数快速估计方法[J]. 物探与化探, 2021, 45(6): 1588-1596. HUANG Yuansheng, WANG Yanguo, LUO Xiao. A fast estimation method of magnetic-source parameters based on the vertical difference of normalized source strength[J]. Geophysical and Geochemical Exploration, 2021, 45(6): 1588-1596. |
| [30] |
BLAKELY R J. Potential Theory in Gravity and Magnetic Applications[M]. Cambridge: Cambridge University Press, 1995.
|
| [31] |
NABIGHIAN M N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section: its properties and use for automated anomaly interpretation[J]. Geophysics, 1972, 37(3): 507-517. DOI:10.1190/1.1440276 |
| [32] |
NABIGHIAN M N. Toward a three-dimensional automatic interpretation of potential field data via genera-lized Hilbert transforms: fundamental relations[J]. Geophysics, 1984, 49(6): 780-786. DOI:10.1190/1.1441706 |
| [33] |
AGARWAL B N P, SHAW R K. Comment on 'An analytic signal approach to the interpretation of total field magnetic anomalies' by Shuang Qin[J]. Geophy-sical Prospecting, 1996, 44(5): 911-914. DOI:10.1111/j.1365-2478.1996.tb00180.x |
| [34] |
LI X. Understanding 3D analytic signal amplitude[J]. Geophysics, 2006, 71(2): L13-L16. DOI:10.1190/1.2184367 |
| [35] |
HSU S K, SIBUET J C, SHYU C T. High-resolution detection of geologic boundaries from potential-field anomalies: an enhanced analytic signal technique[J]. Geophysics, 1996, 61(2): 373-386. DOI:10.1190/1.1443966 |
| [36] |
BAUR O, SNEEUW N, GRAFAREND E W. Methodo-logy and use of tensor invariants for satellite gravity gradiometry[J]. Journal of Geodesy, 2008, 82(4): 279-293. |
| [37] |
DENG X, SHEN W, YANG M, et al. First-order derivatives of principal and main invariants of magnetic gradient tensor of a uniformly magnetized tesseroid and spherical shell[J]. Surveys in Geophysics, 2022, 43(4): 1233-1262. DOI:10.1007/s10712-022-09697-1 |
| [38] |
GUO L, GAO R, ZHANG G. Estimating the magnetization direction of sources through correlation between reduced-to-pole anomaly and normalized source strength[J]. Applied Mechanics and Materials, 2014, 644-650: 3793-3796. DOI:10.4028/www.scientific.net/AMM.644-650.3793 |
| [39] |
PILKINGTON M, BEIKI M. Mitigating remained magnetization effects in magnetic data using the normalized source strength[J]. Geophysics, 2013, 78(3): J25-J32. DOI:10.1190/geo2012-0225.1 |



 杜劲松, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。E-mail:
杜劲松, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。E-mail: