2. 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
2. Key Laboratory of Earth Exploration and Information Technology of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
地震信号是一种非平稳信号,仅在时间域或频率域对非平稳信号进行分析是远远不够的。时频分析[1]作为信号处理领域的基本工具,通过一定的方法将时间域信号变换到时间—频率域,能够清晰地描述频率和时间的关系,时频分析已广泛应用于地震资料处理与解释中。
Gabor[1]将复数道信号的概念引入时频分析中,并提出了短时傅里叶变换;Morlet等[2]提出了连续小波变换,并将其应用于地震信号分析,促进了非平稳地震信号分析的发展;Stockwell等[3]总结了短时傅里叶变换和连续小波变换的优点,在此基础上提出S变换,克服了短时傅里叶变换窗口恒定、不能根据频率自适应选择窗口宽度的局限性,使S变换成为许多科学领域的有效工具。然而,受窗口宽度的影响,S变换的时频分辨率并不理想,低频分量的时间分辨率以及高频分量的频率分辨率均不高。为达到较高的时频分辨率,McFadden等[4]首先提出了使用参数控制任意窗函数的广义S变换,使得窗口函数的调节具有更好的灵活性;高静怀等[5]在S变换的基础上提出了用四个参数调节高斯窗函数的广义S变换,并在薄互层分析中取得了较好的效果;陈学华等[6-8]提出二参数广义S变换,在地震信号处理与油气预测等方面得到了广泛应用;黄忠来等[9-10]提出了同步挤压S变换,能够较好地反映信号中弱振幅的时频特征,并将此方法进一步改进为二阶同步挤压S变换,基于该方法的谱分解技术可检测与天然气相关的谱异常;武迪等[11]结合变分模态分解与包络导数能量算子预测了碳酸盐岩溶洞储层的油气分布;张付瑷等[12]基于实际信号的振幅谱对窗参数优化S变换作进一步改进,在实际资料的河道检测中能更好地刻画河道的空间展布特征,显示更清晰的地质细节特征;朱焱辉等[13]将多窗思想引入到重排平滑伪Wigner-Ville分布中,通过拾取时频脊线从时频谱中提取高频能量,提升识别小型河道、薄扇体以及薄砂体的能力。
近年来,稀疏表示被证明是一种解决非唯一解反问题的有效且具有前途的方法。Flandrin等[14]基于压缩感知中的欠采样数据和L1范数的稀疏表示提出了稀疏Cohen分布;Liu等[15]基于平滑L0范数提出了短时稀疏表示算法。在稀疏表示的基础上,基于稀疏性的时频分析技术得到了进一步发展。Hu等[16]在基于短时傅里叶变换的稀疏时频分解基础上,增加了一个L2范数正则化,调整了稀疏性;Gholami[17]提出了基于混合范数稀疏短时傅里叶变换的TF方法,用于地滚波压制和油气的直接检测;Sattari[18]提出了一种基于稀疏的快速窗口参数优化算法,通过确定最佳窗口长度,从而对窗函数进行稀疏优化,在分辨干扰波和抑制随机噪声方面取得了较好的效果;Chen等[19-20]基于Lp伪范数提出了稀疏频谱反演方法;Wang等[21]将稀疏时频应用于地震数据面波的压制;Luo等[22-23]将稀疏时频分解与AVO反演结合,得到了分辨率更高的频散结果。韩利等[24]利用稀疏反演的地震复频谱分解方法求得高分辨率时频能量谱和相位谱。田琳等[25]用快速投影迭代软阈值投影算法求解稀疏短时傅里叶变换的谱分解,并用于压制地滚波。邢文军等[26]将稀疏反演时频分析与频散属性相结合,提高了纵波频散的分析精度。Kakhki等[27]用组稀疏约束对三分量数据进行稀疏分解,得到具有更高分辨率和稀疏性以及更连续振幅的时频谱。Lin等[28]在稀疏自适应S变换的基础上结合高分辨率同步挤压谱分解方法,提出同步挤压自适应S变换,具有高时频聚焦性和高抗干扰性。Yang等[29]提出基于压缩感知理论的数据驱动稀疏时频表示方法,并在天然气水合物游离气的检测中取得良好效果。上述研究表明,稀疏约束下的时频分解具有更高的分辨率,并在面波压制、低频阴影分析和弹性参数反演等方面均有广泛的应用。
本文将稀疏约束的思想引入时频分析,并根据广义S变换窗参数可灵活调节的特点,构建了一种稀疏约束的广义S变换。合成信号的分析结果表明,本文方法得到的时频分析结果具有更高的分辨率和更好的能量聚焦性。在实际数据的应用中能有效突出“低频阴影”现象,能够提高油气储层预测的精度,有利于储层形态的准确刻画。
1 方法原理S变换方法是将窗函数的固定时窗改为与频率相关的窗(时窗宽度随频率变化,且与频率成反比)。S变换方法中的窗函数表达式为
| $ w(t)=\frac{1}{\sigma \sqrt{2 \rm{ \mathsf{ π} }}} \mathrm{e}^{-\frac{t^2}{2 \sigma^2}} $ | (1) |
式中:t为时间;σ为决定窗函数时间宽度的尺度因子,定义为
| $ \sigma(f)=\frac{1}{|f|} $ | (2) |
式中f为频率。
信号y(t)的S变换为
| $ \mathrm{ST}(\tau, f)=\int_{-\infty}^{\infty} \boldsymbol{y}(t) \frac{|f|}{\sqrt{2 \rm{ \mathsf{ π} }}} \mathrm{e}^{-\frac{f^2(\tau-t)^2}{2}} \mathrm{e}^{-\mathrm{i} 2 \rm{ \mathsf{ π} } \mathit{f t}} \mathrm{~d} t $ | (3) |
式中τ为时间位移。根据陈学华等[6-7]的二参数广义S变换方法,即用含有两个调节参数λ和p的窗函数代替原有的S变换窗函数的尺度因子
| $ \sigma(f)=\frac{1}{\lambda|f|^p} $ | (4) |
由此得到窗函数为
| $ w(t, f)=\frac{\lambda|f|^p}{\sqrt{2 \rm{ \mathsf{ π} }}} \mathrm{e}^{-\frac{\lambda^2 f^{2 p} t^2}{2}} $ | (5) |
式中:0<p≤1.5;λ>0。当p一定时,λ取值越大,时窗宽度随频率呈反比变化的速度加快,窗函数在时间域拉伸,在频率域压缩,其时频分布的时间分辨率降低;当λ一定时,p的取值增大,同样会造成窗函数在时间域拉伸,时频分布的时间分辨率降低。因此,可以根据实际应用的需要合理地选择λ和p以调节时频分辨率。信号y(t)的广义S变换为
| $ \operatorname{GST}(\tau, f)=\int_{-\infty}^{\infty} \boldsymbol{y}(t) \frac{\lambda|f|^p}{\sqrt{2 \rm{ \mathsf{ π} }}} \mathrm{e}^{\frac{-\lambda^2 f^{2 p}(\tau-t)^2}{2}} \mathrm{e}^{-\mathrm{i} 2 \rm{ \mathsf{ π} } \mathit{f t}} \mathrm{~d} t $ | (6) |
对于一个有限长的离散信号Y[nT],n∈[0, 1, …, N-1],其中T为采样周期,N为离散信号的采样点数。则令τ=aT,f=b/NT,其中a、b分别为离散的时间索引号和频率索引号。得到广义S逆变换的离散形式为
| $ \begin{aligned} & \boldsymbol{Y}[n T]= \\ & \sum\limits_{a=0}^{N-1} \sum\limits_{b=0}^{N-1} \operatorname{GST}\left[a T, \frac{b}{N T}\right] w\left(a T-n T, \frac{b}{N T}\right) \mathrm{e}^{\frac{\mathrm{i} 2 \rm{ \mathsf{ π} } \mathit{a b}}{N}} \end{aligned} $ | (7) |
由于λ和p两个调节参数的引入,使得在实际信号处理中对于窗函数的调节更加灵活,因此能够选择最佳的参数值来提高时频分辨率,但仍有一定改进的空间。
将稀疏分解的概念引入时频分析方法中,可以将信号的时频变换过程视为一个稀疏约束下的线性反演问题,然后利用最优化算法可以求得较高分辨率的时频谱。
由于S变换是信号与时频分布之间的线性映射关系,借鉴Gholami[17]离散短时傅里叶逆变换的表示方法,本文将式(7)离散广义S逆变换用矩阵表示为
| $ \boldsymbol{Y}=\boldsymbol{G}_{\mathrm{re}} \boldsymbol{m} $ | (8) |
式中:Gre是一个大小为N×N2的重构矩阵,由窗函数和傅里叶变换矩阵组成;m=[m1, m2, …,mN]T是大小为N2×1的时频振幅谱重新排列的列向量,mi∈RN×1,i=1, 2, …,N,R表示实数集。在求得m后需将它变为[m1, m2, …,mN]的形式作为时频振幅谱。
由于式(7)是一个欠定的线性方程,可以使用不同的约束来获得期望的唯一时频分布。稀疏性促进正则化通过在一个凸约束优化框架中利用最小化的混合L1-L2范数来寻求期望的m的近似值
| $ \begin{aligned} & \boldsymbol{m}=\underset{\boldsymbol{m}}{\operatorname{argmin}}\left(\|\boldsymbol{m}\|_1+\gamma\|\boldsymbol{m}\|_2^2\right) \\ & \text { s. t. } \quad\left\|\boldsymbol{Y}-\boldsymbol{G}_{\mathrm{re}} \boldsymbol{m}\right\|_2^2 \leq \varepsilon \end{aligned} $ | (9) |
式中:‖·‖1和‖·‖2分别表示矩阵的L1范数和L2范数;γ≥0是平衡参数,用于权衡解的L1范数和L2范数,γ→0时,L1范数具有过稀疏解;ε为收敛阈值,一般取1×10-3。
利用Bregman迭代正则化方法[30]解决下式的凸问题
| $ \left\{\begin{array}{l} \boldsymbol{m}^{(k+1)}=\underset{\boldsymbol{m}^{(k)}}{\operatorname{argmin}}\left\{\left\|\boldsymbol{m}^{(k)}\right\|_1+\gamma\left\|\boldsymbol{m}^{(k)}\right\|_2^2+\right. \\ \left.\quad \frac{\mu}{2}\left\|\boldsymbol{G}_{\mathrm{re}} \boldsymbol{m}^{(k)}-\boldsymbol{Y}^{(k)}\right\|_2^2\right\} \\ \boldsymbol{Y}^{(k+1)}=\boldsymbol{Y}^{(k)}+\boldsymbol{Y}-\boldsymbol{G}_{\mathrm{re}} \boldsymbol{m}^{(k+1)} \end{array}\right. $ | (10) |
式中:k为迭代次数;μ>0是拉格朗日乘数,当μ值过大会损失一定的有效信息,而μ值过小则会出现不真实的时频分布信息;Y(0)=Y。
为了减少迭代次数,借鉴Gholami[17]的矩阵分解思想,本文将矩阵Gre分解为
| $ \boldsymbol{G}_{\mathrm{re}}=\mathit{\boldsymbol{ \boldsymbol{\varPhi}}} \boldsymbol{F} $ | (11) |
式中:F是大小为N2×N2的傅里叶变换矩阵;Φ=[φ, φ, …,φ]是一个由窗矩阵φ构成的稀疏块矩阵,尺寸为N×N2。窗矩阵φ是由不同频率的广义S变换窗函数(式(5))基于Toeplitz矩阵原理构建的,即
| $ \boldsymbol{\varphi}=\left[w\left(t, f_1\right), w\left(t, f_2\right), \cdots, w\left(t, f_N\right)\right]^{\mathrm{T}} $ | (12) |
若式(5)中的窗函数参数p=0 (如短时傅里叶变换),则生成的窗矩阵φ为Toeplitz矩阵。
2 模型试算与分析为了验证本文的稀疏广义S变换方法的有效性,设计了两个合成信号进行分析、计算。
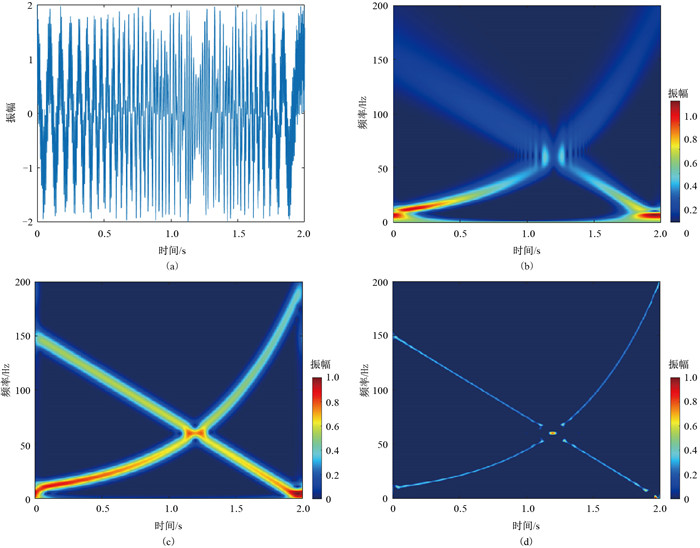
合成信号一是由两个不同的Chirp非平稳信号组成,频率范围为0~200 Hz(图 1a)。对该信号分别做S变换、广义S变换和稀疏广义S变换,得到对应的时频谱分别如图 1b~图 1d所示。由图可见,相较于S变换,广义S变换时频谱有更高的频率分辨率,尤其是高频部分的分辨率优势更加明显;相较于广义S变换,稀疏广义S变换时频谱中信号的能量分布更加均匀,时频谱具有更好的时频聚集性。
|
图 1 合成的Chirp非平稳信号(a)及三种方法处理的时频分布 (b)S变换;(c)广义S变换;(d)稀疏广义S变换 |
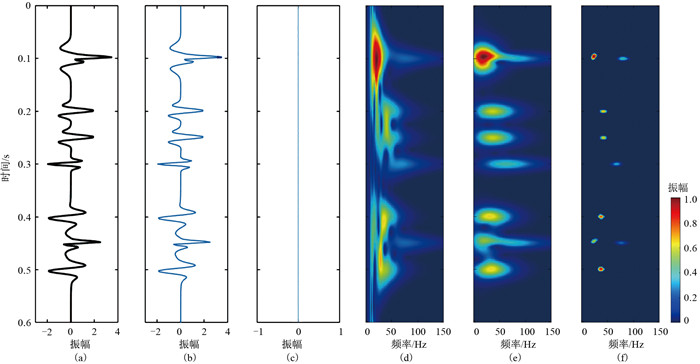
合成信号二如图 3a所示,其是由图 2所示的主频分别为20、35、65、40和75 Hz以及相位分别为0°、135°、170°、20°和90°的Ricker子波叠加而成。图 3b为逆稀疏广义S变换重构的信号,其与原始信号的误差为图 3c。对合成信号二分别做S变换、广义S变换和稀疏广义S变换,得到对应的时频谱分别如图 3d~图 3f所示,可以看出,尽管广义S变换比S变换有更好的时频分辨率,但是在低频和高频的区分上并不理想,精度不高。时间分辨率上能明显地区分不同时间的频率,但是在频率分辨率上对于0.10与0.45 s时的20及75 Hz的Ricker子波,没有明确的区分。稀疏广义S变换结果(图 3f)在时频分辨率上具有明显的优势,其能量更集中在信号频率中心位置,能明显地区分高频分量与低频分量。
|
图 3 图 2合成信号及其时频分布 (a)Ricker子波合成信号;(b)重构信号;(c)图b与图a的误差;(d)S变换;(e)广义S变换;(f)稀疏广义S变换 |
|
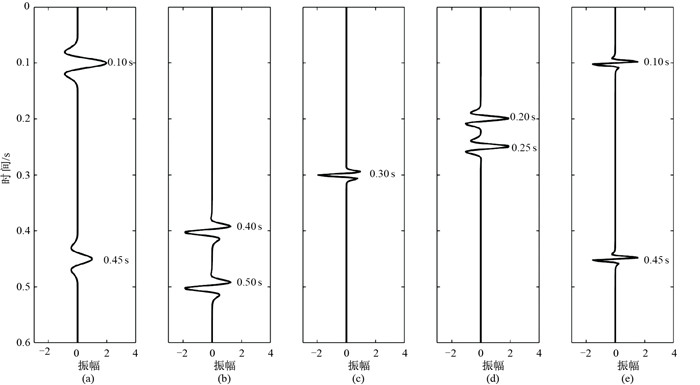
图 2 不同相位Ricker子波的合成信号及其组成分量 (a)0°;(b)135°;(c) 170°;(d) 20°;(e) 90° |
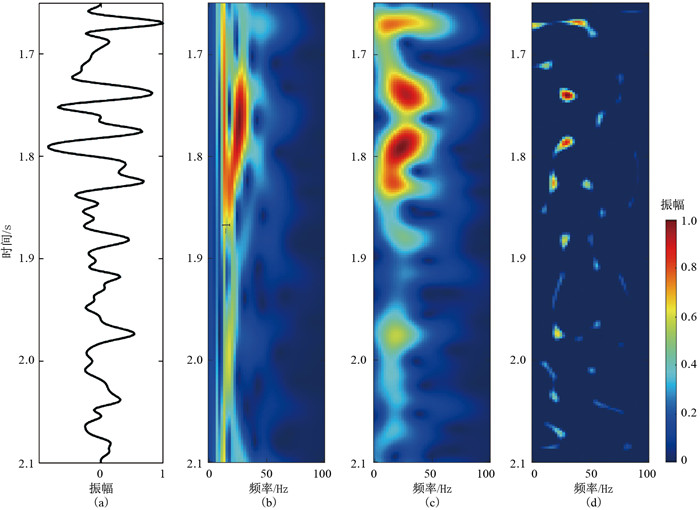
将本文所提出的稀疏广义S变换方法应用到实际地震信号中,取JZ地区单道地震信号如图 4a所示,该地震道为图 5a地震剖面中的第490道(红线处)。图 4b~图 4d分别是该单道地震信号的S变换、广义S变换和稀疏广义S变换的时频分布,可以看出,稀疏广义S变换方法无论在时频分辨率还是能量聚集性上都体现出更明显的优势。
|
图 4 单道地震信号及其不同变换的时频分布 (a)单道地震信号;(b)S变换;(c)广义S变换;(d)稀疏广义S变换 |

|
图 5 实际地震数据剖面及不同方法处理的24Hz瞬时谱剖面 (a)原始地震剖面;(b)S变换;(c)广义S变换;(d)稀疏广义S变换 |
该单道地震信号对应的地震剖面如图 5a所示。其S变换、广义S变换时频和稀疏广义S变换单频(24 Hz)剖面分别如图 5b~图 5d所示。对比分析可知,稀疏广义S变换的时频分布结果无论在纵向还是横向上的分辨率都明显高于前两种方法;特别是在广义S变换已经提高了一定的时频分辨率的基础上,稀疏广义S变换的时频分辨率更高,能量聚集性与连续性更好,对地层刻画地更为清晰。
3.2 低频异常检测作为直接检测油气的手段,“低频阴影”已成为油气储层预测的重要烃类指示因子,而合适的时频分析方法是进行地震信号瞬时谱分析、检测低频阴影的关键[8]。为了说明本文所提出的稀疏广义S变换方法的有效性,将它应用于上述JZ地区实际地震数据中进行对比、分析,应用高时频分辨率研究“低频阴影”现象。
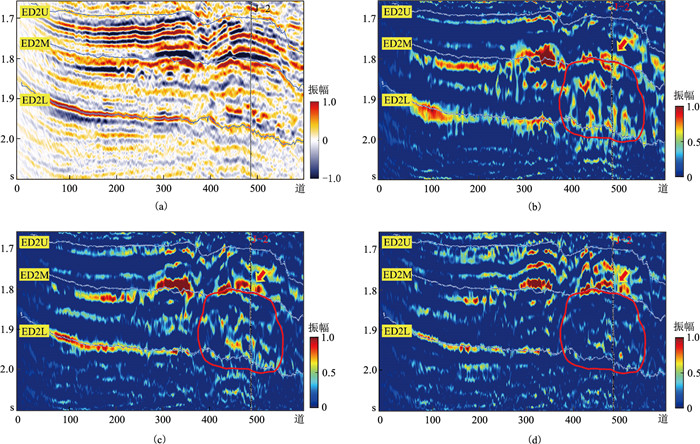
抽取该工区井J-2附近实际三维地震数据进行时频处理。图 6为过井J-2的瞬时谱剖面,图 6b为17 Hz的瞬时谱剖面,油气储层(红色箭头标注)显示为强能量,其下方也有强能量显示(红圈),即认为存在“上强下强”的低频阴影特征;当瞬时频率增加到24 Hz(图 6c),油气储层显示为强能量,但其下方能量有明显减弱的趋势;当频率继续增加到31 Hz时(图 6d),油气储层依然显示为强能量,但其下方位置的能量已经很弱,即“上强下强”的特征。
|
图 6 JZ地区实际地震数据不同瞬时谱剖面低频阴影检测 (a)原始地震剖面;(b)17 Hz;(c)24 Hz;(d)31 Hz |
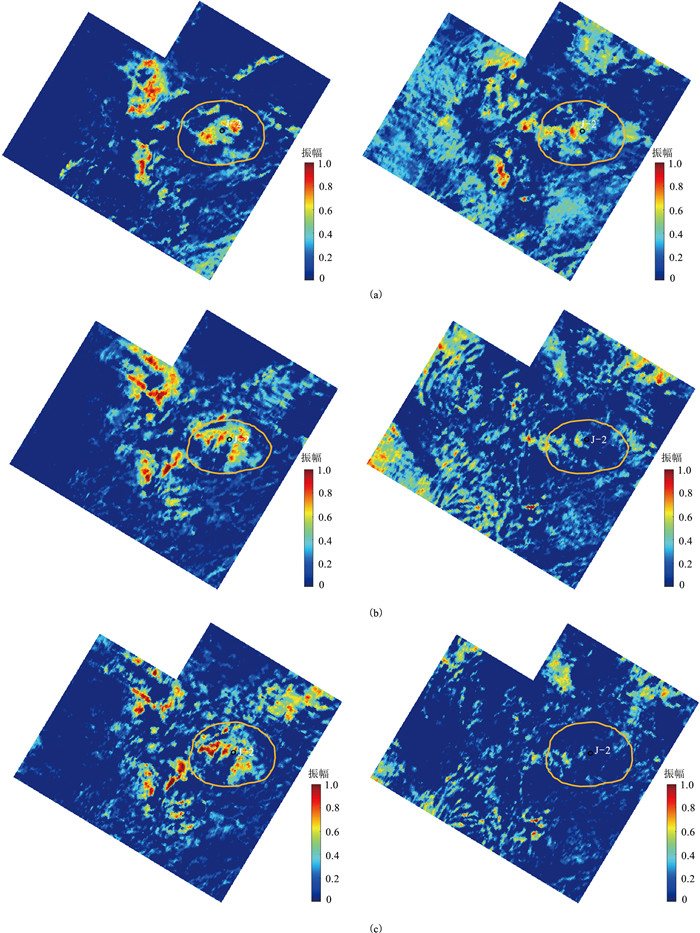
图 7是从同一资料的三维瞬时谱数据体中抽取的沿层切片。图中左列为穿过油气储层的切片,右列是其下延33 ms处的切片。当频率为17 Hz时(图 7a),左边切片油气储层(黄圈)表现为强能量,右边切片中也存在强的低频阴影;当频率达到24 Hz时(图 7b),左边切片能量仍然较强,但右边切片的低频阴影减弱;当频率继续增加到31 Hz时(图 7c),右边切片的低频阴影逐渐消失。在各频率的切片中,左边切片一直存在明显的强能量分布。
|
图 7 穿过油气储层(左)及油气储层下延33 ms(右)的沿层切片上的“低频阴影”检测 (a)17 Hz;(b)24 Hz;(c)31 Hz |
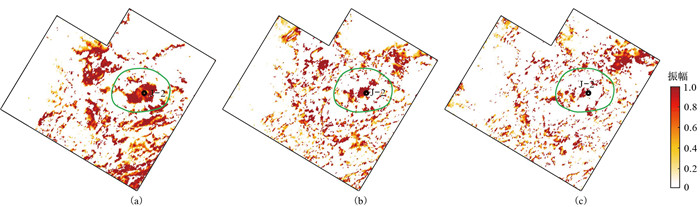
为了更加清晰地说明利用低频能量异常进行油气检测的效果,进一步利用图 7中左列与右列切片低频能量的比值对不同频率的油气异常情况进行对比、分析(图 8)。由图可知,当频率为17 Hz时,比值切片(图 8a)的能量异常最突出,可更加清晰地刻画储层的展布范围,而随着频率增高,图 8b和图 8c的比值切片显示的能量逐渐减弱,强能量显示范围逐渐减小。可见,比值切片的对比结果更加突出了“低频阴影”现象。
|
图 8 图 7穿过油气储层的切片与下延33 ms的低频能量切片之间的低频能量比值 (a)17 Hz;(b)24 Hz;(c)31 Hz |
本文在广义S变换的基础上,引入稀疏约束的思想,通过采用迭代正则化方法解决凸问题,构建了一种稀疏广义S变换方法,将该方法应用于合成信号和实际地震数据中,结果表明本文方法可得到时频分辨率更高和能量聚焦性更好的时频分布,在油气储层的“低频阴影”检测中,能够更加清晰地刻画油气储层的位置和空间展布特征。本文方法更适用于处理复杂地震信号和油气储层的精细刻画,为地震资料的精细解释提供了一种新的技术支撑。该方法在复杂地质体异常精细刻画、高精度频变AVO反演及属性融合等方面具有较大的发展前景。
| [1] |
GABOR D. Theory of communications[J]. Journal of the Institution of Electrical Engineers, 1946, 93: 429-457. |
| [2] |
MORLET J, ARENS G, FOURGEAU E, et al. Wave propagation and sampling theory-Part Ⅰ: complex signal and scattering in multilayered media[J]. Geophy-sics, 1982, 47(2): 203-221. |
| [3] |
STOCKWELL R G, MANSINHA L, LOWE R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [4] |
MCFADDEN P D, COOK J G, FORSTER L M. Decomposition of gear vibration signals by the genera-lised S transform[J]. Mechanical Systems and Signal Processing, 1999, 13(5): 691-707. DOI:10.1006/mssp.1999.1233 |
| [5] |
高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析[J]. 地球物理学报, 2003, 46(4): 526-532. GAO Jinghuai, CHEN Wenchao, LI Youming, et al. Generalized S transform and seismic response analysis of thin interbeds[J]. Chinese Journal of Geophysics, 2003, 46(4): 526-532. DOI:10.3321/j.issn:0001-5733.2003.04.015 |
| [6] |
陈学华, 贺振华. 改进的S变换及在地震信号处理中的应用[J]. 数据采集与处理, 2005, 20(4): 449-453. CHEN Xuehua, HE Zhenhua. Improved S-transform and its application in seismic signal processing[J]. Journal of Data Acquisition and Processing, 2005, 20(4): 449-453. DOI:10.3969/j.issn.1004-9037.2005.04.018 |
| [7] |
陈学华, 贺振华, 黄德济. 基于广义S变换的地震资料高效时频谱分解[J]. 石油地球物理勘探, 2008, 43(5): 530-534. CHEN Xuehua, HE Zhenhua, HUANG Deji. High-efficient time-frequency spectrum decomposition of seismic data based on generalized S transform[J]. Oil Geo-physical Prospecting, 2008, 43(5): 530-534. |
| [8] |
陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测[J]. 地球物理学报, 2009, 52(1): 215-221. CHEN Xuehua, HE Zhenhua, HUANG Deji, et al. Low frequency shadow detection of gas reservoirs in time-frequency domain[J]. Chinese Journal of Geophysics, 2009, 52(1): 215-221. |
| [9] |
黄忠来, 张建中. 同步挤压S变换[J]. 中国科学(信息科学), 2016, 46(5): 643-650. HUANG Zhonglai, ZHANG Jianzhong. Synchro-squeezing S-transform[J]. Scientia Sinica (Informa-tionis), 2016, 46(5): 643-650. |
| [10] |
黄忠来, 张建中, 邹志辉. 二阶同步挤压S变换及其在地震谱分解中的应用[J]. 地球物理学报, 2017, 60(7): 2833-2844. HUANG Zhonglai, ZHANG Jianzhong, ZOU Zhihui. A second-order synchrosqueezing S-transform and its application in seismic spectral decomposition[J]. Chinese Journal of Geophysics, 2017, 60(7): 2833-2844. |
| [11] |
武迪, 宋维琪, 刘军, 等. 变分模态分解与包络导数算子结合的时频分析方法及溶洞储层预测[J]. 石油地球物理勘探, 2021, 56(2): 346-355. WU Di, SONG Weiqi, LIU Jun, et al. Seismic time-frequency analysis based on VMD and envelope deriva-tive operator for fractured-vuggy reservoir prediction[J]. Oil Geophysical Prospecting, 2021, 56(2): 346-355. |
| [12] |
张付瑷, 陈学华, 罗鑫, 等. 改进的窗参数优化S变换及其在河道检测中的应用[J]. 石油地球物理勘探, 2021, 56(4): 809-814.881. ZHANG Fuai, CHEN Xuehua, LUO Xin, et al. Improved window parameter optimized S-transform and its application in channel detection[J]. Oil Geophysical Prospecting, 2021, 56(4): 809-814.881. |
| [13] |
朱焱辉, 张向涛, 刘立峰, 等. 白云凹陷深水区河道砂体分布预测[J]. 石油物探, 2022, 61(5): 888-897. ZHU Yanhui, ZHANG Xiangtao, LIU Lifeng, et al. Prediction of channel sand body distribution in deep water area of Baiyun sag[J]. Geophysical Prospecting for Petroleum, 2022, 61(5): 888-897. |
| [14] |
FLANDRIN P, BORGNAT P. Time-frequency energy distributions meet compressed sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 2974-2982. DOI:10.1109/TSP.2010.2044839 |
| [15] |
LIU Z, YOU P, WEI X, et al. High resolution time-frequency distribution based on short-time sparse representation[J]. Circuits, Systems.and Signal Processing, 2014, 33(12): 3949-3965. |
| [16] |
HU J, HE X, LI W, et al. Parameter estimation of maneuvering targets in OTHR based on sparse time-frequency representation[J]. Journal of Systems Engineering and Electronics, 2016, 27(3): 574-580. |
| [17] |
GHOLAMI A. Sparse time-frequency decomposition and some applications[J]. IEEE Transactions on Geo-science and Remote Sensing, 2013, 51(6): 3598-3604. |
| [18] |
SATTARI H. High-resolution seismic complex trace analysis by adaptive fast sparse S-transform[J]. Geophysics, 2017, 82(1): V51-V67. |
| [19] |
CHEN Y, HE Y, LI S, et al. Seismic spectrum decomposition based on sparse time-frequency analysis[J]. Journal of Applied Geophysics, 2020, 177: 104031. |
| [20] |
CHEN Y, PENG Z, GHOLAMI A, et al. Seismic signal sparse time-frequency representation by Lp-quasinorm constraint[J]. Digital Signal Processing, 2019, 87: 43-59. |
| [21] |
WANG X, WANG H. Application of sparse time-frequency decomposition to seismic data[J]. Applied Geo-physics, 2014, 11(4): 447-458. |
| [22] |
LUO C, LI X, HUANG G. Hydrocarbon identification by application of improved sparse constrained inverse spectral decomposition to frequency-dependent AVO inversion[J]. Journal of Geophysics and Engineering, 2018, 15(4): 1446-1459. |
| [23] |
LUO C, HUANG G, LI X. Frequency-dependent AVO inversion based on sparse constrained inversion spectral decomposition[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 524-528.
|
| [24] |
韩利, 刘春成, 张益明, 等. 地震复谱分解技术及其在烃类检测中的应用[J]. 地球物理学报, 2016, 59(3): 1095-1101. HAN Li, LIU Chuncheng, ZHANG Yiming, et al. Seismic complex spectral decomposition and its application on hydrocarbon detection[J]. Chinese Journal of Geophysics, 2016, 59(3): 1095-1101. |
| [25] |
田琳, 胡津健. 稀疏短时傅里叶变换谱分解方法及应用[J]. 地球物理学进展, 2021, 36(6): 2581-2587. TIAN Lin, HU Jinjian. Sparse short-time Fourier transform spectral decomposition method and its application[J]. Progress in Geophysics, 2021, 36(6): 2581-2587. |
| [26] |
邢文军, 曹思远, 陈思远, 等. 基于L1-L2范数的高分辨率时频分析方法及应用[J]. 地球物理学报, 2022, 65(9): 3623-3633. XING Wenjun, CAO Siyuan, CHEN Siyuan, et al. High-resolution time-frequency analysis based on L1-L2 norm and its application[J]. Chinese Journal of Geo-physics, 2022, 65(9): 3623-3633. |
| [27] |
KAKHKI M K, MOKHTARI A, MANSUR W J. Three-component sparse S transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-7. |
| [28] |
LIN Y, CHEN S, ZHANG G, et al. High-resolution time-frequency analysis based on a synchroextracting adaptive S-transform and its application[J]. Journal of Geophysics and Engineering, 2022, 19(5): 1124-1133. |
| [29] |
YANG Y, GAO J, WANG Z, et al. Data-driven time-frequency method and its application in detection of free gas beneath a gas hydrate deposit[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-13. |
| [30] |
GOLDSTEIN T, OSHER S. The split bregman me-thod for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343. |



 陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email:
陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email: 