2. 中国石油大学(北京)非常规油气科学技术学院, 北京 102249
2. Unconventional Petroleum Research Institute, China University of Petroleum(Beijing), Beijing 102249, China
由于不受倾角、模型复杂程度和偏移孔径的限制,逆时偏移已经成为目前最流行的偏移成像方法之一。相对于声波逆时偏移,弹性波逆时偏移技术考虑了转换波的特征,在一些特殊地质结构成像中,如气藏,发挥了重要作用[1-5]。在弹性波逆时偏移中,耦合在一起的P/S波会造成严重的串扰噪声,因此精确的P/S波解耦技术至关重要[6]。
对于各向同性介质,P/S波解耦常常利用Helmholtz分解理论,将弹性波场分解成标量P波和矢量S波[7],或者从Christoffel方程出发,在波数域模拟P波算子进行求解[8]。Zhang等[9]发展了一种在波数域构建极化向量算子的P/S波解耦方法;Zhu[10]同样提出一种等价的空间域弹性波解耦方法,但需要求解泊松方程;为了提高效率,Zhao等[4]和Yang等[11]提出了一种利用子波和多波记录进行时间积分的方法,避免了求解泊松方程。
对于各向异性介质,由于P/S波的传播方向与极化方向不一致或不垂直,因此不能直接应用传统的Helmholtz方法。各向异性介质中的P/S波极化方向矢量可通过求解Christoffel方程获得[8]。在频率—波数域可以得到精确解,用于P/S波解耦,其结果振幅和相位正确,但难以适用于复杂模型[8-9]。Yan等[12]提出了基于非稳态滤波的P/S波解耦方法,可适用于任意复杂的VTI模型,但大尺度空间滤波算子所需的计算量较大,尤其在三维情况下。另外一种有效解耦P/S波的方法是低秩近似,且成功应用于弹性波逆时偏移[13],但该方法在每一个时间步需做多次傅里叶变换。最近,Yang等[14]发展了一种伪泊松算子分解方法,可以适用于任意复杂模型的TI介质。该方法使用LU分解技术求解各向异性泊松方程,因此在每个时间步骤需要N3次计算(N为网格点数)。
为了提高效率和适应性,本文应用一种VTI介质各向异性Helmholtz解耦方法(简称ani-Helmholtz方法)[15]分离P/S波。该方法首先求解VTI介质Christoffel方程,得到P/S波极化方向矢量,然后将弹性波场投影到极化方向上,得到VTI介质的波数域P/S波解耦公式。最后,利用一阶泰勒展开近似解耦公式中的归一化项。ani-Helmholtz分解方法可以适用于任意复杂模型,在每个时间步骤仅需做三次傅里叶变换。与原始弹性波场相比,该分解方法产生的P/S波场具有正确的振幅和相位。
低频噪声和成像假象是逆时偏移中常见的干扰。前者由同路径波场成像导致,后者因炮点上行波场与检波点下行波场互相关形成[16]。利用无反射波动方程和平滑速度场可以压制低频噪声[17-18],但同时损伤了反射波有效信息。Laplace滤波方法可压制噪声,但易产生高频假象、导致振幅畸变[19]。Poynting矢量可以计算波场传播方向,通过设计滤波器,可以压制大角度噪声[20-21],但当波场复杂时,其计算误差较大。将波场分离为上、下行波,然后利用炮点下行波场与检波点上行波场相关成像,可有效解决低频噪声和成像假象问题[22-29]。
因此,本文将各向异性介质ani-Helmholtz P/S波解耦方法与上下行波波场分离成像技术相结合,用于VTI介质弹性波逆时偏移,有效地压制了成像中的低频噪声和串扰假象。模型数据结果验证了本文方法的有效性。
1 方法原理 1.1 二维ani-Helmholtz解耦算法对各向异性介质的Christoffel方程进行特征分析,其特征值和特征向量代表了P/S波的相速度和极化矢量[28]。各向异性介质中P/S波波场可通过将弹性波场投影到极化方向上获得。
二维VTI介质二阶弹性波动方程为
| $ \left\{\begin{array}{l} \rho \frac{\partial^2 u_x}{\partial t^2}=\left(C_{11} \frac{\partial^2}{\partial x^2}+C_{55} \frac{\partial^2}{\partial z^2}\right) u_x+\left(C_{13}+C_{55}\right) \frac{\partial^2 u_z}{\partial x \partial z} \\ \rho \frac{\partial^2 u_z}{\partial t^2}=\left(C_{13}+C_{55}\right) \frac{\partial^2 u_x}{\partial x \partial z}+\left(C_{55} \frac{\partial^2}{\partial x^2}+C_{33} \frac{\partial^2}{\partial z^2}\right) u_z \end{array}\right. $ | (1) |
式中:ux和uz分别为弹性波位移波场的x和z分量;ρ为密度;C11、C13、C33和C55为VTI介质刚度矩阵系数,可表示为
| $ \left\{\begin{array}{l} C_{11}=(1+2 \varepsilon) \rho v_{\mathrm{P}}^2 \\ C_{33}=\rho v_{\mathrm{P}}^2 \\ C_{55}=\rho v_{\mathrm{S}}^2 \\ C_{13}=\rho \sqrt{\left[(1+2 \delta) v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right]\left[v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right]}-\rho v_{\mathrm{S}}^2 \end{array}\right. $ | (2) |
其中:vP和vS分别为沿对称轴方向的纵波和横波速度;ε和δ为Thomsen各向异性参数[30-31]。
基于局部均匀假设,将式(1)转换到频率—波数域可得到VTI介质的Christoffel方程
| $ \left[\begin{array}{cc} C_{11} k_x^2+C_{55} k_z^2-\lambda & \left(C_{13}+C_{55}\right) k_x k_z \\ \left(C_{13}+C_{55}\right) k_x k_z & C_{55} k_x^2+C_{33} k_z^2-\lambda \end{array}\right]\left[\begin{array}{c} U_x \\ U_z \end{array}\right]=0 $ | (3) |
式中:U(Ux,Uz)为频率—波数域弹性波矢量波场,(Ux,Uz)T也可看作Christoffel方程的特征向量;kx和kz分别为x和z方向的波数;λ为特征值,可表示为
| $ \lambda=\rho \omega^2=\rho k^2 V^2 $ | (4) |
其中:ω为角频率;V为相速度。利用椭圆VTI介质假设求解式(3),可得特征值的近似解[14-15]
| $ \left\{\begin{array}{l} \lambda_1=\rho v_{\mathrm{P}}^2\left[(1+2 \varepsilon) k_x^2+k_z^2\right] \\ \lambda_2=\rho v_{\mathrm{S}}^2\left(k_x^2+k_z^2\right) \end{array}\right. $ | (5) |
与特征向量近似解
| $ \boldsymbol{U}_1=\left[\begin{array}{c} k_x \\ \frac{\sqrt{\left[(1+2 \delta) v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right]\left(v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right)}}{(1+2 \varepsilon) v_{\mathrm{P}}^2-v_{\mathrm{S}}^2} k_z \end{array}\right] $ | (6) |
| $ \boldsymbol{U}_2=\left[\begin{array}{c} \frac{\sqrt{\left[(1+2 \delta) v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right]\left(v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right)}}{(1+2 \varepsilon) v_{\mathrm{P}}^2-v_{\mathrm{S}}^2} k_z \\ -k_x \end{array}\right] $ | (7) |
式中U1和U2分别为P波和S波的极化矢量,二者相互正交。根据Helmholtz分解原理,将弹性波矢量波场U(Ux,Uz)、P波矢量波场
| $ \left\{\begin{array}{l} \boldsymbol{U}_1 \cdot \boldsymbol{U}=\boldsymbol{U}_1 \cdot \boldsymbol{U}^{\mathrm{P}} \\ \boldsymbol{U}_2 \cdot \boldsymbol{U}=\boldsymbol{U}_2 \cdot \boldsymbol{U}^{\mathrm{S}} \\ \boldsymbol{U}_2 \cdot \boldsymbol{U}^{\mathrm{P}}=\bf{0} \\ \boldsymbol{U}_1 \cdot \boldsymbol{U}^{\mathrm{S}}=\bf{0} \end{array}\right. $ | (8) |
为了统一表示,定义算子D=U1,则D·U2=0,式(8)可重写为
| $ \left\{\begin{array}{l} \boldsymbol{D} \cdot \boldsymbol{U}=\boldsymbol{D} \cdot \boldsymbol{U}^{\mathrm{P}} \\ \boldsymbol{D} \times \boldsymbol{U}=\boldsymbol{D} \times \boldsymbol{U}^{\mathrm{S}} \\ \boldsymbol{D} \times \boldsymbol{U}^{\mathrm{P}}=\bf{0} \\ \boldsymbol{D} \cdot \boldsymbol{U}^{\mathrm{S}}=\bf{0} \end{array}\right. $ | (9) |
上式包含了四个方程和四个未知数,展开求解,可得
| $ \left\{\begin{array}{l} U_x^{\mathrm{P}}=\frac{k_x^2 U_x+r k_x k_z U_z}{k_x^2+r^2 k_z^2} \\ U_z^{\mathrm{P}}=\frac{r k_x k_z U_x+r^2 k_z^2 U_z}{k_x^2+r^2 k_z^2} \\ U_x^{\mathrm{S}}=\frac{r^2 k_z^2 U_x-r k_x k_z U_z}{k_x^2+r^2 k_z^2} \\ U_z^{\mathrm{S}}=\frac{-r k_x k_z U_x+k_x^2 U_z}{k_x^2+r^2 k_z^2} \end{array}\right. $ | (10) |
式中
| $ r=\sqrt{\frac{\left[(1+2 \delta) v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right]\left(v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right)}{(1+2 \varepsilon) v_{\mathrm{P}}^2-v_{\mathrm{S}}^2}} $ | (11) |
将式(10)写成向量形式
| $ \left\{\begin{array}{l} \boldsymbol{U}^{\mathrm{P}}=\boldsymbol{D}\left(\boldsymbol{D} \cdot \frac{\boldsymbol{U}}{|\boldsymbol{D}|^2}\right) \\ \boldsymbol{U}^{\mathrm{S}}=-\boldsymbol{D} \times\left(\boldsymbol{D} \times \frac{\boldsymbol{U}}{|\boldsymbol{D}|^2}\right) \end{array}\right. $ | (12) |
利用式(12),可在波数域实现各向异性介质P/S波解耦,但仅局限于均匀介质。因此进一步在式(12)中添加虚数项
| $ \left\{\begin{array}{l} \boldsymbol{U}^{\mathrm{P}}=\mathrm{i} \boldsymbol{D}(\mathrm{i} \boldsymbol{D} \cdot \boldsymbol{W}) \\ \boldsymbol{U}^{\mathrm{s}}=-\mathrm{i} \boldsymbol{D} \times(\mathrm{i} \boldsymbol{D} \times \boldsymbol{W}) \end{array}\right. $ | (13) |
式中W=U/|D|2,为辅助波场。
基于弱各向异性假设,对式(13)中的归一化项在ε=0、δ=0处做一阶泰勒展开,可得
| $ \frac{1}{|\boldsymbol{D}|^2}=\frac{1}{k_x^2+k_z^2}+\frac{k_z^2}{\left(k_x^2+k_z^2\right)^2} \frac{2 v_{\mathrm{P}}^2(2 \varepsilon-\delta)}{v_{\mathrm{P}}^2-v_{\mathrm{S}}^2} $ | (14) |
将式(14)代入式(13),再变换到空间域,可得
| $ \left\{\begin{array}{l} \boldsymbol{u}^{\mathrm{P}}=\nabla^{\mathrm{d}}\left(\nabla^{\mathrm{d}} \cdot \boldsymbol{w}\right) \\ \boldsymbol{u}^{\mathrm{S}}=-\nabla^{\mathrm{d}} \times\left(\nabla^{\mathrm{d}} \times \boldsymbol{w}\right) \end{array}\right. $ | (15) |
| $ \boldsymbol{w}=-\left[\frac{1}{k_x^2+k_z^2}+\frac{k_z^2}{\left(k_x^2+k_z^2\right)^2} \frac{2 v_{\mathrm{P}}^2(2 \varepsilon-\delta)}{v_{\mathrm{P}}^2-v_{\mathrm{S}}^2}\right] \boldsymbol{u} $ | (16) |
式中u(ux,uz)、
(1) 求解VTI弹性波波动方程(式(1))得到弹性波波场u(ux,uz),并进行傅里叶变换得到波数域弹性波场U(Ux,Uz)。
(2) 用波数域弹性波场U(Ux,Uz)计算
| $ \left\{\begin{array}{l} \boldsymbol{U}_{\mathrm{a}}=\boldsymbol{U}\left(U_x, U_z\right) /\left(k_x^2+k_z^2\right) \\ \boldsymbol{U}_{\mathrm{b}}=\boldsymbol{U}\left(U_x, U_z\right) k_z^2 /\left(k_x^2+k_z^2\right)^2 \end{array}\right. $ | (17) |
(3) 将步骤(2)中得到的波场进行逆傅里叶变换得到空间域波场ua和ub,计算辅助波场
| $ \boldsymbol{w}=\boldsymbol{u}_{\mathrm{a}}+\frac{2 v_{\mathrm{P}}^2(2 \varepsilon-\delta)}{v_{\mathrm{P}}^2-v_{\mathrm{S}}^2} \boldsymbol{u}_{\mathrm{b}} $ | (18) |
(4) 对辅助波场进行散度计算,得到矢量P波波场;进行旋度计算获得矢量S波波场。
上述算法在空间—波数域实现,且在每个时间步上仅需三次傅里叶变换(一次正变换,两次反变换),可适用于任意复杂模型。
1.2 上下波场分离成像条件低频噪声是由同路径波场在非成像点处相互关导致,严重降低了成像质量。同时,在强梯度界面处,由于炮点的上行波与检波点下行波的相关成像,会在真实界面上方产生假象。因此引入了上下波场分离成像条件,其主要利用炮点的下行波场与检波点的上行波场进行相关成像。
| $ \left\{\begin{array}{l} I^{\mathrm{PP}}=\int_{t=0}^T \boldsymbol{s}^{\mathrm{P}} \cdot \boldsymbol{r}^{\mathrm{P}} \mathrm{d} t \\ I^{\mathrm{PS}}=\int_{t=0}^T \boldsymbol{s}^{\mathrm{P}} \cdot \boldsymbol{r}^{\mathrm{S}} \mathrm{d} t \end{array}\right. $ | (19) |
式中:IPP和IPS分别为PP波和PS波成像结果;sP为震源P波波场;rP和rS分别为检波点P波和S波波场;T为地震记录长度。由于该成像条件会引入低频噪声和界面假象,引入上下波场分离成像条件
| $ \left\{\begin{array}{l} I^{\mathrm{PP}}=\int_{t=0}^T \boldsymbol{s}_{\mathrm{d}}^{\mathrm{P}} \cdot \boldsymbol{r}_{\mathrm{u}}^{\mathrm{P}} \mathrm{d} t \\ I^{\mathrm{PS}}=\int_{t=0}^T \boldsymbol{s}_{\mathrm{d}}^{\mathrm{P}} \cdot \boldsymbol{r}_{\mathrm{u}}^{\mathrm{S}} \mathrm{d} t \end{array}\right. $ | (20) |
式中:
对于式(18)的上、下行波场,本文采用Shen等[23]的方法求解。首先通过Hilbert变换构建只含正频率的复数波场
| $ \boldsymbol{s}^{\mathrm{c}}(\boldsymbol{x}, t)=\boldsymbol{s}(\boldsymbol{x}, t)+\mathrm{i} H[\boldsymbol{s}(\boldsymbol{x}, t)] $ | (21) |
式中:x表示空间坐标;sc(x, t)为复数波场;s(x, t)为用Ricker子波作为震源的外推波场;H[·]为Hilbert变换后Ricker子波作为震源的外推的波场。将复数波场沿z方向变换到波数域进行上下行波分离
| $ \left\{\begin{array}{l} \boldsymbol{S}_{\mathrm{d}}\left(x, k_z, t\right)= \begin{cases}\boldsymbol{S}^{\mathrm{c}}\left(x, k_z, t\right) & k_z>0 \\ 0 & k_{\mathrm{z}}<0\end{cases} \\ \boldsymbol{S}_{\mathrm{u}}\left(x, k_z, t\right)= \begin{cases}\boldsymbol{S}^{\mathrm{c}}\left(x, k_z, t\right) & k_z<0 \\ 0 & k_z>0\end{cases} \end{array}\right. $ | (22) |
式中:Sc(x, kz, t)是sc(x, t)在z方向的空间傅里叶变换结果;Sd(x, kz, t)和Su(x, kz, t)是波数域下、上行震源波场,对其进行逆傅里叶变换后可得到空间域上、下行震源波场。
检波点波场的上下行波分离过程与震源波场相似,不再赘述。
结合ani-Helmholtz解耦算法和上下波场分离成像条件的VTI弹性波逆时偏移的整体流程如下:
(1) 利用式(1)进行炮点波场模拟,得到弹性位移波场s(x, t);同时利用时间域Hilbert变换子波进行炮点波场模拟,得到弹性波场H[s(x, t)]。
(2) 利用式(1)的伴随方程与接收到的多波地震记录进行检波点波场模拟,得到弹性位移波场r(x, t);同时利用时间域Hilbert变换后的多波记录进行检波点波场模拟,得到弹性波场H[r(x, t)]。
(3) 利用式(21)和式(22)对震源波场和检波点波场进行上、下行波波场分离,得到炮点下行波场sd(x, t)和检波点上行波场ru(x, t)。
(4) 利用ani-Helmholtz算法对弹性波场sd(x, t)和ru(x, t)进行P/S波解耦,得到
(5) 应用式(20)得到成像结果IPP和IPS。
本文首先对波场进行上下行波分离,再对P/S波解耦,共应用上下行波分离两次(震源波场一次、检波点波场一次),P/S波解耦两次(震源波场一次、检波点波场一次)。若先进行P/S波解耦,再进行上下行波分离,则需要P/S波解耦四次(震源波场s(x, t)和H[s(x, t)]各一次、检波点波场r(x, t)和H[r(x, t)]各一次),上下行波分离四次(震源P波波场和S波波场各一次,检波点P波波场和S波波场各一次)。因此,从效率方面考虑,先进行上下行波分离,再进行P/S波模式解耦是必要的。
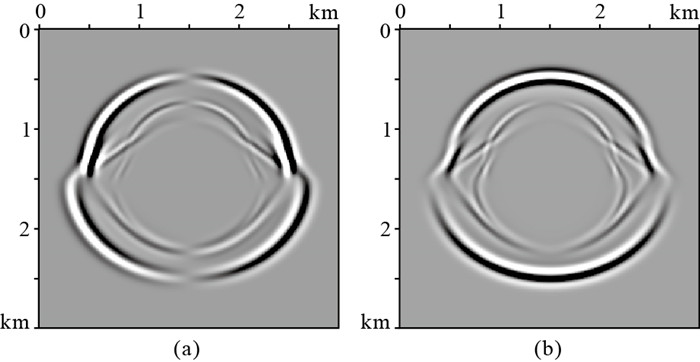
2 数值算例首先建立水平双层均匀VTI模型进行P/S波解耦以及上下行波分离测试。模型网格数为300×300,空间采样步长为10 m,界面深度为1500 m。模型上层参数为:vP=2500 m/s,vS=1800 m/s,ε=0.12,δ=0.10;下层参数为:vP=3200 m/s,vS=2250 m/s,ε=0.18,δ=0.15。采用主频为15 Hz的Ricker子波作为震源激发,使用空间10阶、时间2阶的交错网格有限差分进行模拟。时间采样间隔为1 ms,记录长度为1.5 s。震源位于(1500 m,1400 m)处模拟的原始弹性波波场快照如图 1所示。
|
图 1 双层模型弹性波波场快照 (a)x分量;(b)z分量 |
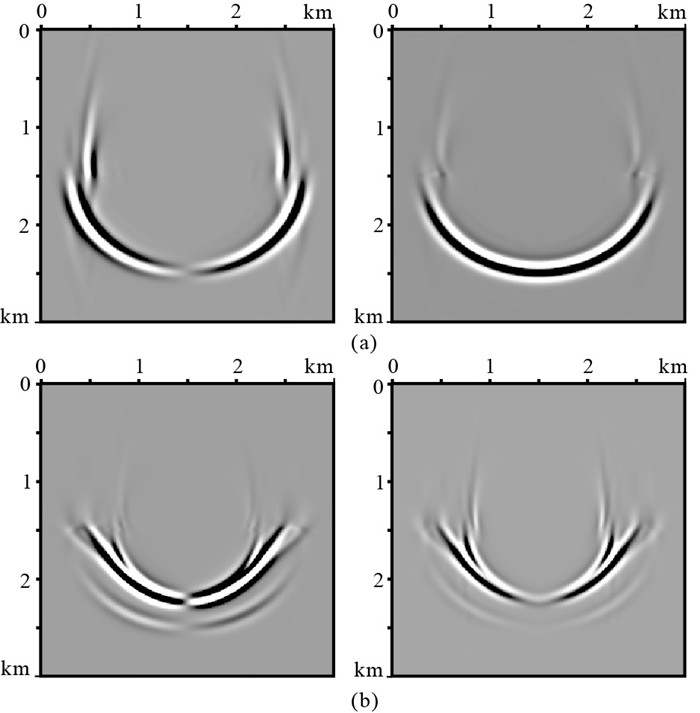
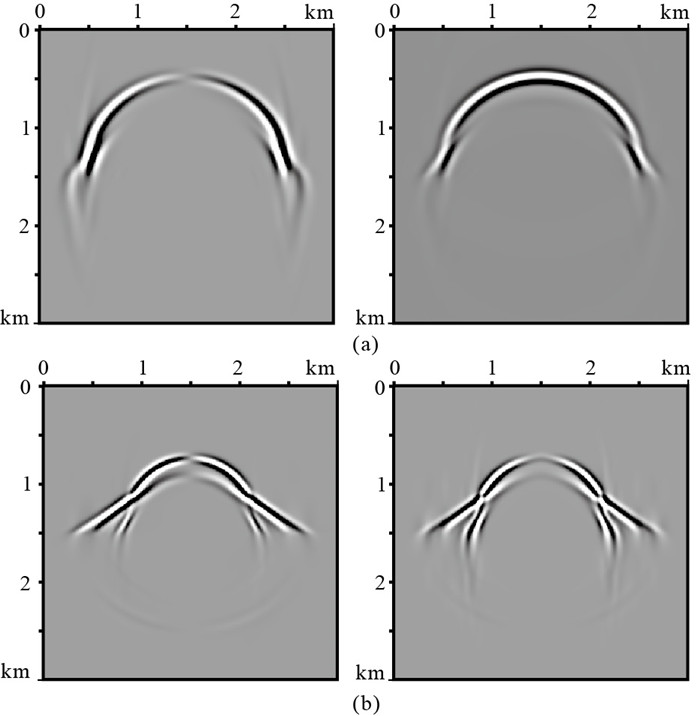
图 2为弹性波波场分离的上、下行波分量,两个方向的行波分离得比较干净。利用ani-Helmholtz解耦方法对图 1波场进行P/S波模式分离,结果如图 3所示,与原始波场(图 1)相比,P波分量(图 3a)得到了完全分离,S波分量(图 3b)有轻微P波残留(箭头所示),这是由于椭圆介质假设导致,在复杂介质成像中该误差可忽略。同样对图 2的上、下行弹性波场进行P/S波模式分离,分离的下行P波和S波快照如图 4所示,上行P波和S波快照如图 5所示。与图 3相比,P/S波上、下行波场同样分离得比较彻底。

|
图 2 双层模型弹性波波场上(a)、下(b)行波分离结果 左为x分量,右为z分量。 |

|
图 3 双层模型弹性波波场P(a)/S(b)波解耦结果 左为x分量,右为z分量。 |
|
图 4 双层模型下行波的P(a)/S(b)波解耦结果 左为x分量,右为z分量。 |
|
图 5 双层模型上行波的P(a)/S(b)波解耦结果 左为x分量,右为z分量。 |
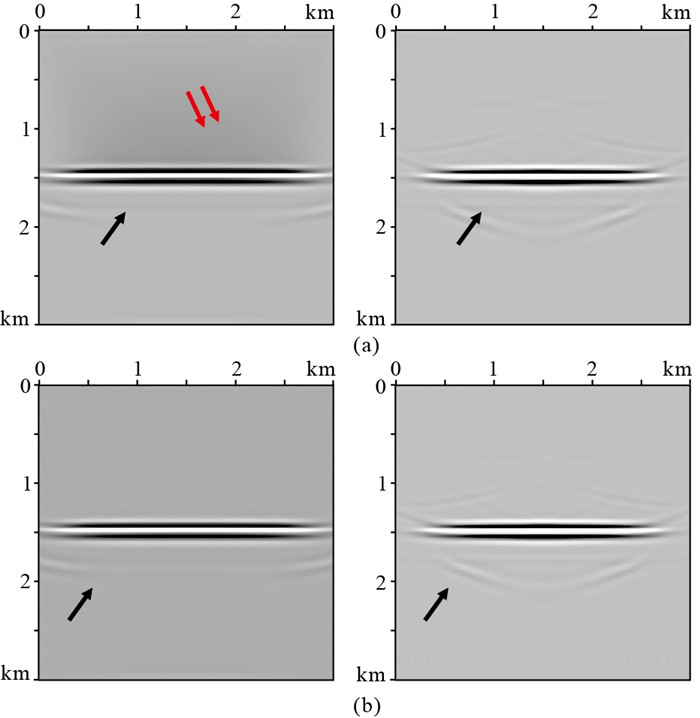
对于两层模型,在地下10 m处均匀布设100个震源,300个检波器均匀分布在地表。100炮模拟数据的不同成像条件VTI介质的弹性波逆时偏移结果如图 6所示。采用传统成像条件(式(19))得到PP波偏移结果界面上方有较多的低频噪声(红色箭头所示),PS成像因模型界面梯度较小并未出现假象(图 6a)。采用上下波场分离成像条件(式(20)) 的PP和PS成像结果如图 6b所示,相比之下,因避免了同路径成像,有效去除了PP波成像结果的低频噪声。值得注意的是,图 6成像结果在界面下方存在着明显的假象(黑色箭头所示),这是由于仅对检波点的反传波场进行了P/S波解耦,但未对用于反传的多分量地震数据进行P/S波模式分离(即分为P波地震数据,S波地震数据),在进行反传时,这些耦合的P/S波地震数据会产生错误走时的转换波,会在界面下方(或上方)产生假象。消除这些假象的有效方法之一是对接收到的地震记录先进行P/S波分离,得到纯P波记录和纯S波记录进行反传,这将是进一步的研究方向。
|
图 6 双层模型不同成像条件的弹性波逆时偏移结果 (a)传统成像条件;(b)波场分离成像条件。左为PP波,右为PS波。 |
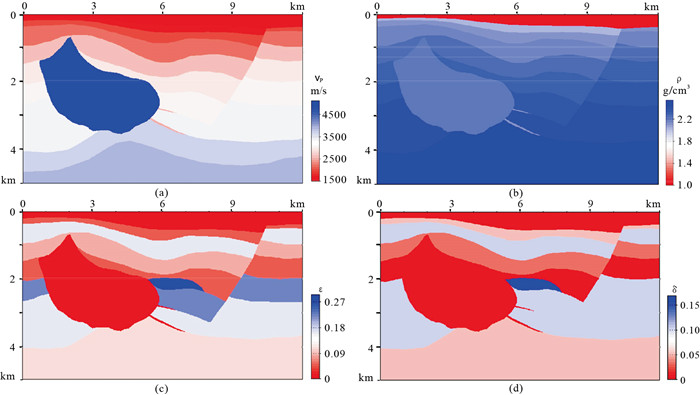
VTI Hess模型(图 7)的盐丘边界具有较大的速度梯度,可用于测试偏移方法的有效性。该模型网格数为1200×500,空间步长为10 m,其中S波速度是P波速度1/2。震源采用主频为15 Hz的Ricker子波,时间采样间隔为0.5 ms。120个炮点均匀分布在地下10 m处,炮间距为100 m。每炮800个检波器接收,间隔为10 m。
|
图 7 VTI Hess模型 (a)P波速度;(b)密度;(c)ε;(d)δ |
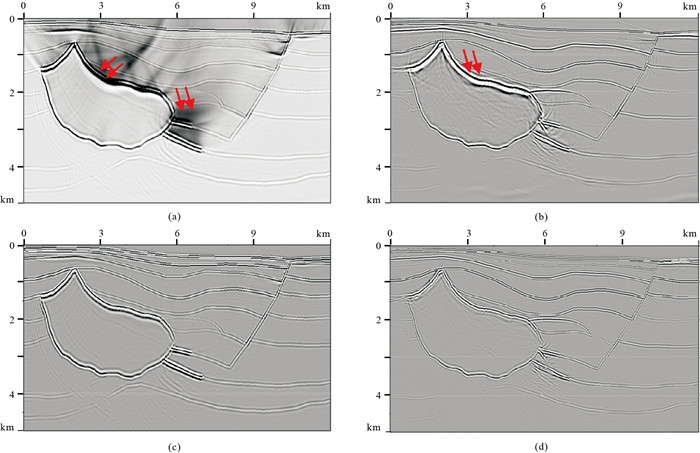
图 8a和图 8b为应用传统成像条件(式(19))得到的PP和PS波成像结果。可以看出,由于同路径成像原因,PP波结果上存在严重的低频噪声干扰(图 8a箭头所示),难以去除。同时,由于盐丘边界梯度较大,应用传统成像条件时,PS波偏移结果存在同路径以及上行震源波场与下行检波点波场互相关成分,在盐丘边界处会形成界面假象和噪声(图 8b箭头所示),这对后续的道集提取和AVO等处理有着较大影响。图 8c和图 8d为采用上下行波分离成像条件(式(20))得到的偏移结果,可以看到,因为仅采用了炮点的下行波场与检波点的上行波场进行互相关,因此避免了由于同路径成像产生的低频噪声,成像质量明显提高。在盐丘边界处,消除了传统方法带来的成像假象和严重噪声污染,验证了本文方法及流程的有效性。
|
图 8 Hess模型不同成像条件的偏移结果 (a)传统成像条件PP波;(b)传统成像条件PS波;(c)上下行波分离成像条件PP波;(d)上下行波分离成像条件PS波 |
本文主要将各向异性ani-Helmholtz解耦算法与上下行波分离方法相结合,并应用于VTI介质各向异性弹性波逆时偏移中,建立了一套高效的成像流程,有效地去除了低频噪声与界面假象,提高了成像质量,合成模型案例证明了本文方法的有效性。
采用各向异性ani-Helmholtz解耦算法,将弹性波场分解为向量P波和S波波场,该算法在每个时间步骤仅需三次傅里叶变换,效率较高,适用于任意复杂模型。且该算法可以轻松推广到三维和TTI介质中,具有明确的物理意义。但同时由于采用了椭圆VTI假设和一阶泰勒展开式,该算法主要适用于弱各向异性介质,当遇上强各向异性介质时可能会产生不可忽视的误差。此外,由于推导过程中基于局部均匀假设,对模型进行适度的平滑是有必要的。由于逆时偏移对初始速度模型有较强的依赖性,本文采用5×5高斯平滑模板应用于Hess模型,对速度和各向异性参数模型反复平滑3次左右,既可以降低强梯度界面带来的P/S波波场解耦误差,又保证了成像的质量。在此基础上更高程度的平滑对成像结果可能会造成不可忽视的误差。
基于显式行波分离技术的成像结果有效压制了低频噪声和成像假象,提高了成像质量。但是,在上下波场分离过程中,波数的截断会在波场快照边界处造成分离假象,这时需要添加一定区域范围的衰减时窗进行压制。但同时也会造成信号的破坏,如何平衡分离误差与信号缺失,是后续需要研究的问题。
尽管本文采用了ani-Helmholtz解耦算法和行波分离成像条件,但同样还存在一定程度的成像误差(图 8),这些误差主要来源于多次波的干扰以及分离过程中的数值误差,且随着模型的复杂化而变得明显。针对后者的数值误差干扰,可应用延长差分算子长度和提高分离算子精度等方法,但同时也会增加较多的计算量。本文成像方法流程的计算量主要包括四次正演(震源端两次,检波点端两次),五次快速傅里叶变换(式(16)三次,式(20)两次),以及散度、旋度计算。为了提高计算效率,本文的模型试算引入了GPU技术,即CUDA(Compute Unified Device Architecture)并行编程平台。CUDA库函数中的cufft API函数可实现并行优化的快速傅里叶变换,大大节省了运行时间。应用GPU技术可将本文方法推广到三维或实际数据成像。
| [1] |
CALDWELL J. Marine multicomponent seismology[J]. The Leading Edge, 1999, 18(11): 1274-1282. DOI:10.1190/1.1438198 |
| [2] |
GRANLI J, ARNTSEN B, SOLLID A, et al. Imaging through gas-filled sediments using marine shear-wave data[J]. Geophysics, 1999, 64(3): 668-677. DOI:10.1190/1.1444576 |
| [3] |
ZHAO Y, LI W. Model-based radiation pattern correction for interferometric redatuming in 4D seismic[J]. Geophysics, 2018, 83(4): Q25-Q35. DOI:10.1190/geo2017-0731.1 |
| [4] |
ZHAO Y, ZHANG H, YANG J, et al. Reducing artifacts of elastic reverse time migration by the deprimary technique[J]. Geophysics, 2018, 83(6): S569-S577. DOI:10.1190/geo2018-0260.1 |
| [5] |
于春玲, 王建民, 付雷, 等. 转换波各向异性速度分析与偏移成像[J]. 石油地球物理勘探, 2010, 45(增刊1): 44-47. YU Chunling, WANG Jianmin, FU Lei, et al. Anisotropic velocity analysis and migration imaging for converted wave[J]. Oil Geophysical Prospecting, 2010, 45(S1): 44-47. |
| [6] |
YAN J, SAVA P. Isotropic angle-domain elastic reverse-time migration[J]. Geophysics, 2008, 73(6): S229-S239. DOI:10.1190/1.2981241 |
| [7] |
MORSE P M, FESHBACH H. Methods of Theoretical Physics[M]. New York: McGraw-Hill Book Company, 1953.
|
| [8] |
DELLINGER J, ETGEN J. Wavefield separation in two-dimensional anisotropic media[J]. Geophysics, 1990, 55(7): 914-919. DOI:10.1190/1.1442906 |
| [9] |
ZHANG Q, MCMECHAN G A. 2D and 3D elastic wavefield vector decomposition in the wavenumber domain for VTI media[J]. Geophysics, 2010, 75(3): D13-D26. DOI:10.1190/1.3431045 |
| [10] |
ZHU H. Elastic wavefield separation based on the Helmholtz decomposition[J]. Geophysics, 2017, 82(2): S173-S183. DOI:10.1190/geo2016-0419.1 |
| [11] |
YANG J, ZHU H, WANG W, et al. Isotropic elastic reverse time migration using the phase- and amplitude-corrected vector P- and S-wavefields[J]. Geophysics, 2018, 83(6): S489-S503. DOI:10.1190/geo2018-0023.1 |
| [12] |
YAN J, SAVA P. Elastic wave-mode separation for VTI media[J]. Geophysics, 2009, 74(5): WB19-WB32. DOI:10.1190/1.3184014 |
| [13] |
CHENG J, Fomel S. Fast algorithms for elastic-wave-mode separation and vector decomposition using low-rank approximation for anisotropic media[J]. Geo-physics, 2014, 79(4): C97-C110. |
| [14] |
YANG J, ZHANG H, ZHAO Y, et al. Elastic wavefield separation in anisotropic media based on eigenform analysis and its application in reverse-time migration[J]. Geophysical Journal International, 2019, 217(2): 1290-1313. DOI:10.1093/gji/ggz085 |
| [15] |
ZHANG L, LIU L, NIU F, et al. A novel and efficient engine for P/S wave-mode vector decomposition for VTI elastic reverse time migration[J]. Geophysics, 2022, 87(4): S185-S207. DOI:10.1190/geo2021-0609.1 |
| [16] |
FEI T, LUO Y, QIN F. An endemic problem in reverse-time migration[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 3811-3815
|
| [17] |
BAYSAL E, KOSLOFF D D, SHERWOOD J W C. A two-way nonreflecting wave equation[J]. Geophysics, 1984, 49(2): 132-141. DOI:10.1190/1.1441644 |
| [18] |
LOEWENTHAL D, STOFFA P L, FARIA E L. Suppressing the unwanted reflections of the full wave equation[J]. Geophysics, 1987, 52(7): 1007-1012. DOI:10.1190/1.1442352 |
| [19] |
ZHANG Y, SUN J. Practical issues of reverse time migration: True amplitude gathers, noise removal and harmonic-source encoding[J]. First Break, 2009, 27(1): 53-59. |
| [20] |
YOON K, MARFURT K. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 2006, 52(2): 102-107. |
| [21] |
YOON K, GUO M H, CAI J, et al. 3D RTM angle ga-thers from source wave propagation direction and dip of reflector[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 3136-3140.
|
| [22] |
LIU F, ZHANG G, MORTON S A, et al. An effective imaging condition for reverse-time migration using wavefield decomposition[J]. Geophysics, 2011, 76(1): S29-S39. DOI:10.1190/1.3533914 |
| [23] |
SHEN P, ALBERTIN U. Up-down separation using Hilbert transformed source for causal imaging condition[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 4175-4179.
|
| [24] |
FEI T, LUO Y, YANG J, et al. Removing false images in reverse time migration: the concept of de-primary[J]. Geophysics, 2015, 80(6): S237-S244. DOI:10.1190/geo2015-0289.1 |
| [25] |
WANG W, MCMECHAN G A, TANG C, et al. Up/down and P/S decompositions of elastic wavefields using complex seismic traces with applications to calculating Poynting vectors and angle-domain common-image gathers from reverse time migrations[J]. Geophysics, 2016, 81(4): S181-S194. DOI:10.1190/geo2015-0456.1 |
| [26] |
XUE H, LIU Y. Reverse-time migration using multidirectional wavefield decomposition method[J]. Applied Geophysics, 2018, 15(2): 222-233. DOI:10.1007/s11770-018-0670-0 |
| [27] |
ZHANG L, LIU Y, JIA W, et al. Suppressing residual low-frequency noise in VSP reverse time migration by combining wavefield decomposition imaging condition with Poynting vector filtering[J]. Exploration Geophysics, 2021, 52(2): 235-244. DOI:10.1080/08123985.2020.1804298 |
| [28] |
徐世刚, 包乾宗, 任志明, 等. 结合泊松算法和波场分解成像条件的各向异性优化纯声波方程逆时偏移[J]. 石油地球物理勘探, 2022, 57(3): 614-623. XU Shigang, BAO Qianzong, REN Zhiming, et al. Reverse-time migration of optimized pure acoustic equation in anisotropic media by combining Poisson algorithm and wavefield decomposition imaging condition[J]. Oil Geophysical Prospecting, 2022, 57(3): 614-623. |
| [29] |
高少武, 孙鹏远, 方云峰, 等. 双检数据上下行波场分离技术研究进展[J]. 石油地球物理勘探, 2021, 56(6): 1419-1429. GAO Shaowu, SUN Pengyuan, FANG Yunfeng, et al. Research progress of up-going and down-going wavefield separation for dual-sensor data[J]. Oil Geophy-sical Prospecting, 2021, 56(6): 1419-1429. |
| [30] |
TSVANKIN I. Seismic Signatures and Analysis of Reflection Data in Anisotropic Media(3rd ed)[M]. Tulsa: SEG, 2012.
|
| [31] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [32] |
陈可洋, 王建民, 关昕, 等. 逆时偏移技术在VSP数据成像中的应用[J]. 石油地球物理勘探, 2018, 53(1): 89-94. CHEN Keyang, WANG Jianmin, Guan Xin, et al. VSP data imaging with reverse time migration[J]. Oil Geo-physical Prospecting, 2018, 53(1): 89-94. |
| [33] |
WANG C, CHENG J, ARNTSEN B. Scalar and vector imaging based on wave mode decoupling for elastic reverse time migration in isotropic and transversely isotropic media[J]. Geophysics, 2016, 81(5): S383-S398. DOI:10.1190/geo2015-0704.1 |



 张乐乐, 北京市昌平区府学路18号中国石油大学(北京)非常规油气科学技术学院, 102249。Email:
张乐乐, 北京市昌平区府学路18号中国石油大学(北京)非常规油气科学技术学院, 102249。Email: 