2. 东方地球物理公司, 河北涿州 072751
2. BGP Inc., CNPC, Zhuozhou, Hebei 072750, China
地震数据处理中面波是一种常见噪声,表现为低频、低速、强能量特征,并具有频散性和多模性。为了更凸显地震数据中的反射和折射波等信息,须有效压制面波噪声。利用面波的低频特征,可在频率域滤除低频成分,如f-k滤波[1]等;也可在变换域分离有效波与面波,包括频率—波数域方法[2]、τ-p滤波[3-4]、Radon变换[5-6]、小波变换[7]、曲波变换[8]、稀疏分解[9]及局部时频分解[10]等;还可利用面波的近似线性特征对其进行消除,如平面波分解[11]、奇异值分解[12]、干涉去除[13]、预测误差滤波器(PEF)[14]等方法。另外,还有基于预测消减策略的其他压制方法,如f-x域建模和反演方法[15]。
上述方法虽得到了很好应用,然而由于使用的前提条件往往难以满足,如规则的炮检分布,或需要辅助处理步骤估计面波时差,以至于诸如面波能量残留、有效信号保真及对空间稀疏采样造成的假频问题等得不到很好解决。
基于频散的面波预测与压制算法,充分利用面波的频散特征,通过对数据进行分析得到频散曲线,进而得到面波模型,最后通过消减方法将面波从数据中消除,这种方法不需任何先验信息,具有很高的灵活性。频散谱的计算及频散关系的拾取是这类方法的关键,常用方法包括倾斜f-k变换法[16]、小波变换法、τ-p变换法[3]、相移法[17],倾斜叠加法[18]、高精度线性Radon法[19]等,这些传统方法获得的频散谱分辨率不高,且在低频段的分辨率更低,影响面波预测的准确性。此外,通过优化参与分析数据的炮检距、道数等问题可提高实际地震数据频散曲线生成精度[20]。Zheng等[21]应用一种非线性信号相似性分析法(MNLSC),得到高低频一致的高精度频散谱,进而预测与压制面波噪声,该方法有望成为一种有效的面波压制方法,但高精度的频散谱计算面临海量数据时耗时太大。
本文介绍一种改进的频散面波压制方法,该方法结合自适应表面波数据提取技术、炮检距相关步长的面波重建技术和噪声模型匹配消减法,充分利用高分辨率频散谱分析方法,使该程序能应用于实际并产生良好效果。实际资料测试结果表明,本文方法可有效地预测和消除频散面波,同时最大程度地保护反射信号,还可很好地解决空间稀疏采样引起的空间混叠现象。
1 方法原理地震记录中,熟知的瑞雷面波广泛存在于半空间、层状介质中,且在传播过程中能量衰减慢,在层状介质中还具有频散特性。实际地震记录的频散曲线可通过面波的频散谱提取,传统的基于波场变换的频率域方法是将时间域面波记录转变为频域的频散谱,面波频散谱中既包含基阶频散,也包含高阶频散,应用该方法在单炮记录中就可较容易地提取面波的频散曲线。
假设时刻t、距离x处的时间域记录为u(x,t),其傅里叶变换为
| $ U(x, \omega)=\int u(x, t) \exp (\mathrm{i} \omega t) \mathrm{d} t $ | (1) |
式中ω为圆频率。
频率—空间域波场U(x,ω)可表示为振幅与相位相乘的形式
| $ U(x, \omega)=A(x, \omega) P(x, \omega) $ | (2) |
式中:P(x,ω)表示相位谱,包含了每个频率的相位信息,即波场的到达时间;A(x,ω)表示振幅谱,包含了波场的衰减、空间扩散等信息;记录U(x,ω)表示每个频率分量的振幅与相位特性。因此,U(x,ω)也可表示为
| $ U(x, \omega)=A(x, \omega) \exp (-\mathrm{i} \mathit\Phi x) $ | (3) |
式中Φ=ω/cω,其中cω表示频率ω处的相速度。对整个单炮记录的U(x,ω)求和
| $ V(\omega, \phi)=\int \frac{U(x, \omega)}{|U(x, \omega)|} \exp (\mathrm{i} \phi x) \mathrm{d} x $ | (4) |
得到关于ω与ϕ的关系式。对于给定的某一频率ω,当ϕ满足
| $ \phi=\mathit\Phi=\frac{\omega}{c_\omega} $ | (5) |
V(ω,ϕ)即取得极大值,此时对应的相速度为该频率处面波的相速度。基于该算法,可计算面波频散谱,通过频散谱拾取频散曲线。一般使用线性信号相似性分析法计算频散谱,所得频散谱在低频部分的分辨率低于高频部分,在面波所处的低频段难以得到可靠时移量,将影响后续面波预测。
本文使用非线性信号相似性分析法(NLSC)[22]计算频散谱,所得频散谱在高、低频段能量都很均衡,且分辨率高于传统方法。NLSC可用
| $ S_{\mathrm{NLSC}}\left(\omega, c_\omega ; \sigma\right)=\frac{S_{\mathrm{NL}}\left(\omega, c_\omega\right)-S_\pi}{1-S_\pi} $ | (6) |
表示,即为某一频率和相速度的地震信号在两个接收点的非线性信号相关。式中:σ为可调整频散谱分辨率的无量纲参数;Sπ为背景值,且有
| $ \begin{aligned} &S_{\mathrm{NL}}\left(\omega, c_\omega\right)=\\ &\;\;\;\;\frac{1}{T} \int_0^T \exp \left(-\frac{\left[\bar{d}_1(t ; \omega)-\bar{d}_x\left(t+\frac{x}{c_\omega} ; \omega\right)\right]^2}{4 \omega^2 \pi^{-2} \sigma^2}\right) \mathrm{d} t \end{aligned}$ | (7) |
式中:dx(t; ω)为地震道数据;T为地震信号长度。
频散谱分析是基于频散类方法的第一步,也是最关键的一步。获取高精度的频散谱,进而得到准确的频散曲线,对面波预测是至关重要的。传统方法所得频散谱的分辨率较低,尤其是低频部分。使用NLSC对地震数据进行比较,就能得到高精度频散谱,但计算相当耗时,当数据量大时无法真正发挥其优势。
对地震数据进行面波时窗定义,在远、近排列自适应地对面波数据进行选取,并根据面波所在的优势频段提取面波数据,能最大限度地减少体波的影响,充分凸显面波的传播特性。结合NLSC,使用滑动步长获取局部域的数据的频散特征,能发挥这种频散谱估计的优势,减小计算量。
图 1显示应用本文方法获得的高分辨率频散谱(图 1c),可见相较于传统方法所得频散谱(图 1b),其分辨率大幅提升,且高、低频的分辨率更一致,这样就显著提高了低频段频散曲线的精细程度。

|
图 1 高精度面波频散谱 (a)原始单炮记录;(b)f-k变换法所得频散谱;(c)本文方法所得高精度面波频散谱 |
利用面波频散曲线获得近地表横波速度的方法广泛地应用于近地表调查,许多学者通过不同方法克服了瑞雷面波频散曲线的非线性与多极性,提高了反演结果的准确性和稳定性[23-25]。从近地表横波速度模型正演得到面波数据,进而从地震数据中对其进行压制,也取得了较好效果[26-27]。不同于这类方法需要首先得到近地表速度场信息,本文使用一种完全数据驱动的方法重建面波数据。得益于高精度的频散谱分析方法,能得到准确的频散关系,基于此可从地震数据中提取面波模型,首先将地震信号进行相位校正,以此消除面波的频散效应,通过此方式将类线性的面波特征变成真线性;再用相邻地震道面波数据的相干性就可完成对面波模型的预测。
面波模型的重建过程可表示为
| $ \begin{aligned} & U(x ; \omega)= \\ & \;\;\;\quad \frac{1}{A} \sum\limits_{x_i=-L \text { (offset) }}^{L(\text { offset) }} a_i \cdot U\left(x_i ; \omega\right) \cdot \mathrm{e}^{-\mathrm{i} \omega \frac{x_i}{c_\omega}} \end{aligned} $ | (8) |
式中:U(x;ω)是预测的某位置面波噪声;L是随炮检距变化的局部域空间窗;ai是权重系数,i为重建时窗的索引;A是某检波点处所有权重系数的和。在此,需考虑不同炮检距对面波重建的影响,采用随炮检距变化的预测窗口,以更准确预测面波噪声。
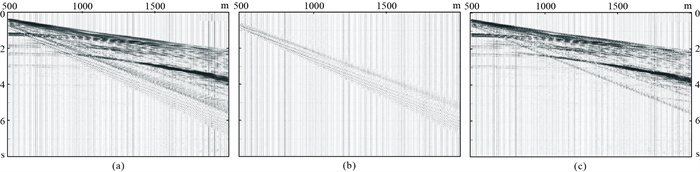
在正演得到的包含面波信息的模型数据(图 2a)上对本文方法进行测试,图 2b为预测的面波噪声,图 2c为去噪后结果,可见面波噪声被准确预测并压制。
|
图 2 模型试算 (a)原始数据;(b)预测噪声;(c)去噪结果 |
从原始地震数据中减去预测出的面波,就可实现对面波噪声的压制。然而,两者并非总是契合得很好,特别是在特殊地表情形下,或是地震道缺失时,直接相减会产生畸点,对有效信号造成破坏。实际应用中,需将预测噪声与地震数据进行相关匹配,进而将其从原始地震数据中减去,能更好地消除面波,突出有效信号。
2 应用效果该方法在实际数据处理中展现出很好的应用效果,对传统去噪方法不能解决的由稀疏采样导致的空间假频问题有很好的适用性。图 3所示资料来自岐口凹陷北大港地区,该区地表复杂,风化层严重,使该地区面波尤为发育,且能量很强,视速度低,严重影响中、深层有效反射(图 3a)。观察用本文方法预测出的假频面波(图 3e),可见去噪结果的信噪比显著改善,三角区的面波能量得到较彻底的压制,反射波的信息得以恢复(图 3b)。而f-k视速度滤波方法对该假频面波却无能为力(图 3c、图 3f),振幅压制方法能有效提高数据的信噪比,但尚有部分面波能量残留(图 3d、图 3g)。对比不同方法所得频谱(图 4),可得到同样的结论。面对低频、低视速度的假频面波,f-k方法无法有效将噪声成分从f-k谱中滤除,而振幅去噪方法有效地压制了低频部分的能量,但仍有一定量的能量残余还可能伤害有效信号。因此,本文方法能很好地压制面波能量,并使有效信号所在频段尽可能地保持不变。

|
图 3 应用效果一 (a)原始炮集;(b)本文方法面波压制后结果;(c)f-k滤波方法去噪结果;(d)振幅压制方法去噪结果;(e)本文方法预测的面波噪声;(f)f-k滤波方法消除的噪声;(g)振幅压制方法消除的噪声 |

|
图 4 不同方法频谱对比 |
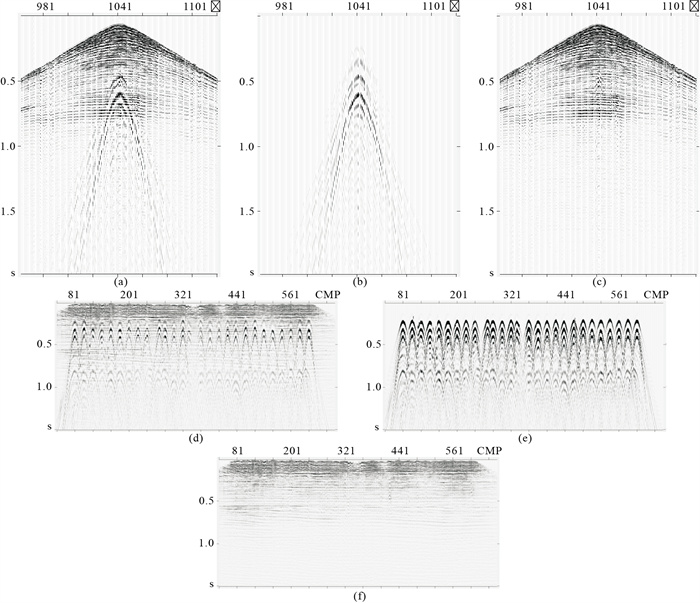
将本文方法应用于安徽淮南M煤矿地区的一个三维高精度数据体。该区表层为稳定的黏土或沙质黏土层,面波为影响最大的噪声,能量较强,与有效信号的频带接近且全区分布。该区目的层煤层反射波稳定,特征明显,同相轴连续性较好,能全区可靠对比追踪,利于检验本文方法效果。针对原始数据炮集(图 5a),应用该方法预测得到的面波噪声(图 5b)形态完整、能量均衡,噪声数据中看不到有效信号损失,去噪结果(图 5c)中噪声得到较彻底压制,同相轴清晰连续,面波噪声的能量残余也处理得很好。对比叠加剖面可见,淹没在原始剖面(图 5d)中的同相轴在去噪后(图 5f)得到清晰显现,噪声剖面(图 5e)中基本无有效信号。
|
图 5 应用效果二 (a)原始炮集;(b)本文方法预测的面波噪声;(c)本文方法面波压制后结果;(d)去噪前叠加剖面;(e)噪声剖面;(f)去噪后叠加剖面 |
这两个实例都证明了该方法在消除频散面波噪声方面的有效性及其在信号保真度方面的优异表现。
3 结束语本文探讨了一种改进的基于频散的面波预测与压制方法。根据面波的固有频散属性,利用非线性信号相似性分析方法获取高精度面波频散谱,进而自动获取频散曲线,利用频散曲线重建面波模型,最后将其从地震数据中减去,以达到压制面波的目的。该流程是一种完全数据驱动的方法,不需任何先验信息,比传统的去面波方法更有效、更灵活,适用于不同类型的近地表情形,在保真度、能量残余和空间假频等方面对预测与压制频散面波有更优异表现,并在实际应用中取得了较好效果。
| [1] |
DUNCAN G, BERESFORD G. Slowness adaptive f-k filtering of prestack seismic data[J]. Geophysics, 1994, 59(1): 140-147. DOI:10.1190/1.1443525 |
| [2] |
ASKARI R, SIAHKOOHI H R. Ground roll attenuation using the S and x-f-k transforms[J]. Geophysical Prospecting, 2008, 56(1): 105-114. |
| [3] |
MCMECHAN G A, YEDLIN M J. Analysis of dispersive waves by wave field transformation[J]. Geophysics, 1981, 46(6): 869-874. DOI:10.1190/1.1441225 |
| [4] |
TURNER G. Aliasing in the tau-p transform and the removal of spatially aliased coherent noise[J]. Geophysics, 1990, 55(11): 1496-1503. DOI:10.1190/1.1442797 |
| [5] |
RUSSELL B, HAMPSON D, CHUN J. Noise elimination and the Radon transform, part 2[J]. The Lea-ding Edge, 1990, 9(11): 31-37. DOI:10.1190/1.1439700 |
| [6] |
HU Y, WANG L, CHENG F, et al. Ground-roll noise extraction and suppression using high-resolution linear Radon transform[J]. Journal of Applied Geophy-sics, 2016, 128: 8-17. DOI:10.1016/j.jappgeo.2016.03.007 |
| [7] |
徐阳, 罗明璋, 王智, 等. 广义S变换与二维离散小波变换联合压制面波[J]. 石油物探, 2018, 57(3): 395-403. XU Yang, LUO Mingzhang, WANG Zhi, et al. Surface wave suppression using generalized S-transform and 2D discrete wavelet transform[J]. Geophysical Pro-specting for Petroleum, 2018, 57(3): 395-403. DOI:10.3969/j.issn.1000-1441.2018.03.009 |
| [8] |
李继伟, 臧殿光, 刁永波, 等. 自适应相减和Curvelet变换组合压制面波[J]. 石油地球物理勘探, 2020, 55(5): 1005-1015. LI Jiwei, ZANG Dianguang, DIAO Yongbo, et al. Combination of adaptive subtraction and Curvelet transform to suppress surface waves[J]. Oil Geophy-sical Prospecting, 2020, 55(5): 1005-1015. |
| [9] |
WANG W, GAO J, CHEN W, et al. Data adaptive ground-roll attenuation via sparsity promotion[J]. Journal of Applied Geophysics, 2012, 83: 19-28. DOI:10.1016/j.jappgeo.2012.04.004 |
| [10] |
LIU Y, FOMEL S. Seismic data analysis using local time-frequency decomposition[J]. Geophysical Prospecting, 2013, 61(3): 516-525. DOI:10.1111/j.1365-2478.2012.01062.x |
| [11] |
FOMEL S. Applications of plane-wave destruction filters[J]. Geophysics, 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [12] |
PORSANI M J, SILVA M G, MELO P E M, et al. SVD filtering applied to ground-roll attenuation[J]. Journal of Geophysics and Engineering, 2010, 7(3): 284-289. DOI:10.1088/1742-2132/7/3/007 |
| [13] |
HALLIDAY D, BILSBY P, WEST L, et al. Scattered ground-roll attenuation using model-driven interfe-rometry[J]. Geophysical Prospecting, 2015, 63(1): 116-132. DOI:10.1111/1365-2478.12165 |
| [14] |
BROWN M, CLAPP R G, MARFURT K. Predictive Coherent Noise Suppression of 3-D Ground Roll[R]. SEP Report, 1999.
|
| [15] |
PERKINS C, ZWAAN M. Ground roll attenuation[C]. Extended Abstracts of 62nd EAGE Conference & Exhibition, 2000, cp-28-00172.
|
| [16] |
SERDYUKOV A S, YABLOKOV A V, DUCHKOV A A, et al. Slant f-k transform of multichannel seismic surface wave data[J]. Geophysics, 2019, 84(1): A19-A24. DOI:10.1190/geo2018-0430.1 |
| [17] |
PARK C B, MILLER R D, XIA J. Imaging dispersion curves of surface waves on multi-channel record[C]. SEG Technical Program Expanded Abstracts, 1998, 17: 1377-1380.
|
| [18] |
XIA J, XU Y, MILLER R D. Imaging dispersive energy by slant stacking[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 1061-1064.
|
| [19] |
LUO Y, XIA J, MILLER R D, et al. Rayleigh-wave dispersive energy imaging using a high-resolution li-near Radon transform[J]. Pure and Applied Geophy-sics, 2008, 165(5): 903-922. DOI:10.1007/s00024-008-0338-4 |
| [20] |
姜福豪, 李培明, 张翊孟, 等. 多道面波频散分析在实际大炮数据中的应用[J]. 石油地球物理勘探, 2018, 53(1): 17-24, 46. JIANG Fuhao, LI Peiming, ZHANG Yimeng, et al. Frequency dispersion analysis of MASW in real seismic data[J]. Oil Geophysical Prospecting, 2018, 53(1): 17-24, 46. |
| [21] |
ZHENG Y, HU H. Nonlinear signal comparison and high-resolution measurement of surface-wave dispersion[J]. Bulletin of the Seismological Society of America, 2017, 107(3): 1551-1556. DOI:10.1785/0120160242 |
| [22] |
HU H, ZHENG Y. Data-driven dispersive surface-wave prediction and mode separation using high-resolution dispersion estimation[J]. Journal of Applied Geophysics, 2019, 171: 103867. DOI:10.1016/j.jappgeo.2019.103867 |
| [23] |
高旭, 于静, 李学良, 等. 自适应权重蜻蜓算法及其在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2021, 56(4): 745-757. GAO Xu, YU Jing, LI Xueliang, et al. Rayleigh wave dispersion curve inversion based on adaptive weight dragonfly algorithm[J]. Oil Geophysical Prospecting, 2021, 56(4): 745-757. |
| [24] |
王一鸣, 宋先海, 张学强. 应用人工神经网络算法的地震面波非线性反演[J]. 石油地球物理勘探, 2021, 56(5): 979-991. WANG Yiming, SONG Xianhai, ZHANG Xueqiang. Research on nonlinear inversion of seismic surface waves based on artificial neural network algorithm[J]. Oil Geophysical Prospecting, 2021, 56(5): 979-991. |
| [25] |
王一鸣, 宋先海, 张学强. 瑞雷面波频散曲线的粒子群蚁群混合优化反演[J]. 石油地球物理勘探, 2022, 57(2): 303-310, 356. WANG Yiming, SONG Xianhai, ZHANG Xueqiang. Inversion of Rayleigh wave dispersion curves based on particle swarm and ant colony hybrid optimization[J]. Oil Geophysical Prospecting, 2022, 57(2): 303-310, 356. |
| [26] |
STROBBIA C, ANDREAS L, VERMEER P, et al. Surface waves: Use them then lose them. Surface-wave analysis, inversion and attenuation in land reflection seismic surveying[J]. Near Surface Geophysics, 2011, 9(6): 503-513. |
| [27] |
STROBBIA C, ZARKHIDZE A, MAY R, et al. Mo-del-based coherent noise attenuation for complex dispersive waves[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 3571-3575.
|



 孙郧松, 河北省涿州市华阳东路物探科技园东方地球物理公司物探技术研究中心, 072751。Email:
孙郧松, 河北省涿州市华阳东路物探科技园东方地球物理公司物探技术研究中心, 072751。Email: 