海底节点(Ocean Bottom Node,OBN)是一种放置在海底,可独立采集、记录地震信号的多分量地震仪[1]。OBN勘探是将节点地震仪布设在海底,记录由水中激发、海底之下地层界面反射的地震信号。由于摆脱了电缆的束缚,OBN地震观测系统设计灵活、多变,可对常规地震勘探盲区进行有效探测与成像,提供对复杂与高速屏蔽构造(如盐下屏蔽)的有效地震成像所必不可少的宽方位角、多方位角、多炮检距地震数据集[2-5]。并且由于节点仪器直接置于海底,因此相对于常规海上拖缆地震数据,OBN地震数据除包含大量纵波信息外,也包含了丰富的转换波信息。该技术可得到全方位纵波及转换横波的信息,能够在海洋底部的构造调查、油气探测中发挥出色的作用[6-8]。
在OBN采集过程中,由于受到海底起伏及洋流等因素的影响,投放到海底的OBN三分量检波器的方向是随机的,因此与诸如垂直地震剖面(Vertical Seismic Profile,VSP)或海底电缆(Ocean Bottom Cable, OBC)等其他多分量数据处理一样,估算三分量检波器的方向以及对三分量数据进行方向校正是OBN多分量数据处理极为关键的步骤之一[9]。通常情况下,OBN的地震传感器内置罗盘和倾角仪,在数据采集时它们会实时记录三分量检波器在海底的方向参数。OBN数据处理需要利用现场记录的三分量检波器的方向参数对OBN三分量数据进行重定向校正,将现场记录的OBN数据的x、y、z三个分量旋转到大地坐标系下的北、东及铅垂方向,以消除由三分量检波器放置姿态引起的记录波场在不同分量上的串扰现象。如果现场记录的三分量检波器定向参数缺失或精度不够,就需对OBN记录进行基于数据的三分量检波器定向分析,估算描述三分量检波器在海底放置姿态的定向参数,并利用估算的定向参数对OBN数据进行三分量检波器重定向处理。针对VSP、OBC或OBN勘探的三分量检波器定向问题已发展出许多不同的方法。Di Siena等[10]、闫有平等[11]在VSP数据处理中通过使直达P波的信号能量最大来确定垂直钻孔中三分量检波器的方位角;Becquey等[12]应用基于偏振分析的方法估算斜井中三分量检波器的方向;Michaels等[13]提出一种基于主成分分析的方法,利用SH波确定检波器的布设方向;Zheng等[14]和马志霞等[15]利用地震道互相关的方法来估算井下相邻检波器之间的相对角度;Li等[16]采用基于初至P波偏振分析的方法确定部署在海底的三分量OBC的检波器方向;Grigoli等[17]给出一种基于复域线性最小二乘反演的三分量检波器定向方法。Zha等[18]给出一种利用瑞利面波极化分析估算海底地震仪(Ocean Bottom Seismometer,OBS)水平分量方向角的方法。对于三分量记录中一个分量的记录波场一致性较好或方向已知的数据(如直井VSP数据或OBC数据,由于前者的z分量均指向垂直方向,后者的x分量受OBC的约束,记录波场的一致性较好),这些方法解决三分量检波器定向问题较容易,效果通常也较好[19];但对于三分量检波器三个分量方向均为未知的OBN数据,特别是对于海水较浅的OBN数据,由于可用于进行定向分析的直达波数据量较少,这些算法的适应性通常较差,难以取得满意的定向分析效果。
本文给出一种综合利用OBN数据不同分量的初至波和反射波进行三分量检波器重定向分析方法,由于利用了初至波和反射波的能量信息,该方法既适应深水也适应浅水OBN数据,且稳定性比常见的基于直达波偏振分析的方法更好。
1 方法原理根据弹性波理论,在均匀各向同性介质中,P波的质点振动方向处于炮点和接收点所在的垂直面内,且与P波的传播方向一致。在OBN数据采集时,如果三分量检波器能够严格按照采集设计方向布设在海底,即将三分量检波器的Z分量都置于铅垂方向,X分量置于平行测线方向或北方向,在这种假设条件下,通过对三分量记录上的直达P波进行偏振分析,得到的P波质点振动方向与炮—检点连线方向是一致的;否则,如果三分量检波器在海底的放置方向偏离设计方向,则会导致直达P波质点振动方向偏离炮—检点连线方向。常见的OBC或OBN三分量检波器定向分析方法就是基于上述原理,通过分析直达P波质点振动方向与炮—检点连线方向之间的偏离估算三分量检波器在海底的放置姿态[20],从而得到三分量检波器重定向所需的定向参数。这种方法通常需拾取高精度的直达P波的初至时间,但是对于海水较浅的OBN数据,通常下行的直达P波在炮检距较小的情况下就会达到临界角,在超过临界角时产生的海底折射波不仅会影响直达P波初至时间的拾取精度,也会与直达P波产生干涉,从而影响三分量检波器定向分析的效果。
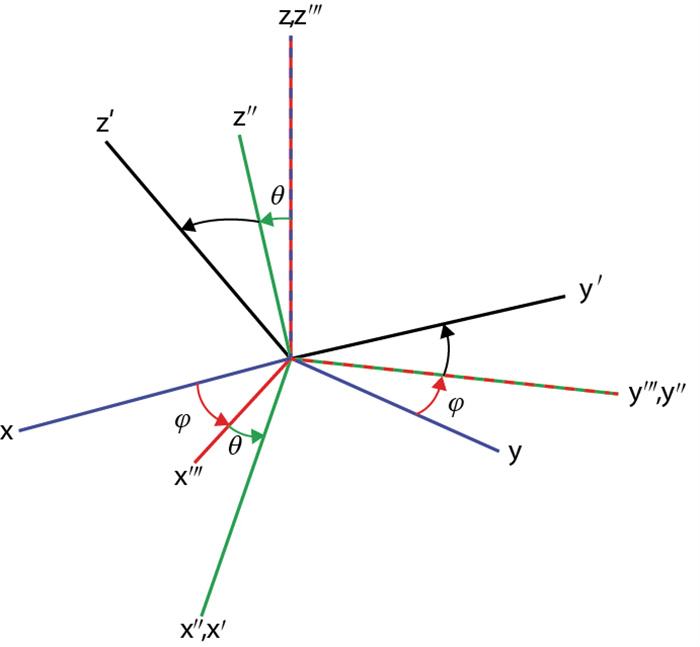
图 1为欧拉角表示的由全局到局部坐标系的旋转过程示意图。该过程可通过3次连续的两分量旋转实现。第一次旋转以z轴为旋转轴,对x、y分量进行旋转,旋转角为方位角φ,将蓝线所示的全局坐标系旋转到红线所示的坐标系;第二次旋转以第一次旋转后的y′′′轴为旋转轴,对第一次旋转后的x′′′和z分量进行旋转,旋转角为倾角θ,得到绿线所示的坐标系;第三次线旋转以第二次旋转后的x″轴为旋转轴,对第二次旋转后的x″和y″分量进行旋转,旋转角为滚动角ϕ,得到黑线所示的局部坐标系。
|
图 1 欧拉角表示的由全局(蓝线)到局部(黑线)坐标系旋转过程示意图 |
不同类型的OBN描述三分量检波器放置姿态的方向参数是不同的,本文采用最常见的θ、ϕ和φ三个欧拉角描述三分量检波器在海底的放置方向。借鉴图 1所示的旋转过程,可由全局坐标系表示OBN的x、y、z三个分量的设计方向,通常x分量指向大地坐标系下的北方向或平行工区测线方向,y分量指向东方向或垂直工区测线方向,x、y分量所在的平面为水平面,z分量指向铅垂方向。按照图 1所示的旋转过程所示,将表示OBN设计方向的x、y、z三个分量依次旋转到红线所示的x′′′、y′′′、z′′′三个方向、绿线所示的x″、y″、z″方向以及黑线所示的表示海底节点真实放置姿态的x′、y′、z′方向。根据欧拉旋转定理[21],三分量旋转可表示为
| $ \left[\begin{array}{l} x^{\prime}(\varphi, \theta, \phi) \\ y^{\prime}(\varphi, \theta, \phi) \\ z^{\prime}(\varphi, \theta, \phi) \end{array}\right]=\boldsymbol{R}(\varphi, \theta, \phi)\left[\begin{array}{l} x \\ y \\ z \end{array}\right] $ | (1) |
式中R(φ, θ, ϕ)为旋转矩阵
| $ \left\{\begin{array}{l} \boldsymbol{R}(\varphi, \theta, \phi)=\left[\begin{array}{ccc} c_\theta c_{\varphi} & c_\theta \mathrm{s}_{\varphi} & -s_\theta \\ s_\phi s_\theta c_{\varphi}-c_\phi s_{\varphi} & s_\phi s_\theta s_{\varphi}+c_\phi c_{\varphi} & s_{\varphi} c_\theta \\ c_\phi s_\theta c_{\varphi}+s_\phi s_{\varphi} & c_\phi s_\theta s_{\varphi}-s_\phi c_{\varphi} & c_{\varphi} c_\theta \end{array}\right] \\ c_\phi=\cos \phi, c_\theta=\cos \theta, c_{\varphi}=\cos \varphi \\ s_\phi=\sin \phi, s_\theta=\sin \theta, s_{\varphi}=\sin \varphi \end{array}\right. $ |
由于|R(φ, θ, ϕ|=1,所以R为非奇异矩阵,存在逆矩阵R-1使得
| $ \left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\boldsymbol{R}^{-1}(\varphi, \theta, \phi)\left[\begin{array}{l} x^{\prime}(\varphi, \theta, \phi) \\ y^{\prime}(\varphi, \theta, \phi) \\ z^{\prime}(\varphi, \theta, \phi) \end{array}\right] $ | (2) |
在定向参数φ、θ和ϕ已知的条件下,利用式(2)可将海底三分量检波器由实际放置方向旋转到设计接收方向,从而实现三分量检波器重定向处理。
设当前炮点相对于当前接收点的方位角为α,可将式(2)中x和y两个水平分量旋转到炮点指向接收点的径向方向和垂直炮点和接收点所在垂直面的切向方向,水平分量旋转采用如下公式进行
| $ \left[\begin{array}{l} R \\ T \end{array}\right]=\left[\begin{array}{cc} \cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] $ | (3) |
式中:R为水平分量旋转后的径向分量;T为水平分量旋转后的切向分量。由式(2)和式(3)可以看出,水平分量旋转后的OBN数据的R、T、z三个分量均与三分量检波器在海底的放置方向有关,描述三分量检波器放置方向的φ、θ和ϕ三个参数的现场采集质量或基于数据的重定向分析精度直接影响OBN数据各个分量的波场特征。
在均匀各向同性介质假设条件下,由不同类型的地震波的偏振特征可知,无论是由气枪震源在海水中激发的直达P波,还是来自于地下地层界面的反射P波或P-SV转换波,其质点振动都在炮点和接收点所在的垂直面内,理论上不存在与该垂直面正交的切向振动,也就是说,利用式(3)对OBN三分量地震记录进行水平分量旋转后,P波和P-SV转换波的能量被旋转到z分量和R分量上,T分量上的能量近似为零。对于实际OBN数据,虽然在T分量的深层部分有明显的记录能量,但直达P波和浅部的反射波能量通常都非常小或近似为零。因此,利用水平分量旋转后的三分量共接收点道集内给定时窗内的能量,可构造如式(4)所示关于三分量检波器定向参数φ、θ、ϕ的函数
| $ F(\phi, \theta, \varphi)=\frac{\sum\limits_\limits{i=1}^m \sum\limits_\limits{t=\tau_1}^{\tau_2} T_i^2(t)}{\sum\limits_\limits{i=1}^m \sum\limits_\limits{t=\tau_1}^{\tau_2} R_i^2(t)+\sum\limits_\limits{i=1}^m \sum\limits_\limits{t=\tau_1}^{\tau_2} z_i^2(t)} $ | (4) |
式中:t为地震数据的采样时间;Ri(t)、Ti(t)和zi(t)分别为水平分量旋转后地震数据的径向、切向和垂直分量,其中i=1, 2,…,m为共接收点道内的炮序号,m为共接收点道集内参与计算的总炮数;τ1和τ2分别为计算时窗的起始时间和终止时间。通过能量扫描的方法求解该函数的极小值,可获得最优的三分量检波器定向参数。对于深水OBN数据,由于共接点道内的可用于直达P波定向分析的道数比较多,且直达P波为初至波,信噪比较高,可拾取高精度的初至,所以通常利用直达P波进行定向分析;对于浅水OBN数据,由于可用于直达P波定向分析的道数较少,可选取包含浅部反射波的计算时窗,综合利用初至P波和反射波的信息进行定向分析,以便提高定向分析结果的稳定性和可靠性。
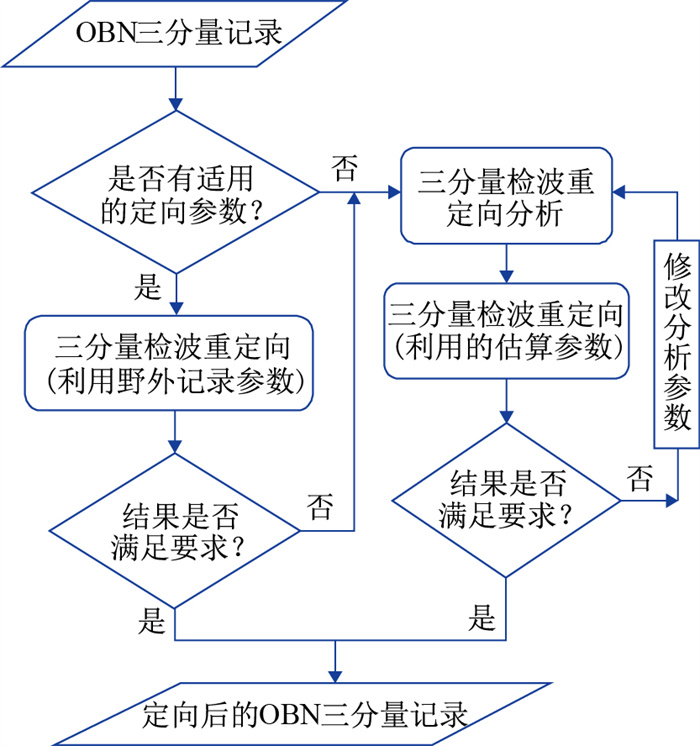
2 技术流程及质控由于实际OBN数据三分量重定向分析需用到OBN三分量记录的振幅以及炮点和接收点的坐标信息,因此在OBN数据三分量数据重定向处理前,需先对OBN数据进行三分量检波器重定位和矢量保真校正等处理,消除因海底节点定位不准和三分量检波器矢量不保真对三分量检波器重定向分析结果的影响。三分量检波器重定向处理包括三个步骤:一是利用OBN数据采集时现场记录的三分量检波器方向参数,对OBN数据直接进行三分量重定向处理;二是利用现场重定向后的OBN三分量记录给定时窗内的振幅信息,进行三分量检波器的剩余重定向分析;三是利用估算的三分量检波器剩余重定向参数,对OBN数据进行三分量剩余重定向处理。在实际OBN数据重定向处理时,建议根据图 2所示的流程对这三个步骤进行选择应用。为了保证最终的三分量检波器重定向应用效果,需利用三分量记录波场的极性、能量、偏振等属性对实际OBN数据三分量重定向效果进行有效质控,最简单且容易操作的方法是通过利用水平分量旋转后的三分量道集进行波场一致性分析,以及利用共接收点道集的T分量进行初至P波剩余能量分析,检验三分量数据重定向分析和校正的效果。
|
图 2 实际OBN数据三分量检波器重定向处理流程图 |
图 3a为实际OBN数据原始三分量共接收点道集。由图可见,受三分量检波器放置方向的影响,波场在各个分量存在明显的能量泄露,横波能量被投影到z分量上,y分量上则存在着明显的纵波。图 3b为对该数据进行水平分量旋转后的三分量共接收点道集,可以看到,在水平分量旋转后的道集上,纵波和横波在各个分量上都混叠在一起,T分量上存在着很强的初至波及反射纵波能量,显示该节点存在着严重的三分量检波器重定向问题。由于该数据在采集时没有记录三分量检波器在海底的放置方向,不能直接利用现场记录的定向参数对该OBN数据进行三分量检波器重定向处理,因此需先利用OBN三分量数据估算检波器的定向参数,然后再对OBN数据进行重定向处理。由于放置该海底节点处的水深较小,本数据只在炮点两侧少数几道存在直达P波,并且受震源激发影响,近炮道记录上的直达P波噪声严重,常规基于直达P波的三分量检波器重定向分析方法难以适用。图 3c为利用本文方法对该数据进行三分量检波器重定向校正并进行水平分量旋转后的共接收点道集,对比图 3b可见,在利用本方法进行三分量检波器重定向后的道集上,初至P波和浅层反P波或P-SV转换波能量在T分量上很微弱,主要能量集中在z和R分量上;反射P波主要分布在z分量上,P-SV转换波主要分布在R分量上,T分量上只在深部有较弱的P-SV波分布,由检波器放置方向导致的各个分量上的波场混叠现象得到有效解决。

|
图 3 OBN原始数据(a)与水平分量旋转(b)及重定向(c)后的三分量共接收点道集 |
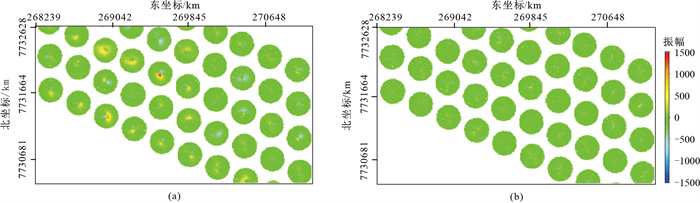
在处理过程中,为了检验该OBN数据三分量检波器重定向效果,抽取如图 4所示的重定向前、后的三分量共炮检距道集,抽取道集的炮检距范围为120~140 m,可以看到,在重定向前的三分量道集上,受三分量检波器放置方向的影响,波场的一致性比较差,T分量上存在很强的能量;在重定向后的道集上,z分量上纵波以及R分量上的转换波的波场一致性有显著改善,T分量上的能量明显减弱。为检验整体的应用效果,绘制了重定向前、后不同节点的共接收点道集T分量给定时窗内的初至波平均振幅。如图 5a和图 5b所示,选取的炮检距范围为0~500 m。由图可见,对于T分量初至波能量较强的节点,重定向后的初至波能量均明显减小。图 6为OBN数据重定向前、后的纵波叠加剖面对比。由图可见,由于z分量上的转换波得到有效分离,在三分量重定向后的叠加剖面上,纵波成像质量在浅层和深层都有明显改善(红圈内),反射同相轴的连续性、数据信噪比都有明显提高。

|
图 4 重定向前(a)、后(b)三分量共炮检距(120~140 m)道集 |
|
图 5 不同节点重定向前(a)、后(b)的T分量初至波平均振幅能量 |

|
图 6 OBN数据重定向前(a)、后(b)的纵波叠加剖面 |
(1) 海底三分量检波器的实际放置姿态若偏离设计的布设方向,会影响数据后续处理效果,导致OBN记录波场在不同分量相互混叠;如果现场记录的检波器定向参数不能满足三分量数据重定向精度要求,则需进行基于数据的三分量检波器定向分析处理。
(2) 在均匀各向同性介质假设条件下,根据P波和P-SV转换波的质点均在炮点和接收点所在垂直面内振动的特点,利用OBN三分量记录的初至波或浅层反射波,通过构造三分量检波器关于由三个欧拉角描述的定向参数的函数,并通过求解该函数的极小值得到最优的三分量检波器定向参数。本文方法综合利用初至波和浅层反射波,既适应深水也适应浅水OBN数据,具有比常规方法更好的数据适应性和稳定性。
(3) 为保证三分量检波器重定向分析和应用效果的可靠性,可利用三分量记录波场的极性、能量、偏振等属性对实际OBN数据三分量重定向进行有效质控。
(4) 三分量检波器重定向处理可有效解决OBN数据因检波器放置姿态引起的波场混叠问题,但对于因海底复杂构造及地下介质各向异性导致的纵、横波和快、慢横波分离问题,还需做进一步的分析和处理。
| [1] |
吴志强, 张训华, 赵维娜, 等. 海底节点(OBN)地震勘探: 进展与成果[J]. 地球物理学进展, 2021, 36(1): 412-424. WU Zhiqiang, ZHANG Xunhua, ZHAO Weina, et al. Ocean Bottom station Nodes (OBN): progress and achievement[J]. Progress in Geophysics, 2021, 36(1): 412-424. |
| [2] |
马力, 李庆春, 马见青. 基于动态惩罚加权的浅水OBN直达波与折射波初至联合二次定位方法[J]. 石油地球物理勘探, 2023, 58(1): 75-82, 177. MA Li, LI Qingchun, MA Jianqing. OBN secondary positioning method jointly by first breaks of direct and refracted waves in shallow water based on dynamic penalty weighting[J]. Oil Geophysical Prospecting, 2023, 58(1): 75-82, 177. |
| [3] |
陈传庚, 刘颖, 王雪玲, 等. OBC与OBN地震勘探差异性浅析[J]. 物探装备, 2019, 29(3): 180-183. CHEN Chuangeng, LIU Ying, WANG Xueling, et al. Difference between OBC and OBN seismic exploration[J]. Equipment for Geophysical Prospecting, 2019, 29(3): 180-183. DOI:10.3969/j.issn.1671-0657.2019.03.010 |
| [4] |
李斌, 冯奇坤, 张异彪, 等. 海上OBC-OBN技术发展与关键问题[J]. 物探与化探, 2019, 43(6): 1277-1284. LI Bin, FENG Qikun, ZHANG Yibiao, et al. Summary of development and key issues of offshore OBC-OBN technology[J]. Geophysical and Geochemical Exploration, 2019, 43(6): 1277-1284. |
| [5] |
白杰, 全海燕, 汪长辉, 等. 水下机器人在深水OBN地震采集中的应用[J]. 石油物探, 2022, 61(2): 286-292. BAI Jie, QUAN Haiyan, WANG Changhui, et al. Application of remotely operated vehicles in deep-ocean OBN seismic acquisition[J]. Geophysical Prospecting for Petroleum, 2022, 61(2): 286-292. DOI:10.3969/j.issn.1000-1441.2022.02.010 |
| [6] |
张明强, 焦叙明, 王炜, 等. OBN资料三维水层相关多次波压制方法研究[J]. 石油物探, 2020, 59(6): 872-879. ZHANG Mingqiang, JIAO Xuming, WANG Wei, et al. 3D water-layer-related multiples attenuation for OBN data[J]. Geophysical Prospecting for Petro-leum, 2020, 59(6): 872-879. DOI:10.3969/j.issn.1000-1441.2020.06.005 |
| [7] |
周吉祥, 杨源, 单瑞, 等. ROV技术在海底地震节点布设中的应用及展望[J]. 海洋地质前沿, 2020, 36(12): 72-77. ZHOU Jixiang, YANG Yuan, SHAN Rui, et al. Application and prospect of ROV technology to submarine seismic node layout[J]. Marine Geology Frontiers, 2020, 36(12): 72-77. |
| [8] |
余本善, 孙乃达. 海底地震采集技术发展现状及建议[J]. 海洋石油, 2015, 35(2): 1-5. YU Benshan, SUN Naida. Current development situations and suggestion on the techniques of ocean bottom seismic acquisition[J]. Offshore Oil, 2015, 35(2): 1-5. DOI:10.3969/j.issn.1008-2336.2015.02.001 |
| [9] |
蔡志东. 井中地震技术: 连接多种油气勘探方法的桥梁[J]. 石油地球物理勘探, 2021, 56(4): 922-934. CAI Zhidong. Borehole seismic: a bridge connecting multiple oil and gas exploration methods[J]. Oil Geophysical Prospecting, 2021, 56(4): 922-934. |
| [10] |
DI SIENA J P, GAISER J E, CORRIGAN D. Horizontal Components and Shear Wave Analysis of Three Component VSP Data, in Vertical Seismic Profiling, Part B: Advanced Concepts[M]. EDS Toksoz, M.N. & Stewart, R.R., Geophysical Press, London, 1984.
|
| [11] |
闫有平, 赵军才, 胡亚东, 等. 应用VSP观测的黄土塬地面地震干扰波研究[J]. 石油地球物理勘探, 2022, 57(5): 1046-1056. YAN Youping, ZHAO Juncai, HU Yadong, et al. Study of surface seismic interference wave in loess tableland based on VSP observation[J]. Oil Geophysical Prospecting, 2022, 57(5): 1046-1056. |
| [12] |
BECQUEY M, DUBESSET M. Three-component sonde orientation in a deviated well[J]. Geophysics, 1990, 55(10): 1386-1388. |
| [13] |
MICHAELS P. Use of principal component analysis to determine downhole tool orientation and enhance SH-waves[J]. Journal of Environmental and Engineering, 2001, 6(4): 175-183. |
| [14] |
ZHENG X, MCMECHAN G A. Two methods for determining geophone orientations from VSP data[J]. Geophysics, 2006, 71(4): V87-V97. |
| [15] |
马志霞, 孙赞东. 两种方法结合实现斜井VSP检波器定向[J]. 石油地球物理勘探, 2010, 45(5): 655-660. MA Zhixia, SUN Zandong. Integration of two methods to realize deviated well VSP geophone orientation[J]. Oil Geophysical Prospecting, 2010, 45(5): 655-660. |
| [16] |
LI X, YUAN J. Geophone orientation and coupling in three-component sea-floor data: a case study[J]. Geophysical Prospecting, 1999, 47(6): 995-1013. |
| [17] |
GRIGOLI F, SIMONE C, TORSTEN D, et al. A complex linear least-squares method to derive relative and absolute orientations of seismic sensors[J]. Geophysical Journal International, 2012, 188(3): 1243-1254. |
| [18] |
ZHA Y, WEBB S C, MENKE W, et al. Determining the orientations of ocean bottom seismometers using virtual sources[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 151-156.
|
| [19] |
GRATACOS B. Reorientation and calibration of non-gimbaled multicomponents sensors[J]. SEG Technical Program Expanded Abstracts, 2003, 22: 838-841. |
| [20] |
张文波, 李建峰, 孙鹏远, 等. 基于直达波偏振分析的三分量检波器定向方法[J]. 石油地球物理勘探, 2017, 52(增刊2): 19-25. ZHANG Wenbo, LI Jianfeng, SUN Pengyuan, et al. A three-component geophone orientation method based on direct P-wave polarization[J]. Oil Geophysical Prospecting, 2017, 52(S2): 19-25. |
| [21] |
ZARE R N, 赖 善桃, 余 亚雄, 丘 应楠. 译角动量: 化学及物理学中的方位问题[M]. 北京: 科学出版社, 1995: 79-84.
|



 张文波, 河北省涿州市华阳东路东方公司科技园物探技术研究中心, 072751。Email:
张文波, 河北省涿州市华阳东路东方公司科技园物探技术研究中心, 072751。Email: 