2. 中国石油勘探开发研究院西北分院, 甘肃兰州 730020
2. Research Institute of Exploration and Development-Northwest, PetroChina, Lanzhou, Gansu 730020, China
地震偏移的核心目标是得到地下构造清晰的像。这首先依赖于满足偏移成像要求的背景(偏移)速度场,更精细的速度建模也严重依赖有效的背景速度模型。
而基于CMP道集的初始叠加速度分析是最稳健的方法。常规的速度谱解释及建模方法常常是依靠人工拾取。人工方法虽然较为精细,保证了横向连续性,但工作量大且耗时。而在当前“两宽一高”采集条件下,CMP道集数量异常庞大,需要发展比较自动、高效的速度估计方法,同时减少人工干预,降低数据处理的时间和人工成本,提高总体的勘探效益[1-2]。核心是自动、智能化的合理速度谱解释。
早在1967年Garotta等[3]提出了基于共反射点双曲时距曲线的速度分析方法。Taner等[4]给出了借助速度谱的叠加速度分析方法。Toldi[5]较早探索了速度谱自动拾取方法,初始模型经过扰动,自动寻找叠加能量最大的速度函数。这种寻找最佳速度的问题,可建立误差泛函并用优化方法求取,Lumley[6]探索了基于Monte Carlo自动拾取方法。考虑到层速度约束,有学者从剩余慢度平方谱中自动拾取层速度用于偏移速度分析[7-8];林年添等[9]提出了向前做最大“能量团”的积分、向后递归计算最优解的方法,Decker等[10]将其转换为变分问题求解。
速度解释也是一个决策过程,很多学者借助有监督或无监督类的智能化方法实现。Smith[11]利用多属性包括AVO、相邻道的连续性等过滤噪声,基于距离聚类分析找到各属性中心作为拾取结果;Chen[12]实现了K均值聚类拾取方法;Waheed等[13]对比了K均值聚类拾取方法与带噪声的基于密度的空间聚类方法;王迪等[14]提出了自适应阈值聚类方法。但这类无监督方法通常基于单道进行,缺乏判断速度合理性的依据。机器学习类方法则通过学习道集或速度谱到速度模型的非线性映射关系[15],如Ma等[16]的卷积神经网络(CNN)方法、Wang等[17]的U-net网络方法、Duque等[18]的对抗网络方法、张兵[19]的多层卷积神经网络方法、韩明亮等[20]的全卷积神经网络方法。但此类方法依赖于训练集的建立,泛化能力难以定量评价。
在人工交互拾取的时候,速度谱解释人员会参考相邻道集,尽量让横向速度变化趋势平滑,但在计算机自动拾取建模时较难实现。多数自动拾取方法是基于单个CMP道集速度谱能量团特征逐次拾取,将相邻道拾取结果排列在一起可能表现出严重的速度跳变现象,这是因为没有利用隐含的结构信息增强横向连续性。
本文构建了一个自动拾取速度的Bayes决策框架,认为背景速度整体是基于层位结构处所解释的速度所控制,将结构信息作为聚类的参考依据,通过均值聚类划分不同的参数估计区域,在各个参数估计域中以速度变化趋势、邻道拾取结果(时间—速度对数据,简称TV对)的统计趋势为速度拾取决策的先验信息,考虑了纵向速度合理性,并且基于横向速度的统计结果进行质量控制,实现智能化的自动背景速度建模。
1 Bayes决策意义下的自动拾取方法 1.1 方法理论背景由于观测信号包含随机噪声,并且观测环境有不可控的干扰,参数估计结果含有随机误差、存在不确定性,要在概率统计基础上提出具体的参数估计方法。速度估计是非线性反问题,如果参数空间不经过先验信息约束,将是十分庞大[21-22]。自动拾取需要基于多尺度的空间信息,利用统计信息和先验认识的约束,在Bayes决策原则下提取合理的TV对。
在Bayes决策原则下,拾取问题是基于观测数据,即高维速度谱数据体D估计速度参数,所估计的参数组合使定义的决策风险最小
| $ R[p(\boldsymbol{\theta} \mid \boldsymbol{D}), a]=\sum\limits_{\boldsymbol{\theta} \in \boldsymbol{\Theta}} L(\boldsymbol{\theta}, a) p(\boldsymbol{\theta} \mid \boldsymbol{D}) $ | (1) |
其中后验概率密度为
| $ p(\boldsymbol{\theta} \mid \boldsymbol{D})=\frac{p(\boldsymbol{D} \mid \boldsymbol{\theta}) p(\boldsymbol{\theta})}{p(\boldsymbol{D})} $ | (2) |
式中:θ表示TV对参数;Θ为参数空间;a代表拾取决策;p(θ)为参数的先验概率分布,反映在观测之前对参数已有的认识;p(D)为数据的先验分布;代价函数L评价了基于不同参数选择下的道集拉平或叠加聚焦的效果;R则反映了基于概率密度函数所生成参数的整体评估表现,根据整体道集拉平的效果评价;p(D|θ)为似然概率分布,表示在已知参数下事件发生的可能性。
通过引入先验概率分布,能够将所估计的参数似然分布调整到更接近真实的概率,后验概率综合了先验概率分布与多次观测样本参数估计的概率密度分布。先验信息的选择来自对问题的认识,在人工交互拾取速度时,通常要考虑拾取速度的合理性:速度范围要符合地质规律,因此反射层结构约束是必不可少的;要考虑相邻点速度的连续性。人工交互拾取解释过程会综合利用多种属性的信息,主要包括:①叠加速度—零炮检距反射时间(vs-t0)域的单道相似系数谱;②叠加速度—CMP坐标(vs-xCMP)域的速度分布信息;③t0-xCMP域的零炮检距旅行时分布信息;④二维叠加剖面中的层位信息。自动拾取可以类比此过程。
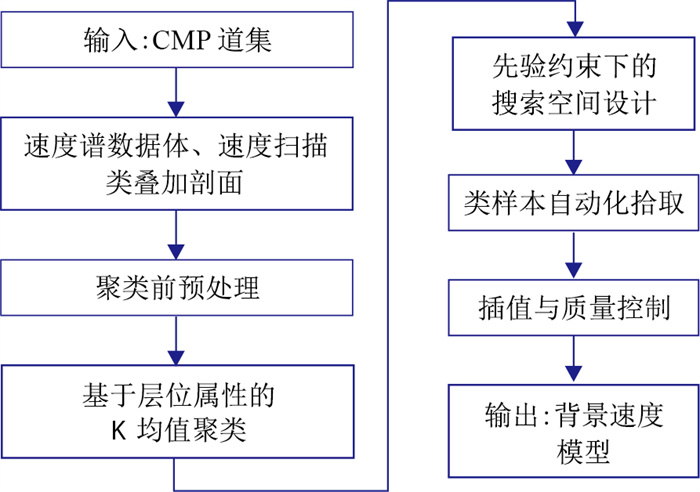
1.2 方法处理流程本文方法的基本步骤(图 1)可描述如下:
|
图 1 速度建模算法的基本流程 |
(1) 先基于数据域CMP道集形成速度谱数据体和类叠加剖面,基于类叠加剖面提取层位结构;
(2) 对于单个CMP道集,利用提取的层位结构,使用K均值聚类算法对局部窗内的速度谱数据体预处理后进行聚类划分,形成不同层位节点的类;
(3) 利用统计信息和先验信息约束拾取范围,以整体拾取点区间内的道集拉平效果最优为拾取目标,拾取点在约束范围内小范围扰动获得最优拾取结果;
(4) 在所有CMP道集拾取完成后,统计邻域同层拾取结果,在结构约束下对拾取点质量进行控制,经过插值和平滑,得到最后的模型。
1.3 多维数据空间的形成首先基于成像域数据相关准则,以某道为中心的邻域范围内所有CMP道集根据双曲时距关系合成速度谱
| $ d\left(t_0, v_{\mathrm{s}}\right)=\frac{\sum\limits_\limits{m=-M / 2}^{M / 2}\;\;\;\;\;\left\{\sum\limits_\limits{n=1}^N I\left[t_n\left(t_{0 m}, v_{\mathrm{s}}, h_n\right), h_n\right]\right\}^2}{N \sum\limits_\limits{m=-M / 2}^{M / 2} \;\;\sum\limits_\limits{n=1}^N\left\{I\left[t_n\left(t_{0 m}, v_{\mathrm{s}}, h_n\right), h_n\right]\right\}^2} $ | (3) |
式中:N为总道数;I为幅值;hn为第n道的半炮检距;M为时窗大小;t0m为时窗内第m个样点的零炮检距旅行时;tn为与t0m对应的第n道的旅行时。
将各CMP速度谱排列在一起形成速度谱数据体。为压缩储存空间、提高计算效率,数据体可以进行降采样处理。
在生成速度谱数据体的同时,生成类叠加剖面
| $ U\left(t_0, x_{\mathrm{CMP}}\right)=\int_{v_{\mathrm{s}}^{\mathrm{d}}}^{v_{\mathrm{s}}^{\mathrm{u}}} w\left(x_{\mathrm{CMP}}\right) u\left(t_0, v_{\mathrm{s}}, x_{\mathrm{CMP}}\right) \mathrm{d} v_{\mathrm{s}} $ | (4) |
式中:U表示类叠加数据;w为加权系数;u表示动校正后的CMP道集数据;vsu、vsd分别为叠加速度的上、下限。生成类叠加剖面是在未知正确叠加速度的情况下获得较高分辨率的层位结构信息的方法:在每个CMP点上,以一定间隔改变速度,用不同速度做动校正和叠加,并将参与叠加的地震道根据不同层位叠加后相对能量大小再进行加权叠加、调整速度积分的上、下限及加权系数,保证浅、中、深层叠加能量均衡,最终获得类叠加剖面。用正确扫描速度的校正叠加结果能够凸显结构,错误速度的叠加结果将相互抵消。
提取层位的方式是基于相干属性[23-24]。二维叠加剖面中各点的相干属性定义为
| $ \sigma=\frac{\sum\limits_\limits{m=-M / 2}^{M / 2}\;\;\;\;\left[\frac{1}{N} \sum\limits_\limits{n=1}^N U_n\left(t_0+m \Delta t-q x_n\right)\right]^2}{\sum\limits_\limits{m=-M / 2}^{M / 2} \;\;\frac{1}{N} \sum\limits_\limits{n=1}^N\left[U_n\left(t_0+m \Delta t-q x_n\right)\right]^2} $ | (5) |
式中:q表示扫描倾角;xn为第n道坐标;qxn表示随道号n变化各道的时移量;Δt为采样间隔。计算二维剖面上各点的相干值,要按照一定间隔改变q进行倾角扫描,取σ最大值作为相干值。
由于浅、中、深层可能存在同相轴能量差异过大的情况,导致某些深度上结构信息缺失,使后续速度拾取不连续,需要对深层同相轴进行增益补偿。通过动态设置阈值,自适应地提取相干属性值较大的区域作为层位的可能位置,在局部窗内统计提取点的数量,基于局部统计结果去除离散点,保留连续线段作为拾取层位;再自适应地减去已提取的部分,降低阈值进一步搜索次强能量的位置,重复这个过程,尽可能使结构信息在浅、中、深层都有体现。
速度拾取思路是从整体到局部,先搜索获得每个道集速度大致的拾取位置及范围,再对每个拾取区间搜索,局部微调以获得最优结果。由于数据中含噪声和多次波,速度谱能量团不一定指示真实叠加速度,因此各道集分开的拾取结果容易出现横向跳变,需添加关于层位和速度的先验约束。而叠加剖面中蕴含的结构,提供了t0的位置信息。层位约束是指:谱点的时间只能位于从叠加剖面所提取的层位对应的时间附近,去除那些不能指示层位的谱点。以层位属性为核心的聚类方法能够发现数据隐藏的内部结构,按照某种度量方式把数据集分成多个类,并使得类内样本尽可能的相似。
本文基于K均值方法对速度谱数据体中的样本依据层位信息实现分类。K均值聚类是将所有J个样本划分到K个类中,计算各个样本到每个中心的距离,使每个样本到其所属类的中心距离最小,类内相似性达到最大。聚类前首先经过阈值滤波去除能量弱的样本,类别数根据提取的层位数量决定,并根据道集上提取的层位位置对每一个速度谱上的样本形成层位属性,反映数据点归类为不同层位的可能性。t0i位置的数据点提取的层位属性ai, k为
| $ {a_{i, k}} = \left\{ {\begin{array}{*{20}{l}} {1 - \frac{{{\tau _i}}}{\varepsilon }}&{{\tau _i} = \left| {{t_{0i}} - {t_{{\rm{layer}}k{\rm{ }}}}} \right|\leqslant\varepsilon }\\ 0&{{\tau _i} > \varepsilon } \end{array}} \right. $ | (6) |
式中:k为层位序号;ε为根据采样时间设置的误差容忍度阈值;tlayerk为第k层的结构时间。
聚类实施过程如下:
(1) 定义每个层位结构所在位置作为初始的聚类中心;
(2) 计算每个样本到每个中心的距离,将所有样本聚集到距离最近的类中,构成聚类结果;
(3) 将每个类中样本坐标的均值作为新的类中心;
(4) 重复步骤(2)和步骤(3),直到聚类结果稳定。
聚类得到的每个类别的所有样本对应该层位速度参数可能的分布范围,单道的拾取可以认为是分别从不同类别抽取一个TV对进行组合,最终需要在基于这些聚类样本的空间中搜索使道集拉平情况达到最优的速度。
1.4 Bayes统计决策下的自动拾取聚类样本所组成的空间依然是比较庞大的,先验信息的引入限制了估计参数分布范围,同时减小了搜索参数的工作量。因此在完成对层位约束的筛选后,可以将人机交互拾取的思想作为拾取范围控制的依据[25-26],包括三个方面。①叠加速度整体递增性,体现在限制拾取同一道集中相邻层位两点vs分布范围。②根据Dix公式将vs转换到层速度时,相邻层速度一般不会有急剧的翻转,转换到vs同样如此。根据工区参考的最大、最小层速度,限制同一道集中相邻两拾取点间的速度曲线斜率范围。③邻道层速度、叠加速度连续性,体现在相邻道拾取点的相对位置不能超过同一层位拾取速度统计的均方误差范围。对于同一个类别中的样本,同时考察这些因素是否满足,将不符合先验假设范围内的谱点去除。
经过速度和层位结构的约束后,每个类内只保留符合约束条件的TV对离散数据。一个道集同相轴拉平的效果与提取的叠加速度有关,本文采取一种各道集分别逐层拾取的方法以保障在不同层位都达到较优的效果。不同层位上采用谱能量最大的点作为初始拾取点,通过
| $ \boldsymbol{\theta}_j=\underset{\boldsymbol{\theta}_j \in \boldsymbol{\Theta}}{\operatorname{argmin}} \sum\limits_{n=1}^N \Delta T_n\left[\boldsymbol{\theta}_j, u_{\mathrm{nmo}}\left(\boldsymbol{\theta}_j\right)\right] $ | (7) |
衡量此点相邻的时窗内的用拾取速度道集拉平的效果。式中:θj为第j个所求参数对;unmo(θj)为基于参数θj的动校正后的道集;ΔTn为互相关值最大时所对应的时延量。
在约束范围内扰动拾取点再次计算道集拉平效果进行比较,利用两道互相关求时延,求取整体时延量最小,取综合目标函数达到极值时的TV对作为最佳拾取值。
1.5 质量控制及插值平滑所有CMP道集拾取完成后,统计邻域同层拾取结果,去除并重新估计远离统计均值的离群点,减少横向速度跃变的出现。再利用整个测线上的离散点实施插值,构造出规则网格下的速度场数据。插值的结果可能不完美,尤其是先转换为层速度再进行插值的情况,可用方向滤波的方式对层速度进行横向高斯平滑。
2 数值实验基于合成数据及实际数据按照上述的实施策略进行智能化的速度分析、建模,评价方法的效果和可靠性。
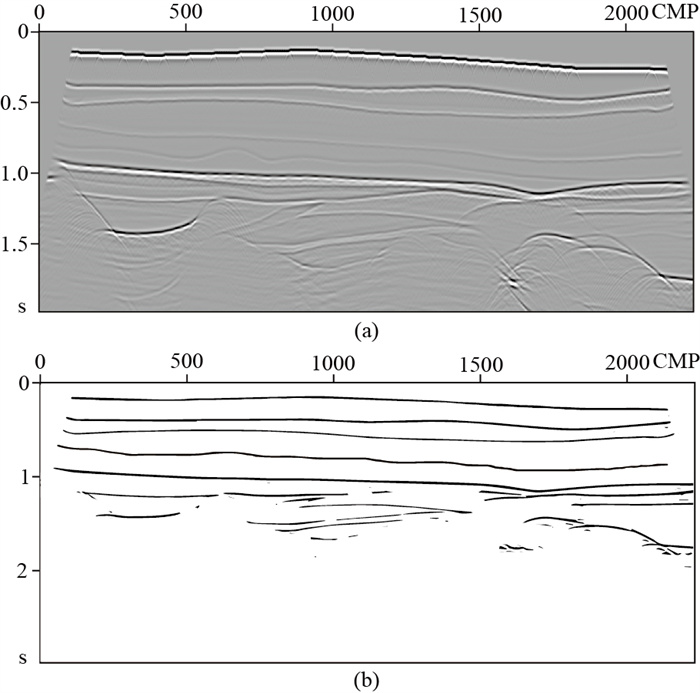
大庆模型深度为3968 m,宽度为30000 m,最大炮检距为2800 m,共调用2237个CMP。首先对每一个CMP生成相似系数谱,排列形成速度谱数据体(图 2),再生成类叠加剖面(图 3a)。为提高提取叠加剖面中层位的效果,先对叠加剖面进行各向异性平滑,再按照式(5)计算相干属性并基于阈值过滤获取层位信息(图 3b),去掉了大部分成像噪声,保留了连续的结构,为K均值聚类提供依据。单CMP的速度谱及聚类结果如图 4所示,深层的能量团聚焦不足,如果不利用先验信息约束很难确定拾取位置。

|
图 2 速度谱数据体 |
|
图 3 类叠加剖面(a)及提取的层位结构(b) |

|
图 4 原始速度谱(a)及层位约束的聚类结果(b) |
对每个CMP道集根据施加关于层位信息、层速度、叠加速度、时间间隔的先验约束,进一步缩小参数范围,如图 5所示。在约束范围内逐层沿结构拾取按照代价函数(式(7))使局部道集拉平的TV对。

|
图 5 约束前(a)、后(b)速度谱类内拾取范围(b)对比 |
对同一测线所有CMP点都进行如上操作,得到全测线的TV对分布(图 6)。由图 6可以看出,横向上各层旅行时有一定连续性的趋势,但是存在一些跳变点,反映了时间约束较为宽松。因此还需要基于所估计同一层位相邻CMP点叠加速度的统计规律对估计参数做质量控制:先以突变点道集为中心,统计邻域道集TV对的参数分布,计算其均值和均方差,突变点的误差会远大于多道统计均方差。将多道统计平均的速度、时间参数作为参考,校正突变点的参数,以提高参数分布横向连续性。

|
图 6 沿测线拾取TV对的时间分布 |
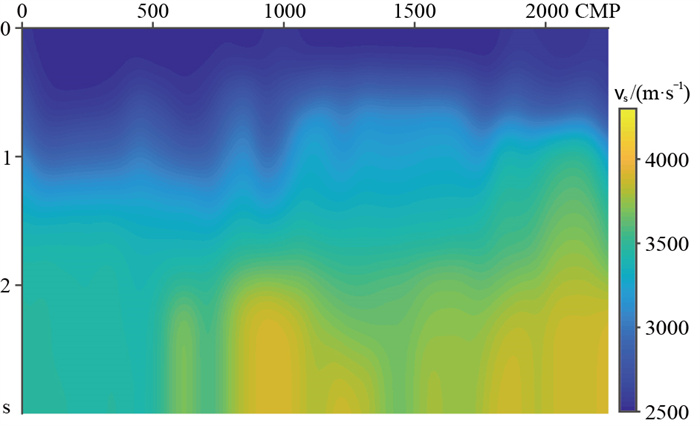
经过关于横向速度变化的质量控制后,线性插值并高斯平滑形成的速度场(图 7),相邻层位拾取的速度也较为连续。该方法中间过程不需要人为干预,用得到的速度模型进行动校、叠加,能够获得同相轴较为清晰的结果(图 8)。
|
图 7 二维剖面智能化速度拾取结果 |

|
图 8 模型叠加剖面 |
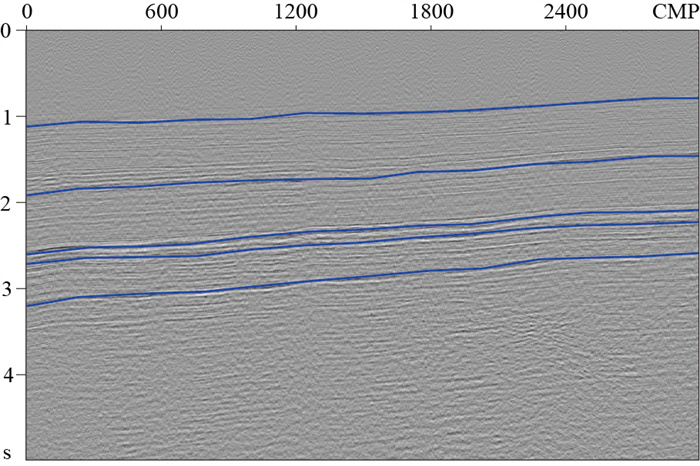
实际资料来自中国西部探区,炮数为1082,可用的CMP道集数量为9000,最大炮检距为6000 m,采样时间为6 s,采样间隔为1 ms。参考的均方根速度范围为4000~7000 m/s,实际速度谱能量团分布范围为4600~5500 m/s。当设置主要结构层数为5时,速度谱及其能量团的聚类结果如图 9所示,先验信息约束了能量发散区域的速度拾取范围。图 10为加权叠加的类叠加剖面,蓝线展示了以五个特征层位为目标提取的层位结构,将作为K均值聚类的依据。

|
图 9 实际资料CMP600的速度谱(a)及其聚类结果(b) |
|
图 10 实际资料的类叠加剖面及提取主要层位示意图 |
图 11为智能化拾取与人工拾取结果的单点对比,二者趋势大致相同,智能化拾取结果同样能够刻画出浅层的速度反转。采取上述的流程对该测线上的所有CMP进行智能化拾取,最后插值平滑得到的时间域叠加速度场(图 12),能够做到逐个CMP点进行拾取,与人工交互拾取结果(图 13)相比,拾取密度增加,消除了横向速度跳变导致的阶梯状现象。
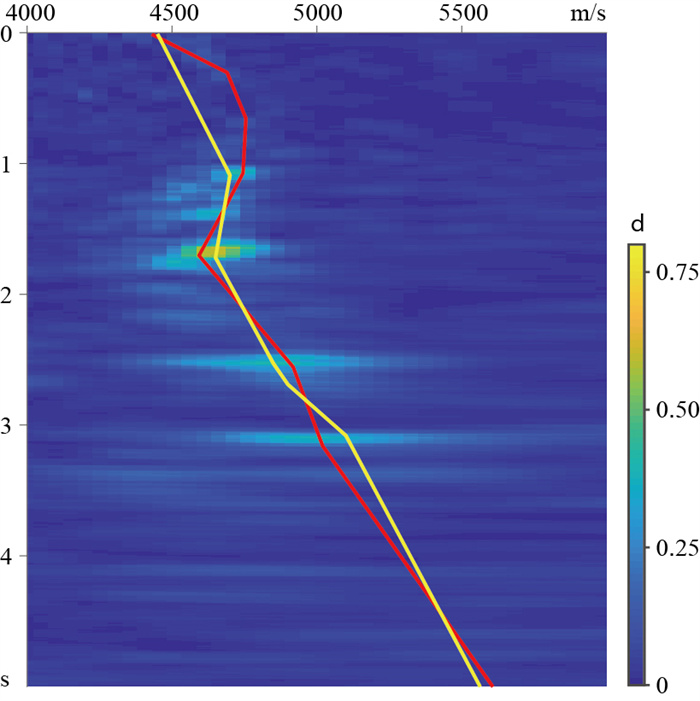
|
图 11 CMP600智能拾取结果(红线)与人工拾取结果(黄线)的对比 |

|
图 12 实际资料智能化拾取结果 |
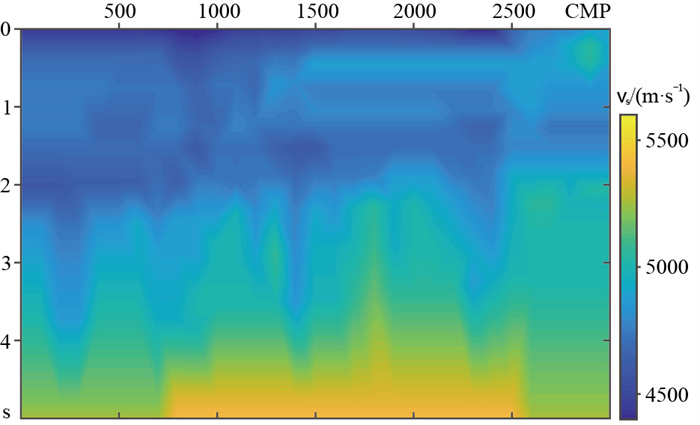
|
图 13 实际资料人工交互拾取结果 |
本文在Bayes最佳决策意义下构建了一套时间—速度对智能拾取策略和方法,目前的实现还是比较基本的,很多具体环节需要完善和提升。例如提高类叠加剖面的信噪比和提高结构提取精度,因为更准确的结构信息会减少后续智能化拾取的工作量。流程中聚类前需要对速度谱进行降采样以降低计算量和为数据体分配内存空间;在设置聚类特征层位数量时,是以剖面中具有一定间隔的强能量反射轴为依据;在设置智能化拾取参数约束范围时,要提前抽取道集的速度谱;质量控制时参与的CMP道集范围也需要根据道间距、CMP间距进行调整,CMP间距越密集统计约束量越可靠。另外本文主要考虑的是二维情况下的速度建模,三维时则需要扩展到估计三维的层位结构,并且综合考虑在Inline和Crossline方向上对速度拾取结果进行统计约束。
用智能算法完美地实现任意复杂情形下的、合理的速度谱解释及初始背景速度建模并不是一件简单的事情。但是,把它归结为Bayes最佳决策问题是合乎逻辑的。本文方法还可以在统计新方法在高维速度谱数据体的应用和多种信息融合等方面进一步完善,最终形成一个普适性强的综合算法。这是一项极有理论意义和工业应用价值的研究。
客观地讲,在较高和中等信噪比情况下,本文的智能拾取结果与人工拾取结果的差异不大,可以达到实用化水平。但在低信噪比和极低信噪比条件下,智能地拾取依然存在极大的挑战。需要在更高维的数据空间中引入更多的层位、统计和人工先验信息,构建更为合理稳健的决策方案。
4 结论“两宽一高”地震数据采集逐渐普及,产生了CMP道集数目庞大的数据体,逐点TV对的人工拾取几乎成了不可能完成的工作。为此,本文提出了一套Bayes决策框架下利用结构信息、统计信息和先验信息的智能化时间速度对拾取方法,其中蕴含了模仿人工交互速度分析的思想。
本文提出的智能化建模方法有以下特点:
(1) 引入了类叠加剖面及基于相干属性提取结构剖面;
(2) 围绕结构特征对速度谱点进行聚类,缩小模型参数空间;
(3) 分别对横、纵向速度的约束进行量化,并引入邻域搜索结果的统计信息,从各个方面约束TV对的搜索空间以保证搜索结果的合理性。
感谢中国石油勘探开发研究院、中海油研究总院和湛江分公司、中石化物探技术研究院和胜利油田分公司对本文研究的支持和资助。
| [1] |
马彦彦, 李国发, 张星宇, 等. 叠前深度偏移速度建模方法分析[J]. 石油地球物理勘探, 2014, 49(4): 687-693. MA Yanyan, LI Guofa, ZHANG Xingyu, et al. Strategy of velocity model building in prestack depth migration[J]. Oil Geophysical Prospecting, 2014, 49(4): 687-693. DOI:10.13810/j.cnki.issn.1000-7210.2014.04.010 |
| [2] |
王华忠, 冯波, 王雄文, 等. 地震波反演成像方法与技术核心问题分析[J]. 石油物探, 2015, 54(2): 115-125, 141. WANG Huazhong, FENG Bo, WANG Xiongwen, et al. Analysis of seismic inversion imaging and its technical core issues[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 115-1285, 141. |
| [3] |
GAROTTA R, MICHON D. Continuous analysis of the velocity function and of the move out corrections[J]. Geophysical Prospecting, 1967, 15(4): 584-597. DOI:10.1111/j.1365-2478.1967.tb01805.x |
| [4] |
TANER M T, KOEHLER F. Velocity spectra-digital computer derivation applications of velocity functions[J]. Geophysics, 1969, 34(6): 859-881. DOI:10.1190/1.1440058 |
| [5] |
TOLDI J L. Velocity analysis without picking[J]. Geo-physics, 1989, 54(2): 191-199. |
| [6] |
LUMLEY D E. Monte Carlo Automatic Velocity Picks[R]. Stanford Exploration Project, 1997.
|
| [7] |
陈志德, 刘桭宽, 李成斌. 三维叠前深度偏移速度分析及蒙特卡洛自动层速度拾取[J]. 地球物理学报, 2002, 45(2): 246-254. CHEN Zhide, LIU Zhenkuan, LI Chengbin. 3-D pre-stack depth migration velocity analysis and automatic Monte Carlo velocity picking in depth[J]. Chinese Journal of Geophysics, 2002, 45(2): 246-254. |
| [8] |
AL-YAHYA K. Velocity analysis by iterative profile migration[J]. Geophysics, 1989, 54(6): 718-729. DOI:10.1190/1.1442699 |
| [9] |
林年添, 刘洪, 李建勇. 基于Viterbi算法的复杂地质体速度约束化自动拾取[J]. 地球物理学进展, 2004, 19(2): 311-316. LIN Niantian, LIU Hong, LI Jianyong. Automatic picking velocity by the Viterbi algorithm for the complex geological case[J]. Progress in Geophysics, 2004, 19(2): 311-316. DOI:10.3969/j.issn.1004-2903.2004.02.017 |
| [10] |
DECKER L, FOMEL S. A variational method for picking velocity surfaces from semblance scans[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 3684-3688.
|
| [11] |
SMITH K. Machine learning assisted velocity auto-picking[J]. SEG Technical Program Expanded Abstracts, 2017, 36: 5686-5690. |
| [12] |
CHEN Y Q. Automatic semblance picking by a bottom-up clustering method[C]. SEG 2018 Workshop: SEG Maximizing Asset Value Through Artificial Intelligence and Machine Learning, 2018, 44-48.
|
| [13] |
WAHEED U B, AL-ZAHRANI S, HANAFY S M. Machine learning algorithms for automatic velocity picking: K-means vs DBSCAN[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 5110-5114.
|
| [14] |
王迪, 袁三一, 袁焕, 等. 基于自适应阈值约束的无监督聚类智能速度拾取[J]. 地球物理学报, 2021, 64(3): 1048-1060. WANG Di, YUAN Sanyi, YUAN Huan, et al. Intelligent velocity picking based on unsupervised clustering with the adaptive threshold constraint[J]. Chinese Journal of Geophysics, 2021, 64(3): 1048-1060. |
| [15] |
HUANG J, CAO J, CHEN G, et al. Automate seismic velocity model building through machine learning[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 1556-1560
|
| [16] |
MA Y, JI X, FEI T, et al. Automatic velocity picking with convolutional neural networks[J]. SEG Technical Program Expanded Abstracts, 2018, 37: 2066-2070. |
| [17] |
WANG W, YANG F, MA J. Velocity model building with a modified fully convolutional network[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2086-2090.
|
| [18] |
DUQUE L, GUTIÉRREZ G, ARIAS C, et al. Automated velocity estimation by deep learning based seismic-to-velocity mapping[J]. Extended Abstracts of 81st EAGE Conference & Exhibition, 2019, 1-5. |
| [19] |
张兵. 基于卷积神经网络和叠加速度谱的地震层速度自动建模方法[J]. 石油物探, 2021, 60(3): 366-375. ZHANG Bing. Automatic seismic interval velocity building based on convolutional neural network and velocity spectrum[J]. Geophysical Prospecting for Petroleum, 2021, 60(3): 366-375. |
| [20] |
韩明亮, 邹志辉, 马锐. 利用反射地震资料和多尺度训练集的深度学习速度建模[J]. 石油地球物理勘探, 2021, 56(5): 935-946. HAN Mingliang, ZOU Zhihui, MA Rui. Deep lear-ning-driven velocity modeling based on seismic reflection data and multi-scale training sets[J]. Oil Geophysical Prospecting, 2021, 56(5): 935-946. |
| [21] |
宋磊, 印兴耀, 宗兆云, 等. 基于先验约束的深度学习地震波阻抗反演方法[J]. 石油地球物理勘探, 2021, 56(4): 716-727. SONG Lei, YIN Xingyao, ZONG Zhaoyun, et al. Deep learning seismic impedance inversion based on prior constraints[J]. Oil Geophysical Prospecting, 2021, 56(4): 716-727. |
| [22] |
张子良, 李振春, 张凯, 等. 地质模型约束的全波形速度建模反演及在复杂断块区的应用[J]. 石油地球物理勘探, 2020, 55(3): 599-606. ZHANG Ziliang, LI Zhenchun, ZHANG Kai, et al. Research of geological model-constrained FWI and application in complex fault-block zones[J]. Oil Geophysical Prospecting, 2020, 55(3): 599-606. |
| [23] |
苑书金. 地震相干体技术的研究综述[J]. 勘探地球物理进展, 2007, 30(1): 7-15. YUAN Shujin. A review of seismic coherence techniques[J]. Progress in Exploration Geophysics, 2007, 30(1): 7-15. |
| [24] |
陈双全, 季敏. 地震数据结构张量相干计算方法[J]. 石油物探, 2012, 51(3): 233-238. CHEN Shuangquan, JI Min. Structure tensor cohe-rence computation method of seismic data[J]. Geophysical Prospecting for Petroleum, 2012, 51(3): 233-238. |
| [25] |
LANDA E, THORE P, SORIN V, et al. Interpretation of velocity estimates from coherency inversion[J]. Geophysics, 1991, 56(9): 1377-1383. |
| [26] |
COVA David, 刘 洋, 丁 成震, et al. 人工智能和视速度约束的地震波初至拾取方法[J]. 石油地球物理勘探, 2021, 56(3): 419-435. |
| [38] |
COVA D, LIU Yang, DING Chengzhen, et al. First break picking method based on artificial intelligence and apparent velocity constraint[J]. Oil Geophysical Prospecting, 2021, 56(3): 419-435. |



 伍国富, 上海市杨浦区四平路街道彰武路100号同济大学彰武校区海洋与地球科学学院, 200092。Email:
伍国富, 上海市杨浦区四平路街道彰武路100号同济大学彰武校区海洋与地球科学学院, 200092。Email: 