2. 中国石油大学(北京)CNPC物探重点实验室, 北京 102249;
3. 中国石油大学(北京)海洋石油勘探国家工程实验室, 北京 102249;
4. 同济大学海洋地质国家重点实验室, 上海 200092
2. CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum(Beijing), Beijing 102249, China;
3. National Engineering Laboratory for Offshore Oil Exploration, China University of Petroleum(Beijing), Beijing 102249, China;
4. State Key Laboratory of Marine Geology, Tongji University, Shanghai 200092, China
在地震勘探中,由于地层的吸收和衰减效应,地震波会发生振幅衰减和相位畸变,导致地震主频向低频移动,高频波能量降低、频带变窄,严重降低了地震资料的分辨率。在资料处理过程中采用衰减补偿方法可有效消除吸收衰减影响。Futterman[1]通过研究地震波能量衰减机制,确立了最基本的Futterman衰减模型。针对衰减补偿开展的相关研究主要分为两大类:①利用波场延拓原理推导的反Q滤波方法,包括Hale[2]完成的全反Q滤波处理;白桦等[3]利用短时傅里叶变换对信号进行分频加权的反Q滤波方法;Wang[4-5]提出了稳定的反Q滤波方法;严红勇等[6]针对VSP资料实施的反Q滤波处理等。在反Q滤波过程中,波场外推时指数函数的存在会放大高频噪声,减弱了补偿方法的稳定性,并且存在振幅补偿不足的缺点。②基于反演思想的衰减补偿,是将补偿问题转化为反问题,可以通过不同的约束方法提高补偿的精度和稳定性。如Zhang等[7]、Wang等[8-10]、王本锋等[11]分别利用Tikhonov正则化和L1、L2范数进行正则化约束以及在贝叶斯理论框架下解决反演问题,提高了衰减补偿的精度和稳定性;Ma等[12]和刘金涛等[13]也分别通过数据驱动结构正则化约束以及全局约束开展了多道衰减补偿,同时兼顾了地震资料的信噪比(SNR)及横向一致性。
针对叠后数据进行衰减补偿的研究较为成熟,但由于未考虑真实的射线传播路径对吸收衰减的影响,因而叠后补偿方法不适用于叠前数据。对于叠前地震数据而言,能量吸收不仅降低了地震分辨率,而且吸收衰减程度会随着传播路径发生变化,进而改变了AVO反射特征,影响后续高精度叠前反演的结果,容易造成AVO解释陷阱。众多团队针对叠前数据开展了衰减补偿研究,Lazaratos等[14]在AVO校正中首次提出了沿炮检距进行地层吸收补偿的思想;任浩然等[15]基于波场延拓的思想,沿射线路径进行吸收与衰减补偿,改善了子波波形的一致性;Bansal等[16]在纵波和转换波联合反演过程中,应用Lazaratos等[14]提出的与炮检距相关的吸收补偿方法,提高了反演精度;Yan等[17]沿射线路径进行波场延拓,将稳定的反Q滤波方法用于叠前纵波与转换波数据;李国发等[18]利用反Q滤波方法分别补偿了与深度或炮检距相关的吸收衰减,消除了衰减对AVO反射特征的影响;Chai等[19]将反Q滤波与叠前AVA反演整合为一体,直接从非稳态叠前数据提取高分辨率参数,避免了反Q滤波的不稳定性。张生强等[20]根据叠前道集高、低频成分的衰减差异,利用低频约束开展了时频—空间域的AVO响应校正,较好地还原了叠前道集的AVO特征。
与叠后数据相比,叠前数据信噪比相对较低,反Q滤波方法更易引起补偿不稳定现象。多位学者也关注到叠前补偿的抗噪性,Li等[21]基于时间和炮检距分量对吸收衰减的不同影响,将地震吸收分解为时间和炮检距两部分,提出了“两步法”方案分别进行补偿,并实施正则化约束提高抗噪性;Aharchaou等[22]利用tau-p变换进行局部角度分解,将Q补偿应用于叠前数据,减弱了非相干噪声和空间混叠的影响,但该方法仅适用于常Q模型,不能用于时空变化的Q值模型,因此存在较大局限性;Cheng等[23]推导出衰减介质中叠前角道集的频率域正演公式,并利用Tikhonov正则化对反问题进行稳定性处理,进而实现叠前数据的衰减补偿。
本文在Wang等[10]提出的衰减补偿方法的基础上,考虑了射线路径对吸收衰减的影响和叠前数据信噪比较低的特点,提出一种基于L1范数正则化约束的叠前数据衰减补偿方法,并利用交替方向乘子算法[24](Alternative Direction Method of Multipliers,ADMM)进行数值求解实现衰减补偿。所提方法不仅能对振幅和相位进行补偿,还能恢复叠前道集的AVA反射特征。通过数值测试将本文方法与叠后衰减补偿[10]、叠前反Q滤波[15, 17-18]方法进行对比分析,结果表明本文方法精度更高、抗噪性更强,能够更稳定、有效地对叠前道集进行衰减补偿。同时,Q值模型敏感度分析实验说明了该方法对Q值模型精度不敏感,仅借助低频Q值模型也能保持较高的补偿精度。实际叠前资料的处理结果进一步验证了该方法的实用性。
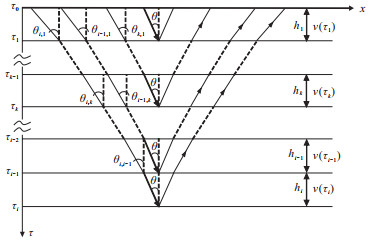
1 方法理论 1.1 衰减介质中叠前数据正演模型如图 1所示,在水平层状介质假设条件下,当入射角为θ时,地下第k层自激自收时间为τk的深度点处激发的简谐波地震记录,就是τk位置的反射系数r(τk, θ)与一系列简谐波ŵ(ω)ejωt的乘积[8]
|
图 1 水平层状介质入射角道集射线路径示意图 v(τk)表示第k层的介质速度,hk表示第k层的厚度。 |
| $ r({\tau _k}, \theta )\hat w(\omega ){{\rm{e}}^{{\rm{j}}\omega t}} $ | (1) |
式中:ω为角频率;ŵ(ω)为地震子波的频谱;j表示虚部。
假设i为总的地层,深度点τi与τi-1之间的厚度为hi,层速度为v(τi),则沿射线路径从τi传播到τi-1位置的简谐波记录为
| $ r({\tau _i}, \theta )\hat w(\omega ){e^{{\rm{j}}\omega t}}{{\rm{e}}^{{\rm{ - j}}\omega \frac{{2{h_i}}}{{v({\tau _i})\cos \theta }}}} $ | (2) |
图 1中θi, k表示深度τi处激发的简谐波传播到第k层τk处的入射角度,θ=θi, i。假设地下层速度已知,当简谐波逐层传播时,各层入射角度可由Snell定律得到
| $ \frac{{\sin {\theta _{i, 1}}}}{{v({\tau _1})}} = \cdots = \frac{{\sin {\theta _{i, k}}}}{{v({\tau _k})}} = \cdots = \frac{{\sin {\theta _{i, i - 1}}}}{{v({\tau _{i - 1}})}} = \frac{{\sin \theta }}{{v({\tau _i})}} $ | (3) |
该简谐波逐层传播至地表即得到合成地震记录
| $ r({\tau _i}, \theta )\hat w(\omega ){{\rm{e}}^{{\rm{j}}\omega t}}{{\rm{e}}^{ - {\rm{j}}\omega \sum\limits_{k = 1}^i {\frac{{2{h_k}}}{{v({\tau _k})\cos {\theta _{i, k}}}}} }} $ | (4) |
采用Wang在2002年描述的模型[4]模拟地震波在衰减介质中的传播,用复速度替换式(4)中的速度v(τk),引入衰减
| $ \frac{1}{{v({\tau _k})}} = \frac{1}{{v({\tau _k}, \omega )}}\left[ {1 - \frac{{\rm{j}}}{{2Q({\tau _k})}}} \right] $ | (5) |
式中:v(τk, ω)为与角频率相关的相速度;Q(τk)为深度点τk处地层品质因子Q值。其中
| $ v({\tau _k}, \omega ) = v({\tau _k}, {\omega _0}){\left| {\frac{\omega }{{{\omega _0}}}} \right|^{{\gamma _k}}} $ | (6) |
| $ {\gamma _k} = \frac{2}{{\rm{ \mathsf{ π} }}}{\tan ^{{\rm{ - }}1}}\left[ {\frac{1}{{2Q({\tau _k})}}} \right] \approx \frac{1}{{{\rm{ \mathsf{ π} }}Q({\tau _k})}} $ | (7) |
式中v(τk, ω0)为主频ω0对应的相速度。
结合式(4)~式(7)得到地震记录
| $ \begin{aligned} & \boldsymbol{s}\left(\tau_i, \omega, t, \theta\right)=\boldsymbol{r}\left(\tau_i, \theta\right) \hat{w}(\omega) \mathrm{e}^{\mathrm{j} \omega t} \times \\ & \exp \left\{-\omega \sum\limits_{k=1}^i\left[\frac{h_k}{v\left(\tau_k, \omega_0\right) \cos \theta_{i, k} Q\left(\tau_k\right)}\left|\frac{\omega_0}{\omega}\right|^{\gamma_k}\right]\right\} \times \\ & \exp \left\{-\mathrm{j} \omega \sum\limits_{k=1}^i\left[\frac{2 h_k}{v\left(\tau_k, \omega_0\right) \cos \theta_{i, k}}\left|\frac{\omega_0}{\omega}\right|^{\gamma_k}\right]\right\} \end{aligned} $ | (8) |
将深度转换为时间,地震波从深度点τk传播到τk-1位置的自激自收时间为
| $ \Delta \tau_k=\frac{2 h_k}{v\left(\tau_k, \omega_0\right)} $ | (9) |
将式(9)代入式(8),考虑到常规叠前角道集数据已经过动校正处理,因此将动校正时间考虑在内,可得到
| $ \begin{aligned} & \boldsymbol{s}\left(\tau_i, \omega, t, \theta\right)=\boldsymbol{r}\left(\tau_i, \theta\right) \hat{\boldsymbol{w}}(\omega) \mathrm{e}^{\mathrm{j} \omega t} \times \\ & \exp \left\{-\omega \sum\limits_{k=1}^i\left[\frac{\Delta \tau_k}{2 \cos \theta_{i, k} Q\left(\tau_k\right)}\left|\frac{\omega_0}{\omega}\right|^{\gamma_k}\right]\right\} \times \\ & \exp \left[-\mathrm{j} \omega \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{\cos \theta_{i, k}}\left|\frac{\omega_0}{\omega}\right|^{\gamma_k}\right)\right] \times \\ & \exp \left[\mathrm{j} \omega \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{\cos \theta_{i, k}}-\Delta \tau_k\right)\right] \end{aligned} $ | (10) |
假设地下有n个深度点,对不同深度点的反射系数r(τi, θ)产生的简谐波求和,即可得到地面接收的地震记录
| $ \begin{aligned} & \boldsymbol{s}(\omega, t, \theta)=\sum\limits_{i=1}^n \boldsymbol{r}\left(\tau_i, \theta\right) \hat{\boldsymbol{w}}(\omega) \mathrm{e}^{\mathrm{j} \omega t} \times \\ & \;\;\;\;\;\;\;\;\exp \left[-\omega \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{2 \cos \theta_{i, k} Q\left(\tau_k\right)}\left|\frac{\omega_0}{\omega}\right|^{\gamma_k}\right)\right] \times \\ & \;\;\;\;\;\;\;\;\exp \left[-\mathrm{j} \omega \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{\cos \theta_{i, k}}\left|\frac{\omega_0}{\omega}\right|^{\gamma_k}\right)\right] \times \\ & \;\;\;\;\;\;\;\;\exp \left[\mathrm{j} \omega \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{\cos \theta_{i, k}}-\Delta \tau_k\right)\right] \end{aligned} $ | (11) |
对式(11)关于角频率ω求和,即可得到衰减介质中叠前数据的时间域正演模型
| $ \begin{aligned} \boldsymbol{s}(t, \theta) & =\int_{-\infty}^{\infty} \mathrm{d} \omega \sum\limits_{i=1}^n \boldsymbol{r}\left(\tau_i, \theta\right) \hat{w}(\omega) \mathrm{e}^{\mathrm{j} \omega t} \times \\ & \exp \left\{-\omega \sum\limits_{k=1}^i\left[\frac{\Delta \tau_k}{2 \cos \theta_{i, k} Q\left(\tau_k\right)}\left|\frac{\omega_0}{\omega}\right|^{\gamma_k}\right]\right\} \times \\ & \exp \left[-\mathrm{j} \omega \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{\cos \theta_{i, k}}\left|\frac{\omega_0}{\omega}\right|^{\gamma_k}\right)\right] \times \\ & \exp \left[\mathrm{j} \omega \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{\cos \theta_{i, k}}-\Delta \tau_k\right)\right] \end{aligned} $ | (12) |
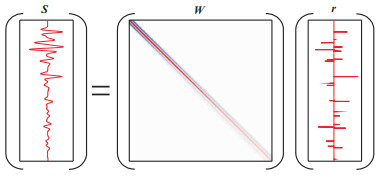
将式(12)矩阵化,得到
| $ \underbrace {\left[ {\begin{array}{*{20}{c}} {s\left( {{t_1}, \theta } \right)}\\ {s\left( {{t_2}, \theta } \right)}\\ \vdots \\ {s\left( {{t_n}, \theta } \right)} \end{array}} \right]}_{\boldsymbol{S}} = \underbrace {\left[ {\begin{array}{*{20}{c}} {w\left( {{t_1}, {\tau _1}, \theta } \right)}&{w\left( {{t_1}, {\tau _2}, \theta } \right)}& \cdots &{w\left( {{t_1}, {\tau _n}, \theta } \right)}\\ {w\left( {{t_2}, {\tau _1}, \theta } \right)}&{w\left( {{t_2}, {\tau _2}, \theta } \right)}& \cdots &{w\left( {{t_2}, {\tau _n}, \theta } \right)}\\ {}& \vdots &{}&{}\\ {w\left( {{t_n}, {\tau _1}, \theta } \right)}&{w\left( {{t_n}, {\tau _2}, \theta } \right)}& \cdots &{w\left( {{t_n}, {\tau _n}, \theta } \right)} \end{array}} \right]}_{\boldsymbol{W}}\underbrace {\left[ {\begin{array}{*{20}{c}} {r\left( {{\tau _1}, \theta } \right)}\\ {r\left( {{\tau _2}, \theta } \right)}\\ \vdots \\ {r\left( {{\tau _n}, \theta } \right)} \end{array}} \right]}_{\boldsymbol{r}} $ | (13) |
式中:S、r分别为离散后的地震记录和反射系数序列;W为经历了大地Q滤波效应的时变衰减子波矩阵,矩阵中元素可以表示为
| $ \begin{aligned} & w\left(t_p, \tau_i, \theta\right)=\sum\limits_{q=1}^{\frac{n}{2}} \hat{\boldsymbol{w}}\left(\omega_q\right) \mathrm{e}^{\mathrm{j} \omega_q t_p} \times \\ & \exp \left[-\omega_q \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{2 \cos \theta_{i, k} Q\left(\tau_k\right)}\left|\frac{\omega_0}{\omega_q}\right|^{\gamma_k}\right)\right] \times \\ & \exp \left[-\mathrm{j} \omega_q \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{\cos \theta_{i, k}}\left|\frac{\omega_0}{\omega_q}\right|^{\gamma_k}\right)\right] \times \\ & \exp \left[\mathrm{j} \omega_q \sum\limits_{k=1}^i\left(\frac{\Delta \tau_k}{\cos \theta_{i, k}}-\Delta \tau_k\right)\right] p, i=1, 2, \cdots, n \end{aligned} $ | (14) |
式中:tp为第p个时间采样点,采样点数共n个;ωq为第q个角频率采样点,采样点数共n/2个。
|
图 2 正向Q滤波示意图 |
本文通过对反射系数序列施加L1范数正则化约束[10],构建了如下目标泛函
| $ J(\boldsymbol{r})=\frac{1}{2}\|\boldsymbol{S}-\boldsymbol{W} \boldsymbol{r}\|_2^2+\lambda\|\boldsymbol{r}\|_1 $ | (15) |
式中:λ > 0为正则化参数。λ是补偿精度与稳定性之间的平衡参数,对于不同信噪比的数据,λ的选择需谨慎。λ太大时噪声被压制,但是补偿结果精度下降,尤其是深层记录会出现补偿不足的现象;λ太小时反演结果因噪声而出现不稳定,导致信噪比严重降低。
为了改善深层补偿效果,提高反演方法精度,引入权重函数[10]
| $ a(t)=\exp \left(\frac{\beta \pi t}{Q}\right) $ | (16) |
式中β > 0为加权因子,控制深层补偿的加权力度。对于深层衰减较为严重的地震资料,β取较大值。但是对于深层信噪比较低的数据,不能只关注深层补偿程度,此时若选取较大的β值可能会放大深层噪声,而应当增大正则化参数λ来压制噪声。
综上,在处理含噪数据时,β与λ有多种不同组合的取值,一般首先确定β的值,然后通过权衡补偿精度与稳定性,进而确定λ的取值。
结合式(15)、式(16)将目标泛函改写为
| $ J(\boldsymbol{r})=\frac{1}{2}\|\boldsymbol{A} \boldsymbol{S}-\boldsymbol{A} \boldsymbol{W} \boldsymbol{r}\|_2^2+\lambda\|\boldsymbol{r}\|_1 $ | (17) |
式中A为权重函数变量。
式(17)可通过ADMM求解[24]。首先,通过引入一个伴随变量z分离式(17)中的L2、L1范数
| $ J(\boldsymbol{r}, \boldsymbol{z})=\frac{1}{2}\|\boldsymbol{A S}-\boldsymbol{A W} \boldsymbol{r}\|_2^2+\lambda\|\boldsymbol{z}\|_1 $ | (18) |
然后,构建增广Lagrangian函数优化式(18),有
| $ \begin{aligned} L_\rho(\boldsymbol{r}, \boldsymbol{z}, \boldsymbol{y})= & \frac{1}{2}\|\boldsymbol{A S}-\boldsymbol{A} \boldsymbol{W} \boldsymbol{r}\|_2^2+\lambda\|\boldsymbol{z}\|_1+ \\ & \boldsymbol{y}^{\mathrm{T}}(\boldsymbol{r}-\boldsymbol{z})+\frac{\rho}{2}\|\boldsymbol{r}-\boldsymbol{z}\|_2^2 \end{aligned} $ | (19) |
式中:y为Lagrangian乘子向量;ρ为惩罚参数,通过对惩罚函数‖r-z‖22的加权,体现惩罚的力度。
最后,通过以下迭代使式(19)最小化
| $ \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{r}}^{(m + 1)}} = \mathop {\min }\limits_r {L_\rho }\left[ {{\boldsymbol{r}}, {{\boldsymbol{z}}^{(m)}}, {{\boldsymbol{y}}^{(m)}}} \right]}\\ {{{\boldsymbol{z}}^{(m + 1)}} = \mathop {\min }\limits_z {L_\rho }\left[ {{{\boldsymbol{r}}^{(m + 1)}}, {\boldsymbol{z}}, {{\boldsymbol{y}}^{(m)}}} \right]}\\ {{{\boldsymbol{y}}^{(m + 1)}} = {{\boldsymbol{y}}^{(m)}} + \rho \left[ {{{\boldsymbol{r}}^{(m + 1)}} - {{\boldsymbol{z}}^{(m + 1)}}} \right]} \end{array}} \right. $ | (20) |
其中
| $ \boldsymbol{r}^{(m+1)}=\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{W}+\rho \boldsymbol{I}\right)^{-1}\left[\boldsymbol{W}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{S}+\rho \boldsymbol{z}^{(m)}-\boldsymbol{y}^{(m)}\right] $ | (21) |
| $ \boldsymbol{z}^{(m+1)}=S_{\frac{\lambda}{\rho}}\left[\boldsymbol{r}^{(m+1)}+\frac{\boldsymbol{y}^{(m)}}{\rho}\right] $ | (22) |
| $ \boldsymbol{y}^{(m+1)}=\boldsymbol{y}^{(m)}+\rho\left[\boldsymbol{r}^{(m+1)}-\boldsymbol{z}^{(m+1)}\right] $ | (23) |
式中m为迭代次数。式(22)是典型的loss问题,利用软阈值算法[24]求解
| $ \boldsymbol{z}_i^{(m+1)}=\operatorname{sgn}\left[\boldsymbol{r}_i^{(m+1)}+\frac{\boldsymbol{y}_i^{(m)}}{\rho}\right] \max \left[\left|\boldsymbol{r}_i^{(m+1)}+\frac{\boldsymbol{y}_i^{(m)}}{\rho}\right|-\frac{\lambda}{\rho}, 0\right] $ | (24) |
式中sgn(·)是符号函数。
初始化设置r(0)=0,z(0)=0,y(0)=0,并重复执行式(21)~式(23),直到满足迭代终止条件‖ r(m+1)-r(m)‖ 2/[1+‖ r(m+1)‖ 2] < ε,其中,ε > 0为容忍误差。得到的最优结果r与震源子波褶积即可实现衰减补偿。
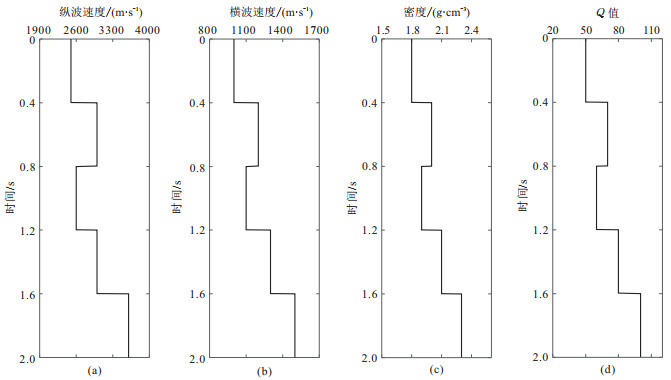
2 数值测试 2.1 可行性分析设计一个五层的水平层状介质模型,模型纵、横波速度、密度及Q值如图 3所示。假设主频为40 Hz的雷克子波,在不考虑几何扩散、透射损失和动校正拉伸的情况下,根据Zoeppritz方程计算得到不同入射角的反射系数,入射角范围为0°~ 50°,间隔为1°。利用式(13)分别合成无衰减和含衰减叠前角道集(图 4)。通过对比发现,由于受能量吸收衰减的影响,在纵向上地震波振幅衰减和相位畸变随着传播时间的增加越来越严重,分辨率降低;横向上地震数据的AVA反射特征发生改变,地震记录的同相性也受到明显影响。
|
图 3 五层地层介质模型 (a)纵波速度;(b)横波速度;(c)密度;(d)品质因子 |

|
图 4 无衰减(a)和含衰减(b)叠前角道集 |
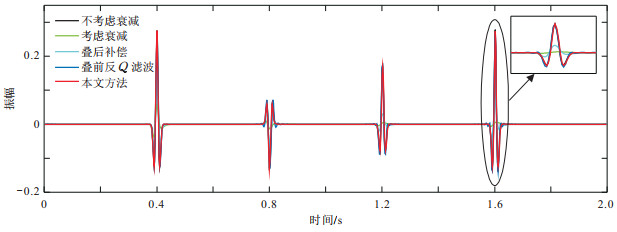
利用本文方法对衰减道集进行补偿,并分别与叠前反Q滤波方法、叠后补偿方法进行对比,补偿结果如图 5所示。由于数据不含噪声,图 5a中测试得到β值为144,可以保证深层得到充分补偿;β确定后,测试选取λ的值为8×10-5,可以保证补偿的稳定性。对比可见,叠后补偿方法虽然进行了振幅补偿和相位校正,但由于未考虑传播路径的影响,在深层和大角度地震道出现了严重的补偿不足现象。而叠前反Q滤波方法与本文方法考虑了射线路径,因此均能充分地对振幅和相位进行补偿。如图 6所示,50°入射角地震道的补偿结果进一步展示了本文方法与叠前反Q滤波方法补偿效果一致。

|
图 5 不同方法补偿结果对比 (a)基于L1范数正则化约束的叠前补偿方法;(b)叠前反Q滤波方法;(c)基于L1范数正则化约束的叠后补偿方法 |
|
图 6 无噪声数据入射角为50°的地震道不同方法补偿结果对比 |
图 7显示最下层同相轴的AVA曲线及主频随角度变化曲线,图 7a中紫色点划线为考虑衰减的AVA曲线增益17倍的细节放大图。由图可见:由于不同角度射线路径的吸收衰减程度不同,地震同相轴的横向反射特征被改变,产生了错误的AVA信息。而叠后补偿方法不能充分还原大角度的AVA信息,但本文方法和叠前反Q滤波方法均可以较好地消除与入射角度相关的吸收差异,恢复AVA反射特征。同样,从图 7b可见:受到衰减影响的反射波主频随入射角增大而降低,减弱了叠前道集的横向一致性。经叠后补偿方法处理后,中角度至大角度道集仍显示补偿不足;而本文方法与叠前反Q滤波方法均能恢复地震反射波主频,且不随入射角变化。通过上述数值模拟实验,充分验证了本文方法处理叠前角道集数据的可行性。

|
图 7 最下层同相轴的AVA曲线(a)与主频随入射角变化曲线(b) |
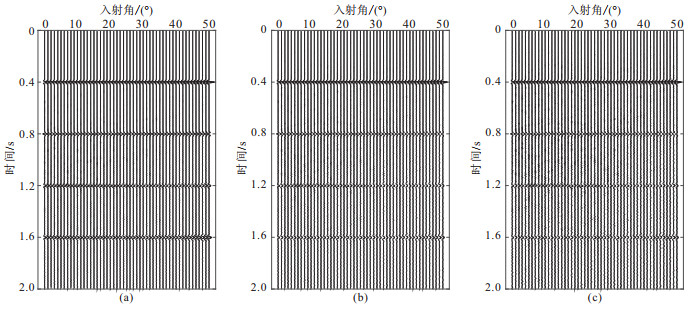
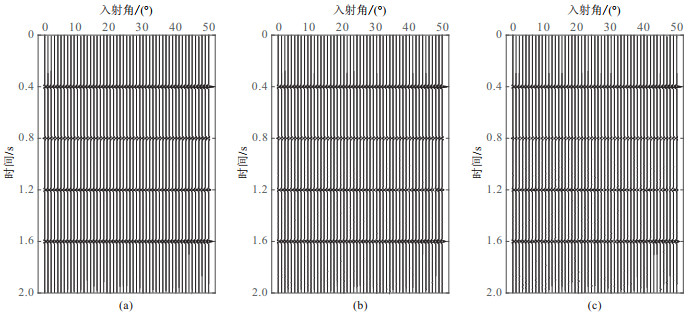
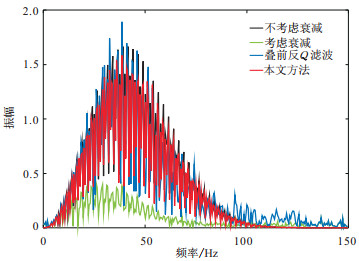
叠前数据的信噪比一般较低,而稳定性和抗噪性是衡量补偿方法的两个标准,本文开展了抗噪性对比实验。如图 8所示,对整个叠前角道集添加高斯随机噪声,使角道集的信噪比分别达到20、10和5 dB。图 9显示叠前反Q滤波补偿结果,图 10显示L1范数正则化约束叠前补偿结果。由于β值会影响深层数据能量及信噪比,因此减小了β的取值。图 10a~图 10c中,首先通过测试确定β为44,然后根据含噪程度的差异分别测试,随着信噪比降低得到λ的取值分别为0.01、0.03和0.06。图 11和图 12分别展示了信噪比为10 dB时,入射角为50°的地震道(细节放大图)不同方法补偿结果对比和入射角为30°的地震道不同方法补偿结果频谱图。

|
图 8 不同信噪比含衰减叠前角道集 (a)SNR=20 dB;(b)SNR=10 dB;(c)SNR=5 dB |
|
图 9 不同信噪比资料叠前反Q滤波方法补偿结果 (a)SNR=20 dB;(b)SNR=10 dB;(c)SNR=5 dB |
|
图 10 不同信噪比资料基于L1范数正则化约束的叠前衰减方法补偿结果 (a)SNR=20 dB;(b)SNR=10 dB;(c)SNR=5 dB |

|
图 11 信噪比10 dB时入射角为50°的地震道不同方法补偿结果对比 |
|
图 12 30°入射角地震道不同方法补偿结果频谱图 |
综合观察图 8~图 12可见,当叠前道集存在噪声时,高频信号的补偿会放大噪声的影响(图 12),尤其对于深层记录,噪声放大较为严重(图 11),补偿结果出现不稳定。但是与叠前反Q滤波方法相比,本文方法具有更强的抗噪性,并未明显放大高频噪声,补偿结果仍具有较高的信噪比。
采用平均相关系数(ACC)和补偿后资料新信噪比(SNRnew)量化描述补偿精度和抗噪性能
| $ \mathrm{ACC}=\frac{1}{N} \sum\limits_{x=1}^N \frac{\boldsymbol{S}_x^{\text {ref }} \boldsymbol{S}_x^{\mathrm{T}}}{\left\|\boldsymbol{S}_x\right\|_2\left\|\boldsymbol{S}_x^{\text {ref }}\right\|_2} $ | (25) |
| $ \mathrm{SNR}_{\text {new }}=10 \lg \frac{\left\|\boldsymbol{S}^{\text {ref }}\right\|_2^2}{\left\|\boldsymbol{S}^{\text {ref }}-\boldsymbol{S}\right\|_2^2} $ | (26) |
式中:Sref和S分别为参考和补偿后的叠前道集;N为道数;Sxref和Sx分别为参考和补偿后的地震道。
表 1和表 2分别统计了两种方法补偿后资料的平均相关系数和新信噪比。
|
|
表 1 不同方法补偿后资料ACC统计 |
|
|
表 2 不同方法补偿后资料SNRnew统计 |
对比可知,随着原始道集信噪比的降低,叠前反Q滤波方法补偿结果出现明显的精度下降、信噪比降低的现象,尤其是对于5 dB含噪数据,补偿结果的ACC低至0.7718,SNRnew低至3.62,深层信号不能得到充分补偿以致严重影响了数据的品质。而利用本文方法补偿后,同样针对5 dB的低信噪比数据,补偿结果仍能保持0.9641的相关度,并且补偿结果的信噪比也提高至10.39。量化分析结果充分证明本文方法具有较高的精度和抗噪性。
此外,叠前数据的衰减补偿也需要关注噪声对横向反射特征AVA曲线以及主频变化的影响。图 13绘制了不同信噪比资料最下层同相轴的AVA曲线,可以看出,叠前反Q滤波方法在保持一定信噪比的前提下,会出现深层补偿不足的现象;而本文方法能更充分地对深层记录进行补偿,恢复原始的AVA反射特征。图 14展示了最下层同相轴主频随入射角变化曲线,同样可见,叠前反Q滤波方法补偿虽然能在一定程度上恢复叠前道集的主频,但由于方法抗噪性较弱,当信噪比较低时会导致主频恢复不足,并且随入射角波动较大,干扰了叠前道集主频的横向一致性;而本文方法补偿结果的主频充分恢复到真值附近,并且在真值附近扰动较小。通过AVA及主频曲线分析,进一步说明本文方法在含噪情况下仍能够充分还原叠前道集的AVA反射特征及主频,并且在一定程度上改善了叠前道集的横向一致性。

|
图 13 不同信噪比资料不同方法补偿结果最下层同相轴的AVA曲线对比 (a)SNR=20 dB;(b)SNR=10 dB;(c)SNR=5 dB |

|
图 14 不同信噪比资料不同方法补偿结果最下层同相轴的主频随入射角变化曲线对比 (a)SNR=20 dB;(b)SNR=10 dB;(c)SNR=5 dB |
在进行衰减补偿时需要用到Q值模型,而实际生产中一般难以得到高精度、高分辨率的Q值模型。为此,开展了Q值模型精度敏感度分析实验,以测试Q值模型精度对补偿结果的影响。首先,对图 3d品质因子Q值模型添加最大幅值20%的高斯随机误差,然后分别对含误差的Q值模型(共1001个采样点)进行了101、301和801点平滑,得到不同的Q值低频模型(图 15)。

|
图 15 加入20%高斯随机误差的Q值模型(a)及其101点(b)、301点(c)和801点(d)平滑结果 |
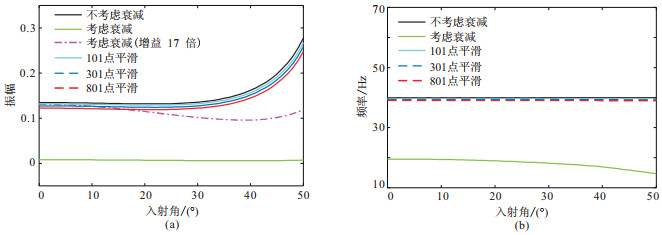
最后,利用本文方法对衰减道集进行补偿,β和λ取值仍为144和8×10-5,补偿结果如图 16所示。由图可见,对于不同的Q值低频模型,本文方法均得到较好的补偿效果。同样绘制了最下层同相轴的AVA曲线(图 17a)及主频随角度变化曲线(图 17b),可以看出,即使利用801点平滑后的Q值模型进行补偿,本文方法也能较好地还原原始道集的AVA特征、提高主频。Q值敏感度分析实验进一步说明本文方法对Q值模型精度敏感度不高,在仅给出一个低频Q值模型时,也能保持较高的补偿精度。

|
图 16 不同Q值模型的补偿结果 (a)101点平滑;(b)301点平滑;(c)801点平滑 |
|
图 17 不同Q值模型补偿结果最下层同相轴的AVA曲线(a)与主频随入射角变化曲线(b) |
应用实际叠前角道集资料验证本文方法的实用性。实际数据来自中国东部油田某工区,工区地下构造为复杂断块,含气砂岩发育。待补偿资料为经过去噪、反褶积、速度分析以及叠前时间偏移等处理后的叠前偏移角道集。
首先通过以下三个步骤进行补偿前的数据准备:①利用Dix公式将均方根速度转换为层速度,得到层速度曲线(图 18a);②利用Cheng等[26]提出的对数谱面积双重差法估计得到低频Q值(图 18b);③利用谱模拟[27]和高阶统计量技术[28]提取浅层子波(图 18c)。然后,分别利用叠前反Q滤波方法及本文方法对实际叠前角道集进行补偿。

|
图 18 补偿前的准备数据 (a)层速度曲线;(b)低频Q值模型;(c)浅层子波 |
为了保证补偿精度及信噪比,通过测试确定了β和λ取值分别为64和0.7。两种方法补偿结果如图 19所示,可以看出两种方法补偿后的叠前道集的深层能量均增强,相位畸变得以校正。本文方法的补偿结果纵向分辨率更高,并且对于大角度的道集补偿更充分,AVA反射特征形态更明显。另外,补偿结果在中、深层的信噪比优于叠前反Q滤波方法。

|
图 19 实际叠前角道集及不同方法补偿结果对比 (a)实际叠前角道集;(b)叠前反Q滤波方法;(c)基于L1范数正则化约束的叠前衰减补偿方法 |
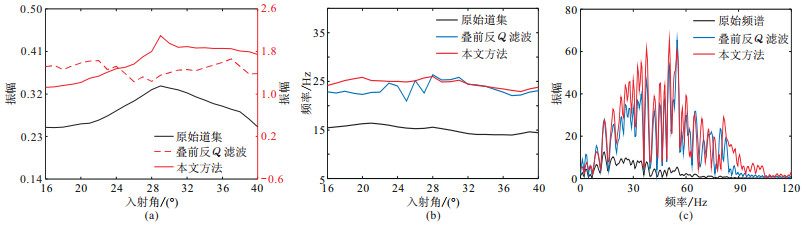
选择图 19中1.4 s处的同相轴(红色箭头指示)进行AVA分析和主频分析。如图 20所示,与叠前反Q滤波方法相比,本文方法补偿后地震同相轴的AVA反射特征得以更好的恢复(图 20a),大角度道集的振幅衰减得到充分补偿,并且更好地还原了主频随入射角变化的趋势(图 20b),补偿后主频受噪声干扰较小,提高了主频的横向一致性。图 20c展示了入射角30°的地震道补偿前、后的频谱对比,可见补偿后道集频谱能量抬升更明显,主频提高,频带拓宽更显著,高频能量得以补偿,并且没有放大高频噪声的干扰。实际资料测试结果进一步验证了本文所提方法的有效性和实用性。
|
图 20 不同方法补偿结果分析 (a)AVA曲线;(b)主频随入射角变化曲线;(c)入射角30°的地震道补偿前、后频谱 |
本文考虑了叠前道集上不同地震道传播路径的差异对吸收衰减带来的影响,利用反演的思想推导出一种基于L1范数正则化约束的叠前角道集衰减补偿方法。通过数值模拟实验和实际数据应用,对比、分析了叠后补偿、叠前反Q滤波方法和本文方法的补偿结果,得到以下结论。
(1) 本文方法有效抑制了补偿过程中的噪声放大现象,在保持高信噪比的同时获得了精度较高的补偿结果,还原了叠前道集的AVA反射特征,一定程度上消除了射线路径对主频横向一致性的影响。
(2) 通过Q值模型精度敏感度分析实验测试了Q值模型精度对本文方法补偿结果的影响,证明本文方法对Q值敏感度不高。为验证本文方法的实用性,对实际叠前道集进行了补偿处理,与叠前反Q滤波方法比较的结果表明,本文方法抗噪能力更强,对大角度地震道的补偿效果更好,AVA反射特征得到了更好地恢复,主频一致性得以提高,为后续叠前高精度反演提供了保证。
(3) 本文方法对低至中等强度的随机噪声具有较好的抗噪性,但过高强度的噪声仍会影响补偿效果。因此,利用本文方法进行处理时首选高信噪比数据,建议在补偿之前进行一定的去噪处理,以保证补偿的精度及稳定性。同时,本文方法需要提前获取地下地层速度、Q值及震源子波以完成补偿前的数据准备,进而实现高精度的衰减补偿。
| [1] |
FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5279-5291. DOI:10.1029/JZ067i013p05279 |
| [2] |
HALE D. An inverse Q-filter[J]. Stanford Exploration Project, 1981, 28(1): 289-298. |
| [3] |
白桦, 李鲲鹏. 基于时频分析的地层吸收补偿[J]. 石油地球物理勘探, 1999, 34(6): 642-648. BAI Hua, LI Kunpeng. Stratigraphic absorption compensation based on time-frequency analysis[J]. Oil Geophysical Prospecting, 1999, 34(6): 642-648. DOI:10.3321/j.issn:1000-7210.1999.06.005 |
| [4] |
WANG Y. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67(2): 657-663. DOI:10.1190/1.1468627 |
| [5] |
WANG Y. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 2006, 71(3): V51-V60. DOI:10.1190/1.2192912 |
| [6] |
严红勇, 刘洋, 赵前华, 等. 一种提高VSP分辨率的反Q滤波方法[J]. 石油地球物理勘探, 2011, 46(6): 873-880. YAN Hongyong, LIU Yang, ZHAO Qianhua, et al. A method for improving VSP resolution by inverse Q filtering[J]. Oil Geophysical Prospecting, 2011, 46(6): 873-880. |
| [7] |
ZHANG C, ULRYCH T J. Seismic absorption compensation: a least squares inverse scheme[J]. Geophysics, 2007, 72(6): R109-R114. DOI:10.1190/1.2766467 |
| [8] |
WANG S. Attenuation compensation method based on inversion[J]. Applied Geophysics, 2011, 8(2): 150-157. DOI:10.1007/s11770-011-0275-3 |
| [9] |
WANG S, SONG H, YANG D. Seismic attenuation compensation by Bayesian inversion[J]. Journal of Applied Geophysics, 2014, 111: 356-363. DOI:10.1016/j.jappgeo.2014.10.012 |
| [10] |
WANG S, CHEN X. Absorption-compensation me-thod by l1-norm regularization[J]. Geophysics, 2014, 79(3): V107-V114. DOI:10.1190/geo2013-0206.1 |
| [11] |
王本锋, 陈小宏, 李景叶, 等. 基于反演的稳定高效衰减补偿方法[J]. 地球物理学报, 2014, 57(4): 1265-1274. WANG Benfeng, CHEN Xiaohong, LI Jingye, et al. A stable and efficient attenuation compensation method based on inversion[J]. Chinese Journal of Geophy-sics, 2014, 57(4): 1265-1274. |
| [12] |
MA X, LI G, LI H, et al. Multichannel absorption compensation with a data-driven structural regularization[J]. Geophysics, 2020, 85(1): V71-V80. DOI:10.1190/geo2019-0132.1 |
| [13] |
刘金涛, 王孝, 王小卫, 等. 全局约束反演多道吸收补偿方法[J]. 石油地球物理勘探, 2021, 56(2): 273-282. LIU Jintao, WANG Xiao, WANG Xiaowei, et al. Multi-channel absorption compensation method based on global constrained inversion[J]. Oil Geophysical Prospecting, 2021, 56(2): 273-282. DOI:10.13810/j.cnki.issn.1000-7210.2021.02.008 |
| [14] |
LAZARATOS S, FINN C. Deterministic spectral ba-lancing for high-fidelity AVO[C]. SEG Technical Program Expanded Abstracts, 2004, 23: 219-223.
|
| [15] |
任浩然, 王华忠, 张立彬. 沿射线路径的波动方程延拓吸收与衰减补偿方法[J]. 石油物探, 2007, 46(6): 557-561. REN Haoran, WANG Huazhong, ZHANG Libin. Compensation for absorption and attenuation using wave equation continuation along ray path[J]. Geophysical Prospecting for Petroleum, 2007, 46(6): 557-561. DOI:10.3969/j.issn.1000-1441.2007.06.006 |
| [16] |
BANSAL R, KHARE V, JENKINSON T, et al. Correction for NMO stretch and differential attenuation in converted-wave data: a key enabling technology for prestack joint inversion of PP and PS data[J]. The Leading Edge, 2009, 28(10): 1182-1190. DOI:10.1190/1.3249772 |
| [17] |
YAN H, LIU Y. Estimation of Q and inverse Q filtering for prestack reflected PP- and converted PS-waves[J]. Applied Geophysics, 2009, 6(1): 59-69. DOI:10.1007/s11770-009-0009-y |
| [18] |
李国发, 张小明, 彭更新, 等. 与炮检距有关的地层吸收对AVO分析的影响及其补偿方法[J]. 石油地球物理勘探, 2014, 49(1): 89-94. LI Guofa, ZHANG Xiaoming, PENG Gengxin, et al. Influence of offset-related absorption on AVO analysis and its compensation[J]. Oil Geophysical Prospecting, 2014, 49(1): 89-94. |
| [19] |
CHAI X, WANG S, WEI X, et al. High resolution prestack nonstationary AVA inversion: Part 1-Theory[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 553-558.
|
| [20] |
张生强, 张志军, 郭军, 等. 时频空间域低频约束AVO响应校正方法[J]. 石油地球物理勘探, 2021, 56(1): 137-145. ZHANG Shengqiang, ZHANG Zhijun, GUO Jun, et al. AVO response correction constrained by low-frequency components in time-frequency-space domain[J]. Oil Geophysical Prospecting, 2021, 56(1): 137-145. |
| [21] |
LI G, LIU Y, ZHENG H, et al. Absorption decomposition and compensation via a two-step scheme[J]. Geophysics, 2015, 80(6): V145-V155. DOI:10.1190/geo2015-0038.1 |
| [22] |
AHARCHAOU M, NEUMANN E. Prestack Q compensation with sparse tau-p operators[J]. Geophy-sics, 2019, 84(5): V295-V305. |
| [23] |
CHENG W, WANG S, ZHOU C, et al. Prestack data attenuation compensation based on inversion[C]. 82nd EAGE Annual Conference & Exhibition, 2021, 1-5.
|
| [24] |
BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2011, 3(1): 1-122. |
| [25] |
MARGRAVE G F. Theory of nonstationary linear filtering in the Fourier domain with application to time-variant filtering[J]. Geophysics, 1998, 63(1): 244-259. DOI:10.1190/1.1444318 |
| [26] |
CHENG W, WANG S, ZHOU C, et al. Q estimation based on the logarithmic spectral area double diffe-rence[J]. Geophysics, 2022, 87(2): V155-V167. DOI:10.1190/geo2021-0040.1 |
| [27] |
LINES L R, ULRYCH T J. The old and the new in seismic deconvolution and wavelet estimation[J]. Geo-physical Prospecting, 1977, 25(3): 512-540. DOI:10.1111/j.1365-2478.1977.tb01185.x |
| [28] |
LAZEAR G D. Mixed-phase wavelet estimation using fourth-order cumulants[J]. Geophysics, 1993, 58(7): 1042-1051. |



 王守东,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email:
王守东,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email: