“相”是岩层生成时的古地理环境及其物质表现的总和[1]。地震相分析的目的是解释区域地层,重塑盆地的沉积史和构造史,预测生、储油相带及构造、地层(岩性)圈闭等[2]。地震相识别是油气藏勘探和储层预测的基础。传统的地震相划分方法通常基于地震属性变化识别地震相,针对不同的地震相需要人工选择突出地震相特征的地震属性。随着地震勘探技术的不断发展及地震数据规模的不断增加,地震相人工解释需要耗费大量的时间和精力。同时,人工解释存在很大的主观性和不确定性,这些都直接影响后期地震资料解释的准确性[3]。
近年来,深度学习技术取得了突破性进展,并广泛用于地震相划分,极大地提高了解释效率。早在1995年,王翠华等[4]使用自组织映射神经网络划分地震相,充分利用地震剖面和相应的三瞬(瞬时振幅、瞬时相位及瞬时频率等)剖面的局部和整体特征,利用样本适当训练网络即可划分地震相,网络训练速度快。然而,自组织映射神经网络的分类效果依赖于初始权值。Dubois等[5]为了划分堪萨斯州西南部Panoma气田地震相,选取基于贝叶斯规则的经典参数方法以及模糊逻辑、k-最近邻和前馈—反馈传播人工神经网络(ANN)的非参数方法,用3600个样本构造训练集和测试集训练网络,其中每个样本带有四个或五个岩相类。实验结果表明:ANN是适合这种特定分类问题的最优分类器,并在很多方面取得了较好效果;但是结构简单且层数较少,仅能获取有限特征,限制了网络表达能力。随后,深度学习因其强大的特征提取和非线性拟合能力受到业界广泛关注。近年来,深度学习在图像分类[6]、语义分割[7]、目标检测[8]等计算机视觉任务中不断突破,并在人脸识别、姿势识别、医疗和无人驾驶等领域取得了巨大成功。
地震资料解释与计算机视觉间存在很多相似性,相应的图像分类、语义分割算法可用于地震相分类及预测等。Qian等[9]使用深度卷积自动编码器(DCAE)从未标记数据中学习非线性、判别式和不变特征,然后使用传统的分类或聚类技术分析地震相。Li等[10]提出了基于深度自编码神经网络(DAE)的地震波形降维方法划分地震相边界。Wang等[11]结合地震地层切片技术与三维卷积神经网络(CNN)模型分析地震相。王树华等[12]使用深度卷积网络(DCNN)识别地震相,不仅很好地保持了地震数据结构特征,还基于多层网络结构挖掘数据的更深层特征,提高了识别结果的可靠性。上述基于CNN的地震相划分模型用一个窗在图像上滑动,依次确定每一个滑动窗的中心像素的类别从而分割整张图像。这种方法计算冗余较大且不易于同时获取像素点的位置信息和上、下文信息。基于全卷积神经网络(FCN)的语义分割模型加入上采样和跳跃层连接很好地解决了上述问题。然而,FCN具有平移不变性,并没有考虑有用的全局上、下文信息。研究表明,全局特征信息或上、下文信息相互作用有助于正确地分类像素,从而更好地进行语义分割[13]。因此,利用上、下文信息进行语义分割的编码器和解码器结构更能胜任分割任务。编码器主要减小特征图大小并捕获更高层次的语义信息;解码器主要通过逐渐恢复特征图细节信息和空间维度进行分割。整个结构利用编码器模块的多尺度特性提取特征,并由解码器模块恢复空间分辨率。U-Net[14]模型和SegNet[15]模型就是典型的编码器—解码器结构。
近年来,基于编码器—解码器结构划分地震相的方法越来越多。Zhang等[16]对人工标注的标签和地震数据进行镜像和裁剪以确保网络可以接受任意大小的输入,然后用数据增广技术生成大量的训练样本,再构建两个独立的基于编码器—解码器结构的网络识别地震相,其中一个网络同时识别所有地震相,另一个网络识别每个模型的单个地震相,并利用集成学习方法优化模型。该方法能提高模型的预测能力,可以较好地描述地震相。Feng等[17]提出在贝叶斯框架下使用CNN预测地震岩相,并量化分类中的不确定性方法;采用变分方法逼近CNN参数的后验分布,以此预测地震相。Mukhopadhyay等[18]提出了基于贝叶斯SegNet的地震相分类编码器、解码器结构,并引入预测熵的概念获取不确定性图。贝叶斯深度学习方法计算量大,耗时较长,不适用于大规模数据。闫星宇等[19]在U-Net模型的末端加入金字塔池化模块(PPM)可提高模型获取全局信息的能力,利用U-Net+PPM方法预测地震相的精度更高并具有更良好的边界刻画能力,但对计算资源的要求较高。常德宽等[20]联合残差神经网络(ResNet)和U-Net架构,构建了由地震数据识别断层的网络架构(SeisFault-Net),利用ResNet解决深层网络梯度弥散问题,有效提高了SeisFault-Net的训练效率。虽然深度学习算法已经广泛用于地震相划分,然而由于地震相出现的模式及其空间尺度的多样性,在保证高分辨率以及高精度的同时提高计算效率仍是一项具有挑战性的任务。
本文提出基于LinkNet的高分辨率地震相划分方法,采用结合多元交叉熵与Tversky的损失函数,改善不均衡数据中少数类地震相边界的刻画精度。此外,LinkNet的解码层可共享编码层的学习特征,使解码层的结构更精简,可大大提高计算效率。在荷兰北海F3区块的测试结果验证了方法的有效性。
1 方法原理 1.1 网络结构LinkNet[21-22]的网络结构借鉴了U-Net的思想,采用编码器—解码器结构(图 1a)。网络共包含2个卷积层(conv)、1个池化层(pool)、2个转置卷积层(deconv)、4个编码层(encoder)、4个解码层(decoder)。在每个卷积层之间使用批归一化,随后是激活函数(ReLU)。网络上半部分主要为编码器结构,是一个18层的残差神经网络(ResNet18),其中4个残差块层构成LinkNet的4个编码层,这是一个相当轻量级的网络,可以使LinkNet的运行效率较高。下半部分主要为解码器结构,解码层将图像特征通道数减少到原来的数量。

|
图 1 LinkNet网络结构 (a) LinkNet编码器—解码器网络结构;(b)编码层结构;(c)解码层结构编码层的结构为ResNet18残差块层,由2个残差块组成,每个残差块包含两个卷积层和一个跳跃连接;通过四个编码层后,图像的特征通道数分别为64、128、256、512。解码层由2个卷积层中间加1个转置卷积层构成,四次解码后图像的特征通道数分别为256、128、64、64,此时图像特征通道数收缩到原来的数量。m为输入图像特征通道数,n为输出图像特征通道数。⊕表示将编码层的特征图叠加到解码层的特征图上。 |
LinkNet的第一层是内核大小为7×7的卷积层,步长为2,输入通道数为1,输出通道数为64。取256×256像素(pixels)大小的数据图像作为网络输入,经第一个卷积层之后,图像大小变为128×128。第二层设置为池化层,池化的作用是在保留主要特征的同时减少参数和计算量,防止过拟合,提高模型的泛化能力,其内核大小为3×3,步长为2,池化方式为最大池化。经池化层之后,图像大小变为原来的一半,通道数保持不变。
从第二个编码层起,每个编码层的输入叠加到对应的解码层的输出,使相应的解码层能共享编码层的学习特征,从而使解码层的结构更简单,使用更少的参数(图 1b)。
与现有的分段网络相比,LinkNet的解码层可共享编码层的学习特征,因而使解码层的结构更精简,大大减少了网络参数,极大地提高了网络的运行效率,基本可实现实时操作(图 1c)。
经编码器—解码器结构之后,图像进入第1个转置卷积层,其内核大小为3×3,步长为2,该过程相当于上采样操作,输出图像大小变为128×128,特征通道数变为32。接着,进入下一个卷积层,其内核大小为3×3,步长为1,图像大小和特征通道数保持不变。最后,进入第二个转置卷积层,其内核大小为2×2,步长为2,输出图像大小变为256×256,通道数变为1,此时输出地震相预测结果。
1.2 损失函数在分类问题中,将实例分为正例和负例两部分。将正例预测为正例,称为真正类(True Positive,TP),将负例预测为正例,称为假正类(False Positive,FP)。与此相反,将负例预测为负例,称为真负类(Ture Negitave,TN),将正例预测为负例,称为假负类(False Negative,FN)[23]。将正例预测为正例的情况占全部实际为正例的比例称为召回率(Recall),表示为
| $ \text { Recall }=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} $ | (1) |
当数据样本不均衡时,需要着重考虑召回率。如当训练模型用于医学的癌症预测时,病人患癌为正例,没患癌为负例,假设模型预测全部病人没有患癌,由于患癌的病人处于少数,所以模型的准确率很高,但模型并未检测出患癌症的病人。
传统的基于深度学习的地震相划分方法使用交叉熵作为损失函数训练网络的目标函数,但交叉熵对于在数据中占比较少的地震相的分割效果较差。训练网络的主要挑战之一是数据不均衡,这在地震相划分中尤为突出,如地质异常体的数量通常远低于正常地质体。使用不均衡数据进行训练可能导致预测结果严重偏向于高准确率及低召回率(敏感性),这是不期望的结果。当训练集中每类像素数量变化较大时,需要根据真实类别对损失加权。为此,在传统的损失函数(交叉熵)基础上加入Tversky[24],通过调节损失函数中FP和FN的权重参数,缓解目标图像分割任务的样本不均衡问题。
传统的损失函数(交叉熵)为
| $ L=-\sum\limits_{c=1}^C \sum\limits_{k=1}^K y_{c, k} \lg \left(p_{c, k}\right) $ | (2) |
其中
| $ {p_{c, k}} = \frac{{{{\rm{e}}^{{z_{c, k}}}}}}{{\sum\limits_{c = 1}^C {{{\rm{e}}^{{z_{c, k}}}}} }} $ | (3) |
式中:C为地震相总类数;K为输入的像素点总数;yc, k为标签中像素点k为第c类对应的值;zc, k为网络最终输出结果,其物理意义为该点预测为第c类地震相的可能性;pc, k为像素点k预测为第c类的概率,是对zc, k进行softmax函数归一化的结果。
由式(2)可见,通过分别计算每个像素点的交叉熵并求和得到L。为了使L取最小值,会更多地关注占比较大的类别,从而忽略占比较小的类别。但在实际应用中,对占比较小的类别的关注度更高。如地震相中盐丘等地质异常体占比较小,但是很重要。为此,在损失函数中引入可以评价整体分割效果的Tversky[24]解决上述问题。Tversky系数是一种度量集合相似度的函数,可以体现两个区域轮廓的相似程度,取值范围为[0, 1]。Tversky系数公式为
| $ \begin{array}{*{20}{l}} {{\rm{Tversky}}(\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{B}}) = }\\ {\frac{{|\mathit{\boldsymbol{A}} \cap \mathit{\boldsymbol{B}}|}}{{|\mathit{\boldsymbol{A}} \cap \mathit{\boldsymbol{B}}| + \alpha |\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}| + \beta |\mathit{\boldsymbol{B}} - \mathit{\boldsymbol{A}}|}}} \end{array} $ | (4) |
式中:A∩B为预测值A和真实值B的交集,|A-B|为FP,|B-A|为FN;α和β为惩罚系数,α+β=1。通过调整α和β可以平衡FP和FN,进而影响召回率等指标。Tversky(A, B)的值越接近1,表示分割结果和标准分割图像之间相似度越高;反之,越接近0则表示相似度越低。α和β均设置为0.5时,Tversky系数即为Dice系数[25],此时FP和FN对损失函数的贡献相同。在地震相分割任务中,地质异常体区域的像素点数量明显小于正常地质体区域,相同的权重参数将无法解决分割图像任务的样本不均衡问题,设置更大的β值将使FN较FP对损失值的贡献更大,使分割结果倾向于FN较少的结果,从而提升召回率。同样,如果设置更大的α值,分割结果将会倾向于FP较少的结果,从而提升精度。
用于地震相预测的损失函数(Tversky)为
| $ \begin{array}{*{20}{l}} {{L_{{\rm{Tversky }}}} = }\\ {\sum\limits_{c = 1}^c {\frac{1}{K}} \left( {1 - \frac{{\sum\limits_{k = 1}^K {{p_{c, k}}} {y_{c, k}} + \varepsilon }}{{\sum\limits_{k = 1}^K {{p_{c, k}}} {y_{c, k}} + \alpha \sum\limits_{k = 1}^K {{p_{c, k}}} {y_{c, \bar k}} + \beta \sum\limits_{k = 1}^K {{p_{c, \bar k}}} {y_{c, k}} + \varepsilon }}} \right)} \end{array} $ | (5) |
式中:pc, k为像素点k不属于第c类的概率;yc, k为标签中像素点k不属于第c类对应的值;ε为平滑值,本文取1。
式(5)可以最大程度地衡量预测结果与标签之间的相似性,使二者尽可能接近,减小不均衡数据对模型训练的影响,增强地震相边界的分割效果。本文将L与LTversky的加权线性组合作为网络的新损失函数,即
| $ L_{\text {loss }}=L+\lambda L_{\text {Tversky }} $ | (6) |
式中λ为LTversky的权重。
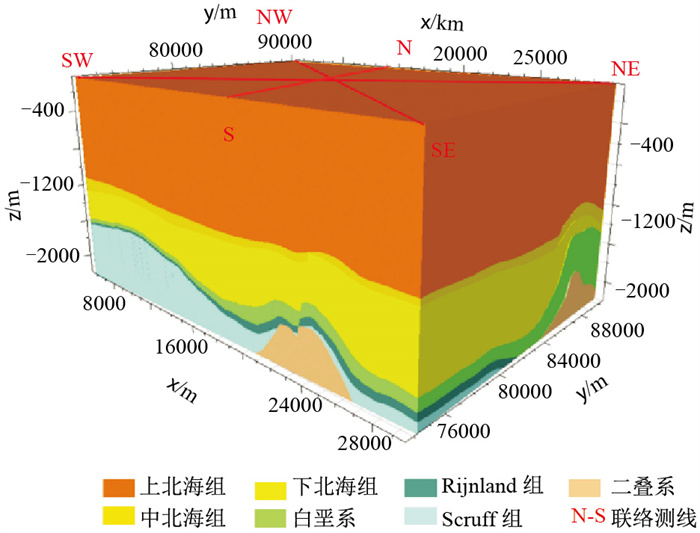
2 应用实例本文选用荷兰北海F3区块公开数据测试所提方法的效果。Alaudah等[26]参考F3区块测井资料,根据岩性差异由人工解释了七组岩石地层单元(图 2),以上述数据作为验证基于深度学习的地震相划分方法的标准数据。
|
图 2 北海F3区块地层模型 上北海组:中新统—第四系,黏土岩、砂岩;下、中北海组:古新统—中新统,砂岩和黏土岩;白垩系:上白垩统—古新统,碳酸盐岩;Scruff组:上侏罗统—下白垩统,黏土岩;Rijnland组:上白垩统,含砂岩黏土层;二叠系:上二叠统,蒸发岩、碳酸盐岩 |
本文也选用上述标准数据验证方法的效果,所用数据属于F3区块第100~第700主测线,共601条剖面,每条剖面701道。将该区块数据体中的第300~第670号主测线剖面作为训练集,第671~第700号主测线剖面作为验证集,第100~ 第299号主测线剖面作为测试集,用于评估模型的预测效果。依据文献[26],将Rijnland组和白垩系合并为一类处理,数据集样本共分为6类。
2.1 数据预处理现有的深度学习方法通过对训练数据进行几何变换、旋转变换、翻转变换、随机擦除等数据增广操作,以增加样本的数量和多样性,但这些方法用于地震数据时往往会破坏地震相原有的形态与空间分布规律。为此,沿三维数据体的主测线、联络测线、SW-NE、NW-SE四个方向划分二维地震剖面,再在每一条地震剖面上选取尺寸为256×256的窗口,通过选取不同的滑动步长截取所需的训练数据,在保证遵循地震相空间分布规律的基础上增加样本的多样性。图 3为截取的一段训练数据样本及标签。

|
图 3 截取的一段训练数据样本(a)及标签(b) |
本文采用平均像素精度(mPA)和平均交并比(mIOU)两项指标评价地震相划分结果,以在数据不均衡的条件下更好地反映模型的预测效果。
mPA为每个类内被正确分类的像素数与总像素数比值的平均,即
| $ \mathrm{mPA}=\frac{1}{C} \sum\limits_{c=1}^c\left|\frac{\boldsymbol{P}_c \cap \boldsymbol{Y}_c}{\left|\boldsymbol{Y}_c\right|}\right| $ | (7) |
式中:Yc为在地震剖面上属于第c类地震相的像素点集合;Pc为被网络模型预测为第c类地震相的像素点集合;运算符|·|表示集合中的元素总数。
mIOU是语义分割的标准度量,为Pc与Yc的交集和并集之比的平均,即
| $ \operatorname{mIOU}=\frac{1}{C} \sum\limits_{c=1}^c\left|\frac{\boldsymbol{P}_c \cap \boldsymbol{Y}_c}{\boldsymbol{P}_c \cup \boldsymbol{Y}_c}\right| $ | (8) |
mIOU考察预测结果和真实标签的重叠程度,由于简洁、代表性强而成为最常用的分类效果度量标准,人们均使用该指标评价分类效果。
2.3 实验结果分析本次训练使用的GPU型号为RTX 3090,在PyTorch框架下训练网络,用GPU加速计算,采用Adam优化算法。学习速率决定了模型训练的效率和精度,学习率太小,导致收敛过慢;反之,学习率太大,容易在目标函数最低点处振荡,也会降低训练效率。本文根据实验经验,设置学习率为5×10-4,训练过程中由人工调试λ以及α、β。
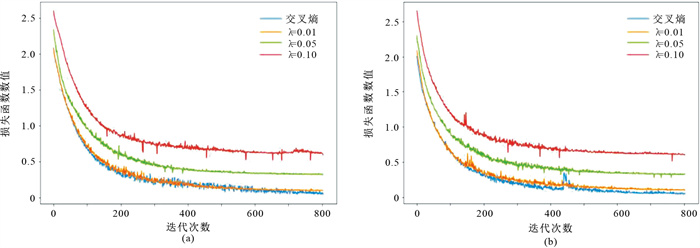
将训练集中的地震数据输入LinkNet深度学习网络模型,用划分结果与对应的地震相标签计算网络的损失函数值、更新网络参数,在验证集度量模型的性能。随着迭代次数增加,训练集的损失函数值越来越小,选择在验证集上损失函数值最小的模型为最优模型。图 4为模型训练损失函数值随迭代次数变化曲线。由图可见,当迭代达到550次,各组损失函数均开始收敛,由于Tversky更关注召回率,导致精度降低,因此当λ增大时,损失函数值也变大。模型运行结果(表 1)表明:LinkNet在λ=0.01、β=0.6时预测效果最好,此时mPA、mIOU值均比U-Net+PPM高;LinkNet迭代130次仅需要8s,而U-Net+PPM则需要150s。此外,LinkNet可在配置更低的笔记本(显卡型号为NVIDIA Quadro T2000 with Max-Q,4G显存)上运行,但是U-Net+ PPM则不行。表 2为测试集中Inline 280剖面评价指标。可见:采用Lloss的LinkNet模型在前四个相的准确率(PA)和其他模型相近,在后两个相的PA相对较高;采用Lloss的LinkNet模型在前两个相的交并比(IOU)和其他模型相近,在后四个相的IOU相对较高。利用训练好的模型逐个预测全部三维数据的二维主测线剖面并最终合成三维数据(图 5)。
|
图 4 模型训练损失函数值随迭代次数变化曲线 (a)β=0.7;(b)β=0.6 |
|
|
表 1 模型运行结果 |
|
|
表 2 测试集中Inline 280剖面评价指标 |
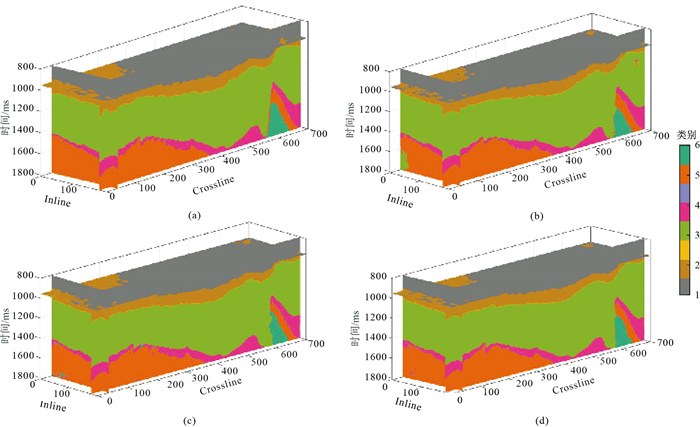
|
图 5 地震相三维切片 (a)真实数据;(b)损失函数为式(2)的LinkNet预测结果;(c)U-Net+PPM预测结果;(d)损失函数为式(6)的LinkNet预测结果(λ=0.01、β=0.6) |
前文使用完整的地震数据对应的地震相标签作为网络的训练集(图 3),实际标签也可以是离散的。为此,在原数据集基础上,每隔3条剖面抽出一条剖面,共抽取200条剖面作为训练集,每隔30条剖面抽出一条剖面,共抽取20条剖面作为验证集训练网络,其余381条剖面作为测试集评估得到的模型。在这种情况下,本文方法在测试集的地震相预测结果的mPA为96.57%、mIOU为93.49%,U-Net+PPM的mPA为96.21%、mIOU为92.24%。
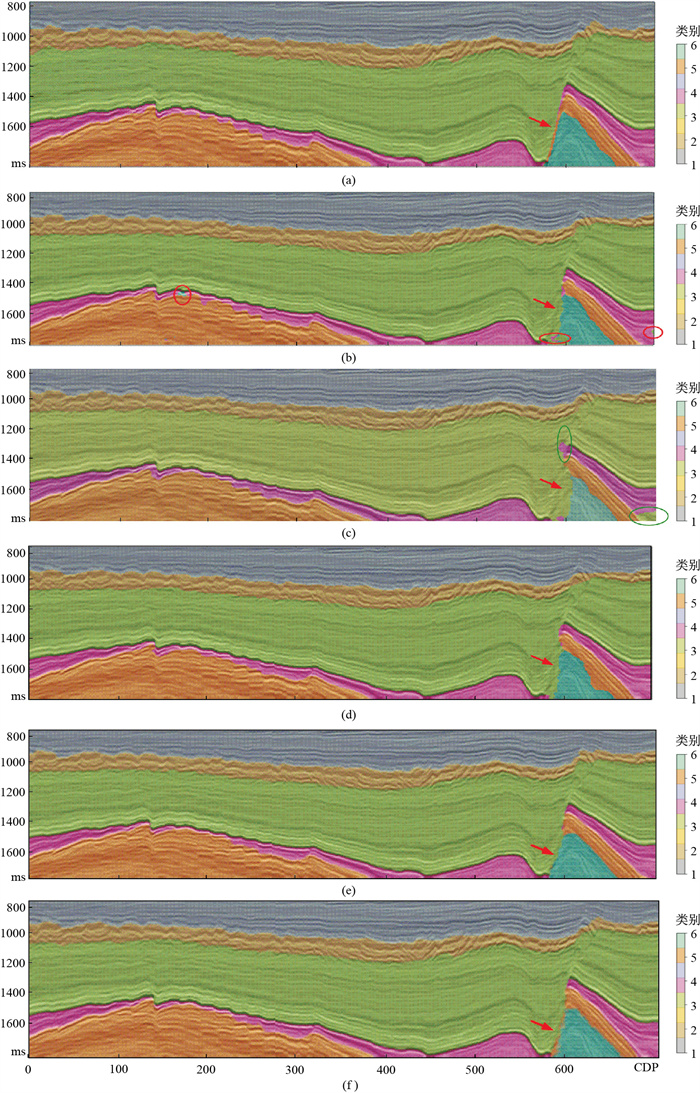
图 6为Inline280剖面地震相预测结果。由图可见:①在预测第4类时,U-Net+PPM(图 6b)在红色椭圆区域出现错误,损失函数为式(2)的LinkNet(图 6c)在蓝色椭圆区域出现错误,而损失函数为式(6)的LinkNet(图 6d)则没有出现错误;②离散训练数据集的损失函数为式(6)的LinkNet的刻画结果(图 6f红色箭头处)较U-Net+PPM(图 6e)更精细;③离散训练数据集的模型预测结果(图 6e、图 6f)优于整块训练数据集(图 6b、图 6d),这得益于前者与测试集剖面相距较近,使网络能够更好地学习数据特征。④U-Net+PPM和LinkNet对红色箭头处的预测精度都不高,这是由于该位置的层太薄、训练数据过少所致。图 6说明在面对不均衡数据时,本文方法对占比较小的类别的关注度更高,并具有更好的边界刻画能力。
|
图 6 Inline280剖面地震相预测结果 (a)真实地震相;(b)U-Net+PPM;(c)损失函数为式(2)的LinkNet;(d)损失函数为式(6)的LinkNet(λ=0.01、β=0.6);(e)U-Net+PPM (离散训练数据集);(f) 损失函数为式(6)的LinkNet (λ=0.01、β=0.6,离散训练数据集) |
本文提出基于LinkNet的地震相自动划分方法,采用多分类交叉熵与Tversky的加权线性组合作为网络训练的损失函数。Tversky通过调整参数平衡假正类和假负类,进而提升召回率等指标提高不均衡数据中少数类地震相边界的刻画精度。LinkNet解码层共享编码层的学习特征,使解码层的结构更精简,大大提高了计算效率。在荷兰北海F3区块的测试结果表明,本文方法刻画地震相的精度高于U-Net+PPM。同时,LinkNet计算速度快,可以在配置更低的设备上运行,较U-Net+PPM更实用。
| [1] |
NIVLET P. Uncertainties in seismic facies analysis for reservoir characterisation or monitoring: causes and consequences[J]. Oil & Gas Science and Technology-Rev.IFP, 2007, 62(2): 225-235. DOI:10.3321/j.issn:0564-3945.2007.02.004 |
| [2] |
JOHN A K, LAKE L, TORRES-VERDIN C, et al. Seismic facies identification and classification using simple statistics[J]. SPE Reservoir Evaluation & Engineering, 2008, 11(6): 984-990. |
| [3] |
顾元, 朱培民, 荣辉, 等. 基于贝叶斯网络的地震相分类[J]. 地球科学——中国地质大学学报, 2013, 38(5): 1143-1152. GU Yuan, ZHU Peimin, RONG Hui, et al. Seismic facies classification based on Bayesian network[J]. Earth Science-Journal of China University of Geoscien-ces, 2013, 38(5): 1143-1152. |
| [4] |
王翠华, 韩德贵, 李志荣. 人工神经网络在地震相划分中的应用[J]. 南方油气地质, 1995, 1(4): 47-51. WANG Cuihua, HAN Degui, LI Zhirong. The application of artificial neural network to the discrimination of seismic facies[J]. Southern China Petroleum Geology, 1995, 1(4): 47-51. |
| [5] |
DUBOIS M K, BOHLING G C, CHAKRABARTI S. Comparison of four approaches to a rock facies classification problem[J]. Computers & Geosciences, 2007, 33(5): 599-617. |
| [6] |
张珂, 冯晓晗, 郭玉荣, 等. 图像分类的深度卷积神经网络模型综述[J]. 中国图象图形学报, 2021, 26(10): 2305-2325. ZHANG Ke, FENG Xiaohan, GUO Yurong, et al. Overview of deep convolution neural networks for image classification[J]. Journal of Image and Graphics, 2021, 26(10): 2305-2325. DOI:10.11834/jig.200302 |
| [7] |
曾文献, 马月, 丁宇, 等. 基于深度学习的图像语义分割方法研究综述[J]. 现代计算机, 2021(21): 115-122. ZENG Wenxian, MA Yue, DING Yu, et al. Survey of image semantic segmentation algorithms based on deep learning[J]. Modern Computer, 2021(21): 115-122. DOI:10.3969/j.issn.1007-1423.2021.21.022 |
| [8] |
赵立新, 邢润哲, 白银光, 等. 深度学习在目标检测的研究综述[J]. 科学技术与工程, 2021, 21(30): 12787-12795. ZHAO Lixin, XING Runzhe, BAI Yinguang, et al. Review on survey of deep learning in target detection[J]. Science Technology and Engineering, 2021, 21(30): 12787-12795. DOI:10.3969/j.issn.1671-1815.2021.30.001 |
| [9] |
QIAN F, YIN M, LIU X Y, et al. Unsupervised seismic facies analysis via deep convolutional autoenco-ders[J]. Geophysics, 2018, 83(3): A39-A43. DOI:10.1190/geo2017-0524.1 |
| [10] |
LI K, LIU Z, SHE B, et al. Orthogonal deep auto-encoders for unsupervised seismic facies analysis[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2023-2028.
|
| [11] |
WANG J, ZHENG X, HUANG H. Seismic facies analysis based on 3D-CNN and seismic stratigraphic slice[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2609-2613.
|
| [12] |
王树华, 于会臻, 谭绍泉, 等. 基于深度卷积神经网络的地震相识别技术研究[J]. 物探化探计算技术, 2020, 42(4): 475-480. WANG Shuhua, YU Huizhen, TAN Shaoquan, et al. Research on seismic phase recognition technology based on deep convolution neural network[J]. Computing Techniques for Geophysical and Geochemical Exploartion, 2020, 42(4): 475-480. DOI:10.3969/j.issn.1001-1749.2020.04.06 |
| [13] |
李梦怡, 朱定局. 基于全卷积网络的图像语义分割方法综述[J]. 计算机系统应用, 2021, 30(9): 41-52. LI Mengyi, ZHU Dingju. Review on image semantic segmentation based on fully convolutional network[J]. Computer System & Application, 2021, 30(9): 41-52. |
| [14] |
张岩, 周一帆, 宋利伟, 等. 基于物理约束U-Net网络的地震数据低频延拓[J]. 石油地球物理勘探, 2023, 58(1): 31-45. ZHANG Yan, ZHOU Yifan, SONG Liwei, et al. Low frequency continuation of seismic data based on physically constrained U-Net network[J]. Oil Geophysical Prospecting, 2023, 58(1): 31-45. |
| [15] |
陈德武, 杨午阳, 魏新建, 等. 基于混合网络U-SegNet的地震初至自动拾取[J]. 石油地球物理勘探, 2020, 55(6): 1188-1201. CHEN Dewu, YANG Wuyang, WEI Xinjian, et al. Automatic picking of seismic first arrivals based on hybrid network U-SegNet[J]. Oil Geophysical Prospecting, 2020, 55(6): 1188-1201. |
| [16] |
ZHANG Y, LIU Y, ZHANG H, et al. Seismic facies analysis based on deep learning[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(7): 1119-1123. |
| [17] |
FENG R, BALLING N, GRANA D, et al. Bayesian convolutional neural networks for seismic facies classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(10): 8933-8940. |
| [18] |
MUKHOPADHYAY P, MALLICK S. Bayesian deep learning for seismic facies classification and its uncertainty estimation[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2488-2492.
|
| [19] |
闫星宇, 顾汉明, 罗红梅, 等. 基于改进深度学习方法的地震相智能识别[J]. 石油地球物理勘探, 2020, 55(6): 1169-1177. YAN Xingyu, GU Hanming, LUO Hongmei, et al. Intelligent seismic facies classification based on an improved deep learning method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1169-1177. |
| [20] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [21] |
杨知, 欧文浩, 刘晓燕, 等. 基于LinkNet卷积神经网络的高分辨率遥感影像水体信息提取[J]. 云南大学学报(自然科学版), 2019, 41(5): 932-938. YANG Zhi, OU Wenhao, LIU Xiaoyan, et al. Water information extraction for high resolution remote sensing image based on LinkNet convolutional neural network[J]. Journal of Yunnan University (Natural Science Edition), 2019, 41(5): 932-938. |
| [22] |
CHAURASIA A, CULURCIELLO E. LinkNet: Exploiting encoder representations for efficient semantic segmentation[C]. 2017 IEEE Visual Communications and Image Processing, 2017, doi: 10.1109/VCIP.2017.8305148.
|
| [23] |
谢文鑫, 苑金辉, 胡晓飞. 基于全卷积神经网络的左心室图像分割方法[J]. 软件导刊, 2020, 19(5): 19-22. XIE Wenxin, YUAN Jinhui, HU Xiaofei. Left ventri-cular image segmentation method based on full convolution neural network[J]. Software Guide, 2020, 19(5): 19-22. |
| [24] |
SALEHI S S, ERDOGMUS D, GHOLIPOUR A. Tversky loss function for image segmentation using 3D fully convolutional deep networks[C]. Interna-tional Workshop on Machine Learning in Medical Ima-ging, 2017, 379-387.
|
| [25] |
唐杰, 孟涛, 韩盛元, 等. 基于多分辨率U-Net网络的地震数据断层检测方法[J]. 石油地球物理勘探, 2021, 56(3): 436-445. TANG Jie, MENG Tao, HAN Shengyuan, et al. A fault detection method of seismic data based on MultiResU-Net[J]. Oil Geophysical Prospecting, 2021, 56(3): 436-445. |
| [26] |
ALAUDAH Y, MICHALOWICZ P, ALFARRAJ M, et al. A machine-learning benchmark for facies classification[J]. Interpretation, 2019, 7(3): SE175-SE187. |



 汪玲玲, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email:
汪玲玲, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email: 