2. 东方地球物理公司研究院大庆物探研究院, 黑龙江大庆 163453
2. PetroChina Daqing Geophysical Research Institute of GRI, BGP, Daqing, Heilongjiang 163453, China
松辽盆地北部古中央隆起带呈近南北向展布,东、西两侧以徐家围子断陷和古龙断陷的控陷断裂为边界,为潜山性质的基岩隆起带[1-3]。古中央隆起带基底上覆地层缺失断陷期沉积层序,基岩暴露地表时间长,风化壳厚度大,埋深小,生储盖组合良好,具有良好的天然气成藏条件,因此是松辽盆地深层天然气的重要资源接替领域。
研究区古中央隆起带自基岩物质形成建造以来,经历了长期的风化、热变质、动力变质等后期改造作用,基底岩石类型多、岩性复杂。综合钻井岩心分析、570块薄片鉴定及测井等资料,确定古中央隆起带基底岩石类型主要为浅变质沉积岩、浅变质火山岩、花岗岩3大类,局部发育动力变质岩,主要由构造运动导致构造断裂带中的原岩发生碎裂、变形作用而形成。基底主要发育花岗岩、变质岩储层,不同类型储层的裂缝发育程度不同。钻井揭示:花岗岩的脆性大,易形成裂缝,花岗岩储层物性最好,属于孔隙—裂缝型储层;基底花岗岩风化壳储层非均质性强,储层物性较差,以裂缝为主。
目前,对于基底风化壳储层地震预测,岩性及储层的岩石物理特征分析尤为重要,为了精确地选择储层反演参数和提取属性,急需建立针对基底复杂岩性、储层的地震预测技术流程[4-8]。目前针对沉积岩、碳酸盐岩及页岩油的岩石物理分析研究较多。邢文军等[9]应用跨频段测试分析研究不同饱和流体砂岩储层,展示了不同的地震波频散规律;庞孟强等[10]针对川西须家河组高含气饱和度致密砂岩,开展超声和地震频段岩石物理测试与孔隙—裂缝衰减岩石物理建模,以预测致密砂岩的孔隙度和裂缝含量;龙腾等[11]、李闯等[12]通过对碳酸盐岩进行跨频段岩石物理测量与频散理论分析,研究不同孔隙结构以及流体对频散与衰减的影响。前人研究成果表明,宽频带岩石物理实验分析对于研究储层与非储层具有重要意义,目前有关基底花岗岩和变质岩的岩石物理弹性参数特征的实验室研究较少。为此,本文通过地震岩石物理特征分析,采用超声频段和地震频段岩样测试方法,建立由地球物理勘探获得的物理量与地下岩石参数的定量对应关系,了解储层流体变化引起的地震响应变化及基底不同岩性的储层弹性参数特征,建立基底孔隙—裂缝型储层的岩石物理模型,以期为基底风化壳储层地震预测奠定研究基础[13-16]。
1 岩石样品的优选本次实验针对古中央隆起带基底的变质安山岩、构造角砾岩、片岩、花岗岩、碎裂花岗岩、糜棱化花岗岩、糜棱化石英闪长岩、长英质糜棱片岩、变质砾岩、蚀变闪长岩及千枚岩,共取岩石样品33块(表 1),其中气层取样7种岩性(共18块岩样),干层取样9种岩性(共15块岩样)。
|
|
表 1 岩石样品取样表 |
为了更好地分析基底的岩石物理特征,本文将基底岩性分为浅变质沉积岩(片岩、变质砾岩、千枚岩、糜棱片岩、砂砾岩)、浅变质中基性岩(蚀变闪长岩、变质安山岩)及花岗岩类(花岗岩、糜棱岩化花岗岩、碎裂花岗岩、构造角砾岩)3大类进行研究和分析。
岩心观察表明,古中央隆起带储层为孔隙—裂缝型,储集空间主要为裂缝和溶蚀孔,以裂缝为主。花岗岩类裂缝最发育,裂缝密度达7条/m,平均孔隙度为2.43%,物性最好(图 1a);浅变质火山岩裂缝较发育,多处见氧化面,局部被方解石充填,裂缝密度为3条/m,平均孔隙度为1.6%(图 1b);浅变质砂泥岩裂缝相对不发育,裂缝密度为2条/m,局部裂缝被方解石脉填充(图 1c),平均孔隙度为0.6%。整体上花岗岩、碎裂花岗岩、构造角砾岩等花岗岩类较浅变质沉积岩和浅变质火山岩的裂缝和溶蚀孔发育,风化壳储层物性最好,是古中央隆起带成储优势岩性。

|
图 1 岩心照片 (a)LT2井花岗岩;(b) LT1井浅变质安山岩;(c) LT1井片岩 |
为了精确测量古中央隆起带岩石样品的物性参数,将样品放入烘干箱中烘干(温度为80℃,历时72 h),以消除孔隙中残留的水汽。利用孔渗测量仪测试样品的渗透率与氦气孔隙度,测量结果表明:基底的储层较致密,孔隙度变化范围为0.8%~3.1%,渗透率变化范围为0.008~0.680 mD。密度—孔隙度交会分析(图 2)表明,浅变质沉积岩、花岗岩类及浅变质中基性岩的密度与孔隙度呈明显的线性负相关。渗透率—孔隙度交会分析(图 3)表明,三类岩石的渗透率与孔隙度整体上呈线性正相关,不同岩石的曲线斜率存在差异。
|
图 2 密度—孔隙度交会分析 |
|
图 3 渗透率—孔隙度交会分析 |
超声波测量技术在中国已经趋于成熟,可测量不同压力与温度条件下岩石样品的超声纵波速度和横波速度。本次实验主要运用透射法,透射方法是在样品两侧分别放置发射高频弹性脉冲波的震源与接收器,用接收器接收超声透射波的初至时间、波形以及振幅。实际操作中,可在岩石样品的两端放置一对超声换能器,测试超声波在岩石样品中的传播时间和波形,对其进行分析、计算获得岩石样品地震波衰减信息。
通过采集超声信号波形拾取初至旅行时,由
| $ v_{\mathrm{P}}=\frac{L}{T_{\mathrm{P}}} $ | (1) |
| $ v_{\mathrm{s}}=\frac{L}{T_{\mathrm{S}}} $ | (2) |
计算超声纵、横波速度。式中:L为样品长度;v、T分别为旅行时、速度,下标P、S分别代表纵波、横波。
通过测量给定材料参数,对比实验测量结果与给定材料参数的参考值之间的差异,以验证整套试验系统的测量精度。本次实验采用标准铝块进行超声标定实验,采用超声探头直接测量和超声探头嵌入探头模具间接测量两种方法。测量结果表明:两种方法得到的波形初至时间基本相同;由于探头模具增加了超声波传播距离,间接测量方法得到的波形振幅低于直接测量方法;两种方法得到的超声纵波速度基本相同(测量值为6430 m/s,参考值为6400 m/s),相对误差为0.5%,表明实验室测量结果精度较高。
2.3 实验与测井数据标定对比低频地震岩石物理测量系统能够直接测量地震频段的岩石弹性参数,对研究地震波传播特征及油气勘探、开发具有重要意义。分析LT1井、LT2井、LTx3井测井数据与实验结果(图 4)表明:①测井纵波速度值域范围为5330~5944 m/s,与实验结果的绝对误差范围为16~119 m/s;测井横波速度值域范围为3153~3710 m/s,与实验结果的绝对误差范围为31~156 m/s。②测井数据与实验结果的绝对误差相对较小,整体上实验值大于测井值。造成上述现象的原因为,基底岩石样品中发育大量微裂隙,当声波穿过含饱和流体岩石后,在微裂隙两端形成压力差引起微观尺度流体流动,造成岩石“干骨架”模量的改变。
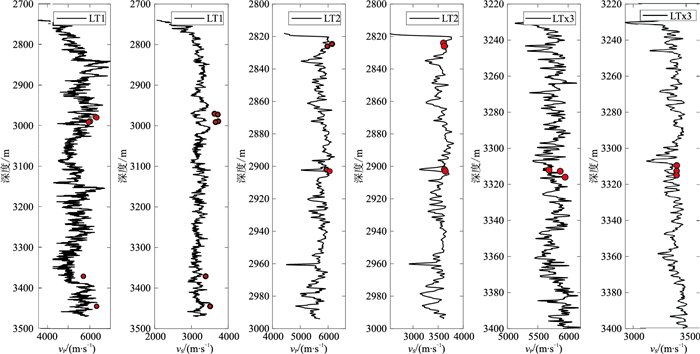
|
图 4 LT1井、LT2井、LTx3井测井数据(黑色曲线)与实验结果(红色点) |
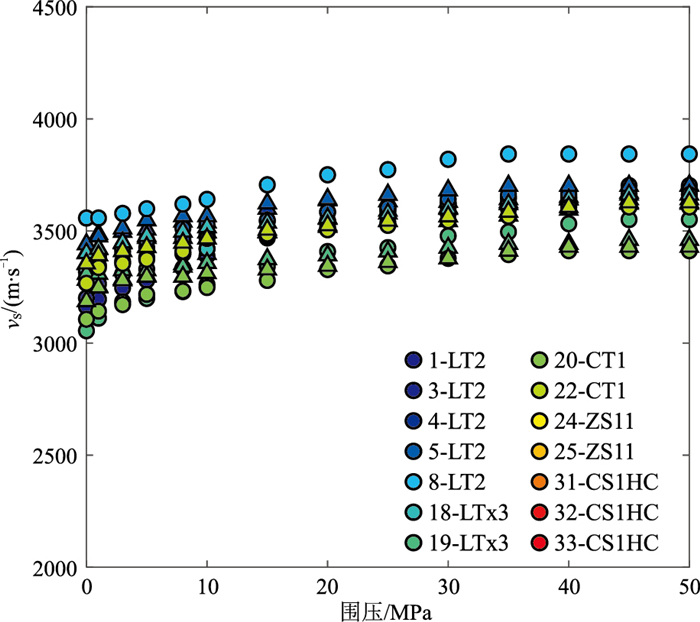
图 5、图 6分别为花岗岩类样品纵、横波速度随围压变化关系。由图可见,随着围压增加,在饱和流体状态下纵、横波速度均增大。具体表现为:①在气饱和状态下,随着围压增大,纵、横波速度呈非线性到线性变化的趋势,其中低压条件非线性关系明显,表明岩石样品发育大量微裂隙;随着压力增大、裂缝闭合,纵、横波速度呈线性变化趋势。②在水饱和状态下,纵、横波速度随围压呈明显的线性变化趋势,表明流体效应抑制了压力的影响。③整体上,在饱和流体状态下横波速度的变化量小(图 6),纵波速度的变化量相对较大(图 5)。
|
图 6 花岗岩类样品横波速度随围压变化关系 |
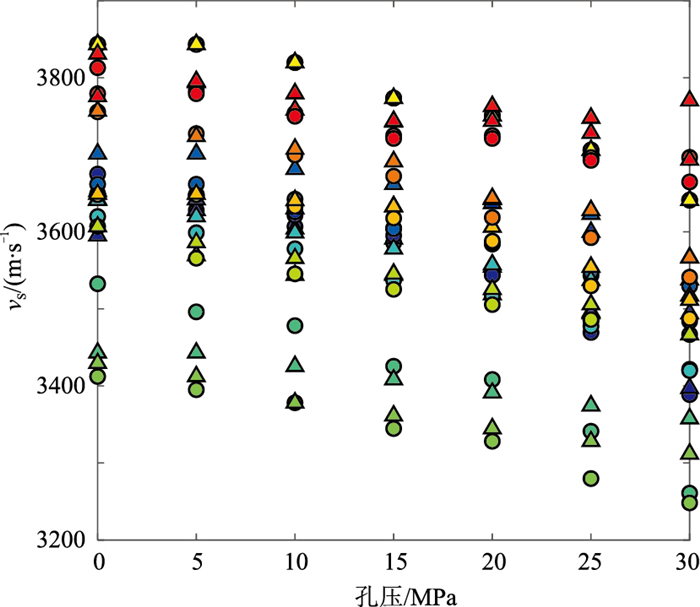
图 7、图 8分别为花岗岩类样品纵、横波速度速度随孔压变化关系。由图可见,随着孔压增大,在饱和流体状态下纵、横波速度均呈降低趋势。具体表现为:随着孔压增大,气饱和状态的纵波速度的变化量较水饱和状态大(图 7);在水饱和状态下,随着孔压增大纵波速度无明显的压力依赖性(图 7),横波速度的变化量较纵波速度小(图 8)。
|
图 8 花岗岩类样品横波速度随孔压变化关系 |
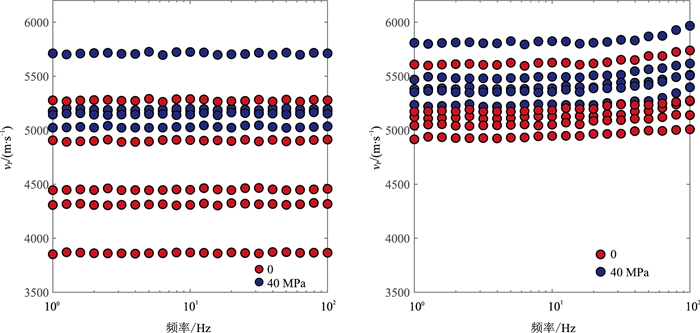
选用5块花岗岩类样和5块浅变质沉积岩样品,温度保持在20℃,围压从0逐渐增至40 MPa,在低频段测量不同流体饱和及不同压力条件的纵波速度随频率的变化。在测量过程中,为了确保岩石均匀受力,在每个压力点间均间隔30 min进行测试。测试结果表明:①花岗岩类(图 9)和浅变质沉积岩(图 10)的纵波速度随频率变化的趋势一致,由于花岗岩裂缝发育,导致整体上浅变质沉积岩的纵波速度变化量较花岗岩类小,说明利用纵波速度和纵波阻抗能较好地识别优质储层;②在气饱和状态下,速度没有发生明显的频散变化,随着压力增大,纵波速度具明显增大趋势(图 9左、图 10左);③在水饱和状态下,纵波速度发生频散变化,随着压力增大,频散范围逐渐向低频方向移动(图 9右、图 10右);④水饱和状态纵波速度的相对变化量(图 9右、图 10右)小于气饱和状态(图 9左、图 10左)。
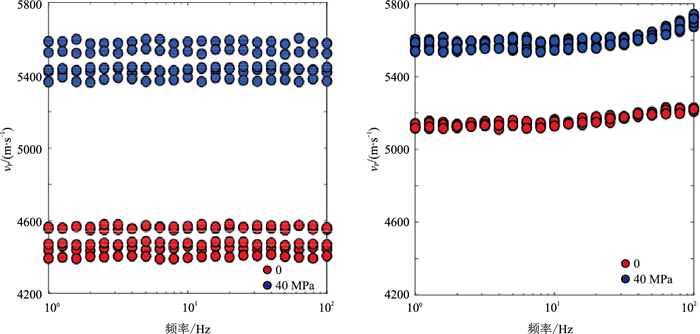
|
图 9 花岗岩类样品气饱和(左)、水饱和(右)状态的纵波速度随频率的变化。 |
|
图 10 浅变质沉积岩样品气饱和(左)、水饱和(右)状态的纵波速度随频率的变化 |
在气饱和状态下,对比、分析在超声频段和地震频段及不同压力条件下,岩样的纵、横波速度随孔隙度的变化关系。结果表明:①压力为40 MPa时纵、横波速度明显高于压力为0时。②随着孔隙度增加,纵波速度变化量增大。③在不同压力条件下,不同频段的纵、横波速度的变化趋势基本相同,其中低压条件的速度差异较高压条件大,这种速度差异变化指示微裂隙是影响频散绝对变化量主要因素;随着压力增大、微裂隙逐渐闭合,孔隙间的流体流动效应减弱,喷射效应降低。
利用David等[17]的方法计算花岗岩类样品的微裂隙参数等,分析在不同压力、流体饱和状态下纵波速度随微裂缝密度、微观孔隙纵横比及软孔隙度的变化规律。通过高压测量的纵、横波速度计算干岩石的体积模量Kstiff和剪切模量μstiff,利用Mori-Tanaka公式(1973)计算软孔隙的孔隙形状表达式Pc和Qc,此时岩石骨架的基质模量由Kstiff和μstiff代替
| $ K_{\mathrm{d}}=K_{\mathrm{stiff}}\left(1+\frac{\phi_{\mathrm{c}}}{1-\phi_{\mathrm{c}}} P_{\mathrm{c}}\right)^{-1} $ | (3) |
| $ \mu_{\mathrm{d}}=\mu_{\mathrm{stiff}}\left(1+\frac{\phi_{\mathrm{c}}}{1-\phi_{\mathrm{c}}} Q_{\mathrm{c}}\right)^{-1} $ | (4) |
式中:ϕc为软孔隙度;Kd和μd分别为干岩石样品的有效体积模量与等效剪切模量;Pc和Qc是以纵横比α为函数的软孔隙形状表达式。软孔隙的孔隙纵横比通常小于0.01,软孔隙的性质通常由裂隙密度εp决定,εp与ϕc的关系为
| $ \varepsilon_p=\frac{3 \phi_{\mathrm{c}}}{4 \pi \alpha} $ | (5) |
通过计算得到不同压力条件的εp,利用
| $ \varepsilon_p=\varepsilon_0 \mathrm{e}^{\frac{-p}{p^{\prime}}} $ | (6) |
拟合裂隙密度—压力关系式。式中:ε0为零压力条件的致密砂岩样品的初始裂隙密度;p为有效压力;p′为裂隙闭合压力。
以30号致密砂岩为例,利用式(6)拟合压力—裂隙密度关系图。利用
| $ \alpha^i=\frac{3}{4 \pi} \int_{\varepsilon_p(a)}^{\varepsilon_0} \frac{p^{\prime}\left[\frac{1}{K_{\mathrm{d}}\left(\varepsilon_p\right)}-\frac{1}{K_{\text {stiff }}}\right]}{\varepsilon_p^2} \mathrm{~d} \varepsilon_p $ | (7) |
计算最小初始纵横比αi。式中:Kd(εp)为干岩石体积模量;εp(α)为某一α对应的裂隙密度。
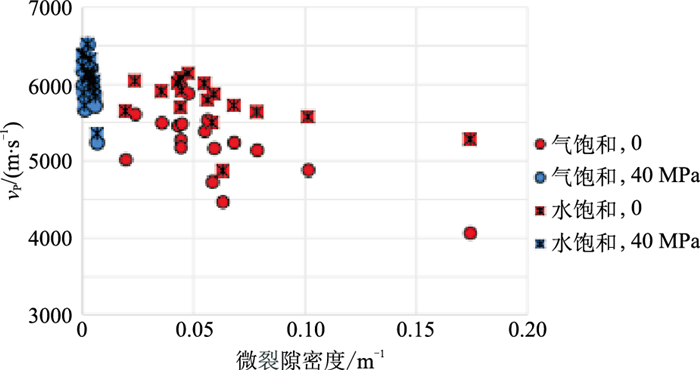
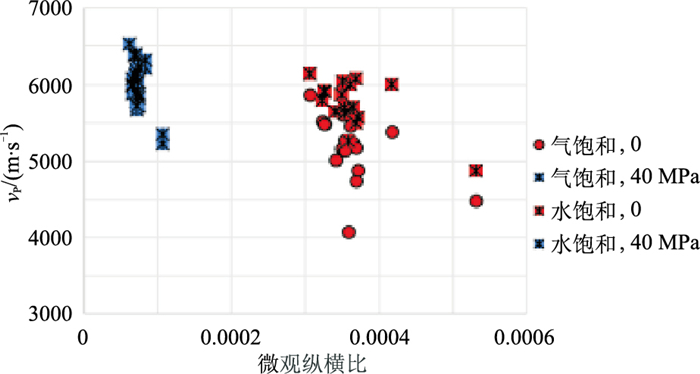
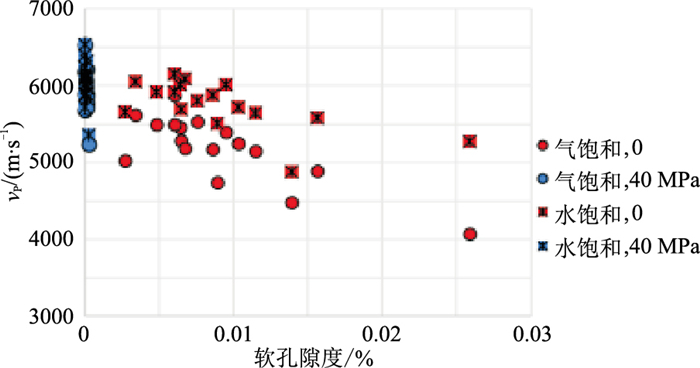
在低压条件下,花岗岩类的水饱和状态的纵波速度值明显高于气饱和状态(图 11~图 13)。随着压力增大,如在压力为40 MPa时,不同流体饱和状态的纵波速度差异较小,主要是由于基底储层裂缝较发育所致,即:在低压条件下,微裂隙密度、孔隙纵横比、软孔隙度较高、分布范围广;随着压力增大,微裂隙逐渐闭合,三种微裂隙参数较小,分布较集中。
|
图 11 不同压力和饱和状态的纵波速度与微裂隙密度的关系 |
|
图 12 不同压力和饱和状态的纵波速度与孔隙纵横比的关系 |
|
图 13 不同压力和饱和状态的纵波速度与软孔隙度的关系 |
为了研究在不同压力和不同流体(气、水)饱和状态下,孔隙度对主要物理参数的影响,对比、分析超声频段和地震频段岩石物理测量结果(图 14、图 15)。在压力为0时,纵、横波速度随孔隙度的变化趋势基本相同:压力越大,则纵、横波速度越大,孔隙度越大,导致纵、横波速度差异越大。在压力为40 MPa时,纵、横波速度随孔隙度呈线性变化趋势,岩样的裂缝基本闭合,饱和流体类型对弹性参数影响较小(图 14、图 15)。

|
图 14 不同压力的孔隙度与纵波速度关系 |
|
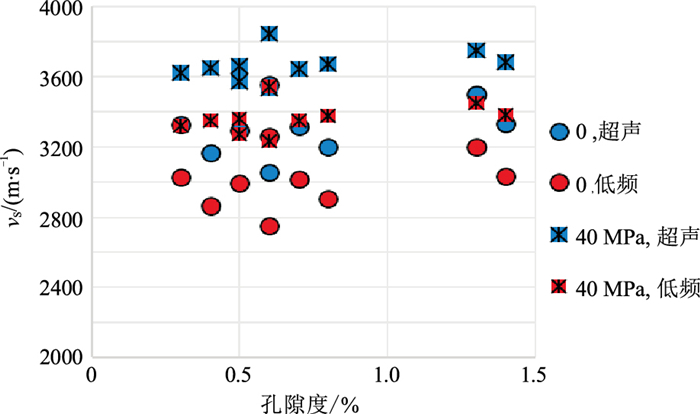
图 15 不同压力的孔隙度与横波速度关系 |
在压力为40 MPa时,测量、分析古中央隆起带基底岩样在不同饱和状态条件下,超声频段和地震频段纵、横波速度随孔隙度的变化关系(图 16、图 17)。不同频段弹性参数随孔隙度变化不明显。具体表现为:①在超声频段水饱和与气饱和的速度差异较大;②在地震频段水饱和与气饱和的速度差异较小;③孔隙度越大,气饱和纵波速度差异越大(图 16),横波速度差异较小(图 17),说明纵波速度对物性较敏感。
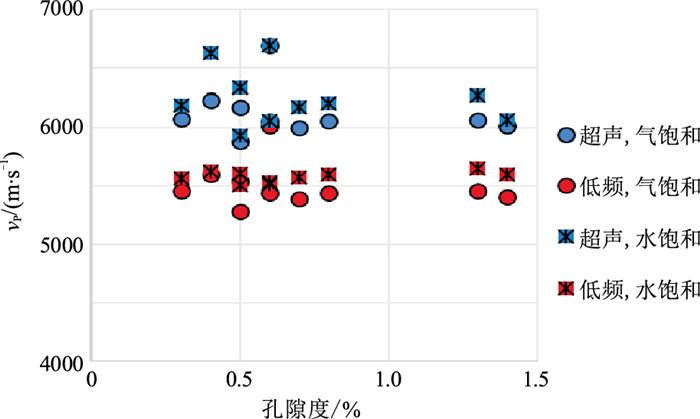
|
图 16 不同饱和状态的纵波速度与孔隙度的关系 |
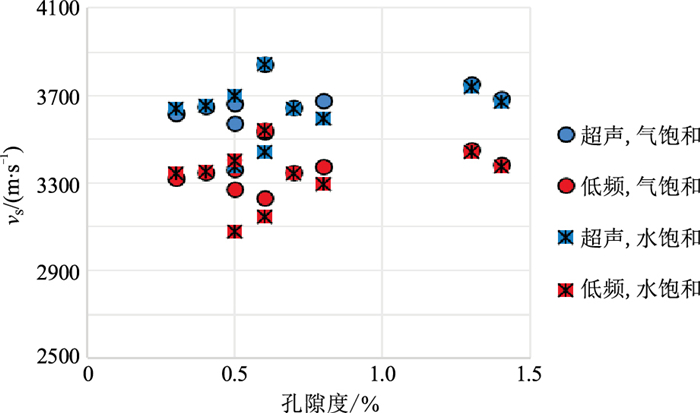
|
图 17 不同饱和状态的横波速度与孔隙度的关系 |
当岩性、孔隙流体性质、流体赋存空间发生改变时,不同的属性参数的变化是有差异的[18],这种差异为利用属性交会图技术识别孔隙流体以及岩性提供了客观依据。通常不能确定哪些属性参数对储层变化较敏感,故选择属性交会图存在一定困难。因此,需要定量评价属性参数对储层变化的敏感性,并描述特定储层参数与盖层参数的相对大小。可用流体指示因子Q定量刻画储层相对于盖层弹性参数的相对变化
| $ Q=\frac{A_{\mathrm{w}}-A_0}{\sigma_0} $ | (8) |
式中:Aw为储层属性参数平均值;A0为盖层属性参数平均值;σ0为盖层属性参数均方差。Q越大,说明属性参数对储层越敏感。
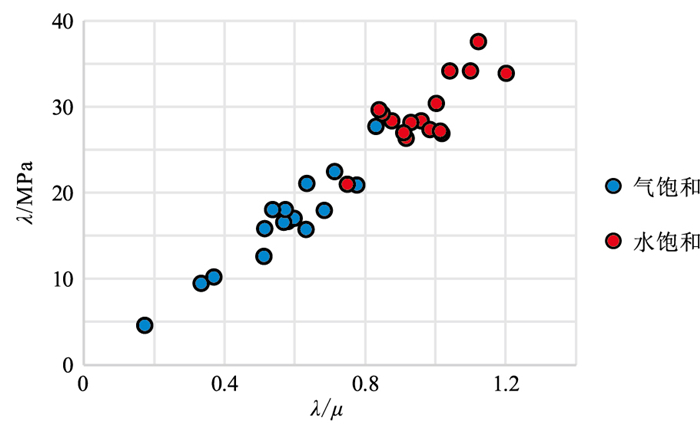
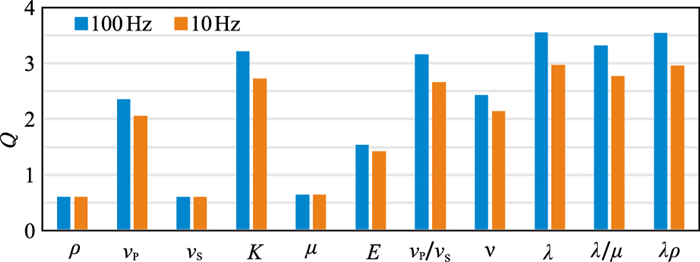
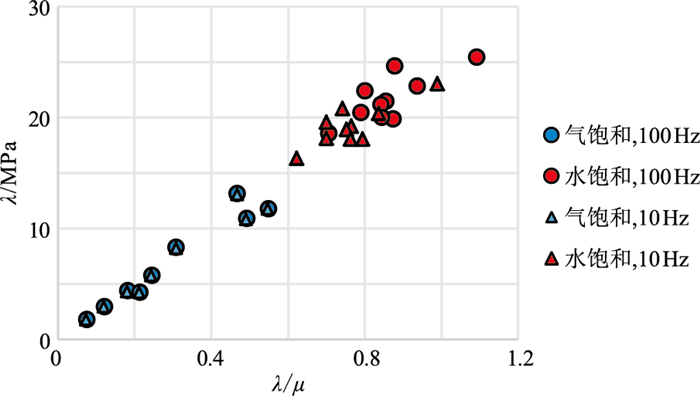
基于超声频段纵、横波速度及密度的实验测试结果计算其他弹性参数,通过计算多种弹性参数的Q(图 18),优选出对基底风化壳储层流体敏感的弹性参数vP/vS、ν、λ、λ/μ、λρ。超声频段λ-λ/μ(图 19)交会分析能有效区分饱和水和饱和气。对比、分析地震频段10 Hz和100 Hz测试结果表明,流体敏感参数与超声频段分析结果基本一致(图 20、图 21)。
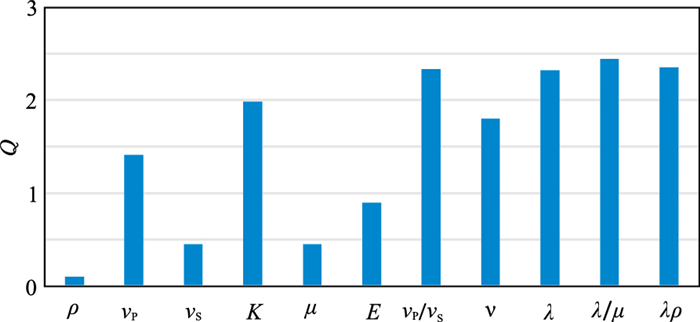
|
图 18 超声频段花岗岩类流体敏感性分析 E为杨氏模量,图 20同。 |
|
图 19 超声频段花岗岩类λ-λ/μ交会图 |
|
图 20 地震频段花岗岩类流体敏感性分析 |
|
图 21 地震频段花岗岩类λ-λ/μ交会图 |
刘晓晶等[19]基于Ruger的方位AVO反射系数近似方程推导了方位弹性阻抗方程,将裂缝介质的界面信息转化为地层内部的弹性信息,方位弹性阻抗差异体现了地层的各向异性。基底风化壳储层为孔隙—裂缝型储层,储集空间以裂缝为主,在裂缝密度为3条/m、裂缝倾角为50°的条件下,建立了饱和度—孔隙度解释图板(图 22)。可见:随着含水饱和度增大,纵波阻抗和λ/μ增加,当含水饱和度趋近1时,纵波阻抗快速上升;随着背景孔隙度减小,模型的纵波阻抗、λ/μ均逐渐升高;实际测井数据的大部分数据点集中分布于背景孔隙度小、含水饱和度大的区域,符合风化壳储层特征及岩石物理规律,确定了基底风化壳储层敏感弹性参数。

|
图 22 饱和度—孔隙度解释图板 Sw为含水饱和度。 |
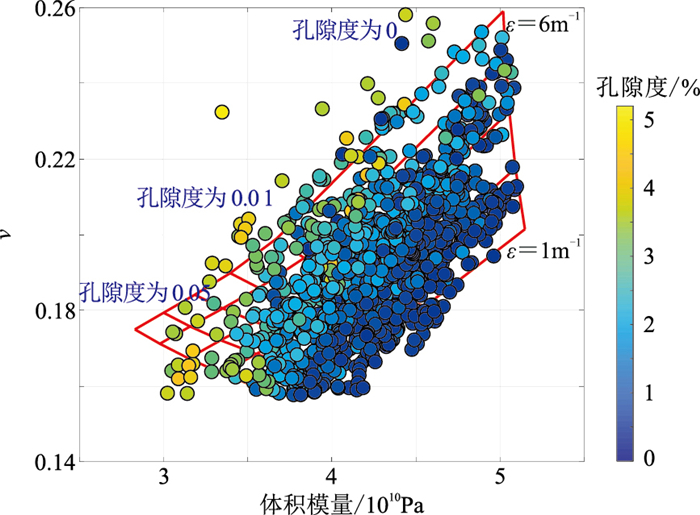
在含水饱和度为50%、裂缝倾角为50°的条件下建立了裂缝密度—孔隙度解释图板(图 23),裂缝密度指示范围为1~6条/m,背景孔隙度指示范围为0~0.05。可见:随着裂缝密度增大、背景孔隙度增大,泊松比、体积模量均逐渐下降;裂缝密度越大,对应的速度变化范围越大;LT2井的实际测井数据和图板数据的一致性很好。
|
图 23 裂缝密度—孔隙度解释图板 |
(1) 对松辽盆地北部古中央隆起带基底33块岩性样品,采用超声频段和地震频段实验测试,测得的标准铝块的超声频段纵波速度(6430 m/s)与参考值(6400 m/s)基本相同,相对误差为0.5%,精度较高。
(2) 随着围压增加,在水饱和和气饱和状态下纵、横波速度均增大,且横波速度变化不大。随着孔压增加,在水饱和和气饱和状态下纵、横波速度均呈降低趋势,且在气饱和状态下纵波速度的变化量大于水饱和状态,在水饱和和气饱和状态下横波速度的下降趋势相似。
(3) 对比、分析超声频段和地震频段在不同压力的速度差异表明:当压力为0时,超声频段和地震频段速度差异较大;当压力为40 MPa时,超声频段和地震频段速度差异减小。不同压力的超声频段和地震频段速度差异表明微裂隙是影响频散绝对变化量的主要因素,随着压力增加,微裂隙逐渐闭合,孔隙间的流体流动效应减弱,喷射效应降低。
(4) 地震频段和超声频段储层敏感参数优选结果相同,即vP/vS、ν、λ、λ/μ、λρ等参数对流体最敏感,可作为识别基底风化壳的储层敏感参数。
(5) 在裂缝密度为3条/m、裂缝倾角为50°的条件下建立了饱和度—孔隙度解释图板,在含水饱和度为50%、裂缝倾角为50°的条件下建立了裂缝密度—孔隙度解释图板,为风化壳孔隙—裂缝型储层预测奠定了理论基础。
| [1] |
冯志强. 松辽盆地庆深大型气田的勘探前景[J]. 天然气工业, 2006, 26(6): 1-5. FENG Zhiqiang. Exploration potential of large Qingshen gas field in the Songliao basin[J]. Natural Gas Industry, 2006, 26(6): 1-5. DOI:10.3321/j.issn:1000-0976.2006.06.001 |
| [2] |
姜传金, 陈树民, 初丽兰, 等. 徐家围子断陷营城组火山岩分布特征及火山喷发机制的新认识[J]. 岩石学报, 2010, 26(1): 63-72. JIANG Chuanjin, CHEN Shumin, CHU Lilan, et al. A new understanding about the volcanic distribution characteristics and eruption mechanism of Yingchen Formation in Xujiaweizi fault depression[J]. Acta Petrologica Sinica, 2010, 26(1): 63-72. |
| [3] |
姜传金, 冯肖宇, 詹怡捷, 等. 松辽盆地北部徐家围子断陷火山岩气藏勘探新技术[J]. 大庆石油地质与开发, 2007, 26(4): 133-137. JIANG Chuanjin, FENG Xiaoyu, ZHAN Yijie, et al. New methodology to explore gas-bearing volcanic re-servoir in Xujiaweizi Fault Depression of the northern Songliao Basin[J]. Petroleum Geology and Oilfield Development in Daqing, 2007, 26(4): 133-137. DOI:10.3969/j.issn.1000-3754.2007.04.034 |
| [4] |
YANG J, MAO H, CHANG X, et al. Mu-rho direct inversion for volcanic rock reservoir prediction: A case study of the Dinan Field, Junggar Basin[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 252-255.
|
| [5] |
WU Q, ZHAO H, LI L, et al. Analysis of rock physics reponse of gas-bearing volcanic reservoir based on three-phase poroelastic theory[J]. Applied Geophysics, 2008, 5(4): 277-283. DOI:10.1007/s11770-008-0035-1 |
| [6] |
陈树民, 李来林, 赵海波. 松辽盆地白垩系火山岩储层岩石物理声学特性分析[J]. 岩石学报, 2010, 26(1): 14-20. CHEN Shumin, LI Lailin, ZHAO Haibo. Physical analysis of acoustic characteristics of Cretaceous volcanic rocks in the Songliao basin[J]. Acta Petrologica Sinica, 2010, 26(1): 14-20. |
| [7] |
张丽华, 潘保芝, 单刚义, 等. 火山岩储层流体性质识别[J]. 石油地球物理勘探, 2008, 43(6): 728-730. ZHANG Lihua, PAN Baozhi, SHAN Gangyi, et al. Method for identifying fluid property in volcanite re-servoir[J]. Oil Geophysical Prespecting, 2008, 43(6): 728-730. DOI:10.3321/j.issn:1000-7210.2008.06.020 |
| [8] |
姜传金, 戴世立, 吴杰, 等. 松辽盆地北部营城组火山岩岩石弹性参数测试及特征分析[J]. 石油地球物理勘探, 2014, 49(5): 916-924. JIANG Chuanjin, DAI Shili, WU Jie, et al. Elastic parameter tests and characteristics analysis of volcanic rocks in Yingcheng Formation, Northern Songliao Basin[J]. Oil Geophysical Prespecting, 2014, 49(5): 916-924. |
| [9] |
邢文军, 吴开龙, 吴鑫, 等. 储层砂岩宽频段地震岩石物理特征的实验研究[J]. 地球物理学进展, 2018, 33(4): 1609-1616. XING Wenjun, WU Kailong, WU Xin, et al. Multi-frequency laboratory measurement of rock physics property on sandstone[J]. Progress in Geophysics, 2018, 33(4): 1609-1616. |
| [10] |
庞孟强, 巴晶, CARCIONE J M, 等. 致密砂岩衰减岩石物理图板分析: 储层微裂隙预测[J]. 地球物理学报, 2020, 63(11): 4205-4219. PANG Mengqiang, BA Jing, CARCIONE J M, et al. Analysis of attenuation rock-physics template of tight sandstones: Reservoir microcrack prediction[J]. Chinese Journal of Geophysics, 2020, 63(11): 4205-4219. |
| [11] |
龙腾, 赵建国, 刘欣泽, 等. 碳酸盐岩跨频段岩石物理测量与理论建模——不同孔隙结构对碳酸盐岩频散与衰减的影响研究[J]. 地球物理学报, 2020, 63(12): 4502-4516. LONG Teng, ZHAO Jianguo, LIU Xinze, et al. Cro-ss-band rock physics measurement and theoretical mo-deling of carbonate rocks: Study on the effect of diffe-rent pore structures on the dispersion and attenuation of carbonate rocks[J]. Chinese Journal of Geophysics, 2020, 63(12): 4502-4516. |
| [12] |
李闯, 赵建国, 王宏斌, 等. 致密碳酸盐岩跨频段岩石物理实验及频散分析[J]. 地球物理学报, 2020, 63(2): 627-637. LI Chuang, ZHAO Jianguo, WANG Hongbin, et al. Multi-frequency rock physics measurements and dispersion analysis on tight carbonate rocks[J]. Chinese Journal of Geophysics, 2020, 63(2): 627-637. |
| [13] |
MAVKO G, MUKERGI T and DVORIKIN J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media[M]. Cambridge University, 1998.
|
| [14] |
WANG Z. Fundamentals of seismic rock physics[J]. Geophysics, 2001, 66(2): 398-412. |
| [15] |
KING M S. Rock-physics developments in seismic exploration: A personal 50-year perspective[J]. Geophysics, 2005, 70(6): 3ND-8ND. |
| [16] |
刘浩杰. 地震岩石物理研究综述[J]. 油气地球物理, 2009, 7(3): 1-8. LIU Haojie. Summarization of seismic rock physics research[J]. Petroleum Geophysics, 2009, 7(3): 1-8. |
| [17] |
DAVID E C, ZIMMERMAN R W. Pore structure model for elastic wave velocities in fluid- saturated sand-stones[J]. Journal of Geophysical Research, 2012, 117(B7): 1-15. |
| [18] |
王迪, 张益明, 牛聪, 等. 储层敏感流体因子反演及烃类检测[J]. 石油地球物理勘探, 2021, 56(1): 146-154. WANG Di, ZHANG Yiming, NIU Cong, et al. Reservoir sensitive fluid factor inversion and its application in hydrocarbon detection[J]. Oil Geophysical Prospecting, 2021, 56(1): 146-154. |
| [19] |
刘晓晶, 陈祖庆, 陈超, 等. 方位弹性阻抗傅里叶级数裂缝预测方法[J]. 石油地球物理勘探, 2022, 57(2): 423-433. LIU Xiaojing, CHEN Zuqing, CHEN Chao, et al. Fracture prediction method based on Fourier series of azimuthal elastic impedance[J]. Oil Geophysical Prospecting, 2022, 57(2): 423-433. |



 戴世立, 黑龙江省大庆市让胡路区科苑路中国石油大庆油田有限责任公司勘探开发研究院, 163712。Email:
戴世立, 黑龙江省大庆市让胡路区科苑路中国石油大庆油田有限责任公司勘探开发研究院, 163712。Email: