2. 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580
2. School of Geosciences, China University of Petroleum (East China), Qingdao, Shandong 266580, China
能源是国民经济发展的重要支撑,能源安全直接影响国家安全、可持续发展以及社会稳定。近年来,油气勘探、开发不断向深水、深地、非常规等复杂油气领域推进,油气藏特征更复杂,其中最典型的裂缝型储层油气识别成为研究前沿和世界级难题。五维数据反演是以宽方位地震五维数据为基础的反演,五维数据是通过炮检距向量片(Offset Vector Tile,OVT)技术处理宽方位地震(横向与纵向排列尺度的比值大于0.5的地震勘探系统)资料得到的道集资料,其显著特点是同时包含高品质炮检距和方位角信息(即空间三维坐标+炮检距+方位角)[1]。五维数据中丰富的方位角及炮检距等信息为裂缝型储层地震预测及油气识别奠定了资料基础,但在实际裂缝型储层五维数据解释方面仍存在挑战[1],瓶颈在于现有裂缝型储层流体识别方法在构建流体敏感参数过程中没有考虑岩石骨架、油气水及裂缝、孔隙(“固液缝”)耦合影响,对五维数据中丰富的方位信息蕴含的流体信息挖掘不够,并且针对裂缝型储层油气识别以间接计算参数为主[2-4]。业界主要针对裂缝型储层地震岩石物理流体因子构建及油气识别方法开展了大量基础研究与应用[5-9]。
裂缝型储层地震流体识别的关键是流体因子构建。基于地震岩石物理模型及储层流体地震响应分析,可将孔隙及裂缝对流体的异常特性表征为各向异性流体因子,进而判识非常规储层含流体类型。人们基于岩石物理理论或裂缝各向异性理论等从不同角度构建了不同的流体敏感参数[10-11],并研究地震信息与流体类型之间的关系,推导地震反射系数与流体敏感参数之间的关系进而由反演预测流体[12-17]。目前利用五维数据研究裂缝型储层含油气性大多以常规油气识别方法在裂缝型储层中的拓展应用为主,包括利用各向异性Gassmann孔隙弹性理论流体体积模量识别含油气性[18-19]以及基于各向异性Gassmann孔隙弹性理论和线性滑动理论构建各向异性流体因子[20]。上述方法从岩石物理及各向异性机理出发构建综合考虑“固液缝”解耦的流体因子,为裂缝型储层各向异性流体识别提供了新途径,本文基于流体因子研究直接反演储层参数的方法。
由于裂缝型储层的特殊性及地下埋藏条件的复杂性,给裂缝型储层流体识别带来挑战。宽方位地震五维数据反演问题本身存在“病态解”及“不确定性”等问题,多裂缝参数同时反演更易导致储层参数反演精度下降。因此,基于间接代数组合的流体因子在计算过程中不可避免地累积计算误差,影响油气识别效果[6-7, 20]。为了有效地结合叠前地震反演与流体识别,人们广泛研究了流体因子直接反演问题,主要包括推导包含流体因子的反射系数线性近似公式及研究直接反演方法[18-19, 21-24]等。针对裂缝型储层,弹性阻抗反演和基于贝叶斯框架的AVAZ反演[25-30]是常用的直接反演方法,除单纯利用地震时间域纵波信号反演外,还包括多波联合反演及非线性反演方法。基于贝叶斯框架的地震反演算法,采取不同的反演策略,充分利用五维数据中多波的特征信息(振幅、频率及相位)直接获取表征储层流体信息异常特性的流体敏感参数,是裂缝型储层流体识别的主要目的。
本文根据裂缝型储层岩石物理及各向异性理论,推导由“固液缝”解耦流体因子直接表征的裂缝型储层方位地震反射系数方程,分析模型的适用条件,从理论上阐明采用该方程获取“固液缝”解耦流体因子的可行性。提出了“固液缝”解耦油气识别方法,采用五维数据时频联合反演方法,基于振幅—频率联合反演策略,在贝叶斯理论框架下构建五维数据振幅—频率联合反演目标泛函,综合利用五维数据的频率和振幅信息及测井、地质资料直接获取“固液缝”解耦流体因子,消除因参数间接运算的累计误差引起的流体识别假象。模型测试及实际资料研究表明,该方法可提高流体识别精度,利用五维数据可直接识别裂缝型储层油气。
1 方法原理 1.1 裂缝型储层“固液缝”解耦流体因子刚度矩阵构建及分析Gurevich[31]在Schoenberg线性滑动模型的基础上,考虑裂缝与背景基质孔隙间的流体流动效应,将各向异性Gassmann方程改写为
| $ C_{i j}^{\text {sat }}=C_{i j}^{\mathrm{dry}}+\beta_i \beta_j K^* \quad i, j=1, \cdots, 6 $ | (1) |
式中:Cijsat为饱和流体裂缝岩石的等效刚度弹性矩阵元素;Cijdry为干裂缝岩石的等效刚度弹性矩阵元素;K*为各向异性Gassmann孔隙空间模量;βi和βj均为各向异性Biot系数,统一用βm表示为
| $ \left\{\begin{array}{l} \beta_m=\left(1-\frac{\sum\limits_{n=1}^3 C_{m n}^{\mathrm{dry}}}{3 K_{\mathrm{g}}}\right) \vartheta_m \\ \vartheta_m= \begin{cases}1 & m=1, 2, 3 \\ 0 & m=4, 5, 6\end{cases} \end{array}\right. $ | (2) |
式中Kg为固体矿物颗粒等效体积模量。
式(1)中K*与干裂缝岩石刚度矩阵有关,结合线性滑动理论,有
| $ K^*=\frac{K_{\mathrm{g}}}{1-\phi-\left(1-\alpha_0\right)\left(1-\frac{K_{\mathrm{d}}}{M_{\mathrm{d}}} \delta_{\mathrm{N}}\right)+\phi \frac{K_{\mathrm{g}}}{K_{\mathrm{f}}}} $ | (3) |
式中:ϕ为总孔隙度;Kf为流体体积模量;Kd为背景干岩石有效体积模量;Md为干岩石纵波模量;α0为各向同性Biot系数;δN为法向裂隙弱度。
将式(2)、式(3)代入式(1),可得含孔隙裂缝介质饱和流体时的刚度矩阵解析表达式
| $ \boldsymbol{C}_{\mathrm{HTI}}^{\text {sat }}=\left(\begin{array}{cccccc} C_{11}^{\text {sat }} & C_{13}^{\text {sat }} & C_{13}^{\text {sat }} & 0 & 0 & 0 \\ C_{13}^{\text {sat }} & C_{33}^{\text {sat }} & C_{23}^{\text {sat }} & 0 & 0 & 0 \\ C_{13}^{\text {sat }} & C_{23}^{\text {sat }} & C_{33}^{\text {sat }} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44}^{\text {sat }} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{55}^{\text {sat }} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{55}^{\text {sat }} \end{array}\right) $ | (4) |
其中
| $ \left\{\begin{array}{l} C_{11}^{\mathrm{sat}}=M_{\mathrm{d}}\left(1-\delta_{\mathrm{N}}\right)+\frac{\alpha_0^2}{\phi} K_{\mathrm{f}}+\frac{2 \alpha_0\left(1-\alpha_0\right)}{\phi} K_{\mathrm{f}} \delta_{\mathrm{N}} \\ C_{13}^{\mathrm{sat}}=\lambda_{\mathrm{d}}\left(1-\delta_{\mathrm{N}}\right)+\frac{\alpha_0^2}{\phi} K_{\mathrm{f}}+\frac{\alpha_0\left(1-\alpha_0\right)}{\phi} K_{\mathrm{f}}(1+\chi) \delta_{\mathrm{N}} \\ C_{23}^{\mathrm{sat}}=\lambda_{\mathrm{d}}\left(1-\chi \delta_{\mathrm{N}}\right)+\frac{\alpha_0^2}{\phi} K_{\mathrm{f}}+\frac{2 \alpha_0\left(1-\alpha_0\right)}{\phi} K_{\mathrm{f}} \chi \delta_{\mathrm{N}} \\ C_{33}^{\mathrm{sat}}=M_{\mathrm{d}}\left(1-\chi^2 \delta_{\mathrm{N}}\right)+\frac{\alpha_0^2}{\phi} K_{\mathrm{f}}+\frac{2 \alpha_0\left(1-\alpha_0\right)}{\phi} K_{\mathrm{f}} \chi \delta_{\mathrm{N}} \\ C_{44}^{\mathrm{sat}}=\mu \\ C_{55}^{\mathrm{sat}}=\mu\left(1-\delta_{\mathrm{T}}\right) \end{array}\right. $ | (5) |
式中:χ=λd/Md,Md和λd分别为干燥岩石纵波模量和拉梅参数;μ为剪切模量;δT为切向裂隙弱度。
令
| $ f_{\text {ani }}=K_{\mathrm{f}} G(\phi)+2 F(\phi) K_{\mathrm{f}} \chi \delta_{\mathrm{N}} $ | (6) |
将式(6)代入式(4),有
| $ \left\{\begin{aligned} C_{11}^{\mathrm{sat}} \approx & M_{\mathrm{d}}\left(1-\delta_{\mathrm{N}}\right)+f_{\mathrm{ani}}+2 F(\phi) K_{\mathrm{f}}(1-\chi) \delta_{\mathrm{N}} \\ C_{12}^{\mathrm{sat}}= & C_{13}^{\mathrm{sat}} \approx \lambda_{\mathrm{d}}\left(1-\delta_{\mathrm{N}}\right)+f_{\mathrm{ani}}+ \\ & F(\phi) K_{\mathrm{f}}(1-\chi) \delta_{\mathrm{N}} \\ C_{22}^{\mathrm{sat}}= & C_{33}^{\mathrm{sat}} \approx M_{\mathrm{d}}\left(1-\chi^2 \delta_{\mathrm{N}}\right)+f_{\mathrm{ani}} \\ C_{23}^{\mathrm{sat}} \approx & \lambda_{\mathrm{d}}\left(1-\chi^2 \delta_{\mathrm{N}}\right)+f_{\mathrm{ani}} \\ C_{44}^{\mathrm{sat}}= & \mu \\ C_{55}^{\mathrm{sat}}= & C_{66}^{\mathrm{sat}}=\mu\left(1-\delta_{\mathrm{T}}\right) \end{aligned}\right. $ | (7) |
为了验证弱各向异性近似刚度参数(式(7))的精度,对比式(7)与精确刚度参数(式(5))的计算结果。假定裂缝型储层模型(岩石由石英和黏土组成,比例为2∶1,含水饱和度分别为30%和70%)裂隙饱含气和水,使用Wood公式计算混合流体模量,并使用VRH方程计算矿物的平均模量。
图 1为不同含气饱和度条件下裂缝型储层模型的刚度参数计算结果。由图可见:①在含气饱和度Sg相同情况下(图 1a与图 1b、图 1c与图 1d),δN越小,则式(7)计算结果越准确,故式(7)更适用于弱各向异性介质;②在δN相同情况下(图 1a与图 1c、图 1b与图 1d),Sg越大,则式(7)计算结果越准确,故式(7)更适用于含气(低体积模量)裂缝型储层。

|
图 1 不同含气饱和度条件下裂缝型储层模型的刚度参数计算结果 (a)Sg=0.2, δN=0.05;(b)Sg=0.2, δN=0.1;(c)Sg=0.8, δN=0.05;(d)Sg=0.8, δN=0.1 |
式(7)是各向同性介质中含一组定向排列的垂直裂缝形成的等效HTI介质饱和流体弹性刚度参数。在此基础上,考虑反射界面两侧弹性参数弱差值近似及弱各向异性近似(即
| $ \Delta \boldsymbol{C}_{\mathrm{HTI}}^{\mathrm{sat}}=\left(\begin{array}{cccccc} \Delta C_{11}^{\mathrm{sat}} & \Delta C_{12}^{\mathrm{sat}} & \Delta C_{13}^{\mathrm{sat}} & 0 & 0 & 0 \\ \Delta C_{12}^{\mathrm{sat}} & \Delta C_{22}^{\mathrm{sat}} & \Delta C_{23}^{\mathrm{sat}} & 0 & 0 & 0 \\ \Delta C_{13}^{\mathrm{sat}} & \Delta C_{23}^{\mathrm{sat}} & \Delta C_{33}^{\mathrm{sat}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \Delta C_{44}^{\mathrm{sat}} & 0 & 0 \\ 0 & 0 & 0 & 0 & \Delta C_{55}^{\mathrm{sat}} & 0 \\ 0 & 0 & 0 & 0 & 0 & \Delta C_{66}^{\text {sat }} \end{array}\right) $ | (8) |
其中
| $ \left\{\begin{aligned} \Delta C_{11}^{\mathrm{sat}} \approx & \Delta M_{\mathrm{d}}-M_{\mathrm{d}} \Delta \delta_{\mathrm{N}}+\Delta f_{\text {ani }}+2 F(\phi) K_{\mathrm{f}}(1-\chi) \Delta \delta_{\mathrm{N}} \\ \Delta C_{12}^{\text {sat }}= & \Delta C_{13}^{\text {sat }} \approx \Delta \lambda_{\mathrm{d}}-\lambda_{\mathrm{d}} \Delta \delta_{\mathrm{N}}+\Delta f_{\text {ani }}+ \\ & F(\phi) K_{\mathrm{f}}(1-\chi) \Delta \delta_{\mathrm{N}} \\ \Delta C_{22}^{\text {sat }}= & \Delta C_{33}^{\text {sat }} \approx \Delta M_{\mathrm{d}}-M_{\mathrm{d}} \chi^2 \Delta \delta_{\mathrm{N}}+\Delta f_{\text {ani }} \\ \Delta C_{23}^{\text {sat }} \approx & \lambda_{\mathrm{d}}-M_{\mathrm{d}} \chi^2 \Delta \delta_{\mathrm{N}}+\Delta f_{\text {ani }} \\ \Delta C_{44}^{\text {sat }}= & \Delta \mu \\ \Delta C_{55}^{\text {sat }}= & \Delta C_{66}^{\text {sat }}=\Delta \mu-\mu \Delta \delta_{\mathrm{T}} \end{aligned}\right. $ |
基于Born积分和稳相方法[21],反射系数与散射函数之间的关系可简单表示为
| $ R_{\mathrm{PP}}(\theta)=\frac{1}{4 \rho \cos ^2 \theta}\left(\Delta \rho \xi^{\mathrm{PP}}+\sum\limits_{i=1}^6 \sum\limits_{j=1}^6 \Delta C_{i j}^{\mathrm{Cat}} \eta_{\mathrm{pp}}^{\mathrm{pp}}\right) $ | (9) |
式中:θ为地震波入射角;ρ为介质密度;ΔCijsat为扰动刚度参数;ξPP和ηijpp可由入射PP波、散射PP波的慢度和极化矢量表示。
将式(8)代入式(9)可以得到(附录A)
| $ \begin{aligned} & R_{\mathrm{PP}}(\theta, \varphi)=a(\theta) \frac{\Delta M_{\mathrm{d}}}{M_{\mathrm{d}}}+b(\theta) \frac{\Delta \mu}{\mu}+c(\theta) \frac{\Delta \rho}{\rho}+ \\ & d(\theta) \frac{\Delta f_{\mathrm{ani}}}{f_{\mathrm{ani}}}+e(\theta, \varphi) \Delta \delta_{\mathrm{N}}+f(\theta, \varphi) \Delta \delta_{\mathrm{T}} \end{aligned} $ | (10) |
其中
| $ \begin{aligned} & a(\theta)=\frac{\gamma_{\mathrm{dry}}^2}{\gamma_{\mathrm{sat}}^2} \frac{\sec ^2 \theta}{4} ; b(\theta)=-\frac{2}{\gamma_{\mathrm{sat}}^2} \sin ^2 \theta \\ & c(\theta)=\frac{1}{2}-\frac{\sec ^2 \theta}{4} ; d(\theta)=\left(1-\frac{\gamma_{\mathrm{dry}}^2}{\gamma_{\mathrm{sat}}^2}\right) \frac{\sec ^2 \theta}{4} \\ & e(\theta, \varphi)=-\frac{\gamma_{\mathrm{dry}}^2}{\gamma_{\mathrm{sat}}^2} \frac{\sec ^2 \theta}{4}\left[\frac{2}{\gamma_{\mathrm{sat}}^2}\left(1-\sin ^2 \theta \cos ^2 \varphi\right)-1\right]^2 \\ & f(\theta, \varphi)=\frac{1}{\gamma_{\mathrm{sat}}^2} \cos ^2 \varphi \sin ^2 \theta\left(1-\tan ^2 \theta \sin ^2 \varphi\right) \end{aligned} $ |
式中:φ为方位角;ΔMd、Δμ、Δρ、Δfani、ΔδN和ΔδT分别为介质扰动参数;γsat2=Ms/μ,γdry2=Md/μ,Ms为含水岩石纵波模量,通过计算井上数据得到。
图 2为Md、μ、ρ、fani、δN及δT扰动变化对RPP的影响,由图可见:fani扰动(图 2d)在θ≤40°范围内对RPP均有贡献,因此可很好地反演fani;Md(图 2a)和μ(图 2b)扰动几乎在所有θ对RPP均有贡献;相比而言,ρ扰动(图 2c)在小θ才对RPP有贡献,而在大θ几乎没有任何贡献;不同θ、φ的δN(图 2e)与δT(图 2f)扰动对RPP贡献较小,但对大θ数据较敏感。因此大入射角或远炮检距数据更利于反演裂缝弱度。

|
图 2 Md(a)、μ(b)、ρ(c)、fani(d)、δN(e)及δT(f)扰动变化对RPP的影响 ΔMd/Md、Δμ/μ、Δρ/ρ、Δfani/fani、ΔδN/δN及ΔδT/δT的取值范围均为[-0.1, 0.1],间隔为0.05。 |
对于五维数据,时间域和频率域地震反演分别考虑不同域中的地震响应与模型合成地震记录的匹配程度,进而搜索拟合数据空间的最优模型参数。时间域地震反演的抗噪性较频率域强,但是时间域地震反演的分辨率不及频率域。为保持频率域地震反演的高分辨率优良特性和解决频率域地震信号对噪声敏感的问题,充分利用带限地震信号的时间域和频率域信息,利用傅里叶变换将地震道由时间域变换到频率域,然后综合时间域和频率域响应特征发展基于贝叶斯框架的时间—频率域联合反演方法。
将式(10)的背景介质参数的相对差值取自然对数近似替换相对差值,即ΔMd/Md≈Δ(lnMd)、Δμ/μ≈Δ(lnμ)、Δρ/ρ≈Δ(lnρ)和Δfani/fani≈Δ(lnfani),假设背景介质参数与裂缝参数变化连续且扰动范围较小,则Δ(lnMd)≈d(lnMd)、Δ(lnμ)≈d(lnμ)和Δ(lnρ)≈d(lnρ),且ΔδN≈dδN、ΔδT≈dδT。
将式(10)分别与时间域和频率域地震子波褶积,得到时间域正演方程
| $ \begin{aligned} & S(t)=W(t) a_{M_{\mathrm{d}}}(\theta) D \ln M_{\mathrm{d}}+W(t) a_\mu(\theta) D \ln \mu+ \\ & W(t) a_\rho(\theta) D \ln \rho+W(t) a_{f_{\mathrm{ani}}}(\theta) D \ln f_{\mathrm{ani}}+ \\ & W(t) a_{\delta_{\mathrm{N}}}(\theta, \varphi) D \delta_{\mathrm{N}}+W(t) a_{\delta_{\mathrm{T}}}(\theta, \varphi) D \delta_{\mathrm{T}} \end{aligned} $ | (11) |
和频率域正演方程
| $ \begin{aligned} & S^{\prime}(\omega)=W^{\prime}(\omega) E a_{M_{\mathrm{d}}}(\theta) D \ln M_{\mathrm{d}}+W^{\prime}(\omega) E a_\mu(\theta) D \ln \mu+ \\ & W^{\prime}(\omega) E a_\rho(\theta) D \ln \rho+W^{\prime}(\omega) E a_{f_{\mathrm{ani}}}(\theta) D \ln f_{\mathrm{ani}}+ \\ & W^{\prime}(\omega) E a_{\delta_{\mathrm{N}}}(\theta, \varphi) D \delta_{\mathrm{N}}+W^{\prime}(\omega) E a_{\delta_{\mathrm{T}}}(\theta, \varphi) D \delta_{\mathrm{T}} \end{aligned} $ | (12) |
式中:S(t)和S′(ω)分别为时间域、频率域地震记录,t为时间,ω为角频率;W(t)和W′(ω)分别为时间域、频率域子波;aMd(θ)、aμ(θ)、aρ(θ)、afani(θ)、aδN(θ, φ)以及aδT(θ, φ)分别对应式(10)中的系数项;E为傅里叶算子;D为差分算子。
将式(11)和式(12)写成矩阵形式
| $ \left(\begin{array}{c} \boldsymbol{S}(t) \\ \boldsymbol{S}^{\prime}(\omega) \end{array}\right)=\left(\begin{array}{cc} \boldsymbol{G}_{\text {iso }}(t) & \boldsymbol{G}_{\text {ani }}(t) \\ \boldsymbol{G}_{\text {iso }}^{\prime}(\omega) & \boldsymbol{G}_{\text {ani }}^{\prime}(\omega) \end{array}\right)\left(\begin{array}{c} \boldsymbol{m}_{\text {iso }} \\ \boldsymbol{m}_{\text {ani }} \end{array}\right) $ | (13) |
式中:Giso (t)、Giso′ (ω)分别为时间域、频率域各向同性正演算子;Gani (t)、Gani′ (ω)分别为时间域、频率域各向异性正演算子;miso、mani分别为各向同性、各向异性模型参数矩阵。
在贝叶斯框架下,基于五维数据时频域分步反演算法,借助目标参数协方差矩阵Ccov的特征值和特征向量U处理Giso (t)、Giso′ (ω)、Gani (t)、Gani′ (ω)及miso、mani,提高待反演参数稳定性,利用奇异值分解Ccov=UΣUT得到U和特征值正定矩阵Σ,即
| $ \begin{aligned} & \left(\begin{array}{ll} \widetilde{\boldsymbol{G}}_{\text {iso }}(t) & \widetilde{\boldsymbol{G}}_{\mathrm{ani}}(t) \\ \widetilde{\boldsymbol{G}}'_{\mathrm{iso}}(\omega) & \widetilde{\boldsymbol{G}'}_{\mathrm{ani}}(\omega) \end{array}\right)= \\ & \left(\begin{array}{cc} \boldsymbol{G}_{\text {iso }}(t) & \boldsymbol{G}_{\text {ani }}(t) \\ \boldsymbol{G}'_{\text {iso }}(\omega) & \boldsymbol{G}'_{\text {ani }}(\omega) \end{array}\right)\left(\operatorname{kron}\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{-\frac{1}{2}} \boldsymbol{U}^{\mathrm{T}}, \boldsymbol{I}_L\right)\right)^{-1} \\ & \end{aligned} $ | (14) |
| $ \left(\begin{array}{c} \widetilde{\boldsymbol{m}}_{\text {iso }} \\ \widetilde{\boldsymbol{m}}_{\text {ani }} \end{array}\right)=\left(\mathrm{kron}\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{-\frac{1}{2}} \boldsymbol{U}^{\mathrm{T}}, \boldsymbol{I}_L\right)\right)\left(\begin{array}{c} \boldsymbol{m}_{\text {iso }} \\ \boldsymbol{m}_{\text {ani }} \end{array}\right) $ | (15) |
因此,地震记录可以写为
| $ \left(\begin{array}{c}\boldsymbol{S}(t) \\ \boldsymbol{S}^{\prime}(\omega)\end{array}\right)=\left(\begin{array}{cc}\widetilde{\boldsymbol{G}}_{\text {iso }}(t) & \widetilde{\boldsymbol{G}}_{\text {ani }}(t) \\ \widetilde{\boldsymbol{G}}_{\text {iso }}^{\prime}(\omega) & \widetilde{\boldsymbol{G}}'_{\text {ani }}(\omega)\end{array}\right)\left(\begin{array}{l}\widetilde{\boldsymbol{m}}_{\text {iso }} \\ \widetilde{\boldsymbol{m}}_{\text {ani }}\end{array}\right) $ | (16) |
式中:kron(·)为Kronecker乘积算子;IL为L阶单位矩阵,L为井曲线采样点数。构建协方差矩阵的方式有多种,本文由统计测井数据获得。在贝叶斯框架下,构建五维数据时频域分步反演目标泛函
| $ \begin{aligned} & F(\tilde{\boldsymbol{m}})=(\boldsymbol{S}-\boldsymbol{G} \tilde{\boldsymbol{m}})^{\mathrm{T}}(\boldsymbol{S}-\boldsymbol{G} \tilde{\boldsymbol{m}})+(\boldsymbol{S}-\widetilde{\boldsymbol{G}} \tilde{\boldsymbol{m}})^{\mathrm{T}}(\boldsymbol{S}'-\boldsymbol{G} \tilde{\boldsymbol{m}})+ \\ & 2 \sigma^2 \sum\limits_{i=1}^6 \ln \left(1+\frac{\widetilde{\boldsymbol{m}}_i^2}{\sigma^2}\right)+\sum\limits_{i=1}^6 \lambda_i\left(\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i-\widetilde{\boldsymbol{P}}_i \widetilde{\boldsymbol{m}}_i\right)^{\mathrm{T}}\left(\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i-\widetilde{\boldsymbol{P}}_i \widetilde{\boldsymbol{m}}_i\right) \end{aligned} $ | (17) |
| $\begin{aligned} & F(\tilde{\boldsymbol{m}})_{\mathrm{ani}}=\left(\boldsymbol{S}-\boldsymbol{S}_{\mathrm{iso}}-\boldsymbol{G} \widetilde{\boldsymbol{m}}_{\mathrm{ani}}\right)^{\mathrm{T}}\left(\boldsymbol{S}-\boldsymbol{S}_{\mathrm{iso}}-\boldsymbol{G} \tilde{\boldsymbol{m}}_{\mathrm{ani}}\right)+ \\ & \left(\boldsymbol{S}^{\prime}-\boldsymbol{S}_{\mathrm{iso}}^{\prime}-\widetilde{\boldsymbol{G}}' \widetilde{\boldsymbol{m}}_{\mathrm{ani}}\right)^{\mathrm{T}}\left(\boldsymbol{S}-\boldsymbol{S}_{\mathrm{iso}}^{\prime}-\boldsymbol{G}' \tilde{\boldsymbol{m}}_{\mathrm{ani}}\right)+ \\ & 2 \sigma^2 \sum\limits_{i=5}^6 \ln \left(1+\frac{\tilde{\boldsymbol{m}}_i^2}{\sigma^2}\right)+\sum\limits_{i=5}^6 \lambda_i\left(\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i-\boldsymbol{P}_i \widetilde{\boldsymbol{m}}_i\right)^{\mathrm{T}}\left(\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_i-\boldsymbol{P}_i \widetilde{\boldsymbol{m}}_i\right) \end{aligned} $ | (18) |
式中:λi为模型参数的约束系数;Pi为积分算子;Λi=ln(Ri/R0)/2,R0为模型参数的初始值;σ2为背景噪声分布方差。反演过程首先将Md、μ、ρ和fani四个参数作为第一步的重点优化参数,然后在此基础上,将δN和δT两个裂缝参数作为第二步的优化目标,从而最终求取全部待反演参数。
2 模型试算及实际资料处理 2.1 模型试算选用A区的一口井的合成方位地震角度道集验证五维数据时频联合反演模型参数的可行性。首先,基于褶积模型及提取的地震子波,并添加高斯随机噪声,合成无噪及信噪比为5∶1、2∶1的不同方位角的地震角度道集(图 3、图 5、图 7)及其反演结果(图 4、图 6、图 8)。由图 4、图 6、图 8可见,模型参数反演结果与实际测井数据吻合较好(平均相对误差较小),验证了五维数据时频联合反演的可行性。

|
图 3 方位角分别为30°(a)、60°(b)、90°(c)、120°(d)、150°(e)和180°(f)的无噪地震角度道集 |

|
图 4 由图 3反演的模型参数 红色曲线为反演结果,蓝色曲线为实际数据,绿色曲线为初始模型曲线,下同。 |

|
图 5 方位角分别为30°(a)、60°(b)、90°(c)、120°(d)、150°(e)和180°(f)的信噪比为5∶1的地震角度道集 |

|
图 6 由图 5反演的模型参数 |

|
图 7 方位角分别为30°(a)、60°(b)、90°(c)、120°(d)、150°(e)和180°(f)的信噪比为2∶1的地震角度道集 |

|
图 8 由图 7反演的模型参数 |
B区地层发育大量高角度裂缝,预测目标为裂缝型非常规页岩油气储层,可将其等效为HTI介质。选取45°、135°方位五维数据,每个方位的叠前炮检距数据均经过AVO保幅处理、从炮检距到角度道集的转换。图 9为45°、135°方位角地震数据小、中、大入射角部分角度叠加剖面,图 10与图 11分别为Md、μ、ρ、fani、δN及δT初始模型剖面与反演剖面。由图 11可见:fani反演剖面的结构与图 9相似,并与测井解释结果一致,A井作为测试井并未参与初始模型的建立以及后期反演,fani反演剖面的低值异常对应测井解释的油气位置,fani解耦流体识别结果的油气界面清晰(红色区域),且与钻井结果吻合,进一步验证了方法的有效性与可靠性。模型参数反演结果与原始测井数据的对比结果表明(图 12),两者吻合较好,进一步验证了方法的有效性。

|
图 9 45°(左)、135°(右)方位角地震数据小(上)、中(中)、大(下)入射角部分角度叠加剖面 小、中、大入射角平均值分别为8°、16°及24°。 |
|
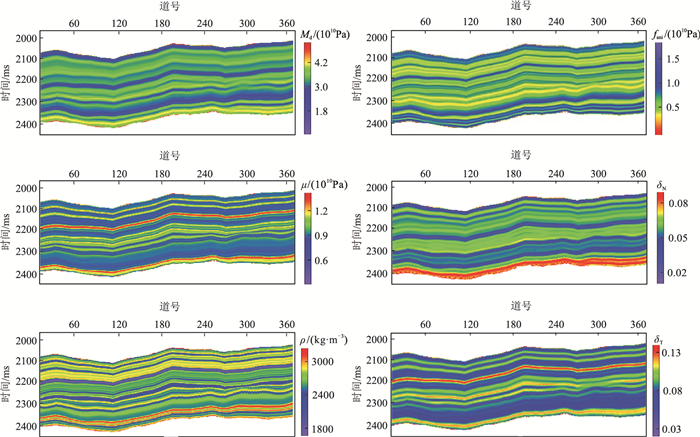
图 10 Md、μ、ρ、fani、δN及δT初始模型剖面 |

|
图 11 Md、μ、ρ、fani、δN及δT反演剖面 右上图的红色虚线椭圆指示裂缝型气藏发育区域。 |

|
图 12 原始测井数据(蓝)与井旁模型参数(红)反演结果对比 |
本文方法旨在从五维数据中直接获取裂缝型储层参数。结合各向异性Gassmann孔隙弹性理论和线性滑动理论,以“固液缝”解耦流体因子为基础,推导了由“固液缝”解耦流体因子直接表征的新的纵波反射系数方程,消除了岩石骨架、裂缝、孔隙及油气水耦合对地震反射特征的影响;分析、讨论了新纵波反射系数方程的适用条件及敏感性,在此基础上,构建贝叶斯框架的地震反演目标函数,并基于时频资料研究五维数据流体识别方法,可直接获得裂缝型储层“固液缝”解耦流体因子,消除了累计误差的影响,提高了预测精度。模型试算及实际资料处理结果表明,所提方法可以合理、可靠地预测裂缝型储层油气分布。
附录A 式(10)的推导过程将式(8)的扰度刚度矩阵代入式(9),得
| $ \begin{aligned} & R_{\mathrm{PP}}(\theta, \varphi)= \\ & \frac{\Delta M_{\mathrm{d}}+\Delta f_{\mathrm{ani}}-4 \Delta \delta_{\mathrm{T}} \mu \cos ^2 \varphi \sin ^2 \theta\left(\sin ^2 \theta \sin ^2 \varphi-\cos ^2 \theta\right)}{4 \rho V_{\mathrm{P}}^2 \cos ^2 \theta}- \\ & \frac{\Delta \delta_{\mathrm{N}} M_{\mathrm{d}}\left(1-\frac{2}{\gamma_{\mathrm{dry}}^2} \sin ^2 \theta \sin ^2 \varphi-\frac{2}{\gamma_{\mathrm{dry}}^2} \cos ^2 \theta\right)^2}{4 \rho V_{\mathrm{P}}^2 \cos ^2 \theta}+ \\ & \frac{\Delta \rho\left(2 \cos ^2 \theta-1\right)}{4 \rho \cos ^2 \theta}-\frac{2 \Delta \mu \sin ^2 \theta}{\rho V_{\mathrm{P}}^2} \end{aligned} $ | (A-1) |
整理可得
| $ \begin{aligned} & R_{\mathrm{PP}}(\theta, \varphi)= \\ & \left(\frac{\gamma_{\mathrm{dry}}^2}{\gamma_{\mathrm{sat}}^2} \frac{\sec ^2 \theta}{4}\right) \frac{\Delta M_{\mathrm{d}}}{M_{\mathrm{d}}}-\left(\frac{2}{\gamma_{\mathrm{sat}}^2} \sin ^2 \theta\right) \frac{\Delta \mu}{\mu}+ \\ & \left(\frac{1}{2}-\frac{\sec ^2 \theta}{4}\right) \frac{\Delta O}{\rho}+\frac{K_{\mathrm{f}} G(\phi)+2 F(\phi) K_{\mathrm{f}} \chi \delta_{\mathrm{N}}}{M_{\rm{s}}} \frac{\sec (\theta)^2}{4} \frac{\Delta f_{\mathrm{ani}}}{f_{\mathrm{ani}}}- \\ & \frac{\gamma_{\mathrm{dry}}^2}{\gamma_{\mathrm{sat}}^2} \frac{\sec ^2 \theta}{4}\left(1+\frac{2}{\gamma_{\mathrm{dry}}^2} \sin ^2 \theta \sin ^2 \varphi-\frac{2}{\gamma_{\mathrm{dry}}^2} \cos ^2 \theta\right)^2 \Delta \delta_{\mathrm{N}}+ \\ & \frac{1}{\gamma_{\mathrm{sat}}^2} \cos ^2 \varphi \sin ^2 \theta\left(1-\tan ^2 \theta \sin ^2 \varphi\right) \Delta \delta_{\mathrm{T}} \end{aligned} $ | (A-2) |
根据各向异性Gassmann流体项F(ϕ)Kf=Ms-Md,而且
| $ \begin{aligned} & R_{\mathrm{PP}}(\theta, \varphi)=a(\theta) \frac{\Delta M_{\mathrm{d}}}{M_{\mathrm{d}}}+b(\theta) \frac{\Delta \mu}{\mu}+c(\theta) \frac{\Delta \rho}{\rho}+ \\ & d(\theta) \frac{\Delta f_{\mathrm{ani}}}{f_{\mathrm{ani}}}+e(\theta, \varphi) \Delta \delta_{\mathrm{N}}+f(\theta, \varphi) \Delta \delta_{\mathrm{T}} \end{aligned} $ | (A-3) |
其中
| $ \begin{aligned} & a(\theta)=\frac{\gamma_{\mathrm{dry}}^2}{\gamma_{\mathrm{sat}}^2} \frac{\sec ^2 \theta}{4} ; b(\theta)=-\frac{2}{\gamma_{\mathrm{sat}}^2} \sin ^2 \theta \\ & c(\theta)=\frac{1}{2}-\frac{\sec ^2 \theta}{4} ; d(\theta)=\left(1-\frac{\gamma_{\mathrm{dry}}^2}{\gamma_{\mathrm{sat}}^2}\right) \frac{\sec ^2 \theta}{4} \\ & e(\theta, \varphi)=-\frac{\gamma_{\mathrm{dry}}^2}{\gamma_{\mathrm{sat}}^2} \frac{\sec ^2 \theta}{4}\left[\frac{2}{\gamma_{\mathrm{sat}}^2}\left(1-\sin ^2 \theta \cos ^2 \varphi\right)-1\right]^2 \\ & f(\theta, \varphi)=\frac{1}{\gamma_{\mathrm{sat}}^2} \cos ^2 \varphi \sin ^2 \theta\left(1-\tan ^2 \theta \sin ^2 \varphi\right) \end{aligned} $ |
| [1] |
印兴耀, 张洪学, 宗兆云. OVT数据域五维地震资料解释技术研究现状与进展[J]. 石油物探, 2018, 57(2): 155-178. YIN Xingyao, ZHANG Hongxue, ZONG Zhaoyun. Research status and progress of 5D seismic data interpretation in OVT domain[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 155-178. |
| [2] |
CARCIONE J M, GUREVICH B, SANTOS J E, et al. Angular and frequency-dependent wave velocity and attenuation in fractured porous media[J]. Pure Applied Geophysics, 2013, 170(11): 1673-1683. DOI:10.1007/s00024-012-0636-8 |
| [3] |
ZONG Z, SUN Q, LI C, et al. Young's modulus variation with azimuth for fracture orientation estimation[J]. Interpretation, 2018, 6(4): T809-T818. DOI:10.1190/INT-2017-0101.1 |
| [4] |
CHEN H. Seismic frequency component inversion for elastic parameters and maximum inverse quality factor driven by attenuating rock physics models[J]. Surveys in Geophysics, 2020, 41(4): 835-857. DOI:10.1007/s10712-020-09593-6 |
| [5] |
SMITH G C, GIDLOW P M. Weighted stacking for rock property estimation and detection of gas[J]. Geophysical Prospecting, 1987, 35(9): 993-1014. DOI:10.1111/j.1365-2478.1987.tb00856.x |
| [6] |
SMITH G C, GIDLOW P M. The fluid factor angle and the crossplot angle[C]. SEG Technical Program Expanded Abstracts, 2003, 22: 185-188.
|
| [7] |
GOODWAY B, CHEN T, DOWNTON J. Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters; "λρ", "μρ", & "λ/μ fluid stack", from P and S inversions[C]. SEG Technical Program Expanded Abstracts, 1997, 16: 183-186.
|
| [8] |
RUSSELL B H, HEDLIN K, HILTERMAN F J, et al. Fluid-property discrimination with AVO: A Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [9] |
QUAKENBUSH M, SHANG B, TUTTLE C. Poisson impedance[J]. The Leading Edge, 2006, 25(2): 128-138. DOI:10.1190/1.2172301 |
| [10] |
HUDSON J A. Wave speeds and attenuation of elastic waves in material containing cracks[J]. Geophysical Journal International, 1981, 64(1): 133-150. DOI:10.1111/j.1365-246X.1981.tb02662.x |
| [11] |
SCHOENBERG M, SAYERS C M. Seismic anisotropy of fractured rock[J]. Geophysics, 1995, 60(1): 204-211. DOI:10.1190/1.1443748 |
| [12] |
CHEN H, JI Y, INNANEN K A. Estimation of modified fluid factor and dry fracture weaknesses using azimuthal elastic impedance[J]. Geophysics, 2018, 83(1): WA73-WA88. DOI:10.1190/geo2017-0075.1 |
| [13] |
CHAPMAN M, LIU E, LI X. The influence of fluid-sensitive dispersion and attenuation on AVO analysis[J]. Geophysical Journal International, 2006, 167(1): 89-105. DOI:10.1111/j.1365-246X.2006.02919.x |
| [14] |
PAN X, ZHANG G, LIU J, et al. Estimating fluid term and anisotropic parameters in saturated transversely isotropic media with aligned fractures[J]. Journal of Seismic Exploration, 2021, 30(1): 65-84. |
| [15] |
王迪, 张益明, 牛聪, 等. 储层敏感流体因子反演及烃类检测[J]. 石油地球物理勘探, 2021, 56(1): 146-154. WANG Di, ZHANG Yiming, NIU Cong, et al. Reservoir sensitive fluid factor inversion and its application in hydrocarbon detection[J]. Oil Geophysical Prospecting, 2021, 56(1): 146-154. DOI:10.13810/j.cnki.issn.1000-7210.2021.01.017 |
| [16] |
ZHANG S, HUANG H, DONG Y, et al. Direct estimation of the fluid properties and brittleness via elastic impedance inversion for predicting sweet spots and the fracturing area in the unconventional reservoir[J]. Journal of Natural Gas Science and Engineering, 2017. DOI:10.1016/j.jngse.2017.04.028 |
| [17] |
RUSSELL B H, HEDLIN K J. Extended poroelastic impedance[J]. Geophysics, 2019, 84(2): N1-N14. DOI:10.1190/geo2018-0311.1 |
| [18] |
PAN X, DU X, ZHAO X, et al. Seismic characterization of decoupled orthorhombic fractures based on observed surface azimuthal amplitude data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021. DOI:10.1109/TGRS.2021.3105724 |
| [19] |
CHEN H, MORADI S, INNANEN K A. Joint inversion of frequency components of PP-and PSV-wave amplitudes for attenuation factors using second-order derivatives of anelastic impedance[J]. Surveys in Geophysics, 2021, 42(4): 961-987. DOI:10.1007/s10712-021-09649-1 |
| [20] |
印兴耀, 张洪学, 宗兆云. 五维地震油气识别方法[J]. 应用声学, 2020, 39(1): 63-70. YIN Xingyao, ZHANG Hongxue, ZONG Zhaoyun. Seismic fluid identification based on 5D seismic data[J]. Journal of Applied Acoustics, 2020, 39(1): 63-70. |
| [21] |
SHAW R K, SEN M K. Use of AVOA data to estimate fluid indicator in a vertically fractured medium[J]. Geophysics, 2006, 71(3): C15-C24. DOI:10.1190/1.2194896 |
| [22] |
YIN X, ZHANG S. Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation[J]. Geophysics, 2014, 79(5): R221-R232. DOI:10.1190/geo2013-0372.1 |
| [23] |
YIN X, ZONG Z, WU G. Research on seismic fluid identification driven by rock physics[J]. Science China Earth Sciences, 2015, 58(2): 159-171. DOI:10.1007/s11430-014-4992-3 |
| [24] |
LI K, YIN X, ZONG Z, et al. Estimation of porosity, fluid bulk modulus, and stiff-pore volume fraction using a multitrace Bayesian amplitude-variation-with-offset petrophysics inversion in multiporosity reservoirs[J]. Geophysics, 2022, 87(1): M25-M41. DOI:10.1190/geo2021-0029.1 |
| [25] |
印兴耀, 张世鑫, 张峰. 针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究[J]. 地球物理学报, 2013, 56(7): 2378-2390. YIN Xingyao, ZHANG Shixin, ZHANG Feng. Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification[J]. Chinese Journal of Geophysics, 2013, 56(7): 2378-2390. |
| [26] |
周爽爽, 印兴耀, 裴松, 等. 地震波形约束的蒙特卡洛-马尔科夫链随机反演方法[J]. 石油地球物理勘探, 2021, 56(3): 543-554, 592. ZHOU Shuangshuang, YIN Xingyao, PEI Song, et al. Monte Carlo-Markov Chain stochastic inversion constrained by seismic waveform[J]. Oil Geophysical Prospecting, 2021, 56(3): 543-554, 592. |
| [27] |
陈超, 印兴耀, 陈祖庆, 等. 基于页岩岩石物理等效模型的地层压力系数预测方法[J]. 石油地球物理勘探, 2022, 57(2): 367-376, 394. CHEN Chao, YIN Xingyao, CHEN Zuqing, et al. Prediction for formation pressure coefficients based on an equivalent petrophysical model of shale[J]. Oil Geophysical Prospecting, 2022, 57(2): 367-376, 394. |
| [28] |
刘晓晶, 陈祖庆, 陈超, 等. 方位弹性阻抗傅里叶级数裂缝预测方法[J]. 石油地球物理勘探, 2022, 57(2): 423-433. LIU Xiaojing, CHEN Zuqing, CHEN Chao, et al. Fracture prediction method based on Fourier series of azimuthal elastic impedance[J]. Oil Geophysical Prospecting, 2022, 57(2): 423-433. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.019 |
| [29] |
顾雯, 印兴耀, 巫芙蓉, 等. 波形驱动下多参数约束高分辨率反演方法——以四川盆地渝西地区龙马溪组页岩气为例[J]. 石油地球物理勘探, 2021, 56(6): 1311-1321. GU Wen, YIN Xingyao, WU Furong, et al. Multi-parameter constrained high-resolution inversion method driven by waveform: A case study of Longmaxi Formation shale gas in western Chongqing, Sichuan Basin[J]. Oil Geophysical Prospecting, 2021, 56(6): 1311-1321. |
| [30] |
ZONG Z, JI L. Model parameterization and amplitude variation with angle and azimuthal inversion in orthotropic media[J]. Geophysics, 2021, 86(1): R1-R14. |
| [31] |
GUREVICH B. Elastic properties of saturated porous rocks with aligned fractures[J]. Journal of Applied Geophysics, 2003, 54(3-4): 203-218. |



 印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 