地震数据重建在地震数据处理环节具有非常重要的作用,是该环节取得良好效果的前提。然而,受经济条件和采集因素(障碍物、复杂地质条件等)制约,野外采集的地震勘探数据在空间上往往呈现不规则和不完整分布[1],将直接影响后续地震资料的处理[2],并最终影响资料解释和油气藏预测。因此,发展有效的地震数据重建方法,对实际地震数据进行高信噪比、高保真的重构具有重要的现实意义。许多学者发展了多种有效的地震数据重建算法,如频率—空间预测滤波方法[3-4]、基于变换域中地震数据稀疏表征的方法。Abma等[5]首先将凸集投影(Projection on Convex Sets, POCS)法引入三维不规则地震数据重建,对不规则缺失数据在傅里叶域进行迭代阈值重建,取得了较好效果。与其他重建算法相比,POCS法最显著的优点是简单、易于实现,并且具有很好的重建效果。在每次迭代中,选择合理的阈值参数对重建效率很重要。Gao等[6]通过使用指数衰减阈值策略使基于傅里叶域的POCS地震重建的计算效率大大提高。金成玫等[7]将POCS算法引入曲波变换的重建方法,通过采用按指数衰减的阈值参数加快了迭代收敛速度。Ge等[8]提出了反比例阈值模型,根据最大迭代次数对频谱能量分布规律进行采样,然后在权重部分根据每个阈值的百分比计算权重值。Wang等[9]提出了一种使用GPU加速POCS重建的计算方案,该方法利用基于GPU的傅里叶变换库加速三维POCS算法中最耗时部分的运行。
由于POCS法与压缩感知[10]中的迭代收缩阈值算法(Iterative Shrinkage Thresholding Algorithm, ISTA)有关,且Yang等[11]证明了ISTA可推导出POCS方法。FISTA保留了ISTA的计算简单性,但是在理论上和实践上都证明了全局收敛速度明显更好[12-13]。与ISTA相比(其收敛速度仅为O(1/k),其中k为迭代次数,FISTA具有全局收敛速度O(1/k2)。因此,可以借鉴压缩感知中快速迭代收缩阈值算法(Fast Iterative Shrinkage Thresholding Algorithm, FISTA)的思想改进POCS算法。
本文借鉴FISTA的思想,提出了基于曲波变换的快速凸集投影算法(Fast POCS,FPOCS),并利用其对三维地震数据进行插值,从优化的角度实现更快收敛。首先,简要阐述了POCS算法的数学原理;然后,参照FISTA算法,给出FPOCS算法并将其引入非均匀采样地震数据重建,由于地震数据通常是由复杂的曲线状元素所构成的,局部特征变化较大,因此在FPOCS重构方法中引入了具有局部性、多尺度和多方向性的曲波变换[15-17],实现稀疏表示,并在重建过程中采用指数衰减的阈值参数提高重建结果;最后,利用模拟和实际数据验证了本文方法的有效性。
1 地震数据重建理论假设缺失地震数据的观测区域是分布在非均匀网格上的。地震数据采集过程在数学上可以通过以下形式来表述
| $ \boldsymbol{Y}^{\text {obs }}=\boldsymbol{P Y}+\boldsymbol{n} $ | (1) |
式中:Yobs表示观测数据(缺失数据);Y表示原始完整的地震数据;n是数据噪声;P是采样矩阵,为一个对角线元素是0或1的对角阵。地震数据重建是从Yobs中恢复出Y。设x=ΦY是某个变换域的系数,若Y在某个变换域(傅里叶域、曲波域等)是稀疏的,则x是稀疏的或者可压缩的,其中Φ表示稀疏变换。曲波变换由于具有多尺度、多方向性的特点,能更好地捕捉到曲线状的奇异特征,进而对地震数据进行最优局部分解。因此本文选择曲波变换作为稀疏变换基。
由于式(1)通常是欠定的,所以数学上通常考虑如下带先验约束的优化问题
| $ \min\limits _{\boldsymbol{x}}\left\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{Y}^{\text {obs }}\right\|_2^2+\alpha g(\boldsymbol{x}) $ | (2) |
式中:A=PCT,C是曲波正交变换;‖Ax-Yobs‖22表示误差拟合项,其中,‖·‖2是L2范数;α是正则化参数;g(x)表示正则化项,本文采用稀疏约束g(x)=‖x‖1,其中‖·‖1是L1范数。
2 基于快速POCS的地震数据重建 2.1 POCS算法POCS算法是一种经典的地震数据重建迭代算法,计算效率高、结果稳定。该算法迭代过程由阈值阶段和缺失数据填充两个阶段组成。阈值化阶段(或滤波阶段),通过变换域(如傅里叶域、曲波域)中的阈值化算子将已知信息代到未知位置。缺失数据填充阶段有助于固定已知位置的振幅。在稀疏约束‖ΦY‖1下,POCS算法求解优化问题式(2)的具体迭代形式如下
| $ \boldsymbol{u}_{k+1}=\boldsymbol{C}^{\mathrm{T}} \boldsymbol{T}_{\lambda_k}\left(\boldsymbol{C} \boldsymbol{Y}_k\right) $ | (3) |
| $ \boldsymbol{Y}_{k+1}=\boldsymbol{Y}^{\text {obs }}+(\boldsymbol{I}-\boldsymbol{P}) \boldsymbol{u}_{k+1} $ | (4) |
式中:I是单位矩阵;Tλk是软阈值算子,表示如下
| $ \boldsymbol{T}_{\lambda k}(x)= \begin{cases}\boldsymbol{x}-\lambda \cdot \operatorname{sgn} \eta & |\eta| \geqslant \lambda \\ 0 & |\eta|<\lambda\end{cases} $ | (5) |
式中:λ表示阈值因子;η为原始阈值。上述迭代过程中,Y1可以由Y或预插值算法初始化。
由于野外实际采集到的地震数据通常含有噪声,虽然在迭代过程中阈值阶段(式(3))对噪声进行了去除,但是噪声又会通过式(4)重新进入重建数据。因此,为了保证重建数据不含噪声,Zhang等[18]提出交换式(3)和式(4)的顺序达到去噪目的。插值过程中可以应用一些技巧,例如使用阈值参数或保持一定百分比的最大系数。在迭代过程中,阈值参数可能会随着迭代线性或指数下降(图 1),以减少截断效应。

|
图 1 指数阈值与线性阈值下降图 |
线性阈值模型一般设置为
| $ \lambda_k=\lambda_{\max }-\frac{k-1}{N-1}\left(\lambda_{\max }-\lambda_{\min }\right) $ | (6) |
指数阈值模型一般设置为
| $ \lambda_k=\lambda_{\max }{\frac{\lambda_{\min }}{\lambda_{\max }}}^{\frac{k-1}{N-1}} $ | (7) |
式中:N是最大迭代次数;λmax和λmin分别是设置的最大和最小阈值。
从图 1可以明显看出,指数阈值模型的衰减快于线性阈值模型,故本文选用指数阈值模型。式(4)可以改写为
| $ \boldsymbol{Y}_{k+1}=\boldsymbol{u}_{k+1}+\delta\left(\boldsymbol{Y}_k-\boldsymbol{P} \boldsymbol{u}_{k+1}\right) $ | (8) |
式中δ为0到1变化的控制因子。当δ=1时,式(8)退化为方程(4)。在迭代中,为了降低原始数据中的噪声,可将δ从1逐渐减小至0。
2.2 迭代收缩阈值算法求解式(8)最常用的方法之一是ISTA。ISTA算法一般可以表示为
| $ \boldsymbol{x}_{k+1}=\boldsymbol{T}_{\lambda k}\left[\boldsymbol{x}_k-2 t \boldsymbol{A}^{\mathrm{T}}\left(\boldsymbol{A} \boldsymbol{x}_k-\boldsymbol{Y}\right)\right] $ | (9) |
式中t是合适的步长。ISTA算法收敛速率仅为O(1/k)。
受文献[13]的启发,结合式(9),给出快速POCS算法(FISTA)
| $ \left\{\begin{array}{l} \boldsymbol{Y}_{k+1}=\boldsymbol{T}_{\lambda k}\left(\boldsymbol{Z}_k\right)+\frac{t_k-1}{\frac{1+\sqrt{1+4 t_k^2}}{2}}\left(\boldsymbol{X}_k-\boldsymbol{X}_{k-1}\right) \\ \boldsymbol{Z}_{k+1}=(\boldsymbol{I}-\boldsymbol{P}) \boldsymbol{Y}_{k+1}+\boldsymbol{P} \boldsymbol{X} \end{array}\right. $ | (10) |
为了测试本文方法对地震数据重建问题的有效性,测试中将信噪比作为地震数据重建性能的评判指标
| $ \mathrm{SNR}=10 \lg \frac{\left\|\boldsymbol{y}^*\right\|_2}{\|\boldsymbol{y}-\hat{\boldsymbol{y}}\|_2} $ | (11) |
式中y*和
为了比较FPOCS算法与POCS算法,选取大小为128×128×128模拟数据进行测试,该数据共128炮,每炮有128道,采样点数为128,道距为10 m。采样间隔为4 ms。分别对炮、检点进行25%随机欠采样。完整数据与欠采样数据如图 2a与图 2b所示。

|
图 2 合成数据(a)及欠采样数据(b) |
基于曲波变换的重建算法存在较严重的周期效应。为有效克服这一问题,在实施重建算法前,对欠采样数据进行零填充,即分别在炮点轴与检波点轴两侧填充一定的零道。本实验在炮点轴与检波点轴分别填充5道,数据大小变为138×138×128。重建完成后,再删除填充的道。经数值实验测试,该方法有效缓解了周期效应对重建效果的影响。此外,在数值实验中拾取了采样道的初至,并使用线性插值近似缺失道的初至。重建完成后,初至以上均赋值0,以进一步优化重建效果。
接下来使用FPOCS、POCS算法对数据进行重建,并采用指数衰减阈值(初值为0.2),两种方法迭代次数均为15,三维曲波的尺度数为4,角度数为8。信噪比随迭代次数的变化趋势如图 3所示,FPOCS及POCS算法均采用指数衰减阈值模型。由图可见,FPOCS算法的重建效果优于POCS,其最终信噪比为16.1631 dB,收敛速度也快,约在第13次迭代即可达到最大信噪比。

|
图 3 信噪比随迭代次数的变化 |
图 4展示了两种方法的重建结果。与图 2a原始数据相比,部分尚未重建好(图中红框所示),这在重建误差中可清楚看到。因此,重建结果和重建信噪比表明了本文方法的有效性。

|
图 4 POCS(a)和FPOCS(b)算法重建结果(上)及重建误差(下)对比 |
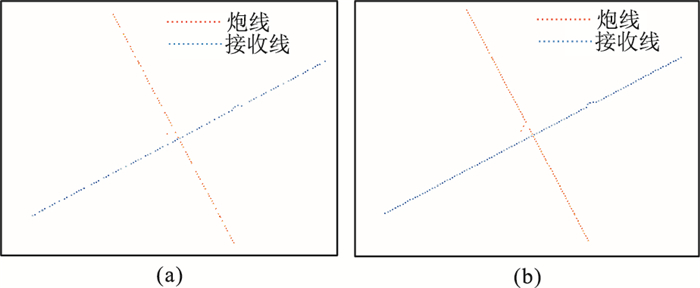
选取某实际压缩感知采集数据的一个十字排列道集进行方法效果测试,图 5a为十字排列数据的观测系统。原始数据尺寸为1501×71×178,检波点和炮点个数分别为178和71。该采集数据在检波点和炮点方向同时做了25%随机欠采样。
|
图 5 实际数据观测系统(a)和理论观测系统(b) |
通过计算炮点和检波点的间隔分布,可以得出炮点和检波点的间隔为50、100或者150 m,其中大部分间隔为50 m。对该十字排列数据进行插值,步骤如下。
第一步: 生成新的理论观测系统—网格化的数据,即观测数据,以该数据为例,炮点和检波点网格化间隔都设置为50 m。原始观测系统分布和新的理论观测系统分布如图 5a和5b所示。
第二步:FPOCS数据重建。根据理论观测系统,得到重建后的数据尺寸为1501×90×240,即缺失率大致为41.50%,其中炮线方向缺失率约为24.47%,检波线方向缺失率约为25.83%。
按上述方式处理数据,所得规则网格尺寸为94×240,即炮点数为94,检波点数为240。图 6a显示了理论观测系统中的原始数据,缺失率大致为41.50%。参数与模拟数据相同,使用FPOCS算法对缺失道进行重建,迭代15次的结果如图 6b所示。

|
图 6 实际观测数据(a)及其对应的FPOCS重建结果(b)对比 |
为了更加清楚地展示插值效果,图 7给出了数据的二维展布图。图 7a中黑色箭头所指为整条排列缺失的数据,可以看出原始数据存在整个排列数据的缺失,同时也存在连续两个排列数据缺失的情况,导致数据重建难度大;图 7b展示的是重建后的数据。对比可以看到整条排列缺失的数据也能够很好地重构。

|
图 7 实际观测系统数据二维展布图(a)及FPOCS重建结果(b)对比 |
本文在压缩感知理论的基础上,提出了基于曲波变换的快速凸集投影(FPOCS)算法,并且将该方法用于压缩感知地震数据重建。该方法保留了POCS算法的简单性,通过利用FISTA算法提高了迭代计算的收敛速度和重构精度。由模拟数据和实际数据重建结果分析可以看出,本文方法可以较好地恢复缺失的地震数据,同时,同相轴连续性得到加强,一些细节信息也得到恢复,验证了本文方法在重建压缩感知地震采集数据方面的有效性。
| [1] |
段中钰, 李婷婷, 肖勇, 等. 基于压缩感知的SR-ADMM地震数据重建[J]. 石油地球物理勘探, 2021, 56(6): 1220-1228. DUAN Zhongyu, LI Tingting, XIAO Yong, et al. Seismic data reconstruction by SR-ADMM algorithm based on compressed sensing[J]. Oil Geophysical Prospecting, 2021, 56(6): 1220-1228. DOI:10.13810/j.cnki.issn.1000-7210.2021.06.003 |
| [2] |
NAGHIZADEH M, SACCHI M D. Beyond alias hiera-rchical scale curvelet interpolation of regularly and irregularly sampled seismic data[J]. Geophysics, 2010, 75(6): WB189-WB202. DOI:10.1190/1.3509468 |
| [3] |
SPITZ S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [4] |
NAGHIZADEH M, SACCHI M D. F-X adaptive seismic-trace interpolation[J]. Geophysics, 2009, 74(1): V9-V16. DOI:10.1190/1.3008547 |
| [5] |
ABMA R, KABIR N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91-E97. DOI:10.1190/1.2356088 |
| [6] |
GAO J, CHEN X, LI J, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 2010, 7(3): 229-238. DOI:10.1007/s11770-010-0246-5 |
| [7] |
金成玫, 陈生昌. 基于压缩感知和深度学习的地震数据重建[J]. 石油物探, 2022, 61(7): 782-792. JIN Chengmei, CHEN Shengchang. Seismic data reconstruction based on compressed sensing and deep learning[J]. Geophysical Prospecting for Petroleum, 2022, 61(7): 782-792. |
| [8] |
GE Z, LI J, PAN S, et al. A fast-convergence POCS seismic denoising and reconstruction method[J]. Applied Geophysics, 2015, 12(2): 169-178. DOI:10.1007/s11770-015-0485-1 |
| [9] |
WANG S, XING G, YAO Z. Accelerating POCS interpolation of 3D irregular seismic data with Graphics Processing Units[J]. Computers & Geosciences, 2010, 36(10): 1292-1300. |
| [10] |
DONOHO D L. Compressed sensing: IEEE Transactions on Information Theory[J]. 2006, 52, 1289-1306.
|
| [11] |
YANG P, GAO J, CHEN W. Curvelet-based POCS interpolation of nonuniformly sampled seismic records[J]. Journal of Applied Geophysics, 2012, 79: 90-99. DOI:10.1016/j.jappgeo.2011.12.004 |
| [12] |
WRIGHT S J, NOWAK R D, FIGUEIREDO M A T. Sparse reconstruction by separable approximation[J]. IEEE Transactions on Signal Processing, 2009, 57(7): 2479-2493. DOI:10.1109/TSP.2009.2016892 |
| [13] |
BECK A, TEBOULLE M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 73(1): 183-202. |
| [14] |
LI C, MOSHER C C, KAPLAN S T. Interpolated compressive sensing for seismic data reconstruction[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-6.
|
| [15] |
MA J. Improved iterative curvelet thresholding for compressed sensing and measurement[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 60(1): 126-136. |
| [16] |
庞洋, 张华, 郝亚炬, 等. 基于加速Bregman方法和阈值迭代法的联合地震数据重建法[J]. 石油地球物理勘探, 2022, 57(5): 1035-1045. PANG Yang, ZHANG Hua, HAO Yaju, et al. Joint seismic data reconstruction based on the accelerated Bregman method and threshold iteration meghod[J]. Oil Geophysical Prospecting, 2022, 57(5): 1035-1045. |
| [17] |
PLONKA G, MA J. Curvelet-wavelet regularized split Bregman iteration for compressed sensing[J]. International Journal of Wavelets, Multiresolution and Information Processing, 2011, 9(1): 79-110. DOI:10.1142/S0219691311003955 |
| [18] |
ZHANG H, YANG X, MA J. Can learning from natural image denoising be used for seismic data interpolation[J]. Geophysics, 2020, 85(4): WA115-WA136. DOI:10.1190/geo2019-0243.1 |



 董烈乾, 河北省涿州市范阳中路307号东方地球物理公司国际勘探事业部, 072751。Email:
董烈乾, 河北省涿州市范阳中路307号东方地球物理公司国际勘探事业部, 072751。Email: 