多波地震勘探是利用纵波、横波、转换波等多种信息精细勘察油气藏的一种勘探技术[1],可以识别薄互层、小断层、低幅度构造,准确预测储层边界和储层物性、监测流体,甚至还可以直接预测油气等。但是转换波静校正尤其在复杂勘探区域是公认的陆上转换波地震勘探难点,因此转换波静校正精度和效果已成为衡量转换波地震资料处理水平的重要标准之一。
转换波静校正量是由激发端P-P波静校正量和接收端转换波P-SV波静校正量组成。由于在同一介质中P-SV波传播速度比P-P波低,且P-SV波传播不受孔隙流体影响,导致同一位置P-SV波静校正量大于P-P波[2]。目前,常规转换波静校正技术主要包括面波反演法[3-4](反演横波速度)、初至波静校正方法(主要包括层析反演法、折射法[5]、初至时差法)、反射波法(主要包括纵波构造约束法、反射波剩余静校正等)等。Muyzert[6]提出利用海上P-SV波地震资料中的Scholte面波反演浅层横波速度结构,进而求取横波静校正量;Bansal等[7]介绍了估计近地表横波速度及转换波长、短波长接收点静校正量的方法;孟小红等[8]利用瑞利波速度反演求取P-SV波静校正量。但是在复杂勘探区域,面波通常不发育,信噪比相对较低,因此面波反演法的实际效果不好。转换波初至经常与纵波初至、纵波折射波等信息混杂,信噪比较低,不易分辨和识别,因此初至波常规静校正算法的转换波静校正的效果不好。由于初至波静校正法和面波反演法在复杂构造探区的静校正效果不好,室内反射波静校正法被广泛应用。其中纵波构造约束转换波静校正方法[9-10]的基本原理是通过纵波反射信息约束转换波反射信息,从而获得纵波共检波点反射层位与转换波共检波点对应反射层位的时差关系,由此计算转换波检波点静校正量。这种方法的实际应用效果很好,但其适用条件严格且计算精度低,不适合复杂构造区静校正。
总之,尽管目前转换波静校正技术方法众多,部分已形成了相应的软件产品,已成为多分量勘探不可或缺的重要组成部分。然而,这些方法还面临一些实际困难和问题:①面波反演法[11]存在面波发散、难以确定频散周期及复杂探区面波信噪比低、频散曲线拾取困难等问题;②初至波静校正方法中的层析反演和折射法的转换波初至信噪比低,尤其在复杂探区拾取初至很难(拾取精度难达到转换波静校正计算的要求);③共检波点道集叠加纵波构造约束法要求地下反射界面变化相对平缓或者水平。因此,上述方法目前都不适合复杂探区转换波资料静校正。为此,本文提出一种复杂构造转换波静校正方法,模型试验和实际资料处理效果很好。
1 纵波构造约束转换波静校正原理多波地震勘探转换波产生机理、传播路径、传播速度与纵波存在一定差异(图 1),当纵波非垂直入射到地下界面时,在反射和透射过程中同时产生P-SV波。转换波静校正与纵波静校正既有一定联系[12]也有差别,表现为:①转换波下行波与纵波完全一致,炮点延迟时相同,转换波炮点静校正量与纵波炮点静校正量完全相同;②由于转换波传播速度、低降速带厚度、高速层顶界面等与纵波存在一定差异,造成转换波检波点静校正量一般都比纵波大(2~10倍),再加上转换波初至易受纵波初至以及噪声的干扰,很难辨认和拾取,纵波资料处理中常用的折射波静校正、层析静校正方法很难满足转换波静校正的要求,尤其在地表和地下条件都较复杂的探区,因此转换波静校正问题严重影响了资料处理效果和质量。
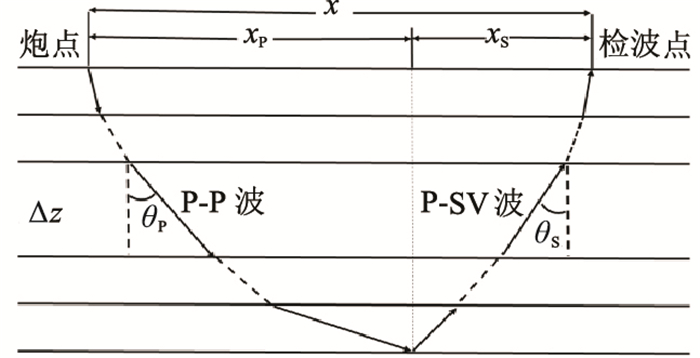
|
图 1 转换波传播路径 x为炮检距;xP为炮点到转换点距离;xS为转换点到接收点距离;θP为纵波入射角;θS为转换波出射角;Δz为地层厚度。 |
目前室内转换波静校正处理主要采用纵波构造约束静校正方法,这种方法的炮点静校正量可由常规的纵波静校正获得,应用转换波炮点静校正量后共检波点道集中每个地震道的剩余静校正量相同,均为对应检波点的静校正量。把经过炮点静校正的共检波点道集数据进行动校正叠加,每个叠加道都包含了对应检波点的转换波静校正量。然后先对P-P波共检波点道集叠加并拾取层位,获得P-P波层位时间,利用速度比把拾取的层位时间转换到P-SV域。同样,可以在P-SV波共检波点道集叠加剖面上拾取与P-P波层位对应的层位时间,然后用P-P波投影到P-SV域的层位时间减去P-SV波拾取的层位时间,时间差就是P-SV波检波点静校正量。这种常规转换波静校正方法的前提条件是:①假设P-SV波炮点静校正问题已经完全解决,地震道剩余校正量均为检波点静校正量;②选择拾取的共检波点道集叠加剖面构造层位基本水平。条件①在复杂构造横向速度变化剧烈情况下,炮点静校正问题没有完全解决,P-P波和P-SV波速度分析精度受到影响,即使在构造层位水平情况下,共检波点也很难同相叠加,容易引起道间动校正误差,这些误差与转换波静校正量交织在一起很难分离,在地下复杂构造区难以保证地震道剩余校正量都为检波点静校正量的假设;条件②对于地下有较大构造起伏的复杂探区很难满足,而且共检波点道集叠加剖面信噪比相对较低、层位拾取困难。为回避纵波构造约束转换波静校正的条件,本文提出了一种复杂构造转换波静校正方法。
2 复杂构造转换波静校正方法常规纵波构造约束转换波静校正方法假设纵波静校正问题已基本解决,P-SV波地震道只存在检波点静校正量。假设转换波共检波点静校正量正确,纵波和转换波共检波点道集叠加剖面在P-SV域的对应层位特征应该相似;相反,如果转换波检波点静校正问题没有解决,则在P-SV域纵波与转换波共检波点道集叠加剖面对应层位应该存在一定时差,这个时差就是转换波检波点静校正量。基于这一原理,可以通过纵波约束转换波的方法准确计算转换波检波点静校正量。但是,如果所选的约束层位构造复杂、起伏较大,转换波静校正效果将受到影响。层位起伏较大,纵波和转换波共检波点同相轴都存在时差(共检波点剖面是一次覆盖剖面),复杂构造层位不能同相叠加,叠加剖面信噪比通常较低,层位拾取困难,这种情况容易造成纵波与转换波共检波点道集叠加剖面的相同层位时差变化不合理,影响转换波静校正计算精度和效果。为了突破构造层位必须水平的限制,本文采用层位拉平和共检波点速度分析的纵波构造约束转换波静校正方法,可以解决复杂构造转换波静校正问题。具体步骤为:①通过层位拉平的方法消除转换波静校正构造项,克服层位基本水平的限制。首先拾取P-P波CMP叠加剖面信噪比较高的构造层位,并计算层位拉平投影时差,用投影时差“拉平”叠前数据。②将层位拉平数据转换到共检波点域并重新完成共检波点P-P波速度分析,以使共检波点道集的每道速度相同,消除复杂构造横向速度剧烈变化及速度分析精度不高造成的道间动校正误差,既可以使共检波点同相叠加、提高信噪比,又减少了速度精度不高对地震道剩余静校正量的影响。③把P-P波构造层位拉平的投影时差转换到P-SV域拉平P-SV波叠前数据,在共检波点域重新完成P-SV波共检波点速度分析,提高P-SV波共检波点道集叠加剖面信噪比和分辨率,最终提高P-SV波共检波点道集叠加层位拾取精度和效率。通过构造层位拉平和共检波点域速度分析,再利用P-P波构造约束转换波静校正方法提高复杂构造转换波静校正计算精度和效率。
根据地表一致性条件,P-SV波各地震道的静校正量tij可分解为四部分[9]
| $ t_{i j}=s_i+g_j+c_k+y_k $ | (1) |
式中:si为i位置炮点静校正量;gj为j位置检波点静校正量;ck为共转换点k位置的动校正剩余正常时差,随炮检距的平方而变化;yk为构造项。
根据转换波传播机理,P-SV波炮点静校正量与P-P波相同。那么,应用P-P波炮点静校正后,地震道剩余静校正量只剩检波点校正量。设不同检波点校正量为tj,可分解为
| $ t_j=g_j+c_k+y_k $ | (2) |
又由于转换波检波点静校正量远大于剩余动校正量,故ck≈0,因此式(2)可简化为
| $ t_j=g_j+y_k $ | (3) |
也可以改写为
| $ t_j-y_k=g_j $ | (4) |
本文在共中心点叠加剖面拾取层位,并通过层位投影获得层位拉平时差,用这个时差对叠前P-P波层位拉平,消除P-P波共中心点构造项;并把P-P波层位拉平时差校正量转换到P-SV域,对P-SV波也进行层位拉平;将P-P波和P-SV波拉平数据在共检波点重新进行速度分析和动校正。拉平P-P波层位的共检波点道集叠加剖面反射层在理论上应该接近水平反射层位,将拉平层位时间Td(理论上为转换波共检波点道集叠加反射层位时间)转换到P-SV域,设T0PS为转换波共检波点道集叠加剖面实际反射层位时间,T0PS是通过P-SV波层位拉平后,在共检波点道集叠加剖面上由层位拾取获得(P-SV波与P-P波拾取层位必须匹配一致),T0PS含转换波检波点校正量。由上述关系式可获得转换波检波点校正量
| $ t_j=T_{\mathrm{d}}-T_{\mathrm{0PS} j} $ | (5) |
因此
| $ T_{\mathrm{d}}-y_k-T_{\mathrm{0PS} j}=g_j $ | (6) |
设拾取转换波共检波点道集叠加剖面层位深度为H,P-P波垂直速度为V0P,P-SV波垂直速度为V0PS,P-P波到达转换点的双程旅行时为T0P,P-SV波从炮点经转换点到达检波点的旅行时为T0PS,则
| $ \frac{H}{V_{\mathrm{0P}}}+\frac{H}{V_{\mathrm{0PS}}}=T_{\mathrm{0PS}} $ | (7) |
| $ \frac{2 H}{V_{\mathrm{0P}}}=T_{\mathrm{0P}} $ | (8) |
因此
| $ T_{\mathrm{0PS}}=\frac{1+\frac{V_{\mathrm{0P}}}{V_{\mathrm{0PS}}}}{2} \times T_{\mathrm{0P}} $ | (9) |
设
| $ \gamma_0=\frac{V_{0 \mathrm{P}}}{V_{\mathrm{0PS}}} $ | (10) |
则
| $ T_{\mathrm{0PS}}=\frac{1+\gamma_0}{2} \times T_{\mathrm{0P}} $ | (11) |
式(6)的Td-yk实际上是P-P波共检波点构造拾取层位在P-SV波共检波点道集叠加剖面上对应层位的投影。如果P-P波静校正问题已经完全解决,构造拉平后构造项消失,那么yk≈0,则投影Td实际上是共中心点构造层位拉平后转换波共检波点道集叠加剖面的理论反射层位时间T0PS,这与Td在理论上完全吻合,即Td是应用转换波静校正后共检波点道集叠加标准层位时间。则式(6)变为
| $ g_j=\frac{T_{\mathrm{0P}j}\left(\gamma_0+1\right)}{2}-T_{\mathrm{0PS} j} $ | (12) |
式中T0P为P-P波构造层位拉平后拾取的层位时间,也就是P-P波到达深度转换点的双程旅行时间,T0P转换到P-SV域的时间T0Pj(γ0+1)/2就是本文理论上P-SV波从炮点经深度转换点到达检波点的旅行时间,这个时间不含转换波校正量。T0PS为转换波共检波点道集叠加剖面实际反射层位时间(含检波点校正量),转换波传播理论时间与实际时间的差即为所求的转换波静校正量。
根据上述原理,复杂构造纵波构造约束静校正技术的实现方案为(图 2):
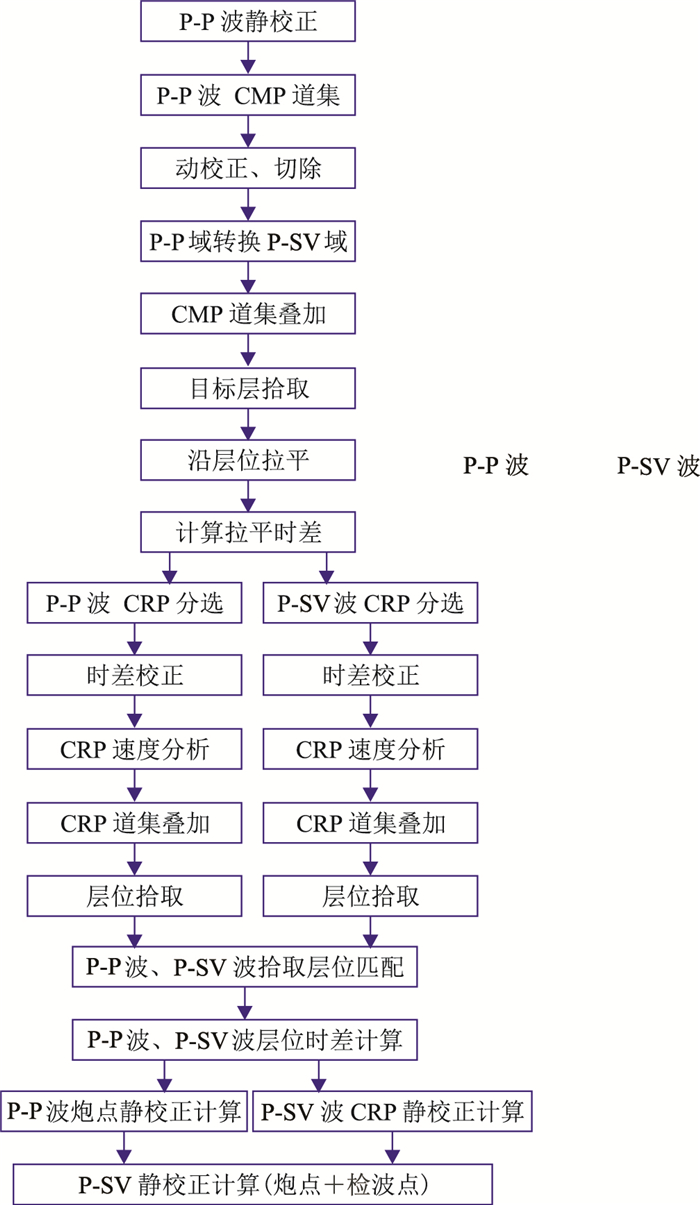
|
图 2 P-SV波静校正计算流程 |
(1) 层位拾取。采集原始三分量地震数据进行前期预处理以及速度分析,估计勘探区域纵横波速度比γ0值;野外静校正后对纵波进行共中心点叠加(已经完成动校正并校正到基准面上),在叠加剖面上选择同相轴相对清晰的层位拾取时间,选择的层位原则上能延续整个工区。如果存在多个符合条件的层位,最好选择相对较浅的层位。
(2) 层位拉平。把步骤(1)拾取的层位时间投影到一条水平直线上获得投影时差,把投影时差应用于纵波动校正前的地震数据上拉平纵波构造层位。然后再把投影时差转换到P-SV域,同样拉平转换波构造层位。
(3) 层位匹配与时差计算。对步骤(2)拉平的叠前地震数据,分别在P-P波和P-SV波共检波点道集上完成速度分析;然后分别进行P-P波和P-SV波共检波点动校正以完成共检波点道集叠加;在P-P波和P-SV波共检波点道集叠加剖面层位上分别拾取构造拉平层位对应的层位,以获得P-P波和P-SV波共检波点层位拾取时间;把P-P波拾取层位时间转换到P-SV域变为T0Pj(已经完成纵波炮点和检波点静校正),P-SV波对应的拾取层位时间为T0PSj(已经应用纵波炮点校正量)。
(4) P-SV波静校正计算。把步骤(3)的拾取结果代入式(12)计算P-SV波检波点静校正量。
3 模型数据试算设计一个P-P波弹性波模拟速度模型(图 3)验证文中介绍的转换波静校正方法。P-SV波速度模型弹性波模拟由P-P波速度模型通过恒定的纵横波速度比(2.5)转换获得。采用弹性波模拟方法同时获得叠前P-P波和P-SV波炮集正演记录,然后把数据分选成共检波点记录进行模型实验。
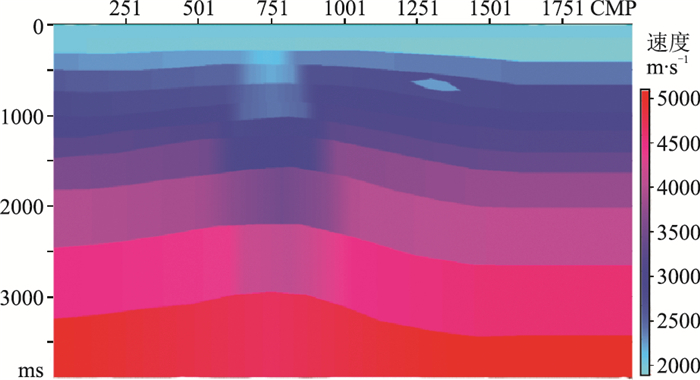
|
图 3 P-P波弹性波模拟速度模型 速度模型地表水平,存在多个反射层位,每个反射层的倾角都不一样,地表最低速度为1800 m/s,近地表第一层横向速度和近地表层厚度都有不同程度的变化。速度模型构造较复杂,速度模型网格尺寸为20 m。 |
图 4为P-P波层位拉平前、后共检波点道集叠加剖面。由于模型数据构造复杂,P-P波(图 5a)、P-SV波(图 5c)共检波点道集NMO动校正后有效信号同相轴不水平,因此很难同相叠加,起伏较大构造部分共检波点道集叠加剖面信噪比偏低,拾取检波点道集叠加剖面层位困难(图 4b),还存在双相位同相轴,很难准确拾取正确的层位。这种复杂构造共检波点道集叠加剖面信噪比低,在很大程度上降低了转换波静校正精度。
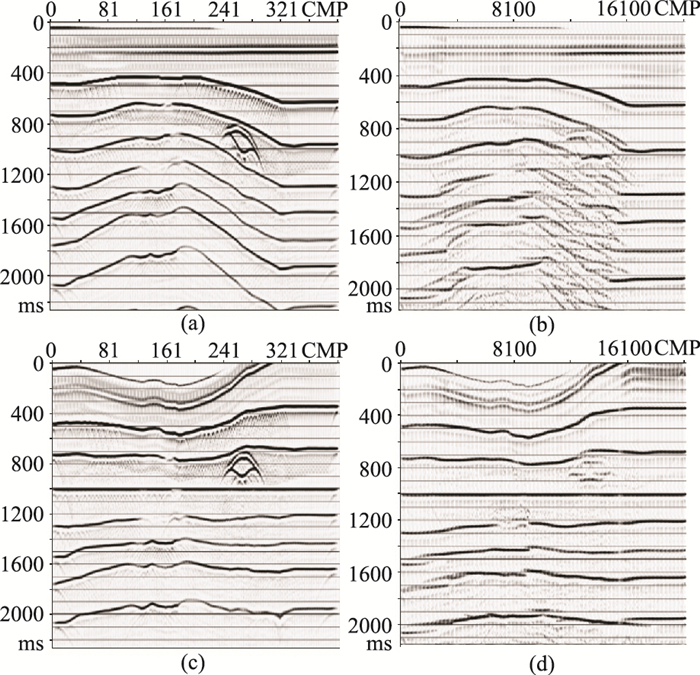
|
图 4 P-P波层位拉平前、后叠加剖面
(a)共中心点;(b)共检波点道集;(c)层位拉平后共中心点;(d)层位拉平后共检波点道集。 图a的炮点和检波点没有引入任何静校正量;图b的预处理包括动校正时差校正。 |
|
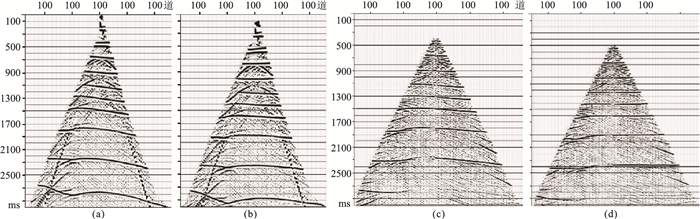
图 5 层位拉平前、后动校正共检波点道集 (a)P-P波层位拉平前;(b)P-P波层位拉平后;(c)P-SV波层位拉平前;(d)P-SV波层位拉平后 |
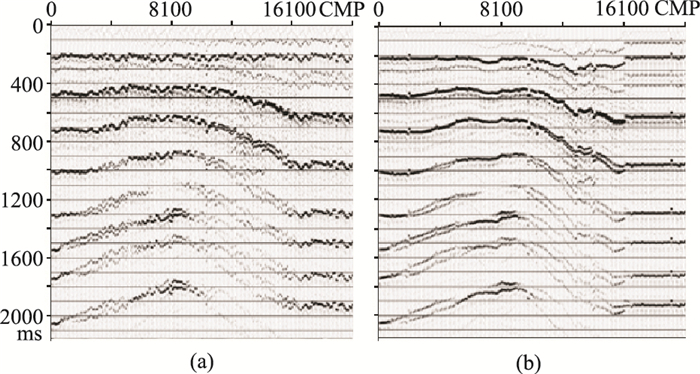
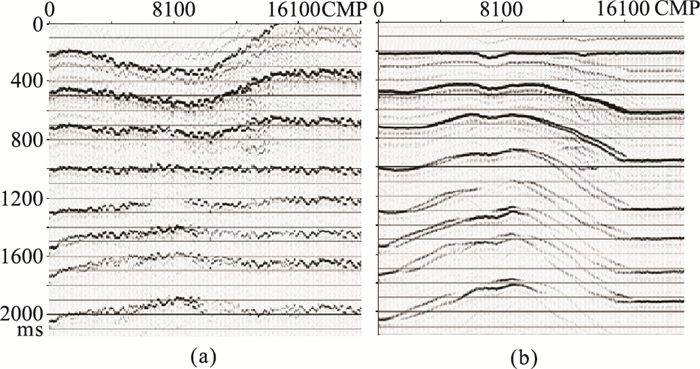
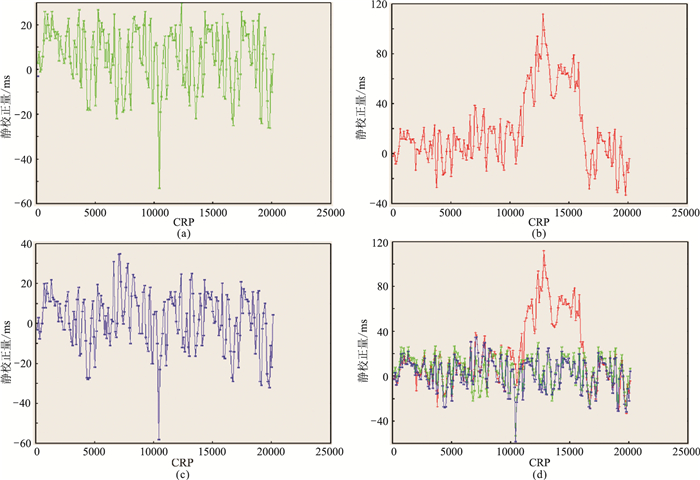
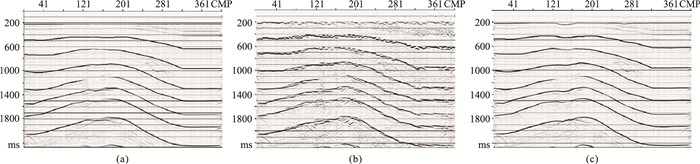
选择1000 ms处的层位(图 4a和图 4c)拉平。对比拉平前(图 4b)、后(图 4d)共检波点道集叠加剖面可见:前者几乎无法识别同相轴;后者的信噪比和分辨率得到很大提高,尤其在构造起伏较大位置,能清楚识别同相轴,明显提高了层位拾取精度,从而可以提高转换波检波点静校正精度。此外,P-P波(图 5a)和P-SV波(图 5c)层位拉平前共检波点道集1000 ms处的同相轴存在一定倾角,不能同相叠加。P-P波(图 5b)、P-SV波(图 5d)层位拉平后共检波点道集1000 ms处的同相轴已经水平,完全可以同相叠加。图 6为静校正效果。由图可见:①P-SV波模型静校正后共检波点道集叠加剖面(图 6a)未经层位拉平,叠加前进行了动校正,且引入了一套转换波检波点静校正扰动量(图 8a);②通过拾取图 6a的层位得到纵波构造约束转换波静校正量(图 8b)及其叠加剖面(图 6b),转换波静校正误差大、同相轴不清晰且欠光滑,还存在部分剩余校正量。通过拉平图 6a得到图 7a,并用本文方法获得转换波静校正量(图 8c)及转换波静校正后共检波点道集叠加剖面(图 7b)。由图 7b可见:同相轴更清晰、光滑,证明本文方法突破了常规构造约束转换波静校正计算的条件限制,获得了更高精度的转换波静校正量,满足复杂构造转换波静校正的精度要求(图 8)。由静校正叠合显示(图 8d)可以明显观察到常规转换波静校正方法得到的校正量在构造复杂层位误差很大,而本文方法完全弥补了这一缺陷,得到的转换波静校正量与引入的原始静校正量基本吻合。图 9为本文方法静校正效果对比。由图可见:模型数据引入图 8b静校正量CCP叠加剖面(图 9b)的同相轴不光滑,而原始正演模型数据CCP叠加剖面(图 9a)与转换波静校正CCP叠加剖面(图 9c)的同相轴非常光滑、相似,证明了本文方法的可靠性;图 9a与图 9c的细微差异,是由人工层位拾取欠准确所致,这也是无法避免的。模型测试结果证明本文的转换波静校正方法的精度较高。
|
图 6 静校正效果 (a)P-SV波模型静校正后共检波点道集叠加剖面;(b)常规纵波构造约束静校正后共检波点道集叠加剖面 |
|
图 7 本文P-SV波层位拉平纵波约束静校正效果 (a)图 6a的层位拉平结果;(b)本文方法静校正后共检波点道集叠加剖面 |
|
图 8 转换波静校正模型实验得到的静校正曲线 (a)引入的共检波点校正量曲线;(b)常规纵波构造约束求取的转换波静校正量曲线;(c)本文方法得到的转换波静校正量曲线;(d)图a、图b、图c叠合显示 |
|
图 9 本文方法静校正效果对比 (a)原始正演模型数据CCP叠加剖面;(b)图a引入图 8b静校正量CCP叠加剖面;(c)对图b进行转换波静校正CCP叠加剖面 |
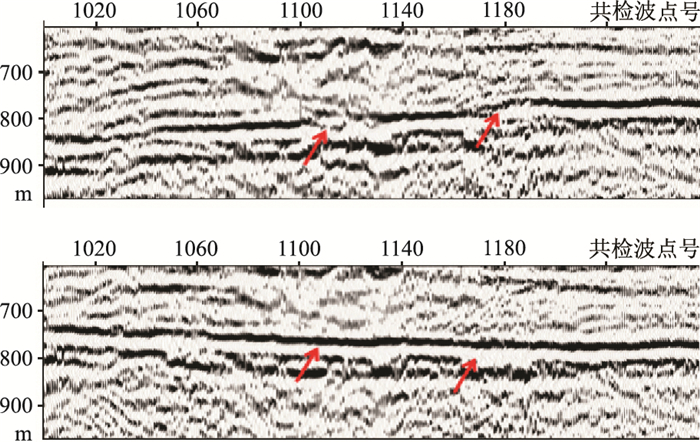
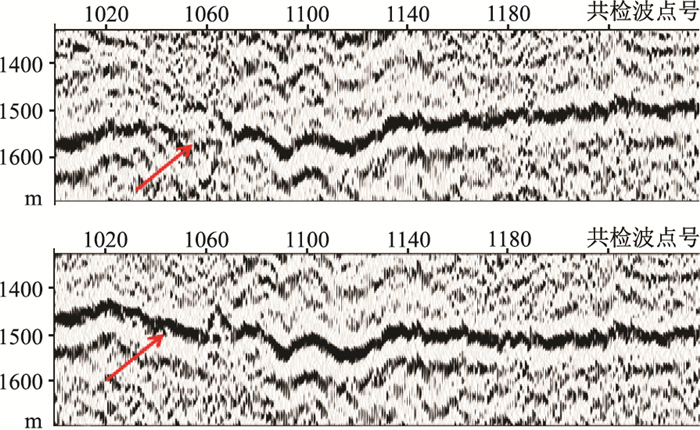
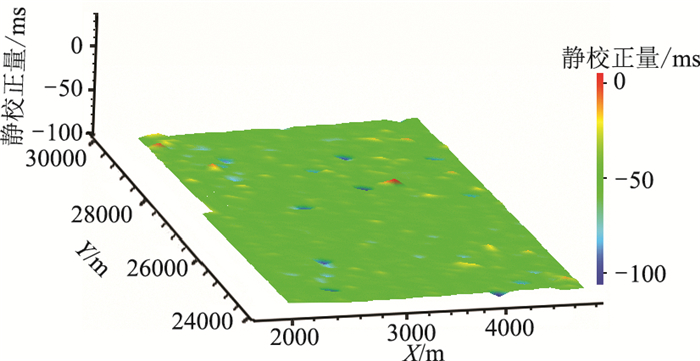
图 10和图 11分别为A区3891检波线层位拉平前、后P-P波和P-SV波共检波点道集叠加剖面。可见:①叠加剖面信噪比偏低,存在一个倾角较大的层位,转换波静校正量大,未做层位拉平的共检波点道集叠加剖面局部成像困难,拾取层位难度大(图 10上、图 11上),精确计算转换波静校正量难度较大;②层位拉平后P-P波、P-SV波共检波点道集叠加剖面的信噪比和分辨率得到明显提高(图 10下、图 11下箭头标注位置)。图 12、图 13分别为第一次迭代、第二次迭代获得的检波点转换波静校正量。由图可见,图 13的检波点转换波静校正量已经很小,这说明检波点转换波静校正计算过程经第二次迭代已经基本收敛,收敛如此之快证明了本文的转换波静校正方法的可靠性。因此应用本文方法可以快速、准确地计算转换波静校量。
|
图 10 A区3891检波线层位拉平前(上)、后(下)P-P波共检波点道集叠加剖面 |
|
图 11 A区3891检波线层位拉平前(上)、后(下)P-SV波共检波点道集叠加剖面 |

|
图 12 第一次迭代获得的检波点转换波静校正量 |
|
图 13 第二次迭代获得的检波点转换波静校正量 |
图 14、图 15分别为A区860检波线P-SV波静校正前、后CCP叠加剖面。可见后者的信噪比和分辨率得到明显提升(图 15),证明了复杂构造转换波静校正方法的可靠性。
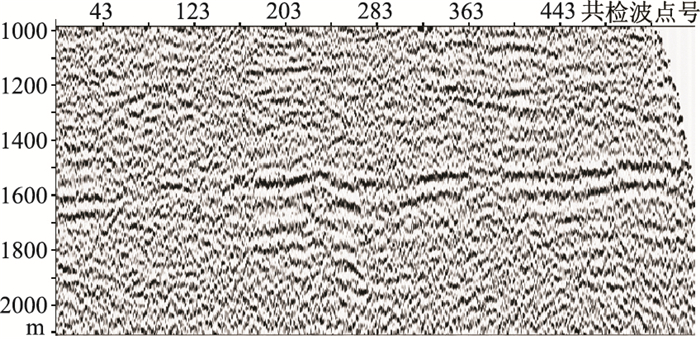
|
图 14 A区860检波线P-SV波静校正前CCP叠加剖面 |
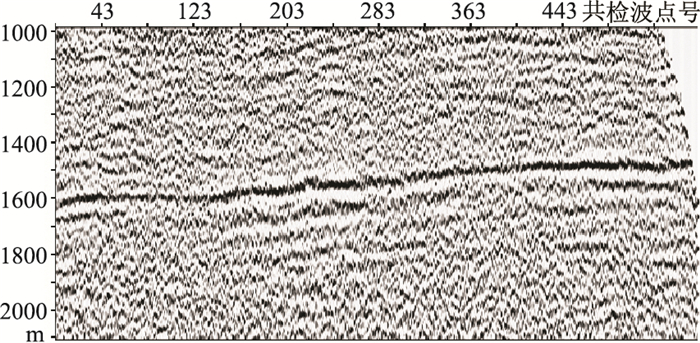
|
图 15 A区860检波线本文方法P-SV波静校正CCP叠加剖面 |
图 16、图 17分别为B区600检波线P-SV波静校正前、后CCP叠加剖面。由图可见:①叠加剖面信噪比较高,存在两个倾角较大的层位;②后者的同相轴连续性强、信噪比更高,证明了复杂构造转换波静校正方法的的有效性。
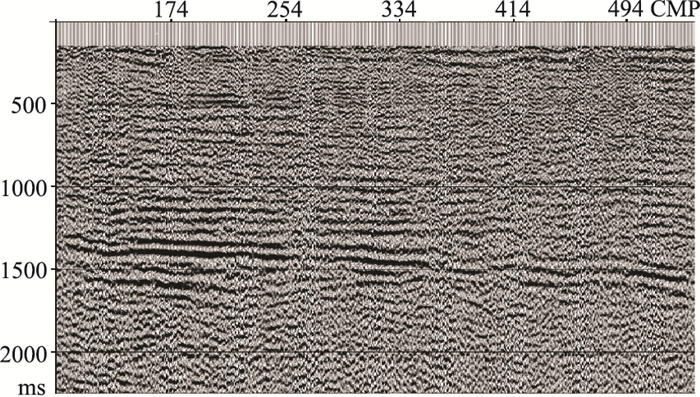
|
图 16 B区600检波线P-SV波静校正前CCP叠加剖面 |

|
图 17 B区600检波线本文方法P-SV波静校正CCP叠加剖面 |
模型数据试算和实际数据应用均严格按照P-SV波静校正计算流程实施,所获结果符合理论认识,证明了本文方法的合理性。影响转换波静校正效果的主要因素是层位拾取,层位拾取精度越高,得到的转换波静校正量越准确。本文的复杂构造转换波静校正方法具有以下优势:
(1) 通过层位拉平方法,突破了常规纵波构造约束法要求构造层位水平的条件限制,可适应地下构造起伏较大的转换波静校正计算。
(2) 本文方法通过P-P波和P-SV波共检波点速度分析,提高了P-P波和P-SV波共检波点道集叠加成像精度、叠加剖面的信噪比和分辨率,从而最终提高层位拾取精度和转换波静校正精度。
(3) 本文方法得到的转换波静校正量精度高,为后续提高反射波静校正量[12]计算精度奠定了坚实基础。为进一步改善转换波静校正效果,转换波静校正后通常还要进行转换波反射法剩余静校正[13],如果前期的转换波静校正精度越高,则建立的反射波静校正模型越精确、剩余静校正精度越高,则反射波静校正迭代更容易收敛、静校正量更可靠。
转换波静校正技术发展到今天,尽管已经具备了部分较成熟的转换波静校正方法[14],但是复杂地表转换波静校正问题在相当长的时期仍然是转换波资料处理的难题和重点之一。随着对转换波静校正问题研究的不断深入,期待逐渐开发更有效的转换波静校正方法。
| [1] |
李庆忠, 王建花. 多波地震勘探的难点与展望[M]. 山东青岛: 中国海洋大学出版社, 2007.
|
| [2] |
董敏煜. 多波多分量地震勘探[M]. 北京: 石油工业出版社, 2002.
|
| [3] |
ROY S, STEWART R R, DULAIJAN K A. S-wave velocity and statics from ground-roll inversion[J]. The Leading Edge, 2010, 29(10): 1250-1257. DOI:10.1190/1.3496915 |
| [4] |
潘树林. P-SV转换波静校正方法研究[D]. 四川成都: 成都理工大学, 2008.
|
| [5] |
MEERSMAN K D, ROIZMAN M. Converted wave receiver statics from first break mode conversions[C]. 2009 CSPG CSEG CWLS Convention Expanded Abstracts, 2009, 219-222.
|
| [6] |
MUYZERT E. Scholte wave velocity inversion for a near surface S-velocity model and PS-statics[C]. SEG Technical Program Expanded Abstracts, 2000, 19, doi: 10.1190/1.1815606.
|
| [7] |
BANSAL R, ROSS W, LEE S, et al. A novel approach to estimating near-surface S-wave velocity and converted-wave receiver statics[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 1192-1196.
|
| [8] |
孟小红, 郭良辉. 利用地震瑞利波速度反演求取P-SV波横波静校正量[J]. 石油地球物理勘探, 2007, 42(4): 448-453. MENG Xiaohong, GUO Lianghui. Using velocity inversion of seismic Rayleigh wave to compute S-wave statics of P-SV wave[J]. Oil Geophysical Prospecting, 2007, 42(4): 448-453. DOI:10.3321/j.issn:1000-7210.2007.04.017 |
| [9] |
CARY P W, EATON D W S. A simple method for resolving large converted-wave(P-SV) statics[J]. Geophysics, 1993, 58(3): 429-433. DOI:10.1190/1.1443426 |
| [10] |
HENLEY D C. Hybrid raypath interferometry: correcting converted wave receiver statics[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 1861-1865.
|
| [11] |
LIU Y, WEI X. Propagation characteristics of converted refracted wave and its application in static correction of converted wave[J]. Science in China Series D: Earth Sciences, 2008, 51(S2): 226-232. DOI:10.1007/s11430-008-6004-y |
| [12] |
赵秀莲, 许士勇, 马在田. 转换波剩余静校正方法与应用[J]. 石油地球物理勘探, 2004, 39(5): 532-538. ZHAO Xiulian, XU Shiyong, MA Zaitian. Method of PS wave residual static corrections and application[J]. Oil Geophysical Prospecting, 2004, 39(5): 532-538. DOI:10.3321/j.issn:1000-7210.2004.05.008 |
| [13] |
王建民, 刘学伟, 王桂水, 等. 转换波组合静校正技术在大庆地区的应用研究[J]. 石油物探, 2008, 47(3): 290-293. WANG Jianmin, LIU Xuewei, WANG Guishui, et al. Application study of combined static technology for P-SV wave in Daqing area[J]. Geophysical Prospecting for Petroleum, 2008, 47(3): 290-293. |
| [14] |
SCHAFER A W. The determination of converted-wave statics using P refractions togather with SV refractions[C]. SEG Technical Program Expanded Abstracts, 1999, 18, doi: 10.1190/1/1889086.
|



 熊定钰, 河北省涿州市华阳东路东方地球物理公司物探技术科技园区, 072751。Email:
熊定钰, 河北省涿州市华阳东路东方地球物理公司物探技术科技园区, 072751。Email: 