水力压裂是非常规油气资源增产的有效手段,它是通过向井筒特定段地层注入高压流体,使岩石发生破裂,可释放微地震信号[1]。微地震监测的目的在于对压裂裂缝整体效果进行评价和解释,以调整压裂参数,提高油气产量[2]。相较于井下监测方式,地面监测具有成本低、施工简单等特点,但同时地面监测数据存在噪声干扰严重、有效信号微弱、信噪比低等缺点[3-4]。信号中存在如随机噪声、强脉冲干扰、工业交流电干扰、压裂设备干扰等多种噪声[5]。微地震数据的品质直接决定着微地震定位的准确性、可靠性及后续的解释工作[6],因此,提高监测数据的信噪比是微地震数据处理的关键一步,对微地震监测技术的应用意义重大。
目前,人们提出了诸多微地震数据降噪方法,如小波变换法、f-k滤波法及奇异值分解法等[7]。这些方法主要是根据有效信号和噪声在变换域中的差异进行降噪,其中变换域和阈值大小的选择会对降噪效果产生极大影响,且对信噪比的提升幅度有限,特别是某些复杂的噪声及与有效信号在变换域重叠的噪声,降噪效果并不明显。
近年来,有学者将不同方法进行结合或改进,提高了算法的降噪性能。贾瑞生等[8]结合经验模态分解和独立成分分析方法,提出了基于盲源分离技术的微地震信号降噪方法;宋维琪等[9]应用τ-p变换有效压制了微地震信号中的线性相关噪声,提高了地面微地震事件的辨识度;程浩等[10]提出了基于小波变换的自适应阈值微震信号降噪方法,最大限度地去除高频噪声、保留低频有效信号;张唤兰等[11]采用自适应奇异值分解对微地震信号进行滤波处理,并采用AIC(Akaike信息准则)自动选取信号初至。
近年来,深度学习算法在众多信号处理任务中取得了优越的成果。其中,循环神经网络(RNN)在处理时间序列问题上表现出极大的优越性,在序列预测、语音识别与去噪[12]等领域得到了广泛的应用。针对RNN的梯度消失问题,Hochreiter等[13]提出了长短期记忆(Long Short-term Memory,LSTM)神经网络,并在序列信号的去噪中取得了显著效果。Shen等[14]利用LSTM网络对受污染的引力波信号进行去噪,能有效去除引力波中的非高斯分布和非平稳噪声,具有较强的泛化性能;汪凯翔等[15]将LSTM网络用于实测地电场数据,信噪比提高了约20 dB;Qiu等[16]利用具有长短时记忆的双向RNN压制了生物医学信号中的电力线干扰。
微地震信号在时域内是一种具有前后相关性的连续变化的序列信号。鉴于上述研究成果,本文利用双向LSTM(Bi-LSTM)网络压制微地震信号的噪声,为微地震降噪提供一种新的技术手段。仅用合成信号构建的数据集训练网络难以在实际信号降噪中取得理想结果,与前人的应用不同,本文在训练集中对合成信号添加大量的实测噪声,以期提高网络对实际监测数据的泛化能力。通过模型对微地震信号进行特征提取,在训练过程中学习到含噪信号与无噪信号之间的映射关系,以达到去噪的目的。合成信号和实际信号的处理结果表明,本文方法可以有效压制微地震信号中的多类噪声,降噪前、后数据的地震发射层析(Seismic Emission Tomography,SET)成像定位精度验证了本文方法的效果。
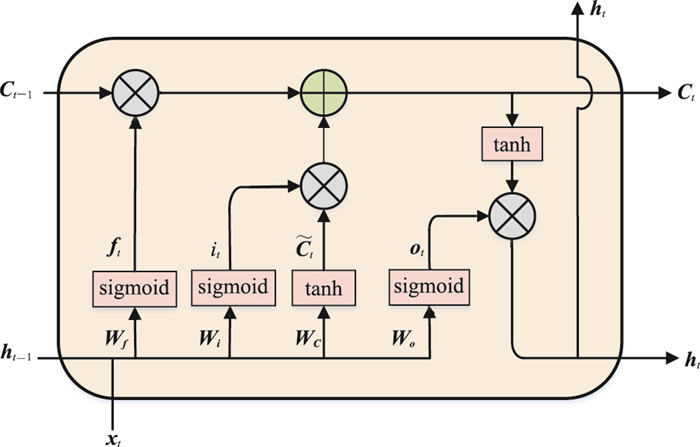
1 LSTM神经网络概述 1.1 LSTM神经网络LSTM网络是RNN的一种改进模型,有效解决了训练过程中因内部梯度受时间步长的影响而引起的梯度消失问题,在处理时序信号中具有良好表现[17]。与其他传统神经网络相比,最大的区别和优势是LSTM单元之间的循环连接使其具有记忆功能。LSTM网络包含若干个LSTM单元,每个单元由一个单元状态和三个控制单元状态的门结构组成,分别是遗忘门、输入门和输出门。LSTM网络的基本单元结构如图 1所示。
|
图 1 LSTM基本单元结构 |
LSTM网络的训练过程分为前向传播和反向传播,前向传播的过程为[18]
| $ \boldsymbol{f}_t=\operatorname{sigmoid}\left(\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right] \cdot \boldsymbol{W}_\boldsymbol{f}+\boldsymbol{b}_\boldsymbol{f}\right) $ | (1) |
| $ \boldsymbol{i}_t=\operatorname{sigmoid}\left(\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right] \cdot \boldsymbol{W}_\boldsymbol{i}+\boldsymbol{b}_\boldsymbol{i}\right) $ | (2) |
| $ \boldsymbol{o}_t=\operatorname{sigmoid}\left(\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right] \cdot \boldsymbol{W}_\boldsymbol{o}+\boldsymbol{b}_\boldsymbol{o}\right) $ | (3) |
| $ \widetilde{\boldsymbol{C}}_t=\tanh \left(\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right] \cdot \boldsymbol{W}_\boldsymbol{C}+\boldsymbol{b}_\boldsymbol{C}\right) $ | (4) |
| $ \boldsymbol{C}_t=\boldsymbol{f}_t \odot \widetilde{\boldsymbol{C}}_{t-1}+\boldsymbol{i}_t \odot \boldsymbol{C}_t $ | (5) |
| $ \boldsymbol{h}_t=\boldsymbol{o}_t \odot \tanh \left(\boldsymbol{C}_t\right) $ | (6) |
式中:xt是t时刻输入向量;ft、it、ot分别是遗忘门、输入门、输出门的控制状态;
通过反向传播减少模型输出和标签之间的损失值调整网络的参数。微地震信号降噪问题属于回归问题,选用均方误差函数作为损失函数,即
| $ L=\frac{1}{m N} \sum\limits_{i=1}^m \sum\limits_{j=1}^N\left(\hat{y}_{i j}-y_{i j}\right)^2 $ | (7) |
式中:m为样本个数;N为样本数据的长度;
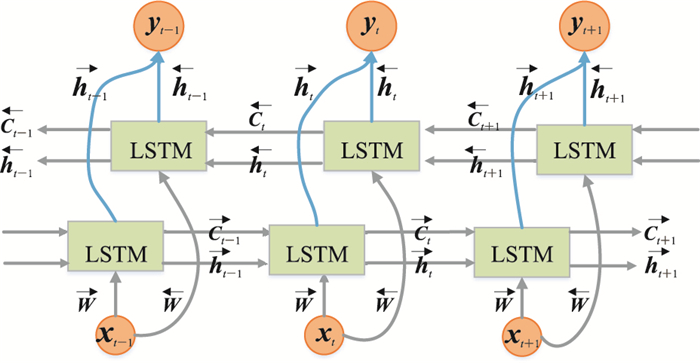
LSTM网络仅能由上一刻的数据预测该时刻之后的数据。Bi-LSTM网络[19]的创新之处在于网络中引入了未来时刻的数据信息对当前时刻的影响,综合考虑了波形数据前、后两方向的特征影响,更充分地提取微地震监测数据的时间特征。该模型工作原理如图 2所示,Bi-LSTM网络利用两个时序相反、相互独立的LSTM模型,分别参与正向计算和反向计算。网络得到两个方向的输出
|
图 2 Bi-LSTM网络结构 |
| $ \overrightarrow{\boldsymbol{h}}_t=g_1\left(\left[\boldsymbol{x}_t, \boldsymbol{h}_{t-1}\right] \cdot \overrightarrow{\boldsymbol{W}}+\boldsymbol{b}_{\vec{\boldsymbol{h}}}\right) $ | (8) |
| $ \overleftarrow{\boldsymbol{h}}_t=g_1\left(\left[\boldsymbol{x}_t, \boldsymbol{h}_{t-1}\right] \cdot \overleftarrow{\boldsymbol{W}}+\boldsymbol{b}_{\boldsymbol{h}}^{\leftarrow}\right) $ | (9) |
| $ \boldsymbol{y}_t=g_2\left(\boldsymbol{W}_1 \overrightarrow{\boldsymbol{h}}_t+\boldsymbol{W}_2 \overleftarrow{\boldsymbol{h}}_t+\boldsymbol{b}_{\boldsymbol{y}}\right) $ | (10) |
式中:
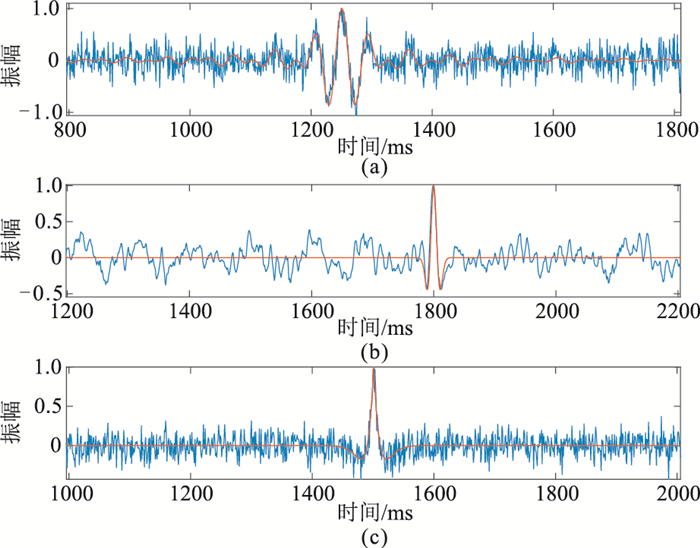
本文使用的实际数据源于川渝地区LG172油气井压裂地面微地震监测[20]。由于地面微地震监测现场会产生各种噪声,采集理想的无噪声数据极其困难,因此本文应用合成信号构建样本数据集。为了构造与真实微地震信号相似的数据集,选择与地面微地震信号特征相似的Ricker子波、可控震源子波及宽带Ricker子波进行算法仿真。假设某个震源点破裂、发生微地震事件,根据理论旅行时合成幅值不等的三种子波作为地面接收的无噪声信号[21]。其中,子波的主频范围设为35~45 Hz,采样间隔为1 ms,考虑到计算机内存及训练效率,将记录长度均设置为2.5 s。对所有合成的子波数据叠加噪声模拟实际监测到的含噪声信号,所加噪声包括不同信噪比(-14~7 dB)的高斯白噪及在原始监测信号中截取的各类实际噪声(图 3)。
|
图 3 部分合成的含噪信号(蓝色)及其标签(红色) (a)可控震源子波叠加高斯白噪;(b)Ricker子波叠加实际背景噪声;(c)宽带Ricker子波叠加实际背景噪声 |
将合成的含噪声信号作为网络的输入,对应的无噪声信号作为标签。由于微地震信号的振幅差距过大,在输入模型前需对每一组含噪信号及其标签同时进行标准化处理[22],以提高模型的收敛速度及精度,消除参数量纲差异带来的影响。本文共合成2357个样本,随机选取1900个作为训练集,457个作为测试集。
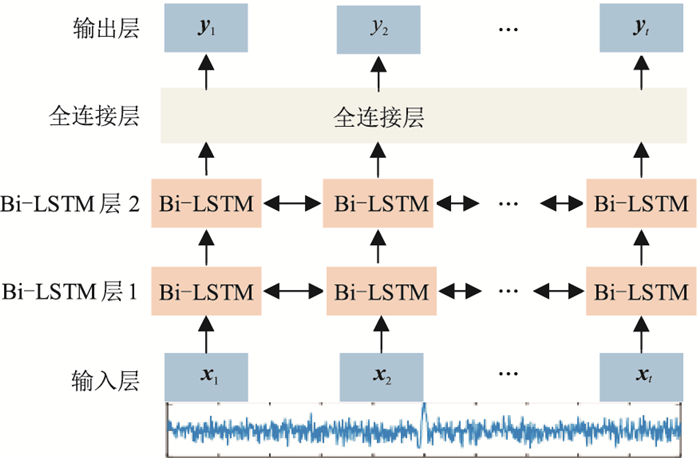
2.2 模型构建结合Bi-LSTM网络模型的相关理论,针对本文所建立的数据集,搭建的微地震信号降噪网络模型如图 4所示,包括一个输入层、两个Bi-LSTM层、一个全连接层和输出层。数据经过标准化处理后,输入层输入预处理好的2500×1的微地震信号,在每个时间点按顺序接收相应的时间序列值。两个Bi-LSTM层从输入的信号中自动学习并提取非线性特征,每个隐藏层中的双向LSTM单元循环次数为2500。由于每个LSTM单元的输入均为一维数据,将LSTM单元的的隐藏节点数设为64,过多的神经元可能会导致模型过拟合。全连接层将Bi-LSTM层2中所有神经元的输出值ht加权求和得到模型的输出,其输出结果为每一个时间节点的预测值,由输出层输出2500×1的序列数据,得到降噪后的微地震信号。
|
图 4 基于Bi-LSTM的微地震信号降噪模型 |
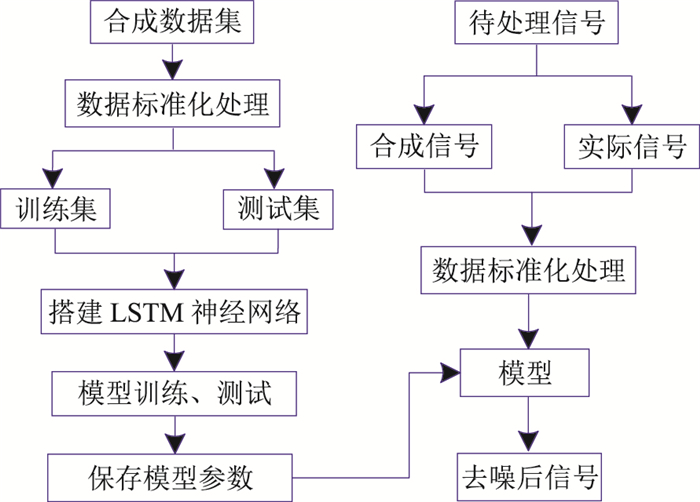
应用Bi-LSTM网络的微地震信号降噪算法流程如图 5所示,主要包括数据集构建、网络训练和实际数据测试三部分。具体步骤如下:
|
图 5 应用Bi-LSTM网络的微地震信号降噪算法流程 |
(1) 对应用Ricker子波、可控震源子波、宽带Ricker子波合成的微地震记录分别叠加高斯噪声和实际背景噪声生成数据样本,将数据进行标准化处理后划分训练集和测试集;
(2) 搭建Bi-LSTM模型,初始化模型参数;
(3) 通过训练集训练网络模型,利用测试集验证网络的性能,以找到效果最好、最合适的参数,并保存模型;
(4) 将模拟数据和实际数据分别输入到训练好的模型中得到降噪后的信号。
3 模型训练及实验分析 3.1 模型训练本文采用Python语言和Tensorflow架构作为编程环境,完成模型的训练,采用Adam算法优化参数。训练方式采用小批量输入方式(训练中设置为20个样本)以降低运算复杂度,同时在全连接层引入随机失活(Dropout)策略防止过拟合,失活率设为0.5。经过测试,学习率设为0.0001时模型降噪性能最好。经过60次迭代后损失函数值趋于收敛,然后对模型进行测试。训练和测试过程中的损失函数变化曲线如图 6所示,训练集和测试集的最终损失值分别降至0.000104、0.000249。

|
图 6 训练集和测试集损失函数变化曲线 |
为定量说明本文所提基于Bi-LSTM方法的降噪效果,应用含噪信号降噪前后的信噪比和均方根误差两个参数进行评价,其定义分别为
| $ \mathrm{SNR}=10 \lg \frac{\sum\limits_{i=1}^N y_j^2}{\sum\limits_{j=1}^N\left(y_j-\hat{y}_j\right)^2} $ | (11) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{j=1}^N\left(y_j-\hat{y}_j\right)^2} $ | (12) |
为了验证Bi-LSTM网络降噪方法的有效性,以Ricker子波为例,合成不同信噪比的微地震数据进行多组实验,并与经验模态分解(EMD)法、奇异值分解(SVD)法、常规LSTM网络法进行对比。
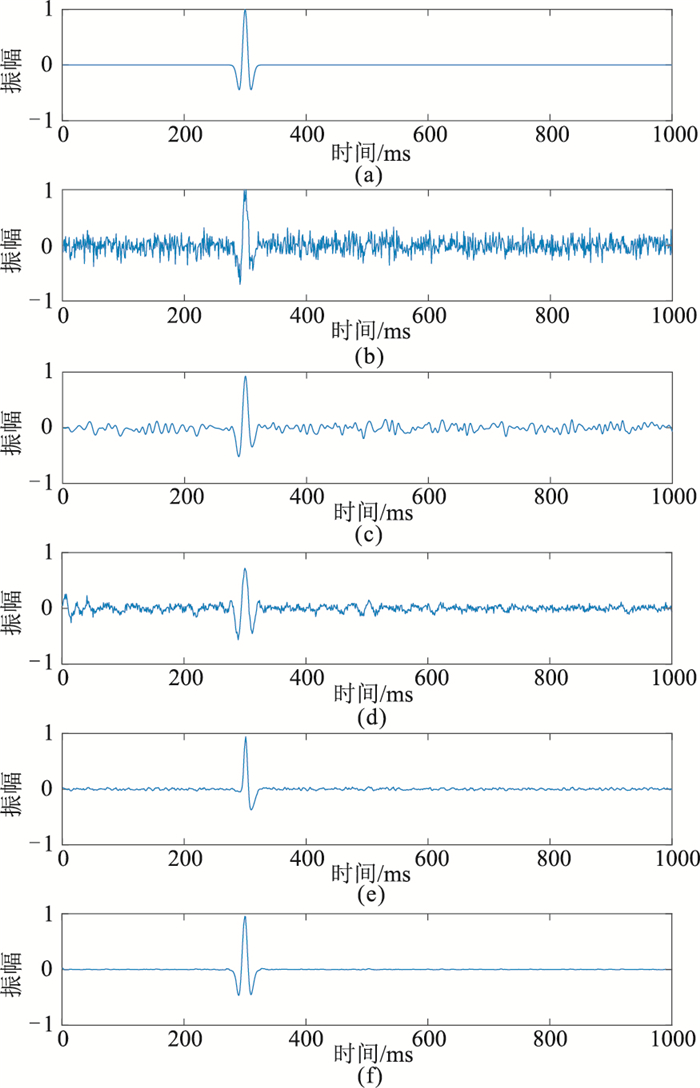
首先用Ricker子波(图 7a)与高斯噪声叠加合成信噪比分别为2、-3、-7和-11 dB微地震信号,分别记为信号1、信号2、信号3和信号4,其中信号3如图 7b所示。信号3经过EMD后,直接滤除高频成分的模态分量,虽然噪声在一定程度上得到了抑制,但仍有较多残留(图 7c)。将信号3进行SVD,设置奇异值阈值为45,重构后的信号如图 7d所示,可以看出,其有效信号的幅值与原始信号相差较大且噪声去除并不彻底。图 7e和图 7f分别为常规LSTM网络和本文的Bi-LSTM网络对信号3的降噪结果,二者均具有良好的降噪效果,但Bi-LSTM网络的噪声去除更彻底。
|
图 7 信号3不同方法降噪结果对比 (a)无噪声信号;(b)信号3;(c)EMD方法;(d)SVD方法;(e)常规LSTM方法;(f)本文的Bi-LSTM方法 |
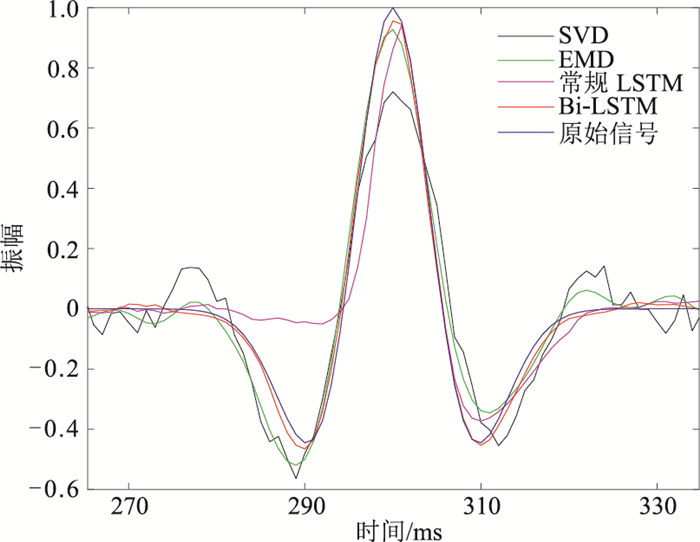
将无噪声信号及经4种降噪方法降噪结果进行局部放大对比,如图 8所示。相比于Bi-LSTM算法,由LSTM算法降噪后的信号初至较原始信号发生了变化,有效信号的形状也产生了畸变。本文方法的降噪效果在时域波形上优于EMD、SVD和常规LSTM方法,不仅噪声几乎完全被消除,且降噪后的信号与原信号的整体特征及幅值基本保持一致,局部细节更完整。Bi-LSTM方法对4道信号的降噪时间均在1 s内,效率高于SVM和EMD法。由于Bi-LSTM网络结构比LSTM复杂,训练时间略长,但降噪效果更好。
|
图 8 有效信号放大对比 |
4个不同SNR信号的四种方法降噪结果的SNR、RMSE统计如表 1所示,可见,无论降噪前信噪比高低,本文方法降噪结果的SNR都提升了20 dB以上,SNR最高、RMSE最小。本文方法可用同一个网络模型实现对不同SNR信号降噪,降噪效果最好。
|
|
表 1 不同信噪比信号四种方法降噪性能对比 |
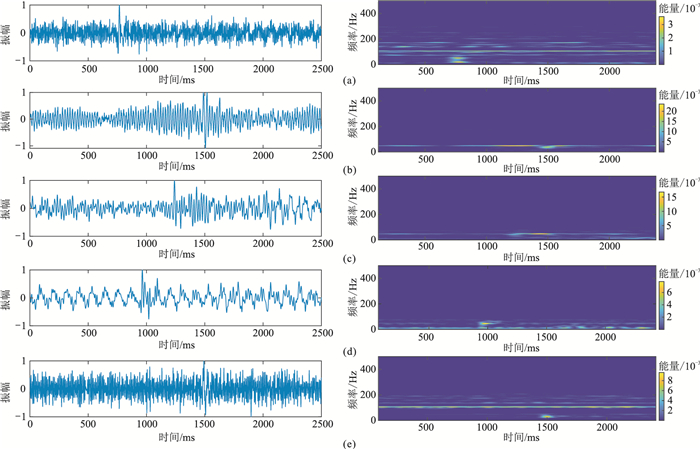
将Bi-LSTM网络降噪方法应用于LG172井的实际地面微地震监测数据,验证其实用性。首先选取五道含不同类型噪声的典型信号,从中截取包含有效信号的2500个样点。将截取后的五道信号分别输入到已训练好的网络进行降噪,并采用短时傅里叶变换分析降噪前、后的时频特性。五道信号降噪前、后的时域波形及时频谱分别如图 9和图 10所示。
|
图 9 五道实际微地震信号波形(左)及时频谱(右) (a)第一道;(b)第二道;(c)第三道;(d)第四道;(e)第五道 |
|
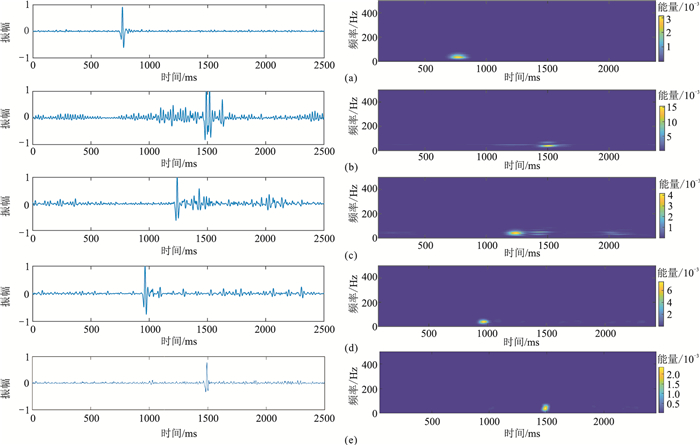
图 10 五道实际微地震信号本文方法降噪结果的波形(左)及时频谱(右) (a)第一道;(b)第二道;(c)第三道;(d)第四道;(e)第五道 |
第一道信号中所含噪声为频率分布在0~300 Hz的随机噪声,有效信号几乎淹没于噪声之中(图 9a);降噪后的时域波形有效信号清晰可见,消除了大量随机噪声,从时频图中可以清晰看出有效信号的分布(图 10a)。第二道的噪声在时域中表现为波浪型分布,是典型的压裂设备干扰(图 9b);经本文方法降噪之后,基本保留了有效信号的原始特征,去除了压裂干扰(图 10b)。第三道和第四道的噪声属于低频噪声,即使噪声与有效信号的频带重叠(图 9c、图 9d),模型也具有良好的降噪效果,滤除了信号中、低频噪声(图 10c、图 10d)。第五道的噪声主要为固定频率噪声(图 9e),频率为100、150和180 Hz的噪声均被消除(图 10e)。由此可见,本文方法能有效消除实际微地震信号中的各类噪声,精确保持了有效信号形态,提高了微地震监测数据的品质。
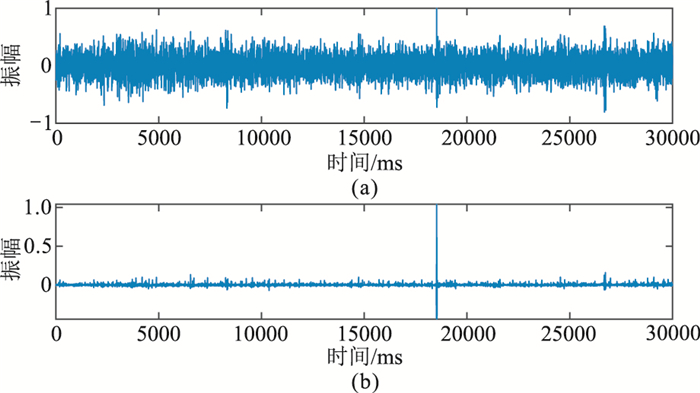
网络每次输入的波形长度是有限的,仅为2500个样点,一般实际数据长度约为30~60 s。图 11a为一道经数据标准化处理后的完整微地震监测数据,长度为30 s。若实现对该信号的降噪,需将其截断为12段数据,每段长度均为2500个样点;再按顺序输入到训练好的网络;最后将每一段降噪后的数据进行拼接后得到该道信号完整的降噪波形,如图 11b所示。
|
图 11 完整实际微地震信号(a)及本文方法降噪结果(b) |
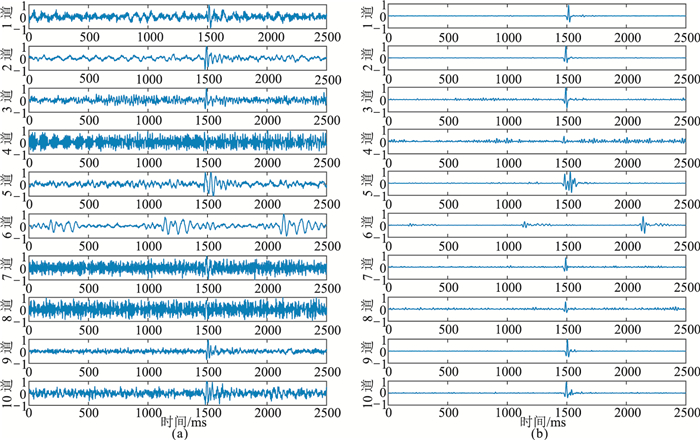
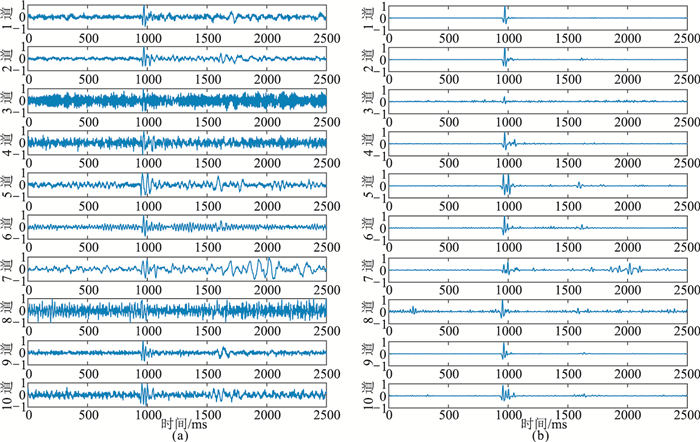
将本文方法用于多道实际微地震信号降噪。LG172井采用33个地面站点进行微地震压裂监测。本文将33道微地震数据分为3组,其中第1组和第2组原始数据如图 12a、图 13a所示。本文方法的降噪结果如图 12b、图 13b所示。对比降噪前、后波形可见,降噪后的曲线突出了有效信号,随机噪声、压裂设备干扰等均被压制。总体来看,网络对于信噪比越高的信号降噪效果越好,如第1组实测数据中的第2、第3、第9道信号,噪声几乎被完全消除;对于信噪比较低的信号,仍会存在少量残留噪声,如第1组实测数据的第3和第8道。由于设置的样本的信噪比跨度很大,且模型提取的是所有信号的共同特征,所以会造成每道信号的噪声压制程度各不相同。另外,网络在某些情况下会出现误判现象,由微地震信号的相关性[21]可知,第2组实测数据仅有一个微地震事件,而第7道信号降噪后检测出两个微地震信号。原因可能是其噪声的特征与有效信号特征极为相似而被网络错误识别为有效信号。总之,本文方法在很大程度上提高了微地震数据的信噪比,有利于后续震源定位。
|
图 12 LG172井第1组原始监测数据(a)及本文方法降噪结果(b) |
|
图 13 LG172井第2组原始监测数据(a)及本文方法降噪结果(b) |
提高震源定位精度是微地震信号降噪的目的。因此,分析微地震信号降噪前、后的定位精度是检验本文算法有效性和实用性的有力凭证。SET成像是一种地面微地震监测的震源定位方法,当监测站点数固定时,信噪比越高,成像越聚焦,定位越准确;相反,信噪比越低,成像的聚焦性就越差[23-25]。
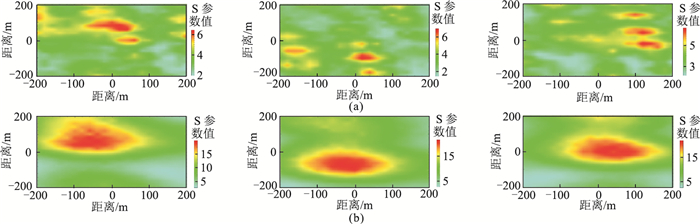
第1组~第3组实测数据的33道原始信号与降噪后信号的定位结果如图 14所示。第1组实测数据降噪前成像虽有较明显的焦点,但受噪声的影响定位误差较大。第2组和第3组实测数据降噪前的SET成像聚焦性较差,强噪声造成图中具有多个局部聚焦点,定位结果不可靠;而降噪后的成像图能量聚焦性明显提高,可以准确定位震源位置。由此可见,微地震信号降噪有效解决了噪声导致的SET成像定位不准确问题。
|
图 14 LG172井3组实测数据降噪前(a)、后(b)SET成像结果对比 左、中、右分别为第1、第2、第3组数据。 |
利用常规降噪方法处理微地震信号存在一定的局限性,难以解决海量微地震信号降噪问题。本文提出了一种应用Bi-LSTM网络的微地震信号降噪方法,为了减小训练集和测试集之间的分布差异,利用合成信号和实际噪声构造样本数据集对模型进行训练和测试。使用训练好的Bi-LSTM网络对不同信噪比的合成数据以及川渝地区LG72井微地震监测数据进行降噪,取得了较好效果。
(1) 合成信号和实际信号的降噪结果表明,信噪比越高,对噪声的压制程度越大。而信噪比较低的信号降噪后可能会存在一些残留噪声,但即使完全被噪声淹没的信号降噪后仍然可以清晰地识别有效信号。由此可见,本文的降噪方法对噪声程度具有良好的适应性。
(2) 微地震信号作为一种时间序列数据,Bi-LSTM网络相较于LSTM网络能更充分地提取时间特征信息,挖掘序列前、后相关性。与EMD、SVD、常规LSTM方法相比,无论是定性分析还是定量结果,Bi-LSTM网络都具有更强的降噪性能。与传统方法相比,本文方法避免了变换域的选择、阈值大小设定等一系列繁杂流程,在训练过程中自动提取特征。将33道实际信号输入网络中可在1 s内输出降噪结果,面对海量数据可以短时间内完成多道信号的降噪。
(3) 本文构建的数据集有限,对其他地区压裂微信号降噪效果不理想。通过添加新的监测井数据补充训练集,以识别更多的噪声特征以提高模型的降噪性能。
| [1] |
段银鹿, 李倩, 姚韦萍. 水力压裂微地震裂缝监测技术及其应用[J]. 断块油气田, 2013, 20(5): 644-648. DUAN Yinlu, LI Qian, YAO Weiping. Microseismic fracture monitoring technology of hydraulic fracturing and its application[J]. Fault-Block Oil & Gas Field, 2013, 20(5): 644-648. |
| [2] |
邵晓光, 董宏丽, 代丽艳. 微地震监测技术综述[J]. 吉林大学学报(信息科学版), 2018, 36(1): 55-61. SHAO Xiaoguang, DONG Hongli, DAI Liyan. Review of microseismic monitoring technology[J]. Journal of Jilin University (Information Science Edition), 2018, 36(1): 55-61. |
| [3] |
张晟瑞, 任朝发, 李星缘, 等. 地面微地震资料噪声压制方法[J]. 地球物理学进展, 2018, 33(6): 2522-2527. ZHANG Shengrui, REN Chaofa, LI Xingyuan, et al. Denoising method of surface microseismic data[J]. Progress in Geophysics, 2018, 33(6): 2522-2527. |
| [4] |
刁瑞, 吴国忱, 尚新民, 等. 地面微地震有源噪声自动识别与匹配压制方法[J]. 石油地球物理勘探, 2018, 53(2): 311-319. DIAO Rui, WU Guochen, SHANG Xinmin, et al. Microseismic active noise automatic identification and matching denoising[J]. Oil Geophysical Prospecting, 2018, 53(2): 311-319. |
| [5] |
刁瑞, 吴国忱, 尚新民, 等. 地面阵列式微地震数据盲源分离去噪方法[J]. 物探与化探, 2017, 41(3): 521-526. DIAO Rui, WU Guochen, SHANG Xinmin, et al. The blind separation denoising method for surface array micro-seismic data[J]. Geophysical and Geochemical Exploration, 2017, 41(3): 521-526. |
| [6] |
唐杰, 张文征, 梁雨薇, 等. 自适应数据驱动的紧框架微地震数据随机噪声压制[J]. 石油地球物理勘探, 2019, 54(5): 954-961. TANG Jie, ZHANG Wenzheng, LIANG Yuwei, et al. A random-noise suppression approach with self-adaptive data-driven tight frame for microseismic data[J]. Oil Geophysical Prospecting, 2019, 54(5): 954-961. |
| [7] |
代丽艳, 董宏丽, 李学贵. 微地震数据去噪方法综述[J]. 吉林大学学报(地球科学版), 2019, 49(4): 1145-1159. DAI Liyan, DONG Hongli, LI Xuegui. Review of microseismic data denosing methods[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(4): 1145-1159. |
| [8] |
贾瑞生, 赵同彬, 孙红梅, 等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报, 2015, 58(3): 1013-1023. JIA Ruisheng, ZHAO Tongbin, SUN Hongmei, et al. Microseismic signal denoising method based on empi-rical mode decomposition and independent component analysis[J]. Chinese Journal of Geophysics, 2015, 58(3): 1013-1023. |
| [9] |
宋维琪, 刘太伟. 地面微地震资料τ-p变换噪声压制[J]. 石油地球物理勘探, 2015, 50(1): 48-53. SONG Weiqi, LIU Taiwei. Surface microseismic noise suppression with τ-p transform[J]. Oil Geophysical Prospecting, 2015, 50(1): 48-53. |
| [10] |
程浩, 袁月, 王恩德, 等. 基于小波变换的自适应阈值微震信号去噪研究[J]. 东北大学学报(自然科学版), 2018, 39(9): 1332-1336. CHENG Hao, YUAN Yue, WANG Ende, et al. Study of hierarchical adaptive threshold micro-seismic signal denoising based on wavelet transform[J]. Journal of Northeastern University (Natural Science), 2018, 39(9): 1332-1336. |
| [11] |
张唤兰, 朱光明, 王保利. Hankel矩阵滤波在微地震数据处理中的应用[J]. 煤田地质与勘探, 2014, 42(1): 72-75. ZHANG Huanlan, ZHU Guangming, WANG Baoli. Application of Hankel matrix filtering in microseismic data processing[J]. Coal Geology & Exploration, 2014, 42(1): 72-75. |
| [12] |
XU Y, DU J, DAI L R, et al. An experimental study on speech enhancement based on deep neural networks[J]. IEEE Signal Processing Letters, 2014, 21(1): 65-68. |
| [13] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. |
| [14] |
SHEN H Y, GEORGE D, HUERTA E A, et al. Denoising gravitational waves with enhanced deep recurrent denoising auto-encoders[C]. IEEE International Conference on Acoustics, Speech and Signal Proces-sing (ICASSP), 2019, 3237-3241.
|
| [15] |
汪凯翔, 黄清华, 吴思弘. 长短时记忆神经网络在地电场数据处理中的应用[J]. 地球物理学报, 2020, 63(8): 3015-3024. WANG Kaixiang, HUANG Qinghua, WU Sihong. Application of long short-term memory neural network in geoelectric field data processing[J]. Chinese Journal of Geophysics, 2020, 63(8): 3015-3024. |
| [16] |
QIU Y, HUANG, XIAO F, et al. A segment-wise reconstruction method based on bidirectional long short term memory for power line interference suppression[J]. Biocybernetics and Biomedical Engineering, 2018, 38(2): 217-227. |
| [17] |
张荣, 李伟平, 莫同. 深度学习研究综述[J]. 信息与控制, 2018, 47(4): 385-397, 410. ZHANG Rong, LI Weiping, MO Tong. Review of deep learning[J]. Information and Control, 2018, 47(4): 385-397, 410. |
| [18] |
GOODFELLOW I, BENGIO Y, COURVILLE A. Deep Learning[M]. Cambridge: The MIT Press, 2016.
|
| [19] |
GRAVES A, SCHMIDHUBER J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures[J]. Neural Networks, 2005, 18(5-6): 602-610. |
| [20] |
盛立, 徐西龙, 王维波, 等. 基于时频分析和卷积神经网络的微地震事件检测[J]. 中国石油大学学报(自然科学版), 2021, 45(5): 54-63. SHENG Li, XU Xilong, WANG Weibo, et al. Detection of microseismic events based on time-frequency analysis and convolutional neural network[J]. Journal of China University of Petroleum (Edition of Natural Science), 2021, 45(5): 54-63. |
| [21] |
王维波, 徐西龙, 盛立, 等. 卷积神经网络微地震事件检测[J]. 石油地球物理勘探, 2020, 55(5): 939-949. WANG Weibo, XU Xilong, SHENG Li, et al. Detection of microseismic events based on convolutional neural network[J]. Oil Geophysical Prospecting, 2020, 55(5): 939-949. |
| [22] |
许滔滔, 王中兴, 肖卓伟, 等. 基于LSTM循环神经网络的大地电磁工频干扰压制[J]. 地球物理学进展, 2020, 35(5): 2016-2022. XU Taotao, WANG Zhongxing, XIAO Zhuowei, et al. Magnetotelluric power frequency interference suppression based on LSTM recurrent neural network[J]. Progress in Geophysics, 2020, 35(5): 2016-2022. |
| [23] |
KUGAENKO Y, SALTYKOV V, SINITSYN V, et al. Passive seismic monitoring in hydrothermal field: seismic emission tomography[C]. Proceedings World Geothermal Congress 2005, 2005, 1-6.
|
| [24] |
CHAMBERS K, KENDALL J M, BRANDSBERG-DAHL S, et al. Testing the ability of surface arrays to monitor microseismic activity[J]. Geophysical Prospecting, 2010, 58(5): 821-830. |
| [25] |
王维波, 官强, 高明, 等. 利用残差网络和地震发射层析成像的微地震事件检测[J]. 石油地球物理勘探, 2022, 57(2): 251-260. WANG Weibo, GUAN Qiang, GAO Ming, et al. Detection of microseismic events based on residual network and seismic emission tomography[J]. Oil Geophysical Prospecting, 2022, 57(2): 251-260. |



 盛立, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)控制科学与工程学院, 266580。Email:
盛立, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)控制科学与工程学院, 266580。Email: 