2. 中国石油天然气集团物联网重点实验室, 甘肃兰州 730020;
3. 中国科学技术大学地球和空间科学学院, 安徽合肥 230026
2. Key Laboratory of Internet of Things, CNPC, Lanzhou, Gansu 730020, China;
3. School of Earth and Space Sciences, University of Science and Technology of China, Hefei, Anhui 230026, China
地震反射层位的精确解释是建立地下构造和地层模型的前提。为了从地震数据体中提取地震反射层位,很多学者提出了不同的自动或半自动追踪算法,如地震瞬时相位[1]、地震波形分类[2]、追踪反射层方向[3]等。尽管这些方法能够处理横向相干反射,但对反射结构和地层的不连续性比较敏感,通常难以正确追踪被断层错断的层位。
相对地质时间(Relative Geological Time,RGT)体估计是由Stark[1]提出的一种从地震数据中提取构造信息的技术。在RGT体中,每一个采样点被赋予一个相对地质时间值,相邻的具有相同地质时间的采样点的集合可表征一个地层界面。因此,一旦获得了精确的RGT体,就可以在其中提取所有类型的地质构造,如地震反射层位可以由RGT体的等值面表示等。为了获得RGT体,有学者提出了利用地震道瞬时相位信息计算RGT体的相位展开方法[1];此外,也可以利用平面波重建(PWD)方法计算的局部反射斜率估算RGT体[4]。尽管这些方法能够正确地捕捉局部结构特征,但始终遵循横向反射层是连续的这一条件,因此无法追踪被断层明显错断的反射层。
深度学习技术[5]依据数据驱动,从标签数据或过去的经验中得到输入与输出之间的映射函数。其中监督学习的深度学习方法能够从训练数据集中提取相关特征和知识,以捕获高度复杂和强非线性的关系[6]。很多学者从自然图像智能处理[7-11]中受到启发,将深度学习方法成功用于地球物理问题的解决,如河道体解释[12-13]、溶洞识别[14]、断层检测[15]、波形反演[16]和噪声衰减[17]等。Geng等[18]证明了为自然图像分割任务设计的U形网络结构可以成功地用于二维RGT体的估计。该网络通过处理多尺度结构特征,逐步提取地震数据体的高度抽象表示和信息,通过多层级处理,网络的输出能从一个全局的感受野收集空间信息,以表征地震数据体中所有的结构。为了提高该方法表征非线性关系的能力,在编码器—解码器框架中使用多级联的残差学习模块构建一个非常深的网络。尽管网络深度被认为是许多计算机视觉问题的一个核心因素[19-20],但简单地堆叠残差模块形成更深的网络很难使算法获得进一步的改善,并且更深的网络通常更难被训练。因此,一个更复杂的网络是否对RGT体估计有积极作用,以及如何构建一个可训练的深度网络,都还有待研究。另外,过度使用下采样处理会在网络中产生非常小的特征图像,使结构信息几乎无法保存,并显著增加模型参数。三维地震数据体处理需要的大量计算成本(GPU内存),导致该方法的应用受到限制。另一方面,该网络缺少对不同特征图进行区分学习的能力,因此它会平等地对待每个通道特征,可能不会关注具有不同形状、大小的地震反射结构。并且,Geng等[18]使用的传统的逐点比较的损失函数也无法准确区分目标与预测RGT体之间的结构差异。
为了克服Geng等[18]方法的缺陷,本文提出一种简化的三维深度神经网络,它具有编码器—解码器结构和注意力机制,能够从输入的地震波形逐点预测相对地质时间,以实现精确的地质结构解释,同时不需要花费大量的计算成本。该网络首先将多次下采样得到的特征连接在不同的空间尺度上,然后系统地聚合下采样得到的低频信息与上采样得到的高频信息捕获特征细节并保持原来的空间分辨率,进一步借助注意力机制在自主学习和增强相关特征的同时抑制无关特征,最终实现准确的RGT体预测。
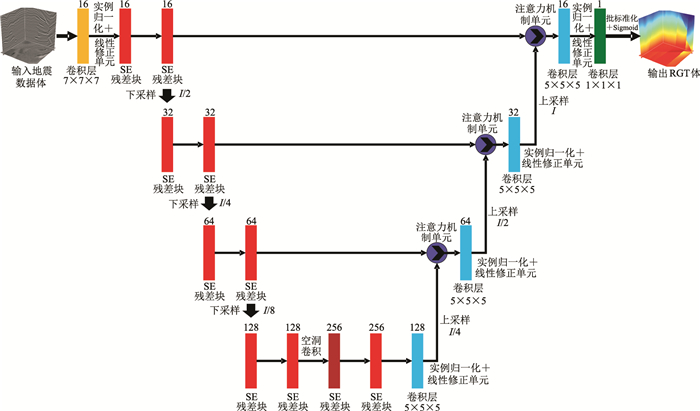
1 自动相对地质时间体估计网络架构本文网络(图 1)使用编码器—解码器框架[2],编码器由21个卷积层组成,以系统地聚合多尺度结构特征。网络从7×7×7卷积层开始,后接实例归一化层和修正线性单元。在输入地震数据体后,第一个卷积层计算其16个局部平移不变的低层特征数据,然后将它们输入多级联残差学习模块。连续的两个压缩和激励(Squeeze-and-Excitation,SE)残差块(图 1中红色矩形块)用于对特征数据进行下采样,以扩大卷积层的感受野。如图 1所示,通过系统地分析四个下采样率(分别为2、4、8、16)的多尺度模式,逐步提取抽象的知识表达,每个特征尺度由两个SE残差块组成,这种多尺度结构分析方法不仅提高了预测精度,而且有效地节省了计算量。
|
图 1 实现自动RGT体估计的深度神经网络架构 I表示输入地震数据体的尺寸。 |
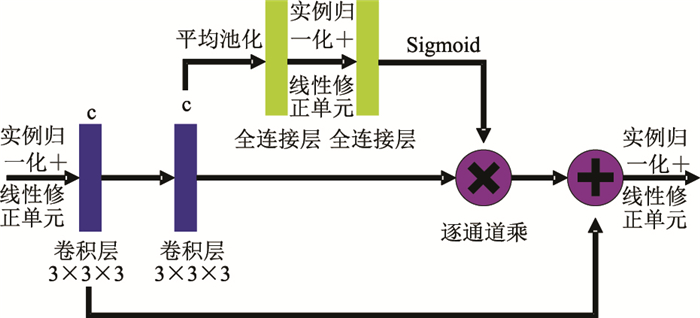
目前主流的基于卷积神经网络(Convolutional Neural Network,CNN)的方法均以渐进的方式对特征数据进行下采样,以获得足够大的感受野,从而稳健地拟合标签数据。然而,当过多的下采样处理消除了局部构造信息后,便很难从地震数据中准确地捕捉到所有的构造特征。为了保持原来的空间分辨率和多尺度感受野,在编码器最后一个尺度级别用空洞卷积[21]操作替换下采样(图 1),避免产生过小尺寸的特征数据。如图 2所示,每个SE残差块[22]由两个具有相同核尺寸(3×3×3)的卷积层组成,其后连接实例归一化层和线性修正单元。在这两个卷积层上增加一个跳跃连接,将SE残差块表示为残差学习函数,可以有效地在整个网络中反向传播梯度信息。
|
图 2 SE残差块架构 |
在标准的CNN中,残差通过融合所有特征数据得到,不同通道间的相关关系相互纠缠,阻碍了网络的表征能力。而本文SE残差块使用通道注意力机制(Channel-Wise Attention)[22-24]学习不同特征数据之间的关系,使其中相关特征被强调,不相关特征被抑制。
通道注意力机制通过压缩和释放两个步骤实现。在压缩步骤中,将从上一卷积层中提取的带m个通道的残差特征输入平均池化层,该池化层聚集跨空间维度的结构信息以产生全局特征响应的嵌入编码。在释放步骤中,以该嵌入编码作为输入,通过两个全连接层和Sigmoid激活函数生成归一化的通道权重集合。计算出的权值用于对残差特征进行跨通道的校正,从而估算出每个SE残差块的输出。此外,即使对于大尺寸地震数据体,执行这样的特征校正也只是稍微增加模型的复杂性和计算成本,这对于三维地震数据处理尤为重要。
解码器主要执行上采样和特征提取,以将编码特征映射回输入尺寸,并对地震数据体上所有采样点的RGT体值进行预测。在每个尺度上,使用简单的三线性插值进行上采样,采用无需训练的参数补偿两个串联特征之间尺寸的不匹配。上采样后的特征数据输入到一个5×5×5卷积层、实例归一化层和线性修正单元函数,以进一步提取特征。编码器和解码器通过3个不同尺度的跳跃连接相连,不仅补偿了空间分辨率,且聚合了多尺度的结构模式。在输出层应用线性变换(1×1×1卷积层)融合所有解码的特征,即可得到最终的预测结果。一旦获得了精确的RGT体,便可以在相应的地震数据体中提取所有类型的地质结构,例如地震反射层位可以由RGT体的等值面表示等。
2 损失函数和评价指标相对地质时间体的估计是一个标准的回归问题,其中地震数据体中每一采样点上的相对地质时间值对应其振幅值。在许多回归问题中,均方误差(Mean-Square-Error,MSE)是一种常用的度量准则,用于逐像素地比较预测结果与实际标签之间的差异。其表达式为
| $ \mathrm{MSE}=\frac{1}{N} \sum\limits_{i=1}^N\left(x_i-y_i\right)^2 $ | (1) |
式中:xi和yi分别表示第i个预测结果和实际标签;N是训练样本的总数。
地震数据体由强相关特征组成,这些相关性存在于承载地质结构空间特征的振幅信息中。一般来说,均方误差具有加速优化求解和稳定计算过程的优点,但不适用于表征结构误差,尤其是对于如断层、层位等结构。例如,当所有地震反射层位都得到正确解释时,断层可以简单地视为横跨多个层位的不连续面。由于MSE这种逐点度量的方式不足以准确表示这些关系,具有类似误差的两个预测结果可能含有显著不同的结构特征。
为了正确度量RGT体估计的误差,本文使用基于结构相似性的性能准则(Structrual Similarity Index Metric,SSIM)[25]作为损失函数。SSIM最初是一个基于自然图像结构退化的度量指标,用于量化畸变图像与参考图像之间误差的可见性,在各种计算机视觉任务中表现出了良好的性能。在三维RGT体估计问题中,将SSIM定义为
| $ \operatorname{SSIM}=\frac{\left(2 \mu_x \mu_y+C_1\right)\left(2 \sigma_{x y}+C_2\right)}{\left(\mu_x^2+\mu_y^2+C_1\right)\left(\sigma_x^2+\sigma_y^2+C_2\right)} $ | (2) |
式中:C1、C2是两个由输入RGT体的平均动态范围l确定的常数因子,用于稳定计算,其中C1=(k1×l)2,C2=(k2×l)2,本文设置k1=0.01,k2=0.03,l=0.5;μ、σ分别为RGT体的均值和标准差,下标x、y分别表示预测RGT体和实际RGT体标签;σxy为两个RGT体的协方差。
本文从μ、σ和σxy三个方面评价结构相似性。为了估计SSIM,首先构建一个尺寸为11×11×11样本的3D高斯窗,然后逐点移动该窗,并在每次窗口滑动时根据式(2)计算对应的局部结构相似度,从而得出整个数据体上每个采样点的SSIM系数。将所有SSIM系数的平均数作为预测结果与标签RGT体之间的全局结构相似性,即SSIM误差。仅在两个RGT体完全相同的情况下,估计的SSIM才能达到最大值1,即表示完全一致的结构相似性;相反,当SSIM值为0时,则表示二者之间几乎没有结构相似性。因此,本文在训练中最小化RGT损失函数以优化网络性能
| $ L_{\mathrm{RGT}}=1-|\mathrm{SSIM}| $ | (3) |
在训练RGT体估计网络的过程中,本文使用多种类型的评价指标,包括平均绝对误差(MAE)、均方根误差(RMSE)和平均相对百分比差异(MRPD),从多个角度定量地评估预测结果。具体如下
| $ \mathrm{MAE}=\frac{1}{n} \sum\limits_{i=1}^n\left|x_i-y_i\right| $ | (4) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(x_i-y_i\right)^2} $ | (5) |
| $ \mathrm{MRPD}=\frac{2}{n} \sum\limits_{i=1}^n \frac{\left|x_i-y_i\right|}{\left|x_i\right|+\left|y_i\right|} $ | (6) |
式中:n表示输入的地震数据体中所有采样点的数量;|·|表示取绝对值运算。RMSE和MAE用于逐点计算标签与预测结果之间的差异,而MRPD表示它们的百分比差异的平均值。与MAE相比,RMSE由于额外的平方运算而对预测误差的变化程度更为敏感。
3 网络的训练与验证RGT体估计是一个有监督的学习任务,这意味着训练网络通常需要大量带标注的数据才能获得期望的效果。然而,对一个在工区采集的实际数据,很难完整地标注所有地质结构。为了在实际数据稀少的情况下训练网络,本文利用Wu等[26]提出的方法,通过对初始水平模型进行褶皱和断裂变形,生成具有逼真构造特征的合成训练数据集和验证数据集;分别使用1000对和100对合成的三维地震数据体以及相应的RGT体标签对本文网络进行训练和验证,每个数据体的尺寸为128×128×128。为了保证网络的收敛性和泛化能力,对所有的地震数据体和RGT体均进行了标准化处理,即将输入地震数据体和输出RGT体的数值范围都归一化到0~1.0。
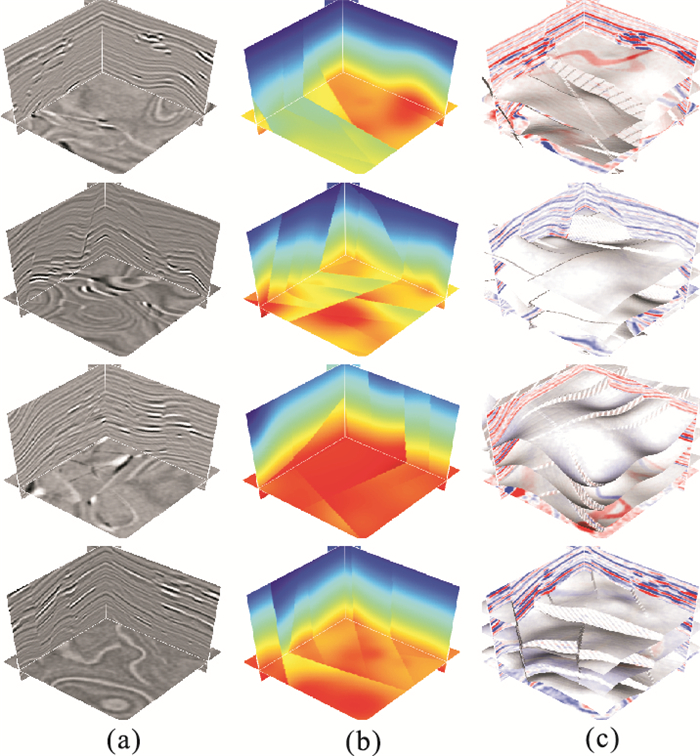
图 3给出了合成训练数据集中的4个样本。由图可见,利用准确RGT体能够在复杂构造背景下一次性地获得多个表征地层空间形态的地震反射层位。
|
图 3 合成训练数据集中的4个样本 (a)合成地震数据体;(b)准确标注RGT体;(c)利用准确RGT体同时追踪的三个层位 |
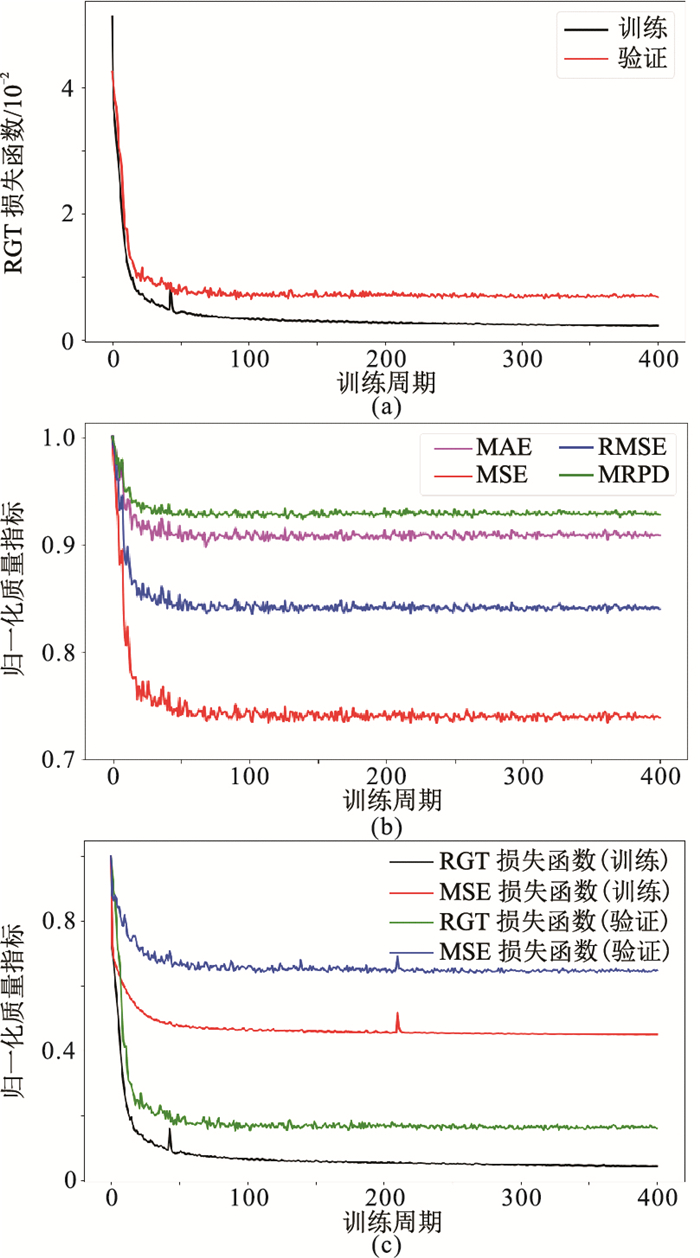
采用自适应步长的自适应矩估计(Adam)优化算法[27]最优化网络。在训练网络时,总的训练周期设置为400,在每一个训练周期内分批次将训练数据集中的所有样本输入到网络中进行训练,并将批次大小设置为4(总样本数=批次数×批次大小)。初始学习率设置为0.001,当预先定义的指标性能停止改善时,学习率自动降低,即当准则性能在两个训练周期内停滞时,将学习率降低至原来的95%。由图 4可见,当经过400个训练周期后优化停止,训练过程和验证过程的损失曲线逐渐收敛,分别小于0.004和0.01(图 4a);网络在验证集上的RMSE、MSE、MAE和MRPD四种归一化质量指标也下降到稳定水平(图 4b),这表明网络已成功捕获了输入地震数据体中的结构模式;其损失函数无论是在收敛性方面,还是在稳定性方面,都显著优于MSE损失函数(图 4c)。
|
图 4 自动RGT体估计网络的性能分析 (a)训练和验证数据集上的RGT损失函数曲线;(b)训练过程中验证数据集上多种归一化质量指标的变化;(c)训练和验证数据集上的不同损失函数曲线比较 |
为了验证训练网络的性能,在验证数据集中随机选择4个地震数据体(图 5a)作为网络的输入并预测地震数据体相应的RGT体(图 5e)。由图可见,预测结果具有与标签(图 5b)一致的结构模式。同样,图 4a也反映了经过400个训练周期后,二者损失函数值之间的误差非常小。
|
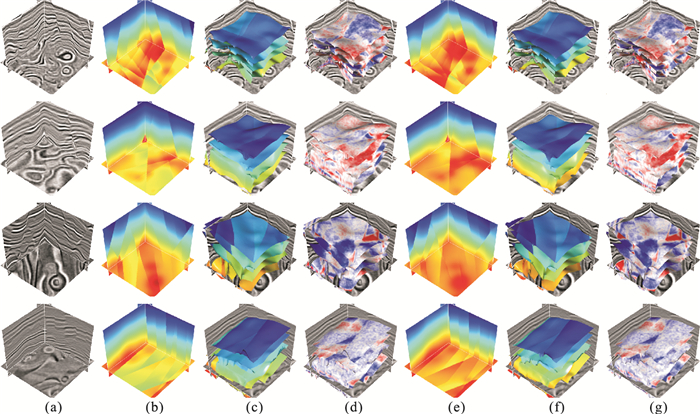
图 5 随机选择的4个地震数据体及相应的预测结果 (a)合成地震数据体;(b)准确标注RGT体;(c)利用准确RGT体同时追踪的三个层位;(d)利用追踪层位(c)提取的沿层振幅;(e)网络预测的RGT体;(f)利用网络预测RGT体同时追踪的三个层位;(g)利用图f追踪层位提取的沿层振幅 |
如前所述,地震反射层位可以用RGT体的等时面表示。为了进一步确定本文方法层位追踪的有效性,从每个预测的RGT体中提取一组等时面(将RGT体中给定相对地质时间值的所有采样点连接起来便可形成一个等时面)。从图 5c、图 5f可见,这些提取的等值面即使在穿过断层位置时也始终严格遵循地质结构的快速空间变化,这表明网络能够正确地提取结构信息;同时,从图 5d、图 5g中提取的沿层振幅具有较好的一致性,也可进一步证明本文RGT体预测网络的有效性和准确性。
4 实际资料应用利用多个实际地震数据体进行测试,进一步验证本文网络对实际资料的泛化能力。其中两个实际地震数据体的测试结果如下。
为了与训练数据集保持一致,对所有的输入地震数据体进行相同的标准化处理,即将输入数据体的数值范围标准化到0~1.0。为了进行比较,在没有任何已知地质模型的情况下,应用目前广泛使用的基于局部斜率的方法[4]作为参考预测实际地震数据体所对应的RGT体。
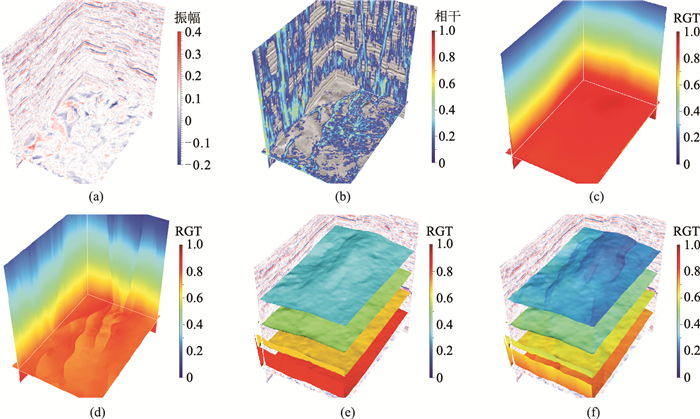
如图 6所示,实际陆上地震数据体的尺寸为535×361×257(图 6a),从相干属性结果(图 6b)可见实际数据体中多组交叉断层密集排列,这使得构造复杂化;参考方法计算的RGT体(图 6c)显示出与地震数据体一致的构造趋势,但它无法准确追踪穿过断层的层位;本文网络预测的RGT体(图 6d)对复杂交错且密集分布的断层可准确地预测;除此之外,提取RGT体等值面计算的地震反射层位(图 6f)与地震数据体中的复杂构造变化趋势高度契合,在断层附近被错断且伴有较大的断距,表明了断层在RGT体中被正确地估计。这主要是因为本文方法除了在标签数据中包含大量准确标注的复杂断层外,网络的特征注意力机制以及恰当的损失函数也使断层的特征得到准确的表达。
|
图 6 第一个实际数据体及不同方法的预测结果 (a)地震数据体;(b)地震数据体与相干体的叠合;(c)参考方法计算的RGT体;(d)本文网络预测的RGT体;(e)利用参考方法计算的RGT体追踪的多个层位;(f)利用本文网络预测的RGT体追踪的多个层位 |
图 7为另一个实际陆上地震数据体应用实例,数据体的尺寸为210×381×351。由图可见,即使地层被断层所错断(图 7c),所预测的RGT体也能严格地遵循构造的快速空间变化且层位地震反射(图 7e)的相位变化较为一致;与参考方法(图 7b和图 7d)相比,估计的RGT体和提取的层位更准确,进一步验证了利用本文方法进行自动层位追踪的有效性和准确性。

|
图 7 第二个实际数据体及不同方法的预测结果 (a)地震数据体;(b)参考方法计算的RGT体;(c)本文网络预测的RGT体;(d)利用参考方法计算的RGT体提取的多个沿层振幅;(e)利用本文网络预测的RGT体提取的多个沿层振幅 |
本文提出了一个具有注意力和残差学习机制的、由编码器—解码器框架组成的自动RGT体估计网络,可以自动、准确地从地震数据体中估计RGT体,且无需任何手动选取约束,为多层位自动追踪奠定了坚实的数据基础。RGT体的估计是一个标准的回归问题,考虑到地震数据体由强相关特征组成,这些相关性存在于承载地质结构空间特征的振幅信息中,因此为了正确度量RGT体估计的误差,在优化网络时使用基于结构相似性的准则作为损失函数。仅使用合成数据集训练网络,该网络不仅在验证数据集上显示出优越的性能,而且在实际地震数据体上应用效果较好,所预测的RGT体能成功地捕获复杂的结构特征。两个实际地震数据体的应用实例表明,本文方法的性能明显优于传统方法,具有较好的泛化能力和广阔的应用前景。
| [1] |
STARK T J. Unwrapping instantaneous phase to ge-nerate a relative geologic time volume[C]. SEG Technical Program Expanded Abstracts, 2003, 22: 1707-1710.
|
| [2] |
WU H, ZHANG B, LIN T, et al. Semiautomated seismic horizon interpretation using the encoder-decoder convolutional neural network[J]. Geophysics, 2019, 84(6): B403-B417. DOI:10.1190/geo2018-0672.1 |
| [3] |
PARKS D. Seismic Image Flattening as a Linear Inverse Problem[D]. Colorado School of Mines, Golden, 2010.
|
| [4] |
FOMEL S. Applications of plane-wave destruction filters[J]. Geophysics, 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [5] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [6] |
KAPPLER K, KUZMA H A, RECTOR J W. A comparison of standard inversion, neural networks and support vector machines[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 1725-1727.
|
| [7] |
CIREGAN D, MEIER U, SCHMIDHUBER J. Multi-column deep neural networks for image classification[C]. 2012 IEEE Conference on Computer Vision and Pattern Recognition, 2012, 3642-3649.
|
| [8] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [9] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]. 3rd International Conference on Learning Representations, 2015, 1-14.
|
| [10] |
CHEN L, PAPANDREOU G, KOKKINOS I, et al. DeepLab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs[J]. IEEE Transactions on Pattern Ana-lysis and Machine Intelligence, 2018, 40(4): 834-848. DOI:10.1109/TPAMI.2017.2699184 |
| [11] |
BADRINARAYANAN V, KENDALL A, CIPOLLA R. SegNet: a deep convolutional encoder-decoder architecture for image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(12): 2481-2495. DOI:10.1109/TPAMI.2016.2644615 |
| [12] |
PHAM N, FOMEL S, DUNLAP D. Automatic channel detection using deep learning[J]. Interpretation, 2019, 7(3): SE43-SE50. DOI:10.1190/INT-2018-0202.1 |
| [13] |
GAO H, WU X, LIU G. Channel simulation and deep learning for channel interpretation in 3D seismic images[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 1449-1453.
|
| [14] |
闫星宇, 李宗杰, 顾汉明, 等. 基于深度卷积神经网络的地震数据溶洞识别[J]. 石油地球物理勘探, 2022, 57(1): 1-11. YAN Xingyu, LI Zongjie, GU Hanming, et al. Identification of karst caves in seismic data based on deep convolutional neural network[J]. Oil Geophysical Prospecting, 2022, 57(1): 1-11. |
| [15] |
王静, 张军华, 芦凤明, 等. 构建三维深度监督网络的断层检测方法[J]. 石油地球物理勘探, 2021, 56(5): 947-957. WANG Jing, ZHANG Junhua, LU Fengming, et al. Research on fault detection method based on 3D deeply supervised network[J]. Oil Geophysical Prospecting, 2021, 56(5): 947-957. DOI:10.13810/j.cnki.issn.1000-7210.2021.05.002 |
| [16] |
WU Y, MCMECHAN G A. Parametric convolutional neural network-domain full-waveform inversion[J]. Geophysics, 2019, 84(6): R881-R896. DOI:10.1190/geo2018-0224.1 |
| [17] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, WU Jie, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [18] |
GENG Z, WU X, SHI Y, et al. Deep learning for relative geologic time and seismic horizons[J]. Geophy-sics, 2020, 85(4): WA87-WA100. |
| [19] |
HE K, ZHANG X, REN S, et al. Deep residual lear-ning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, 770-778.
|
| [20] |
LAINA I, RUPPRECHT C, BELAGIANNIS V, et al. Deeper depth prediction with fully convolutional residual networks[C]. 2016 Fourth International Conference on 3D Vision (3DV), 2016, 239-248.
|
| [21] |
YU F, KOLTUN V. Multi-scale context aggregation by dilated convolutions[DB/OL]. (2016-04-30)[2022-03-14]. https://arxiv.org/abs/1511.07122.
|
| [22] |
HU J, SHEN L, ALBANIE S, et al. Squeeze-and-excitation networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(8): 2011-2023. DOI:10.1109/TPAMI.2019.2913372 |
| [23] |
ZHANG Y, LI K, LI K, et al. Image super-resolution using very deep residual channel attention networks[C]. Computer Vision - ECCV 2018, 2018, 294-310.
|
| [24] |
CHEN L, ZHANG H, XIAO J, et al. SCA-CNN: spatial and channel-wise attention in convolutional networks for image captioning[C]. 2017 IEEE Confe-rence on Computer Vision and Pattern Recognition (CVPR), 2017, 6298-6306.
|
| [25] |
WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Proces-sing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
| [26] |
WU X, GENG Z, SHI Y, et al. Building realistic structure models to train convolutional neural networks for seismic structural interpretation[J]. Geophysics, 2020, 85(4): WA27-WA39. DOI:10.1190/geo2019-0375.1 |
| [27] |
吴丹, 吴海莉, 李群, 等. 应用自适应矩估计的快速最小二乘逆时偏移[J]. 石油地球物理勘探, 2022, 57(2): 386-394. WU Dan, WU Haili, LI Qun, et al. Fast least-squares reverse-time migration with adaptive moment estimation[J]. Oil Geophysical Prospecting, 2022, 57(2): 386-394. |



 李海山, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email:
李海山, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email: 