2. 山东省物化探勘查院, 山东济南 221116;
3. 海洋矿产资源评价与探测技术功能实验室, 青岛海洋科学与技术国家实验室, 山东青岛 266237
2. Shandong Institute of Geophysical & Geochemical Exploration, Jinan, Shandong 221116, China;
3. Qingdao National Laboratory for Marine Science and Technology, Functional Laboratory for Marine Mineral Resources Evaluation and Exploration Technology, Qingdao, Shandong 266237, China
初至拾取质量直接影响后续折射波静校正[1]、地震剖面解释和地震层析成像[2-3]等。随着地震采集技术的提高及勘探地形的日益复杂,地震数据呈几何级增长且信号也越来越复杂。传统的初至自动拾取方法对中、低信噪比数据的拾取准确率和精度不高,需大量的人工操作进行调整,耗时耗力、效率低下。因此,对于海量的中、低信噪比数据,亟需一种能够同时满足工业化精度标准和效率的初至智能拾取方法。
传统的初至拾取方法主要有人工手动拾取和算法自动拾取两类。人工手动拾取方法主要根据操作者经验手动标记初至位置,主观性强、一致性差、效率低下[4];算法自动拾取方法是根据波形在能量、频率等方面的不同特征识别初至,常用方法有能量比值法[5-6]、相关法[7-8]、图像处理法[9-10]、神经网络法[11-12]等。这些方法大多基于单道数据拾取,欠考虑多道数据之间的相关性,因此对于信噪比较低的地震数据拾取效果不佳。
目前深度学习技术发展迅速,并广泛应用于地震勘探领域[13-17]。初至拾取从原理上可看作是一个二分类问题,高精度的初至拾取方法可结合计算机视觉中的语义分割技术对地震数据的每一个信号时刻进行分类,最终得到初至位置。目前,应用在初至拾取上的神经网络大多是以全卷积网络(Fully Convolutional Networks, FCN)[18]、SegNet[19]、U-Net[20]等为基础进行改进的编码—解码结构[21-22]。刘佳楠等[23]提出基于FCN的地震初至波拾取方法,由于网络结构简单,拾取初至的精度有限。陈德武等[24]提出基于混合网络U-SegNet的地震初至自动拾取方法,融合了U-Net和SegNet两个网络结构,但为节约时间和内存,去掉通过学习参数上采样的反卷积操作,在一定程度上降低了拾取的精度。潘英杰等[25]提出一种基于地震图像深度语义分割的初至拾取方法,但该方法需先将数据转化为图像并对图像处理,再转化为数据,过程繁琐,应用效率较低。
针对上述神经网络方法在地震资料初至拾取上存在精度不够和效率低的问题,本文在充分分析U-Net结构基础上,结合残差学习模块及亚像素卷积方法,提出一种面向地震波初至智能拾取的超分辨率深度残差方法(SD-Net)。残差学习模块扩展了网络深度并克服了深层网络退化的问题,提升网络的学习能力以更好地学习目标特征;亚像素卷积方法通过卷积和多通道间的像素重组扩大特征图,实现特征图由低分辨率空间到超分辨率空间的转化,解决了反卷积作为上采样运算效率低和还原特征图精度低的问题;同时,具有长跳跃连接的编、解码结构结合浅层和深层的特征图,实现了不同尺度特征的融合。本文结合残差学习模块、亚像素卷积方法以及编、解码网络中长跳跃连接的各个优势,使网络具有更强的学习能力及更高的推理效率。另外,结合迁移学习增强网络泛化能力,实现了高精度、高效率、普适性的地震数据初至智能拾取。
1 方法原理 1.1 残差学习模块神经网络的深度对模型的效果有至关重要的影响,增加神经网络的深度可提高网络学习能力,使其更好地学习地震数据特征[26-28]。但是,直接堆叠更多的层数会导致梯度弥散、梯度爆炸、网络退化等问题,使网络出现更高的训练误差[29]。
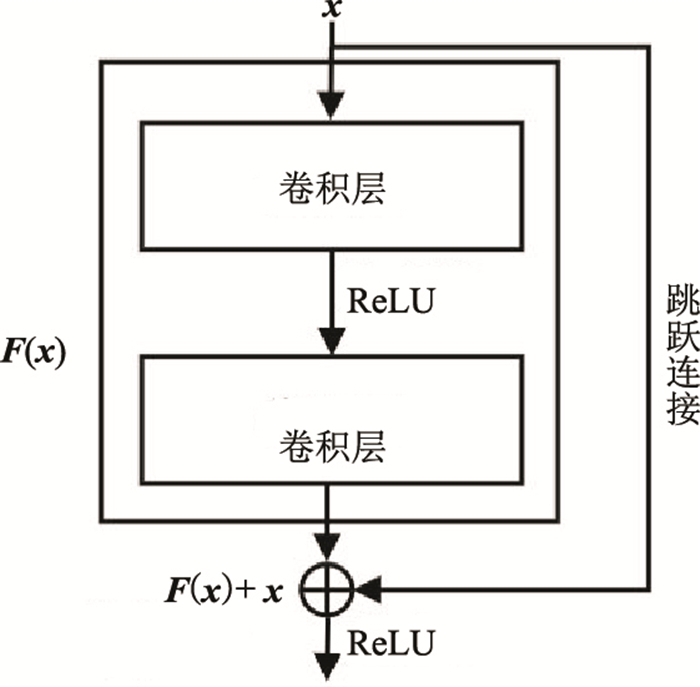
为解决深层网络性能下降的问题,He等[30]提出了残差学习模块。如图 1所示,原始输入为x,期望输出为F(x)+x,x经两个卷积层,其中第一个卷积层使用修正线性单元(Rectified Linear Unit,ReLU),输出F(x),同时右侧跳跃连接直接将输入的x传送给F(x),二者进行加法操作并经过ReLU,最后的输出结果变为H(x)=F(x)+x,而网络需要学习的映射函数由恒等映射函数转化为残差映射函数F(x)=H(x)-x。
|
图 1 残差学习模块示意图 |
He等[30]指出,如果网络层数达到了最优深度,残差函数F(x)将推理为0,即通过残差学习后的输出与输入相同,从而变为恒等映射。残差学习方法解决了网络层数加深造成的梯度弥散、梯度爆炸及网络退化的问题,提高了网络的学习能力以及训练效率。
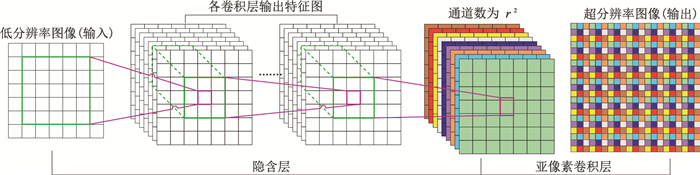
1.2 亚像素卷积方法神经网络通过卷积操作提取目标特征后,输出的特征图尺寸会变小,需通过上采样还原特征图分辨率,以达到分割的效果。目前广泛使用的上采样方法包括插值法和反卷积法。其中基于插值的上采样方法是一个固定运算,计算复杂度较高;基于反卷积的上采样方法使用带权重的网络层学习参数,但反卷积层具有“非均匀重叠效应”,会导致还原后的特征图带有棋盘纹理。Shi等[31]提出的高效亚像素卷积神经网络中使用亚像素卷积方法,具有图像从低分辨率到超分辨率转化的效果(图 2)。该网络通过隐含层对图像进行特征提取,生成r×r通道的特征图,其中r为上采样倍数。使用亚像素卷积层将每个像素的r2个通道重新排列成一个r×r的区域,对应超分辨率图像中一个r×r大小的子块,从而将大小为H×W× r2的特征图像重新排列成同样大小的超分辨率图像,其中H和W分别为特征图的高和宽。
|
图 2 高效亚像素卷积神经网络流程图(修改自文献[31]) |
高效亚像素卷积神经网络通过卷积和多通道间的像素重组,使特征图完成由低分辨率空间到超分辨率空间的转化。亚像素卷积层可学习到更好、更复杂的推理方式,提高特征图的分辨率,从而更加精准地定位初至区域,有效降低了计算复杂度,在拾取效果及训练效率上均有很大提升。
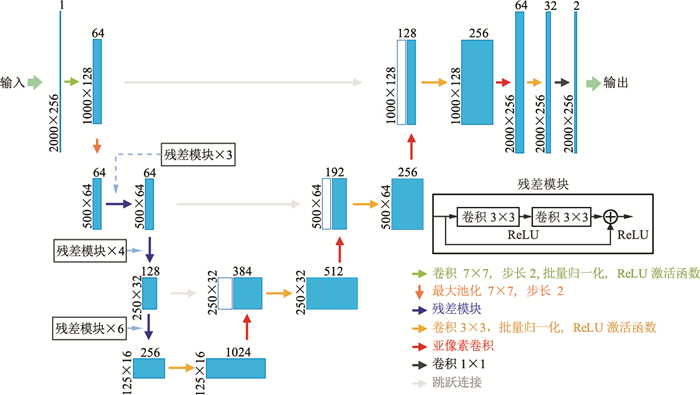
1.3 SD-Net结构本文设计的SD-Net结构(图 3)与传统语义分割网络U-Net结构形状类似,也是由编码器和解码器两部分组成。编码器子网络学习输入的地震数据并提取特征图谱,解码器子网络对得到的特征图谱进行特征优化和任务处理,逐步实现每一个像素的类别标注。在特征图分辨率相同的层间建立跳跃连接,将具有空间信息的低级特征和具有语义信息的高级特征进行融合,从而提高初至定位的准确度。
|
图 3 SD-Net网络结构图 |
与U-Net不同的是,SD-Net的编码器部分使用一个尺寸为7×7的卷积核和最大池化处理输入数据,大尺寸卷积核具有更大的感受野,有助于提取浅层信息间的相关性;池化操作可缩减特征图尺寸,减少深层网络的计算复杂度;使用残差模块以增加网络深度,通过卷积控制步长代替池化进行下采样操作,保留更多的特征信息。残差模块由两个3×3卷积层和一个跳跃连接组成,卷积层后添加批量归一化[32]和ReLU激活函数,提高了模型的训练效率,增强了模型的鲁棒性和泛化能力,编码器具体参数见表 1。残差学习模块的残差函数定义为
|
|
表 1 编码器参数 |
| $ R\left(x_i\right)=F\left(x_i\right)+x_i $ | (1) |
| $ x_{i+1}=f\left[R\left(x_i\right)\right] $ | (2) |
式中:xi和xi+1分别表示残差学习模块的输入和输出,其中i∈N,N为卷积层数;R(xi)为恒等映射;F(xi)为要学习的残差映射;f为ReLU激活函数。
在解码器部分,使用亚像素卷积对多通道特征图进行像素重组实现上采样,还原特征图尺寸。上采样因子设置为2,即特征图每次经过上采样后尺寸变为原来的2倍。输入特征图首先在顶、底部与左、右侧边缘分别填充1行或1列零元素;其次经过一个卷积核尺寸为3×3的卷积层,输出特征图尺寸不变,通道数变为原来的4倍;最后经过亚像素卷积层进行4通道的像素重组,对一个像素的4个通道进行拼接,形成一个2×2大小的新像素块,完成特征图尺寸的2倍放大。解码器具体参数见表 2。亚像素卷积方法可表示为
|
|
表 2 解码器参数 |
| $ I^{\mathrm{SR}}=f^l\left(I^{\mathrm{LR}} ; W_l, b_l\right) $ | (3) |
| $ f^l\left(I^{\mathrm{LR}} ; W_l, b_l\right)=\sigma\left[W_l \times f^{l-1}\left(I^{\mathrm{LR}}\right)+b_l\right] $ | (4) |
式中:ISR为处理后的特征图;fl为像素重组;Wl是学习网络的权值,l∈(1, N-1),为一大小为nl-1×nl×kl×kl的2D卷积张量,其中nl、kl分别是第l层的特征数量和卷积大小;bl是长度为nl的偏置;σ为非线性函数;ILR表示输入的特征图。
具有空间信息的低级特征和具有语义信息的高级特征对于网络的目标识别能力均起着至关重要的作用。因此,在SD-Net的编码器和解码器之间建立3个长跳跃连接,将来自编码器浅层低级特征和来自解码器的深层高级特征在通道维度上融合,增强网络的识别能力,提高初至拾取的准确度。网络最后用一个1×1的卷积层及Sigmoid激活函数输出初至取值范围为[0, 1]的概率值。
2 模型训练与测试 2.1 构建样本集模型训练采用的数据集是经去噪处理后的实际地震数据,由于资料数据量过大,无法直接输入网络中训练,因此需对其进行预处理。为保持地震道之间的连续性及炮记录中的初至波特征,将SEG-Y数据按照连续炮号整体划分,提取单炮记录为单一样本数据,并将其尺寸裁剪为2000×256,其中256表示地震道数,2000表示每一地震道的样本点数,若单炮记录地震道数超过256,则以炮点为中心进行裁剪;若单炮记录地震道数不足256,则将其舍弃。采样间隔为2 ms,经处理后,最终得到每道4000个样本数据,然后利用这些样本数据制作网络训练所需的样本集,具体过程如下。
(1) 使用传统算法,如长、短时窗平均比(STA/LTA)法,自动拾取4000个样本数据的初至,并采用人工修正错误初至。
(2) 根据初至时刻生成对应标签。为避免样本类别不均衡导致网络训练过程中的过拟合或欠拟合,采用以初至波为边界的二分类标注方式,将初至之前的样点值设为0,初至及初至后的样点值设为1。
(3) 为加快网络训练过程中梯度下降的求解速度,使用归一化操作将样本值控制在[0, 1]范围内,具体方法为
| $ x_{a, b}^{\prime}=\frac{X_{a, b}-X_{\min }}{X_{\max }-X_{\min }} $ | (5) |
式中:Xa, b、x′a, b分别表示归一化前、后第b道第a个采样点的值;Xmax、Xmin分别表示样本中的最大值和最小值。
(4) 样本集划分。将所有单炮数据及其对应的标签文件按8:1:1的比例划分为训练集、验证集和测试集,供网络模型训练使用。训练集、验证集和测试集所包含数据个数分别为3200、400、400。
2.2 训练网络模型训练网络模型参数见表 3,模型训练使用交叉熵损失函数
|
|
表 3 模型训练参数表 |
| $ \begin{aligned} \operatorname{Loss}= & -\frac{1}{n} \sum\limits_{m=1}^n \times \\ & {\left[y_m \lg p_m+\left(1-y_m\right) \lg \left(1-p_m\right)\right] } \end{aligned} $ | (6) |
式中:n表示训练样本的总个数;m表示当前训练样本批次中的第m个样本;ym表示第m个样本对应的标签;pm表示第m个样本预测为ym的概率。
利用适应性矩估计(Adaptive moment estimation, Adam)算法优化网络参数,最小化损失。为防止训练过程中出现训练数据过拟合的现象,每当训练集完成4次迭代训练后,使用优化后参数对验证集进行1次验证,训练迭代次数设置为100,并使用早停机制自动提前终止网络模型的训练,终止条件为:当连续5次使用验证集进行验证的结果中,错误率没有下降,则停止训练,并只保存最好的结果。
模型效果的评估标准使用语义分割中最常用的均交并比(Mean Intersection over Union, MIoU),MIoU是计算真实值与预测值两个集合的交集和并集之比
| $ \mathrm{MIoU}=\frac{1}{h+1} \sum\limits_{u=0}^h \frac{p_{u u}}{\sum\limits_{v=0}^h p_{u v}+\sum\limits_{v=0}^h\left(p_{v u}-p_{u u}\right)} $ | (7) |
式中:puv表示标签值为u、被预测为v的数量;pvu表示标签值为v、被预测为u的数量;puu表示预测正确的数量;h+1为类别总数。
本文使用样本集分别对U-Net、SD-Net进行训练和验证,并记录训练过程中的损失值Loss与MIoU值。
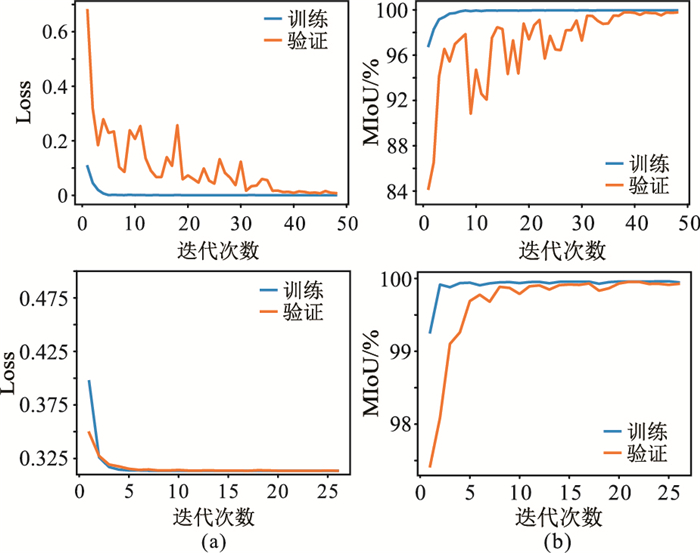
使用样本集对U-Net模型进行训练,在48次迭代后触发早停机制,总共用时14.2 h,其验证结果如图 4(上)。U-Net模型在验证集上的MIoU达到99.78%。然而在前期网络模型训练过程中,模型在训练集上的Loss及MIoU已趋于稳定,但是在验证集上Loss曲线和MIoU曲线存在抖动现象,直到第35次迭代后才收敛,表明U-Net模型对于地震数据特征的学习能力略有不足。
|
图 4 U-Net(上)与SD-Net(下)模型训练的Loss曲线(a)和MIoU曲线(b) |
使用样本集对SD-Net模型进行训练,在26次迭代后触发早停机制,总共用时4.5 h,其验证结果如图 4(下),模型在验证集上的MIoU达到99.96%,而且SD-Net的Loss曲线和MIoU曲线在训练过程很稳定,网络收敛较快,表明SD-Net具有更强网络学习能力与更好的初至拾取效果。
2.3 测试网络模型分别使用U-Net和SD-Net模型对未参与训练过程的测试集数据进行预测,共400个地震数据,每个数据256道,共102400道。表 4为U-Net和SD-Net网络总参数、准确率和训练用时的对比,能够客观地度量网络的性能。由表可见,相较于U-Net,SD-Net的参数总数量更少,约为U-Net参数总量的2/5,模型拾取初至准确率更高,训练用时更短,推理速度更快。
|
|
表 4 U-Net、SD-Net模型性能对比 |
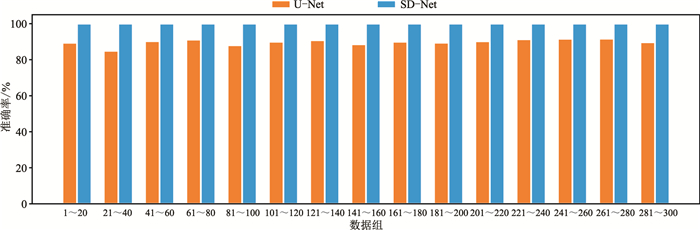
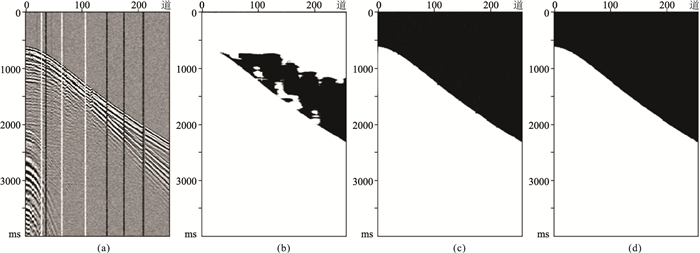
为验证SD-Net模型的鲁棒性,选取300个与训练集尺寸、剖面特征、信噪比均不同的数据制作新测试集,数据尺寸为2000×128,数据包含炮点在测线中间以及两端的情况,并对数据添加不同程度的随机噪声、坏道等干扰信号。图 5为SD-Net与U-Net对新测试集数据初至拾取的预测结果对比,每20个数据为一组,共15组,取每组准确率的平均值,使用本文方法得到的初至拾取结果平均准确率为99.75%(蓝条),而U-Net得到的平均准确率为89.80%(黄条);图 6为两种方法对新测试集数据中单个样本的预测结果,可见U-Net受噪声影响较大,将部分初至前类别识别为初至后类别,而SD-Net几乎不受影响,基本可以做到准确分类。
|
图 5 U-Net和SD-Net法预测准确率对比 |
|
图 6 单个样本U-Net和SD-Net法预测结果对比 (a)原始地震数据;(b)U-Net;(c)SD-Net;(d)标签值 |
综上所述,SD-Net法在训练效率、拾取精度以及鲁棒性方面均优于U-Net法。
3 实际应用效果分析 3.1 SD-Net法与STA/LTA法对比使用业内常用的STA/LTA法拾取初至,STA/LTA法可表示为
| $ \mathrm{SL}(t)=\frac{\frac{1}{n_{\mathrm{s}}} \sum\limits_{z=t-n_{\mathrm{s}}}^t \mathrm{CF}(z)}{\frac{1}{n_1} \sum\limits_{z=i-n_1}^t \mathrm{CF}(z)} $ | (8) |
分子、分母分别为短、长时窗信号平均值。式中:t为采样时刻;nl、ns、分别为长、短时窗的长度;CF(z)为z时刻的特征函数值,表征地震数据的振幅、能量或者其他变化;SL为设定的触发阈值,超过该阈值时,认为出现有效信号。需根据经验设置ns、nl计算SL的值,该值影响地震信号的识别和拾取效果。
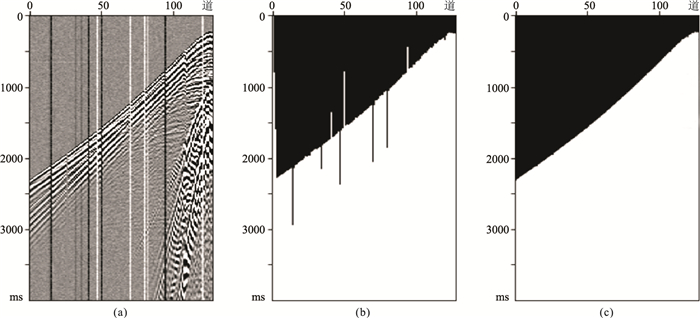
图 7为STA/LTA法与SD-Net法拾取初至的结果,可见,当地震数据含有随机噪声和坏道时,STA/LTA法拾取的初至存在上、下跳变,拾取精度不高,而SD-Net法拾取的初至不存在跳变问题,能够精确地拾取初至,表明SD-Net的初至拾取能力优于STA/LTA法。
|
图 7 STA/LTA与SD-Net法拾取初至对比 (a)地震数据;(b)STA/LTA;(c)SD-Net |
使用与训练样本集数据特征不同的地震资料试验,分析初至特征和子波类型的变化对模型拾取初至的影响,测试SD-Net模型的泛化能力。
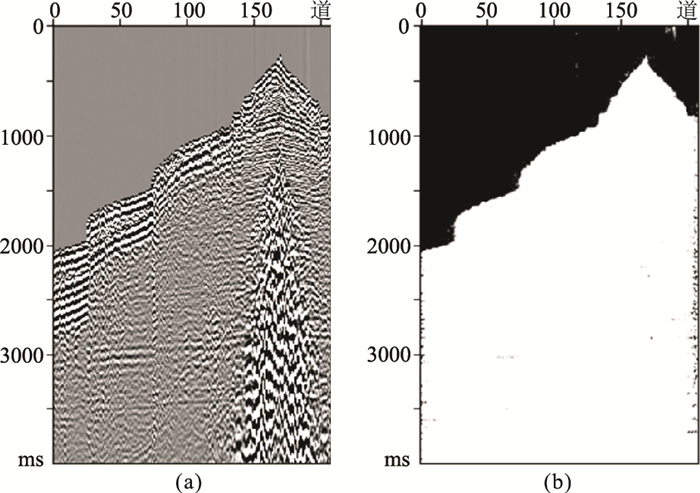
为分析模型对初至连续性特征的依赖性,判断模型是否会因初至错断而出现拾取错误的情况,使用网络模型预测带有地表起伏的地震数据,预测结果如图 8所示。由于模型未学习过该类数据的特征信息,故会出现部分错误分类的现象,但模型能够基本正确地分割初至边界,证明模型对初至连续性特征依赖性较低,初至错断的情况不会影响模型的拾取能力。
|
图 8 SD-Net对带有地表起伏的地震数据预测结果 (a)带有地表起伏的地震数据;(b)模型分割结果 |
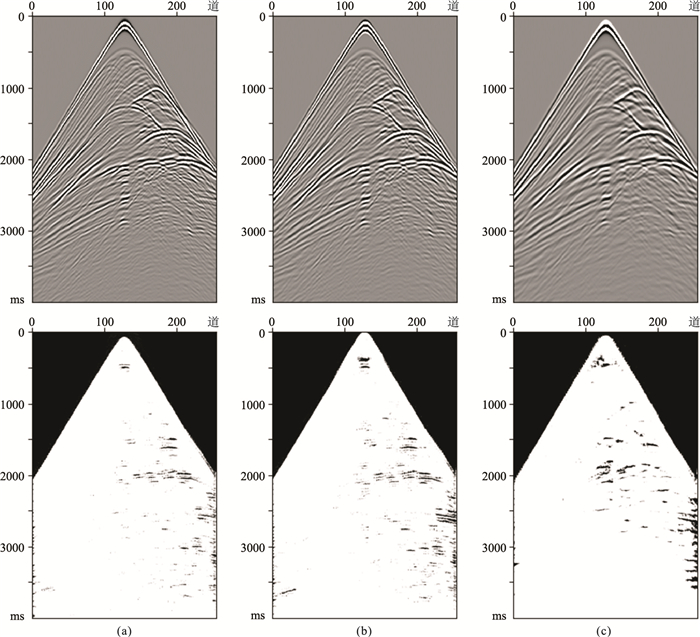
为分析不同子波类型对模型初至拾取的影响,以Marmousi2模型作为速度场,选用15 Hz理论Ricker子波、Puzirov子波和Symmetrical子波分别进行正演实验。三种不同子波模型正演结果及预测效果如图 9所示。由图可见,对于三种不同类别子波正演的地震数据,虽然内部存在部分分类错误的情况,但均可准确地分割初至边界,证明子波类型的改变不会影响模型初至拾取的效果。
|
图 9 不同类型子波正演(上)与模型分割(下)结果 (a)Ricker子波;(b)Puzirov子波;(c)Symmetrical子波 |
上述试验证明,SD-Net模型具有较强的泛化能力。
3.3 迁移学习应用效果分析实际应用中,因各工区地质环境不同,故使用一个工区数据训练好的网络模型,无法有效地对另一个工区数据进行初至拾取。且在勘探环境复杂的地区,由于各种噪声干扰,得到的地震数据信噪比较低,通过高信噪比数据训练得到的初至拾取模型也无法很好地应用于低信噪比数据。
迁移学习是利用不同数据之间的相关性,将存储已有问题的解决模型应用在其他不同但有相关性的问题上,以提高网络适应性和泛化能力。使用少量的新数据样本对原有网络模型进行迁移学习,模型即可对新数据进行有效初至拾取。
为模拟新工区数据,对原始地震数据进行加噪处理。添加的噪声来源于实际数据的裁切,将实际地震数据中的各类噪声抽取出来组成一个噪声库,然后从噪声库中随机选择噪声并赋予不同的权重,添加到原始数据中,得到不同信噪比的新数据。信噪比公式如下
| $ \mathrm{SNR}=101 \mathrm{~g} \frac{\sum\limits_{a=1}^{M_1} \sum\limits_{b=1}^{M_2} c_{a, b}^2}{\sum\limits_{a=1}^{M_1} \sum\limits_{b=1}^{M_2}\left(d_{a, b}-c_{a, b}\right)^2} $ | (9) |
式中:ca, b、da, b分别表示加噪前、后的地震数据;M1、M2分别代表当前数据的总行数和总列数。
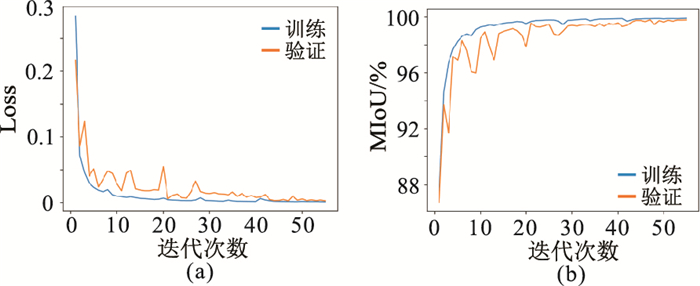
选取200个已标注好的样本,其中160个作为训练集,40个作为验证集,使用原始数据训练好的网络模型对新数据进行迁移学习,训练过程中的Loss和MIoU分别如图 10a、图 10b所示,可见网络收敛较快,模型经过55个训练周期后Loss趋于稳定并触发早停机制,总共用时45 min,模型在验证集上的MIoU达到99.69%。
|
图 10 迁移学习训练过程Loss曲线(a)及MIoU曲线(b) |
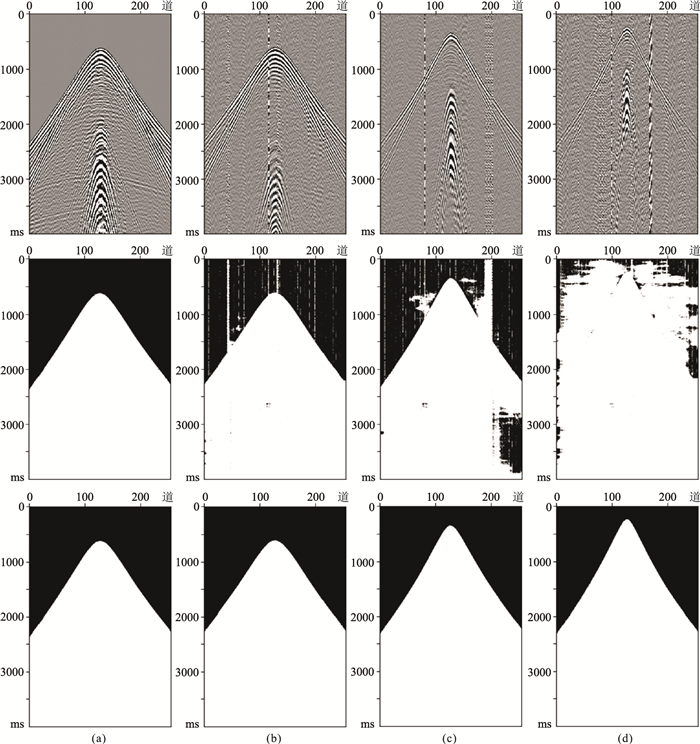
分别使用迁移学习前、后的网络模型,对未参与训练的加噪数据(不同信噪比)和原始数据做测试,验证迁移学习效果(图 11)。由图可见,随着地震数据信噪比的降低,迁移学习前网络模型的拾取效果逐渐变差,而迁移学习后的网络模型学习了低信噪比数据的特征,对不同信噪比的地震数据均可以准确拾取初至。试验表明,经过迁移学习后的模型不仅可以正确拾取之前学习的高信噪比的地震数据初至,同时也能够正确拾取加噪后的不同信噪比的地震数据初至。
|
图 11 原始数据及不同信噪比的加噪数据(上)迁移学习前(中)、后(下)模型预测结果 (a)原始数据;(b)信噪比为3.3582 dB;(c)信噪比为-1.4353 dB;(d)信噪比为-4.1402 dB |
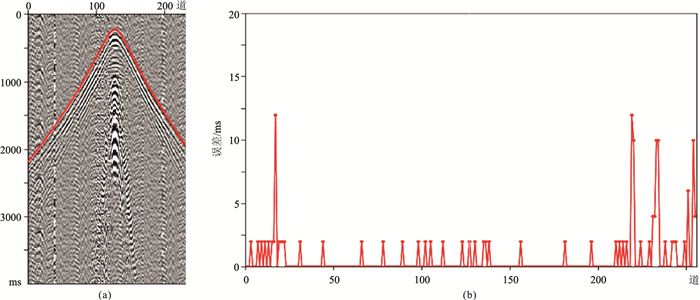
为清晰展示初至拾取结果,将预测结果所得分割图中初至位置的坐标信息提取出来,映射到原始地震资料上,并对比、分析预测结果与人工拾取的结果(图 12)。图 12a为提取预测的初至位置映射到地震数据的效果图,图 12b为网络模型预测初至位置与人工拾取初至位置的误差,平均误差为0.8906 ms。算例结果显示迁移学习后得到的模型对原始数据和加噪数据均具有很好的初至拾取效果,表明该网络可通过迁移学习不断提取新工区的地震数据特征,即只需对新工区数据做少量标注就能训练得到适应该工区的初至拾取模型,证明SD-Net模型具备较强的适应性和泛化能力,易于工业化生产,具有很好的应用前景。
|
图 12 初至映射地震数据(a)及迁移学习后模型预测与人工拾取误差(b) |
本文基于深度学习的U-Net网络提出了一种面向地震波初至智能拾取的超分辨率深度残差方法(SD-Net),通过引入残差学习模块增强了网络对地震数据的学习能力,同时使用亚像素卷积方法提高了特征图的分辨率,从而实现初至精准定位。通过SD-Net法的长跳跃连接操作对多尺度特征信息进行融合。最后使用迁移学习增强了网络泛化能力,并取得了较好效果。主要结论如下:
(1) 实际地震资料数据集的训练和测试结果以及量化评估指标表明,U-Net和本文方法在同一测试集上的预测准确率分别为99.35%和99.97%,且U-Net的训练用时约为本文方法的3倍,证明了本文提出的SD-Net模型比U-Net模型具有更高的初至拾取精度和更快的训练速度;
(2) 使用与训练集尺寸、剖面特征、信噪比均不同的数据所构成的新测试集对U-Net和SD-Net进行试验与分析,结果表明二者对新测试集数据初至拾取的平均准确率分别为89.80%和99.75%,证明本文提出的SD-Net模型比U-Net模型具有更强的鲁棒性;
(3) 将训练的网络模型分别应用于含地表起伏的地震数据以及不同子波正演生成的合成数据上,均可准确地分割初至边界,得到良好的初至拾取效果,证明本文提出的SD-Net模型具有较强的泛化能力;
(4) 对地震数据进行加噪处理模拟新工区数据,使用少量标注样本即可训练得到适用于新数据的初至拾取模型,随机选取的测试集数据与人工标注的初至平均误差统计结果表明,本文方法有效实现了对地震数据初至的准确拾取,证明了本文方法易于工业化生产,具有良好的应用前景。
| [1] |
曾庆才, 曾同生, 欧阳永林, 等. 复杂山地层析反演静校正新方法及应用[J]. 石油地球物理勘探, 2017, 52(3): 418-425. ZENG Qingcai, ZENG Tongsheng, OUYANG Yonglin, et al. A new tomograhpic inversion for static corrections in complex mountain areas[J]. Oil Geophysical Prospecting, 2017, 52(3): 418-425. |
| [2] |
谢春, 刘玉柱, 董良国, 等. 基于声波方程的有限频伴随状态法初至波旅行时层析[J]. 石油地球物理勘探, 2015, 50(2): 274-282. XIE Chun, LIU Yuzhu, DONG Liangguo, et al. First arrival tomography with finite frequency adjoint-state method based on acoustic wave equation[J]. Oil Geophysical Prospecting, 2015, 50(2): 274-282. |
| [3] |
王立歆, 李海英, 李弘, 等. 复杂地质条件下超深层碳酸盐岩断控缝洞体成像及预测技术[J]. 石油物探, 2022, 61(5): 865-875. WANG Lixin, LI Haiying, LI Hong, et al. Imaging and prediction technology of fault-karst reservoirs in ultra-dep carbonate rocks under complex geological conditions[J]. Geophysical Prospecting for Petroleum, 2022, 61(5): 865-875. DOI:10.3969/j.issn.1000-1441.2022.05.011 |
| [4] |
林彬华, 金星, 康兰池, 等. 基于卷积神经网络的地震震级测定研究[J]. 地球物理学报, 2021, 64(10): 3600-3611. LIN Binhua, JIN Xing, KANG Lanchi, et al. The research of earthquake magnitude determination based on Convolutional Neural Networks[J]. Chinese Journal of Geophysics, 2021, 64(10): 3600-3611. |
| [5] |
陈金焕, 曹永生, 孙成龙, 等. 基于二分法的地震波初至自动拾取算法[J]. 地球物理学进展, 2015, 30(2): 688-694. CHEN Jinhuan, CAO Yongsheng, SUN Chenglong, et al. The algorithm for automatic first-breaks picking on seismic traces based on Dichotomy[J]. Progress in Geophysics, 2015, 30(2): 688-694. |
| [6] |
王议迎, 丁仁伟, 李建平, 等. 联合改进STA/LTA与MLoG算子的微震P波到时自动拾取方法[J/OL]. 山东科技大学学报(自然科学版), 2021, 40(6): 1-10. WANG Yiying, DING Renwei, LI Jianping, et al. Automatic pickup of microseismic P-wave arrival based on improved STA/LTA and MLoG operators[J/OL]. Journal of Shandong University of Science and Technology (Na-tural Science), 2021, 40(6): 1-10. |
| [7] |
江国明, 张贵宾, 徐峣. 远震相对走时数据快速计算方法及应用[J]. 地球物理学报, 2012, 55(12): 4097-4105. JIANG Guoming, ZHANG Guibin, XU Yao. A fast method for calculating relative residuals of teleseismic data and its application[J]. Chinese Journal of Geophysics, 2012, 55(12): 4097-4105. |
| [8] |
刘腾蛟, 高阳, 储仿东, 等. 最小二乘曲线拟合的微地震初至优化拾取方法及应用[J]. 石油地球物理勘探, 2018, 53(S2): 124-129. LIU Tengjiao, GAO Yang, CHU Fangdong, et al. Microseismic first arrival picking based on least square curve fitting[J]. Oil Geophysical Prospecting, 2018, 53(S2): 124-129. |
| [9] |
李辉峰, 邹强, 金文昱. 基于边缘检测的初至波自动拾取方法[J]. 石油地球物理勘探, 2006(2): 150-155. LI Huifeng, ZOU Qiang, JIN Wenyu. Method of automatic first breaks pick-up based on edge detection[J]. Oil Geophysical Prospecting, 2006(2): 150-155. |
| [10] |
牛沛琛, 张建中. 基于数字图像处理的地震波初至时间检测[J]. 计算机与现代化, 2007(4): 27-30. NIU Peichen, ZHANG Jianzhong. First Arrival Pic-king Based on Image Processing Methods[J]. Compu-ter and Modernization, 2007(4): 27-30. |
| [11] |
宋建国, 李赋真, 徐维秀, 等. 改进的神经网络级联相关算法及其在初至拾取中的应用[J]. 石油地球物理勘探, 2018, 53(1): 8-16. SONG Jianguo, LI Fuzhen, XU Weixiu, et al. An improved neural-network cascade-correlation algorithm and its application in seismic first break picking[J]. Oil Geophysical Prospecting, 2018, 53(1): 8-16. |
| [12] |
曹晓莉, 刘斌, 王淑荣, 等. 综合动量法和可变学习速度的BP神经网络地震初至拾取[J]. 石油地球物理勘探, 2020, 55(1): 71-79. CAO Xiaoli, LIU Bin, WANG Shurong, et al. Seismic first-break picking based on BP neural network integrated with momentum method and adaptive learning rate method[J]. Oil Geophysical Prospecting, 2020, 55(1): 71-79. |
| [13] |
COVA D, 刘洋, 丁成震, 等. 人工智能和视速度约束的地震波初至拾取方法[J]. 石油地球物理勘探, 2021, 56(3): 419-435. COVA D, LIU Yang, DING Chengzhen, et al. First break picking method based on artificial intelligence and apparent velocity constraint[J]. Oil Geophysical Prospecting, 2021, 56(3): 419-435. |
| [14] |
杨晶, 丁仁伟, 林年添, 等. 基于深度学习的地震断层智能识别研究进展[J]. 地球物理学进展, 2022, 37(1): 298-311. YANG Jing, DING Renwei, LIN Niantian, et al. Research progress of intelligent identification of seismic faults based on deep learning[J]. Progress in Geophysics, 2022, 37(1): 298-311. |
| [15] |
张岩, 李新月, 王斌, 等. 基于深度学习的鲁棒地震数据去噪[J]. 石油地球物理勘探, 2022, 57(1): 12-25. ZHANG Yan, LI Xinyue, WANG Bin, et al. Robust seismic data denoising based on deep learning[J]. Oil Geophysical Prospecting, 2022, 57(1): 12-25. |
| [16] |
李祺鑫, 罗亚能, 马晓强, 等. 基于深度嵌入网络的地震相聚类技术[J]. 石油地球物理勘探, 2022, 57(2): 261-267. LI Qixin, LUO Yaneng, MA Xiaoqiang, et al. Seismic facies clustering technology based on deep embedding network[J]. Oil Geophysical Prospecting, 2022, 57(2): 261-267. |
| [17] |
唐杰, 韩盛元, 刘英昌, 等. 基于去噪卷积神经网络的面波噪声压制方法[J]. 石油物探, 2022, 61(2): 245-252. TANG Jie, HAN Shengyuan, LIU Yingchang, et al. Seismic surface wave atenuation based on denoising convolutional neural networks[J]. Geophysical Prospecting for Petroleum, 2022, 2022, 61(2): 245-252. |
| [18] |
LONG J, SHELHAMER E, DARRELL T. Fully convolutional networks for semantic segmentation[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, 3431-3440.
|
| [19] |
BADRINARAYANAN V, KENDALL A, CIPOLLA R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation[J]. IEEE transactions on pattern analysis and machine intelligence, 2017, 39(12): 2481-2495. |
| [20] |
RONNEBERGER O, FISCHER P, BROX T. U-net: Convolutional networks for biomedical image segmentation[C]. International Conference on Medical image computing and computer-assisted intervention. Springer, Cham, 2015, 234-241.
|
| [21] |
赵明, 陈石, 房立华, 等. 基于U形卷积神经网络的震相识别与到时拾取方法研究[J]. 地球物理学报, 2019, 62(8): 3034-3042. ZHAO Ming, CHEN Shi, FANG Lihua, et al. Earthquake phase arrival auto-picking based on U-shaped convolutional neural network[J]. Chinese Journal of Geophysics, 2019, 62(8): 3034-3042. |
| [22] |
张逸伦, 喻志超, 胡天跃, 等. 基于U-Net的井中多道联合微地震震相识别和初至拾取方法[J]. 地球物理学报, 2021, 64(6): 2073-2085. ZHANG Yilun, YU Zhichao, HU Tianyue, et al. Multi-trace joint downhole microseismic phase detection and arrival picking method based on U-Net[J]. Chinese Journal of Geophysics, 2021, 64(6): 2073-2085. |
| [23] |
刘佳楠, 武杰. 基于全卷积神经网络的地震初至波拾取[J]. 信息技术与网络安全, 2018, 37(11): 58-63. LIU Jia'nan, WU Jie. Seismic first arrival picking based on fully convolutional networks[J]. Information Technology and Network Security, 2018, 37(11): 58-63. |
| [24] |
陈德武, 杨午阳, 魏新建, 等. 基于混合网络U-SegNet的地震初至自动拾取[J]. 石油地球物理勘探, 2020, 55(6): 1188-1201. CHEN Dewu, YANG Wuyang, WEI Xinjian, et al. Automatic picking of seismic first arrivals based on hybrid network U-SegNet[J]. Oil Geophysical Prospecting, 2020, 55(6): 1188-1201. |
| [25] |
潘英杰, 许银坡, 倪宇东, 等. 一种基于地震图像深度语义分割的初至拾取方法[J]. 地球物理学进展, 2022, 37(3): 1122-1131. PAN Yingjie, XU Yinpo, NI Yudong, et al. First break picking method based on deep learning semantic segmentation of seismic image[J]. Progress in Geophysics, 2022, 37(3): 1122-1131. |
| [26] |
王维波, 官强, 高明, 等. 利用残差网络和地震发射层析成像的微地震事件检测[J]. 石油地球物理勘探, 2022, 57(2): 251-260. WANG Weibo, GUAN Qiang, GAO Ming, et al. Detection of microseismic events based on residual network and seismic emision tomography[J]. Oil Geophysical Prospecting, 2022, 57(2): 251-260. |
| [27] |
SZEGEDY C, LIU W, JIA Y, et al. Going deeper with convolutions[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, 1-9.
|
| [28] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[J]. arXiv preprint arXiv: 1409.1556, 2014.
|
| [29] |
HE K, JIAN S. Convolutional neural networks at constrained time cost[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, 5353-5360.
|
| [30] |
HE K, ZHANG X, REN S, et al. Deep residual lear-ning for image recognition[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Re-cognition, 2016, 770-778.
|
| [31] |
SHI W, CABALLERO J, F HUSZ?R, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, 1874-1883.
|
| [32] |
OFFE S, SZEGEDY C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]. International conference on machine learning, PMLR, 2015, 448-456.
|



 丁仁伟, 山东省青岛市黄岛区前湾港路579号山东科技大学地球科学与工程学院, 266590。Email:
丁仁伟, 山东省青岛市黄岛区前湾港路579号山东科技大学地球科学与工程学院, 266590。Email: 