2. 西南石油大学地球科学与技术学院,四川成都 610500
2. School of Geoscience and Technology, Southwest Petroleum University, Chengdu, Sichuan 610500, China
塔里木盆地库车和塔西南山前受构造挤压、沉积风化等因素影响,地表发育山体、沟壑等多种地形,施工条件复杂[1-5]。在地震采集项目部署、技术方案论证、工程造价测算等环节均需对山地地形地类进行详细划分。传统方法通常采用多轮次联合野外踏勘方式,在踏勘效率、成本、安全性与全面性等方面均存在较大不足,主要体现在:①室内地形地类划分以遥感信息和人工目视解译为主,多为定性评价,对地形、地貌信息的定量表征较少;②野外踏勘能够到达的实际区域受限,存在“以偏概全、以点概面”的问题;③室内地形地类划分需收集大量资料,同时需要人工识别和统计,耗时较长;④野外踏勘需要大量人力和物力,同时难以进入尚未修路的工区,短期内难以实现精细分区。
近年来,随着中秋1、博孜9等油气藏的相继发现,复杂山前构造带勘探力度持续加大,地震采集呈现出工作量大、周期短、节奏快、复杂程度日趋增高等特点[6-9],仅仅通过野外踏勘划分地形地类已无法满足油田生产快节奏、科学化的发展需求,亟需探索一种科学合理、客观、经济高效、可重复性强的地形地类划分方法,以便准确地掌握复杂山地工区的炮、检点地形地类构成,从而更好地满足地震采集项目成本测算的需求。
高精度遥感信息广泛运用于国土资源调查、区域地貌研究、地质灾害预防、地震采集方案优选等方面。封志明等[10]利用遥感信息研究地形起伏度与人口分布的相关性;朗玲玲等[11]提出多尺度数字高程模型(Digital Elevation Model,DEM)提取起伏度划分低山丘陵区地形、地貌;牛全富等[12]从坡度、起伏度等地形特征要素中优选敏感因子实现了黄土区滑坡灾害分级预测;叶勇等[13]为改善高、陡山地极低信噪比地区测线的采集条件和可实施性,通过人工加权高程、坡度、相对湿度、岩性等信息计算出评价因子优选地震测线部署方案;陈学强等[14]、张友焱等[15]提出利用高程、坡度等逐点优选检波点改善地震资料品质;赵邦六等[16]、陈德武等[17]介绍了遥感技术在地震采集方面发挥的重要作用,并指出遥感信息在地震勘探中的应用潜力需进一步挖掘。山地地形地类划分通常根据海拔高程并结合坡度、起伏度,由于地区特性和研究需要不同,划分方式和标准也大不相同。前人的研究由于计算地理尺度较大,同时地震采集施工难度表征具有一定特殊性,无法直接应用,但为本次研究提供了“利用DEM数据体来划分山地地形地类”的技术思路。
结合多年生产实践,本文提出一种基于高精度DEM数据体炮、检点地形地类量化评价方法,通过提取遥感信息中的坡度、起伏度、纵深距离等地形特征要素定量表征野外施工难度,并在当前塔里木盆地地震采集工程造价水平下,依据不同要素特点,合理建立地类划分区间,实现地形地类的准确划分。
1 方法原理目前影响塔里木盆地山地地震采集项目施工难度的主要因素有山地高大程度、山体风化破碎程度、山地纵深距离、山地地表岩性等。其中地表岩性主要影响钻井施工,而该部分在工程造价中已有明确的补偿系数,因此在地形地类中暂不考虑。在近年山地地形地类划分实践过程中,将地形特征要素中的起伏度、坡度和纵深距离作为划分地貌类型的3个重要指标。
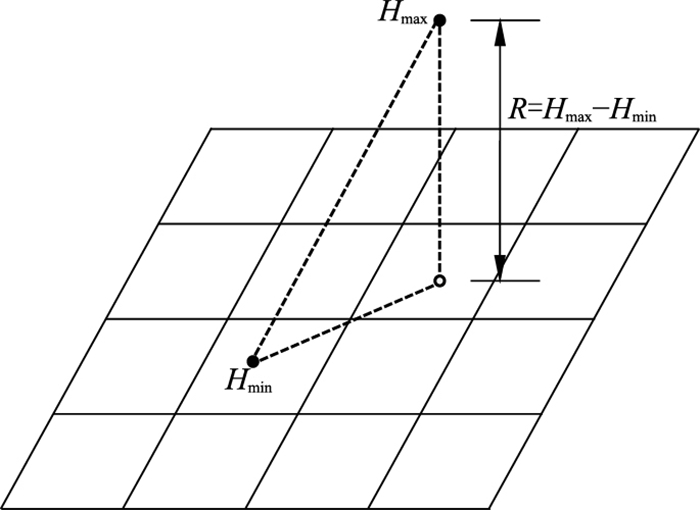
1.1 地形特征要素基本概念 1.1.1 起伏度起伏度是指在当前位置一定空间范围内,最高点与最低点海拔高度的差值[18],可作为地震地形地类划分过程中描述山体区域地形特征的宏观指标,主要反映山体高大程度(图 1)。它表征地震施工纵向上采集设备搬迁等施工难度。地形起伏度R的计算公式为
| $ R=H_{\max }-H_{\min } $ | (1) |
|
图 1 地形起伏度计算示意图 |
式中Hmax、Hmin分别表示计算范围内DEM高程栅格数据体的最大值、最小值。
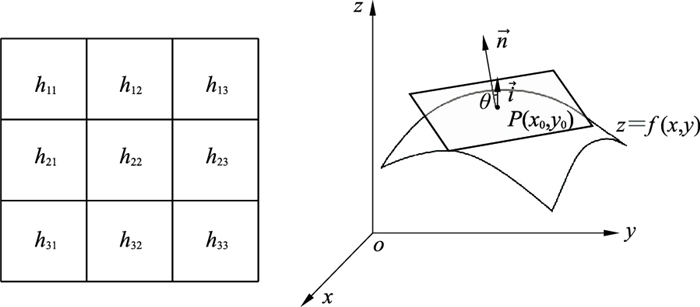
1.1.2 坡度坡度是指当前位置一定空间范围内切平面和水平面间的最大倾角[18],可作为地震地形地类划分过程中山体地表单元陡缓程度的微观指标,主要反映山体受雨水风化切割破碎的严重程度(图 2)。它表征地震施工横向上采集设备搬迁等施工难度。假设任意位置高程记作z=f(x, y),则位置P(x0, y0)的坡度为该点切平面与水平面的夹角θ,即该点法向量
| $ \theta=\frac{\pi}{180} \arctan \sqrt{\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2} $ | (2) |
|
图 2 高程网格(左)及地形坡度计算示意图(右) |
利用三阶反距离平方权差分代替微分,则离散形式为
| $ \begin{aligned} \frac{\partial f}{\partial x} & =\frac{\Delta H_x}{\Delta x} \\ & =\frac{\left(h_{13}-h_{11}\right)+2\left(h_{23}-h_{21}\right)+\left(h_{33}-h_{31}\right)}{8 \mathrm{~d} x} \end{aligned} $ | (3) |
| $ \begin{aligned} \frac{\partial f}{\partial y} & =\frac{\Delta H_y}{\Delta y} \\ & =\frac{\left(h_{31}-h_{11}\right)+2\left(h_{32}-h_{12}\right)+\left(h_{33}-h_{13}\right)}{8 \mathrm{~d} x} \end{aligned} $ | (4) |
式中:h11、h12、h13、⋯、h32、h33为对应高程栅格数据的值;dx为栅格间距,即DEM数据体的精度;Hx、Hy分别为x、y方向差分算子。
1.1.3 纵深距离为完善起伏度、坡度两个地形特征要素在表征山地纵、横向上施工搬迁难度的不足,引入纵深距离的概念,其为从当前位置沿山体边界法线方向向内延伸的距离,它也是描述山体区域地形特征的一个宏观指标,在起伏度和坡度划分结果的基础上调整地类,从而更准确的表征野外施工难度。
为计算方便,利用角平分线法将山体按照不同距离建立若干个与山体边界等距离区域,即多个山体边界纵深距离分析区。纵深距离分析区内任意位置沿其法线方向距离山体边界相等。
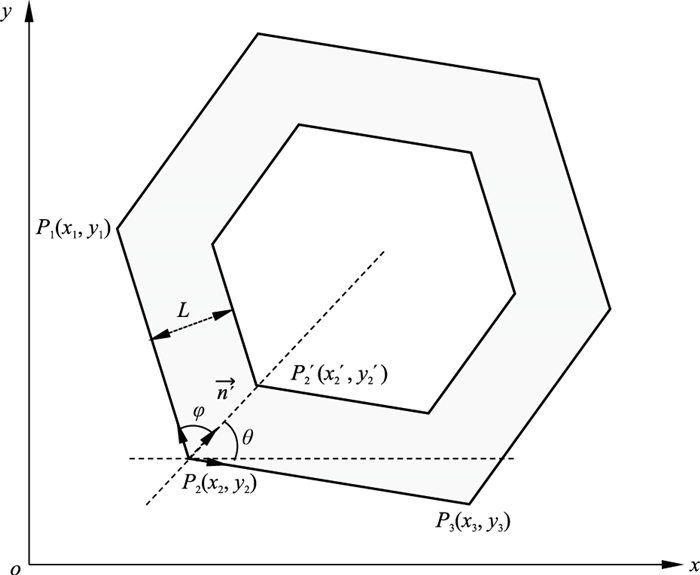
如图 3所示,P1、P2、P3分别为山体边界上相邻的三个点,P2′为距离山体边界L处对应的纵深距离分析区边界上的点,L为纵深距离,φ为∠P1P2P3的平分角,P2到P2′之间的距离为
| $ \overrightarrow{n^{\prime}}=\frac{\overrightarrow{P_2 P_1}+\overrightarrow{P_2 P_3}}{\left|\overrightarrow{P_2 P_1}+\overrightarrow{P_2 P_3}\right|} $ | (6) |
|
图 3 山体边界纵深距离分析示意图 |
为确保
| $ k=\operatorname{sgn}\left(\frac{\overrightarrow{P_1 P_2} \times \overrightarrow{P_2 P_3}}{\left|\overrightarrow{P_1 P_2}\right| \cdot\left|\overrightarrow{P_2 P_3}\right|}\right) $ | (7) |
式中k>0表示
| $ \sin \varphi=\left|\frac{\overrightarrow{n^{\prime}} \times \overrightarrow{P_2 P_3}}{\left|\overrightarrow{P_2 P_3}\right|}\right| $ | (8) |
同时由
| $ \overrightarrow{O P_2^{\prime}}=\overrightarrow{O P_2}+\overrightarrow{P_2 P_2^{\prime}}=\overrightarrow{O P_2}+\overrightarrow{P_2 P_2^{\prime}} \cdot\left(k \cdot \overrightarrow{n^{\prime}}\right) $ | (9) |
重复计算式(6)~式(9)即可求得纵深距离为L的分析区边界点坐标。
1.2 邻域大小计算和地类划分区间确定方法上述起伏度、坡度、纵深距离等地形特征要素能否准确表征山体施工难度,关键在于3个方面:DEM数据体的分辨率大小;地形特征要素中起伏度、坡度的最佳邻域大小;各地形特征要素的地类划分区间。
由于地形地类划分主要应用于地震采集技术经济技术一体化评价,侧重于地震采集工程造价,不需采集方案设计中炮、检点优化选点布设那么高要求如(大于或等于5 m的DEM数据体分辨率),同时结合数据体获取难度和近年生产实践,认为DEM数据体分辨率大于或等于10 m即可。
为适应塔里木盆地山地复杂多样,这里分别采用数理统计中的两种方法:一是均值变点法,用于求取地形特征要素的计算邻域大小;二是自然间断分级法,用于求取地形特征要素的地类划分区间。
1.2.1 均值变点法均值变点法是一种非线性系统输出数据序列单变点分析方法[19]。将工区地形特征要素的平均值作为均值变点法的非线性系统输出数据序列{Xt, t=1, 2, ⋯, m},其中m为序列长度。令i=2, 3, ⋯, m,对每个i将序列分为X1, X2, ⋯, Xi-1和Xi, Xi+1, ⋯, Xm两段,计算每段序列的算术平均值
| $ S_i=\sum\limits_{t=1}^{i-1}\left(X_t-\bar{X}_{i 1}\right)^2+\sum\limits_{t=i}^n\left(X_t-\bar{X}_{i 2}\right)^2 $ | (10) |
| $ S=\sum\limits_{t=1}^{i=1}\left(X_t-\bar{X}_{i 2}\right)^2 $ | (11) |
| $ T_i=S-S_i $ | (12) |
当Ti取最大值时对应位置为变点位置,即最佳的地形特征要素计算邻域。
1.2.2 自然间断分级法自然间断法是地理信息中的一种分类区间确定方法[20],该方法能依据数据的分布特征,将数据按照区间内相似性最高、区间之间差异性最大划分为多个区间。
数据序列平均值的偏差平方和SDAM记作
| $ \operatorname{SDAM}=\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)^2 $ | (13) |
式中
| $ \mathrm{SDCM}_1=\mathrm{SDCM}_{i_1}+\mathrm{SDCM}_{i_2}+\cdots+\mathrm{SDCM}_{i_k} $ | (14) |
同理分别求出其他分组情况SDCM2, ⋯, SDCMCnk的值,并求取它们的最小值SDCMmin=min{SDCMi, t=1, 2, ⋯, Cnk},最小值对应分组情况即为最优分类。
最后利用方差拟合优度GVF验证
| $ \mathrm{GVF}=1-\frac{\mathrm{SDCM}_{\min }}{\mathrm{SDAM}} $ | (15) |
GVF的取值范围为0~1,其值越大表示组间差异越大。在地形地类划分中,一般认为GVF≥0.7时,自然间断法计算的分类结果较好。
1.3 综合划分地形地类依照中国石油天然气集团公司现行定额标准,塔里木盆地地形地类有山地、戈壁、平原农田、沼泽水网和沙漠共5种地表类型。山地地震项目一般包括山地地表类型与戈壁、农田、沼泽水网3种非山地地表类型。山地地形划分标准如表 1所示,当前划分标准多为定性描述,受主观因素影响大。
|
|
表 1 塔里木盆地山地地形地类划分现行定额标准 |
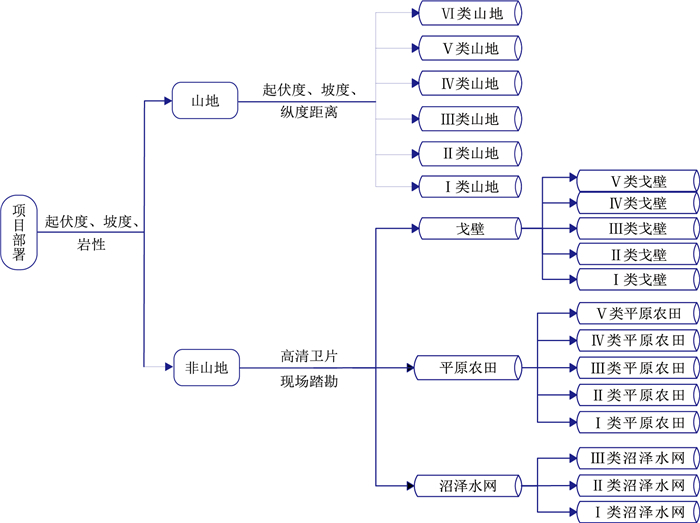
为使山地地类划分工作在现行定额下相对客观合理、划分过程利于量化统一,提出了一种划分方法(图 4),利用10 m精度DEM数据体计算坡度、起伏度、纵深距离,并依据施工难度将山地地类由小到大划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ及Ⅵ类;非山地由于区域连续且范围较小,可直接通过高清卫片结合现场踏勘情况划分地表类型及难度类别。
|
图 4 塔里木油田地震项目地形地类划分示意图 |
首先利用起伏度、坡度划分地形地类,将任意DEM数据体栅格位置由起伏度地类划分结果记作IR(x, y),坡度地类划分结果记作Iθ(x, y),取值为0、1、2、3、4、5、6,分别对应非山地、Ⅰ类山地、Ⅱ类山地、Ⅲ类山地、Ⅳ类山地、Ⅴ类山地、Ⅵ类山地等7种地类,计算起伏度、坡度两者划分结果最大值,得到的地类记作YZ0(x, y),即
| $ Y_{Z_0}(x, y)=\max \left[I_R(x, y), I_\theta(x, y)\right] $ | (16) |
式中YZ0(x, y)表征山地施工难度。实际生产表明,Ⅲ类及Ⅲ类以上山体包围的区域(如山间相对平坦的区域或更加陡峭的区域)施工难度会较该区域直接计算结果大,为进一步刻画此类区域搬迁距离对施工难度的影响,利用纵深距离对YZ0(x, y)做一定调整。沿Ⅲ类山体边界建立3个不同纵深距离分析区,不同纵深距离地类调整因子记作D0(x, y),即
| $ D_0(i, j)=\left\{\begin{array}{lc} 0 & \;\;\;\;\;\;\;L <2.0 \mathrm{~km} \\ 1 & 2.0 \mathrm{~km} \leqslant L <3.5 \mathrm{~km} \\ 2 & \;\;\;\;\;\;\;L \geqslant 3.5 \mathrm{~km} \end{array}\right. $ | (17) |
山体地类随着纵深距离的增加需适当上调,调整后的地类记作YZ0′(x, y)。由于在实际生产中YZ0′(x, y)越大,工程造价增幅越大,因此当D0(x, y)>0时,还需将地类划分为0≤YZ0′(x, y)≤4、YZ0′(x, y)=5、YZ0′(x, y)=6三个层次,当地类达到IV类后,地类越高上调地类幅度越小,具体计算公式如下
| $ \begin{aligned} & Y_{Z_0}^{\prime}(i, j)= \\ & \begin{cases}Y_{Z_0}(x, y)+D_0(x, y) & 0 \leqslant Y_{Z_0}(x, y) \leqslant 4 \\ Y_{Z_0}(x, y)+D_0(x, y)-1 & Y_{Z_0}(x, y)=5 \\ Y_{Z_0}(x, y) & Y_{Z_0}(x, y)=6\end{cases} \end{aligned} $ | (18) |
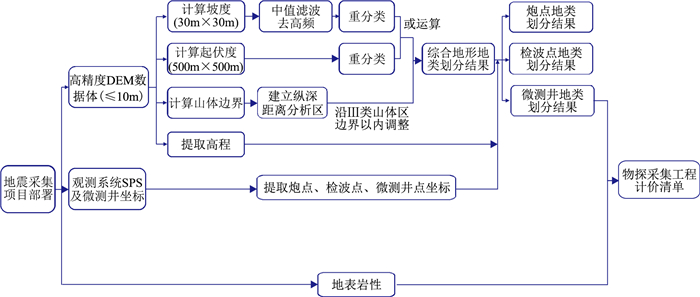
图 5为山地地形地类自动划分的计算流程,在利用上述方法计算部署地震采集项目综合地形地类之后,根据炮点、检波点、微测井点坐标提取、统计每个点对应地类,结合地表岩性即可快速得到地震采集工程计价清单,从而实现高效测算项目工程造价,在采集设计阶段完成经济技术一体化评价,从而优选采集设计方案。
|
图 5 塔里木油田山地地形地类自动划分计算流程 |
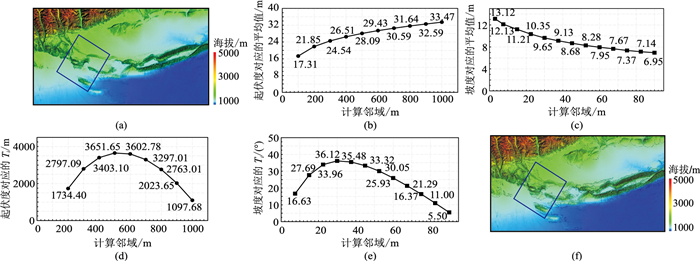
为确定地形地类划分中坡度、起伏度的最佳计算邻域,选取秋里塔格构造带典型山地地表西秋—却勒—佳木段中的佳木地区作为分析数据(图 6a蓝色区域),并利用前文介绍的均值变点法分别计算(采用航拍的1 m精度DEM数据体)100 m×100 m、200 m×200 m、⋯、1000 m×1000 m范围下的起伏度平均值和3.0 m×3.0 m、7.5 m×7.5 m、15.0 m×15.0 m、⋯、90.0×90.0 m范围下坡度平均值作为均值变点分析序列。
|
图 6 坡度、起伏度对应的计算邻域 (a)西秋—却勒—佳木段DEM数据体;(b)不同计算邻域起伏度平均值;(c)不同计算邻域坡度平均值;(d)不同计算邻域起伏度均值变点分析结果;(e)不同计算邻域坡度均值变点分析结果;(f)山地区域(黑色阴影部分) |
如图 6所示,计算结果表明起伏度平均值随邻域大小增加而增加,变点位置对应邻域大小为500 m,坡度平均值随邻域大小增加而减小,变点位置计算邻域大小为30 m,即起伏度、坡度对应的最佳计算邻域大小分别为500 m和30 m。
根据近年塔里木油田地震采集现场地形地类划分经验,将塔里木盆地地震采集地形地类划分中山地定义为:500 m计算范围内起伏度大于30 m或30 m计算范围内坡度大于5°(以DEM数据体分辨率≥10 m计算)的地表或第四系西域组以下老地层出露区。
依据上述定义计算出的西秋—却勒—佳木段山地区域(图 6f黑色阴影部分)与DEM数据体吻合较好,同时秋里塔格构造带和克拉苏构造带划分出的山地分布区域与现场实际地形高度吻合,表明此类山地与非山地划分方法可行、有效。
2.2 起伏度、坡度地类划分区间确定为得到适用于整个塔里木盆地山地地类坡度和起伏度的合理划分区间,选取近三年新采集且具有代表性的6个地震采集项目用于分析,包括库车山前的佳木3、却勒4、克深1三维,柯坪地区的柯坪4、沙井子二维以及塔西南山前的乌泊尔二维。将山地地形地类划分为非山地和山地共7种类型,利用自然间断法分别计算坡度和起伏度计算划分区间,并计算方差拟合优度,计算结果见表 2、表 3。计算结果表明,采用自然间断法分类计算出的各项目起伏度、坡度方差拟合优度为0.96~0.98,表明该方法在山地地类划分中是有效的。各项目之间的划分结果虽然存在一定差异,但整体比较接近。由于二维项目工区跨度大于三维项目,其区间划分范围较三维项目稍大一些。
|
|
表 2 自然间断法起伏度分析结果 |
|
|
表 3 自然间断法坡度分析结果 |
为统一地类划分的标准,同时与当前塔里木油田地震采集工程造价水平和现有地类划分认识相适应,需对坡度和起伏度地类划分区间做出一定调整,调整后分类方案如表 2、表 3所示。从表可见,调整后所有项目方差拟合优度均大于0.91,表明调整后地类划分区间的聚类效果仍然合理。
3 应用实例——以库北1三维为例库北1三维构造位置位于库车坳陷北部构造带库北单斜带,南部紧邻克拉苏构造带,位于阿克苏地区拜城县境内,部署工作量偏移处理前的满覆盖面积为194.72 km2,其中东西长19.8 km、南北宽9.4 km。
工区地形地貌以山地地表(图 7)为主,中部主体为一般山地,北部为落差较大的高难山体,非山体地表为戈壁。高密度采集中炮点范围海拔高程为1550~2750 m,检波点范围海拔高程为1450~2900 m,属于库车山前典型的复杂山地地表类型。以往利用野外踏勘与卫片结合的方式划分地形地类,难以高效准确地表征项目施工难度。

|
图 7 库北1三维工区地理信息 (a)卫星影像;(b)海拔高程 |
工区选取5处典型地表位置(图 8a中的A~E处)现场验证标定,并利用起伏度和坡度划分地形地类(图 8b),仔细对比可以看出,划分结果与实际地表情况基本相符,但工区北部和中部Ⅲ类及Ⅲ类以上包围的高难山体区域局部地类偏低(图 8b中的C和E处),沿Ⅲ类山体边界建立不同纵深距离分析区(图 8c)来调整地类,并依据纵深距离大小对地形地类进行调整,调整后的地类(图 8d)与实际地表更加吻合,划分结果与现场标定结果一致。

|
图 8 库北1三维工区地形地类划分 (a)5处标记点位置现场照片;(b)纵深距离调整前地形地类划分;(c)Ⅲ类及Ⅲ类以上山体不同纵深距离分析区;(d)纵深距离调整后地形地类划分 |
在地震采集部署设计阶段,一般会结合地质任务和工区特点提出2或3种采集方案,库北1三维工区共有2种设计了2种采集方案(表 4)。
|
|
表 4 库北1三维观测系统设计方案 |
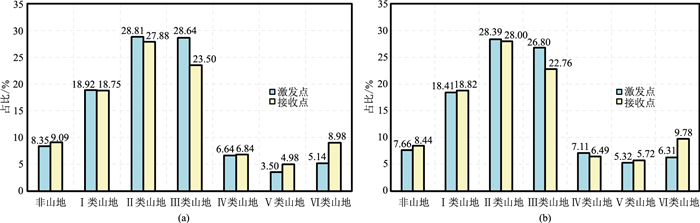
分别根据2种方案炮点、检波点坐标位置提取对应的地类,并统计得到炮点点、接收点不同地类占比(图 9)。两种方案不同地表类型炮点、接收点占比较为接近,非山地约占8%,Ⅰ类~Ⅲ类山体约占72%,Ⅳ类~Ⅵ类山体占20%。
|
图 9 库北1三维工区激发点、接收点不同地类占比柱状图 (a)采集方案1;(b)采集方案2 |
在观测系统参数基础上结合激发参数、接收参数和近地表岩性及厚度情况,即可快速获得量化后的用于项目工程造价测算清单,为经济技术一体化评价优选出最佳采集方案提供决策依据。
依据塔里木油田地震项目工程计价标准分别计算表 4和表 5测算清单工程造价,方案1较方案2在炮道密度提升36.64万道/km2的同时,每平方公里地震采集项目施工费用单价降低0.99%,节约成本约115.94万元。综合考虑成本和采集效果,方案1明显优于方案2,这种“以道换炮”提高炮道密度、降低勘探成本的策略在塔里木探区山地地震采集经常用到。
|
|
表 5 库北1三维项目采集方案1测算清单 |
|
|
表 6 库北1三维项目采集方案2测算清单 |
目前基于起伏度、坡度、纵深距离三地形特征要素的复杂山地炮、检点地形地类高效划分方法已经应用到塔里木油田近3年全部山地地震采集项目经营测算和经济技术一体化评价中,并以此研发了基于GIS平台的复杂山地地震智能工程造价系统。该方法大大提高了地形地类划分的客观性和科学性,野外踏勘周期从1周以上缩短至1天,同时踏勘范围也从以往全工区踏勘转变成安全有效的局部针对性踏勘,整个采集项目地类划分周期由以往的1周以上缩减至2天以内。
4 结束语针对山地地形地类存在的诸多问题,创新性地提出了一种利用起伏度、坡度、纵深距离高效划分山地地形地类的方法,将地形地类划分周期缩短至2天以内,大幅提高了经济技术一体化评价工作的效率和科学性。
实际应用表明,引入纵深距离这一地形特征要素后,标定结果更加精准,有效弥补了仅采用起伏度、坡度一些特殊区域(Ⅲ类及Ⅲ类以上山体包围区的施工困难区)地类划分存在的不足,可进一步提高地形地类划分结果的可靠性。
此次地形地类划分方法研究工作主要建立在塔里木探区工程造价水平上,各探区地震工程造价水平存在一定差异,其他探区通过结合自身工程造价水平适当调整地类划分参数后,该技术具备较好的推广应用潜力。
| [1] |
符力耘, 肖又军, 孙伟家, 等. 库车坳陷复杂高陡构造地震成像研究[J]. 地球物理学报, 2013, 56(6): 1985-2001. FU Liyun, XIAO Youjun, SUN Weijia, et al. Seismic imaging studies of complex high and steep structures in Kuqa depression[J]. Chinese Journal of Geophy-sics, 2013, 56(6): 1985-2001. |
| [2] |
范增辉, 欧阳诚, 刘树根, 等. 塔里木盆地西南部黄土塬地区地震采集技术[J]. 石油地球物理勘探, 2014, 49(4): 627-633. FAN Zenghui, OUYANG Cheng, LIU Shugen, et al. Seismic acquisition in loess area, Southwestern Tarim Basin[J]. Oil Geophysical Prospecting, 2014, 49(4): 627-633. |
| [3] |
陈学强, 王彦峰, 吕景峰, 等. 库车坳陷复杂山地地震采集适用技术及应用效果[J]. 石油地球物理勘探, 2022, 57(4): 806-814. CHEN Xueqiang, WANG Yanfeng, LYU Jingfeng, et al. Seismic exploration technologies and applications in complex mountaion areas of Kuqa Depression[J]. Oil Geophysical Prospection, 2022, 57(4): 806-814. |
| [4] |
崔庆辉, 尚新民, 腾厚华, 等. 西部山前带黄土砾石区静校正方法[J]. 石油地球物理勘探, 2022, 57(2): 226-233. CUI Qinghui, SHANG Xinmin, TENG Houhua, et al. Research on static correction method for the loess and gravel area in western foothill telt[J]. Oil Geophysical Prospection, 2022, 57(1): 194-205. |
| [5] |
彭更新, 刘威, 郭念民, 等. 基于时空域交错网格有限差分法的应力速度声波方程数值模拟[J]. 石油物探, 2022, 61(1): 156-165. PENG Genxin, LIU Wei, GUO Nianmin, et al. A time-space domain dispersion-relationship-based staggered-grid finite-difference scheme for modeling the stress-velocity acoustic wave equation[J]. Geophysical Prospecting for Petroleum, 2022, 61(1): 156-165. DOI:10.3969/j.issn.1000-1441.2022.01.016 |
| [6] |
徐兆辉, 徐振平, 张荣虎, 等. 表腹双复杂构造区深层砂岩有效储层定量预测——以塔里木盆地中秋里塔格地区巴什基奇克组为例[J]. 石油地球物理勘探, 2022, 57(1): 194-205. XU Zhaohui, XU Zhenping, ZHANG Ronghu, et al. Quantitative prediction of deep effective sandstone reserveoir in geomorphologic and techonic complicated area: An example from Bashenjiqike Formation of Middle Qiulitage Area in Tarim Basin[J]. Oil Geophysical Prospection, 2022, 57(1): 194-205. |
| [7] |
李剑, 李谨, 谢增业, 等. 塔里木盆地秋里塔格构造带中秋1圈闭油气来源与成藏[J]. 石油勘探与开发, 2020, 47(3): 512-522. LI Jian, LI Jin, XIE Zengye, et al. Oil and gas source and accumulation of Zhongqiu 1 trap in Qiulitage structural belt, Tarim Basin, NW China[J]. Petroleum Exploration and Development, 2020, 47(3): 512-522. |
| [8] |
田军, 杨海军, 吴超, 等. 博孜9井的发现与塔里木盆地超深层天然气勘探潜力[J]. 天然气工业, 2020, 40(1): 11-19. TIAN Jun, YANG Haijun, WU Chao, et al. Discovery of well Bozi 9 and ultra-deep natural gas exploration potential in the Kelasu tectonic zone of the Tarim Basin[J]. Natural Gas Industry, 2020, 40(1): 11-19. |
| [9] |
杜金虎, 田军, 李国欣, 等. 库车坳陷秋里塔格构造带的战略突破与前景展望[J]. 中国石油勘探, 2019, 24(1): 16-23. DU Jinhu, TIAN Jun, LI Guoxin, et al. Strategic breakthrough and prospect of Qiulitag structural belt in Kuqa depression[J]. China Petroleum Exploration, 2019, 24(1): 16-23. |
| [10] |
封志明, 唐焰, 杨艳昭, 等. 中国地形起伏度及其与人口分布的相关性[J]. 地理学报, 2007, 62(10): 1073-1082. FENG Zhiming, TANG Yan, YANG Yanzhao, et al. The relief degree of land surface in China and its correlation with population distribution[J]. Acta Geographica Sinica, 2007, 62(10): 1073-1082. |
| [11] |
郎玲玲, 程维明, 朱启疆, 等. 多尺度DEM提取地势起伏度的对比分析——以福建低山丘陵区为例[J]. 地球信息科学, 2007, 9(6): 1-6. LANG Lingling, CHENG Weiming, ZHU Qijiang, et al. A comparative analysis of the multi-criteria DEM extracted relief taking Fujian low mountainous region as an example[J]. Geo-information Science, 2007, 9(6): 1-6. |
| [12] |
牛全福, 冯尊斌, 党星海, 等. 黄土区滑坡研究中地形因子的选取与适宜性分析[J]. 地球信息科学学报, 2017, 19(12): 1584-1592. NIU Quanfu, FENG Zunbin, DANG Xinghai, et al. Suitability analysis of topographic factors in Loess landslide research[J]. Journal of Geo-Information Science, 2017, 19(12): 1584-1592. |
| [13] |
叶勇, 雷迎春, 张友焱, 等. 基于遥感信息的地震测线优选方法[J]. 石油勘探与开发, 2008, 35(6): 704-709. YE Yong, LEI Yingchun, ZHANG Youyan, et al. A method to optimize seismic layout based on remote sensing information[J]. Petroleum Exploration and Development, 2008, 35(6): 704-709. |
| [14] |
陈学强, 白文杰, 钟海. 沙漠区高信噪比地震采集方法[J]. 石油地球物理勘探, 2010, 45(3): 321-325. CHEN Xueqiang, BAI Wenjie, ZHONG Hai. High signal-to-noise ratio seismic acquisition methods in desert area[J]. Oil Geophysical Prospecting, 2010, 45(3): 321-325. |
| [15] |
张友焱, 雷迎春, 叶勇, 等. 利用高精度遥感信息辅助设计检波器点位[J]. 石油地球物理勘探, 2009, 44(1): 7-13. ZHANG Youyan, LEI Yingchun, YE Yong, et al. Using high-precision remote information for auxiliary design of geophone point[J]. Oil Geophysical Prospecting, 2009, 44(1): 7-13. |
| [16] |
赵邦六, 杜小弟, 张友焱, 等. 高精度遥感影像数据在复杂地表区地震勘探工程中的应用[J]. 中国石油勘探, 2005, 10(2): 33-35, 52, 64. ZHAO Bangliu, DU Xiaodi, ZHANG Youyan, et al. The application of high precision remote sensing data in seismic survey for complicated topography area[J]. China Petroleum Exploration, 2005, 10(2): 33-35, 52, 64. |
| [17] |
陈德武, 何欣, 王万里, 等. 一种基于ArcGIS的地震采集质量分析评价技术[J]. 物探化探计算技术, 2016, 38(2): 259-263. CHEN Dewu, HE Xin, WANG Wanli, et al. A comprehensive analysis and evaluation technology of seismic acquisition quality based on ArcGIS[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2016, 38(2): 259-263. |
| [18] |
汤国安, 杨昕. ArcGIS地理信息系统空间分析实验教程(2版)[M]. 北京: 科学出版社, 2012: 362-364. TANG Guoan, YANG Xin. ArcGIS GIS Spatial Analysis Experiment Tutorial(2nd ed)[M]. Beijing: Science Press, 2012: 362-364. |
| [19] |
项静恬, 史久恩. 非线性系统中数据处理的统计方法[M]. 北京: 科学出版社, 1997: 3-6. XIANG Jingtian, SHI Jiuen. Statistic Method of Data Analysis of Non-Liner System[M]. Beijing: Science Press, 1997: 3-6. |
| [20] |
李乃强, 徐贵阳. 基于自然间断点分级法的土地利用数据网格化分析[J]. 测绘通报, 2020(4): 106-110, 156. LI Naiqiang, XU Guiyang. Grid analysis of land use based on natural breaks (jenks) classification[J]. Bulletin of Surveying and Mapping, 2020(4): 106-110, 156. |



 杨连刚, 新疆维吾尔自治区库尔勒市石化大道26号塔指小区勘探开发研究院,841000。Email:
杨连刚, 新疆维吾尔自治区库尔勒市石化大道26号塔指小区勘探开发研究院,841000。Email: 