2. 青岛国家海洋科学与技术实验室,山东青岛 266100;
3. 中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛 266100
2. Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266100, China;
3. Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Qingdao, Shandong 266100, China
精确求取初至波旅行时对于实现静校正[1-2]、基尔霍夫积分偏移[3]、旅行时反演[4-9]、地震定位[10]、偏移成像[11]等具有重要意义。传统求取初至波旅行时方法采用射线追踪类算法,包括试射法[12-14]和弯曲法[15-16],但计算效率较低。由于复杂速度模型中两点之间的射线路径存在多种可能,计算极易陷入局部收敛,为了克服射线追踪类算法的缺陷,程函方程类算法得以发展。Vidale[17]基于盒式扩张的思想提出采用有限差分法求解二维程函方程,但这种算法并不完全符合波前传播规律,在因果性方面存在缺陷,由于忽略了初至能量可能迂回传播的情况,致使该算法存在不稳定性,不能取得真正的全局最小旅行时,当网格间距较小时还会带来巨大的计算量;Qin等[18]使用波前扩张理论改进了有限差分算法的因果性;VanTrier等[19]使用迎风有限差分算子提高了算法的稳定性;Sethian[20]提出快速推进法(Fast Marching Method, FMM),利用逆风差分格式求解局部程函方程, 采用窄带延拓重建旅行时波前, 利用堆选排技术保存旅行时, 将最小旅行时放在堆的顶部,显著缩短了寻找极小值的时间; Qian等[21]将快速清理法(Fast Sweeping Method, FSM)用于二维程函方程求解,进一步提高了有限差分算法的计算效率,其主要思想是基于因果关系将旅行时波场传播的方向分成有限个组, 对每一组分别利用Gauss-Seidel迭代方法求解非线性逆风差分格式离散化后的方程组。一些学者提出因式分解形式的程函方程[22-23],解决了震源奇异性问题,进一步提高了有限差分算法的准确度。Vidale[24]还将有限差分算法扩展到三维,此后便成为求取三维旅行时最常用的方法; Soukina等[25]将三维有限差分算法应用于各向异性介质旅行时的求取;Hole等[26]使用三维有限差分算法求解反射波旅行时。相对于二维模型,求取三维地震旅行时对计算精度和效率要求更高,而高精度的高阶有限差分会导致巨大的计算成本[27-28]。如何在求解三维程函方程时平衡精确度与计算成本是求解旅行时亟待解决的问题。
深度学习技术的蓬勃发展为解决以上问题拓展了新途径。20世纪90年代,诸多学者提出了用神经网络求解偏微分方程的想法[29-30]。Sirignano等[31]提出使用全连接神经网络(Fully Connected Neural Network, FCNN)求解偏微分方程的无网格化方法;Tompson等[32]使用卷积神经网络提高了稀疏线性偏微分方程的求解效率,得到Navier-Stokes方程的数值解。针对传统神经网络没有考虑偏微分方程本身携带的物理信息并且缺少物理意义可解释性的缺陷,Raissi等[33]提出物理信息驱动的神经网络(Physics-informed Neural Network,PINN)。与传统深度学习网络不同,PINN在利用FCNN的函数拟合功能实现偏微分方程近似的基础上,在神经网络训练过程中加入偏微分方程和实际物理条件的约束,使求解偏微分方程的结果更具实际物理意义。近年来,PINN在地球物理领域得到了广泛的应用。Xu等[34]将PINN应用于速度模型的反演;Karimpouli等[35]使用PINN求解波动方程进行正演模拟;Song等[36]将PINN用于VTI介质频率域声波方程的求解;Waheed等[37]使用PINN求解二维程函方程并将其应用于层析成像,结果显示PINN在二维初至波旅行时的求取中表现出高于传统方法的效率和准确度。
本文基于PINN实现了三维程函方程的高效、高精度求解。模型实验结果显示,基于PINN的三维初至波旅行时计算方法相对于传统的有限差分法有更高的精度和更高的计算效率。
1 程函方程的有限差分数值解三维形式的程函方程为
| $ \begin{array}{r} {\left[\frac{\partial T(x, y, z)}{\partial x}\right]^2+\left[\frac{\partial T(x, y, z)}{\partial y}\right]^2+} \\ {\left[\frac{\partial T(x, y, z)}{\partial z}\right]^2=\frac{1}{v^2(x, y, z)}} \end{array} $ | (1) |
式中:T(x, y, z)为(x, y, z)处的地震波旅行时;v(x, y, z)为(x, y, z)处的速度。
为了便于表示,式(1)可写为
| $ \left\{\begin{array}{r} |\nabla T(x, y, z)|^2=s^2(x, y, z) \\ T\left(x_{\mathrm{s}}, y_{\mathrm{s}}, z_{\mathrm{s}}\right)=0 \end{array}\right. $ | (2) |
式中:∇为梯度算子;(xs, ys, zs)表示震源位置;T(xs, ys, zs)为震源处的旅行时;s(x, y, z) 表示慢度,其表达式为
| $ s(x, y, z)=\frac{1}{v(x, y, z)} $ | (3) |
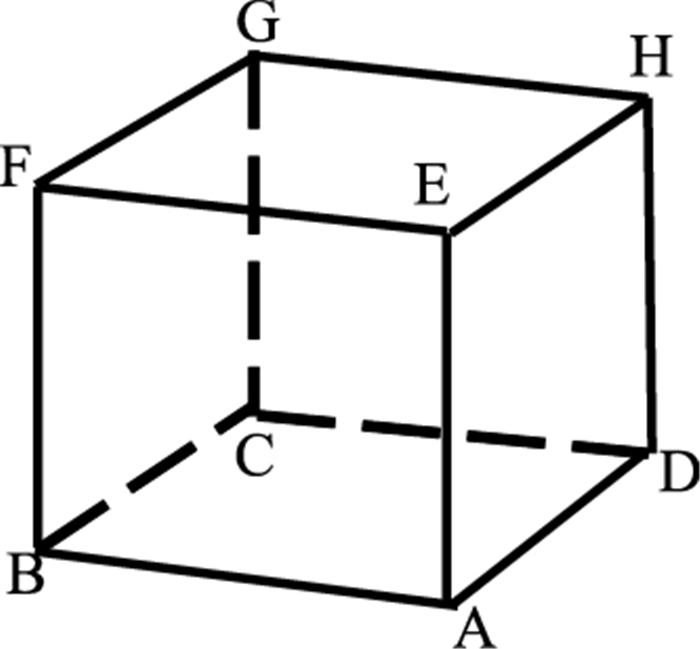
为求解三维程函方程,Vidale[24]提出了有限差分算法,将三维速度模型剖分为如图 1所示的若干正方体网格。假设已知A点旅行时和各网格点的速度,且网格间距为h,则有
| $ T_{\mathrm{B}}=T_{\mathrm{A}}+h s_{\mathrm{B}} $ | (4) |
| $ T_{\mathrm{C}}=T_{\mathrm{A}}+\sqrt{2 h^2 s_{\mathrm{C}}^2-\left(T_{\mathrm{B}}-T_{\mathrm{D}}\right)^2} $ | (5) |
| $ T_{\mathrm{G}}=T_{\mathrm{A}}+\frac{1}{\sqrt{2}} \times \sqrt{6 h s_{\mathrm{G}}-\left(T_{\mathrm{E}}-T_{\mathrm{D}}\right)^2-\left(T_{\mathrm{D}}-T_{\mathrm{B}}\right)^2-\left(T_{\mathrm{B}}-T_{\mathrm{E}}\right)^2-\left(T_{\mathrm{H}}-T_{\mathrm{F}}\right)^2-\left(T_{\mathrm{F}}-T_{\mathrm{C}}\right)^2-\left(T_{\mathrm{C}}-T_{\mathrm{H}}\right)^2} $ | (6) |
|
图 1 三维差分网格示意图 |
式(4)~式(6)分别为一维、二维、三维有限差分算子,使用以上算子对所有网格点进行差分计算,即可求得整个计算区域的旅行时。
有限差分算法凭借较高的精度和计算效率得到了广泛的应用,但该方法存在不可避免的震源奇异性问题[28]。为此,需要将程函方程转化为因式分解形式[29-30],即将待求解旅行时T(x, y, z) 分解为两个因式,有
| $ T(x, y, z)=T_0(x, y, z) \tau(x, y, z) $ | (7) |
式中:T0(x, y, z)是被指定的已知因式;τ(x, y, z) 是需要求解的旅行时未知因式。
将式(7)代入式(2)即可得到因式分解形式的程函方程
| $ \begin{aligned} & T_0^2(x, y, z)|\nabla \tau(x, y, z)|^2+ \\ & \tau^2(x, y, z)\left|\nabla T_0(x, y, z)\right|^2+ \\ & 2 T_0(x, y, z) \tau(x, y, z) \times \\ & \left|\nabla T_0(x, y, z) \nabla T(x, y, z)\right| \\ & =s^2(x, y, z) \tau\left(x_{\mathrm{s}}, y_{\mathrm{s}}, z_{\mathrm{s}}\right)=1 \end{aligned} $ | (8) |
式中τ(xs, ys, zs)为震源位置的未知因式。
T0(x, y, z)用以下解析式指定
| $ \begin{aligned} & T_0(x, y, z)=s\left(x_{\mathrm{s}}, y_{\mathrm{s}}, z_{\mathrm{s}}\right) \times \\ & \;\;\;\;\; \sqrt{\left(x-x_{\mathrm{s}}\right)^2+\left(y-y_{\mathrm{s}}\right)^2+\left(z-z_{\mathrm{s}}\right)^2} \end{aligned} $ | (9) |
式中s(xs, ys, zs) 为震源处的慢度。
因式分解形式的程函方程有效解决了震源奇异性问题,但三维有限差分算法计算精度有限,而具有更高计算精度的高阶有限差分的计算成本也随之提升[27-28]。因此,本文尝试将深度学习与旅行时计算相结合,提出兼具精度与计算效率的基于PINN的地震旅行时求取方法。
2 基于PINN求取地震旅行时 2.1 PINN简介由通用近似算法[38]可知,一个输入层有n个神经元、输出层有m个神经元的神经网络可以用来表示任意一个多维非线性函数u:Rn → Rm,而偏微分方程的建模过程也是寻找满足约束条件的非线性函数,两者具有相通之处。得益于在深度神经网络(DNN)中广泛使用的自动微分技术,在设计神经网络的损失函数时,可以融入偏微分方程中微分形式的约束条件,以获得包含物理模型约束的神经网络,即PINN。PINN的基本结构是通过FCNN近似表示一个函数,再利用自动微分技术求出偏微分方程残差和初边值残差约束,并作为正则项添加至损失函数中,最后利用梯度下降法等优化算法获得神经网络权重参数和偏微分方程物理参数。
为了更好地描述FCNN的结构,假设一个有l层的神经网络,输入层为第1层,输出层为第l层,中间有l-1个隐藏层。每层的神经元数量为k0=n, k1, …, kl=m。连接第l-1层中的第i个神经元和第l层中的第j个神经元之间的权重为wjil。对于层中的每个神经元,都有一个相关的偏置项bi, i=1, …, kl。每个神经元代表一个数学运算,即每个神经元输入值的加权总和与偏置项求和,并通过激活函数对求和结果进行非线性映射。第l层中第k个神经元的输出为[39]
| $ u_k^l = \sigma \left( {\sum\limits_{j = 1}^{{k_l} - 1} {w_{kj}^l} u_j^{l - 1} + b_k^l} \right) $ | (10) |
式中σ(·)表示激活函数。常用的激活函数是Sigmoid、Tanh和ReLu等。
本文构建了一个FCNN并进行训练,以表示给定速度模型中输入空间坐标(x, y, z)与输出程函方程未知因式τ(x, y, z)之间的映射关系。然而仅建立映射关系是不够的,求解程函方程还需用反向传播算法调整权重值wkjl和偏置项bkl,使得损失函数的值最小。
自动微分的反向模式就是反向传播算法的一般化,其思路是根据计算路径从后向前计算,依次得到对每个中间变量节点的偏导数,直至自变量节点处。在每个节点处根据其后续节点计算导数值,整个过程对应于多元复合函数求导时从最外层逐步向内侧求导。自动微分不涉及差分近似误差,因此能够较准确地计算导数,从而求出程函方程残差和初边值残差约束作为损失函数,再通过合适的优化算法进行神经网络参数的迭代优化,当损失函数达到最小时即实现了程函方程的精确求解。
2.2 基于PINN的三维程函方程求解利用神经网络近似表示函数映射关系求解三维程函方程,定义一个损失函数,使训练集中的因式分解形式程函方程的残差最小。求解过程主要包括:
(1) 利用FCNN近似旅行时未知因式τ(x, y, z);
(2) 定义包含了三维程函方程的损失函数,并在随机分配的网格上进行采样,构建用于神经网络训练的数据集;
(3) 通过DNN的自动微分算法计算τ(x, y, z) 相对于空间坐标的偏导数;
(4) 选择合适的优化器,通过更新网络参数来最小化损失函数。
为了便于描述,本文假设震源(xs, ys, zs)处有τ(xs, ys, zs)=1。用多层深度神经网络
| $ \tau(x, y, z) \approx \hat{\tau}(x, y, z)=\mathscr{R}(x, y, z ; \boldsymbol{\theta}) $ | (11) |
式中:
本文采用隐藏层数为10、每层包含20个神经元的全连接神经网络,以实现对旅行时未知因式τ(x, y, z)的近似,并通过全批量优化方法实现神经网络的损失函数最小化。输入层由3个神经元组成,每个空间坐标(x, y, z)有1个神经元。输出层有1个神经元,用来输出神经网络计算得到的旅行时未知因式
激活函数在神经网络参数的优化中也起重要作用。许多研究证明,局部自适应激活函数比传统的固定激活函数具有更好的学习能力[40],因此除了在最后一层使用ReLu线性激活函数外,所有的隐藏层都使用了局部自适应反正切(locally adaptive arctangent)函数,如此可在每个神经元的激活函数中使用可扩展参数,改变激活函数的斜率以提高网络的学习效率。
使用均方差(MSE)构建损失函数
| $ \begin{aligned} \widetilde{S}= & \frac{1}{N_{\boldsymbol{I}^*}} \sum\limits_{\boldsymbol{X}^*\in \boldsymbol{I}}\|L\|_2^2+ \\ & \frac{1}{N_{\boldsymbol{I}}} \sum\limits_{\boldsymbol{X}^* \in \boldsymbol{I}}\|\operatorname{sgn}[-\hat{\tau}(x, y, z)]|\hat{\tau}(x, y, z)|\|_2^2+ \\ & \|\hat{\tau}(x, y, z)-1\|_2^2 \end{aligned} $ | (12) |
式中:I表示所有采样点的集合;NI为采样点的数量;X*表示采样点位置坐标;L为因式分解形式程函方程的残差,其表达式为
| $ \begin{aligned} L= & T_0{ }^2(x, y, z)|\nabla \hat{\tau}(x, y, z)|^2+ \\ & \hat{\tau}^2(x, y, z)\left|\nabla T_0(x, y, z)\right|^2+ \\ & 2 T_0(x, y, z) \hat{\tau}(x, y, z) \times \\ & \left|\nabla T_0(x, y, z) \nabla \hat{\tau}(x, y, z)\right|- \\ & s^2(x, y, z) \end{aligned} $ | (13) |
式(12)第一项定义了在给定的训练集I中的因式分解形式程函方程的有效性;第二项通过使用符号函数sgn(·) 将旅行时输出结果修正为非负数;最后一项要求震源(xs, ys, zs)处的输出结果是一致的,因为因式分解形式的程函方程应当满足
| $ \mathop {\arg \min }\limits_\mathit{\boldsymbol{\theta }} {\rm{ }}\widetilde S(x, y, z;\mathit{\boldsymbol{\theta }}) $ | (14) |
在PINN的优化过程中,损失函数中不同组成部分的收敛效率存在差异[41]。针对损失函数各部分的权值分配方法有两种,即自适应权重和固定权重。Waheed等[37]证明了在PINN的学习过程中,自适应权重分配方法能够有更佳的收敛效率。因此,本文采取自适应权重分配策略,即通过反向传播的梯度值调整分配给损失函数中的不同项的权重,从而提高收敛效率。
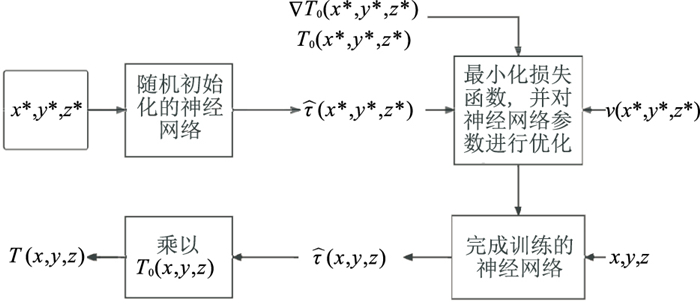
基于PINN求解三维程函方程的流程如图 2所示,(x*, y*, z*)表示训练集中随机选择的各点坐标。将这些点的坐标输入到随机初始化的神经网络中进行训练,并将各点对应的速度v(x*, y*, z*)、已知旅行时参数T0(x*, y*, z*)及空间导数∇T0(x*, y*, z*)作为网络的已知信息,通过最小化损失函数的过程实现对神经网络参数的迭代优化。神经网络训练完成后,输入待求位置的坐标(x, y, z),使用神经网络预测并输出未知旅行时因式
| $ T(x, y, z)=\hat{\tau}(x, y, z) T_0(x, y, z) $ | (15) |
|
图 2 基于PINN求解三维程函方程的流程图 |
本文提出的三维旅行时求解方法无需进行差分近似,而是通过深度神经网络的自动微分直接求解空间导数,理论上可以消除差分近似带来的误差,并且避免了离散网格密集情况下的巨大计算量。另外与传统深度学习方法不同,本文使用的神经网络不需要任何标签数据集,只需对网络参数进行随机初始化,计算出训练集中各点的输出值; 然后将输出结果代入损失函数, 计算与物理方程的拟合程度; 最后基于损失值的最小化优化网络的权重wkjl和偏置项bkl,使其满足三维程函方程。
3 数值模拟实验与讨论为了研究本文所提基于PINN的三维旅行时计算方法的适用性,设计均匀速度模型、水平层状等速度梯度模型、倾斜层状等速度梯度模型及局部三维Marmousi模型, 开展模拟实验,并将本文方法与三维有限差分法计算结果进行了比较。所有模型实验均在Intel(R) Core(TM) i7-4720HQ的CPU上进行,模型参数见表 1。
|
|
表 1 模型参数统计表 |
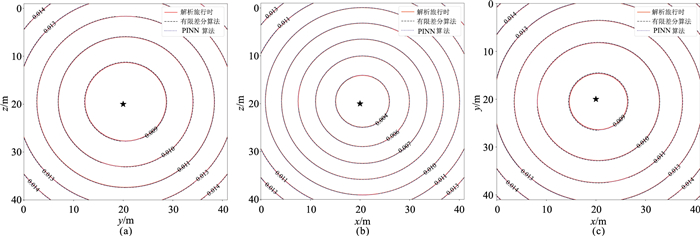
均匀模型中的初至波解析旅行时可以通过距离与速度之比直接求出。截取x=3 m、y=14 m、z=36 m三个剖面分别展示PINN计算的旅行时结果与有限差分法计算结果及解析值的对比。如图 3所示,在三个剖面中PINN计算结果都与理论旅行时相差无几,而有限差分求解结果则在接近模型边界的个别位置相对于解析值出现了偏差。
|
图 3 均匀模型3种方法旅行时计算结果对比(★为震源位置,下同) (a)x=3 m剖面;(b)y=14 m剖面;(c)z=36 m剖面 |
图 4展示了上述三个剖面应用有限差分法(图 4上) 与本文方法(图 4下)的计算结果相对于解析旅行时的绝对误差。可以看到,基于PINN求解的旅行时计算结果绝对误差较小。

|
图 4 均匀模型有限差分法(上)、本文方法(下)计算结果相对于解析旅行时的绝对误差 (a)x=3 m剖面; (b)y=14 m剖面; (c)z=36 m剖面 |
本次模型实验中,采用PINN方法训练过程共耗费约19 min,训练完成后对待求旅行时进行预测仅需3 s,而使用有限差分法进行相同操作则需要约5 min。虽然在神经网络的训练过程耗时较多,但三维旅行时的应用通常需要计算多个震源的旅行时,随着震源数量的增加,本文提出的方法会展现更明显的效率优势。
3.2 水平层状等速度梯度模型对于具有恒定速度梯度的模型,解析旅行时的方程为[42]
| $ T^{\prime}(x, y, z)=\frac{1}{\sqrt{g_x^2+g_y^2+g_z^2}} \arccos \left\{h\left\{1+\frac{\left(g_x^2+g_y^2+g_z^2\right)\left[\left(x-x_{\mathrm{s}}\right)^2+\left(y-y_{\mathrm{s}}\right)^2+\left(z-z_{\mathrm{s}}\right)^2\right]}{2 v(x, y, z) v\left(x_{\mathrm{s}}, y_{\mathrm{s}}, z_{\mathrm{s}}\right)}\right\}\right\} $ | (16) |
式中:T′(x, y, z)是从震源(xs, ys, zs)到某个网格点(x, y, z)的解析旅行时;gx、gy、gz分别表示沿x、y、z三个方向的速度梯度分量。
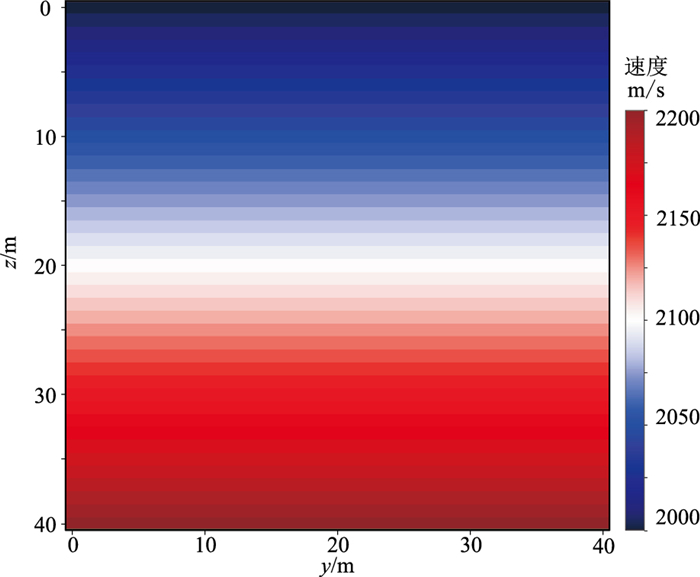
创建的水平层状等速度梯度模型在x方向的剖面如图 5所示,设gx=gy=0、gz=5 s-1,速度在z方向以5 m/s的梯度递增。
|
图 5 水平层状等速度梯度模型(x=1 m剖面) |
取x=10 m、y=20 m、z=35 m三个剖面展示PINN求取旅行时的结果与有限差分法计算结果及解析值的对比(图 6)。可以看到,在三个剖面中PINN计算结果都与理论旅行时几乎相等,而有限差分求解结果则在震源附近的个别位置相对于解析值出现了细微偏差,并且该偏差沿同一方向影响了整个速度模型的旅行时计算结果。

|
图 6 水平层状等速度梯度模型3种方法旅行时计算结果对比 (a)x=10 m剖面;(b)y=20 m剖面;(c)z=35 m剖面 |
图 7为上述三个剖面的有限差分算法计算结果(图 7上)和本文所用方法计算结果(图 7下)相对于解析旅行时的绝对误差。由图可见,基于PINN求解的旅行时绝对误差仍然小于有限差分法计算结果。

|
图 7 水平层状模型有限差分法(上)、本文方法(下)计算结果相对于解析旅行时的绝对误差 (a)x=10 m剖面;(b)y=20 m剖面;(c)z=35 m剖面 |
本次模型实验中,PINN方法训练过程共耗费约25 min,训练完成后对整个速度模型的旅行时预测耗时4 s,而有限差分法计算旅行时约耗时5 mim。本文方法在多炮计算效率方面展现出巨大潜力。
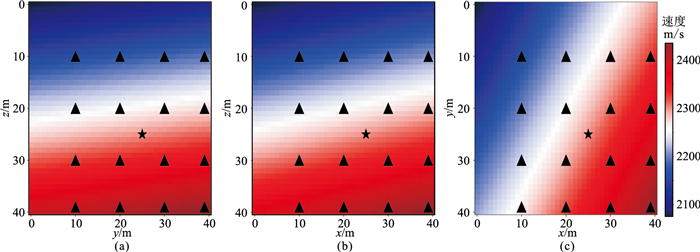
3.3 倾斜层状等速度梯度模型为了证明本文方法的泛化性以及在多震源计算中的效率优势,建立一个倾斜层状等速度梯度模型,x、y、z三个方向的速度变化梯度分别为gx=1 s-1、gy=8 s-1、gz=5 s-1。选择如图 8三个剖面中的三角形所示的48个位置作为训练集震源,生成旅行时训练集数据;以不属于训练集的位置(25 m,25 m,25 m)作为测试集的震源。
|
图 8 倾斜层状等速度梯度模型 (a)x=15 m剖面; (b)y=30 m剖面; (c)z=20 m剖面 |
本文在模型实验中对神经网络进行了修改,将待求空间坐标(x, y, z)和震源位置一并作为输入,通过神经网络模型训练学习并建立震源位置(xs, ys, zs)和待求空间坐标(x, y, z)与相应的输出旅行时参数
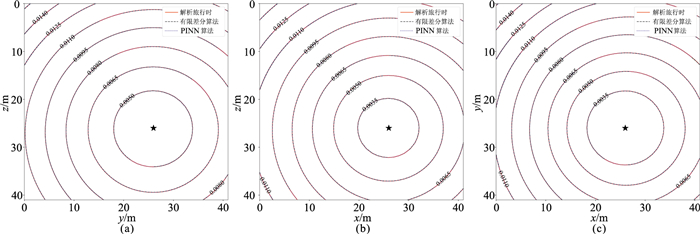
选取x=15 m、y=30 m、z=20 m三条剖面展示PINN法求取旅行时的结果与有限差分法计算结果以及解析值的对比。如图 9所示,在三个剖面中PINN法计算结果都与理论旅行时几乎完全拟合,而有限差分求解结果在对角线方向相对于解析值出现了较明显的偏差。
|
图 9 倾斜层状等速度梯度模型3种方法旅行时计算结果对比 (a)x=15 m剖面; (b)y=30 m剖面; (c)z=20 m剖面 |
图 10为上述三个剖面中有限差分法计算结果(图 10上)与本文方法计算结果(图 10下)相对于解析旅行时的绝对误差。可见在较复杂的速度模型中,基于PINN求解的旅行时的精度仍然优于有限差分法计算结果。

|
图 10 倾斜层状模型有限差分法(上)与本文方法(下)计算结果相对于解析旅行时的绝对误差 (a)x=15 m剖面; (b)y=30 m剖面; (c)z=20 m剖面 |
为了验证多震源计算的效率优势,在y=11 m、y=12 m、y=13 m三个剖面上选取123个网格点作为震源,且这三个剖面上的点均与训练集中的震源点无重合。使用本文方法和有限差分法分别计算所有震源的旅行时,图 11为截取(11 m, 17 m, 19 m)、(12 m, 18 m, 21 m)、(12 m, 37 m, 5 m)、(13 m, 28 m, 16 m)四个点作为震源时,x=20 m剖面上的旅行时计算结果。在该模型试验123炮的计算中,PINN方法训练、预测过程共耗时约68 min,而有限差分法计算旅行时共耗时约458 min,PINN方法体现出了相当明显的效率优势。

|
图 11 多震源位置3种方法旅行时计算部分计算结果对比(x=20 m剖面) (a)震源(11 m, 17 m, 19 m); (b)震源(12 m,18 m,21 m); (c)震源(12 m,37 m,5 m); (d)震源(13 m,28 m,16 m) |
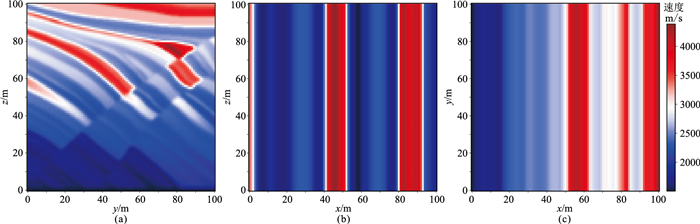
选取x=40 m、y=60 m、z=50 m三条剖面,将二维Marmousi模型中速度变化十分复杂的部分拼接为如图 12所示的局部三维Marmousi模型。
|
图 12 倾斜层状等速度梯度模型 (a)x=40 m剖面;(b)y=60 m剖面;(c)z=50 m剖面 |
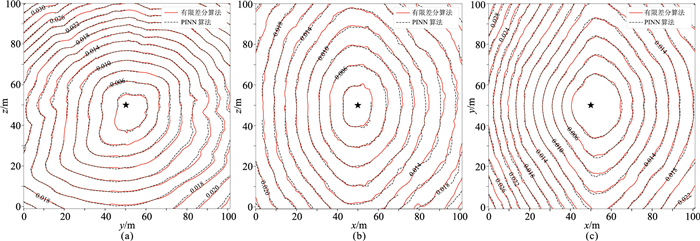
图 13展示了训练完成的神经网络的旅行时预测结果与有限差分法计算结果的对比,可以看到,在三个剖面中PINN计算结果都与有限差分法计算结果基本吻合。
|
图 13 三维Marmousi模型2种方法旅行时计算结果对比 (a)x=40 m剖面;(b)y=60 m剖面;(c)z=50 m剖面 |
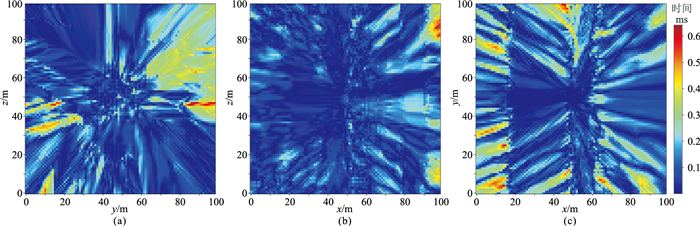
图 14为上述三个剖面中有限差分法计算结果与本文所用方法计算结果之间的绝对误差。由于无法计算Marmousi模型的解析旅行时,故而无法进行精度的对比,但是通过本文方法与有限差分法所求结果的绝对误差,可以验证PINN方法即使对于复杂构造模型也具有较高的稳定性。另外,该模型试验中有限差分法计算旅行时用时约536 min,而PINN方法训练、预测过程共耗时约145 min,在复杂模型中同样表现出明显的效率优势。
|
图 14 三维Marmousi模型中有限差分法与本文方法旅行时求解结果的绝对误差 (a)x=40 m剖面;(b)y=60 m剖面;(c)z=50 m剖面 |
通过数值模拟实验,证明了PINN算法具有效率上的绝对优势,且在简单速度模型中应用精度也有所提高。但对于复杂模型则无法验证所求解旅行时的准确度,只能说明PINN算法能够得到与有限差分算法相似的结果。
4 结束语本文提出一种基于PINN深度神经网络在三维速度模型中计算初至波旅行时的方法。经不同速度模型实验,结果表明本文所提方法求解的旅行时比目前常用的有限差分法计算结果更准确或结果相似,并且适用于复杂的三维速度模型。相对于传统深度学习算法,本文构建的神经网络是基于物理模型驱动的,即在损失函数中加入了三维程函方程,使计算结果更符合物理规律。此外,在给定三维速度模型中选择一部分网格点作为震源位置进行训练学习后,即可输入任意震源位置迅速求解地震波旅行时,在多震源应用中表现出有限差分法不可比拟的效率优势。
| [1] |
LAWTON D C. Computation of refraction static corrections using first-break traveltime differences[J]. Geophysics, 1989, 54(10): 1289-1296. DOI:10.1190/1.1442588 |
| [2] |
SCHIJNS H, HEINONEN S, SCHMITT D R, et al. Seismic refraction traveltime inversion for static corrections in a glaciated shield rock environment: a case study[J]. Geophysical Prospecting, 2009, 57(6): 997-1008. DOI:10.1111/j.1365-2478.2009.00798.x |
| [3] |
ALKHALIFAH T. Efficient traveltime compression for 3D prestack Kirchhoff migration[J]. Geophysical Prospecting, 2011, 59(1): 1-9. DOI:10.1111/j.1365-2478.2010.00886.x |
| [4] |
MAUFROY E, GAFFET S, OPERTO S, et al. Travel time inversion from ground level to gallery: protocol for the characterization of P-wave seismic signature in a fractured-porous Urgonian platform at hectometric scale[J]. Near Surface Geophysics, 2014, 12(6): 697-708. DOI:10.3997/1873-0604.2014025 |
| [5] |
ALVARO R, AKHIL D G, BALLIN P. Assisted history matching in the presence of frequent well intervention using generalize travel time inversion[J]. Journal of Petroleum Science and Engineering, 2011, 78(2): 415-430. DOI:10.1016/j.petrol.2011.06.002 |
| [6] |
ZHAO C J, ZHANG L L, YU P, et al. Combined inversion of first-arrival travel times and reflection travel times[J]. Geophysical Prospecting, 2019, 67(7): 1764-1777. DOI:10.1111/1365-2478.12791 |
| [7] |
NASR M, GIROUX B, DUPUIS J C. A hybrid ap proach to compute seismic travel times in three-dimensional tetrahedral meshes[J]. Geophysical Prospecting, 2020, 68(4): 1291-1313. DOI:10.1111/1365-2478.12930 |
| [8] |
JIANG W B, ZHANG J. First-arrival traveltime tomo graphy with modified total-variation regularization[J]. Geophysical Prospecting, 2017, 65(5): 1138-1154. DOI:10.1111/1365-2478.12477 |
| [9] |
GIROUX B, GLOAGUEN E. Geostatistical traveltime tomography in elliptically anisotropic media[J]. Geophysical Prospecting, 2012, 60(6): 1133-1149. DOI:10.1111/j.1365-2478.2011.01047.x |
| [10] |
GRECHKA V, DE LA PENA A, SCHISSELÉ-REBEL E, et al. Relative location of microseismicity[J]. Geophysics, 2015, 80(6): WC1-WC9. |
| [11] |
LOEWENTHAL D, HU L Z. Two methods for computing the imaging condition for common-shot prestack migration[J]. Geophysics, 1991, 56(3): 378-381. DOI:10.1190/1.1443053 |
| [12] |
SAMBRIDGE M S, KENNETT B L N. Boundary va-lue ray tracing in a heterogeneous medium: a simple and versatile algorithm[J]. Geophysical Journal International, 1990, 101(1): 157-168. DOI:10.1111/j.1365-246X.1990.tb00765.x |
| [13] |
ERVENY V, PŠENČIK I. Gaussian beams and paraxial ray approximation in three-dimensional elastic inhomogeneous media[J]. Journal of Geophysics, 1983, 53(1): 1-15. DOI:10.3321/j.issn:0001-5733.1983.01.001 |
| [14] |
COMAN R, GAJEWSKI D. Traveltime computation by wavefront-orientated ray tracing[J]. Geophysical Prospecting, 2005, 53(1): 23-36. DOI:10.1111/j.1365-2478.2005.00429.x |
| [15] |
JULIAN B R, GUBBINS D. Three-dimensional seismic ray tracing[J]. Journal of Geophysics, 1977, 43(1): 95-113. |
| [16] |
UM J, THURBER C. A fast algorithm for two-point seismic ray tracing[J]. Bulletin of the Seismological Society of America, 1987, 77(3): 972-986. DOI:10.1785/BSSA0770030972 |
| [17] |
VIDALE J. Finite-difference calculation of travel times[J]. Bulletin of the Seismological Society of America, 1988, 78(6): 2062-2076. |
| [18] |
QIN F H, LUO Y, OLSEN K B, et al. Finite-difference solution of the eikonal equation along expanding wavefronts[J]. Geophysics, 1992, 57(3): 478-487. DOI:10.1190/1.1443263 |
| [19] |
VAN TRIER J, SYMES W W. Upwind finite-difference calculation of traveltimes[J]. Geophysics, 1991, 56(6): 812-821. DOI:10.1190/1.1443099 |
| [20] |
SETHIAN J A. Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science[M]. 2nd ed. Cambridge: Cambridge University Press, 1999.
|
| [21] |
QIAN J L, ZHANG Y T, ZHAO H K. Fast sweeping methods for eikonal equations on triangular meshes[J]. SIAM Journal on Numerical Analysis, 2007, 45(1): 83-107. DOI:10.1137/050627083 |
| [22] |
FOMEL S, LUO S T, ZHAO H K. Fast sweeping method for the factored eikonal equation[J]. Journal of Computational Physics, 2009, 228(17): 6440-6455. DOI:10.1016/j.jcp.2009.05.029 |
| [23] |
LUO S T, QIAN J L. Factored singularities and high-order Lax-Friedrichs sweeping schemes for point-source traveltimes and amplitudes[J]. Journal of Computational Physics, 2011, 230(12): 4742-4755. DOI:10.1016/j.jcp.2011.02.043 |
| [24] |
VIDALE J E. Finite-difference calculation of travel times in three dimensions[J]. Geophysics, 1990, 55(5): 521-526. DOI:10.1190/1.1442863 |
| [25] |
SOUKINA S M, GAJEWSKI D, KASHTAN B M. Traveltime computation for 3D anisotropic media by a finite-difference perturbation method[J]. Geophysical Prospecting, 2003, 51(5): 431-441. DOI:10.1046/j.1365-2478.2003.00385.x |
| [26] |
HOLE J A, ZELT B C. 3-D finite-difference reflection travel times[J]. Geophysical Journal International, 1995, 121(2): 427-434. DOI:10.1111/j.1365-246X.1995.tb05723.x |
| [27] |
孙章庆, 孙建国, 岳玉波, 等. 基于快速推进迎风双线性插值法的三维地震波走时计算[J]. 地球物理学报, 2015, 58(6): 2011-2023. SUN Zhangqing, SUN Jianguo, YUE Yubo, et al. 3D traveltime computation using fast marching upwind bilinear interpolation method[J]. Chinese Journal of Geophysics, 2015, 58(6): 2011-2023. |
| [28] |
HU J T, CAO J X, WANG H Z, et al. 3D traveltime computation for quasi-P-wave in orthorhombic media using dynamic programming[J]. Geophysics, 2018, 83(1): C27-C35. DOI:10.1190/geo2016-0558.1 |
| [29] |
LAGARIS I E, LIKAS A, FOTIADIS D I. Artificial neural networks for solving ordinary and partial differential equations[J]. IEEE Transactions on Neural Networks, 1998, 9(5): 987-1000. DOI:10.1109/72.712178 |
| [30] |
LEE H, KANG I S. Neural algorithm for solving differential equations[J]. Journal of Computational Physics, 1990, 91(1): 110-131. DOI:10.1016/0021-9991(90)90007-N |
| [31] |
SIRIGNANO J, SPILIOPOULOS K. DGM: a deep learning algorithm for solving partial differential equation[J]. Journal of Computational Physics, 2018, 375: 1339-1364. DOI:10.1016/j.jcp.2018.08.029 |
| [32] |
TOMPSON J, SCHLACHTER K, SPRECHMANN P, et al. Accelerating eulerian fluid simulation with convolutional networks[C]. Proceedings of the 34th International Conference on Machine Learning, 2017, 3424-3433.
|
| [33] |
RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707. DOI:10.1016/j.jcp.2018.10.045 |
| [34] |
XU Y R, LI J Y, CHEN X H. Physics informed neural networks for velocity inversion[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2584-2588.
|
| [35] |
KARIMPOULI S, TAHMASEBI P. Physics informed machine learning: seismic wave equation[J]. Geoscience Frontiers, 2020, 11(6): 1993-2001. DOI:10.1016/j.gsf.2020.07.007 |
| [36] |
SONG C, ALKHALIFAH T, WAHEED U B. Solving the frequency-domain acoustic VTI wave equation using physics-informed neural networks[J]. Geophysical Journal International, 2021, 225(2): 846-859. DOI:10.1093/gji/ggab010 |
| [37] |
WAHEED U B, HAGHIGHAT E, ALKHALIFAH T, et al. PINNeik: eikonal solution using physics-informed neural networks[J]. Computers & Geosciences, 2021, 155: 104833. |
| [38] |
HORNIK K, STINCHCOMBE M, WHITE H. Multilayer feedforward networks are universal approximators[J]. Neural Networks, 1989, 2(5): 359-366. DOI:10.1016/0893-6080(89)90020-8 |
| [39] |
BISHOP C M. Pattern Recognition and Machine Learning[M]. Springer, New York, 2006.
|
| [40] |
JAGTAP A D, KAWAGUCHI K, EM KARNIADAKIS G. Locally adaptive activation functions with slope recovery for deep and physics-informed neural networks[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2020, 476(2239): 20200334. DOI:10.1098/rspa.2020.0334 |
| [41] |
WANG S F, YU X L, PERDIKARIS P. When and why PINNs fail to train: a neural tangent kernel perspective[J]. Journal of Computational Physics, 2022, 449: 110768. DOI:10.1016/j.jcp.2021.110768 |
| [42] |
SLOTNICK M M. Lessons in Seismic Computing[M]. Society of Exploration Geophysicists, Tulsa, 1959: 178-196.
|



 谭军, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院,266100。Email:
谭军, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院,266100。Email: