海底节点(Ocean Bottom Nodes,OBN)在海洋地震勘探中表现出巨大优势,不仅能获取宽方位、大炮检距、含有转换横波的高质量地震数据,在施工中也不受调查船设备配置和电缆连接的限制,尤其灵活适用于船只和作业平台密集的海域[1]。在实际作业中,根据GPS及其他定位系统按照预设测线位置布设,称为一次OBN定位。在OBN布设过程中,由于受到人工抛掷误差、船速变化、沉降速度、洋流潮汐引起的漂移等影响,实际沉放位置往往偏离设计位置,即使布设位置准确,在勘探工期内,渔船、气候变化、海洋生物等也可能会影响海底节点位置[2]。若忽略节点位置变化,仍使用一次定位结果处理地震数据,将会直接影响CMP面元划分及动校正等处理环节的精度,对地震资料成像将造成较大误差,因此需要通过二次定位获取海底节点的真实位置[3-4]。
目前,主要的二次定位方法有声波定位和地震波定位。声波定位使用声学设备及系统,能快速得到较精确的定位结果,但设备昂贵、定位成本较高[5]。利用地震波定位手段灵活,能满足施工的精度要求,同时可实现炮检双向定位,比较典型的方法有基于地震波场的波场模拟法[6]、波场延拓法[7],基于直达波初至的近正四面体法[8]、搜索法[9]、曲面扫描拟合法[10]、混合定位法[11]、矢量叠加法[12]等。基于波场的定位方法需从波场出发进行模拟或外推延拓,计算量较大、计算速度慢、定位效率较低;基于直达波初至定位广泛应用于深水域,在浅海地区存在许多问题,如浅海域海底坚硬、地形平坦时容易形成稳定的折射面,折射波较发育,地震波数据记录中的初至主要是折射波,直达波初至数量少、方位分布不均且因炮端的干扰,初至难以准确拾取,单一利用直达波初至定位会降低定位的精度,甚至定位失败。因此,人们尝试引入具有宽方位、数据量丰富的折射波初至进行检波器二次定位[13-15]。
基于浅海OBN资料直达波初至少、折射波发育的特点,本文提出一种应用动态惩罚加权函数联合两种初至的定位方法。针对多目标优化问题,选择使用两个加权因子构建联合定位的总目标函数,采用变系数动态加权,根据每次迭代的分目标函数值不断变化权值,以加速优化过程[16-18]。该方法充分利用了地震资料中的直达波与折射波信息,可在准确计算浅海OBN实际位置的同时,反演得到海水和海底速度。
1 方法原理 1.1 目标函数构建在图 1中,激发点坐标为Si(xi, yi, zi),检波点坐标为R(X, Y, Z),L1、L2+L3分别为直达波、折射波传播路径, α为折射波初至临界角。设海水中和海底的地震波传播速度分别为v1、v2,则根据图中几何关系及地震波传播的Snell定律计算临界距离d=h×
| $ t_{\mathrm{d} i}=\frac{1}{v_1} \times \sqrt{\left(x_i-X\right)^2+\left(y_i-Y\right)^2+\left(z_i-Z\right)^2} $ | (1) |
| $ \begin{aligned} t_{\mathrm{r}i}= & \left(z_i-Z\right) \times \frac{\sqrt{v_2^2-v_1^2}}{v_1 v_2}+ \\ & \frac{1}{v_2} \times \sqrt{\left(x_i-X\right)^2+\left(y_i-Y\right)^2} \end{aligned} $ | (2) |

|
图 1 浅海地震波传播路径示意图 |
检波器接收来自多个炮点的地震波。在共检波点道集上,设有N1道的初至为直达波,拾取的直达波初至为Tdj,其中j=1, 2, ⋯, N1;设有N2道的初至为折射波,拾取的折射波初至为Trk,显然k=1, 2,⋯,N2。由式(1)、式(2)中直达波、折射波理论初至tdj和trk,应用最小二乘法可构建直达波误差函数Qd和折射波误差函数Qr
| $ Q_{\mathrm{d}}=\frac{1}{N_1} \sum\limits_{j=1}^{N_1}\left(T_{\mathrm{d} j}-t_{\mathrm{d} j}\right)^2 $ | (3) |
| $ Q_{\mathrm{r}}=\frac{1}{N_2} \sum\limits_{k=1}^{N_2}\left(T_{\mathrm{r} k}-t_{\mathrm{r}k}\right)^2 $ | (4) |
式(3)为直达波的定位公式,当Qd最小时可求得检波器的坐标X、Y、Z和海水速度v1;式(4)为折射波的定位公式,当Qr最小时可求得检波器的坐标X、Y、Z和海水速度v1、海底速度v2。为实现联合定位,本文采用加权平方和方法将两个目标函数转化为一个总目标函数,也称为评价函数,这样就把求解多目标最优化问题转化为求解单目标最优化问题[16-17],总目标函数即为
| $ \begin{aligned} Q= & w_1 \times Q_{\mathrm{d}}+w_2 \times Q_{\mathrm{r}} \\ = & w_1 \times \frac{1}{N_1} \sum\limits_{j=1}^{N_1}\left(T_{\mathrm{d} j}-t_{\mathrm{d} j}\right)^2+ \\ & w_2 \times \frac{1}{N_2} \sum\limits_{k=1}^{N_2}\left(T_{\mathrm{r} k}-t_{\mathrm{r}k}\right)^2 \end{aligned} $ | (5) |
式中w1、w2为加权因子。
当式(5)中的Q最小时,对应的X、Y、Z、v1、v2即为真实值。这样不仅实现了检波器的定位,还能反演得到海水、海底介质的地震波速度。
1.2 权因子动态设计式(5)中的两个加权因子是未知的,加权因子的设置也是联合定位的一个关键。多目标优化中对多个分目标函数加权的方法有常系数加权和变系数加权(动态加权),动态加权的方法包括动态满意度加权[17]、动态惩罚加权[18]等。经过充分试验,本文选择动态惩罚加权有效地将联合定位问题转化为一个无约束单目标优化问题。
动态惩罚加权法是根据每次迭代后各分目标的值Fi(x)确定各分目标对应的加权因子wi(i=1, 2, ⋯, n),与期望值相差较大的分目标对应的权重越高,即给予该分目标一个较大的惩罚因子,使其在迭代中加速优化。在未达到最优解时,每次迭代后各分目标的值不同,则wi在迭代过程中是动态的,当迭代过程逼近最优时,各分目标值变化微小,此时权因子也趋于稳定。分目标Fi(x)对应的权因子表达式[18]为
| $ w_i=\frac{\left|F_i(x)-F_i\right|}{\sum\limits_{i=1}^n\left|F_i(x)-F_i\right|} $ | (6) |
式中Fi为每个分目标的期望值。
在定位公式(式(3)、式(4))中,当计算值等于真实值时,目标函数为0,所以式(6)中的目标期望值可设为0,因此联合定位中的两个权因子设置为
| $ \left\{\begin{array}{l} w_1=\frac{Q_{\mathrm{d}}}{Q_{\mathrm{d}}+Q_{\mathrm{r}}} \\ w_2=\frac{Q_{\mathrm{r}}}{Q_{\mathrm{d}}+Q_{\mathrm{r}}} \end{array}\right. $ | (7) |
求式(5)中Q最小时对应的检波器位置和海水速度及海底速度,实质上是求一个无约束单目标最优化问题。对于此类问题,常用方法有单纯形法(Nelder-Mead)、最速下降法、牛顿法、模拟退火法(SA)、遗传算法(GA)和粒子群算法(PSO)等,每个算法都有其特点,均可实现对本文方法的求解。上述方法中,模拟退火算法是将物理过程与组合优化相结合的一种随机迭代寻优算法,是一种非导数优化算法。它由某一较高初始温度开始,利用概率特性与抽样策略在解的空间中进行随机搜索,随着温度不断下降重复抽样,最终得到全局最优解[16, 19]。模拟退火法具有收敛快、跳过局部最优等优势,经试验对比选用它求解该问题。
联合定位的求解主要包括以下步骤: ①初始化设置模拟退火的参数,有初始温度、退火因子、上下限、初始值等;②将直达波初至和折射波初至分别代入式(3)和式(4),构建两个分目标函数Qd、Qr,并随机生成初始权因子w1、w2;③将两个分目标函数及两个权因子分别代入式(5),构建总目标函数;④在设置的上、下限范围内随机产生新解,使用模拟退火法计算,包括判断Q值、是否接受新解及降低温度;⑤通过迭代条件判断新解是否满足要求,若满足则输出结果;否则,更新权因子,用新解重新构建Qd、Qr,返回步骤③进行迭代计算, 直到满足迭代条件并得到最优解。
2 理论模型试验为了验证该方法的可行性,设计了一个浅海平坦海底模型,海水深度为100 m。在海底设计1条测线,布设21个节点,检波点间距为100 m。在海面布设7条炮线,每条炮线激发101炮,炮线间距为100 m,炮间距为50 m,图 2表示第11号节点(R11)及各炮点的平面位置关系。假设地震波在海水中的传播速度为1500 m/s,海底以下介质地震波速为2000 m/s。通过理论旅行时计算公式,可获取各节点接收每个震源激发的初至波走时。从R11节点接收到各炮点的初至波走时图(图 3),可知走时场关于检波点呈对称分布。

|
图 2 R11及各炮点位置分布(红色圆点为炮点,蓝色方点为检波点) |

|
图 3 R11接收到的各炮点初至 |
初至联合二次定位首先是在共检波点道集上拾取初至,拾取后的初至根据检波器的预设位置、临界距离d及地震记录的形态特征将直达波初至和折射波初至分离形成直达波初至集合和折射波初至集合。再根据检波点的预设位置选择一定炮检距范围内的炮点作为定位的待选炮点,主要以中近炮检距的炮点为主,以便保证待选炮点中包含两种类型的初至波。检波点的反演计算依赖于炮点的位置分布,待选炮点相对于检波点需要宽方位、均匀分布,以保证定位的精度。确定好定位的待选炮点后还需对初至异常的炮点剔除,得到定位的有效炮点。异常炮点的判断可以炮检距为x轴,以拾取的初至时间为y轴,绘制并拟合得到关系曲线,将偏离关系曲线一定范围的炮点视为异常炮点。
以R11为例,说明联合二次定位的具体方法及其测试结果。在该模型测试中,R11的理论坐标为(3500,1300,100),初至使用计算得到的理论值。在图 2中line2、line3、line4、line5、line6五条炮线上各选择7个炮点作为定位炮点。定位炮点与R11的位置关系如图 4,黑色圆圈为临界距离,R11接收到圈内、圈外炮点的初至波分别为直达波、折射波。R11接收到定位炮点的初至走时如图 5所示。

|
图 4 R11及定位炮点位置分布 |

|
图 5 R11接收到定位炮点的初至走时 |
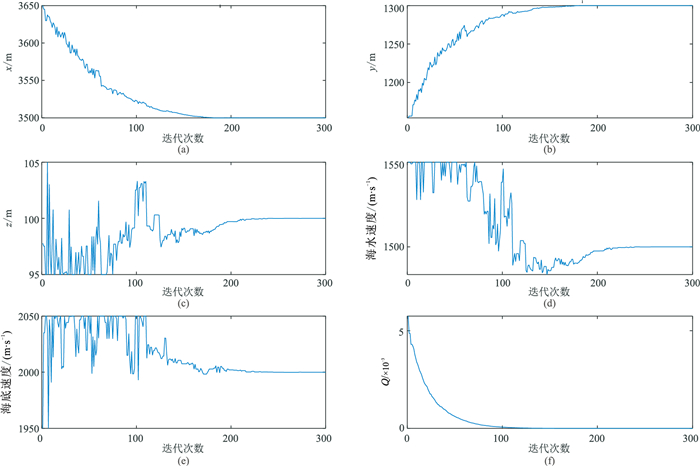
以偏离于真实位置的坐标(3650,1150,95)、海水速度(1450 m/s)和海底速度(1950 m/s)作为迭代初始值,设定模拟退火的参数,利用本文方法代入理论初至时间反演计算。迭代过程如图 6所示,从图中可以看出,随着迭代次数的逐渐增加,各参量逐渐趋于稳定,总目标函数收敛于一个较小值,位置最后稳定在(3500,1300,100),海水速度和海底速度分别稳定在1500 m/s和2000 m/s,反演结果与模型的理论值一致。
|
图 6 零初至误差迭代过程 (a)x坐标迭代过程;(b)y坐标迭代过程;(c)z坐标迭代过程;(d)海水速度迭代过程;(e)海底速度迭代过程;(f)总目标函数Q迭代过程 |
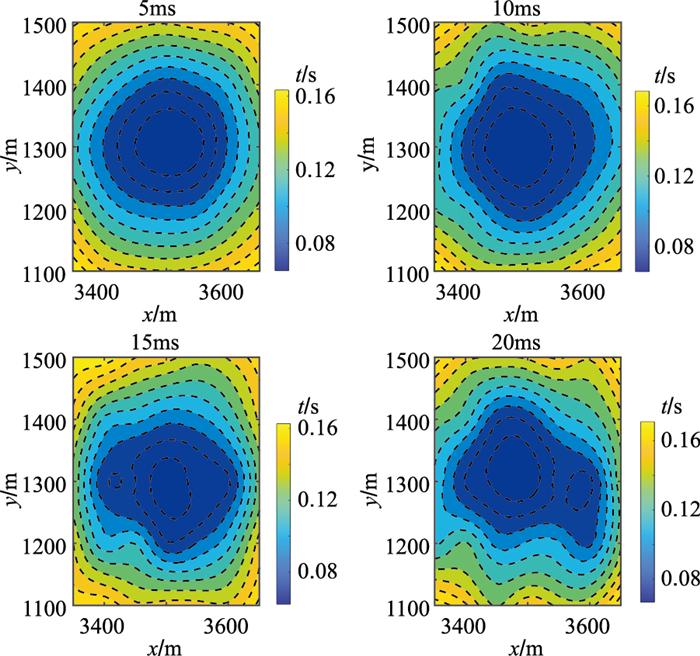
在利用实际资料初至波定位时,从地震数据中拾取的初至并不准确,这直接影响反演结果的准确性。为进一步检验算法的稳定性,对理论计算的初至值加入不同程度的随机误差进行测试,分析方法对初至拾取误差的敏感性。试验中对理论初至值分别加入±5、±10、±15、±20 ms范围的扰动误差,得到相应的初至走时图(图 7),可见此时走时等值线被扭曲而不再对称。
|
图 7 定位炮点不同误差的初至走时 |
控制相同参数设置,加入误差后的试算结果在表 1中列出,可以看出,随着初至误差的增大,目标函数值Q、二维方向的偏离量Dxy、三维方向的偏离量Dxyz逐渐增大,即初至越精确,计算结果越接近真实值,也进一步验证了初至的准确拾取是定位的关键。表中也可看出,当初至值误差值在10 ms范围(为平均初至时间的7.95%)时,Dxy、Dxyz均小于5 m,说明该方法在10 ms的初至误差范围内能够有效地实现定位,验证了基于动态惩罚加权的联合定位方法的稳定性和可靠性。
|
|
表 1 不同初至误差下的计算结果 |
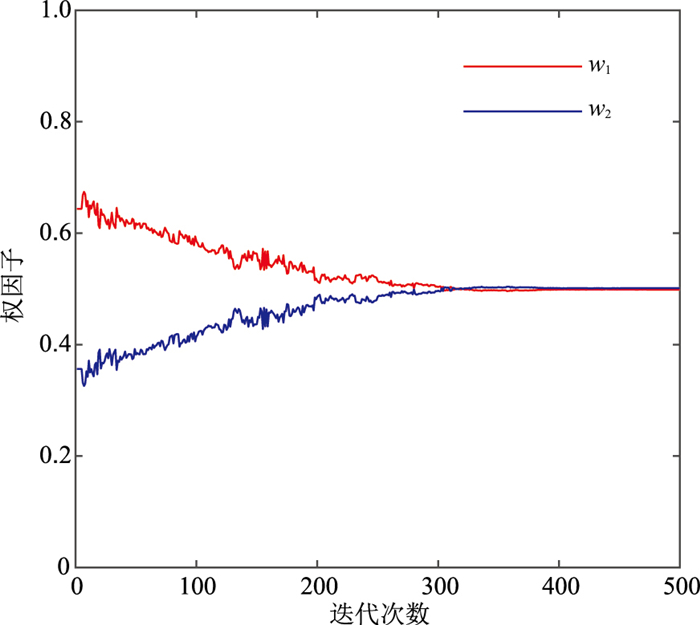
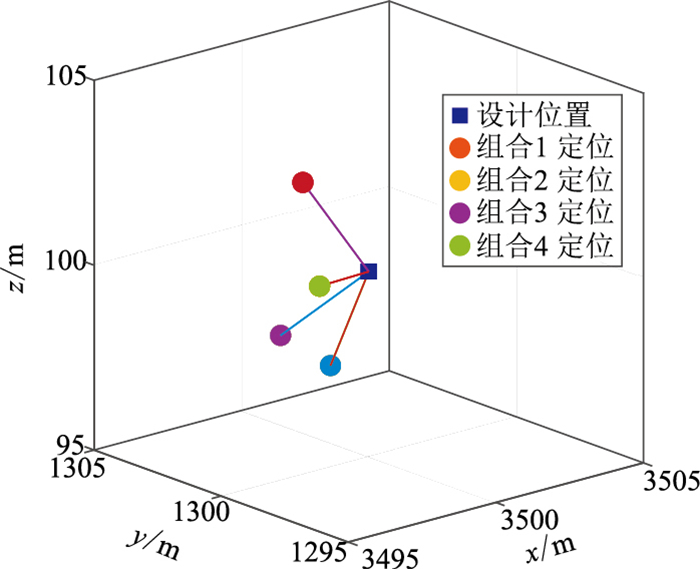
使用直达波初至和折射波初至不同组合方式定位检波点,对权因子的变化进行监控,进一步测试算法的稳定性,各组合选择的定位炮点均遵循全方位的原则。初至的组合方式及计算的稳定权值在表 2中列出,可见两个权因子的大小与初至的数量及其精确程度有关,当初至的数量增加和精度降低时,权值相应地变大,这也符合动态惩罚加权的思想。组合1使用相同数量、相同精度级别的初至定位,在迭代中,两个权因子根据惩罚加权的方法不断修正、动态调整,最终稳定在0.5附近(图 8)。各个组合的定位误差均在设计位置上5 m范围内(图 9),说明动态惩罚加权方法会根据直达波、折射波初至的质量、数量自动调整权因子的大小,最终实现准确定位。
|
|
表 2 不同初至组合定位的稳定权值 |
|
图 8 组合1定位中权因子的变化 |
|
图 9 不同初至组合定位结果 |
将该方法应用于中国M海域节点地震勘探二次定位中,数据采集使用组合气枪震源在海面激发,采用绳系OBN方式采集海底四分量数据,图 10为部分OBN观测系统示意图。由声呐设备测得的该海域的深度约为80~85 m,为浅海环境。

|
图 10 炮点及OBN位置分布 |
对第100号节点检波器(OBN100)做定位试验,选取line1、line4、line17作为定位炮线,在其对应的共检波点道集上拾取初至。再根据前期资料中海水和海底速度、水深计算直达初至与折射初至的临界炮检距,结合地震资料将直达初至与折射初至分离成相应集合。从OBN100预设位置选取3条定位炮线上的部分炮点作为定位炮点,组成一个矩形定位炮点阵列。图 10展示的观测系统中,红色星号表示从普通炮点(黑色星号)中选择的定位炮点。以预设位置(1205,1469)及声呐测量水深(80 m)、海水速度(1500 m/s)和海底速度(1700 m/s)作为初值,设定上、下限及迭代条件,使用联合定位方法反演得到OBN空间位置(1115.90,1516.13,81.82)及海水速度(1517.28 m/s)和海底速度(1709.30 m/s)。
利用同样的步骤对另外两个节点OBN36和OBN66做定位试验,仍选择line1、line4、line17三条炮线作为定位炮线。三个节点的定位结果在图 10中展示,蓝色十字为预设位置,蓝色方点为二次定位位置。可以看出,三个节点的真实位置相较于预设位置都有一定量的漂移,OBN100的漂移量最大,OBN36次之,OBN66最小。
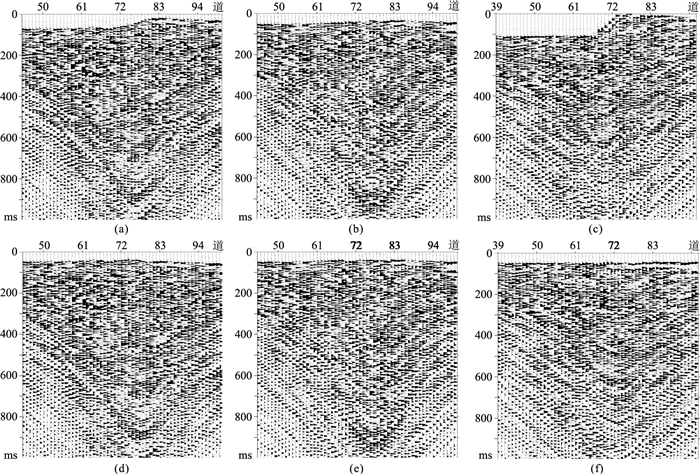
为了验证计算结果的准确性,使用线性动校正(LMO)在三个节点对应的line1地震记录上检验二次定位结果。对比使用预设位置(图 11a~图 11c)与使用二次定位位置(图 11d~图 11f)的LMO结果可知:OBN36和OBN100预设位置动校正后的初至波呈明显的起伏形态,OBN100的起伏最大,这也与其漂移量最大对应,两个节点用二次定位位置动校正后的初至波形态均趋于一条直线。OBN66漂移量较小,预设位置和二次定位位置动校正后的初至也比较接近,可见二次定位结果LMO“拉平”效果相对更好,说明二次定位位置更接近于节点的真实位置。通过以上三个不同漂移量的节点实际数据测试,说明反演得到的二次定位位置是准确的,也验证了本文所提联合定位方法的有效性和适用性。
|
图 11 二次定位结果线性动校正检验(line1) (a)OBN36预设位置;(b)OBN66预设位置;(c)OBN100预设位置;(d)OBN36二次定位位置;(e)OBN66二次定位位置;(f)OBN100二次定位位置 |
在浅海OBN勘探中,准确获取OBN在海底的位置至关重要,而浅海直达波初至数量少、方位分布不均及炮端干扰等问题对准确定位带来挑战,本文利用动态惩罚加权的方法将直达波初至与折射波初至联合实现二次定位。应用于浅海、高速水平海底的模型测试表明该方法是有效的。同时,在不同的初至误差下试算定位结果,说明联合定位的方法在初至有一定误差时也能准确地定位海底检波器位置。使用不同的初至组合监控权因子的变化,说明该方法会根据直达波、折射波初至的质量、数量自动调整权因子的大小,实现准确定位。最终,将该方法应用于M海域OBN实际资料,计算得到的位置与预设位置相比有一定量的偏离。通过线性动校正对结果检验,证明了定位结果真实有效,说明是检波器在投放后发生了漂移。同时,反演得到的海水速度、海底介质速度,可以用于后续海底节点地震资料处理中。
| [1] |
吴志强, 张训华, 赵维娜, 等. 海底节点(OBN)地震勘探: 进展与成果[J]. 地球物理学进展, 2021, 36(1): 412-424. WU Zhiqiang, ZHANG Xunhua, ZHAO Weina, et al. Ocean Bottom Station Nodes(OBN): progress and achievement[J]. Progress in Geophysics, 2021, 36(1): 412-424. |
| [2] |
韩立强, 常稳. 海底电缆初至波二次定位技术的应用[J]. 石油物探, 2003, 42(4): 501-504, 512. HAN Liqiang, CHANG Wen. Application of first break second positioning technique in OBC[J]. Geophysical Prospecting for Petroleum, 2003, 42(4): 501-504, 512. DOI:10.3969/j.issn.1000-1441.2003.04.015 |
| [3] |
徐维秀. 浅水域检波点自动重定位技术[J]. 石油地球物理勘探, 2011, 46(1): 6-11. XU Weixiu. Automatic repositioning technique for shallow water receiver points[J]. Oil Geophysical Prospecting, 2011, 46(1): 6-11. |
| [4] |
葛晓丹. 浅海地震勘探海底电缆初至波二次定位方法研究[D]. 山东青岛: 中国海洋大学, 2015. GE Xiaodan. A Study on the Second Positioning Technique for the First Break in OBC Seismic Exploration of Shallow Sea[D]. Ocean University of China, Qingdao, Shandong, 2015. |
| [5] |
曾湘轶, 杨文艳. 浅析海底电缆地震采集作业二次定位系统[J]. 石油地球物理勘探, 2001, 36(2): 220-226. ZENG Xiangyi, YANG Wenyan. Brief analysis of se-condary positioning system in seismic sea-bottom cable acquisition[J]. Oil Geophysical Prospecting, 2001, 36(2): 220-226. DOI:10.3321/j.issn:1000-7210.2001.02.012 |
| [6] |
SMIT F, PERKINS C, LEPRE L, et al. Seismic data acquisition using ocean bottom seismic nodes at the Deimos Field, Gulf of Mexico[C]. SEG Technical Program Expanded Abstracts, 2008, 27(1): 998-1002.
|
| [7] |
黄龙泽. 基于波动方程的检波点二次定位[J]. 海洋石油, 2011, 31(2): 34-38. HUANG Longze. The secondary positioning of receiver based on wave equation[J]. Offshore Oil, 2011, 31(2): 34-38. DOI:10.3969/j.issn.1008-2336.2011.02.034 |
| [8] |
杨正华, 张慧静. 海底电缆地震勘探中近正四面体法二次定位技术[J]. 石油地球物理勘探, 2013, 48(2): 163-170. YANG Zhenghua, ZHANG Huijing. An approximate tetrahedron method for the secondary positioning in OBC seismic survey[J]. Oil Geophysical Prospecting, 2013, 48(2): 163-170. |
| [9] |
倪成洲, 全海燕, 陈刚, 等. 一种高精度初至波二次定位新方法——搜索法[J]. 石油地球物理勘探, 2008, 43(2): 131-133, 157. NI Chengzhou, QUAN Haiyan, CHEN Gang, et al. A new method for high-precision first break secondary positioning-search method[J]. Oil Geophysical Prospecting, 2008, 43(2): 131-133, 157. |
| [10] |
肖永新, 杨海申, 蒋先艺, 等. OBC勘探中扫描拟合二次定位方法[J]. 石油地球物理勘探, 2012, 47(3): 366-370. XIAO Yongxin, YANG Haishen, JIANG Xianyi. A secondary positioning method by grid scanning and curved-surface fitting in OBC survey[J]. Oil Geophy-sical Prospecting, 2012, 47(3): 366-370. |
| [11] |
马德堂, 赵会兵, 伍忠良. 基于直达波旅行时的OBS混合定位方法[J]. 石油地球物理勘探, 2013, 48(5): 677-681. MA Detang, ZHAO Huibing, WU Zhongliang. An OBS positioning mixed method based on travel-time of direct wave[J]. Oil Geophysical Prospecting, 2013, 48(5): 677-681. |
| [12] |
杨海申, 徐丽军, 马洁, 等. 矢量叠加初至波定位方法及精度评价[J]. 石油地球物理勘探, 2021, 56(1): 49-56. YANG Haishen, XU Lijun, MA Jie, et al. First-break positioning and accuracy evaluation based on vector superposition[J]. Oil Geophysical Prospecting, 2021, 56(1): 49-56. |
| [13] |
张振宇. 折射波法检波器二次定位[J]. 西南石油学院学报, 2005, 27(2): 22-24. ZHANG Zhenyu. The receiver secondary location using refraction wave method[J]. Journal of Southwest Petroleum Institute, 2005, 27(2): 22-24. |
| [14] |
高云, 凡正才, 王民, 等. 折射波法检波器二次定位技术应用研究[J]. 石油物探, 2008, 47(3): 285-289. GAO Yun, FAN Zhengcai, WANG Min, et al. Application research on geophone re-location technology by refraction wave method[J]. Geophysical Prospecting for Petroleum, 2008, 47(3): 285-289. |
| [15] |
ZINN N D. Reintroducing refracted first breaks into ocean-bottom seismic positioning[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 135-139.
|
| [16] |
刘华伟, 陈耀元, 叶莹. 多目标优化的新方法——幂加权和法及数值仿真[J]. 武汉理工大学学报: 交通科学与工程版, 2007, 31(5): 835-838. LIU Huawei, CHEN Yaoyuan, YE Ying. New method of multi objective optimization: sum of weighted power and numerical emluator[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2007, 31(5): 835-838. |
| [17] |
王海光. 满意度动态加权法在多目标拓扑优化中的应用研究[J]. 汽车实用技术, 2016, 41(4): 45-47. WANG Haiguang. Application research of satisfaction dynamic weighting method on the optimization of multi-objective topology[J]. Automobile Applied Technology, 2016, 41(4): 45-47. |
| [18] |
施进发, 洪昌银, 张玉川. 一种新型的加权方法——动态惩罚加权法[J]. 重庆建筑工程学院学报, 1992, 14(3): 94-99. SHI Jinfa, HONG Changyin, ZHANG Yuchuan. A new weighting method: the weighting method of dynamic penalty[J]. Journal of Chongqing Architecture University, 1992, 14(3): 94-99. |
| [19] |
吕进国, 姜耀东, 赵毅鑫, 等. 基于稳健模拟退火—单纯形混合算法的微震定位研究[J]. 岩土力学, 2013, 34(8): 2195-2203. LYU Jinguo, JIANG Yaodong, ZHAO Yixin. Study of microseismic positioning based on steady simulated annealing-simplex hybrid algorithm[J]. Rock and Soil Mechanics, 2013, 34(8): 2195-2203. |



 马见青, 陕西省西安市雁塔路南段126号长安大学雁塔校区,710054。Email:
马见青, 陕西省西安市雁塔路南段126号长安大学雁塔校区,710054。Email: