2. 海洋油气勘探国家工程研究中心,北京 100028
2. National Engineering Research Center of Offshore Oil and Gas Exploration, Beijing 100028, China
在地震勘探或探地雷达(Ground Probing Radar,GPR)探测中,当地震波或电磁波在地下介质传播过程中到达岩石弹性参数突变位置时,根据惠更斯原理,突变点将作为新震源以球面波的形式向四周传播,形成绕射波[1]。在物理地震学中,广义绕射是最基本的球面波传播形式; 而反射波是反射界面上所有面元产生的绕射波叠加总和。因此,物理地震学能够通过研究地震波运动学和动力学特征,对复杂的地质体产生的反射和绕射波场做出合理解释。当地质体的尺度接近或小于1/4波长时,传统的反射波勘探无法做到精细成像;而小尺度、非均质异常体产生的绕射波由于具有明显的指示特征,可以达到针对碳酸盐储层缝洞、破碎带、尖灭点、侵入体等的高分辨率成像要求[2-4]。因此,基于绕射波成像技术在实现超高分辨率地质体勘探方面具有重要的实际意义。
众所周知,反射波勘探发展至今已成为成熟的区域地球物理勘探技术,在油气藏识别成像及工程勘探方面具有完整的理论体系支撑。但由于受地震波或电磁波主频及第一菲涅耳带半径因素影响,反射波数据体的分辨率提升相对困难。在非连续性小尺度构造和岩石突变等非均质体成像方面,绕射波成像具有独特优势,其重要性在20世纪后期被专家学者们所认识,相关的研究也逐步展开。首先是Krey[5]发现在断层发育地带产生的绕射波能够准确指示断面信息。伴随着多次覆盖技术的提出,地震数据体的信噪比得以提升,因此绕射波在叠加处理流程中能量增强,通过单纯的绕射波提取速度信息成为可能。随后,针对绕射波的一系列基础性研究陆续开展[6-7]。常规数据处理流程中主要考虑反射波,而其他波场均被定性为干扰波并进行了压制。此外,绕射波振幅相较于反射波相差约一个数量级,即便进行偏移处理使双曲线收敛,其最终仍会被反射信息掩盖[8]。动校正(Normal Move Out,NMO)及速度分析等处理方式均围绕反射波同相轴展开,目的是将双曲线校正至共中心点处的回声时间水平从而获得速度模型。但绕射波由于时差不同,动校正结果仍为曲线形态[9]。因此,获得单纯绕射波所携带的超高分辨率信息,需以动力学和运动学为基础,开发专门针对绕射波场的数据处理技术。随着平面波理论的发展,学者们提出一系列波场分离成像方法。由于在不同数据处理阶段波形特征存在变化,涌现出的新技术所依托的数学物理基础有所差异。同时,针对不同地质异常体的地震波响应,这些方法也采取了相应的发展改进。
基于绕射波成像的地质异常体识别可以通过两种不同的思路来实现。一方面,是在偏移成像过程中直接针对绕射或散射波场进行成像。根据绕射波与其他波形能量特征及传播路径差异,修改相应成像条件或权重赋值,在包含全波场数据中实现绕射能量提取及反射波能量衰减。针对传统的Kirchhoff积分偏移流程,加权函数及滤波器的应用使得绕射波能量集中,反射波得以压制[10]。在不同变换域下两种波形的能量分布差异同样有助于偏移成像中加权滤波器的设计及修正[11]。在偏移过程中,当两种波的线性特征及相位不同时,相应成像方法的提出成为针对绕射波能量凸显的重要研究方向[12-13]。但由于干扰及前期处理流程存在不确定因素和算法的复杂度影响了成像步骤的实现效率,因此偏移中单独针对绕射波的成像技术研究不够深入。
另一方面,根据不同道集中反射波与绕射波的差异,学者们将绕射波分离与成像进行了分步实现。同样是依据两种波场形态特征及能量变化,在不同数据处理流程或不同道集中实现提取绕射波目的。较早提出且广泛应用的是Radon变换在叠前炮集记录中根据不同波形的顶点位置差异实现绕射波与反射波分离[14-15]。同样,在叠前炮集记录中采用Focusing-Defocusing方法定位产生绕射波的虚震源位置,通过聚焦能量识别和提取绕射波[16-17]。当然,在叠前炮集中进行两种波场的分离可避免相关处理流程对最终结果的影响,但由于炮集记录中反射波和绕射波形态相似,且存在干扰,波场分离结果并不理想。因此,在其他处理流程阶段开发相应技术依然具有价值。Fomel等[18]通过使用平面波解构(Plan Wave Decomposition, PWD)滤波器,针对绕射波和反射波在叠加剖面或自激自收剖面上的倾角差异来设计合适的倾角滤波器进行滤波,最终实现了绕射波的分离。为了消除干扰,Berkovitch等[19]采用多聚焦绕射叠加方法,通过在叠前道集上计算绕射波前出射角及曲率半径,在叠加剖面上同时压制随机干扰及反射波能量,实现了只包含散射体产生的相应信号的输出。Zhao等[20]基于PWD框架,利用机器学习领域里的字典学习技术,实现了GPR数据的反射波压制及去噪处理,并最终输出了单纯的绕射波。
针对绕射波成像,在复杂地层速度条件下,基于Kirchhoff的小尺度散射体成像无法准确实施,因此Silvestrov等[21]引入逆时偏移技术,对倾角域的共成像点道集进行绕射波分离及速度分析,相比于Kirchhoff积分偏移,基于波动方程的逆时偏移能更准确地获得偏移速度模型。Lin等[22]通过最小方差、相干因子及相关属性改进速度分析判定准则,由PWD技术得到的绕射波生成相关偏移角道集,最终完成偏移速度分析,生成偏移速度模型及单纯绕射波偏移数据体。在共炮检距道集中,反射波同相轴具有线性而绕射波同相轴具有近似双曲线特征,据此,Yu等[23]利用稀疏约束对构建的波场函数中的反射系数模型进行了估计,同时将信赖域反射算法(Subspace Trust Region)用于求解该非线性反问题,最终输出深度域绕射波偏移结果。Decker等[24]在共炮检距道集引入斜率变量,将偏移速度外推至时间—空间—斜率域,在斜率域测量绕射波的平直度来实现时间域的偏移速度分析,得到不同炮检距下的速度模型与绕射波收敛图像。同样,当菲涅耳带宽在深部增加时,对于无损提取弱绕射波相对困难,尤其是在三维情况下。为此,Zhao等[25]基于反射和散射在运动学和振幅上的差异,将地震数据体变换至方位角—倾角域得到图像矩阵,再通过低秩稀疏矩阵分解方法实现三维绕射波分离,对于深部弱能量的绕射或散射体,该方法能够准确捕获。
本文提出基于深度神经网络(Deep Neural Networks, DNN)的复杂异常体绕射波分离成像技术。通过引入基于空洞卷积(Atrous Convolution)和深度可分离卷积(Depthwise Separable Convolution),以Encoder-Decoder为基本网络框架完成对绕射或散射波场的分离、提取。对网络输出的单纯绕射波场进行偏移速度分析及成像处理,最终得到高分辨率的偏移剖面及偏移速度模型。
1 基于Encoder-Decoder框架的深度神经网络波场分离方法相较于其他波场,绕射波在能量和形态方面存在较为明显的差异。绕射波振幅与反射波振幅相差约一个数量级;而在不同的原始道集或合成道集中,绕射波与其他类型波在形态方面存在差异。原始道集中绕射波和反射波均为双曲线形态,依据该特征拾取绕射波相对困难。经过常规数据处理后在叠加或自激自收剖面上反射波具有线性特征。而绕射波在叠加过程中能量增强,仍然保持类双曲线特征。因此,本文针对叠后记录或自激自收数据体中的绕射波进行拾取,通过深度学习技术构建整个波形拾取流程。利用并改进深度学习领域内语义分割(Semantic Segmentation)相关技术,实现对数据体中不同波形及背景场的分离。在数据中异常的细节和轮廓勾勒方面,基于Encoder-Decoder的空洞可分离卷积网络(Encoder-Decoder with Atrous Separable Convolution)[26]表现出更好的性能。其中空洞卷积能够在降低算法复杂度的同时增大感受野;深度可分离卷积能够在保持相同特征图数量的条件下减少运算步骤。凭借空间金字塔池化的策略,新技术能够容忍变维度数据输入,实现多尺度目标分析。在主网络选则方面使用相对成熟的ResNet V2-101,依托其101层深度的精细特征图计算,新方法能够实现目标体不同分辨率、不同特性方面的刻画捕捉。
1.1 Encoder-Decoder框架常规深度神经网络中的卷积运算对于输出特征图的大小由卷积核尺寸(Kernel size)、卷积步长(Stride)以及边缘填充尺寸(Padding)决定。对于二维数据体,若输入尺寸为n×n,卷积核尺寸为f×f,卷积步长为s,边缘填充尺寸为p,则当前卷积层输出特征图尺寸为
使用空洞卷积能够保证与传统卷积运算相同计算量的情况下感受野的指数级增长。因此,捕获目标在不同数据体尺度变化情况下,新框架能够输出更为精确的结果。基于空洞和深度可分离卷积的绕射波分离整体框架如图 1所示。

|
图 1 基于深度神经网络基本框架的绕射波分离 |
图 1中Encoder(编码)部分,利用主骨网络(ResNet V2)实现绕射波波形特征抽取,选取不同尺寸(1×1,3×3)和不同扩张率(0,6,12,18)的组合定义4种卷积核(Conv),每种卷积核深度为256。另外,对原始数据体进行池化(Pooling)操作,降低维度。最终得到5种特征图。利用空间金字塔池化方法连接各个特征图。而Decoder(解码)部分,首先对空间金字塔池化输出的特征图进行一个系数为4的双线性上采样(Upsample),其结果与主骨网络结构中输出的低特征图相连接。然后,使用3×3的卷积核进行进一步细化,并再次进行系数为4的双线性上采样。最终实现特征图输出与实际输入相同大小的绕射波分离系统。
1.2 模型训练对于Encoder-Decoder神经网络的训练,本文采用合成理论数据并添加绕射波标签,形成用于训练及验证的数据体。为涵盖可能出现的绕射波场,设计相应模型需考虑实际地下地层模型及背景干扰。共考虑三种地下产生绕射波情况的地质模型:单一小尺度异常体、有限长度水平地层以及复杂异常体组合。因模型对应的单一绕射波场生成相对准确,避免了人为拾取标签对模型训练结果的影响。对于水平地层将会在边界处产生绕射波。
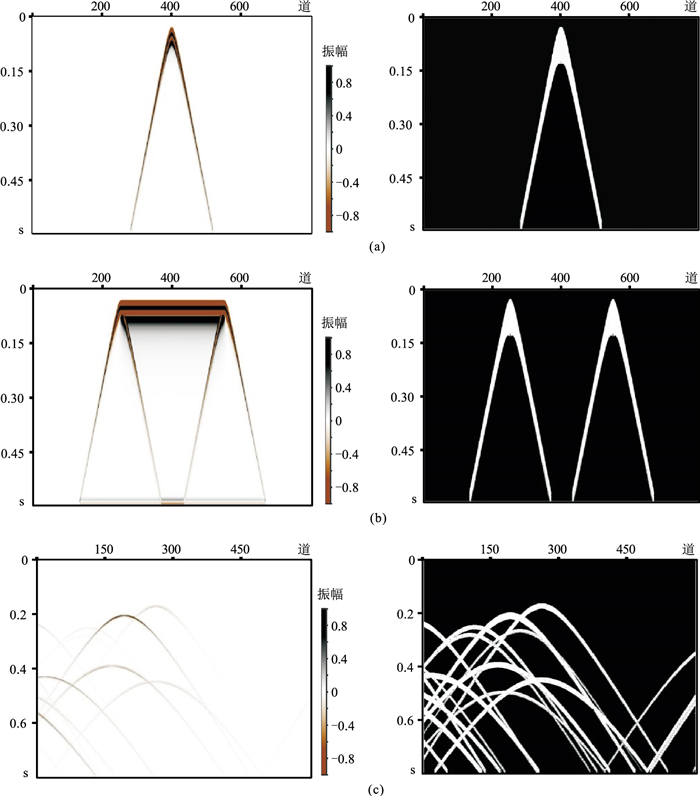
由于子波主频、相位以及地下背景速度场不同,绕射波在形态、振幅方面存在差异,故模型数据的生成充分考虑上述参数的变化。采用震源子波为Ricker子波,固定相位为零,主频以5 Hz为间隔在5~80 Hz之间变化。为方便后续正演模拟,背景速度场统一为常数,且以100 m/s为间隔在1000~8800 m/s之间递增。因此,生成用于训练的理论模型数据体共3792个,其中3500个用于模型训练,292个用于模型验证。需要强调的是,特征图记录的是根据采样点处是否包含绕射波而生成的逻辑值。若数据体中该采样点处包含绕射波场成分,则对应同样大小的特征图中该位置的记录为1,否则记录为0。图 2为三种模型对应固定速度为4000 m/s、子波主频为40 Hz的数据体及相应标签展示图中黑色区域特征值为0,即不包含绕射波波形的区域;白色区域特征值为1,即该区域内存在相关绕射波信号。根据白色区域相应位置的索引可以从原始剖面上提取绕射波波形。
|
图 2 不同模型产生的绕射波数据体(左)及对应标签(右) (a)单一绕射波场;(b)有限边界水平层波场;(c)异常体组合产生的绕射波场 |
本文单纯通过理论合成数据进行网络训练,尽量涵盖不同绕射波类型。考虑到人为给定单纯绕射波特征图所带来的不准确性,故不采用实际数据进行网络参数校正。训练和验证在GPU平台进行完成,其具体型号为Nvidia Tesla K80;训练基本参数为:批大小(batch_size)=4, 轮次(epoch)=2, 迭代次数(iteration)=30000。最终得到用于提取绕射波场的DNN。对于弱绕射及波型重叠情况,新策略能够实现绕射波的准确提取。需要强调的是,训练得到的网络通过添加新的训练数据集可以进一步改进,从而使得绕射波分离精度进一步提高。该机制也是DNN区别于现阶段常规分离方法的重要特征。
2 基于速度连续变化的单纯绕射波成像完成绕射波场提取后,需要进行相关偏移速度分析及偏移流程设计。对于准确的空间变化偏移速度场,绕射波在偏移后将收敛。本次研究采用局部收敛方法获得每个采样点的偏移速度。首先对分离得到的绕射波场进行不同偏移速度的偏移处理。该流程通过速度连续方法实现[18]。
对于准确的偏移速度,单纯绕射波偏移结果具有收敛性,这意味着信号与常数1的相关性低,进而表现为方差极大范数ϕ的值较高[27]。对于信号s,有
| $ \phi=\frac{N \sum\limits_{i=1}^N s_i^4}{\left(\sum\limits_{i=1}^N s_i^2\right)^2} $ | (1) |
式中:N为信号s的样点数;si为信号s的第i个样点。
序列a与常数1的相关性可以表示为
| $ c[\boldsymbol{a}, 1]=\frac{\sum\limits_{i=1}^N a_i}{\sqrt{N \sum\limits_{i=1}^N a_i^2}} $ | (2) |
式中ai为序列a的第i个元素。此时ϕ可以表示为
| $ \left\{\begin{array}{l} \phi=\frac{1}{c\left[\boldsymbol{s}^2, 1\right]^2}=\frac{1}{p q} \\ p=\frac{\sum\limits_{i=1}^N s_i^2}{N}, \quad q=\frac{\sum\limits_{i=1}^N s_i^2}{\sum\limits_{i=1}^N s_i^4} \end{array}\right. $ | (3) |
将p和q的求取公式抽象为平方最小化问题,即
| $ \left\{\begin{array}{l} p=\min\limits _p \sum\limits_{i=1}^N\left(s_i^2-p\right)^2 \\ q=\min\limits _q \sum\limits_{i=1}^N\left(1-q s_i^2\right)^2 \end{array}\right. $ | (4) |
而对于连续变化属性
| $ \begin{aligned} p_i & =\min _{p_i}\left[\sum\limits_{i=1}^N\left(s_i^2-p_i\right)^2+\mathrm{R}\left(p_i\right)\right] \\ q_i & =\min _{p_i}\left[\sum\limits_{i=1}^N\left(1-q_i s_i^2\right)^2+\mathrm{R}\left(q_i\right)\right] \end{aligned} $ | (5) |
式中R是正则化算子。此次实验采用整形正则化约束[19]。针对每个偏移图像中的每个点计算连续变量属性ϕi,最终输出的是收敛图像的地震道集,通过拾取属性最大值可确定相应准确的速度值,最终得到偏移速度数据体。最后利用生成的偏移速度模型对数据体进行偏移处理,进而得到高分辨率偏移剖面。
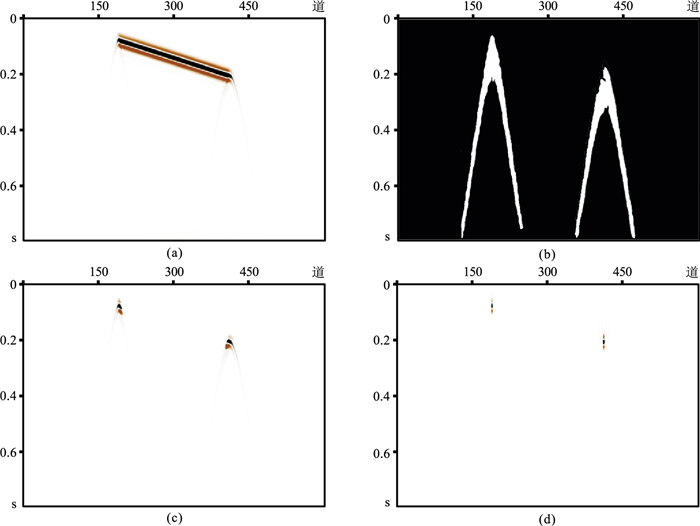
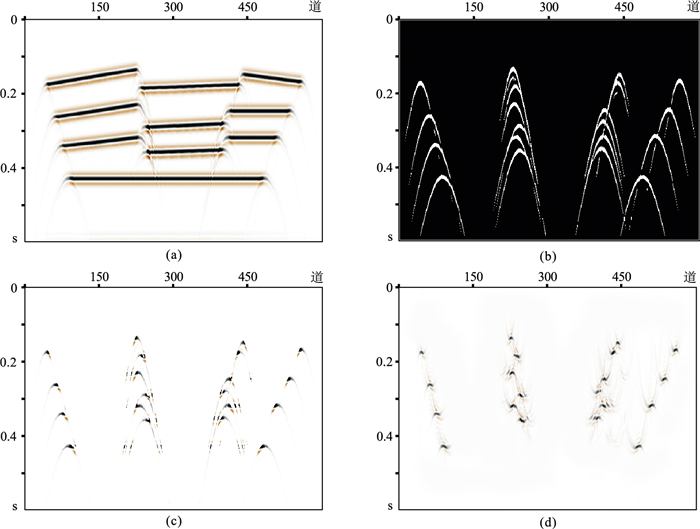
3 数据测试为验证网络的稳定性和准确性,首先通过理论合成数据对方法进行测试。设计包含绕射波的倾斜地层对应的地震波场数据(图 3a)以及多套地层叠加对应的波场(图 4a)作为输入,考察网络对线性信号和非线性信号的分离能力。最终分离得到的绕射波如图 3b、图 4b所示。利用绕射波空间分布的索引(图 3b中白色区域)提取得到的绕射波场如图 3c、图 4c所示。由图 3c和图 4c可以看出,对于反射界面边界处反射波和绕射波重叠情况,新方法能够准确识别并保留绕射波同相轴。图 3d为倾斜地层最终绕射波场的偏移结果。偏移后绕射波形收敛,能量集中,指示了倾斜地层的边界位置,这与实际边界位置处的道集保持一致。图 4d为多套地层叠加分离出的绕射波偏移结果,同样绕射波相对收敛,能够很好指示地层边界位置。由于能量的差异导致偏移波形出现轻微上抛现象,但对异常体的刻画影响较小。
|
图 3 倾斜地层模型绕射波分离成像测试结果 (a)倾斜界面波场;(b)训练模型输出绕射波索引;(c)根据图b提取的绕射波;(d)单纯绕射波偏移成像结果 |
|
图 4 复杂地层模型下绕射波分离成像测试结果 (a)多套地层产生的地震波场;(b)训练模型输出绕射波索引;(c)根据图b提取得到的绕射波;(d)单纯绕射波偏移成像结果 |
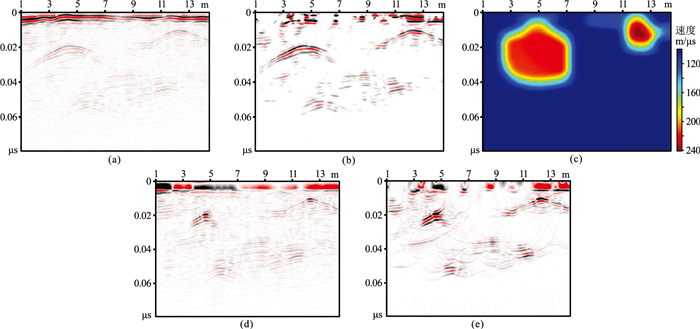
为进一步说明基于DNN的绕射波分离成像流程的高效性及适用性,采用实际GPR数据进行验证,采用无人机贴地飞行采集。已知地下1.5 m埋有两条输气管道,直径为1.2 m,材质为金属,介电常数较小,因此电磁波传播速度接近光速。而常规土壤或岩石介电常数相对较大,电磁波传播速度相对较低,因此最终得到的偏移剖面中应当包含两个高速异常。图 5a为采集到的GPR数据体,包含800道,时间采样点数为505,采样间隔为1.63×10-10 s。从原始剖面上可以看到地表强能量的反射波以及由于输气管道异常存在产生的具有双曲线特征的绕射波(图 5a黑色箭头指示位置)。正如前文提到的,将原始剖面作为输入,经过训练完成的绕射波分离模型,最终输出绕射波场对应的时间采样索引,提取到的单纯绕射波数据如图 5b所示。可以看到单纯绕射波剖面上包含输气管道产生的绕射信号,并且存在具有一定弯曲形态的干扰波,但能量相对较弱。针对分离得到的绕射波数据进行偏移速度分析,根据方差极大范数确定对应偏移速度模型,最终结果如图 5c所示。从图中可以准确识别输气管道引起的高速异常。在偏移成像方面,利用偏移速度剖面对原始剖面进行处理,最终得到的偏移数据体如图 5d所示。同样通过偏移剖面可以确定输气管道引起的剖面波型异常, 对应的绕射波波形收敛,能量集中。通过该剖面能够准确识别地下地质异常体的空间位置及具体展布。图 5e是单纯绕射波场的偏移结果展示,同样可以看到绕射波收敛、能量增强的特点。新流程得到的速度剖面和偏移剖面作为辅助材料,对于后续的解释工作提供准确的数据保障。
|
图 5 实际GPR数据测试结果 (a)原始剖面;(b)模型输出单纯绕射波场;(c)单纯绕射波生成的偏移速度模型;(d)原始剖面偏移成像结果; (e)单纯绕射波偏移成像结果 |
本文通过生成包含绕射波的合成数据,并添加绕射波标签,构建了用于训练及验证深度神经网络的数据库。基于Encoder-Decoder框架的神经网络结构能够准确捕获不同尺度目标体及其边界信息,因此对于绕射波特征提取及波场分离具有独特的优势。该方法单纯通过合成数据训练网络,不对实际数据进行人为判定,并添加标签作为输入训练网络,避免了网络参数训练受到人为因素的干扰。同时,经过训练及验证后的深度神经网络能够更高效地处理后续新数据,无需重新针对特定数据设计算法。对于网络卷积核参数的更新、改进可通过加入更庞大、精确的复杂波场数据及其对应的绕射波特征图进一步完善网络,达到分离网络的泛化性,使其能够适应更为复杂的数据种类。利用分离得到的绕射波场进行偏移速度分析及处理,生成用于解释的高分辨率偏移速度及偏移数据体。相较于传统零炮检距剖面,完成偏移成像的单纯绕射波数据体具有更高的空间分辨率,针对异常体亦具有更高的成像精度,可为解释工作提供可靠的数据。针对GPR数据或地震叠加数据提出的新流程,对于其他道集的数据体同样可以通过深度神经网络进行识别提取以及改变速度分析及成像流程,完成基于绕射波的地质异常体识别成像。
| [1] |
BAKER B B, COPSON E T. The Mathematical Theory of Huygens' Principle[M]. American Mathematical Society, Washington, USA, 2003.
|
| [2] |
朱生旺, 曲寿利, 魏修成, 等. 通过压制共散射点道集映射噪声改善绕射波成像分辨率[J]. 石油物探, 2010, 49(2): 107-114. ZHU Shengwang, QU Shouli, WEI Xiucheng, et al. To improve imaging resolution by mapping noise attenuation on CSP gathers[J]. Geophysical Prospecting for Petroleum, 2010, 49(2): 107-114. DOI:10.3969/j.issn.1000-1441.2010.02.001 |
| [3] |
栾锡武, 杨佳佳. 地震绕射波波场分离与成像方法综述[J]. 石油物探, 2022, 61(5): 761-770. LUAN Xiwu, YANG Jiajia. A review of seismic diffraction wavefield separation and imaging methods[J]. Geophysical Prospecting for Petroleum, 2022, 61(5): 761-770. DOI:10.3969/j.issn.1000-1441.2022.05.001 |
| [4] |
肖曦, 周鹏, 张益明, 等. 基于绕射信息提取技术的断裂识别方法及应用[J]. 石油地球物理勘探, 2021, 56(5): 1130-1136. XIAO Xi, ZHOU Peng, ZHANG Yiming, et al. Research and application of fracture identification me-thod based on diffraction information extraction technology[J]. Oil Geophysical Prospecting, 2021, 56(5): 1130-1136. DOI:10.13810/j.cnki.issn.1000-7210.2021.05.019 |
| [5] |
KREY T. The significance of diffraction in the investigation of faults[J]. Geophysics, 1952, 17(4): 843-858. DOI:10.1190/1.1437815 |
| [6] |
KUNZ B F J. Diffraction problems in fault interpretation[J]. Geophysical Prospecting, 1960, 8(3): 381-388. DOI:10.1111/j.1365-2478.1960.tb01722.x |
| [7] |
HARLAN W S, CLAERBOUT J F, ROCCA F. Signal/noise separation and velocity estimation[J]. Geophysics, 1984, 49(11): 1869-1880. DOI:10.1190/1.1441600 |
| [8] |
YILMAZ Ö. Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data[M]. Society of Exploration Geophysicists, Tulsa, USA, 2001.
|
| [9] |
BANSAL R, IMHOF M G. Diffraction enhancement in prestack seismic data[J]. Geophysics, 2005, 70(3): V73-V79. DOI:10.1190/1.1926577 |
| [10] |
MOSER T J, HOWARD C B. Diffraction imaging in depth[J]. Geophysical Prospecting, 2008, 56(5): 627-641. DOI:10.1111/j.1365-2478.2007.00718.x |
| [11] |
KLOKOV A, FOMEL S. Separation and imaging of seismic diffractions using migrated dip-angle gathers[J]. Geophysics, 2012, 77(6): S131-S143. DOI:10.1190/geo2012-0017.1 |
| [12] |
ZHU X S, WU R S. Imaging diffraction points using the local image matrices generated in prestack migration[J]. Geophysics, 2010, 75(1): S1-S9. DOI:10.1190/1.3277252 |
| [13] |
ZHANG J F, ZHANG J J. Diffraction imaging using shot and opening-angle gathers: a prestack time migration approach[J]. Geophysics, 2014, 79(2): S23-S33. DOI:10.1190/geo2013-0016.1 |
| [14] |
NOWAK E J and IMHOF M G. Diffractor localization via weighted Radon transforms[C]. SEG Technical Program Expanded Abstracts, 2004, 23: 2108-2111.
|
| [15] |
罗腾腾, 徐基祥, 孙夕平. 应用迭代收缩高分辨率Radon变换的绕射波分离与成像方法[J]. 石油地球物理勘探, 2021, 56(2): 313-322. LUO Tengteng, XU Jixiang, SUN Xiping. Diffraction wave separation and imaging based on high-resolution Radon transform on an iterative model shrinking approach[J]. Oil Geophysical Prospecting, 2021, 56(2): 313-322. DOI:10.13810/j.cnki.issn.1000-7210.2021.02.013 |
| [16] |
KHAIDUKOV V, LANDA E, MOSER T J. Diffraction imaging by focusing-defocusing: an outlook on seismic superresolution[J]. Geophysics, 2004, 69(6): 1478-1490. DOI:10.1190/1.1836821 |
| [17] |
杨城增, 张宣堂, 盛同杰, 等. 绕射波叠前共虚震源道集分离方法[J]. 石油地球物理勘探, 2022, 57(4): 847-854. YANG Chengzeng, ZHZNG Xuantang, SHENG Tongjie, et al. Diffraction separation method in the prestack common virtual source gather[J]. Oil Geophysical Prospecting, 2022, 57(4): 847-854. |
| [18] |
FOMEL S, LANDA E, TANER M T. Poststack velocity analysis by separation and imaging of seismic diffractions[J]. Geophysics, 2007, 72(6): U89-U94. DOI:10.1190/1.2781533 |
| [19] |
BERKOVITCH A, BELFER I, HASSIN Y, et al. Diffraction imaging by multifocusing[J]. Geophysics, 2009, 74(6): WCA75-WCA81. DOI:10.1190/1.3198210 |
| [20] |
ZHAO J T, YU C X, PENG S P, et al. Online dictionary learning method for extracting GPR diffractions[J]. Journal of Geophysics and Engineering, 2019, 16(6): 1116-1123. DOI:10.1093/jge/gxz081 |
| [21] |
SILVESTROV I, BAINA R, LANDA E. Post-stack diffraction imaging using reverse-time migration[J]. Geophysical Prospecting, 2016, 64(1): 129-142. DOI:10.1111/1365-2478.12280 |
| [22] |
LIN P, PENG S P, ZHAO J T, et al. Accurate diffraction imaging for detecting small-scale geologic discontinuities[J]. Geophysics, 2018, 83(5): S447-S457. DOI:10.1190/geo2017-0545.1 |
| [23] |
YU C X, ZHAO J T, WANG Y F, et al. Separation and imaging diffractions by a sparsity-promoting model and subspace trust-region algorithm[J]. Geophysical Journal International, 2017, 208(3): 1756-1763. |
| [24] |
DECKER L, MERZLIKIN D, FOMEL S. Diffraction imaging and time-migration velocity analysis using oriented velocity continuation[J]. Geophysics, 2017, 82(2): U25-U35. DOI:10.1190/geo2016-0141.1 |
| [25] |
ZHAO J T, YU C X, PENG S P, et al. 3D diffraction imaging method using low-rank matrix decomposition[J]. Geophysics, 2020, 85(1): S1-S10. |
| [26] |
CHEN L C, ZHU Y K, PAPANDREOU G, et al. Encoder-decoder with atrous separable convolution for semantic image segmentation[C]. Computer Vision-ECCV 2018, 2018, 833-851.
|
| [27] |
FOMEL S. Shaping regularization in geophysical-estimation problems[J]. Geophysics, 2007, 72(2): R29-R36. DOI:10.1190/1.2433716 |



 包乾宗, 陕西省西安市雁塔路126号长安大学地质工程与测绘学院,710054。Email:
包乾宗, 陕西省西安市雁塔路126号长安大学地质工程与测绘学院,710054。Email: 