2. 中国石油大学(北京) 油气资源与探测国家重点实验室,北京 102249
2. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum (Beijing), Beijing 102249, China
孔隙度(ϕ)作为储层预测和油藏描述的重要物性参数之一,可以为含油气性预测、储层品质评估和储量计算等提供较为可靠的参考依据[1-3]。孔隙度受到不同地质因素的影响,包括构造位置、埋藏深度、成岩程度、沉积环境和岩性变化等。通过钻井取心并进行岩石物理分析获取孔隙度是最为直接、准确和有效的方法[4-5],但由于取样和测试成本太高而不适合于大规模应用。在利用测井资料预测孔隙度方面,通常采用基于多种岩石物理模型的方法[6-7]。Luo等[8]在Xu-White模型的基础上提出了改进的岩石物理模型以预测储层的孔隙度。Li等[9]基于Gassmann方程和多孔岩石物理模型建立了新的三维岩石物理模板以定量表征孔隙度。Wang等[10]基于软孔隙度模型与Gassmann方程实现了储层孔隙度的预测。除了采用岩石物理模型外,还存在基于经验关系[11]、统计关系以及引入贝叶斯理论的孔隙度预测模型[12],如通过数据驱动的方式,利用大量测井资料建立测井曲线与孔隙度之间统计性、经验性的岩石物理关系,以实现孔隙度预测[13];在岩石物理理论的基础上,根据贝叶斯理论实现孔隙度的概率估计[14-15]。
随着人工智能和大数据挖掘等技术广泛应用于石油行业,人工智能算法开始应用于测井孔隙度的预测。该类方法选择测井数据作为输入,以专家精细解释的孔隙度曲线作为标签,利用人工智能数据驱动类算法建立多种测井属性与孔隙度之间的非线性关系,在此基础上再进行孔隙度预测。支持向量机[16-17]、随机森林(Random Forest,RF)[18-19]、极度梯度提升树(Extreme Gradient Boosting, XGBoost)[20]、深度神经网络[21-22]、卷积神经网络[23]以及长短期记忆网络[24-26]等数据驱动类方法能建立高维度的多尺度特征与孔隙度之间的复杂联系,但是不同岩性的测井曲线与孔隙度之间的非线性关系相差较大,仅利用数据驱动的人工智能算法可能对不同岩性的非线性关系拟合效果较差。同时,在人工解释砂岩储层孔隙度时,专家通常仅解释储层段的孔隙度而无法获取全井段的孔隙度曲线。此外,高昂的钻井成本导致智能孔隙度预测方法存在标签数量不足和测井样本空间分布不均衡等问题,极大地制约了智能化孔隙度预测精度的提高以及其进一步的推广。因此,需要在孔隙度预测时考虑岩相控制,通过岩相划分砂岩与泥岩,再分别进行砂岩段和泥岩段的孔隙度预测。为此,本文提出了一种基于半监督高斯混合模型与梯度提升树(Gradient Boosting Decision Tree,GBDT)的相控孔隙度预测方法。首先利用少量具岩相标签的测井数据确定高斯混合模型的初始聚类中心及对应的岩相类别;其次利用大量无标签测井数据优化高斯混合模型,实现砂岩与泥岩的正确划分;再次基于地质认识将泥岩孔隙度解释为固定的极小值,从而后续只开展砂岩孔隙度预测;然后将岩石物理方法导出的孔隙度先验信息和测井敏感属性作为梯度提升树算法的多源输入信息,通过学习统计性岩石物理关系建立砂岩孔隙度的计算模型;最终根据岩相结果将砂岩段与泥岩段的孔隙度进行组合得到相控孔隙度。实际工区的测井资料测试表明该方法应用效果较好。
1 方法原理 1.1 测井相控孔隙度智能预测流程如图 1所示,本文提出的基于半监督高斯混合模型与梯度提升树的相控孔隙度预测方法的主要步骤包括:测井数据预处理、基于半监督高斯混合模型的岩相分类、基于梯度提升树与岩石物理模型约束的相控孔隙度预测。具体流程为:①对测井数据进行岩性敏感属性与孔隙度敏感参数的筛选,再对测井岩性敏感属性进行高通滤波处理,消除低频趋势的同时保留高频细节信息;②利用有岩相标签的敏感属性建立岩相分类的初始模型,并结合无岩相标签的敏感属性构建半监督高斯混合模型,进行岩相(砂岩与泥岩)的划分;③根据上一步的岩相结果将测井曲线分成砂岩段和泥岩段两部分,再分别开展孔隙度预测。

|
图 1 测井相控孔隙度智能预测流程 |
本文的目标储层为常规的砂岩储层,因此可将泥岩段孔隙度统一设置为一个极小的常数。针对砂岩段孔隙度预测,首先根据前期优选的孔隙度敏感参数,建立测井敏感参数与孔隙度之间的岩石物理模型;再基于岩石物理模型粗糙估算孔隙度;然后将估算的粗糙孔隙度与其他孔隙度敏感参数(如声波时差AC、井径CAL等)作为集成学习算法的多源输入信息,训练梯度提升树模型,预测砂岩段的孔隙度;最终将砂岩孔隙度与泥岩孔隙度进行组合即可得到相控孔隙度。
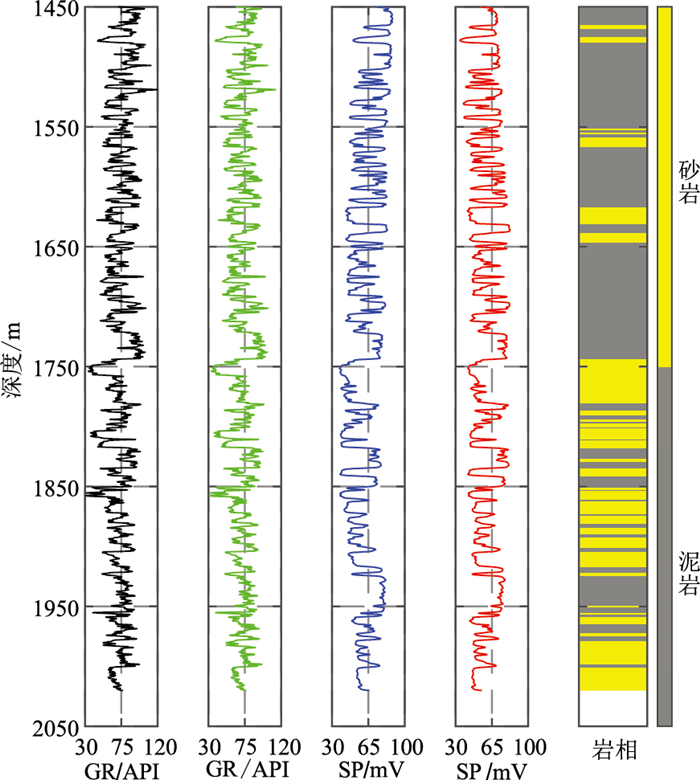
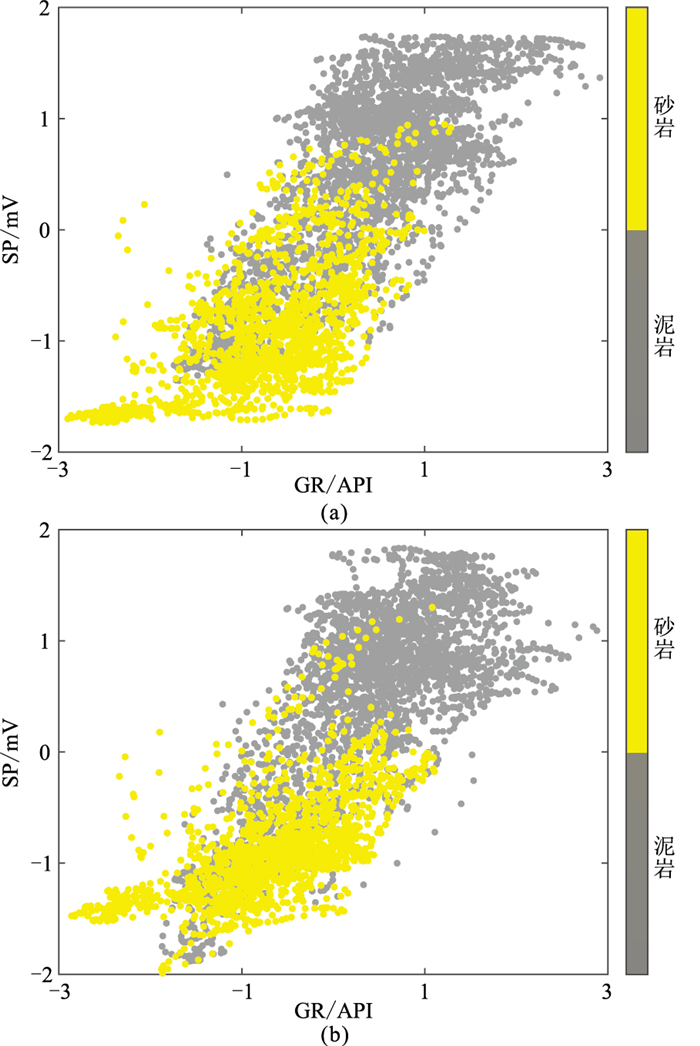
1.2 基于高通滤波的测井数据预处理为降低相控孔隙度预测的难度,本文将相控孔隙度预测分为岩相分类解释和孔隙度预测两个任务。专家在对测井曲线进行岩相解释时,通常只关注测井曲线的某一部分并利用该部分测井曲线的差异判断岩相。这一过程相当于在测井曲线中设置了一个时窗,通过时窗内的曲线变化判断局部岩性。将该时窗沿着测井曲线进行滑动,可以实现整条测井曲线的岩性解释。但是,一些常规的机器学习方法(如聚类算法、决策树算法和支持向量机算法等)无法根据局部的测井曲线差异判断岩性,而是需要考虑整条测井曲线的差异。尽管图 2中的自然伽马(GR)和自然电位(SP)参数与岩性具有较好的对应关系,但是将整条GR和SP曲线交会时,却无法区分岩性(图 3a)。
|
图 2 高通滤波处理前(左)、后(右)的测井曲线对比 |
|
图 3 高通滤波处理前(a)、后(b)GR与SP交会分析 |
多种滤波方法已广泛应用于测井曲线的处理与解释[27-29]。如图 2所示,GR和SP随着深度的增加存在低频变化趋势,这可能缘于地层的沉积环境的变化[30]。为了使机器学习算法在训练过程中更好地实现岩性的分类,本文使用高通滤波对低频趋势进行处理。由图 2可见,高通滤波处理后的测井曲线消除了低频趋势,保留了高频的局部信息。通过交会图(图 3)分析,高通滤波处理后砂岩、泥岩的重合部分减少(图 3b),说明处理后的砂岩和泥岩的GR、SP测井响应差异更大。因此,后续采用处理后的GR和SP参数作为岩相划分的敏感属性。
1.3 基于半监督高斯混合模型的岩相分类聚类方法已广泛应用于测井数据岩性解释。本文使用高斯混合模型对高斯滤波处理后的GR和SP曲线进行岩性分类。初始模型的选取是无监督聚类算法的关键,其质量的好坏不仅影响效率,而且影响精度。因此,本文提出了一种基于半监督高斯混合模型的岩相分类方法。即在传统高斯混合模型的基础上,增加具有岩性解释的测井曲线,计算带有岩性标签的初始模型,实现一种半监督的聚类算法。在理论上,通过多个高斯分布线性组合可以拟合出地层岩性的分布[31]。假设测井参数样本x中每个簇样本的特征服从多元高斯分布,则x的概率密度函数为
| $ \begin{aligned} & p\left(\boldsymbol{x} \mid c_k, \boldsymbol{\mu}_k, {\mathit{\Sigma}}_k\right)=\sum\limits_{k=1}^K c_k N\left(\boldsymbol{x}_k \mid \boldsymbol{\mu}_k, {\mathit{\Sigma}}_k\right) \\ & \;\;\;\;\;\;\;\;\;\;= \sum\limits_{k=1}^K \frac{c_k}{(2 {\rm{ \mathsf{ π} }})^{\frac{D_k}{2}}} \frac{1}{\left|{\mathit{\Sigma}}_k\right|^{\frac{1}{2}}} \\ & \;\;\;\;\;\;\;\;\;\;\exp \left[-\frac{1}{2}\left(\boldsymbol{x}_k-\boldsymbol{\mu}_k\right)^{\mathrm{T}} {\mathit{\Sigma}}_k^{-1}\left(\boldsymbol{x}_k-\boldsymbol{\mu}_k\right)\right] \end{aligned} $ | (1) |
式中:p(·)表示概率函数;K为样本中簇的总数;ck为第k个高斯模型(或簇)对应的系数;N(·)表示高斯分布;μk为第k个簇的样本分布的均值;Σk表示第k个簇的样本分布的协方差;Dk表示数据的维度;上标T表示转置。均值μk描述的是不同岩性对应测井参数的均值,而协方差Σk描述的是每一簇样本的分布形态,反映测井参数的分布情况。
根据式(1)可计算出测井参数每个样本的概率密度函数,通过最大化所有样本的概率密度函数的乘积(最大似然估计法)可求得模型的最佳参数。从本质上讲,最大化所有样本的概率密度函数的乘积等同于最大化所有样本对数概率密度函数的和,即最大化
| $ \begin{array}{l} \lg {L_1}\left( {{\mathit{\boldsymbol{\mu }}_k}, {\mathit{\Sigma }_k}} \right)\\ \;\;\;\;\;\;\;\; = \sum\limits_{j = 1}^J {\lg } \left[{\sum\limits_{k = 1}^K {{c_k}} p\left( {\mathit{\boldsymbol{x}}\mid {\mathit{\boldsymbol{\mu }}_k}, {\mathit{\Sigma }_k}} \right)} \right] \end{array} $ | (2) |
可获得高斯混合模型中的最佳均值和方差。式中:L1是高斯混合模型的目标函数;J表示样本总个数。式中有众多相加项不能通过偏导直接获得其最大值[32],因此在高斯混合模型的参数求解中广泛选用最大期望(EM) 算法,通过迭代的思想求解高斯混合模型参数。具体步骤如下。
(1) 基于具有专家岩性解释的测井敏感特征结果初始化K个高斯分布的均值μk与协方差Σk,并随机初始化混合系数ck。
(2) 遍历所有测井曲线x的所有样本点,计算第i个样本点xi(i=1,2,…,J)属于第k个高斯分布的概率
| $ \begin{aligned} & \gamma_{i, k}=p\left(\boldsymbol{x}_i \mid z_i=k\right) \\ & =\frac{1}{(2 {\rm{ \mathsf{ π} }})^{\frac{d}{2}}\left|{\mathit{\Sigma}}_k\right|^{\frac{1}{2}}} \exp \left[-\frac{1}{2}\left(\boldsymbol{x}_i-\boldsymbol{\mu}_k\right)^{\mathrm{T}} {\mathit{\Sigma}}_k^{-1}\left(\boldsymbol{x}_i-\boldsymbol{\mu}_k\right)\right] \end{aligned} $ | (3) |
式中:zi表示xi所属的类;d为xi的维度。
(3) 按照下式更新μk′和Σk′,即不断优化不同岩相的聚类中心位置
| $ \boldsymbol{\mu}_k{ }^{\prime}=\frac{\sum\limits_{i=1}^J \gamma_{i, k} \boldsymbol{x}_i}{\sum\limits_{i=1}^N \gamma_{i, k}} $ | (4) |
| $ {\mathit{\Sigma}}_k{ }^{\prime}=\frac{\sum\limits_{i=1}^J \gamma_{i, k}\left(\boldsymbol{x}_i-\boldsymbol{\mu}_k{ }^{\prime}\right)\left(\boldsymbol{x}_i-\boldsymbol{\mu}_k{ }^{\prime}\right)^{\mathrm{T}}}{\sum\limits_{i=1}^J \gamma_{i, k}} $ | (5) |
(4) 重复步骤(2)和步骤(3),直到高斯混合模型参数收敛为止,从而找到不同岩相对应的聚类中心,完成对测井数据的岩相分类。
1.4 基于梯度提升树的砂岩孔隙度预测在利用半监督高斯混合模型划分砂岩和泥岩的基础上,设置泥岩孔隙度为固定常数0.01,后续采用梯度提升树算法预测砂岩孔隙度。梯度提升树算法和随机森林算法都是基于决策树的集成算法。在随机森林算法的基础上,梯度提升树算法“提升”了其内部使用的多个决策树之间的相关性,并使用梯度算法快速求解目标函数。
| $ F_M\left(\boldsymbol{x}^{\mathrm{W}}\right)=\sum\limits_{m=1}^M T\left(\boldsymbol{x}^{\mathrm{W}} ; \theta_m\right) $ | (6) |
式中:FM(xW)为预测的孔隙度, xW为输入的砂岩段测井数据;M为决策树总个数;T(xW; θm)表示第m个决策树,其中θm为第m个决策树的参数。模型采用向前分步算法,具体步骤如下。
(1) 首先确定初始提升树
| $ F_0\left(\boldsymbol{x}^{\mathrm{W}}\right)=0 $ | (7) |
(2) 采用向前分步算法,得到第m步的模型,即
| $ F_m\left(\boldsymbol{x}^{\mathrm{W}}\right)=F_{m-1}\left(\boldsymbol{x}^{\mathrm{W}}\right)+T\left(\boldsymbol{x}^{\mathrm{W}} ; \theta_m\right) $ | (8) |
式中:Fm-1(xW)、Fm(xW)分别表示第m-1步、第m步建立的梯度提升树模型。
(3) 利用经验风险最小化确定下一棵决策树的参数
| $ \theta_m=\underset{\theta_m}{\arg \min } \sum\limits_{i=1}^J L_2\left[\boldsymbol{y}_i, F_{m-1}\left(\boldsymbol{x}_i^{\mathrm{W}}\right)+T\left(\boldsymbol{x}^{\mathrm{w}} ; \theta_m\right)\right] $ | (9) |
式中:L2表示梯度提升树的损失函数;yi表示第i个孔隙度样本点;xiW表示测井数据xW的第i个样本点。当采用平方误差损失函数时
| $ L_2\left[\boldsymbol{y}, F_m\left(\boldsymbol{x}^{\mathrm{W}}\right)\right]=\left[\boldsymbol{y}-F_m\left(\boldsymbol{x}^{\mathrm{W}}\right)\right]^2 $ | (10) |
结合式(8),可得
| $ L_2\left[\boldsymbol{y}, F_m\left(\boldsymbol{x}^{\mathrm{W}}\right)\right]=\left[\boldsymbol{y}-F_{m-1}\left(\boldsymbol{x}^{\mathrm{W}}\right)-T\left(\boldsymbol{x}^{\mathrm{W}} ; \theta_m\right)\right]^2 $ | (11) |
由于决策回归器模型的自身特点,即使数据中的输入与输出之间存在着复杂关系,多个回归器的线性组合也可以很好地拟合孔隙度敏感参数与孔隙度之间的非线性关系。由待测试数据输入建立的梯度提升树孔隙度预测模型后,即可获得砂岩段的孔隙度结果。最终得到的相控孔隙度为砂岩孔隙度与泥岩孔隙度的组合。
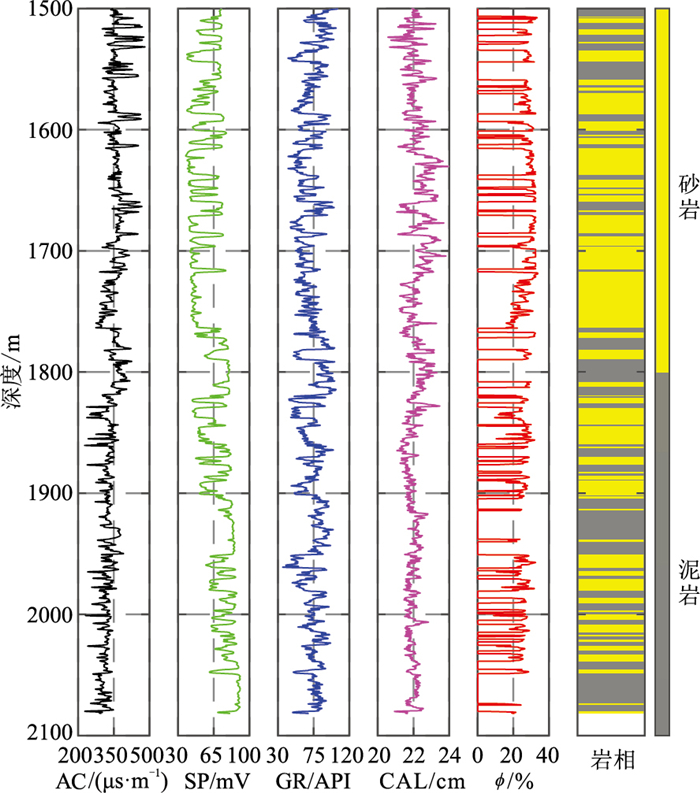
2 实例应用将本文相控孔隙度预测方法应用于中国东部D油田的18口井(分别命名为W1~W18井)。测井段深度为1500~2100 m,岩性主要为砂岩和泥岩。测井曲线主要包括AC、GR、CAL和SP。18口井已做了岩性解释和孔隙度解释。选择其中的W10井进行展示(4条常规测井曲线和专家解释的孔隙度曲线、地层岩性),如图 4所示。选择W1井的测井岩性敏感属性和标签计算半监督聚类算法的初始模型。选择16口井(W1~W16井)的测井数据训练相控孔隙度预测模型(即训练集),其余2口井(W17、W18井)测试相控孔隙度预测模型的性能(即测试集)。
|
图 4 W10井的测井曲线及岩性解释结果 |
在人工解释时,专家通常仅解释储层段(即砂岩)的孔隙度,因此需先划分岩性,再根据岩性的识别结果分段预测孔隙度。如图 5a所示,对16口井的测井曲线进行交会分析。根据不同测井曲线对砂岩与泥岩的区分程度,本文选择了GR、SP作为测井岩性敏感属性。

|
图 5 W1~W16井的测井曲线分布与相关性分析 (a)关于岩性的敏感测井曲线分析;(b)储层段(砂岩段)测井曲线与孔隙度的相关性分析 |
根据训练集中的岩性解释结果提取储层段(即砂岩段)的测井曲线。图 5b显示了16口井储层段测井曲线的分布与相关性。基于曲线相关性结果,选择砂岩段的AC和SP作为砂岩孔隙度敏感属性,它们与孔隙度的相关系数分别为0.95和0.42。
在训练和测试过程中,对测井曲线进行标准化,其定义为
| $ X^*=\frac{X-X_{\text {mean }}}{X_{\text {std }}} $ | (12) |
式中:X、X*分别为标准化前、后的测井曲线;Xmean为测井曲线的平均值;Xstd为测井曲线的标准差。本文将测井敏感属性、砂岩孔隙度敏感属性以及砂岩孔隙度进行归一化处理。
2.2 基于半监督高斯混合模型的岩性识别如图 5a所示,虽然岩性敏感属性可以较好地区分砂岩与泥岩,但是两者之间存在重叠部分,需要对归一化后的岩性敏感属性进行高通滤波处理,从而提高敏感属性的岩性区分效果。
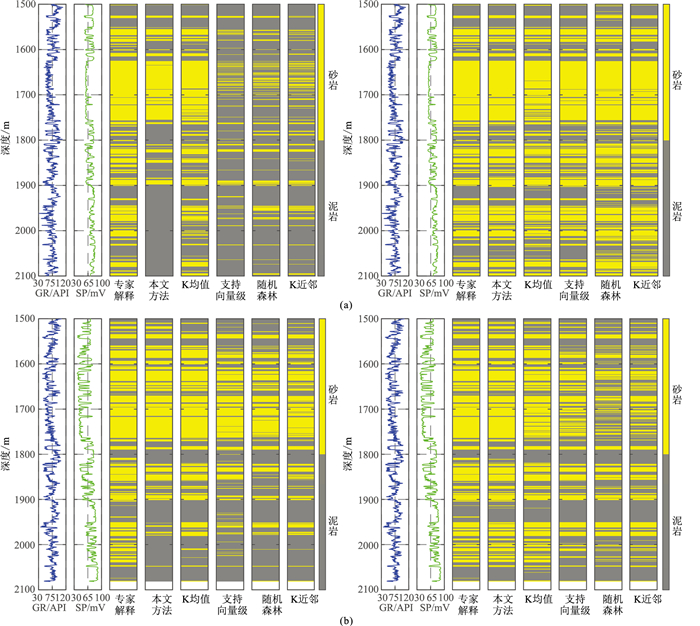
选择W1井的岩性敏感属性与岩性解释结果计算得到带有标签的初始模型,将初始模型与其余测井的岩性敏感属性(W2~W16井)输入半监督高斯混合模型中进行迭代,并使用W17、W18井的岩性敏感属性(滤波处理后)测试模型性能。同时,使用W17井未经滤波处理的岩性敏感属性进行半监督高斯混合模型的岩性识别。然后,将其与常规的机器学习模型(K均值算法、支持向量机、随机森林和K近邻算法)进行对比(图 6)。
|
图 6 W17井(a)、W18井(b)滤波处理前(左)、后(右)的不同方法岩性预测结果对比 |
预测结果的准确率如表 1所示。岩性敏感属性通过高通滤波处理后,岩性识别的准确率有了明显提升,解决了1500~1800 m岩性识别效果较差的问题(图 6)。同时,本文采用的半监督高斯混合模型对岩性的识别准确率均达到了94%以上,高于常规的机器学习模型。
|
|
表 1 W17、W18井不同方法预测结果的准确率对比 |
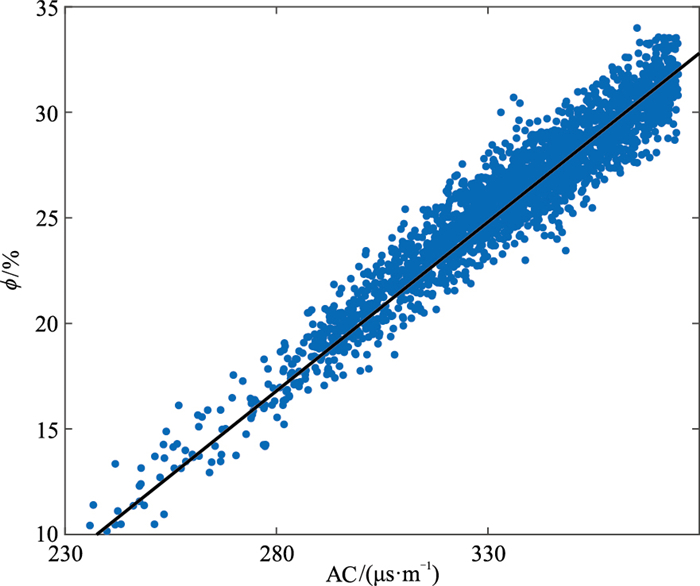
针对砂岩储层,将训练集16口井的砂岩段声波时差与专家解释的真实孔隙度进行交会分析(图 7,黑线表示最小二乘法拟合得到的孔隙度计算模型),可见两者之间具有较好的线性关系。通过最小二乘法建立的孔隙度预测模型为
| $ \phi=\mathrm{AC} \times 0.16-29 $ | (13) |
|
图 7 16口井的砂岩段孔隙度与声波时差的交会分析 |
根据该模型,利用训练集16口井砂岩段的AC可以初步估算砂岩孔隙度。将最小二乘法估算的孔隙度与砂岩孔隙度敏感属性作为多源信息输入梯度提升树,并以砂岩段的真实孔隙度作为标签,建立砂岩孔隙度精确预测模型。
应用相关系数作为预测结果的评价标准,即
| $ r=\frac{\sum\limits_{i=1}^n\left(\phi_{\mathrm{pre}}^{(i)}-\overline{\phi_{\mathrm{pre}}}\right)\left(\phi_{\text {label }}^{(i)}-\overline{\phi_{\text {label }}}\right)}{\sqrt{\sum\limits_{i=1}^n\left(\phi_{\mathrm{pre}}^{(i)}-\overline{\phi_{\mathrm{pre}}}\right)^2} \sqrt{\sum\limits_{i=1}^N\left(\phi_{\text {label }}^{(i)}-\overline{\phi_{\text {label }}}\right)^2}} $ | (14) |
式中:r表示相关系数;n表示数据点的数量;ϕpre(i)、ϕlabel(i)分别表示孔隙度预测值和实际值;
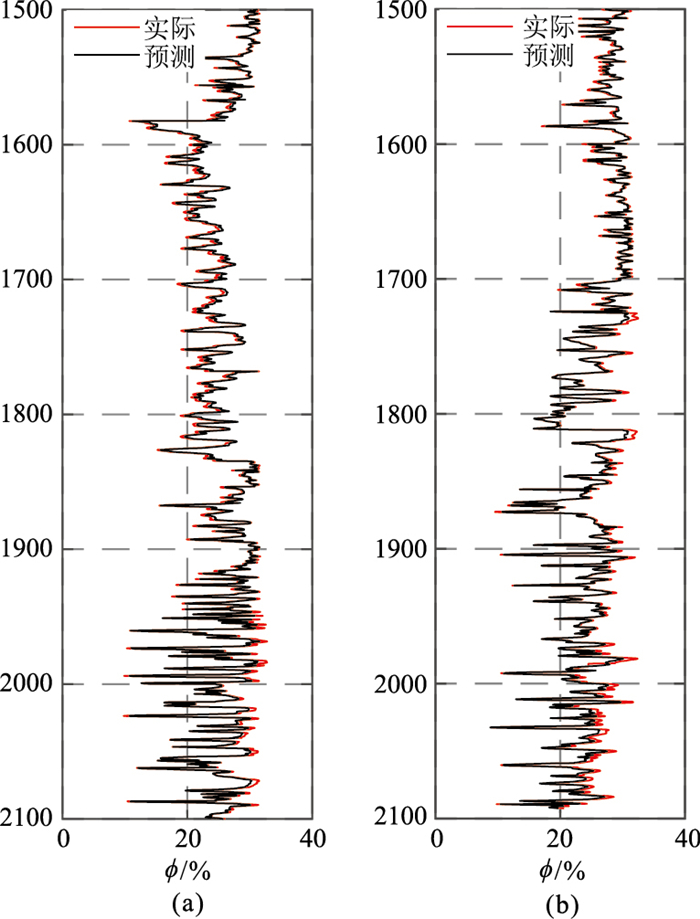
本文方法预测的W17和W18井的砂岩孔隙度与实际结果(图 8)的相关系数均为0.97;而最小二乘法使用式(13)在2口井上估计的砂岩孔隙度与实际结果的相关系数分别为0.95、0.94。由于本文所使用的测井数据中声波时差与砂岩孔隙度的相关系数高达0.95,因此使用最小二乘法和梯度提升树算法预测砂岩孔隙度精度相当。本文将最小二乘法估计的孔隙度、声波时差和井径三种参数(即多源信息)共同作为梯度提升树算法的输入,因此与最小二乘法相比,梯度提升树算法提高了砂岩段孔隙度预测准确率。
|
图 8 W17井(a)、W18井(b)本文方法砂岩孔隙度预测结果与实际结果对比 |
将砂岩的孔隙度预测结果与泥岩的孔隙度进行组合,可得W17、W18井整段的相控孔隙度预测结果(图 9)。W17、W18井本文方法预测的孔隙度与实际结果较吻合,两者相关系数分别为0.77、0.84。虽然砂岩段的孔隙度预测结果精度较高,但是由于岩相控制过程中砂、泥岩划分中存在误差,因此整段相控孔隙度的预测结果与实际结果的相关系数略有下降。

|
图 9 两口井不同方法的预测孔隙度与真实孔隙度的对比 (a)W17井本文方法(左)、不考虑岩性控制而直接应用梯度提升树方法(中)的预测孔隙度、实际孔隙度对比和专家解释岩相(右);(b)W18井本文方法(左)、不考虑岩性控制直接使用梯度提升树(中)的相控孔隙度、实际孔隙度对比和专家解释岩相(右) |
在不考虑岩性控制的情况下,利用训练数据直接使用梯度提升树算法进行模型训练,同样利用W17、W18井2口井进行测试(图 9),预测结果与实际结果的相关系数分别为0.80、0.30。由于W18井的预测结果在1500~1700 m的范围内无法对岩性进行有效划分,导致孔隙度预测结果更偏向于砂岩,因此导致整段预测结果与实际结果的相关系数大大降低。因此,在不考虑岩性控制的情况下,直接利用梯度提升树模型进行拟合会导致预测精度与泛化能力下降。这可能需要深度学习构建更加深层、更加复杂的结构改善这一情况。同时,该结果说明本文提出的基于半监督高斯混合模型与梯度提升树的相控孔隙度预测方法具有更高的准确率和更强的泛化能力。
3 结论本文提出了一种基于半监督高斯混合模型与梯度提升树的测井相控孔隙度预测方法,得出以下结论。
(1) 测井曲线的低频趋势干扰地层岩相的正确划分,经过高通滤波处理消除低频趋势后,不同岩相的测井响应差异更为明显。因此,高通滤波预处理可为半监督高斯混合模型提供更好的分类特征,提升岩相分类的准确率。
(2) 相比于无监督岩相分类算法和有监督岩相分类算法,半监督高斯混合模型能最大化利用有标签数据和无标签数据,引入待测试数据,优化簇类中心位置,从而获得更好的岩相识别效果。
(3) 不同岩相孔隙度的差异将增加智能孔隙度预测模型的建模难度。在考虑相控的情况下,孔隙度预测可简化为岩性分类和砂岩孔隙度预测两个子问题,缓解了孔隙度与测井敏感属性之间非线性关系的复杂度。在岩相识别准确的前提下,相控方法预测的孔隙度与真实结果具有更高的吻合度。
| [1] |
ANGELERI G P, CARPI R. Porosity prediction from seismic data[J]. Geophysical Prospecting, 1982, 30(5): 580-607. DOI:10.1111/j.1365-2478.1982.tb01328.x |
| [2] |
DOYEN P M. Porosity from seismic data: a geostatistical approach[J]. Geophysics, 1988, 53(10): 1263-1275. DOI:10.1190/1.1442404 |
| [3] |
LEITE E P, VIDAL A C. 3D porosity prediction from seismic inversion and neural networks[J]. Computers & Geosciences, 2011, 37(8): 1174-1180. |
| [4] |
韩学辉, 张浩, 毛新军, 等. 基于岩心室应力应变和不确定度分析的致密储层氦孔隙度测量方法[J]. 地球物理学报, 2021, 64(1): 289-297. HAN Xuehui, ZHANG Hao, MAO Xinjun, et al. A method of gas porosity measurement for tight reservoirs based on mechanical analysis of core chamber[J]. Chinese Journal of Geophysics, 2021, 64(1): 289-297. |
| [5] |
邓继新, 王欢, 周浩, 等. 龙马溪组页岩微观结构、地震岩石物理特征与建模[J]. 地球物理学报, 2015, 58(6): 2123-2136. DENG Jixin, WANG Huan, ZHOU Hao, et al. Microtexture, seismic rock physical properties and modeling of Longmaxi Formation shale[J]. Chinese Journal of Geophysics, 2015, 58(6): 2123-2136. |
| [6] |
KHAKSAR A, GRIFFITHS C M. Porosity form so-nic log in gas-bearing shaly sandstones: field data versus empirical equations[J]. Exploration Geophysics, 1998, 29(3-4): 440-446. DOI:10.1071/EG998440 |
| [7] |
未晛, 杨志芳, 晏信飞, 等. 改进型随机斑块饱和模型及其在致密气层检测中的应用[J]. 石油地球物理勘探, 2018, 53(6): 1227-1234. WEI Xian, YANG Zhifang, YAN Xinfei, et al. Modified continuous random patchy-saturation model in tight gas detection[J]. Oil Geophysical Prospecting, 2018, 53(6): 1227-1234. |
| [8] |
LUO Y N, HUANG H D, JAKOBSEN M, et al. Prediction of porosity and gas saturation for deep-buried sandstone reservoirs from seismic data using an improved rock-physics model[J]. Acta Geophysica, 2019, 67(2): 557-575. DOI:10.1007/s11600-019-00274-6 |
| [9] |
LI H B, ZHANG J J. Well log and seismic data analysis for complex pore-structure carbonate reservoir using 3D rock physics templates[J]. Journal of Applied Geophysics, 2018, 151: 175-183. DOI:10.1016/j.jappgeo.2018.02.017 |
| [10] |
WANG P, CHEN X H, LI J Y, et al. Accurate porosity prediction for tight sandstone reservoir: a case study from North China[J]. Geophysics, 2020, 85(2): B35-B47. DOI:10.1190/geo2018-0852.1 |
| [11] |
ARCHIE G E. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Transactions of the AIME, 1942, 146(1): 54-62. DOI:10.2118/942054-G |
| [12] |
牛聪, 张益明, 王迪, 等. LA地区盒8段优质储层的特征与分布预测[J]. 石油地球物理勘探, 2017, 52(3): 591-598. NIU Cong, ZHANG Yiming, WANG Di, et al. Prediction of high-quality reservoir characteristics and distribution in the area LA[J]. Oil Geophysical Prospecting, 2017, 52(3): 591-598. |
| [13] |
AVSETH P, LEHOCKI I, KJØSNES Ø, et al. Data-driven rock physics analysis of North Sea tertiary re-servoir sands[J]. Geophysical Prospecting, 2021, 69(3): 608-621. DOI:10.1111/1365-2478.12986 |
| [14] |
BACHRACH R. Joint estimation of porosity and sa-turation using stochastic rock-physics modeling[J]. Geophysics, 2006, 71(5): O53-O63. DOI:10.1190/1.2235991 |
| [15] |
GRANA D. Probabilistic approach to rock physics modeling[J]. Geophysics, 2014, 79(2): D123-D143. DOI:10.1190/geo2013-0333.1 |
| [16] |
ZHANG Z, ZHANG H, LI J, et al. Permeability and porosity prediction using logging data in a heterogeneous dolomite reservoir: an integrated approach[J]. Journal of Natural Gas Science and Engineering, 2021, 86: 103743. DOI:10.1016/j.jngse.2020.103743 |
| [17] |
YASIN Q, SOHAIL G M, KHALID P, et al. Application of machine learning tool to predict the porosity of clastic depositional system, Indus Basin, Pakistan[J]. Journal of Petroleum Science and Engineering, 2021, 197: 107975. DOI:10.1016/j.petrol.2020.107975 |
| [18] |
YU H, CHEN G X, GU H M. A machine learning methodology for multivariate pore-pressure prediction[J]. Computers & Geosciences, 2020, 143: 104548. |
| [19] |
王光宇, 宋建国, 徐飞, 等. 不平衡样本集随机森林岩性预测方法[J]. 石油地球物理勘探, 2021, 56(4): 679-687. WANG Guangyu, SONG Jianguo, XU Fei, et al. Random forests lithology prediction method for imba-lanced data sets[J]. Oil Geophysical Prospecting, 2021, 56(4): 679-687. |
| [20] |
闫星宇, 顾汉明, 肖逸飞, 等. XGBoost算法在致密砂岩气储层测井解释中的应用[J]. 石油地球物理勘探, 2019, 54(2): 447-455. YAN Xingyu, GU Hanming, XIAO Yifei, et al. XGBoost algorithm applied in the interpretation of tight-sand gas reservoir on well logging data[J]. Oil Geophysical Prospecting, 2019, 54(2): 447-455. |
| [21] |
谷宇峰, 张道勇, 鲍志东. 测井资料PSO-XGBoost渗透率预测[J]. 石油地球物理勘探, 2021, 56(1): 26-37. GU Yufeng, ZHANG Daoyong, BAO Zhidong. Per-meability prediction using PSO-XGBoost based on logging data[J]. Oil Geophysical Prospecting, 2021, 56(1): 26-37. |
| [22] |
CHEN L, LIN W B, CHEN P, et al. Porosity prediction from well logs using back propagation neural network optimized by genetic algorithm in one heterogeneous oil reservoirs of Ordos Basin, China[J]. Journal of Earth Science, 2021, 32(4): 828-838. |
| [23] |
杨柳青, 陈伟, 查蓓. 利用卷积神经网络对储层孔隙度的预测研究与应用[J]. 地球物理学进展, 2019, 34(4): 1548-1555. YANG Liuqing, CHEN Wei, ZHA Bei. Prediction and application of reservoir porosity by convolutional neural network[J]. Progress in Geophysics, 2019, 34(4): 1548-1555. |
| [24] |
杨午阳, 杨佳润, 陈双全, 等. 基于U-Net深度学习网络的地震数据断层检测[J]. 石油地球物理勘探, 2021, 56(4): 688-697. YANG Wuyang, YANG Jiarun, CHEN Shuangquan, et al. Seismic data fault detection based on U-Net deep learning network[J]. Oil Geophysical Prospecting, 2021, 56(4): 688-697. |
| [25] |
CHEN W, YANG L Q, ZHA B, et al. Deep learning reservoir porosity prediction based on multilayer long short-term memory network[J]. Geophysics, 2020, 85(4): WA213-WA225. |
| [26] |
安鹏, 曹丹平, 赵宝银, 等. 基于LSTM循环神经网络的储层物性参数预测方法研究[J]. 地球物理学进展, 2019, 34(5): 1849-1858. AN Peng, CAO Danping, ZHAO Baoyin, et al. Reservoir physical parameters prediction based on LSTM recurrent neural network[J]. Progress in Geophysics, 2019, 34(5): 1849-1858. |
| [27] |
杨怀杰. 测井数据的小波分析方法研究——CCSD主孔数据为例[D]. 北京: 中国地质大学(北京), 2016. YANG Huaijie. Study on Method of Wavelet Transformation in Geophysical Well Log-Evidence from Chinese Continental Scientific Drilling Main Hole[D]. China University of Geosciences(Beijing), Beijing, 2016. |
| [28] |
赵军龙, 刘建建. 常规测井曲线的小波和希尔伯特—黄变换滤波效果分析[J]. 石油地球物理勘探, 2016, 51(4): 801-808. ZHAO Junlong, LIU Jianjian. Conventional well logging data filtering with wavelet transformation and Hilbert-Huang transformation[J]. Oil Geophysical Prospecting, 2016, 51(4): 801-808. |
| [29] |
薛波, 杨青, 张超虹. 基于形态学滤波与小波变换的测井曲线自动分层方法[J]. 地球物理学进展, 2020, 35(1): 203-210. XUE Bo, YANG Qing, ZHANG Chaohong. Automa-tic stratification method of logging curve based on morphological filtering and wavelet transform[J]. Progress in Geophysics, 2020, 35(1): 203-210. |
| [30] |
房文静. 测井多尺度分析方法及应用研究[D]. 山东青岛: 中国石油大学(华东), 2007. FANG Wenjing. Research on Multi-Scale Analysis and Its Application to Well Logging[D]. China University of Petroleum(East China), Qingdao, Shan-dong, 2007. |
| [31] |
NOWAKOWSKA E, KORONACKI J, LIPOVETSKY S. Clusterability assessment for Gaussian mixture mo-dels[J]. Applied Mathematics and Computation, 2015, 256: 591-601. |
| [32] |
DEMPSTER A P, LAIRD N M, RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1977, 39(1): 1-22. |



 袁三一, 北京市昌平区府学路18号中国石油大学(北京)油气资源与探测国家重点实验室,102249。Email:
袁三一, 北京市昌平区府学路18号中国石油大学(北京)油气资源与探测国家重点实验室,102249。Email: