2. 东北石油大学物理与电子工程学院,黑龙江大庆 163318;
3. 东北石油大学人工智能能源研究院,黑龙江大庆 163318
2. School of Physics and Electronic Engineering, Northeast Petroleum University, Daqing, Heilongjiang 163318, China;
3. Institute of Artificial Intelligence Energy Research, Northeast Petroleum University, Daqing, Heilongjiang 163318, China
当今油气资源勘探的重心逐渐向复杂构造、碳酸盐岩和非常规储层等领域转移[1-2],对地下构造成像质量的要求越来越高。在地震勘探中,频带宽度对地震数据十分重要,特别是地震数据低频部分携带信息的可靠度要远大于高频部分。低频成分的质量很大程度上决定了深部地层的成像效果[3-7]。
目前,速度分析、层析成像和全波形反演是利用采集到的地震数据进行物性反演的主要方法。其中全波形反演综合利用地震波场的运动学特征与动力学特征,是目前公认的地震勘探领域精度最高的反演方法[8]。全波形反演是强非线性的,极其依赖初始条件,如初始速度模型和地震数据的低频分量[9-11]。然而在实际地震数据采集过程中,由于大地的滤波作用和人工震源自身局限性,以及检波器畸变等干扰,采集到的地震数据通常损失大量低频成分,使全波形反演结果易陷入局部极小值,极大降低了地震信号处理与解释的精度。
尽管在解决地震数据低频信息缺失问题上,新的低频可控震源取得较大进展,实现可控震源的宽频激发,并采用“两宽一高”地震勘探技术进行地震数据采集、处理,大幅度提高了地震资料品质[12],但由于其施工成本较高而无法作为常规震源。对于大量通过常规震源和技术采集到的地震数据,进行低频恢复主要有两类方法:
(1) 基于模型驱动的方法。可查阅的代表性文献包括:管路平等[13]利用可靠的中间频带对低频部分做自回归预测,通过正向、反向误差和最小原则进行频谱外推[14];Smith等[15]利用连续小波变换拓展地震数据的有效带宽,补偿地震数据低频段;韩立国等[16]基于压缩感知理论建立并求解L1范数约束的稀疏反演问题,实现地震数据的低频补偿;张盼等[17]通过利用被动源地震数据的低频信息重构主动源地震数据的低频缺失部分,实现能量匹配的低频补偿,但被动源噪声干扰严重而难以去除;魏继东[18]利用反褶积方法恢复低频成分,但同时增加了相应(有效频段外)的噪声,降低了数据的信噪比,应用难度较大;丁燕等[2]基于压缩感知理论,通过自适应计算L1范数权重因子并构建改进的俞式低通整形滤波器以补偿地震低频信息;毛博等[19]通过相似性现象结合褶积与反褶积原理重构地震低频数据。此类低频恢复方法的基本原理为利用地震波传播过程物理参数(振幅、频谱)的变化规律进行建模并求解。实际应用时容易出现子波求取困难、噪声干扰严重、参数求解复杂等问题。
(2) 基于数据驱动的方法。目前深度学习的方法在地球物理领域得到快速发展,在岩性识别[20]、断层识别[21]、数据去噪[22]等领域都取得相应研究成果,表明深度学习方法在地球物理应用中具有很强的适应性。Ovcharenko等[23]对随机地下模型的海洋地震勘探进行数值模拟并利用深度卷积神经网络完成中高频—低频的映射,通过波数分析得到单炮二维地震数据比单道一维地震数据低频外推具有更广泛的适用性。Fang等[24]构建了12层的CNN网络,通过输入中高频的二维模拟地震数据预测相应的低频数据,并在反演测试中取得了较好的应用结果;Ovcharenko等[25]利用U-Net神经网络完成二维地震数据从中高频—低频的非线性映射,实现了地震数据的低频恢复。毛博[26]通过搭建卷积神经网络实现单道地震数据的低频拓展,网络的输出与真实地震数据低频分量较接近。Nakayama等[27]在监督学习框架下设计深度卷积神经网络,通过时域进行地震数据低频外推,外推频率与先前存在的频率之间的误差较小。随后,Sun等[28]合成多分量弹性波低频地震数据,设计卷积神经网络并通过扩大卷积获取大的感受野,利用粒子速度的垂直分量和水平分量两个数据集在时域做数据低频外推且获得较好效果。Jin等[29]基于稀疏促进带宽拓展算法提出了低频外推渐进式迁移深度学习算法,具有较高效率和精度,并有较强泛化能力。Zhang等[30]通过将测井数据与地震数据相结合,利用深度卷积神经网络的非线性映射能力将叠后地震数据映射到更宽频带并得到阻抗,取得了较好效果。上述深度学习网络可较好地恢复低频地震数据的时域信息,主要问题在于忽略了地震波传播过程频率与相位等物理参数的变化规律,导致恢复的地震数据低频部分中频率和相位信息的精度不高。
针对该问题,为了提高地震数据低频延拓的精度,本文根据物理模型约束数据驱动的思想,提出改进残差模块的U-Net卷积神经网络,通过地震信号传播过程的物理参数联合约束,在提高信噪比的同时,保持低频地震信号频率、相位信息。
1 方法原理 1.1 应用深度学习恢复地震数据低频成分深度学习的应用领域不断拓展,在地震数据处理方面得到广泛使用。目前应用深度卷积神经网络解决地震数据低频延拓问题的方法过程归纳如下。
1.1.1 样本组织样本集D由输入网络的中高频地震数据x和作为标签的低频地震数据y组成,即D ={ xn, yn}n=1N(N为样本集数量),样本数据集包括三个互斥集合,分别为训练集S、测试集T和验证集V,即D = S∪T∪V且S∩T∩V =∅。
设网络模型为Net,通过监督学习大量中高频地震数据与低频地震数据的非线性映射关系,得到训练好的网络模型。输入中高频地震测试数据,生成预测的低频地震数据
| $ \tilde{\boldsymbol{y}}=\operatorname{Net}(\boldsymbol{x}, \theta) $ | (1) |
式中θ为网络参数。
1.1.2 神经网络拓频原理在有监督学习过程中,神经网络通过训练大量样本数据学习与标签的映射关系,它以S上的平均损失作为经验风险,记为
| $ R_{\mathrm{emp}}(\mathrm{Net})=\frac{1}{N_{\mathrm{s}}} \sum\limits_{i=1}^{N_{\mathrm{s}}} L\left[\operatorname{Net}\left(\boldsymbol{x}_i, \theta\right), \boldsymbol{y}_i\right] $ | (2) |
式中:L为损失函数;Ns为训练集样本数量。神经网络算法以最小化经验风险为目标,通过大量数据为驱动而建立模型。低频延拓的目标是从已知的大量中高频地震数据和低频地震数据中建立非线性映射关系,然后对未知样本进行回归预测。因此,在经验风险最小化的指导下,用于地震数据低频延拓的网络优化目标函数J为
| $ J(\boldsymbol{x}, \theta, \boldsymbol{y})=\underset{\theta}{\arg \min } \sum\limits_i L\left[\operatorname{Net}\left(\boldsymbol{x}_i, \theta\right), \boldsymbol{y}_i\right] $ | (3) |
针对J,直接求取卷积神经网络的最优解相对困难,通常使用梯度下降法利用迭代思想逼近最优解,并将网络参数θt+1表示为
| $ \theta_{t+1}=\theta_t+\mu\left[\nabla \theta_{i=1, 2, \cdots, t} J\left(\boldsymbol{x}, \theta_i, \boldsymbol{y}\right)\right] $ | (4) |
式中:θt为第t次迭代后神经网络参数;μ指更新方向;∇θi=1, 2, …, t为J相对于参数θi的梯度。
1.1.3 损失函数设计神经网络在训练学习期间,用损失函数表征模型预测输出的低频成分与真实的低频成分的拟合程度。常见的损失函数的计算方法有平均绝对值误差(Mean Absolute Error,MAE)和均方误差(Mean Square Error,MSE),分别称为L1 loss和L2 loss,具体定义式分别为
| $ L_{\mathrm{MAE}}(\tilde{\boldsymbol{y}}, \boldsymbol{y})=\frac{1}{b} \sum\limits_{i=1}^b\left|\tilde{\boldsymbol{y}}_i-\boldsymbol{y}_i\right| $ | (5) |
| $ L_{\mathrm{MSE}}(\tilde{\boldsymbol{y}}, \boldsymbol{y})=\frac{1}{b} \sum\limits_{i=1}^b\left(\tilde{\boldsymbol{y}}_i-\boldsymbol{y}_i\right)^2 $ | (6) |
式中:b表示网络batch尺寸大小。损失函数
目前此类纯数据驱动的、利用深度学习模型进行地震数据低频恢复的方法,避免了传统方法假设条件苛刻、求取参数复杂等问题,并且结果具有一定可靠性。但深度学习本质是一个优化问题,求解地震勘探中低频延拓具有多解性,将地震波传输过程中的物理参数变化规律作为约束降低多解性是一个重要方法。
1.2 地震信号物理参数分析全波形反演将地质勘探中的反演问题,转换为以正演模拟数据和观测数据残差的L2范数误差最小的优化问题,属于一个强非线性问题。通过Born近似[31],将地震数据的扰动与地下介质模型参数的扰动线性化。由Born近似可知,全波形反演的误差主要由高阶散射引起,高阶散射场对总场影响越小,Born近似越容易满足。因此,低频波场在Born近似下的误差较小,有利于全波形反演的进行。
地震波是非平稳信号,波形、频率和相位实际上是随时间具有一定的变化规律。这种变化规律反映地震波在地下传播介质的位置、结构和地层岩性等信息[32],且频率和相位信息对精确的反演同样十分重要[33]。在地震勘探逐渐向高精度、高保真发展的情况下,准确地恢复地震数据的波形、频率和相位是一个发展趋势。
傅里叶变换是地震数据频谱分析的主要工具。快速傅里叶变换(Fast Fourier Transform,FFT)是利用计算机实现离散傅里叶变换(Discrete Fourier Transform,DFT)的高效、快速计算方法。设第i道地震数据xi的采样点数为N,采样频率为Fs,其傅里叶变换后展开为复数形式
| $ \begin{gathered} X_i[k]=\sum\limits_{n=0}^{N-1} x_i[n] \mathrm{e}^{-\mathrm{j} \frac{2 {\rm{ \mathsf{ π} }}}{N} k n} \\ k=0, 1, \cdots, N-1 \end{gathered} $ | (7) |
由欧拉定理可得实部和虚部分别为
| $ \operatorname{real}[k] =\sum\limits_{n=0}^{N-1} x_i[n] \cos \left(n \frac{2 {\rm{ \mathsf{ π} }}}{N} k\right) $ | (8) |
| $ \operatorname{imag}[k] =\sum\limits_{n=0}^{N-1}-x_i[n] \sin \left(n \frac{2 {\rm{ \mathsf{ π} }}}{N} k\right) $ | (9) |
那么振幅谱和相位谱计算公式分别为
| $ \begin{aligned} & |f[k]| \\ & \quad=\left\{\begin{array}{lc} \frac{1}{N} \sqrt{\operatorname{real}^2[k]+\operatorname{imag}^2[k]} & k=0 \\ \frac{2}{N} \sqrt{\operatorname{real}^2[k]+\operatorname{imag}^2[k]} & k=1, \cdots, N-1 \end{array}\right. \end{aligned} $ | (10) |
| $ \varphi[k]=\arctan \frac{\operatorname{imag}[k]}{\operatorname{real}[k]} $ | (11) |
式中:|f[k]|为每一道地震数据中不同频率对应波形能量;φ[k]为不同频率对应的相位值。
如针对一维信号
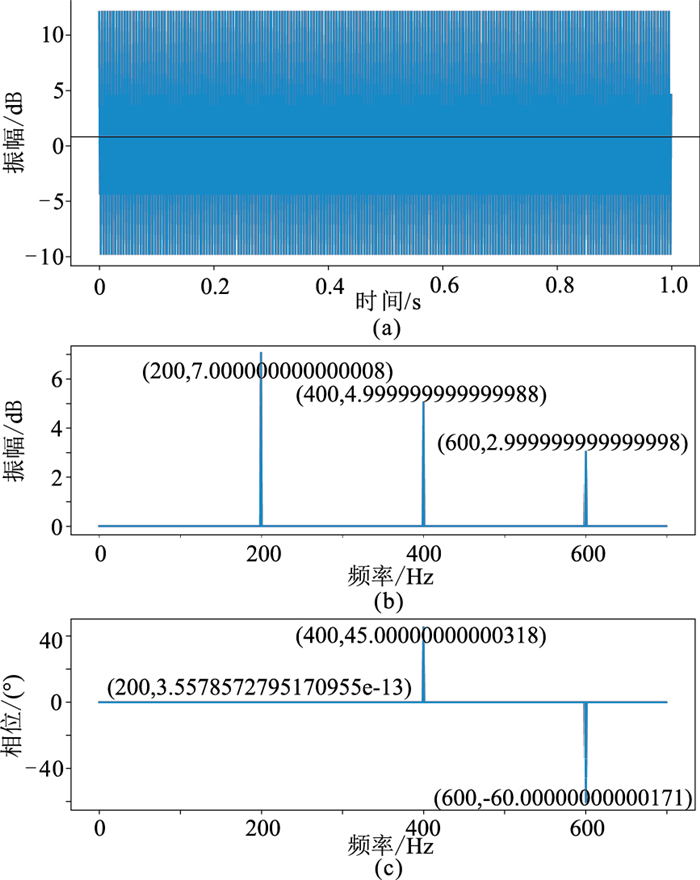
|
图 1 一维信号的波形(a)、振幅谱(b)和相位谱(c) |
由图 1可见:地震信号在时域上的信息仅描述波形能量随时间变化规律;而振幅谱包含主要波形的频率成分信息,更重要的是与信号的相位谱描述一定的频谱成分和波形的运动状态,三者结合可更完备地表征地震信号的信息。
2 基于物理约束的U-Net网络模型地球物理勘探领域的应用场景相对于传统深度学习领域而言,更具有复杂性。考虑地震数据样本的特殊性,有针对性地改进传统通用网络模型可有效提高结果的准确性。
U-Net网络是Ronneberger等[34]在2015年提出的网络结构,最初用于医学图像分割,是一种经典的编—解码器结构,该网络在地震数据超分辨率[35]、地震断层检测[36-37]和地震相识别[38]等应用中具有较好效果。
U-Net网络结构包括三个主要部分:①下采样——网络中前半部分进行4次下采样,每次由两个3×3的卷积层、两个ReLU激活函数及一个最大池化层组成,主要功能是进行特征提取与压缩;②上采样——后半部分进行4次上采样,每次由两个3×3的卷积层、两个ReLU激活函数及一个反卷积操作组成,主要功能是进行数据恢复与重建;③特征融合——U-Net网络在每一次上采样后都会与对应特征提取部分相同尺度的特征图在通道上进行拼接。但浅层网络描述的是结构特征,与上采样部分的高级语义特征具有一定的差别,直接拼接容易影响网络的后续处理效果。
为保持低频信息的主要特征,本文对U-Net网络进行以下改进(图 2):
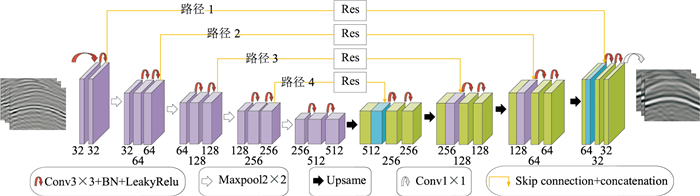
|
图 2 本文改进的U-Net网络模型 |
(1) 通过对称补零操作使卷积前后的数据大小不变,避免特征融合时的裁剪操作,加强对地震数据边缘特征的提取;
(2) 在卷积层与激活函数之间加入批标准化层(Batch Normalization layer,BN),以加快网络收敛速度,减小对初始化参数的依赖,提高网络泛化能力;
(3) 激活函数用来提高神经网络模型的非线性表达能力,考虑到地震数据的类型为实数,而使用ReLU激活函数会使网络中过多的神经元失活(输出为0),因此本文使用LeakyReLU激活函数;
(4) 利用残差模块(图 2中Res部分)缩小下采样与上采样的语义差别,使网络模型能更容易学习低频信息特征。图 3所示残差模块结构由两组卷积、BN和LeakyReLU激活函数构成,以提高网络特征融合的效果,改进传统U-Net的跳跃连接。
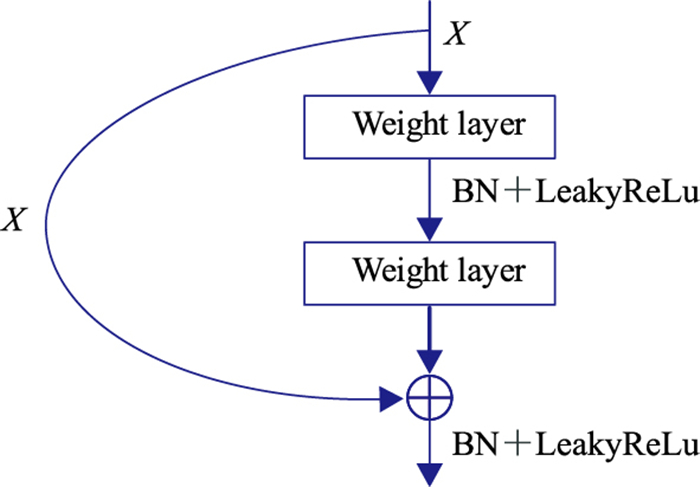
|
图 3 Res残差块结构 |
损失函数是深度神经网络优化目标的学习准则,在一定程度上决定了网络的优化方向与解空间的大小,因此损失函数与实际问题的关联程度非常重要。本文通过设计联合损失函数实现地震波物理参数多维度的约束,进一步提高改进后U-Net网络模型的低频延拓效果。
联合损失函数由时域、频率、相位3个维度的误差组成。其中,时域误差使用L2 loss计算方法,而在频率、相位损失上使用L1 loss计算方法,保证网络能充分学习到地震波传播过程中的3个维度物理参数及其变换规律。基于物理约束的联合损失函数由加权平均的形式定义为
| $ \begin{aligned} L= & \frac{1}{b}\left[\sum\limits_{i=1}^b\left(\tilde{y}_i-y_i\right)^2+\alpha \sum\limits_{i=1}^b\left|f\left(\tilde{y}_i\right)-f\left(y_i\right)\right|+\right. \\ & \left.\beta \sum\limits_{i=1}^b\left|\varphi\left(\tilde{y}_i\right)-\varphi\left(y_i\right)\right|\right] \end{aligned} $ | (12) |
式中:f、φ分别为振幅谱和相位谱算子;α、β分别是振幅谱和相位谱的权重系数。本文整体的网络处理流程如图 4所示。
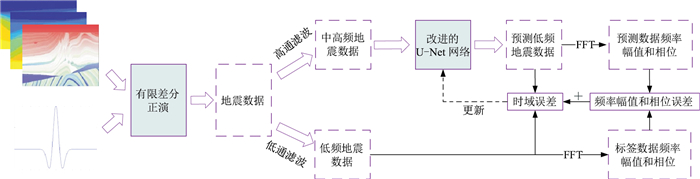
|
图 4 低频延拓整体处理流程图 |
为获得不同特征的地震数据样本,根据理论引导数据科学的思路,利用大量不同特征速度模型,通过有限差分法正演模拟出大量地震数据进行训练测试,以保证输入样本和标签的多样性与准确性。在制作输入样本和标签的过程中,使用8阶巴特沃斯滤波器以6 Hz为截止频率将地震数据划分为低频成分和中高频成分两部分,整体数据处理流程见图 4。数据集D由低频数据和中高频数据构成,即D ={xn, yn}n=1N,N为数据集样本数量,并按照3∶1∶1划分为训练集、测试集和验证集,任取一个数据样本如图 5所示。
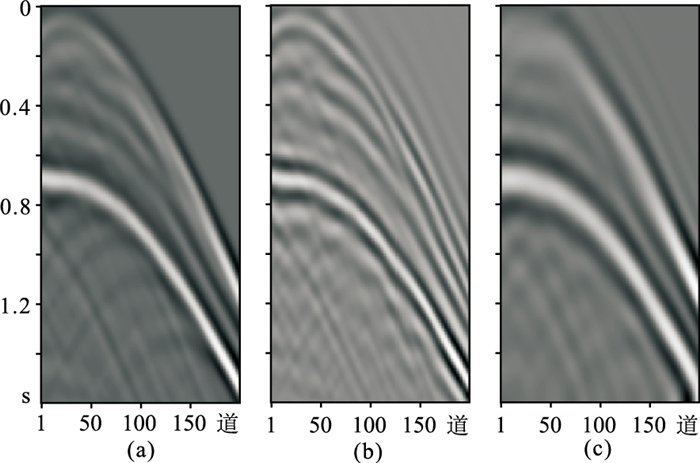
|
图 5 样本数据展示 (a)完整地震数据;(b)中高频成分;(c)低频成分 |
本文基于Pytorch框架搭建网络模型,网络训练采用Adam算法优化目标函数,学习率设置为0.01。迭代次数(Epoch)为300,批大小为8,网络输入输出均为400×200。恢复效果的衡量标准用均方误差MSE和信噪比(Signal to Noise Ratio,SNR)表征,对应表达式为
| $ \mathrm{MSE}=\frac{\sum\limits_{t=1}^M \sum\limits_{s=1}^N\left(\boldsymbol{y}_{t, s}-\tilde{\boldsymbol{y}}_{t, s}\right)^2}{M N} $ | (13) |
| $ \mathrm{SNR}=10 \lg \frac{\sum\limits_{t=1}^M \sum\limits_{s=1}^N\left(\boldsymbol{y}_{t, s}\right)^2}{\sum\limits_{t=1}^M \sum\limits_{s=1}^N\left(\boldsymbol{y}_{t, s}-\tilde{\boldsymbol{y}}_{t, s}\right)^2} $ | (14) |
两式中:M为时间采样总数;N此处为地震道采样总数;yt, s为y中坐标为(t, s)的采样点值。
3.3 物理约束策略与参数设置 3.3.1 约束函数测试本文将物理约束通过损失函数结合到深度学习网络中并对权重参数进行调整,在保证延拓的低频地震数据时域部分具有较好恢复效果的基础上,提高振幅谱和相位谱的效果。而多约束联合损失函数优化在机器学习中属于多任务学习范畴,通过利用相关任务训练特征中包含的特定维度信息(振幅谱和相位谱)改善网络性能及泛化。由于不同约束的损失值对网络的影响不同,对应的数量级很可能存在较大差异,因此将各部分联合损失直接相加的方式可能导致多任务学习过程被某个任务所主导而偏离网络的逼近方向。本文结合多任务学习的思想与实践经验实现地震数据低频延拓联合约束损失函数的权重参数分析与调整。
首先测试地震波物理参数对网络模型的约束效果。将只采用时域约束的模型Ⅰ、联合相位谱约束的模型Ⅱ、联合振幅谱约束的模型Ⅲ及同时联合振幅谱、相位谱约束的模型Ⅳ进行对比测试,各约束的损失函数权重参数均设为1。训练时在时域上初次损失值达到104~105数量级,而在振幅谱和相位谱上初次损失值数量级在102。在训练集上每训练3次在验证集上验证1次,共验证100次。验证集上SNR曲线如图 6所示,可见模型Ⅱ和模型Ⅲ的SNR高于模型Ⅰ,但模型Ⅲ的SNR曲线整体波动幅度较大;而模型Ⅳ的SNR略高于模型Ⅰ,说明加入物理参数约束对模型效果产生一定的影响。具体在时域、振幅谱和相位谱上的MSE指标如表 1所示。

|
图 6 不同模型SNR曲线对比 |
|
|
表 1 不同模型测试结果MSE |
由表 1可见模型Ⅱ、模型Ⅲ在时域、振幅谱、相位谱的MSE均低于模型Ⅰ,且具有较高的SNR,说明网络在低频地震信号恢复处理过程中,结合振幅谱、相位谱约束的引导具有较好效果,但后者约束的有效性高于前者。原因在于,震源激发的地震波在地下介质中传播过程中,在地质界面处发生散射和反射后由检波器接收,振幅谱体现的是不同频率成分的能量,同类地质模型和震源条件下观测得到的地震数据振幅谱分布具有一定的相似性,而相位谱反映信号在空间的状态信息,可更充分表征地下介质的差异。模型Ⅳ在时域和振幅谱的MSE低于模型Ⅰ,高于模型Ⅱ、模型Ⅲ,原因在于多约束条件下结果偏向均衡化,影响低频延拓整体结果,通过进一步研究不同约束权重的合理比例,提高最终效果。
2.3.2 权重比例设置为考察不同权重参数对网络性能的影响,分别进行不同比例实验测试。对于模型Ⅱ,分析各约束损失值的数量级,要保证时域损失为主要loss,因此β值控制在100以内。通过分段评估的方法,相位谱约束权重β分别设置为5、10、20、50、100进行对比,结果如表 2所示,可以看出:
|
|
表 2 模型Ⅱ不同权重时MSE与SNR |
(1) 当β=5、10、20、50时,相位的MSE均低于β=1时,β=10时最小,β=5时时域和振幅谱MSE值最小,但随着权重的增大,时域与振幅谱MSE有升高的趋势,导致SNR降低,其中在β=50时时域和振幅谱MSE值相对较大;
(2) 当β=100时,时域、振幅谱和相位谱的MSE都有增加的趋势,导致SNR相对较低。
为方便展示实验效果,给出β=1、10、100时网络训练过程中后60次验证在时域上的loss值曲线和100次验证在相位上的loss值曲线(未乘β,图 7)。由图 7a可知,当β=1时,时域的loss曲线有小幅波动,当β为10和100时,loss曲线波动较大但后期较为平稳,且当β=10时loss最小;同样图 7b相位谱loss曲线中,β=10时曲线下降最快。由此也说明β过大会影响时域和相位谱的恢复效果,但适当增大可以在保证时域恢复的情况下提高相位谱的恢复效果。

|
图 7 模型Ⅱ不同权重在时域(a)和相位谱(b) 上的验证loss曲线 |
结果表明,合理设定β取值范围(100以内)模型效果优于不联合物理约束情况,地震数据低频延拓效果得到相应提升,再次说明物理约束的有效性。而在调节β取值时发现,当β≤20时相较于不加物理约束,结果在时域、振幅谱和相位谱上的误差均有大幅度减小;虽然和β=1相比,在时域和振幅谱上的误差有上升趋势,但在相位谱上误差有相应的减小,且减小幅度相对较大,使得低频延拓在相位谱恢复上的效果较好。
显然,适当提高β的比例(20以内较为合理)可以强化低频延拓结果在相位谱上的精度,但β的比例过大(50、100)会较大影响时域与振幅谱的效果,甚至对相位谱的恢复会起到反作用。
为进一步分析振幅谱和相位谱联合约束的合理性,在模型Ⅳ的基础上分别对振幅谱约束权重参数与相位谱约束权重参数β,进行不同的配比测试,α∶β=1∶1为初始权重,共设置了13组对比实验,结果如表 3。对比表 3中结果可得出:
|
|
表 3 模型Ⅳ不同权重下MSE与SNR |
(1) 当α<β时,相位谱的MSE比初始权重情况下有所降低,当α∶β=5∶10时降低到最小,且在时域和振幅谱上的MSE低于初始权重。在α∶β为5∶10和20∶50时,时域、振幅谱、相位谱的整体误差低于模型Ⅱ。
(2) 当α≥β,振幅谱与相位谱MSE在α∶β为10∶5和10∶10时,下降相对明显;在α∶β为20∶5、50∶20、80∶50、100∶100情况下,时域、振幅谱、相位谱误差变化较小且有增加的趋势。
分别给出网络训练过程中后60次迭代验证时域loss曲线和100次迭代验证相位谱loss曲线(未乘α、β)如图 8所示。可知当α∶β=5∶10时,在时域和相位谱上均下降最快收敛最好,而α∶β= 100∶100时下降缓慢,时域loss曲线波动较大,说明当权重过大时,网络训练在时域上的收敛性有所下降,拟合效果不理想,最终在时域恢复及SNR上表现较差,同时也影响到了相位谱上loss的收敛效果,导致在相位谱上的MSE值有所上升。

|
图 8 模型Ⅳ不同权重在时域(a)和相位谱(b)上验证loss曲线 |
以上实验表明,加入振幅谱和相位谱的物理约束与无物理约束相比有明显提升,且在调节α∶β的取值时发现,α与β取值50以内时在时域、振幅谱和相位谱上误差均有减小的趋势,但和只有相位谱约束的模型Ⅱ相比部分实验效果接近。当α≤20、β≤50且α<β时,模型预测结果在时域、振幅谱和相位谱上误差降低幅度较明显,SNR相对较高,对地震数据低频延拓效果有大提升。可见,联合振幅谱与相位谱的约束后,通过调节α和β权重参数比例,可达到同时提高地震数据低频延拓结果在时域、振幅谱与相位谱上的效果。综合比较,取α∶β=5∶10相对合理,SNR达到31.807dB,且时域、振幅谱与相位谱综合MSE达到最小。
3.4 U-Net网络改进效果测试 3.4.1 改进残差模块测试为证明改进U-Net残差块的网络结构对低频延拓的有效性,与传统U-Net网络进行性能对比,SNR结果如图 9所示。在模型Ⅰ中使用改进残差跳跃连接整体波动性更小,具有较高的SNR。模型Ⅳ(权重比例为5∶10)下,使用残差跳跃连接后收敛较快,迭代75次后就逐渐趋于平稳且收敛于较高的SNR。
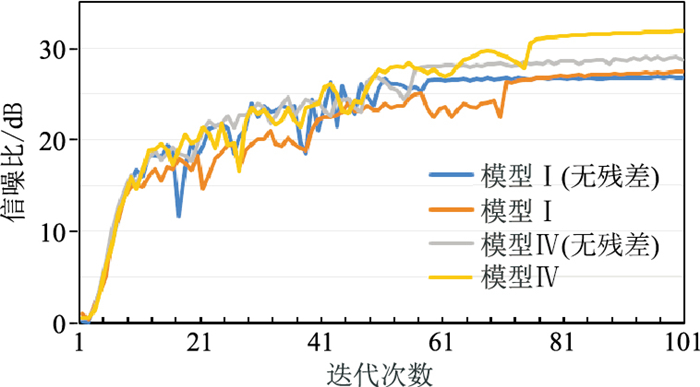
|
图 9 改进残差模块的网络SNR曲线对比 |
为了直观分析数据在提出的网络处理过程中的特征变化,研究网络模型的中间状态,任选1个测试集样本(图 10)在模型Ⅳ(5∶10)第1、3、4次下采样的特征提取阶段和第2、4次上采样的特征恢复中的部分特征图进行可视化输出(图 11)。从图 11a~图 11c中可见,在下采样过程中可以有效提取测试样本的主要特征,且随着网络的加深,提取的特征从浅层的形状纹理信息逐渐抽象。从图 11d~图 11e可见,在上采样过程中,逐步将压缩的样本特征进行映射恢复,恢复的特征随着网络的加深,从抽象特征逐渐恢复出低频信息,最终输出延拓的低频地震数据。输出结果如图 12,可见网络可以较好地从地震数据中高频部分,学习延拓低频成分的非线性逼近关系,并具有较高的恢复精度。
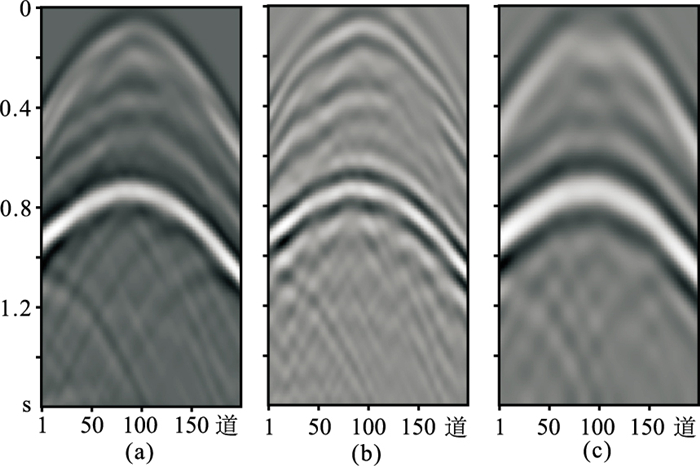
|
图 10 测试数据 (a)完整地震样本数据;(b)中高频成分样本;(c)低频成分样本 |
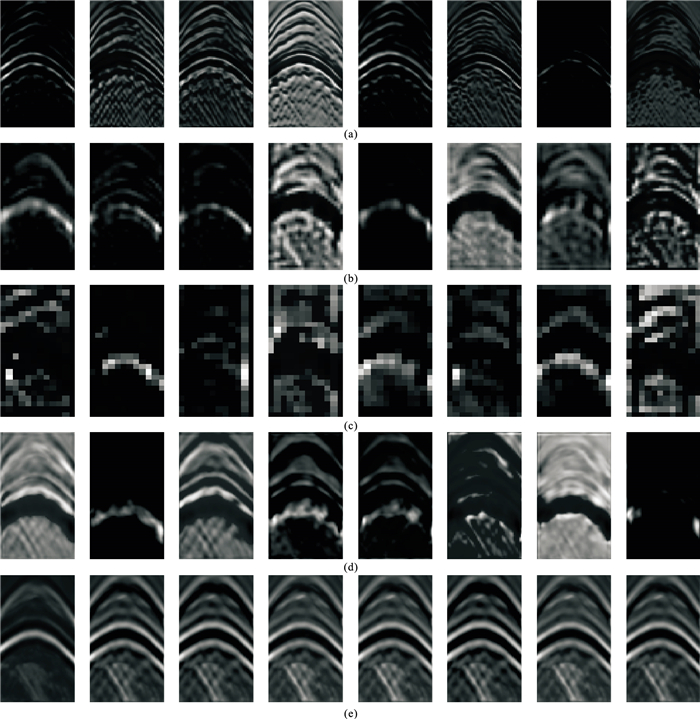
|
图 11 五种采样方式下网络不同层的部分特征 (a)第1次下采样;(b)第3次下采样;(c)第4次下采样;(d)第2次上采样;(e)第4次上采样 |
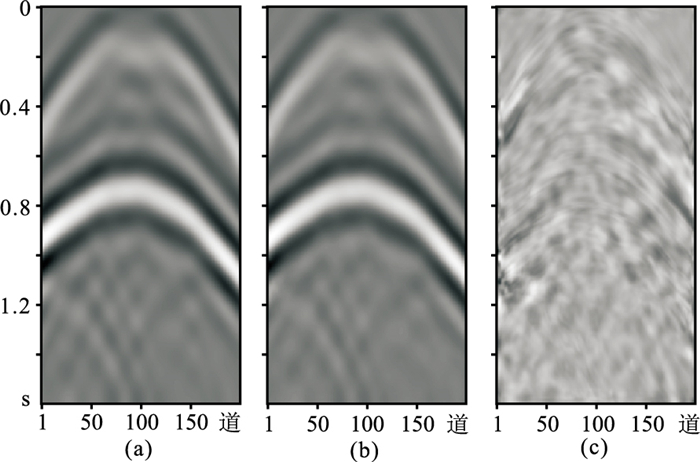
|
图 12 网络测试结果及残差图 (a)测试数据标签;(b)网络输出;(c)残差剖面 |
图 13是第105道地震信号的时域、频率、相位延拓结果(相位谱中由于相位本身计算方式和精度问题导致有效频率外有误差产生),可见本文网络模型恢复地震低频信号过程中,在保持时域与频率恢复效果的同时,具有较高的相位恢复精度。
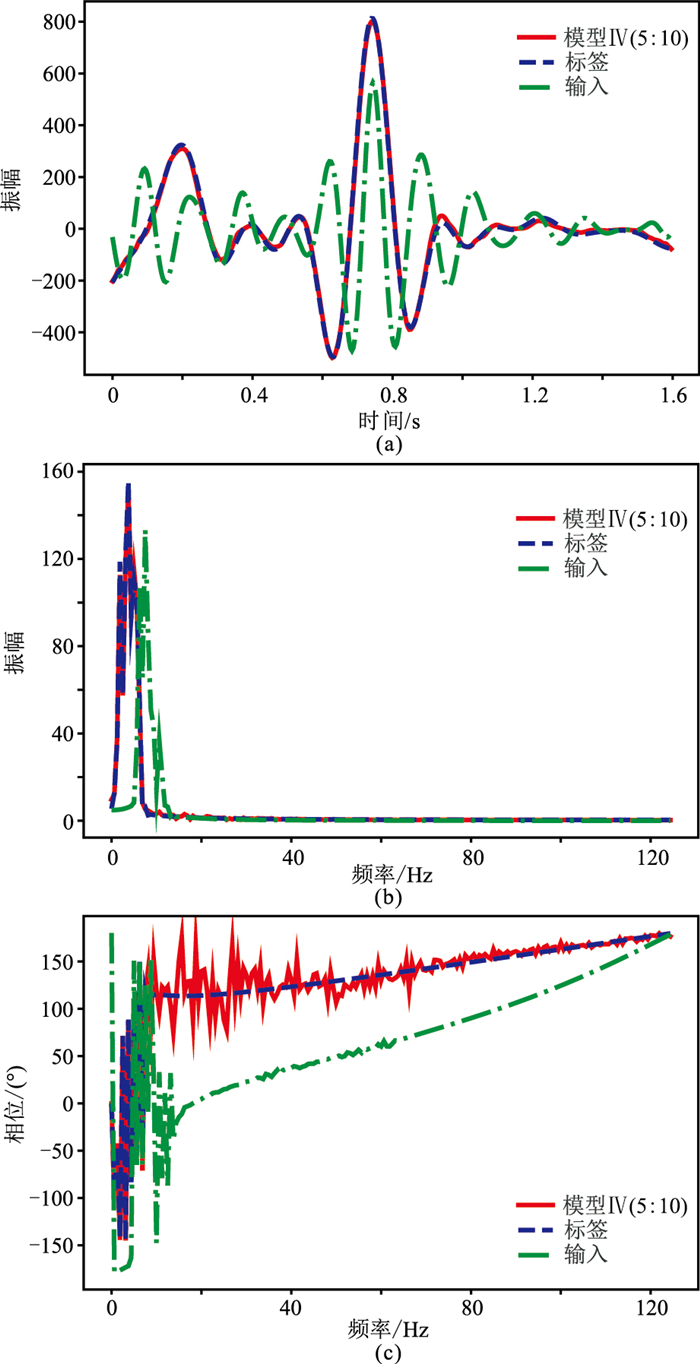
|
图 13 第105道地震数据的时域波形(a)、振幅谱(b)和相位谱(c) |
图 14展示U-Net网络中传统跳跃连接下的特征融合结果和本文所用残差跳跃连接下的特征融合结果。可见相较于U-Net的传统跳跃连接,残差跳跃连接特征融合结果有更完整的特征信息。残差模块的添加改善了下采样特征与上采样特征间的语义差别,使得低频延拓效果有进一步提高。
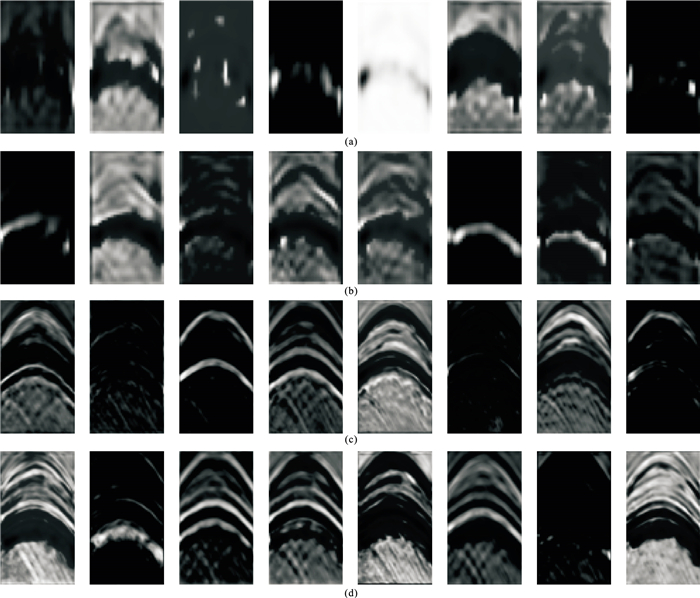
|
图 14 普通跳跃连接(U-Net)与本文使用残差的跳跃连接网络特征融合恢复结果对比 (a)、(c)为普通U-Net网路跳跃连接路径1、路径2特征融合结果;(b)、(d)为本文网络模型残差跳跃连接路径1、路径2特征融合结果 |
现将本文提出的模型Ⅳ(α∶β=5∶10)与当前比较先进的同类算法:原始U-Net网络、VDSR网络、文献[24]的网络模型及文献[26]的低频延拓网络模型的输出效果进行对比。使用相同的数据集训练后,在验证集上MSE结果如表 4,可见本文网络模型在时域、振幅谱、相位谱上的误差均小于其他四个模型。用测试数据(图 10)进行测试,图 15可见VDSR网络的输出结果相对模糊,信息损失严重;文献[24]中网络的输出结果较VDSR有所提升,但细节处仍有较严重的损失;文献[26]中网络模型由于输入、输出的是单道地震数据,因此最后拼接出的二维地震数据有明显竖纹,未考虑地震道间的相关性;U-Net网络输出结果与本文模型Ⅳ(α∶β=5∶10)在时域、振幅谱和相位谱上相对较差。对比时域、振幅谱、相位谱的误差,本文网络模型效果相对较好。抽取第160道地震数据在时域、振幅谱、相位谱上进行对比(图 16),可知在时域、振幅谱恢复上,本文网络模型优于其他方法,且在相位的恢复效果方面具有大幅度提升。
|
|
表 4 各模型MSE结果与SNR值对比 |

|
图 15 不同算法对地震低频数据的恢复效果对比 (a)标签数据;(b)本文模型输出结果;(c)U-Net模型输出结果;(d)VDSR模型输出结果;(e)文献[24]模型输出结果;(f)文献[26]模型输出结果 |
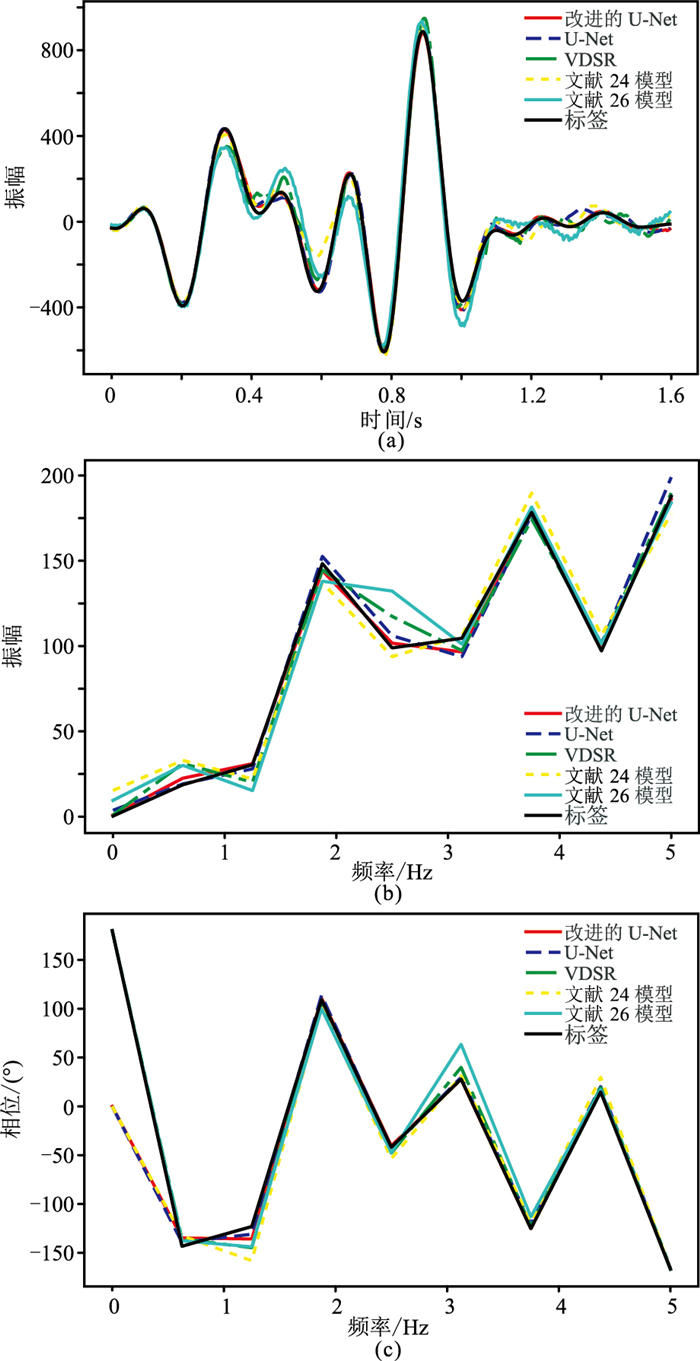
|
图 16 不同模型第160道地震数据的时域波形(a)、频率谱(b)、相位谱(c)效果对比 |
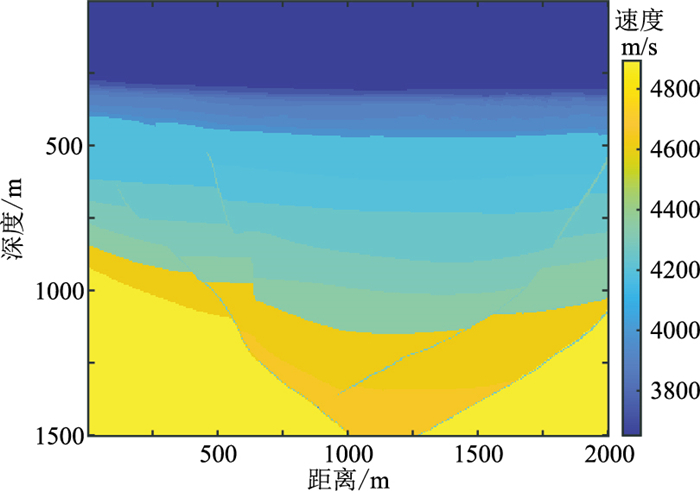
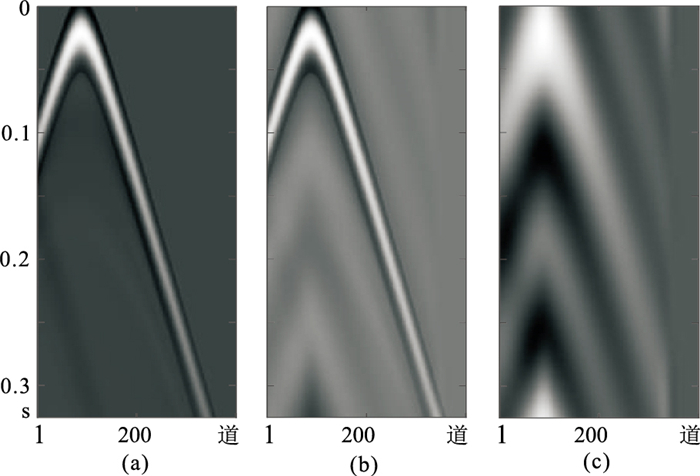
考虑到实际地震样本难以获得,容易导致训练样本特征覆盖不充分的问题。为测试本文模型的应用前景,选取一个深层断裂速度模型(图 17),通过有限差分正演生成地震数据作为测试地震样本,以迁移学习的方法采用本文预训练好的模型参数初始化网络权重,然后利用少量中、高频地震数据和低频地震数据对网络模型进行再训练(图 18),经过微调参数后再对地震数据进行低频延拓。
|
图 17 速度模型 |
|
图 18 迁移学习训练数据 (a)原始生成数据;(b)网络输入中、高频数据;(c)低频成分标签 |
|
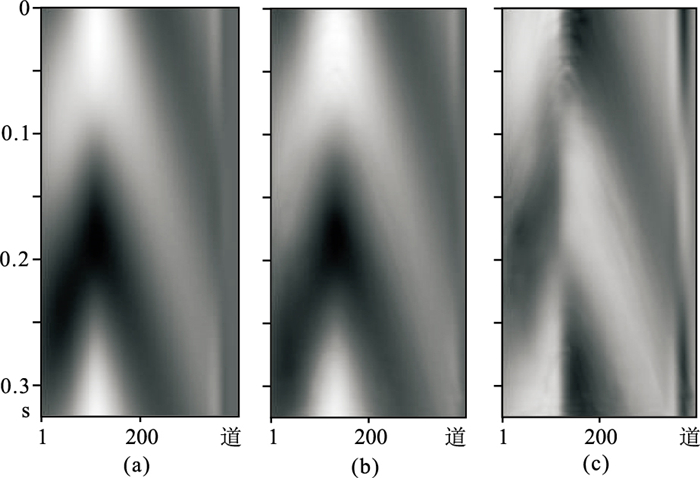
图 19 15 Hz雷克子波生成地震数据测试结果 (a)低频成分标签;(b)网络输出;(c)残差剖面 |
网络模型经再训练精调参数后,样本测试发现网络能较准确地延拓出低频地震数据。另外,对主频为20和30 Hz的雷克子波生成的地震数据进行测试(表 5)。可见模型对不同主频的雷克子波生成的地震数据有较好恢复作用,具有一定泛化能力。
|
|
表 5 不同主频雷克子波下延拓结果MSE |
由表 5可见,使用迁移学习方法可在一定程度上减小因训练数据与实际测试数据的差异,而对本文模型产生的不利影响,且在实际应用中凭借相对少量训练样本和训练时间,就可得到较准确结果。
4 结论本文提出一种基于物理约束的改进U-Net网络进行地震资料低频恢复的方法,得出以下结论:
(1) 联合时域、振幅谱与相位谱信息,可以利用地震波的物理参数约束多维度的恢复效果,考虑到权重比例对网络模型结果的影响,通过大量实验得出较好的权重比例,使网络在联合约束下延拓出的低频地震数据不仅具有较高的时域恢复效果,还能保持频率与相位恢复特征。
(2) 使用残差模块改进U-Net网络的跳跃连接部分,通过中间层分析可见,改进后的网络模型提高下采样与上采样间的语义差别,使网络恢复的特征更丰富,增强恢复效果。
(3) 迁移学习与本文网络模型的结合,使其具有较高的实用性,可以利用少量样本延拓出相对精确的低频地震数据,节省制作样本标签时间和人力成本,实现高效、自动化地震数据低频延拓。
综上所述,本文网络模型具有较好的地震资料低频恢复效果,在提升时域与频率恢复的基础上,着重提升了网络模型在相位方面的恢复效果。
| [1] |
宁宏晓, 唐东磊, 皮红梅, 等. 国内陆上"两宽一高"地震勘探技术及发展[J]. 石油物探, 2019, 58(5): 645-653. NING Hongxiao, TANG Donglei, PI Hongmei, et al. The technology and development of "WBH" seismic exploration in land, China[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 645-653. DOI:10.3969/j.issn.1000-1441.2019.05.002 |
| [2] |
丁燕, 杜启振, 刘力辉, 等. 基于压缩感知和宽带俞式低通整形滤波器的地震低频信息特征分析与补偿[J]. 地球物理学报, 2019, 62(6): 2267-2275. DING Yan, DU Qizhen, LIU Lihui, et al. Feature analysis and compensation of seismic low-frequency based on compressed sensing and broad-band Yu-type low-passing shaping filter[J]. Chinese Journal of Geophysics, 2019, 62(6): 2267-2275. |
| [3] |
TEN KROODE F, BERGLER S, CORSTEN C, et al. Broadband seismic data — The importance of low frequencies[J]. Geophysics, 2013, 78(2): WA3-WA14. DOI:10.1190/geo2012-0294.1 |
| [4] |
张军华, 张在金, 张彬彬, 等. 地震低频信号对关键处理环节的影响分析[J]. 石油地球物理勘探, 2016, 51(1): 54-62. ZHANG Junhua, ZHANG Zaijin, ZHANG Binbin, et al. Low frequency signal influence on key seismic data processing procedures[J]. Oil Geophysical Prospecting, 2016, 51(1): 54-62. DOI:10.13810/j.cnki.issn.1000-7210.2016.01.008 |
| [5] |
孙夕平, 张研, 张永清, 等. 地震拓频技术在薄层油藏开发动态分析中的应用[J]. 石油地球物理勘探, 2010, 45(5): 695-699. SUN Xiping, ZHANG Yan, ZHANG Yongqing, et al. Application of seismic frequency expanding technique in dynamic analysis of thin reservoir development[J]. Oil Geophysical Prospecting, 2010, 45(5): 695-699. |
| [6] |
张彬彬, 张军华, 吴永亭. 地震数据低频信号保护与拓频方法研究[J]. 地球物理学进展, 2019, 34(3): 1139-1144. ZHANG Binbin, ZHANG Junhua, WU Yongting. Research on protection and extension for seismic low frequencies[J]. Progress in Geophysics, 2019, 34(3): 1139-1144. |
| [7] |
ZHANG J H, ZHANG B B, ZHANG Z J, et al. Low-frequency data analysis and expansion[J]. Applied Geophysics, 2015, 12(2): 212-220. DOI:10.1007/s11770-015-0484-2 |
| [8] |
王华忠, 王雄文, 王西文. 地震波反演的基本问题分析[J]. 岩性油气藏, 2012, 24(6): 1-9. WANG Huazhong, WANG Xiongwen, WANG Xiwen. Analysis of the basic problems of seismic wave inversion[J]. Lithologic Reservoirs, 2012, 24(6): 1-9. DOI:10.3969/j.issn.1673-8926.2012.06.002 |
| [9] |
张盼. 基于低频地震波场重构的全波形反演研究[D]. 吉林长春: 吉林大学, 2018. ZHANG Pan. The Study on Full Waveform Inversion based on Low-frequency Seismic Wavefield Reconstruction[D]. Jilin University, Changchun, Jilin, 2018. |
| [10] |
乔凤远, 覃素华, 张宁, 等. 地震低频信息在反演中的作用[J]. 石油地球物理勘探, 2018, 53(增刊2): 266-271. QIAO Fengyuan, QIN Suhua, ZHANG Ning, et al. Low-frequency seismic information applied in inversion[J]. Oil Geophysical Prospecting, 2018, 53(S2): 266-271. |
| [11] |
靳中原, 韩立国, 胡勇, 等. 基于低频信息补偿的数据驱动Marchenko成像[J]. 地球物理学报, 2017, 60(9): 3601-3615. JIN Zhongyuan, HAN Liguo, HU Yong, et al. Low frequency information compensation based data-driven Marchenko imaging[J]. Chinese Journal of Geophy-sics, 2017, 60(9): 3601-3615. |
| [12] |
张丽艳, 李昂, 于常青. 低频可控震源"两宽一高"地震勘探的应用[J]. 石油地球物理勘探, 2017, 52(6): 1236-1245. ZHANG Liyan, LI Ang, YU Changqing. Application of broadband, wide-azimuth, and high-density 3D seismic exploration[J]. Oil Geophysical Prospecting, 2017, 52(6): 1236-1245. |
| [13] |
管路平, 唐权钧. 地震信号的高低频成分补偿[J]. 石油物探, 1990, 29(3): 35-45. GUAN Luping, TANG Quanjun. High/Low frequency compensation of seismic signal[J]. Geophysical Prospecting for Petroleum, 1990, 29(3): 35-45. |
| [14] |
孙成禹. 地震资料的双约束频谱补偿方法[J]. 石油物探, 2000, 39(1): 35-41. SUN Chengyu. Dual constraint frequency spectrum compensation of seismic data[J]. Geophysical Prospecting for Petroleum, 2000, 39(1): 35-41. |
| [15] |
SMITH M, PERRY G, STEIN J, et al. Extending seismic bandwidth using the continuous wavelet transform[J]. First Break, 2008, 26(6): 97-102. |
| [16] |
韩立国, 张莹, 韩利, 等. 基于压缩感知和稀疏反演的地震数据低频补偿[J]. 吉林大学学报(地球科学版), 2012, 42(增刊3): 259-264. HAN Liguo, ZHANG Ying, HAN Li, et al. Compressed sensing and sparse inversion based low-frequency information compensation of seismic data[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(S3): 259-264. |
| [17] |
张盼, 韩立国, 刘强, 等. 主动源与被动源地震数据插值及联合数据成像[J]. 地球物理学报, 2015, 58(5): 1754-1766. ZHANG Pan, HAN Liguo, LIU Qiang, et al. Interpolation of seismic data from active and passive sources and their joint migration imaging[J]. Chinese Journal of Geophysics, 2015, 58(5): 1754-1766. |
| [18] |
魏继东. 检波器反褶积对低频信息的补偿作用[J]. 石油地球物理勘探, 2016, 51(2): 224-231. WEI Jidong. Geophone deconvolution low-frequency compensation for seismic data[J]. Oil Geophysical Prospecting, 2016, 51(2): 224-231. |
| [19] |
毛博, 韩立国. 基于相似性重构低频数据的金属矿频域全波形反演[J]. 地球物理学报, 2019, 62(10): 4010-4019. MAO Bo, HAN Liguo. Full waveform inversion in the frequency domain of low-frequency seismic data based on similarity reconstruction for exploration of deep metallic ores[J]. Chinese Journal of Geophysics, 2019, 62(10): 4010-4019. |
| [20] |
安鹏, 曹丹平. 基于深度学习的测井岩性识别方法研究与应用[J]. 地球物理学进展, 2018, 33(3): 1029-1034. AN Peng, CAO Danping. Research and application of logging lithology identification based on deep learning[J]. Progress in Geophysics, 2018, 33(3): 1029-1034. |
| [21] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [22] |
张岩, 李新月, 王斌, 等. 基于联合深度学习的地震数据随机噪声压制[J]. 石油地球物理勘探, 2021, 56(1): 9-25, 56. ZHANG Yan, LI Xinyue, WANG Bin, et al. Random noise suppression of seismic data based on joint deep learning[J]. Oil Geophysical Prospecting, 2021, 56(1): 9-25, 56. |
| [23] |
OVCHARENKO O, KAZEI V, KALITA M, et al. Deep learning for low-frequency extrapolation from multi-offset seismic data[J]. Geophysics, 2019, 84(6): R989-R1001. |
| [24] |
FANG J W, ZHOU H, LI Y E, et al. Data-driven low-frequency signal recovery using deep learning predictions in full-waveform inversion[J]. Geophysics, 2020, 85(6): A37-A43. |
| [25] |
OVCHARENKO O, KAZEI V, PLOTNITSKIY P, et al. Extrapolating low-frequency prestack land data with deep learning[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 1546-1550.
|
| [26] |
毛博. 基于卷积神经网络的地震数据重构与模型构建研究[D]. 吉林长春: 吉林大学, 2020. MAO Bo. Research on Seismic Data Reconstruction and Model Construction Based on Convolutional Neural Network[D]. Jilin University, Changchun, Jilin, 2020. |
| [27] |
NAKAYAMA S, BLACQUIERE G. Machine-learning-based data recovery and its contribution to seismic acquisition: Simultaneous application of deblending, trace reconstruction, and low-frequency extrapolation[J]. Geophysics, 2021, 86(2): P13-P24. |
| [28] |
SUN H Y, DEMANET L. Deep learning for low frequency extrapolation of multicomponent data in elastic FWI[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-11. |
| [29] |
JIN Y C, HU W Y, WANG S R, et al. Efficient progressive transfer learning for full waveform inversion with extrapolated low-frequency reflection seismic data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-10. |
| [30] |
ZHANG H R, YANG P, LIU Y, et al. Deep learning-based low-frequency extrapolation and impedance inversion of seismic data[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [31] |
WU R S, ZHENG Y C. Non-linear partial derivative and its De Wolf approximation for non-linear seismic inversion[J]. Geophysical Journal International, 2013, 196(3): 1827-1843. |
| [32] |
赵淑红, 朱光明. 相位在地震勘探中的用途及研究[J]. 地球科学与环境学报, 2005, 27(4): 87-89. ZHAO Shuhong, ZHU Guangming. Application and research of phase in seismic prospecting[J]. Journal of Earth Sciences and Environment, 2005, 27(4): 87-89. |
| [33] |
胡勇, 潘冬明, 吴如山, 等. 时频域振幅相位联合的最小二乘逆时偏移[J]. 地球物理学报, 2021, 64(1): 209-223. HU Yong, PAN Dongming, WU Rushan, et al. Joint least square reverse time migration of phase and amplitude in the time-frequency domain[J]. Chinese Journal of Geophysics, 2021, 64(1): 209-223. |
| [34] |
RONNEBERGER O, FISCHER P, BROX T. U-Net: convolutional networks for biomedical image segmentation[C]. Medical Image Computing and Computer Assisted Intervention-MICCAI 2015, Springer, 2015, 234-241.
|
| [35] |
孙永壮, 黄鋆, 俞伟哲, 等. 基于U-Net网络的端到端地震高分辨率处理技术[J]. 地球物理学进展, 2021, 36(3): 1297-1305. SUN Yongzhuang, HUANG Yun, YU Weizhe, et al. End-to-end high-resolution seismic processing method based on U-Net network[J]. Progress in Geophysics, 2021, 36(3): 1297-1305. |
| [36] |
杨午阳, 杨佳润, 陈双全, 等. 基于U-Net深度学习网络的地震数据断层检测[J]. 石油地球物理勘探, 2021, 56(4): 688-697. YANG Wuyang, YANG Jiarun, CHEN Shuangquan, et al. Seismic data fault detection based on U-Net deep learning network[J]. Oil Geophysical Prospecting, 2021, 56(4): 688-697. |
| [37] |
唐杰, 孟涛, 韩盛元, 等. 基于多分辨率U-Net网络的地震数据断层检测方法[J]. 石油地球物理勘探, 2021, 56(3): 436-445. TANG Jie, MENG Tao, HAN Shengyuan, et al. A fault detection method of seismic data based on MultiRes U-Net[J]. Oil Geophysical Prospecting, 2021, 56(3): 436-445. |
| [38] |
张逸伦, 喻志超, 胡天跃, 等. 基于U-Net的井中多道联合微地震震相识别和初至拾取方法[J]. 地球物理学报, 2021, 64(6): 2073-2085. ZHANG Yilun, YU Zhichao, HU Tianyue, et al. Multi-trace joint downhole microseismic phase detection and arrival picking method based on U-Net[J]. Chinese Journal of Geophysics, 2021, 64(6): 2073-2085. |



 董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院,163318。Email:
董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院,163318。Email: