2. 成都理工大学地球勘探与信息技术教育部重点实验室,四川成都 610059
2. Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
在地震勘探中,由于受环境条件的限制,如障碍物、禁区等,采集的地震数据往往是不规则或缺失的。在地震数据处理时,剔除坏道也会造成地震数据的缺失。而原始数据的完整性是后续处理和解释的基础,因此对缺失地震数据进行重建是地震数据处理的关键。现有的地震数据重建方法包括两大类:一是基于固定数据或物理模型的方法,主要包括基于波动方程[1-4],基于预测滤波[5-8]和基于变换域重建[9-12]等;二是利用机器学习和深度学习的人工智能的方法[13-15]。生成对抗网络(GAN)是深度学习方法的一种,也常用于地震数据重建。Oliveira等[16]最先将条件生成网络应用于地震数据重建;Gulrajani等[17]在GAN中应用了梯度惩罚项;Donahue等[18]设计了一种双向GAN。可见GAN在地震数据重建中取得了一定效果。但王静[19]指出普通GAN深度学习模型的输出结果常出现模糊、假频等缺点,该问题在图像重建领域依然存在。主要原因包括[20-21]:①若输入数据缺失较多,卷积结果受到较多0区域的影响,而已知区域对卷积结果的影响较小,从而使卷积值偏离正确结果;②普通卷积模型属于局部操作,卷积结果主要受卷积核覆盖范围内数据的影响,相隔距离较远的数据对其影响不大。为了解决上述问题,Liu等[21]提出了一种部分卷积机制放缩卷积结果,Yu等[20]建立了一种上下文注意力(Contextual attention)机制。
本文在深度学习模型中同时引入部分卷积和注意力机制。所用部分卷积是根据卷积核窗口内的有效信息及其含量进行选择性卷积,并设计了一个比例因子r放缩卷积结果。
常规卷积过程是局部操作,卷积核的感知范围受限于卷积核的大小,卷积结果主要受卷积核覆盖范围内数据的影响。在网络模型中引入注意力机制即是为了弥补此缺点。首先,对于一个前景(待重建)数据特征,先用注意力机制计算它与所有背景数据(待重建数据以外的整体数据)特征的相似度;然后,通过softmax把相似度转换为注意力得分(加权模型),用背景数据特征和注意力得分计算得到平均数据特征;最后,将平均数据特征结果与卷积下采样得到的数据特征进行像素融合,即可弥补常规卷积的上述缺点。
注意力机制在判断前景数据特征和背景数据特征的相似程度时,常用方法包括欧式距离、点积、余弦距离等。由于待重建区域的真实数据的值是未知的,且余弦距离只受角度大小的影响,所以本文选择余弦距离表征相似度。
1 方法原理 1.1 GAN神经网络模型本文所用网络模型是基于GAN,由一个生成网络G和一个判别网络D构成。G通过学习样本,能生成与训练数据相同分布的新数据,而D的目标则是区分真实数据与生成数据。GAN网络模型应用广泛,发展迅速,衍生出很多子网络。本文则是基于深度卷积生成对抗网络(DCGAN)进行改进。
通过DCGAN进行数据修复训练时,常用掩码M作为标记。训练数据Iinput是完整的原始输入数据,M与Iinput的形状、大小相同。M中已知区域标记为1,缺失区域标记为0。Iinput与M同时作为网络的输入,二者进行数乘即可得到缺失数据I。G对缺失数据I′重建并以Iinput为目标样本。D将对重建结果进行判别,并将判别结果反馈给G,两个网络之间相互影响,共同提升网络性能。
GAN的损失函数由G的损失和D的损失两个部分组成。G的总损失由空洞损失、平滑损失和感知损失三者组成。
(1) 空洞损失。表示为
| $ \boldsymbol{L}_{\text {hole }}=\left\|(\boldsymbol{I}-\boldsymbol{M}) \odot\left(\boldsymbol{I}_{\text {out }}-\boldsymbol{I}_{\text {input }}\right)\right\|_1 $ | (1) |
| $ \boldsymbol{L}_{\text {valid }}=\boldsymbol{M} \odot\left(\boldsymbol{I}_{\text {out }}-\boldsymbol{I}_{\text {input }}\right) \|_1 $ | (2) |
式中:Iout为G的输出;Lhole为缺失区域的L1范数损失,表征缺失区域重建结果与目标样本间的差距;Lvalid为已知区域的L1损失,对应已知区域在进入G前与通过G后的差距。
(2) 平滑损失。表达式为
| $ \begin{aligned} \boldsymbol{L}_{\mathrm{tv}}= & \sum\limits_{(i, j) \in p, (i, j+1) \in p}\left\|\boldsymbol{I}_{(i, j+1)}^{\text {out }}-\boldsymbol{I}_{(i, j)}^{\text {out }}\right\|_1+ \\ & \;\; \;\;\sum\limits_{(i, j) \in p, (i, j+1) \in p}\left\|\boldsymbol{I}_{(i+1, j)}^{\text {out }}-\boldsymbol{I}_{(i, j)}^{\text {out }}\right\|_1 \end{aligned} $ | (3) |
式中:p代表数据的一个区域;(i, j)是p区域内一点。平滑损失表示p区域内每一个数据与该数据紧邻的右侧和下侧数据的L1损失之和,用于表征相邻数据在水平和垂直方向的差异。
(3) 感知损失。表达式为
| $ {\mathit{\boldsymbol{L}}_{{\rm{perceptual }}}} = \sum\limits_{i = 1}^N {\frac{1}{{{H_i}{W_i}{C_i}}}} {\left| {\phi _{{\rm{pool }}_i^{}}^{{\rm{input}}{{\rm{ }}_i}} - \phi _{{\rm{pool}}{{\rm{ }}_i}}^{{\rm{out}}{{\rm{ }}_i}}} \right|_1} $ | (4) |
式中:ϕpooli表示VGG-16网络池化层映射的第i个特征;Hi、Wi、Ci分别表示第i个特征的高度、宽度和通道大小。式(4)表征的感知损失对应一个固定网络参数的VGG-16网络[22](图 1)。在感知损失网络的某一层,同时取出生成数据与目标样本的特征向量,将两个特征向量进行对比,以获得更深层次的特征差异。
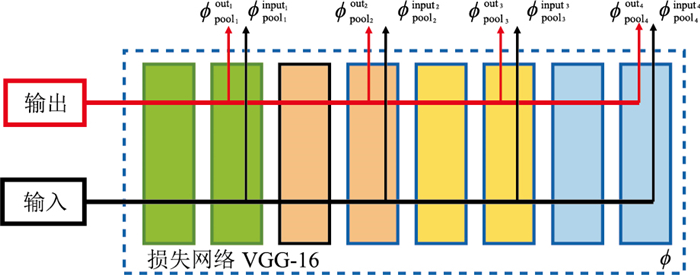
|
图 1 感知损失模型 |
将以上三种损失函数乘以对应的系数后,组合得到G的总损失为
| $ \boldsymbol{L}_G=\lambda_1 \boldsymbol{L}_{\text {hole }}+\lambda_2 \boldsymbol{L}_{\text {valid }}+\lambda_3 \boldsymbol{L}_{\mathrm{tv}}+\lambda_4 \boldsymbol{L}_{\text {perceptual }} $ | (5) |
在实际操作中,可根据不同损失函数的精度和总损失的梯度变化等进行超参数λ的调节。
D中损失函数表示为
| $ \min : \lg \left(1-D_{\boldsymbol{I}_{\text {out }}}\right)^2+\lg D_{{\bf{I}}_{\text {input }}}^2 $ | (6) |
该式为二元交叉熵损失,常用于二分类问题。D对Iinput和Iout进行判别,Iinput作为目标样本,在输入D时会被打上恒定标记1,DIout的结果在0和1之间。
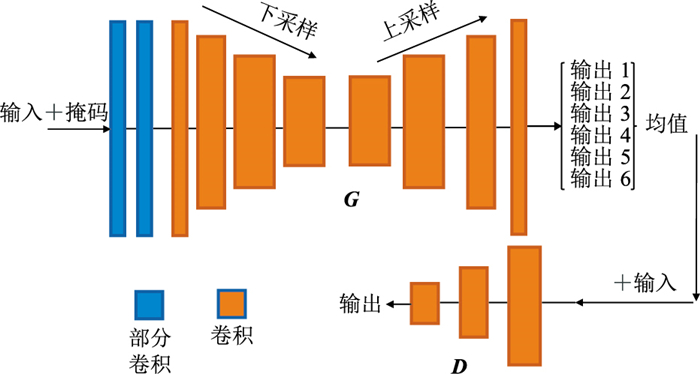
1.2 本文网络模型由于传统的DCGAN网络在数据重建时存在上文所述的缺点,在数据重建方面并不能得到很好的效果。本文对G进行了改进,加入部分卷积和注意力机制提升了网络性能。改进后的生成网络模型G如图 2中的G,网络左端为输入接口,同时输入原始数据与掩码,处理结果从网络的右端输出。下文将详述网络的新模块。
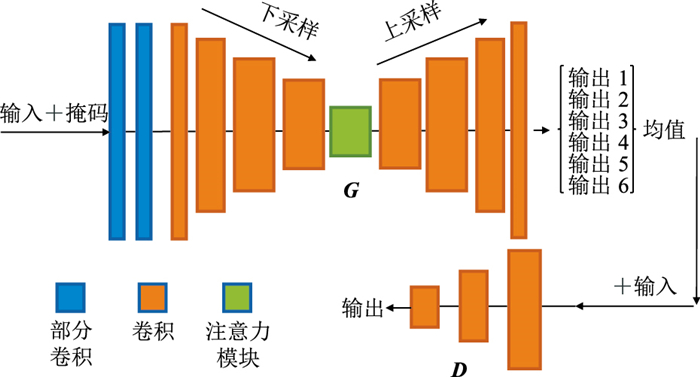
|
图 2 本文网络模型示意图 |
部分卷积(PCONV)是由Liu等[21]提出的一种新的卷积方式,常用于数据修复。部分卷积模块分为数据部分和掩码部分。部分卷积的实现过程(图 3)由下式表示
| $ \boldsymbol{I}_{(i, j)}^{\prime}= \begin{cases}\boldsymbol{W}^{\mathrm{T}}\left(\boldsymbol{I}_{(i, j)} \odot \boldsymbol{M}_{(i, j)}\right) r_{(i, j)} & \left.\| \boldsymbol{M}_{(i, j)}\right) \|_1>0 \\ 0 & \text { 其他 }\end{cases} $ | (7) |
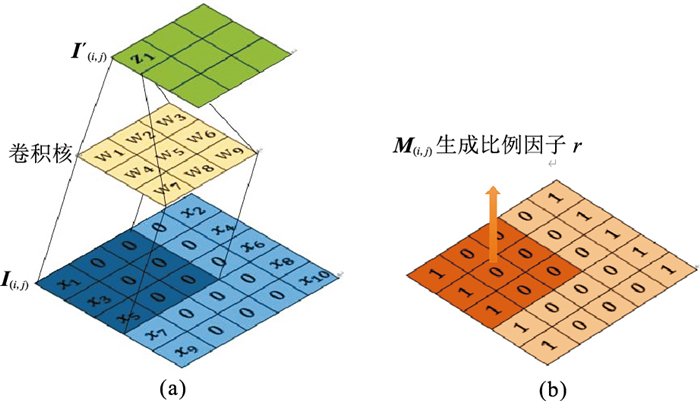
|
图 3 部分卷积示意图 (a)数据部分; (b)掩码部分 |
其中
| $ r_{(i, j)}=\frac{\left\|{\bf{1}}_{(i, j)}\right\|_1}{\left\|\boldsymbol{M}_{(i, j)}\right\|_1} $ | (8) |
当卷积核在输入数据I上滑动做卷积时,(i, j)此时代表卷积核覆盖范围内的中心位置,对应的I(i, j)为卷积核覆盖范围内的输入数据,I′(i, j)为卷积后的输出,M(i, j)对应I(i, j)区域的掩码,掩码内已知区域标记1,缺失区域标记0,1(i, j)代表与M(i, j)大小相同的元素全为1的矩阵。W是卷积计算的参数矩阵。从式(7)可看出,每次卷积计算的结果只受已知元素的影响。同时,根据M(i, j)内已知区域标记1的含量生成比例因子r(式(8)),并通过r调控有效信息的缩放。
每次进行数据部分卷积操作后,数据尺寸和缺失区域范围都会发生变化,为了让M与数据依然保持对应关系,需更新M。更新公式为
| $ m^{\prime}=\left\{\begin{array}{cc} 1 & \left\|\boldsymbol{M}_{(i, j)}\right\|_1>0 \\ 0 & \text { 其他 } \end{array}\right. $ | (9) |
式中m′代表更新后的掩码值。只要M(i, j)有一个元素是已知的,每次部分卷积后的掩码值为1 (图 4)。只要卷积层数足够,通过多次卷积,掩码中代表缺失标记的0会越来越少,最终完全消失。

|
图 4 掩码更新过程示意图 (a)第一次卷积; (b)第二次卷积 |
余弦距离是空间中两点相似度的评价方法,通过将空间中两点映射为向量,并计算向量夹角的余弦值评价相似程度。当余弦值接近1,夹角趋于0°,表明两个向量相似度高;余弦值接近于0,夹角趋于90°,表明两个向量相似度低。本文利用一种基于余弦距离的注意力模型,该模型计算前景数据和背景数据的余弦相似度,并通过softmax将相似度转化为注意力得分(score)。本文注意力机制模块的执行过程如图 5。

|
图 5 注意力模块执行流程 |
输入数据经过下采样后得到n个特征向量,这些特征向量组合定义为F。其中,一个特征向量上(x, y)处的值定义为fx, y,(x′, y′)代表除(x, y)外的任意一点。首先,由下式计算同一个特征向量上任意一点与其余各点之间的余弦相似性
| $ \overbrace{\operatorname{sim}_{x, y ; x^{\prime}, y^{\prime}}}=\left\langle\frac{f_{x, y}}{\left\|f_{x, y}\right\|}, \frac{f_{x^{\prime}, y^{\prime}}}{\left\|f_{x^{\prime}, y^{\prime}}\right\|}\right\rangle $ | (10) |
式中
| $ {\mathop{\rm sim}\nolimits} _{x, y;{x^\prime }, {y^\prime }}^\prime = \frac{{\sum\limits_{i, j \in \{ - k, \cdots , k\} } {\overbrace {{{{\mathop{\rm sim}\nolimits} }_{x + i, y + j, {x^\prime }, {y^\prime }}}}^{}} }}{{k \times k}} $ | (11) |
式中:k代表窗口大小;sim′x, y; x′, y′代表均值滤波处理后(x, y)与(x′, y′)两点间的相似性。
之后,通过softmax函数将点(x, y)的所有相似性结果进行映射,得到同一个向量上其余点位关于点(x, y)的权重系数,即注意力得分,记为score。softmax表达式如下
| $ \operatorname{score}_i=\frac{\mathrm{e}^i}{\sum\limits_j \mathrm{e}^j} $ | (12) |
式中:i为点(x, y)的相似性结果中的一个元素;e为自然常数;scorei为元素i的映射结果。
然而,随着神经网络的迭代,得分并不是固定的。定义经过次迭代后的最终分数为scorei,scorei与scorei-1的关系如下
| $ \operatorname{score}_i=\lambda \operatorname{score}_i^{\prime}+(1-\lambda) \operatorname{score}_{i-1} $ | (13) |
式中:score′i代表第i次迭代过程中通过softmax函数产生的分数;scorei-1为上一轮迭代的最终分数; λ为迭代过程中可学习的参数。
将最终得分score作为加权模型作用于原始的特征向量组合F,从而产生新的特征向量组合
| $ \overset\frown{f_{x, y}}=\sum\limits_{x^{\prime} \in 1, \ldots, w ; y^{\prime} \in 1, \ldots, h} \operatorname{score}_{x, y ; x^{\prime}, y^{\prime}} f_{x^{\prime}, y^{\prime}} $ | (14) |
最后,将新特征向量组合
为了验证本文的网络模型在地震数据重建方面的能力,利用合成数据及实际数据进行验证,并与DCGAN网络模型对比。此外,为了探究部分卷积模块和注意力模块对网络模型数据重建能力影响的差异,还分别设计了DCGAN网络只与部分卷积模块结合的GAN+PCONV模型(图 6),以及DCGAN网络只与注意力模块结合的GAN+attention模型(图 7)。
|
图 6 GAN+PCONV模型 |
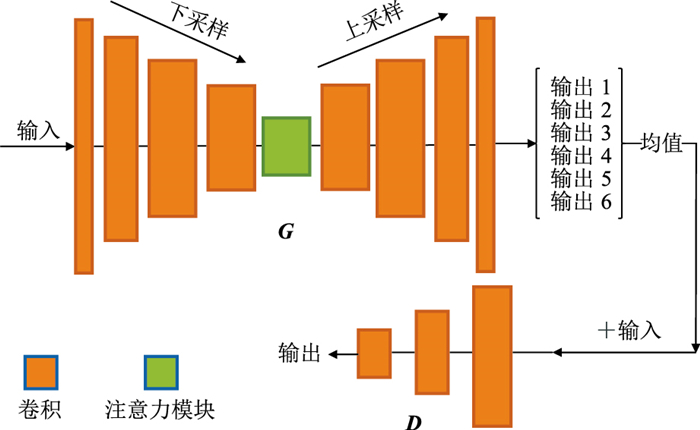
|
图 7 GAN+attention模型 |
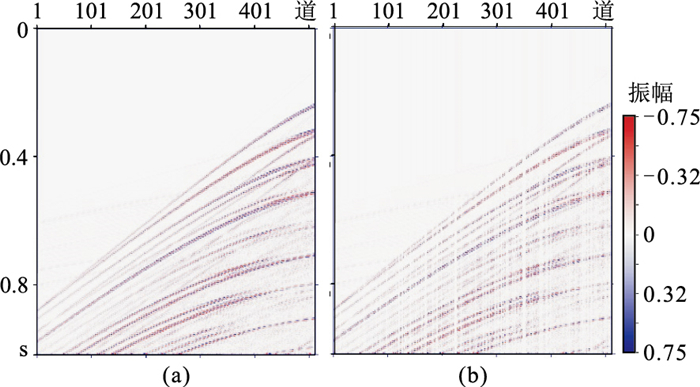
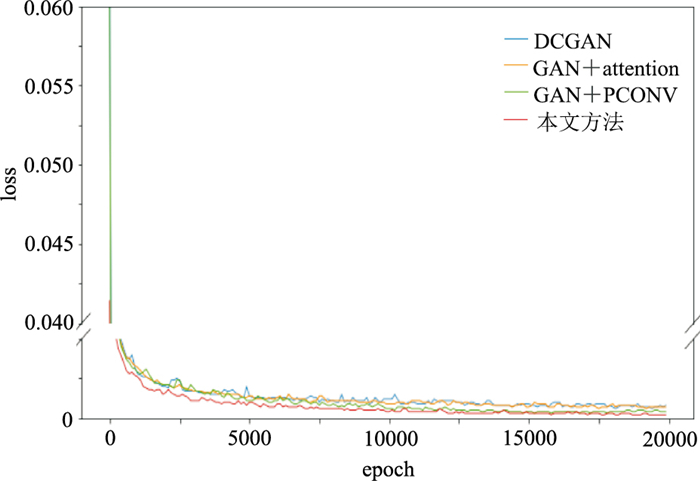
合成数据实验采样自SEG BP94模型,道间距为25 m,采样率为4 ms。合成数据切分为20000个训练切片、200个验证切片、200个测试切片,各切片尺寸均为512×256。为了使合成数据更贴近真实数据,切片载入网络模型时,会被赋予大小为0~10的噪声方差,同时被随机抹去30%~50%的地震道。前文所述网络模型经20000次训练,G的损失变化(loss)如图 8所示。在20000次训练过程中,GAN+attention、GAN+PCONV和本文方法的损失值均比DCGAN的低,其中本文方法获得的损失值最低。图 9a是测试集一中的切片,展示不同网络模型重建效果。

|
图 8 不同网络模型生成网络G的损失曲线 |
|
图 9 测试集一的切片(a)及随机缺失50%(b) |
四种不同模型的数据实验结果如图 10所示。DCGAN网络重建结果如图 10a,其SNR为9.31 dB。重建结果中存在大量的假频,缺失区域并未完全有效地恢复,同相轴连续性较差且模糊,在对应的差值剖面(图 10e)中可见残留有大量的有效信息。GAN+PCONV网络重建结果(图 10b)的SNR为20.51 dB,其同相轴清晰,且假频已经显著减少,其差值剖面图(图 10f)中残留信息较少。GAN+attention网络重建结果(图 10c)的SNR为16.51 dB,重建结果中存在一些假频,其同相轴清晰度和细节表现相较于DCGAN的重建结果有了提升,但差值剖面(图 10g)中残留有大量有效信息。本文方法的重建结果如图 10d,其SNR为23.01 dB,重建结果中的假频显著小于前三者,恢复的细节也优于前三者,在差值剖面中(图 10h)只有少量信息残留。进一步观察四种重建结果的f-k谱(图 11)得知:DCGAN的重建结果(图 11a)中低频区域存在假频;GAN+attention的重建结果(图 11c)中低频区域的假频减少,但在背景上又出现了新的假频;GAN+PCONV的重建结果(图 11b)较好,低频区域的假频减少,没有出现新的假频;本文方法重建结果的f-k谱(图 11d)最清晰,假频最少,说明重建结果最优。该实验说明部分卷积模块和注意力模块均可提升网络重建能力,且部分卷积模块比注意力模块的提升效果更明显。将这两种模块同时融合到网络模型中也能大幅提升重建能力。
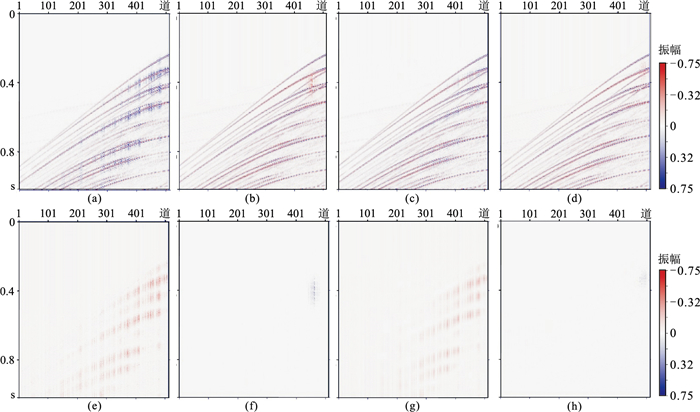
|
图 10 不同方法合成数据重建结果及对应差值 (a)DCGAN重建结果;(b)GAN+PCONV重建结果;(c)GAN+attention重建结果;(d)本文方法重建结果;(e)DCGAN重建差值;(f)GAN+PCONV重建差值;(g)GAN+attention重建差值;(h)本文方法重建差值 |

|
图 11 合成数据四种模型方法重建结果及原始数据的f-k谱 (a)DCGAN;(b)GAN+PCONV;(c)GAN+attention;(d)本文方法;(e)原始数据 |
|
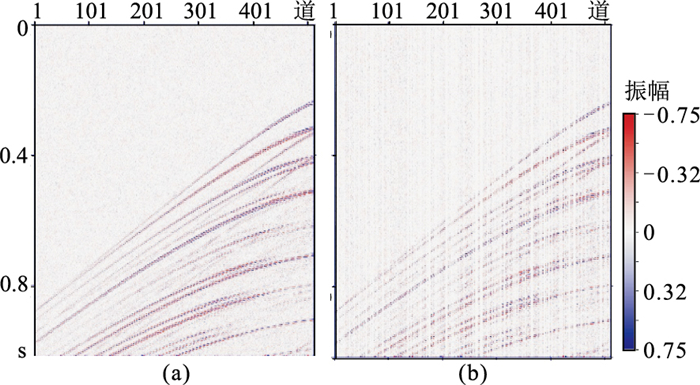
图 12 测试集一的加噪切片(a)及随机缺失50%(b) |
为验证网络在切片含噪情况下的数据重建效果,将测试集随机加噪。加噪后的重建测试结果如图 13。DCGAN的重建结果中(图 13a)存在大量的假频和噪声,细节信息几乎没有得到恢复,重建结果的SNR为7.1 dB,其对应的差值剖面(图 13e)中残留有大量有效信息。GAN+attention网络的重建结果(图 13c)的SNR为9.3 dB,重建结果在细节信息上相较于DCGAN有一定的提升,但仍有大量假频和噪声存在,其差值剖面(图 13g)中也有大量有效信息残留。GAN+PCONV模型提升明显(图 13b),重建结果的SNR为12.3 dB,假频和噪声已经大量减少,同相轴清晰,差值剖面(图 13f)上仍有部分有效信息残留。本文方法相比于GAN+PCONV模型有进一步提升,重建结果的SNR为18.1 dB,重建结果中存在少量聚集的假频,但细节信息比GAN+PCONV丰富。
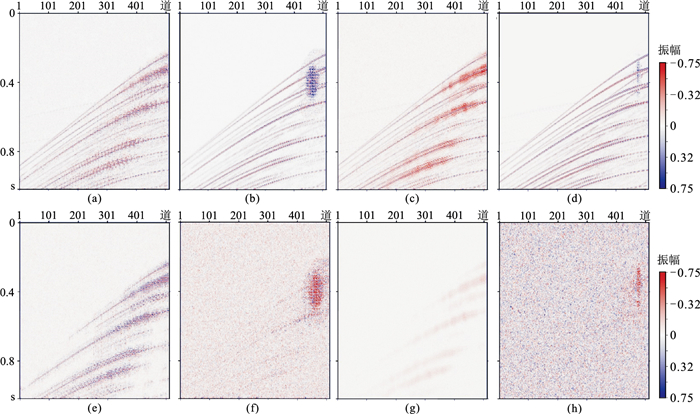
|
图 13 含噪合成数据重建结果 (a)DCGAN重建结果;(b)GAN+PCONV重建结果;(c)GAN+attention重建结果;(d)本文方法重建结果;(e)DCGAN重建差值;(f)GAN+PCONV重建差值;(g)GAN+attention重建差值;(h)本文方法重建差值 |
四种方法重建结果的f-k谱如图 14。可见DCGAN重建结果(图 14a)的高频和背景区域中存在假频,GAN+attention重建结果(图 14c)的高频和背景区域的假频减少,但在低频区生成了新假频。GAN+ PCONV重建结果(图 14b)的高频和背景区域的假频大量减少,低频区域有部分假频。本文方法重建结果(图 14d)中假频明显小于GAN+PCONV。
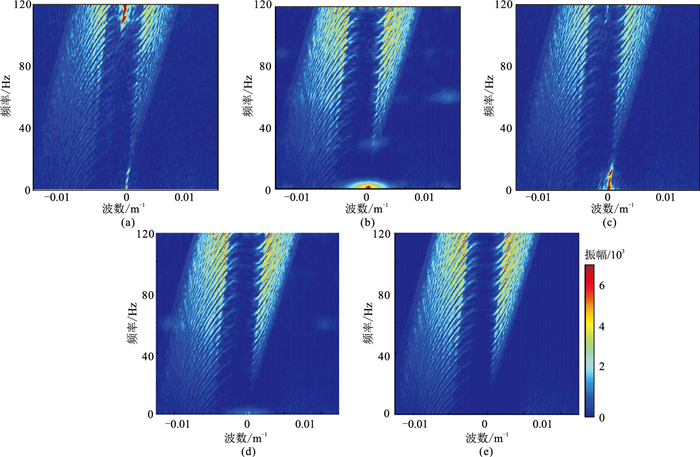
|
图 14 含噪合成数据四种模型重建结果及原始数据的f-k谱 (a)DCGAN;(b)GAN+PCONV;(c)GAN+attention;(d)本文方法;(e)原始数据 |
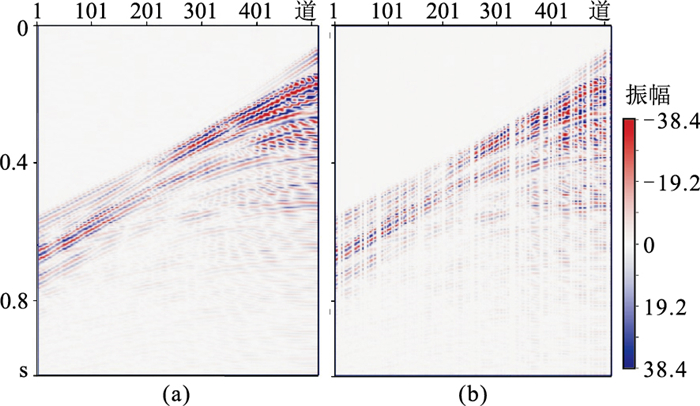
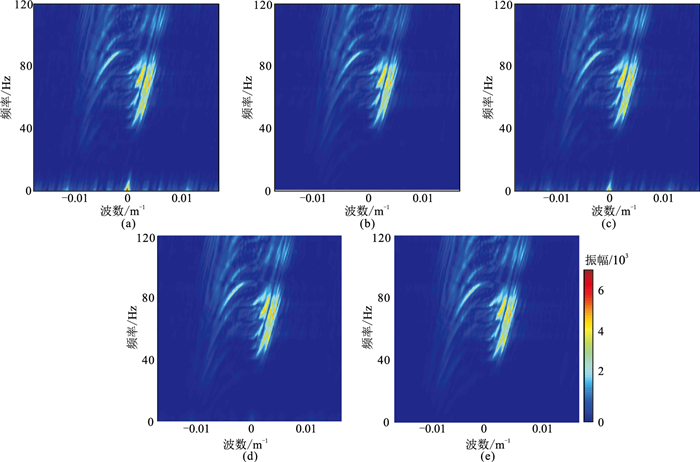
为了说明方法的实用性,利用M地区的实际地震资料进行测试。实际地震数据共3280000道,其道间距为50 m,采样率为4 ms。将其分割为6400个大小为512×256的切片。其中训练集6000个,验证集200个。采用相邻区块的地震数据制成200个测试集。将上文的四种模型在相同的训练集下进行相同次数的训练。训练过程的生成网络G的损失变化(loss)如图 15。可见GAN+PCONV和本文方法的损失值均比DCGAN低,但GAN+attention的损失值降低不明显。图 16a为测试集二的切片,四种不同模型的数据实验结果如图 17所示。DCGAN网络重建结果(图 17a)的SNR为11.3 dB,其同相轴较模糊,且有假频存在,在差值剖面(图 17e)中可见大量有效信息残留。GAN+attention网络重建结果(图 17c)的SNR为12.3 dB,其同相轴的清晰程度较DCGAN重建结果有一定提升,但差值剖面(图 17g)中仍有有效信息残留。GAN+PCONV网络重建结果(图 17b)的SNR为19.1 dB,其同相轴清晰程度大幅提升,假频减少,同时差值剖面(图 17f)中的有效信息已经大量减少。本文方法的重建结果(图 17d)的SNR为20.6 dB,其同相轴清晰程度进一步提升,重建结果的细节恢复效果优于前三者,差值剖面(图 13h)中也只有少量信息残留。观察四种重建结果的f-k谱(图 18)可见:DCGAN(图 18a)和GAN+attention(图 18c)重建结果中的低频区域存在假频;GAN+PCONV重建结果(图 18b)中,低频区域的假频大量减少但背景上仍存在假频;本文方法重建结果中假频最少(图 18d)。实际数据实验也表明,部分卷积模块和注意力模块均可提升网络重建能力,且部分卷积模块比注意力模块提升效果更明显。将这两种模块同时融合到网络模型中也能大幅提升重建能力。
|
图 15 不同网络模型的G损失曲线 |
|
图 16 测试集二的切片(a)及随机缺失50%(b) |

|
图 17 实际数据测试 (a)DCGAN重建结果;(b)GAN+PCONV重建结果;(c)GAN+attention重建结果;(d)本文方法重建结果;(e)DCGAN重建差值;(f)GAN+PCONV重建差值;(g)GAN+attention重建差值;(h)本文方法重建差值 |
|
图 18 实际数据四种模型方法重建结果及原始数据的f-k谱 (a)DCGAN;(b)GAN+PCONV;(c)GAN+attention;(d)本文方法;(e)原始数据 |
普通DCGAN神经网络存在缺陷,其重建结果中存在模糊、假频等缺点。本文针对这些缺陷及其产生的原因,重新设计了DCGAN网络,提出了一种融合部分卷积和注意力机制的对抗网络模型地震数据重建方法。部分卷积根据卷积核内的有效数据量生成比例因子r,并通过比例因子r放缩卷积结果。除此以外,本文使用注意力机制利用背景信息计算出一个平均数据特征,并将该平均数据特征与卷积结果融合,从而使更多的信息能影响卷积结果。
本文的处理结果表明,部分卷积模块和注意力机制均能提高对抗网络模型性能,减少重建过程中模块的模糊、假频,且部分卷积模块比注意力模块提升效果更明显。将这两种机制同时融合到对抗网络模型中也能大幅提升网络性能。
另外,本文的训练模型在含噪较多的数据上依然会出现假频,后续研究将聚焦本文模型针对含噪较多的数据的重建能力。
| [1] |
NAHIZADEH M, SACCHI M D. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data[J]. Geophysics, 2010, 75(6): W189-W202. DOI:10.1190/1.3509468 |
| [2] |
SPAGNOLINI U, OPRENI S. 3-D shot continuation operator[C]. SEG Technical Program Expanded Abstracts, 1996, 15: 439-442.
|
| [3] |
DEREGOWSKI S M. What is DMO?[J]. Fist Break, 1986, 4(7): 7-24. |
| [4] |
FOMEL S. Seismic reflection data interpolation with differential offset and shot continuation[J]. Geophy-sics, 2003, 68(2): 733-744. |
| [5] |
张军华, 仝兆岐, 何潮观, 等. 在f-k域实现三维波场道内插[J]. 石油地球物理勘探, 2003, 38(1): 27-30. ZHANG Junhua, TONG Zhaoqi, HE Chaoguan, et al. 3-D seismic trace interpolation in f-k domain[J]. Oil Geophysical Prospecting, 2003, 38(1): 27-30. DOI:10.3321/j.issn:1000-7210.2003.01.006 |
| [6] |
SPITZ S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [7] |
LU L. Application of local slant-stack to trace interpolation[C]. SEG Technical Program Expanded Abstracts, 1985, 4: 560-562.
|
| [8] |
国九英, 周兴元, 俞寿朋. F-X域等道距道内插[J]. 石油地球物理勘探, 1996, 31(1): 28-34. GUO Jiuying, ZHOU Xingyuan, YU Shoupeng. Iso-interval trace interpolation in F-X domain[J]. Oil Geophysical Prospecting, 1996, 31(1): 28-34. |
| [9] |
TRAD D, ULRCH T J, SACCHI M D. Latest views of the sparse Radon transform[J]. Geophysics, 2003, 68(1): 386-399. DOI:10.1190/1.1543224 |
| [10] |
ZWARTJES P and GISOLF A. Fourier reconstruction with sparse inversion[J]. Geophysical Prospecting, 2007, 55(2): 199-221. |
| [11] |
CANDÈS E J, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [12] |
DONOHO D L. Compressed sensing[J]. IEEE Tran-sactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [13] |
JIA Y N, MA J W. What can machine learning do for seismic data processing? An interpolation application[J]. Geophysics, 2017, 82(3): V163-V177. DOI:10.1190/geo2016-0300.1 |
| [14] |
WANG B F, ZHANG N, LU W K, et al. Deep-learning-based seismic data interpolation: A preliminary result[J]. Geophysics, 2019, 84(1): V11-V20. |
| [15] |
杨冠雨, 王璐, 孟凡顺. 基于深度卷积神经网络的地震数据重建[J]. 地球物理学进展, 2020, 35(4): 1497-1506. YANG Guanyu, WANG Lu, MENG Fanshun. Seismic data reconstruction via deep convolution neural network[J]. Progress in Geophysics, 2020, 35(4): 1497-1506. |
| [16] |
OLIVEIRA D A B, FERREIRA R S, SILVA R, et al. Interpolating seismic data with conditional generative adversarial networks[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(12): 1952-1956. |
| [17] |
GULRAJANI I, AHMED F, ARJOVSKY M, et al. Improved training of wasserstein GANs[C]. Procee-dings of the 31st International Conference on Neural Information Processing Systems, 2017, 5769-5779.
|
| [18] |
DONAHUE J, KRÄHENBÜHL P, DARRELL T. Adversarial feature learning[C]. 5th International Conference on Learning Representations, ICLR 2017, 2017, 1-18.
|
| [19] |
王静. 基于生成对抗网络的地震数据差值[D]. 黑龙江哈尔滨: 哈尔滨工业大学, 2019.
|
| [20] |
YU J H, LIN Z, YANG J M, et al. Generative image inpainting with contextual attention[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2018, 5505-5514.
|
| [21] |
LIU G L, REDA F A, SHIH K J, et al. Image inpain-ting for irregular holes using partial convolutions[C]. Computer Vision — ECCV(European Conference on Computer Vision) 2018, 2018, 85-100.
|
| [22] |
JOHNSON J, ALAHI A, LI F F. Perceptual losses for real-time style transfer and super-resolution[C]. Computer Vision — ECCV(European Conference on Computer Vision) 2016, 2016, 694-711.
|



 陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室,610059。Email:
陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室,610059。Email: