2. 长江大学油气资源与勘探技术教育部重点实验室,湖北武汉 430100
2. Key Laboratory of Exploration Technologies for Oil and Gas Resources, Ministry of Education, Yangtze University, Wuhan, Hubei 430100, China
含水饱和度是煤的一个重要物性参数,对煤层气渗流、瓦斯解吸、预测指标凸显等有较大影响,常被作为煤矿瓦斯灾害治理和预防、瓦斯抽采等工作的重要指标,对于煤炭资源的勘探开发有着重要的指导作用[1-2]。煤层含水饱和度通常可利用电阻抗、声阻抗、放射性等测量参数进行定性或定量评价[3-6]。作为发展最早和应用最广泛的勘探手段之一,电法勘探通过测量储层的电性参数,可为煤储层解释和评价提供较好的地球物理信息[7]。然而,煤体的导电性受骨架、矿物颗粒和孔隙流体等多种因素的影响,其导电机理复杂多样,高温、高压条件下煤层含水饱和度的定量评价存在较大困难[8]。
频率域激发激化法作为一种电法勘探手段,广泛应用于矿产勘查及水文地质调查等领域[9]。相较于传统的单一频率的电阻率测量方法,频率域激发极化数据所含的地层信息更丰富[10]。近年来,一些专家学者开始探索利用频率域激发极化数据评价油气储层饱和度等物性参数。范宜仁等[11]发现极化效应会导致岩石出现电频散现象,该极化效应随含水饱和度的降低而增强,随溶液矿化度的增高而减弱。苏庆新等[12]研究发现岩石界面极化频率与含水饱和度呈线性正相关关系,对应的虚部电阻率模值与含水饱和度呈线性负相关关系。李建军等[13]以泥质砂岩为研究对象,得到不同矿化度溶液和不同饱和度岩样与复电阻率频散的关系,认为复电阻率的虚部对饱和度评价更具参考价值。Xu等[14]针对含油岩石复电阻率开展了研究,提出了一种利用界面极化频率评价含油饱和度的方法。Li等[15]研究了人造砂岩和泥质砂岩零频电阻率和弛豫时间与孔隙度及含水饱和度的关系。Jia等[16]研究了砂岩复电阻率虚部模值最大值与含水饱和度及孔隙度的关系,并证实了基于遗传算法的饱和度评价模型的可行性。Lei等[17]研究了常温、常压条件下变质煤复电阻率实部和虚部随含水饱和度的变化关系。
前人在岩石激发激化理论、复电阻率评价模型等方面做了较深入的研究,揭示了岩石电性参数与储层物性参数的相关性。然而,大多数的研究对象是含油岩石,并且都是在常温、常压条件下开展实验研究,尚未形成有效的高温、高压条件下煤样含水饱和度的定量评价模型。
本文通过对河南焦作地区煤样开展高温、高压条件下的电频谱实验测量,得到煤样在不同温度、压力及含水饱和度条件下的电频谱曲线。基于Cole-Cole模型反演提取煤样的低频复电阻率、高频复电阻率、弛豫时间等参数,进而计算得到界面极化频率和频散度,分析了温度、压力及含水饱和度对煤样电频散曲线的影响,据此提出了一种利用界面极化频率和频散度评价煤样含水饱和度的新方法,为煤储层电法勘探提供了实验基础与理论依据。
1 煤样电频谱实验 1.1 煤样的采集和处理受构造运动的影响,煤层的渗透率、孔隙度、含气饱和度、含水饱和度等参数与埋藏深度、厚度、煤阶等属性关系密切[18-19]。图 1中煤样取自河南焦作地区的原生结构煤。煤体颜色为黑色,宏观煤岩类组分以暗煤为主,占比为65%~70%,亮煤占比为30%~35%。宏观煤岩类型为半暗煤,煤样煤级主要为烟煤,煤样的地质参数如表 1所示。
|
图 1 焦作地区煤样照片 |
|
|
表 1 煤样基本参数 |
根据实际测量条件及煤样层理、隔理的发育情况,将煤样切割为直径25 mm、长度25~40 mm的柱塞样。煤样加工要求端面平整度小于0.02 mm,以保证与测量电极耦合良好。将加工后的标准煤样依序完成烘干、抽真空加压饱和(2000 mg/L的NaCl溶液)。为保持煤样的原生结构,样品在50℃下烘干,并于15 MPa压力下抽真空加压饱和。预处理过程中对岩心严格保湿,保持样品岩心离子通道内溶液稳定,以避免保湿过程带来的实验不利因素。
1.2 电频谱实验岩石的频散机理是复电阻率法勘探的理论基础,不同频率范围内岩石的频散机理并不相同。极化是岩石复电阻率出现频散现象的根本原因,即电介质内部的正、负离子在外加电场的作用下重新组合,形成附加电场。外加电场与附加电场相互作用引起电介质两端实际电压发生变化。在应用地球物理领域,岩石的电频散机理从低频到高频分别占主导地位的依次是:离子双电层极化、界面极化、分子极化以及电子极化[17]。
在界面极化主导的频率范围内,岩石的复电阻率与孔隙度、渗透率、含水饱和度、温度及流体矿化度等因素有关[20]。在此频率区间,岩石的电频谱参数难以进行量化分析,因而传统的解释方法往往将这些效应等效为宏观极化矢量P,代入Maxwell方程,得到位移电流
| $ \boldsymbol{D}=\varepsilon_0 \boldsymbol{E}+\boldsymbol{P}=\varepsilon_0 \varepsilon_{\mathrm{r}} \boldsymbol{E} $ | (1) |
式中:E表示电场强度;ε0和εr分别表示真空介电常数和相对介电常数。
时谐电磁场中,磁场强度H的旋度等于位移电流D的导数与电流密度j之和
| $ \nabla \times \boldsymbol{H}=\frac{\partial \boldsymbol{D}}{\partial t}+\boldsymbol{j} $ | (2) |
对于时谐电磁场,可将上式中对时间的导数
| $ \nabla \times \boldsymbol{H}=\mathrm{i} \omega\left(\varepsilon-\mathrm{i} \frac{\sigma}{\omega}\right) \boldsymbol{E} $ | (3) |
式中ε是介电常数。
在频率域激发激化测量中,煤体可等效为电容。在外加ω=2πf的电磁场(f表示频率)中,等效电容的复介电常数ε*(ω)可表示为
| $ \varepsilon^*(\omega)=\varepsilon-\mathrm{i} \frac{\sigma}{\omega} $ | (4) |
同理,煤体可等效为导体,其复电导率为
| $ \sigma^*(\omega)=\mathrm{i} \omega \varepsilon^*=\sigma+\mathrm{i} \omega \varepsilon $ | (5) |
上式表明介质电导率可表示为随频率变化的复数[21]。
高温、高压煤样电频谱实验系统主要由高精度阻抗分析仪、驱替泵、岩心夹持器、饱和度测量装置、围压泵和计算机(阻抗分析仪程序控制系统)组成(图 2)。电频谱实验中,将预处理好的煤样放入夹持器,将一对测量电极对称放置在煤样两端,与煤样端面充分贴合。在阻抗分析仪上设置扫频范围为20~10M Hz,对数等间隔地扫描101个频点,测量煤样的电压和电流矢量,并据此计算阻抗,进而得到煤样复电阻率的实部和虚部。

|
图 2 煤样复电阻率测量系统示意图 |
分别在不同的温度、压力和含水饱和度条件下测量煤样复电阻率频谱数据。基于焦作地区煤样脆度较大的物理特性及实验室测试条件,本次实验最高温度和最大压力分别设定为90℃和9.0 MPa,驱替压力最高为1.2 MPa。
将高温、高压电频谱仪器设置为恒压3 MPa,之后依次测量饱含水煤样在27℃(室温)、50℃、70℃、90℃等不同温度(T)下的复电阻率,每次改变温度的时间间隔不小于2h,以确保煤样温度稳定。不同温度下实验得到的煤样电频谱曲线见图 3,可见随着温度的升高,煤样电频散明显增强,复电阻率变化幅度增加,虚部电阻率曲线极值点对应的界面极化频率向低频方向移动。
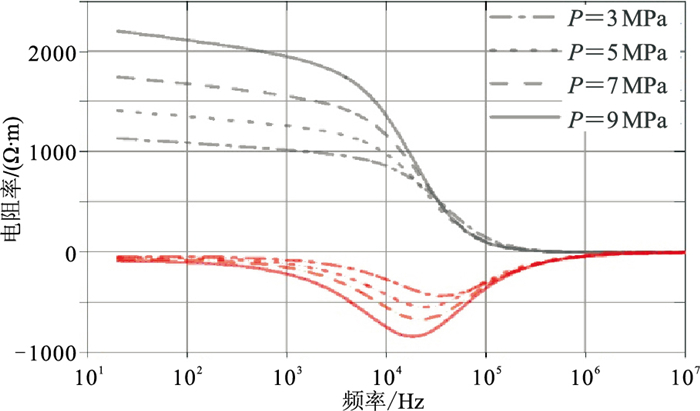
同理,将高温、高压电频谱仪器设置为室温27℃,依次测量饱含水煤样在3、5、7、9 MPa等不同压力(P)下的复电阻率,得到不同压力条件下煤样的电频谱数据(图 4)。每次改变围压时都需保证岩心腔内压力达到稳定状态至少5 min后再开始记录数据。从图 4可见,随着压力的增大,煤样电频散明显增强,复电阻率变化幅度增加,虚部电阻率曲线极值点对应的界面极化频率向低频方向移动。
|
图 4 27℃时不同压力条件下煤样复电阻率频谱曲线 |
通过气(N2)驱法控制煤样的含水饱和度,测量驱替过程中排出液体的重量,进而得到煤样的含水饱和度。在不考虑煤样孔隙中气体质量的情况下,煤样含水饱和度为
| $ S_{\mathrm{w}}=\frac{m_1-m_2-m_3}{V \phi \rho_{\mathrm{w}}} $ | (6) |
式中:ϕ表示煤样孔隙度;m1、m2、m3分别表示饱和条件下煤样、干煤样及煤样排出液体的质量;ρw表示孔隙流体的密度;V表示煤样体积。
将高温、高压电频谱仪器设置为室温27℃、恒压3 MPa,依次将驱替压力设置为0.1、0.2、0.4、0.6、0.8、1.0、1.2 MPa,使煤样含水饱和度Sw逐步降低,直至达到束缚水状态。煤样不同含水饱和度条件下的复电阻率曲线见图 5。

|
图 5 不同含水饱和度条件下煤样复电阻率频谱曲线 |
从图 5可见,随着含水饱和度的增大,煤样的电频散特征明显减弱,复电阻率虚部变化幅度大幅增加,虚部电阻率曲线上极值点对应的界面极化频率向低频方向移动。
1.3 煤样等效电路模型煤岩的导电性主要受煤骨架和孔隙中流体的影响。由于煤骨架与孔隙流体具有不同的导电特性,研究煤岩导电性时常将煤岩各组分导电性加权叠加。电频散研究中,等效电路作为使用最广泛的评价模型,可将岩石各组分等效为串联或并联的电阻或电容,便于精确描述岩石的导电性。Cole-Cole模型广泛应用于岩石复电阻率频谱特性的描述,取得较好效果[22]。
根据Cole-Cole模型等效电路,煤样阻抗Z的数学表达式为
| $ Z=R_0\left\{1-\eta\left[1-\frac{1}{1+({\rm{i}} \omega \tau)^c}\right]\right\} $ | (7) |
式中:η=1-RH/R0表示极化率,其中R0表示煤样零频电阻率,RH表示煤样高频电阻率;τ表示弛豫时间常数;c表示频率相关系数。
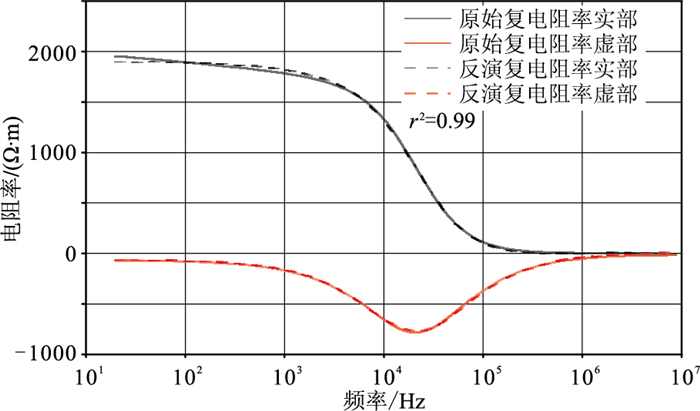
图 6为岩石Cole-Cole模型等效电路示意图。基于Cole-Cole模型,在20~10M Hz频率范围内对所选煤样的电频谱数据采用最小二乘法进行反演,拟合结果见图 7。可见反演得到的煤样复电阻率实部、虚部与实测值的拟合优度r2达到0.99。

|
图 6 岩石Cole-Cole模型等效电路示意图 R表示连通的孔隙,NR表示不连通的孔隙,iωτ表示金属离子表面作用。 |
|
图 7 基于Cole-Cole模型的焦作煤样复电阻率反演拟合结果 |
基于Cole-Cole模型反演可得到煤样的弛豫时间、极化率等电频谱参数,重点分析界面极化频率和频散度与煤样温度、压力及含水饱和度的定量关系。
随着频率的增大,在低频段煤样复电阻率虚部幅值急剧增大,其极大值对应的频率(界面极化频率,FI)常用来评价岩石的频散特性[23]。根据等效电路模型,煤样界面极化频率FI与弛豫时间τ的关系[24]为
| $ \tau=\frac{1}{2 \pi \mathrm{FI}} $ | (8) |
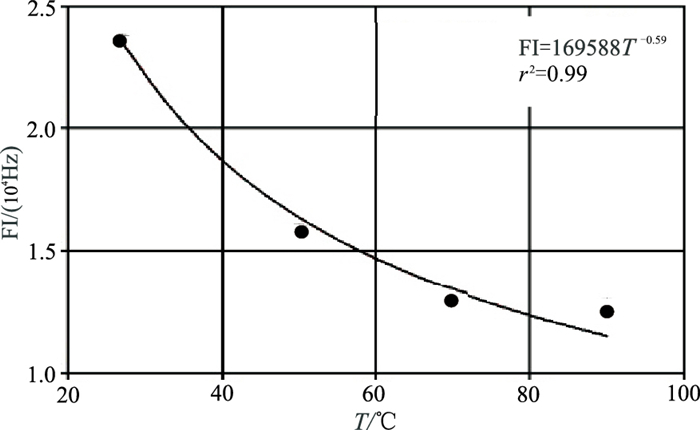
目前,大量实验研究表明岩石的复电阻率受温度、压力和含水饱和度等因素影响较大。图 8是实验得到的煤样温度T与界面极化频率FI的交会图。可以看出,随着温度T的不断升高,煤样界面极化频率FI先迅速降低,后缓慢降低,总体上呈复杂的幂函数关系。
|
图 8 不同温度条件下煤样界面极化频率曲线 |
在不考虑煤样骨架导电性的条件下,随着煤样外部围压的增大,煤样中的孔隙会受到不同程度的压缩,导致煤样导电性减弱,电阻率增高,频散效应增强。图 9是实验得到的煤样压力P与界面极化频率FI的交会图。可以清楚地看出,随着压力P的不断增大,煤样界面极化频率FI降低,二者呈明显的线性负相关关系。

|
图 9 不同压力条件下煤样界面极化频率曲线 |
煤样含水饱和度降低,说明其导电通道变少,煤样导电性随之减弱,电阻率增高,频散效应增强。图 10是煤样含水饱和度Sw与界面极化频率FI的交会图,可见随着煤样含水饱和度的不断增大,界面极化频率降低,二者呈明显的线性负相关关系。

|
图 10 不同含水饱和度条件下煤样界面极化频率曲线 |
岩心实部频散度与电频散特征之间存在多解性,难以定量评价煤样的电频散特征,因此利用实部频散度定量评价岩心电频散特征不具有普适性。但是,岩心复电阻率的虚部信息可以较好地表征煤样的电频散特征。定义复电阻率虚部频散度为[25]
| $ \mathrm{PFE}=\frac{\left|R_{\mathrm{LX}}\right|-\left|R_{\mathrm{HX}}\right|}{\left|R_{\mathrm{LX}}\right|} \times 100 \% $ | (9) |
式中|RLX|和|RHX|分别表示低频和高频复电阻率虚部的模值。PFE主要表征的是界面极化效应的频散特征。基于Cole-Cole模型反演可得到煤样的低频和高频复电阻率的虚部,代入上式可计算煤样的频散度。煤样的频散度与温度、压力及含水饱和度的响应关系分别见图 11、图 12和图 13。

|
图 11 不同温度条件下煤样频散度曲线 |
|
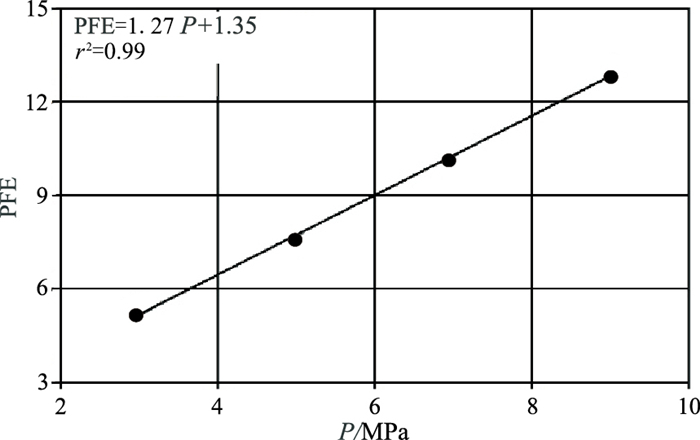
图 12 不同压力条件下煤样频散度曲线 |

|
图 13 不同含水饱和度条件下煤样频散度曲线 |
由图 11可见,随着温度T的升高,煤样频散度PFE不断增大,T与PFE呈明显的线性关系。由图 12可见,随着压力P的增大,煤样频散度PFE不断增大,两者同样呈现出明显的线性关系。由图 13可见,随着含水饱和度Sw的增加,煤样频散度PFE不断减小,两者也呈明显的线性关系。因此,利用复电阻率虚部频散度PFE可较好地评价煤样的含水饱和度。
3 结论本文通过对河南焦作地区原生结构煤样开展高温、高压条件下电频谱实验测量,研究了复电阻率频谱与温度、压力及含水饱和度的关系,得到以下认识。
(1) 煤样界面极化频率与温度呈复杂的幂函数关系,与压力及含水饱和度呈明显的线性负相关关系。
(2) 基于煤样低频和高频复电阻率的虚部模值得到的频散度与温度、压力及含水饱和度均呈明显的线性关系,据此可较好地评价煤样的含水饱和度。
(3) 本文研究结果提供了一种高温、高压条件下评价煤层含水饱和度的新方法,为频率域激发极化法在煤矿勘探中的应用提供了理论及实验基础。
| [1] |
吕明哲. 强突出煤层不同含水率条件煤与瓦斯突出试验研究[D]. 江苏徐州: 中国矿业大学, 2020. LYU Mingzhe. Experimental Study on Coal and Gas Outburst in Strong Outburst Coal Seam with Diffe-rent Moisture Content[D]. China University of Mining and Technology, Xuzhou, Jiangsu, 2020. |
| [2] |
王凤林, 袁玉, 张遂安, 等. 不同含水及负压条件下煤层气等温吸附解吸规律[J]. 煤炭科学技术, 2019, 47(6): 158-163. WANG Fenglin, YUAN Yu, ZHANG Suian, et al. Iso-thermal adsorption and desorption of coalbed me-thane under different water saturation and negative pressure[J]. Coal Science and Technology, 2019, 47(6): 158-163. |
| [3] |
谭廷栋. 测井解释煤层气藏[J]. 测井技术, 1999, 23(2): 83-88. TAN Tingdong. Evaluating coal-bed gas reservoir with log data[J]. Well Logging Technology, 1999, 23(2): 83-88. |
| [4] |
彭苏萍, 杜文凤, 殷裁云, 等. 基于AVO反演技术的煤层含气量预测[J]. 煤炭学报, 2014, 39(9): 1792-1796. PENG Suping, DU Wenfeng, YIN Caiyun, et al. Coal-bed gas content prediction based on AVO inversion[J]. Journal of China Coal Society, 2014, 39(9): 1792-1796. |
| [5] |
傅雪海, 周荣福, 廖斌琛, 等. 地勘阶段煤与瓦斯突出区域预测的理论和方法: 以淮南潘一煤矿为例[M]. 江苏徐州: 中国矿业大学出版社, 2014, 68. FU Xuehai. Theories and Techniques of Regional Forecast of Coal and Gas Outburst During Coal Exploration: Take Panyi Coal Mine in Huainan as an Exa-mple[M]. China University of Mining and Technology Press, Xuzhou, Jiangsu, 2014, 68. |
| [6] |
王学军, 张庆辉, 傅雪海. 山西省煤层气储层物性特征及资源评价[M]. 北京: 煤炭工业出版社, 2015: 60-90. WANG Xuejun, ZHANG Qinghui, FU Xuehai. Physical Characteristics and Resource Evaluation of Coalbed Methane Reservoirs in Shanxi Province[M]. Beijing: China Coal Industry Publishing House, 2015: 60-90. |
| [7] |
ARCHIE G E, 张庚骥. 电阻率测井在确定某些储层特性中的作用[J]. 测井技术, 2007, 31(3): 197-202. ARCHIE G E, ZHANG Gengji. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Well Logging Technology, 2007, 31(3): 197-202. |
| [8] |
刘之的, 王伟, 杨珺茹, 等. 煤及煤层气储层导电特性研究综述与展望[J]. 地球物理学进展, 2020, 35(4): 1415-1423. LIU Zhide, WANG Wei, YANG Junru, et al. Review and prospect of study on conductive properties of coal and CBM reservoirs[J]. Progress in Geophysics, 2020, 35(4): 1415-1423. |
| [9] |
柯马罗夫 B.A.. 激发极化法电法勘探[M]. 修订增补第二版. 北京: 地质出版社, 1983. KОМАРОВ B A. Induced Polarization Electrical Exploration[M]. Revised and Supplemented the Second Edition. Beijing: Geology Press, 1983. |
| [10] |
向葵, 胡文宝, 严良俊, 等. 川黔地区页岩复电阻率的频散特性[J]. 石油地球物理勘探, 2014, 49(5): 1013-1019. XIANG Kui, HU Wenbao, YAN Liangjun, et al. Complex resistivity dispersion characteristics of shale samples in Sichuan and Guizhou area[J]. Oil Geophysical Prospecting, 2014, 49(5): 1013-1019. |
| [11] |
范宜仁, 陆介明, 王光海, 等. 岩石电阻率频散现象的实验研究[J]. 石油大学学报(自然科学版), 1994(1): 17-23. FAN Yiren, LU Jieming, WANG Guanghai, et al. Experimental study on the dispersion of rock resistivity[J]. Journal of the University of Petroleum (Edition of Natural Science), 1994(1): 17-23. |
| [12] |
苏庆新, 柯式镇, 冯启宁, 等. 100Hz~10MHz频段含油水两相岩石电阻抗的研究[J]. 地球物理学进展, 1999, 14(1): 93-103. SU Qingxin, KE Shizhen, FENG Qining, et al. An experimental study on the impedance spectra of rocks saturated with oil and water in frequency 100Hz~10MHz[J]. Progress in Geophysics, 1999, 14(1): 93-103. |
| [13] |
李建军, 邓少贵, 范宜仁, 等. 岩样复电阻率影响因素研究[J]. 测井技术, 2005, 29(1): 11-14. LI Jianjun, DENG Shaogui, FAN Yiren, et al. Study on influential factors on core's complex resistivity[J]. Well Logging Technology, 2005, 29(1): 11-14. |
| [14] |
XU W, KE S, YIN C, et al. Measurement and inversion of complex resistivity spectra for different core samples[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 3015-3019.
|
| [15] |
LI J, KE S, YIN C, et al. A laboratory study of complex resistivity spectra for predictions of reservoir properties in clear sands and shaly sands[J]. Journal of Petroleum Science and Engineering, 2019, 177: 983-994. |
| [16] |
JIA J, KE S, REZAEE R, et al. The frequency exponent of artificial sandstone's complex resistivity spectrum[J]. Geophysical Prospecting, 2021, 69(4): 856-871. |
| [17] |
LEI D, ZHAO C, ZHANG Y, et al. Experimental study on characteristics of water containing coal complex resistivity dispersion[J]. Journal of Loss Prevention in the Process Industries, 2018, 56: 328-333. |
| [18] |
高和群, 韦重韬, 申建, 等. 沁水盆地南部含气饱和度特征及控制因素分析[J]. 煤炭科学技术, 2011, 39(2): 94-97. GAO Hequn, WEI Chongtao, SHEN Jian, et al. Gas content saturation features of seams and control factors analysis in southern part of Qinshui basin[J]. Coal Science and Technology, 2011, 39(2): 94-97. |
| [19] |
韦重韬, 秦勇, 姜波, 等. 华北残留盆地煤层气成藏动力学过程研究——以沁水盆地和鄂尔多斯盆地东缘为例[J]. 地质学报, 2008, 82(10): 1363-1367. WEI Chongtao, QIN Yong, JIANG Bo, et al. Dynamic accumulation process of coalbed methane in residual basins of North China: A case study of the Qinshui basin and the eastern margin of Ordos basin[J]. Acta Geologica Sinica, 2008, 82(10): 1363-1367. |
| [20] |
HIZEM M, BUDAN H, DEVILLÉ B, et al. Dielectric dispersion: a new wireline petrophysical measurement[C]. SPE Annual Technical Conference and Exhibition, 2008, SPE-116130-MS.
|
| [21] |
WEIR W B. Automatic measurement of complex di-electric constant and permeability at microwave frequencies[J]. Proceedings of the IEEE, 1974, 62(1): 33-36. |
| [22] |
林小稳, 柯式镇, 贺秋丽, 等. 岩石复电阻率频谱反演研究[J]. 测井技术, 2016, 40(2): 142-146. LIN Xiaowen, KE Shizhen, HE Qiuli, et al. Inversion study on complex resistivity spectrum of rocks[J]. Well Logging Technology, 2016, 40(2): 142-146. |
| [23] |
段威, 许巍, 刘俊博, 等. 高温高压煤复电阻率各向异性实验研究[J]. 科学技术与工程, 2022, 22(21): 9223-9230. DUAN Wei, XU Wei, LIU Junbo, et al. Complex resistivity anisotropy of coal sample under high tempera-ture and high pressure[J]. Science Technology and Engineering, 2022, 22(21): 9223-9230. |
| [24] |
刘俊博, 许巍, 段威, 等. 高温高压条件煤复电阻率频散特性实验研究[J]. 当代化工, 2022, 51(10): 2300-2306. LIU Junbo, XU Wei, DUAN Wei, et al. Complex resistivity dispersion characteristics of coal under high temperature and high pressure[J]. Contemporary Chemical Industry, 2022, 51(10): 2300-2306. |
| [25] |
童茂松, 李莉, 王伟男, 等. 泥质砂岩的复电阻率实验研究[J]. 测井技术, 2005, 29(3): 188-190. TONG Maosong, LI Li, WANG Weinan, et al. Experimental study on complex resistivity of shaly sands[J]. Well Logging Technology, 2005, 29(3): 188-190. |



 许巍, 湖北省武汉市蔡甸区蔡甸街大学路111号长江大学地球物理与石油资源学院,430100。Email:
许巍, 湖北省武汉市蔡甸区蔡甸街大学路111号长江大学地球物理与石油资源学院,430100。Email:
