目前,面波勘探以其低成本、高效率等诸多优势成为浅地表地震勘探的热门方法之一。而对面波基础理论做充分研究是面波勘探达到理想效果的前提和条件。1885年,Rayleigh[1]首次在理论上证明Rayleigh面波的存在,自此面波成为地球物理学家研究的热点之一。面波具有能量强,传播远,浅层分辨率高,抗干扰能力强等优点,且在层状介质中表现出频散特性。由于面波的频散曲线能反映地层的速度及厚度,基于频散方程的数值模拟算法得以快速发展。Haskell[2]提出Haskell正演数值算法,并推导出Rayleigh波频散方程。Abo-Zena[3]提出Abo-Zena算法,解决了Thomson-Haskell及Knopoff算法出现的高频数值频散问题。但基于频散方程的面波正演方法只适用于波形和走时信息的计算,无法计算波场各分量的振幅值,更无法得到全波场。
基于波动方程的数值模拟方法是另一种实现面波正演的重要手段。其中,有限差分数值模拟法[4-9]能模拟自由表面边界条件[10-11]下的三维波场及可视化地震波在介质中的传播过程[12]。Mittet[13]提出基于交错网格有限差分的自由边界处理方案,但生成的Rayleigh波出现严重的频散现象。周竹生等[14]使用有限差分实现二维全波场正演,揭示了面波的形成机理和传播规律。
在波场模拟中,体波波场是由点震源激发产生的三维球状波场。但由于三维数值计算的工作量大,对硬件要求高,其计算效率难以满足实际生产的需要。因此,为提高计算效率,通常在二维条件下研究三维波场的相关特性。
在二维波动方程正演中,Rayleigh面波常以平面纵波与平面垂直极化横波的干涉波场形式出现,Love波以平面水平极化横波形式出现,理论研究中所使用的波函数也是平面波形式。傅承义[15]在平面波的基础上利用位移函数和波动方程探索面波的频散关系及衰减现象。但实际观测到的面波,无论是其纵波分量还是其横波分量,都不可能表现为平面波形式。在水平层状介质条件下,面波各分量均表现为柱面波形式,这与其在二维直角坐标中呈现的平面波形式明显不同。因此,在二维直角坐标下正演所得的波场存在如下问题:①模拟得到的面波与体波的振幅变化分别为平面波与柱面波特征,而实际的面波与体波分别为柱面波与球面波,两者之间不相符;②模拟得到的面波以平面波形式向外传播时,其振幅不具备空间几何衰减特征,而实际中的面波是以柱面波形式向外传播,其振幅存在空间的几何衰减特征。因此,基于平面波理论的二维直角坐标下的波动方程对波场的描述存在不足,正演结果难以反映真实波场特征。
本文使用柱对称条件处理线震源所激发的柱面波,在二维平面内实现球面波的等价模拟。其中,柱坐标由于自然贴合柱面网格及其柱对称性质,多用于流体运动研究[16]和仪器制造[17]。相较于地震波场正演中直角坐标的广泛应用,柱坐标的相关研究较少。何柏荣等[18]利用二维柱坐标研究圆柱状地质体中地震波的绕射问题。张碧星等[19]引入柱坐标系分析三维水平层状介质的Rayleigh波频散特征。
本文使用柱对称条件将三维问题简化为二维问题,首先推导了柱坐标系下的弹性波波动方程,利用弹性波的基础理论,分析正演所得弹性波场,验证使用二维算法实现三维波场模拟的合理性和可行性。然后分别计算直角坐标系和柱坐标系下的面波波场,对比两种坐标系下面波波场振幅、波形及走时特征,分析柱对称条件下面波的传播特性和模拟优势。
1 柱对称条件下弹性波波场正演模拟 1.1 柱坐标下弹性波波动方程柱坐标系rθz中,r、z、θ分别对应水平坐标、垂直坐标和角度坐标。有如下关系
| $ \left\{\begin{array}{l} \varepsilon_r=\frac{\partial u}{\partial r} \\ \varepsilon_\theta=\frac{1}{r} \frac{\partial e}{\partial \theta}+\frac{u}{r} \\ \varepsilon_z=\frac{\partial w}{\partial z} \\ \eta_{\theta z}=\frac{1}{r} \frac{\partial w}{\partial \theta}+\frac{\partial e}{\partial z} \\ \eta_{r z}=\frac{\partial w}{\partial r}+\frac{\partial u}{\partial z} \\ \eta_{\theta \theta}=\frac{1}{r} \frac{\partial e}{\partial r}+\frac{1}{r} \frac{\partial u}{\partial \theta}-\frac{e}{r} \end{array}\right. $ | (1) |
| $ \left\{\begin{array}{l} \sigma_{r r}=\lambda\left(\varepsilon_r+\varepsilon_\theta+\varepsilon_z\right)+2 \mu \varepsilon_r \\ \sigma_{\theta \theta}=\lambda\left(\varepsilon_r+\varepsilon_\theta+\varepsilon_z\right)+2 \mu \varepsilon_\theta \\ \sigma_{z z}=\lambda\left(\varepsilon_r+\varepsilon_\theta+\varepsilon_z\right)+2 \mu \varepsilon_z \end{array}\right. $ | (2) |
| $ \left\{\begin{array}{l} \rho \frac{\partial^2 u}{\partial t^2}=\frac{\partial \sigma_{r r}}{\partial r}+\frac{1}{r} \frac{\partial \tau_{r \theta}}{\partial \theta}+\frac{\partial \tau_{r z}}{\partial z}+\frac{\sigma_{r r}-\sigma_{\theta \theta}}{r} \\ \rho \frac{\partial^2 e}{\partial t^2}=\frac{\partial \tau_{r \theta}}{\partial r}+\frac{1}{r} \frac{\partial \sigma_{\theta \theta}}{\partial \theta}+\frac{\partial \tau_{\theta z}}{\partial z}+\frac{2 \tau_{r \theta}}{r} \\ \rho \frac{\partial^2 w}{\partial t^2}=\frac{\partial \tau_{z r}}{\partial r}+\frac{1}{r} \frac{\partial \tau_{\theta z}}{\partial \theta}+\frac{\partial \sigma_{z z}}{\partial z}+\frac{\tau_{z r}}{r} \end{array}\right. $ | (3) |
式中:t为时间;εm为正应变;ηmn为切应变(m, n=r、θ、z, m≠n);σmm为正应力;τmn为切应力;u、e、w为直角坐标系下的位移分量,都是r、θ、z、t的函数;λ、μ是拉梅常数;ρ是介质密度。
将柱坐标下的几何方程[20](式(1))和本构方程(式(2))代入柱坐标下的三维运动平衡方程[21](式(3))中,在柱对称条件下各变量与θ无关,波动方程满足
| $ \left\{\begin{aligned} \rho \frac{\partial^2 u}{\partial t^2}= & \frac{\partial}{\partial r}\left[(\lambda+2 \mu) \frac{\partial u}{\partial r}+\lambda\left(\frac{u}{r}+\frac{\partial w}{\partial z}\right)\right]+ \\ & \frac{\partial}{\partial z}\left[\mu\left(\frac{\partial w}{\partial r}+\frac{\partial u}{\partial z}\right)\right]+\frac{2 \mu}{r}\left(\frac{\partial u}{\partial r}-\frac{u}{r}\right) \\ \rho \frac{\partial^2 w}{\partial t^2}= & \frac{\partial}{\partial r}\left[\mu\left(\frac{\partial w}{\partial r}+\frac{\partial u}{\partial z}\right)\right]+\frac{\partial}{\partial z}\left[(\lambda+2 \mu) \frac{\partial w}{\partial z}+\right. \\ & \left.\lambda\left(\frac{\partial u}{\partial r}+\frac{u}{r}\right)\right]+\frac{\mu}{r}\left(\frac{\partial w}{\partial r}+\frac{\partial u}{\partial z}\right) \end{aligned}\right. $ | (4) |
纵横波速度与弹性参数的转换关系为
| $ \left\{\begin{array}{l} v_{\mathrm{P}}=\sqrt{\frac{\lambda+2 \mu}{\rho}} \\ v_{\mathrm{S}}=\sqrt{\frac{\mu}{\rho}} \end{array}\right. $ | (5) |
式中vP、vS分别是纵波、横波速度。
在rOz平面中,震源位于r0处,r-r0表示计算点与震源之间的水平距离。将式(5)代入式(4),即得到柱坐标下的二维弹性波波动方程
| $ \left\{\begin{array}{c} \frac{\partial^2 u}{\partial t^2}=v_{\mathrm{P}}^2 \frac{\partial^2 u}{\partial r^2}+\left(v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right) \frac{\partial^2 w}{\partial r \partial z}+v_{\mathrm{S}}^2 \frac{\partial^2 u}{\partial z^2}+ \\ \quad \frac{v_{\mathrm{P}}^2}{r-r_0}\left(\frac{\partial u}{\partial r}-\frac{u}{r-r_0}\right) \\ \frac{\partial^2 w}{\partial t^2}=v_{\mathrm{P}}^2 \frac{\partial^2 w}{\partial z^2}+\left(v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right)\left[\frac{\partial^2 u}{\partial r \partial z}+\frac{1}{r-r_0} \frac{\partial u}{\partial z}-\right. \\ \left.\frac{u}{\left(r-r_0\right)^2}\right]+v_{\mathrm{S}}^2\left[\frac{\partial^2 w}{\partial r^2}+\frac{1}{r-r_0} \frac{\partial w}{\partial r}+\frac{u}{\left(r-r_0\right)^2}\right] \end{array}\right. $ | (6) |
此外,针对柱坐标系下弹性波场在r-r0→0处出现的极点问题。本文在差分处理有关r-r0的方程时,将常规差分网格沿径向偏移半个网格点[22]以避免r-r0→0处出现数值奇异的情况。
1.2 ADE-PML边界本文选用基于辅助微分方程(ADE)的完全匹配层(PML)方法处理吸收边界[23],即为ADE-PML边界算法。在二维情况下,使用该吸收边界算法分别处理质点的垂直位移分量和水平位移分量。
1.2.1 直角坐标形式以直角坐标系中x方向为例,在频率域利用变换空间求导算子
| $ \frac{\partial}{\partial x}=\frac{1}{s_x} \frac{\partial}{\partial x} $ | (7) |
将波动方程拉伸至复数域。式中sx=dx/jω,是x方向的复拉伸变量,其中j为虚数单位,ω是角频率,dx是人工吸收边界的衰减参数。
ADE-PML边界中,通过下式
| $ d_x=-\frac{3 v_{\max }}{2 L} \ln R\left(\frac{l}{L}\right)^2 \quad 0<l<L $ | (8) |
得到迭代衰减波场的系数
| $ \left\{\begin{array}{c} c_{x 1}=\frac{1-\frac{d_x \Delta t}{2}}{1+\frac{d_x \Delta t}{2}} \\ c_{x 2}=\frac{\frac{d_x}{\Delta x} \Delta t}{1+\frac{d_x \Delta t}{2}} \\ c_{x 3}=\frac{d_x \Delta t}{1+\frac{d_x \Delta t}{2}} \end{array}\right. $ | (9) |
式中:dx是x方向的衰减系数;vmax是弹性波的最大传播速度;L为PML边界的厚度;R是理论反射系数(设为0.001);l是计算点与计算边界之间的距离;cx1、cx2、cx3均为比例系数;Δx和Δt分别为空间和时间步长。
由式(8)可知,边界匹配层越厚,则衰减系数越小,边界的吸收效果越好。因此,可通过改变PML的厚度灵活控制边界的吸收效果[24-29]。
令p=jω+dx,引入频率域辅助变量
| $ \left\{\begin{aligned} \hat{u}_{x 3}= & \frac{d_x^{\prime}}{p} \frac{\partial \hat{u}}{\partial x} \\ \hat{u}_{x 2}= & \frac{d_x}{p} \frac{\partial^2 \hat{u}}{\partial x^2}+\frac{2 d_x^{\prime}}{p} \frac{\partial \hat{u}}{\partial x}-d_x \hat{u}_{x 3} \\ \hat{u}_{x 1}= & v_{\mathrm{P}}^2\left(\frac{d_x^{\prime}}{p} \frac{\partial \hat{u}}{\partial x}+\frac{2 d_x}{p} \frac{\partial^2 \hat{u}}{\partial x^2}+d_x \frac{\partial^2 w}{\partial x \partial z}-d_x \hat{u}_{x 2}\right)- \\ & v_{\mathrm{S}}^2 d_x \frac{\partial^2 w}{\partial x \partial z} \end{aligned}\right. $ | (10) |
| $ \left\{\begin{array}{l} u_3^{k+\frac{1}{2}}=c_{x 1} u_3^{k-\frac{1}{2}}+c_{x 2} \frac{\partial u^k}{\partial x} \\ u_2^{k+\frac{1}{2}}=c_{x 1} u_2^{k-\frac{1}{2}}+2 c_{x 2} \frac{\partial u^k}{\partial x}+c_{x 3}\left(\frac{\partial^2 u^k}{\partial x^2}-u_3^{k+\frac{1}{2}}\right) \\ u_1^{k+\frac{1}{2}}=c_{x 1} u_1^{k-\frac{1}{2}}+c_{x 2} \frac{\partial u^k}{\partial x}+c_{x 3}\left(2 \frac{\partial^2 u^k}{\partial x^2}-u_2^{k+\frac{1}{2}}\right) \end{array}\right. $ | (11) |
式中:dx′是dx对x的导数;
基于Ma等[23]提出的ADE-PML算法,将其推广至柱坐标系。以柱坐标下波动方程的水平分量r为例,将波动方程的水平分量拉伸至复数域
| $ \begin{aligned} (\mathrm{j} \omega)^2 \hat{u}= & v_{\mathrm{P}}^2 \frac{1}{s_r} \frac{\partial}{\partial r}\left(\frac{1}{s_r} \frac{\partial \hat{u}}{\partial r}\right)+\left(v_{\mathrm{P}}^2-v_{\mathrm{S}}^2\right) \frac{1}{s_r} \frac{\partial^2 \hat{w}}{\partial r \partial z}+ \\ & v_{\mathrm{S}}^2 \frac{\partial^2 \hat{u}}{\partial z^2}+\frac{v_{\mathrm{P}}^2}{r-r_0}\left(\frac{1}{s_r} \frac{\partial \hat{u}}{\partial r}-\frac{\hat{u}}{r-r_0}\right) \end{aligned} $ | (12) |
式中
| $ \left\{\begin{aligned} \hat{u}_{r 3}= & \frac{d_r^{\prime}}{q} \frac{\partial \hat{u}}{\partial r} \\ \hat{u}_{r 2}= & \frac{d_r}{q} \frac{\partial^2 \hat{u}}{\partial r^2}+\frac{2 d_r^{\prime}}{q} \frac{\partial \hat{u}}{\partial r}-d_r \hat{u}_{r 3} \\ \hat{u}_{r 1}= & v_{\mathrm{P}}^2\left(\frac{d_r^{\prime}}{q} \frac{\partial \hat{u}}{\partial r}+\frac{2 d_r}{q} \frac{\partial^2 \hat{u}}{\partial r^2}+\right. \\ & \left.d_r \frac{\partial^2 w}{\partial r \partial z}-d_r \hat{u}_{r 2}\right)-v_S^2 d_r \frac{\partial^2 w}{\partial r \partial z} \end{aligned}\right. $ | (13) |
式中:dr=dx;dr′=dx/Δr,则dr′是dr对r求导。
1.3 弹性波波正演模拟在直角坐标系xyz下,假设模型沿y轴无限延伸,二维波场与坐标y无关,垂直分量为z分量,水平分量为x分量。在柱坐标系rθz下,假设模型关于炮点所在轴呈柱对称分布,二维波场与坐标θ无关,垂直分量为z分量,水平分量为r分量。
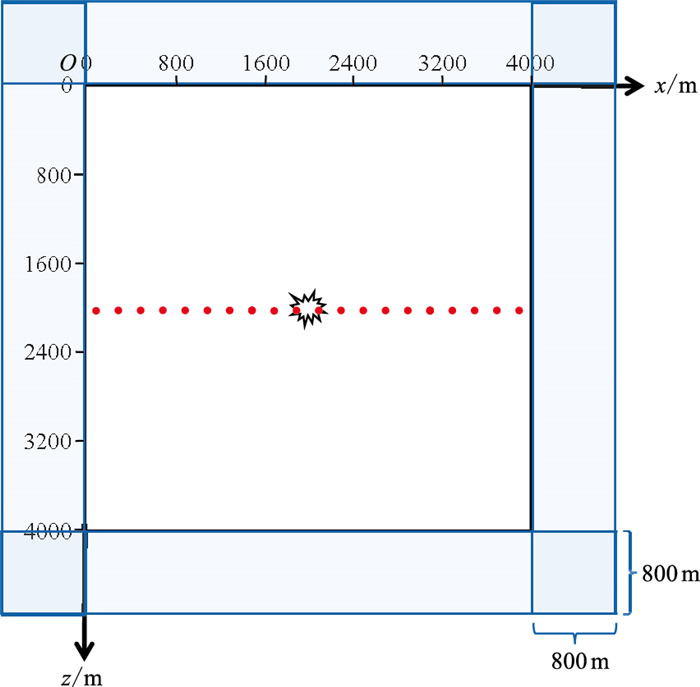
1.3.1 简单模型为验证柱坐标系正演模拟的可行性,建立区域范围为4000 m×4000 m、网格数为800×800,网格采样步长为5 m×5 m的模型。为保证模拟结果具有可比性,该剖面位于相同规格的三维直角坐标模型的y=0处。时间采样率为0.5 ms,总采样时间为0.5 s。介质的纵、横波速度分别为4000、2000 m/s,介质密度为2000 kg/m3。采用ADE-PML吸收边界。在柱坐标系和直角坐标系中分别施加主频为20 Hz的雷克子波,并将震源置于模型中心位置(图 1,其中爆破符号表示震源,红点对应检波点。下同)。
|
图 1 简单模型 |
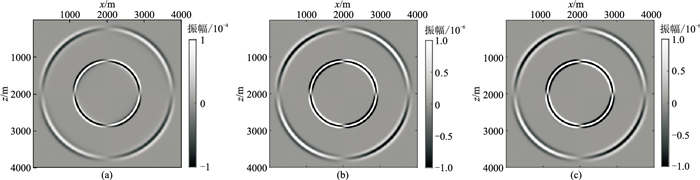
结合弹性波在均匀各向同性介质中的传播特征,分别对比图 2~图 5可知,无论是波场快照还是炮集记录,二维柱坐标与三维直角坐标的正演结果都一致。而在二维模型中,虽然两种坐标系下弹性波各分量的波场快照和地震记录结果都保持一致,但两种坐标系下二维波场增益强度相差两个数量级(参见色标数值)。而二维柱坐标与三维直角坐标的增益强度是相同的。由此可知,采取不同对称系统的二维坐标系对正演波场的能量有明显影响。
|
图 2 水平分量0.5 s波场快照 (a)二维直角坐标;(b)二维柱坐标;(c)三维直角坐标 |

|
图 3 垂直分量0.5 s波场快照 (a)二维直角坐标;(b)二维柱坐标;(c)三维直角坐标 |
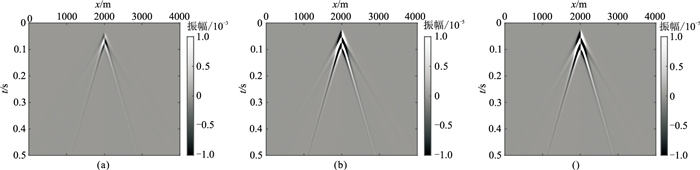
|
图 4 水平分量地震记录 (a)二维直角坐标;(b)二维柱坐标;(c)三维直角坐标 |

|
图 5 垂直分量地震记录 (a)二维直角坐标;(b)二维柱坐标;(c)三维直角坐标 |
由于地震波在传播过程中存在波前几何扩散现象,均匀介质中球面波的扩散因子为1/r。但在二维直角坐标系下,由于只有x和z两个自由度,球面波的波前面由三维的球面变成二维的圆,计算得到的球面扩散因子1/r也相应地变成柱面扩散因子
| $ G(\beta r)=\sqrt{\frac{2}{\pi \beta r}} \mathrm{e}^{\mathrm{j}\left(\beta r+\frac{\pi}{4}\right)} $ | (14) |
式中β为rOz平面内柱面波的波数。本文所用柱坐标算法是基于式(14)述及的柱面扩散因子
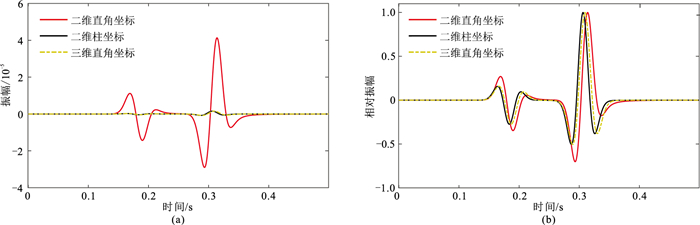
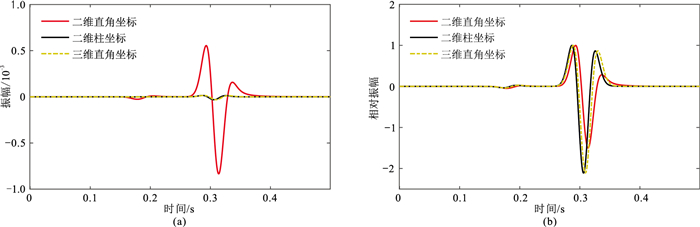
为更直观地观察波场正演的模拟精度,提取两种坐标系下地震记录第500道的检波器信号进行对比。通过图 6、图 7可看出:不同试验中相同位置处接收到的波形基本相同,其中三维直角坐标和二维柱坐标下波的振幅与相位基本一致,二维直角坐标下波的相位明显滞后于其他两条波形曲线。比较二维波形曲线最大振幅处的数据可知:两条曲线振幅大小相差约两个数量级,走时差为0.0075 s。
|
图 6 第500道接收的水平分量 (a)绝对振幅记录;(b)相对振幅记录 |
|
图 7 第500道接收的垂直分量 (a)绝对振幅记录;(b)相对振幅记录 |
对比球面波波场与柱面波波场的解析式可知后者多一个因子
因此,均匀介质中的弹性波在二维直角坐标下表现为柱面波形式,二维柱坐标下弹性波波场表现为球面波。通过该结果能够解释振幅差是由于二维柱坐标下波场以球面形式扩散,二维直角坐标下波场以柱面形式扩散,而在同等震源条件下球面波波前上一点能量比柱面上小。时差主要是二维直角坐标的平面波近似导致的相位差。进而验证二维直角坐标下正演波场与实际三维分布不符。
结合刘君等[30]关于波动方程坐标变换会引入误差的相关研究可知,柱坐标和直角坐标下波动方程的数值计算结果会存在微小误差,这是由于两种坐标系波场在每个时间片计算产生的误差来源不同、累计程度也不同。本文的正演结果也验证这一结论。从图中可见,二维柱坐标与三维直角坐标的正演结果间存在着约0.00125 s的微小走时误差,这正是波动方程坐标变换的离散采样造成的。
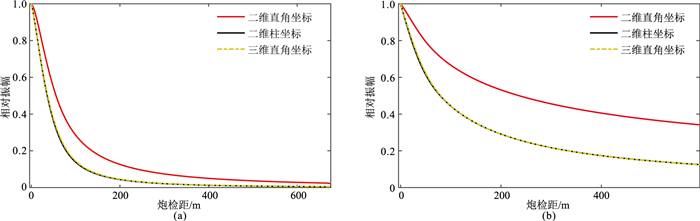
由图 8可知,随炮检距增加,弹性波振幅在柱坐标下比在二维直角坐标下衰减得更快。试验结果满足同等震源条件下球面扩散比柱面扩散速度更快的传播规律,进一步验证柱坐标下正演结果符合实际波场传播中能量的变化规律。
|
图 8 相对振幅随炮检距变化曲线 (a)水平分量;(b)垂直分量 |
对比简单模型中两种二维坐标系波场模拟的结果可知,柱坐标不仅能够表征现有二维直角坐标下的弹性波场特征,而且能够表征实际弹性波传播的能量、相位特征。通过波场快照及波形曲线两个角度的对比分析可见,二维柱坐标与三维直角坐标下的波场特征基本一致,但二维柱坐标下的波场正演更节省计算成本,正演速度更快。因此,对简单模型下利用柱坐标系进行波场正演研究具有准确、高效的优点。
1.3.2 Marmousi模型为进一步验证柱坐标系应用的可行性,采用Marmousi模型。网格尺寸为248×248,网格采样步长为5 m×5 m。时间采样率为0.5 ms,总采样时间为1.5 s。边界为ADE-PML吸收边界。在柱坐标系和直角坐标系中分别施加主频为20 Hz雷克子波。为适应实际的炮集处理流程,模拟单边接收,将震源放置在模型左上边界处(图 9),红点表示检波点。

|
图 9 局部Marmousi模型 |
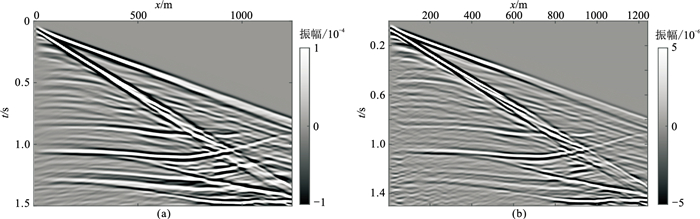
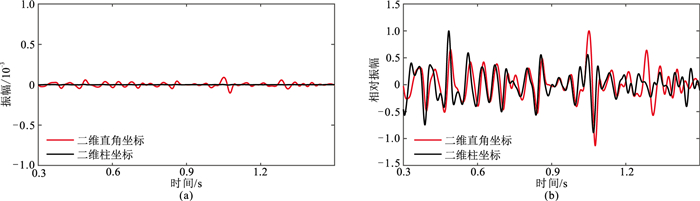
分析对比图 10、图 11,可知在两种坐标系下复杂模型的1.5 s全波场快照和地震记录除波场增益外差别不大。由图 12a可见,全波场中直达波能量过强无法清晰得到反射波波形,且柱坐标下反射波振幅小于直角坐标下的振幅。为进一步研究复杂模型下的反射波,分析去除直达波后的相对波形记录(图 12b)。在复杂模型中柱坐标下波的相位仍滞后于直角坐标,且随着时间增加,柱坐标下波形振幅衰减比直角坐标快。复杂模型下的反射波场与简单模型下的正演结果一致。

|
图 10 两种坐标系下水平分量1.5 s波场快照 (a)直角坐标;(b)柱坐标 |
|
图 11 两种坐标系下水平分量地震记录 (a)直角坐标;(b)柱坐标 |
|
图 12 第30道反射波水平分量 (a)波形记录;(b)相对波形记录 |
至此,通过均匀介质模型和Marmousi模型的正演波场,验证柱坐标系对两种模型下均能保证正演效果,实现波场正演,并体现三维弹性波波场的能量扩散特征及相位特征。
2 Rayleigh面波波场正演模拟 2.1 自由表面与面波生成机理地表空气与地球接触面是一个强阻抗界面。由于空气阻抗与固体地球阻抗相比非常小,故可将地表看作是自由表面[31-33],利用矩形网格可直接描述水平自由表面。本文使用隐式差分法处理边界条件,规避差分边界溢出问题。基于弹性波波动方程(式(6)),在自由边界处利用下式生成面波[5, 12, 34]
| $ \begin{aligned} & -\frac{\gamma}{16} u_{i+2, 0}^k+\left(1+\frac{\gamma}{8}\right) u_{i, 0}^k-\frac{\gamma}{16} u_{i-2, 0}^k \\ & =\frac{\gamma}{16} u_{i+2, 1}^k+\left(1-\frac{\gamma}{8}\right) u_{i, 1}^k+\frac{\gamma}{16} u_{i-2, 1}^k+ \\ & \quad \frac{1}{2}\left(w_{i+1, 1}-w_{i-1, 1}\right) \\ & -\frac{\gamma}{16} w_{i+2, 0}^k+\left(1+\frac{\gamma}{8}\right) w_{i, 0}^k-\frac{\gamma}{16} w_{i-2, 0}^k \\ & =\frac{\gamma}{16} w_{i+2, 1}^k+\left(1-\frac{\gamma}{8}\right) w_{i, 1}^k+\frac{\gamma}{16} w_{i-2, 1}^k+ \\ & \quad \frac{1}{2}\left(u_{i+1, 1}-u_{i-1, 1}\right) \end{aligned} $ | (15) |
式中:i为自由表面任一横向网格点位置;γ=λ/(λ+2μ)。
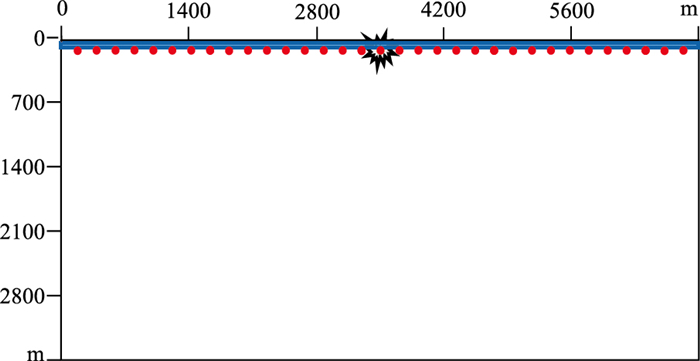
2.2 模型试验与分析假设模型顶面为自由表面,均匀上覆地层以下是均匀基底,模型上方为真空。建立坐标轴xOz(或rOz),为计算方便,假设x轴(或r轴)沿着顶面向右为正方向,z轴向下为其正方向。模型区域范围是7000 m×3500 m,网格采样步长为2 m×2 m,试验时间采样率为0.5 ms,总采样时间为1.5 s。模型中上覆地层深10 m,上覆地层纵波波速为2000 m/s,横波波速为1100 m/s;下伏地层纵波波速为2200 m/s,横波波速为1200 m/s,介质密度为2000 kg/m3。震源使用主频25 Hz的雷克子波,置于上覆地层底面中心处(图 13)所示。
|
图 13 面波试算模型 |
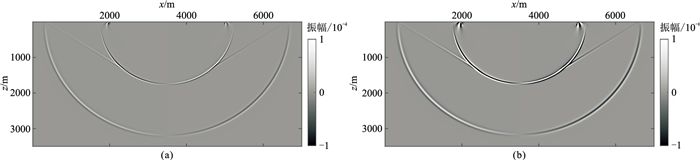
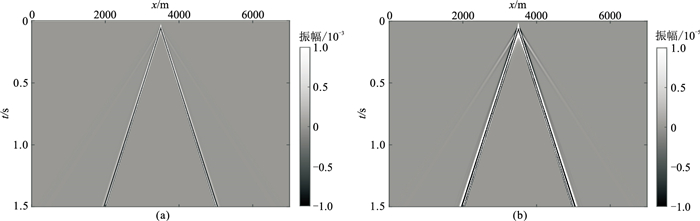
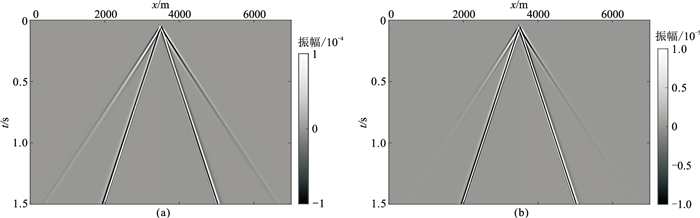
由图 14~图 17可见,两种坐标系下的波场快照和地震记录都基本相同。这表明地震波场在柱坐标系和直角坐标系下有相同的波场模拟效果,进一步验证柱坐标系能够模拟地震波的传播。但不同坐标系下波场增益范围有明显区别(参见色标数值),柱坐标下的面波波场比直角坐标下小近两个数量级,即坐标系变化对面波波场有明显影响。
|
图 14 水平分量1.5 s波场快照 (a)直角坐标;(b)柱坐标 |

|
图 15 垂直分量1.5 s波场快照 (a)直角坐标;(b)柱坐标 |
|
图 16 垂直分量地震记录 (a)直角坐标;(b)柱坐标 |
|
图 17 两种坐标系下水平分量地震记录 (a)直角坐标;(b)柱坐标 |
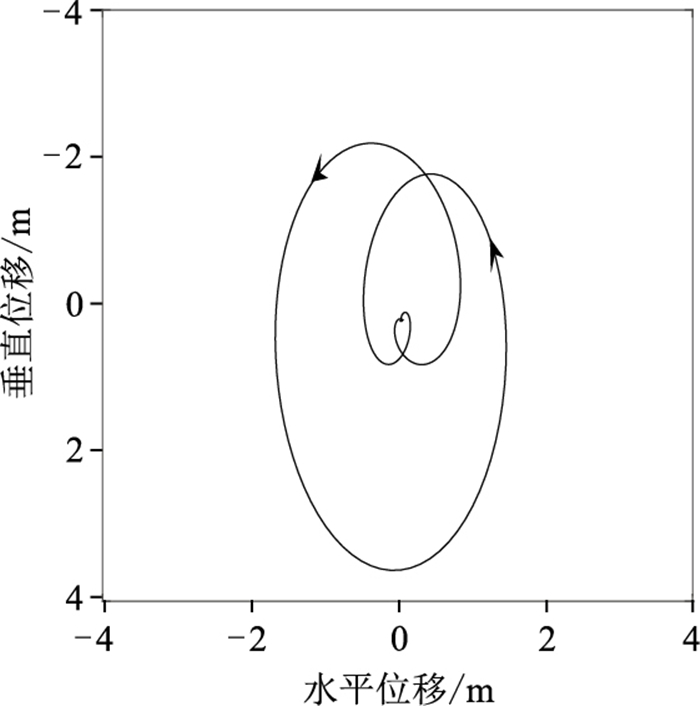
抽取4500 m处质点在不同时刻的位移(图 18),可见质点沿逆时针方向运动,其方向与波的传播方向相反,其轨迹形状近似为主轴垂直的椭圆。该结果表明地表质点运动轨迹与理论一致,模拟所得波场为面波。
|
图 18 地表4500 m处质点的运动轨迹 |
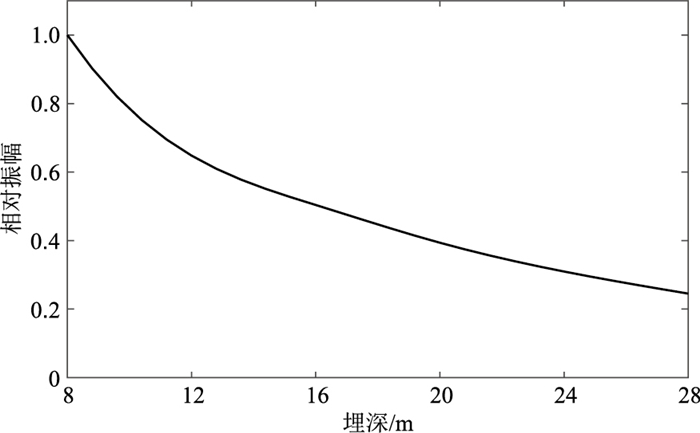
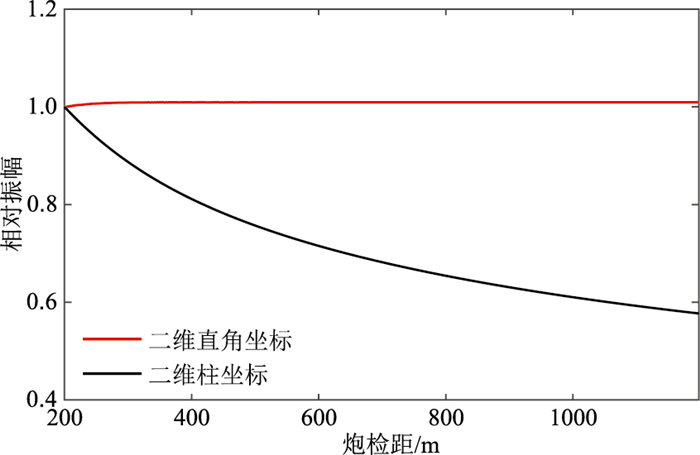
此外,采用不同深度激发、同一点接收的方式研究模拟激发深度对面波能量的关系,得到面波振幅与激发深度之间的关系(图 19)。从图中可见地表激发时会产生较强的面波,随着炮点埋深的增加,产生的面波振幅迅速减小。从图 16中提取面波的垂直振幅,得到振幅随炮检距的变化关系如图 20所示。可以看出,随炮检距的增加,柱坐标系下模拟得到的面波振幅发生衰减,而直角坐标系下模拟得到的面波振幅基本不变。由于二维柱坐标下面波以柱面形式传播,二维直角坐标下面波以平面形式传播,而随着波前的扩散,柱面波波前上一点能量越来越小,平面波没有几何扩散效应,其波前上一点能量不会发生改变。结合邓瑞[35]利用势函数求解波动方程,其在均匀介质中的计算结果显示面波在水平方向具有衰减现象。上述结果说明柱坐标的模拟结果体现三维空间中面波波场能量的几何扩散特征,符合实际情况。
|
图 19 垂直分量波形振幅随炮点埋深变化曲线 |
|
图 20 垂直分量波形振幅随炮检距变化曲线 |
本文研究实现柱对称条件下弹性波传播及面波正演,并对比二维柱坐标系与二维直角坐标系下的地震波场。模型试验和理论分析结果表明:
(1) 在均匀模型和Marmousi模型中,两种坐标系下模拟结果的波形基本一致,即利用柱坐标实现二维波场模拟具有可行性;
(2) 在均匀模型中,二维直角坐标下波形曲线比二维柱坐标的相位超前45°、振幅小两个数量级。结合理论分析可验证二维直角坐标下的模拟波场在能量和相位特征上与实际不符。而利用柱坐标系可等效模拟三维空间中地震波传播的振幅几何衰变,在能量和相位的变化上具备基本的三维特征,可提高正演效率,降低三维模拟的计算成本。
本文提出利用柱坐标实现波场正演的方法能够推动对实际波场的相关研究,有可能获得新的认识,或新的实际应用方案,但其相对于常规二维直角坐标的波场在计算上更复杂。因此,在后续的研究中可考虑将柱坐标方法拓展到层状介质正反演中,进一步发挥柱坐标的优势,提高计算效率。
| [1] |
RAYLEIGH L. On waves propagated along the plane surface of an elastic solid[J]. Proceedings of the London Mathematical Society, 1885, s1-17(1): 4-11. DOI:10.1112/plms/s1-17.1.4 |
| [2] |
HASKELL N A. The dispersion of surface waves on multilayered media[J]. Bulletin of the Seismological Society of America, 1953, 43(1): 17-34. DOI:10.1785/BSSA0430010017 |
| [3] |
ABO-ZENA A. Dispersion function computations for unlimited frequency values[J]. Geophysical Journal International, 1979, 58(1): 91-105. DOI:10.1111/j.1365-246X.1979.tb01011.x |
| [4] |
席超强. 复杂地形条件下面波探查技术研究与应用[D]. 安徽淮南: 安徽理工大学, 2017. XI Chaoqiang. Surface Wave Detection Research and Application Technology of Complex Terrain Condition[D]. Anhui University of Science and Technology, Huainan, Anhui, 2017. |
| [5] |
唐圣松. 二维起伏地表模型瑞雷波场正演研究[D]. 湖南长沙: 中南大学, 2009. TANG Shengsong. Study on Rayleigh-wave Filed Forward of Two-dimensional Rolling Ground Modal[D]. Central South University, Changsha, Hunan, 2009. |
| [6] |
冀月飞. 粘弹介质瑞利面波模拟及频散特征研究[D]. 陕西西安: 长安大学, 2012. JI Yuefei. Forward Modeling of Rayleigh Waves under Viscoelastic Medium and It's Dispersion Characteristics[D]. Chang'an University, Xi'an, Shaanxi, 2012. |
| [7] |
董晋. 粘弹介质勒夫波频散曲线正反演研究[D]. 陕西西安: 长安大学, 2017. DONG Jin. Inversion and Dispersion Curve Simulation of Love Waves in Viscoelastic Media[D]. Chang'an University, Xi'an, Shaanxi, 2017. |
| [8] |
贾宗锋, 吴国忱, 李青阳, 等. 标量波方程广义有限差分正演模拟[J]. 石油地球物理勘探, 2022, 57(1): 101-110. JIA Zongfeng, WU Guochen, LI Qingyang, et al. Forward modeling of scalar wave equation with genera-lized finite difference method[J]. Oil Geophysical Prospecting, 2022, 57(1): 101-110. |
| [9] |
吴悠, 吴国忱, 李青阳, 等. 频率—空间域非均质声波有限差分模拟[J]. 石油地球物理勘探, 2022, 57(2): 342-356. WU You, WU Guochen, LI Qingyang, et al. A finite-difference scheme in frequency-space domain to solve heterogeneous acoustic wave equation[J]. Oil Geophysical Prospecting, 2022, 57(2): 342-356. |
| [10] |
杨尚倍, 白超英, ZHOU Bing. 时间域广义2.5D一阶波动方程曲网格有限差分法数值模拟[J]. 石油地球物理勘探, 2021, 56(6): 1262-1278. YANG Shangbei, BAI Chaoying, ZHOU Bing. Curvilinear-grid finite-difference numerical simulation method for generalized first-order 2.5D timedomain wave equation[J]. Oil Geophysical Prospecting, 2021, 56(6): 1262-1278. |
| [11] |
杨凌云, 吴国忱, 李青阳. 高效优化非分裂PML边界二阶标量波方程数值模拟方法[J]. 吉林大学学报(地球科学版), 2019, 49(6): 1755-1767. YANG Lingyun, WU Guochen, LI Qingyang. Efficient optimization of second order scalar wave equation numerical simulation for non-splitting PML boundary[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(6): 1755-1767. |
| [12] |
袁士川, 宋先海, 蔡伟, 等. 瑞雷波有限差分数值模拟中不同自由表面边界条件的对比[J]. 石油地球物理勘探, 2017, 52(6): 1156-1169. YUAN Shichuan, SONG Xianhai, CAI Wei, et al. Comparison of different free-surface boundary conditions for Rayleigh waves finite-difference modeling[J]. Oil Geophysical Prospecting, 2017, 52(6): 1156-1169. |
| [13] |
MITTET R. Free-surface boundary conditions for elastic staggered-grid modeling schemes[J]. Geophy-sics, 2002, 67(5): 1616-1623. |
| [14] |
周竹生, 刘喜亮, 熊孝雨. 弹性介质中瑞雷面波有限差分法正演模拟[J]. 地球物理学报, 2007, 50(2): 567-573. ZHOU Zhusheng, LIU Xiliang, XIONG Xiaoyu. Finite-difference modelling of Rayleigh surface wave in elastic media[J]. Chinese Journal of Geophysics, 2007, 50(2): 567-573. |
| [15] |
傅承义. 地球介质中的面波与导波(综述)[J]. 声学学报, 1965, 2(2): 49-55. FU Chengyi. Surface and guided waves in the earth medium (review)[J]. Acta Acustica, 1965, 2(2): 49-55. |
| [16] |
HIXON R, SHIH S H, MANKBADI R R. Numerical treatment of cylindrical coordinate centerline singula-rities[J]. International Journal of Computational Fluid Dynamics, 2001, 15(3): 251-263. DOI:10.1080/10618560108970032 |
| [17] |
朱翠玉. 感应加热技术的应用及有限差分研究[D]. 辽宁沈阳: 沈阳航空航天大学, 2013. ZHU Cuiyu. Application of Induction Heating Technology and Research of Finite Difference[D]. Shen-yang Aerospace University, Shenyang, Liaoning, 2013. |
| [18] |
何柏荣, 冯德益. 柱坐标系下求解三维弹性波场的部分分离变量—分步差分方法[J]. 计算物理, 1993, 10(3): 297-308. HE Bairong, FENG Deyi. The partial separation of variables-fractional steps difference method for solving 3-dimensional elastic wave field in cylindrical coor-dinate system[J]. Chinese Journal of Computation Physics, 1993, 10(3): 297-308. |
| [19] |
张碧星, 喻明, 熊伟. 多层介质地层中有低速层出现时的陷模研究[J]. 中国有色金属学报, 1998, 8(2): 340-346. ZHANG Bixing, YU Ming, XIONG Wei. Trapped modes in multilayered media included a low velocity formation[J]. The Chinese Journal of Nonferrous Metals, 1998, 8(2): 340-346. |
| [20] |
BUCHANAN G R. Free vibration of an infinite magneto-electro-elastic cylinder[J]. Journal of Sound and Vibration, 2003, 268(2): 413-426. |
| [21] |
陈江义, 陈花玲. 多层电磁弹性圆柱壳内波的轴向传播[J]. 应用力学学报, 2007, 24(2): 175-179. CHEN Jiangyi, CHEN Hualing. Wave propagation along axis of magneto-electro-elastic multilayered cy-linder[J]. Chinese Journal of Applied Mechanics, 2007, 24(2): 175-179. |
| [22] |
田保林. 柱坐标下Euler方程数值边界条件的一种处理方法[J]. 计算物理, 2006, 23(6): 717-720. TIAN Baolin. Numerical boundary condition of euler equations in cylindrical coordinate[J]. Chinese Journal of Computational Physics, 2006, 23(6): 717-720. |
| [23] |
MA Y M, YU J H, WANG Y Y. A novel unsplit perfectly matched layer for the second-order acoustic wave equation[J]. Ultrasonics, 2014, 54(6): 1568-1574. |
| [24] |
WENG C C, WEEDON H W. A 3D perfectly matched medium from modified maxwell's equations withstretched coordinates[J]. Microwave and Optical Technology Letters, 1994, 7(13): 599-604. |
| [25] |
FRANCIS C, CHRYSOULA T. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307. |
| [26] |
孙成禹, 闫月锋, 蓝阳. 基于CFS-CPML边界处理的LOVE面波有限差分模拟[J]. 地球物理学进展, 2015, 30(6): 2558-2565. SUN Chengyu, YAN Yuefemg, LAN Yang. Finite difference modeling of Love waves based on CFS-CPML boundary processing[J]. Progress in Geophy-sics, 2015, 30(6): 2558-2565. |
| [27] |
马友能, 余锦华, 汪源源. 二阶声场波动方程的非分裂完全匹配层算法[J]. 声学学报, 2013, 38(6): 681-686. MA Youneng, YU Jinhua, WANG Yuanyuan. Unsplit perfectly matched layer for acoustic field simulation based on second-order wave equation[J]. Acta Acustica, 2013, 38(6): 681-686. |
| [28] |
李佩笑, 林伟军, 张秀梅, 等. 常规分裂和非分裂完全匹配层吸收边界比较研究[J]. 声学学报, 2015, 40(1): 44-53. LI Peixiao, LIN Weijun, ZHANG Xiumei, et al. Comparisons for regular splitting and non-splitting perfectly matched layer absorbing boundary conditions[J]. Acta Acustica, 2015, 40(1): 44-53. |
| [29] |
姚铭, 汪勇, 杨晓柳, 等. 不同边界条件下的二维声波方程数值模拟[J]. 科学技术与工程, 2017, 17(32): 11-16. YAO Ming, WANG Yong, YANG Xiaoliu, et al. Numerical simulation of two-dimensional acoustic equation under different boundary conditions[J]. Science Technology and Engineering, 2017, 17(32): 11-16. |
| [30] |
刘君, 魏雁昕, 韩芳. 有限差分法的坐标变换诱导误差[J]. 航空学报, 2021, 42(6): 1-16. LIU Jun, WEI Yanxin, HAN Fang. Coordinate transformation induced errors of finite difference method[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(6): 1-16. |
| [31] |
张立. 近地表介质对勘探地震波场的影响研究[D]. 山东青岛: 中国石油大学(华东), 2012. ZHANG Li. Influence of Near-surface Media on Seismic Wave Field in Exploration[D]. China University of Petroleum(East China), Qingdao, Shandong, 2012. |
| [32] |
王周, 李朝晖, 龙桂华, 等. 求解弹性波有限差分法中自由边界处理方法的对比[J]. 工程力学, 2012, 29(4): 77-83. WANG Zhou, LI Zhaohui, LONG Guihua, et al. Comparison among implementations of free-surface boun-dary in elastic wave simulation using the finite-difference method[J]. Engineering Mechanics, 2012, 29(4): 77-83. |
| [33] |
LAN H Q, ZHANG Z J. Comparative study of the free-surface boundary condition in two-dimensional finite-difference elastic wave field simulation[J]. Journal of Geophysics and Engineering, 2011, 8(2): 275-286. |
| [34] |
ZHANG Y, PING P, DENG P, et al. A free surface formulation for finite difference modeling of surface waves in porous media[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 2406-2411.
|
| [35] |
邓瑞. 横向非均匀介质多模态瑞利面波波场数值模拟研究[D]. 四川成都: 西南交通大学, 2020. DENG Rui. Finite Element Numerical Simulation of the Wave Field of Multiple-mode Rayleigh Wave for Lateral Inhomogeneous Medium[D]. Southwest Jiaotong University, Chengdu, Sichuan, 2020. |



 孙成禹, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
孙成禹, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email: