随着勘探程度的不断加深,断层、裂缝、孔洞、尖灭等小尺度地质体对于油气勘探至关重要,而散射波场能够精确刻画这些非均质的小尺度地质体[1-2]。渤中A凝析气田目的层主要为太古界变质岩潜山[3],平均埋深为4500 m,上覆砂砾岩、火成岩,内幕地质体难以准确识别。常规基于反射波处理的地震资料信噪比低,且潜山地震速度建模精度低,潜山内幕地震反射难以准确归位,成像效果差,仅依靠反射信息难以有效预测内幕裂缝储层的展布规律。在地震数据处理过程中,散射波场常视为噪声而被滤除。为充分利用散射波场信息,在叠前将散射波从全波场数据中分离出来,单独偏移成像,能够有效提高非均质小尺度地质体成像分辨率。
地球物理学家Krey[4]最早在研究断层、尖灭等不连续地质体时发现反射波与散射波混叠。近几十年来,对散射波的重视程度不断加深,根据散射波场的动力学和运动学特征,学者们提出众多叠后、叠前散射波分离方法。常规叠后提取方法主要通过识别散射波在叠加或偏移剖面上的振幅、相位等特征与反射波的差异,进行散射信息分离,如基于共反射面的分离方法[5]、基于偏移倾角域的分离方法[6-10]和主成分分析法[11]、扩散滤波方法[12]等。叠前散射波分离方法主要有基于不同域内的倾角滤波分离方法[13-16]、基于平面波域的滤波分离方法[17-18]等,主要利用了变换域内反射波与散射波存在的特征差异实现反射波与散射波的分离。
近年来,基于倾角滤波的分离方法被广泛应用,其主要利用变换域内散射波与反射波的倾角差异进行滤波,但散射波能量损失大,成像后保幅效果差,且变换过程中易产生假频噪声,导致散射波场包含大量噪声干扰,难以在处理过程中滤除。2016年,陈杰[19]首次将数学形态学方法应用于叠后散射波场分离,取得了较好效果。
本文提出在叠前共炮检距道集上利用形态滤波实现散射波分离。首先在叠前共炮检距道集分析、确定散射波与反射波的形态特征差异,散射波表现为双曲线,反射波则表现为线性;然后利用这一形态差异构建直线形结构元素;再沿空间方向做形态滤波,获得反射波;最后将反射波从原始波场中减去,就得到了散射波。模型正演数据测试验证了本文方法的有效性,避免了常规倾角滤波方法导致的散射波能量损失大的问题。
将本文方法应用于渤中A凝析气田太古界潜山内幕地震资料,散射波成像结果能够有效预测潜山内幕裂缝储层的展布规律,与已钻井结果吻合,为渤中A凝析气田太古界潜山的勘探开发提供了有力的支持。
1 方法原理数学形态学滤波是一种信号处理方法,为膨胀、腐蚀、开启和闭合四个基本运算的平均组合,运算过程是求矩阵的极小和极大。王润秋等[20-21]将数学形态学引入地震资料处理中并得到广泛应用,为使用形态滤波方法进行地震信号处理提供了理论基础。
将任意时刻的共炮检距道集地震数据记为g={g(n′)},n′∈[0,M],M为道数;将结构元素记为s={s(n)},n∈[-N,N],2N为结构元素宽度。
将用s对g进行膨胀运算定义为
| $ \boldsymbol{g} \oplus \boldsymbol{s}=\max \left\{g\left(n^{\prime}-n\right)+s(n)\right\} $ | (1) |
式中“⊕”为膨胀运算符。膨胀运算可以表述为反折、平移结构元素与地震数据对应求和再求极大。
用s对g进行腐蚀运算定义为
| $ \boldsymbol{g} \Theta \boldsymbol{s}=\min \left\{g\left(n^{\prime}+n\right)-s(n)\right\} $ | (2) |
式中“Θ”为腐蚀运算符。腐蚀运算可以表述为反折、平移结构元素与地震数据对应求差再求极小。
开启运算和闭合运算是膨胀和腐蚀运算的组合。用s对g进行开启运算定义为
| $ \boldsymbol{g} \circ \boldsymbol{s}=(\boldsymbol{g} \Theta \boldsymbol{s}) \oplus \boldsymbol{s} $ | (3) |
式中“
| $ \boldsymbol{g} • \boldsymbol{s}=(\boldsymbol{g} \oplus \boldsymbol{s}) \Theta \boldsymbol{s} $ | (4) |
式中“•”为闭合运算符号。
数学形态学滤波可表示为开启运算和闭合运算的组合再取平均,即
| $ F(\boldsymbol{g})=\frac{1}{2}[(\boldsymbol{g} \circ \boldsymbol{s} • \boldsymbol{s})+(\boldsymbol{g} • \boldsymbol{s} \circ \boldsymbol{s})] $ | (5) |
由式(5)可以看出,结构元素是形态滤波方法的唯一变量,影响滤波效果。所以,针对不同的信号选取不同的结构元素进行滤波至关重要,以达到最好的分离效果。
结构元素可以是任意形态的信号,但考虑到地震信号的波形特征,定义结构元素为非凹函数,并关于原点对称。常使用的三种结构元素:直线形结构元素、半椭圆形结构元素和三角形结构元素,分别为
| $ s_1(x)=A $ | (6) |
| $ s_{\mathrm{e}}(x)=A \sqrt{1-\left(\frac{x}{W}\right)^2} $ | (7) |
| $ s_{\mathrm{t}}(x)=A\left(1-\left|\frac{x}{W}\right|\right) $ | (8) |
式中:A是高度,对应地震信号的振幅;W是结构元素宽度,对应地震信号的道数。
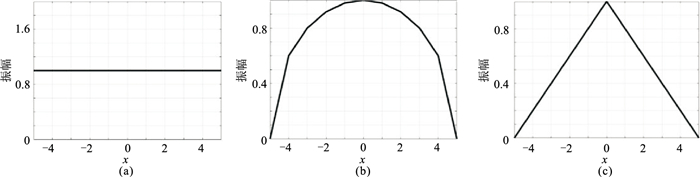
假设结构元素的高度和宽度分别为1和11,常用的三种结构元素如图 1所示,可以看出皆为非凹图形。三种结构元素形态特征有差别,改变其形状、高度和宽度可以影响滤波效果。
|
图 1 常用的三种结构元素 (a)直线形;(b)半椭圆形;(c)三角形 |
在叠前共炮检距道集上,散射波与反射波的显著差异是时距曲线形态不同,后者为直线,前者为双曲线,根据这一明显差异,本文选择直线形结构元素。
结构元素的形态尺度是数学形态学滤波方法分离散射波与反射波的关键,越接近信号的形态尺度,越能分离出完整的信号。结构元素的选取要根据实际地震数据测试具体参数,以达到最好滤波效果。
用直线形结构元素沿空间方向对地震数据进行数学形态学滤波,可获得反射波数据;用原始地震数据减去反射波数据,就得到散射波。
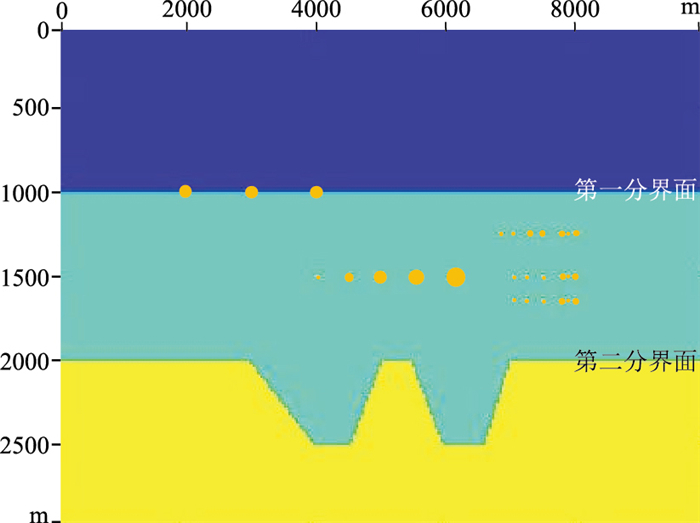
2 数据测试 2.1 模型数据测试为了直观表征散射波分离和成像效果,设计了简单层状模型(图 2)。三层的速度分别为3000、3500、4000 m/s,密度使用经验公式计算。在第一分界面上每隔1000 m加入三个直径为15 m的孔洞,速度为4000 m/s;在第二层中部每隔500 m加入直径为5、10、15、20、30 m的五个孔洞,相隔1000 m加入一破碎带,速度均为4000 m/s;第二界面存在四条断层。使用主频为30 Hz的Ricker子波,利用声波方程正演了141炮数据,起始炮点位于(0,0),炮间距为50 m,道间距为25 m,最小炮检距为0,最大炮检距为3000 m,单边接收,时间采样间隔为2 ms。抽取炮检距为1500 m的道集,如图 3所示。
|
图 2 简单模型 |
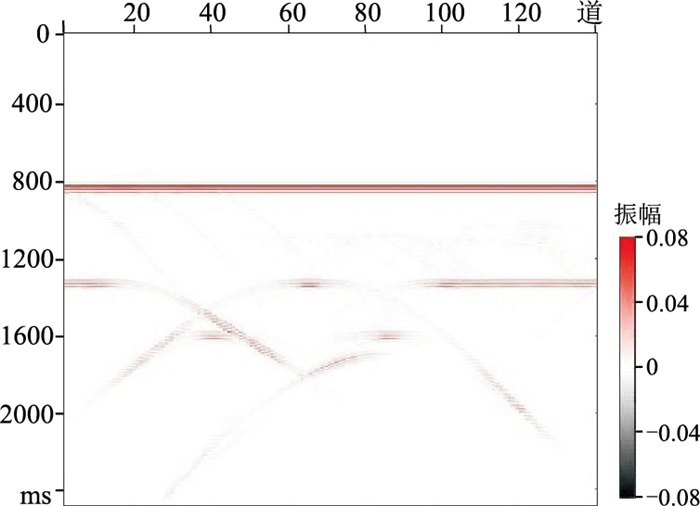
|
图 3 简单模型正演的共炮检距道集 |
对比图 2与图 3可以看出,水平地层、大断层在全波场中表现为反射波,形态特征为直线。孔洞、破碎带等小的地质体表现为散射波,形态特征为双曲线,能量明显弱于反射波,较难以分辨。
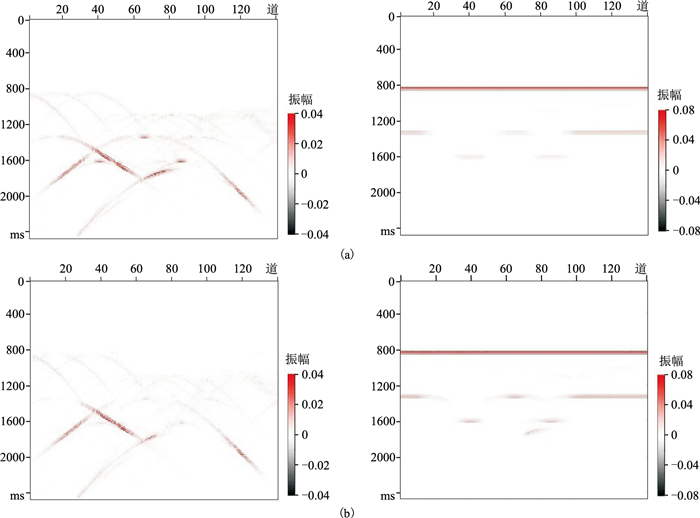
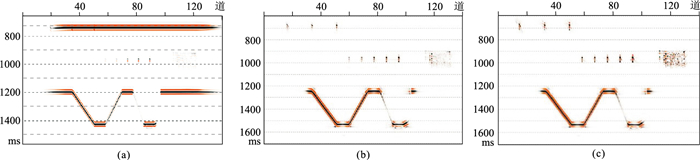
用直线形结构元素对共炮检距道集数据沿空间方向进行形态滤波,分离后的散射波和反射波如图 4a所示,与倾角滤波方法的分离结果(图 4b)相比,形态滤波方法分离的散射波顶点能量损失更小,波场更完整,精度更高。与全波场叠前时间偏移剖面(图 5a)相比,散射波成像结果(图 5b、图 5c)对小尺度、非均匀地质体,如孔洞、破碎带、断层等不连续地质体,具有明显的成像优势。基于形态滤波的散射波成像结果(图 5c)由于保留了更丰富的散射波信息,与图 5b相比,能量更强。
|
图 4 模型数据形态滤波(a)和倾角滤波(b)分离的散射波(左)与反射波(右)结果 |
|
图 5 模型数据成像结果对比 (a)全波场;(b)倾角滤波的散射波;(c)形态滤波的散射波 |
受构造运动影响,渤中A凝析气田太古界潜山内幕裂缝储层发育。成像测井解释内幕裂缝密度为2~5条/m,走向以北东向为主,倾角范围为38°~55°。内幕裂缝储层速度为4800~5300 m/s,密度为2.55~2.65 g/cm3,孔隙度为0.2%~21.9%(均值为4.4%),渗透率为(0.003~614.784)×10-3 μm2(均值为5.050×10-3 μm2),非均质性强。在基于反射波处理的地震资料中,潜山内幕整体呈杂乱断续反射特征,局部可见明显断续、高陡反射特征,受散射影响较大,难以准确预测裂缝储层。
图 6a为渤中A凝析气田的共炮检距(1500 m)道集,存在散射波和反射波,但散射波能量明显较弱,且深层地震信号更弱,难以识别有效波场信息。利用局部倾角滤波方法分离的散射波如图 6b所示,能够有效提取深层的散射波能量,但散射波断续,在反射波与散射波重合处,散射波很难有效分离。利用形态滤波方法分离的散射波如图 6c所示,同样能够有效提取深层的散射波能量,与图 6b相比,散射波保留得更完整,更有利于非均质地质体的成像。

|
图 6 实际资料不同方法分离的散射波共炮检距道集对比 (a)全波场;(b)倾角滤波;(c)形态滤波 |
图 7a为原始的全波场数据叠前时间偏移剖面,潜山内幕裂缝带表现为杂乱断续反射,高陡反射不明显,裂缝储层发育处反射能量弱,无法准确识别裂缝储层。局部倾角和形态滤波法分离的散射波成像结果分别如图 7b、图 7c所示,内幕裂缝带表现为高陡反射,分辨率高,储层发育处散射波能量强,能有效表征裂缝储层发育特征,改善了深层断裂与裂缝发育带的成像效果。与图 7b相比,图 7c对高陡断裂、裂缝带等非均质体的成像更清晰,为深层不同尺度裂缝储层精细表征提供了较好的资料基础。

|
图 7 实际资料不同方法分离的散射波偏移剖面对比 (a)全波场;(b)倾角滤波散射波波场;(c)形态滤波散射波波场 |
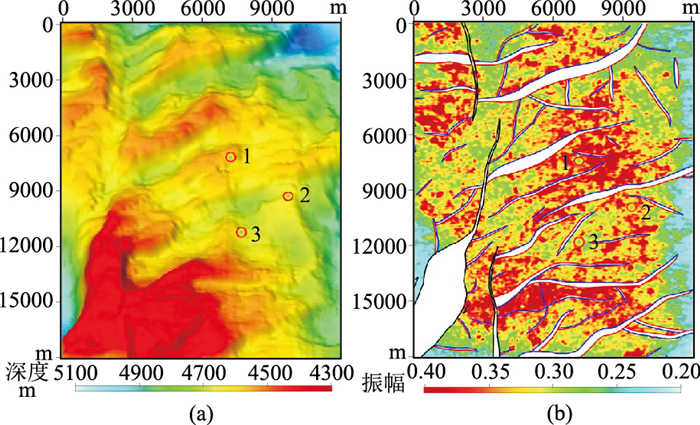
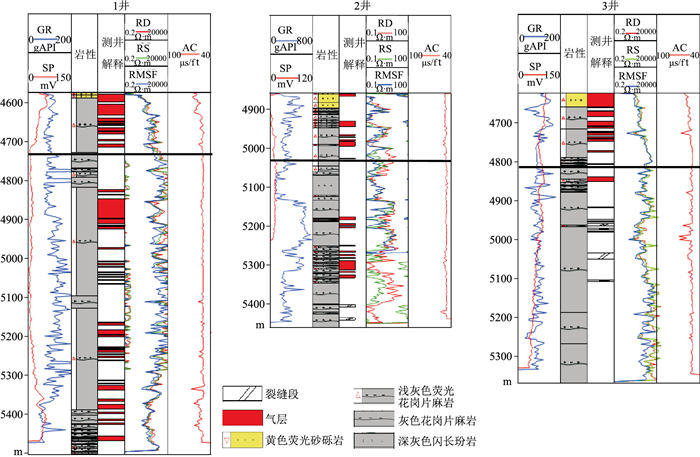
通过提取平面振幅属性并对比潜山面构造特征与已钻井结果,进一步验证本文方法裂缝储层的表征效果。通过地震构造解释获得潜山面的构造图如图 8a所示,1、2、3井均靠近断层,但1、2井在构造高点,3井在斜坡上。对使用形态滤波方法提取的散射波数据成像结果沿潜山面以下50 ms提取时窗长度为200 ms的均方根振幅,得到潜山内幕的散射波振幅属性,如图 8b所示。1井处于大范围裂缝发育区的构造高点,储层发育;2井裂缝也相对发育;3井处,裂缝较不发育。1、2和3井的钻、测井结果如图 9所示,1、2和3井在潜山内幕钻遇裂缝储层的净毛比分别为18.4%、14.5%和8.7%。分析图 8、图 9可以看出,裂缝带储层主要集中发育在构造高部位和断层附近。平面振幅属性与构造圈闭、三口已钻井结果吻合较好。基于形态滤波的潜山内幕裂缝储层预测结果为渤中A凝析气田井位部署提供了技术支持。
|
图 8 潜山顶面构造图(a)与内幕裂缝储层分布预测结果(b) 图b蓝色实线为断层上盘,红色实线为断层下盘,高振幅指示裂缝发育区。 |
|
图 9 1、2和3井的太古界钻、测井解释结果 黑色实线以下为潜山内幕。GR、SP、RD、RS、RMSF、AC分别为自然伽马、自然电位、深侧向电阻率、浅侧向电阻率、微侧向电阻率、声波时差测井曲线。 |
本文利用反射波与散射波的形态差异构建直线形结构元素,在叠前共炮检距道集沿空间方向进行形态滤波,实现了散射波与反射波的分离。由模型和实际地震资料处理结果可得出以下结论。
(1) 相较于常规基于倾角滤波的散射波分离方法,本文的基于形态滤波分离方法得到的散射波场较完整,精度更高,改善了散射波的分离效果。
(2) 对于潜山内幕裂缝带储层,常规反射波方法表征效果差、精度低;本文方法的散射波成像结果保留了更多的由于地层非均质性引起的散射信息,有效改善了潜山内幕成像效果。
(3) 与反射波成像相比,散射波成像分辨率高,高陡界面成像清晰,可用于描述裂缝带储层,对海上潜山勘探、评价具有较高的应用、推广价值。
| [1] |
徐德奎, 何玉, 郑江峰. 基于绕射波的断层识别方法应用[J]. 物探与化探, 2016, 40(4): 783-787. XU Dekui, HE Yu, ZHENG Jiangfeng. A method based on diffraction wave for fault identification and its application[J]. Geophysical and Geochemical Exploration, 2016, 40(4): 783-787. |
| [2] |
陈明政, 邓光校, 朱生旺, 等. 绕射波分离成像技术在塔河油田碳酸盐岩地震弱反射储层预测中的应用[J]. 石油物探, 2015, 54(2): 234-240. CHEN Mingzheng, DENG Guangjiao, ZHU Shengwang, et al. Application of diffraction wave separation and imaging technique in weak seismic reflection of carbonate reservoir prediction in Tahe Oilfield[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 234-240. DOI:10.3969/j.issn.1000-1441.2015.02.016 |
| [3] |
薛永安, 李慧勇. 渤海海域深层太古界变质岩潜山大型凝析气田的发现及其地质意义[J]. 中国海上油气, 2018, 30(3): 1-9. XUE Yongan, LI Huiyong. Large condensate gas field in deep Archean metamorphic buried hill in Bohai sea: discovery and geological significance[J]. China Offshore Oil and Gas, 2018, 30(3): 1-9. |
| [4] |
KREY T. The significance of diffraction in the investigation of faults[J]. Geophysics, 1952, 17(4): 843-858. DOI:10.1190/1.1437815 |
| [5] |
ASGEDOM E G, GELIUS L J, AUSTENG A, et al. A new approach to post-stack diffraction separation[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 3861-3865.
|
| [6] |
罗腾腾, 徐基祥, 秦臻, 等. 混合域高分辨率Radon变换及其在绕射波分离与成像中的应用[J]. 石油物探, 2020, 59(6): 890-900. LUO Tengteng, XU Jixiang, QIN Zhen, et al. Hybrid-domain high-resolution Radon transform and its application in diffraction wave separation and imaging[J]. Geophysical Prospecting for Petroleum, 2020, 59(6): 890-900. DOI:10.3969/j.issn.1000-1441.2020.06.007 |
| [7] |
罗腾腾, 徐基祥, 孙夕平. 应用迭代收缩高分辨率Radon变换的绕射波分离与成像方法[J]. 石油地球物理勘探, 2021, 56(2): 313-322. LUO Tengteng, XU Jixiang, SUN Xiping. Diffraction wave separation and imaging based on high-resolution Radon transform on an iterative model shrinking approach[J]. Oil Geophysical Prospecting, 2021, 56(2): 313-322. DOI:10.13810/j.cnki.issn.1000-7210.2021.02.013 |
| [8] |
ZHU X S, WU R S. Imaging diffraction points using the local image matrices generated in prestack migration[J]. Geophysics, 2010, 75(1): S1-S9. DOI:10.1190/1.3277252 |
| [9] |
严天凡, 刘伊克. 角度域裂缝散射波成像及参数反演[C]. 第四届油气地球物理学术年会论文集, 2021, 561-564. YAN Tianfan, LIU Yike. Scattered wave imaging and parameter inversion of fractures in angle domain[C]. Proceedings of the Fourth Annual Conference on Oil and Gas Geophysics, 2021, 561-564. |
| [10] |
朱万怡, 王华忠, 吴成梁, 等. 基于行波分解的绕射波成像方法研究[J]. 石油物探, 2020, 59(2): 226-235. ZHU Wanyi, WANG Huazhong, WU Chengliang, et al. Diffraction imaging based on wavefield decomposi-tion[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 226-235. DOI:10.3969/j.issn.1000-1441.2020.02.008 |
| [11] |
张志军, 肖广锐, 李尧. 渤中19-6油田变质岩潜山内幕裂缝地震响应特征及预测技术[J]. 石油地球物理勘探, 2021, 56(4): 845-852. ZHANG Zhijun, XIAO Guangrui, LI Yao. Seismic response characteristics and prediction of fractured re-servoir inside metamorphic buried hill of Bozhong 19-6 oilfield[J]. Oil Geophysical Prospecting, 2021, 56(4): 845-852. DOI:10.13810/j.cnki.issn.1000-7210.2021.04.018 |
| [12] |
陈可洋, 杨微, 吴清岭, 等. 地震反射波与散射波波场分离方法初探[J]. 岩性油气藏, 2013, 25(2): 76-81. CHEN Keyang, YANG Wei, WU Qingling, et al. Preliminary study on wave field separation of seismic reflection wave and scattered wave[J]. Lithologic Re-servoirs, 2013, 25(2): 76-81. DOI:10.3969/j.issn.1673-8926.2013.02.013 |
| [13] |
LANDA E, SHTIVELMAN V, GELCHINSKY B. A method for detection of diffracted waves on common-offset sections[J]. Geophysical Prospecting, 1987, 35(4): 359-373. DOI:10.1111/j.1365-2478.1987.tb00823.x |
| [14] |
LANDA E, KEYDAR S. Seismic monitoring of diffraction images for detection of local heterogeneities[J]. Geophysics, 1998, 63(3): 1093-1100. DOI:10.1190/1.1444387 |
| [15] |
朱生旺, 李佩, 宁俊瑞. 局部倾角滤波和预测反演联合分离绕射波[J]. 地球物理学报, 2013, 56(1): 280-288. ZHU Shengwang, LI Pei, NING Junrui. Reflection/diffraction separation with a hybrid method of local dip filter and prediction inversion[J]. Chinese Journal of Geophysics, 2013, 56(1): 280-288. |
| [16] |
BANSAL R, IMHOF M G. Diffraction enhancement in prestack seismic data[J]. Geophysics, 2005, 70(3): V73-V79. DOI:10.1190/1.1926577 |
| [17] |
TANER M T, FOMEL S, LANDA E. Separation and imaging of seismic diffractions using plane-wave decomposition[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2401-2405.
|
| [18] |
KONG X, WANG D Y, LI Z C, et al. Diffraction separation by plane-wave prediction filtering[J]. Applied Geophysics, 2017, 14(3): 399-405. DOI:10.1007/s11770-017-0634-9 |
| [19] |
陈杰. 形态学在地震解释构造特征提取中的应用研究[D]. 北京: 中国石油大学(北京), 2016. CHEN Jie. Mathematical Morphology Used in Extraction of Tectonic Feature When Interpreting Seismic Data[D]. China University of Petroleum (Beijing), Beijing, 2016. |
| [20] |
王润秋, 郑桂娟, 付洪洲, 等. 地震资料处理中的形态滤波去噪方法[J]. 石油地球物理勘探, 2005, 40(3): 277-282. WANG Runqiu, ZHENG Guijuan, FU Hongzhou, et al. Noise-eliminated method by morphologic filtering in seismic data processing[J]. Oil Geophysical Prospecting, 2005, 40(3): 277-282. DOI:10.3321/j.issn:1000-7210.2005.03.013 |
| [21] |
WANG R Q, LI Q, ZHANG M. Application of multi-scaled morphology in denoising seismic data[J]. Applied Geophysics, 2008, 5(3): 197-203. DOI:10.1007/s11770-008-0033-3 |



 张羽茹, 天津市滨海新区海川路2121号中海石油(中国)有限公司天津分公司渤海石油研究院300459。Email:
张羽茹, 天津市滨海新区海川路2121号中海石油(中国)有限公司天津分公司渤海石油研究院300459。Email: