2. 中国石油吐哈油田公司勘探开发研究院,新疆哈密 839009;
3. 中国石油西南油气田公司页岩气研究院,四川成都 610056
2. Research Institute of Petroleum Exploration and Development, Tuha Oil and Gas Field Company, PetroChina, Hami, Xinjiang 839009, China;
3. Shale Gas Research Institute, PetroChina Southwest Oil & Gas Field Company, Chengdu, Sichuan 610056, China
反褶积作为一种提高分辨率的处理方法,一直是研究的热点。Ramachandran等[1]给出了褶积的一般原则,为反褶积方法的发展奠定了基础。Ulrych[2]首次将同态变换应用于地震子波分离。乌尔里克等[3]进一步将同态理论应用于反褶积,取得了较好的效果。同态反褶积不需要假设子波为最小相位,也不需要假设反射系数具有白噪特征,因此受到了广泛关注。凌云等[4]提出了零相位同态反褶积算法;郭向宇等[5]利用同态反褶积法对混合相位子波进行了相位估算和矫正;王君等[6]将统计法同态反褶积与几种已有的方法结合起来,使混合相位反褶积向实用化更进了一步。
同态变换由于特有的优势得到了广泛应用。Liao等[7]将混合同态反褶积方法应用于实际断裂模型分析;王丹等[8]利用同态反褶积提取子波,以定位管道泄露;De Macedo等[9]结合同态反褶积和确定性估计的优势,结合测井数据更准确地预估了子波。同时,同态反褶积在医学信号处理领域也发挥了重要作用,Hernández[10]将同态反褶积算法应用于胎儿心率信号的分析;同态反褶积在声源定位中也能起到关键的作用[11]。
虽然同态反褶积具有较好的适用性,但是其抗噪能力较差,影响了应用效果。Jin等[12]首次从理论和实验两个方面分析了噪声对同态反褶积处理结果的影响,并对方法进行了改进。在实际数据中由于噪声的存在,很难准确确定子波和反射系数在同态谱中的界限,限制了方法的使用。因此,目前同态反褶积研究的关键问题是如何在同态域分离子波与反射系数。
模态分解方法是一种有效分析不同特征信号的方法。Huang等[13]提出了一种适用于非线性平稳信号分析的经验模态分解(EMD)方法,在信号处理研究中起到了重要的作用。Wu等[14]针对模态混叠现象提出了改进的EMD算法——集合经验模态分解方法(EEMD);Yeh等[15]对EEMD算法做了进一步改进,提出了一种互补集合经验模态分解方法,蔡俊雄等[16]将该方法用于地震数据去噪。Jegadeeshwaran等[17]提出的变分模态分解(Variational Mode Decomposition,VMD)方法,能够自适应地实现信号的频域划分及各分量的有效分离,表现出更强的抗噪能力。方江雄等[18]提出了基于频率域内全局自适应的VMD的地震随机噪声压制方法,实现了信号频带的高分辨率、自适应剖分;武迪等[19]提出了一种联合VMD与包络导数能量算子的高精度时频分析方法,能够将地震信号自适应、非递归地分解为一系列具有带限性质的固有模态函数(IMF),最终获取的时频分布能够追踪地震信号的能量变化,从而预测缝洞型储层。胡瑞卿等[20]将VMD方法应用于地震资料去噪,有效压制了随机背景噪声,同时对陡倾角线性干扰有明显的压制效果。针对VMD方法参数确定较难的问题,李华等[21]提出了基于信息熵的参数确定方法,马洪斌[22]采用包络熵与蛙跳算法相结合的优化方式,验证了以包络熵为判断标准确定最优预设参数的可行性。目前VMD方法主要应用于地震资料去噪处理,未见其他方面的应用。
本文利用VMD方法在信号分离方面的优势,结合同态变换特点,提出了一种基于VMD的同态反褶积方法,在同态域采用VMD算法自动分离子波与反射系数,以达到提高地震资料分辨率的目的。
1 方法原理 1.1 同态反褶积根据褶积模型,地震记录可以表示为
| $ x(t)=b(t) * r(t) $ | (1) |
式中:b(t)为地震子波;r(t)表示反射系数。将式(1)变换到频率域,为
| $ X(\omega)=B(\omega) \cdot R(\omega) $ | (2) |
再对两边取对数,可得
| $ \ln X(\omega)=\ln B(\omega)+\ln R(\omega) $ | (3) |
分别用
| $ \hat{X}(\omega)=\hat{B}(\omega)+\hat{R}(\omega) $ | (4) |
对式(4)进行反傅里叶变换,可得
| $ \hat{x}(t)=\hat{b}(t)+\hat{r}(t) $ | (5) |
| $ \hat{b}(t)= \begin{cases}\hat{x}(t) & |t| \leqslant L \\ 0 & |t|>L\end{cases} $ | (6) |
| $ \hat{r}(t)= \begin{cases}0 & |t| \leqslant L \\ \hat{x}(t) & |t|>L\end{cases} $ | (7) |
式中L为截止时间,一般取较小值。然后进行同态反变换就可获得时间域的子波和反射系数,即
| $ \left\{\begin{array}{l} \hat{R}(\omega)=\int \hat{r}(t) \exp (-\mathrm{i} \omega t) \mathrm{d} t \\ \hat{B}(\omega)=\int \hat{b}(t) \exp (-\mathrm{i} \omega t) \mathrm{d} t \end{array}\right. $ | (8) |
| $ \left\{\begin{array}{l} R(\omega)=\exp [\hat{R}(\omega)] \\ B(\omega)=\exp [\hat{B}(\omega)] \end{array}\right. $ | (9) |
| $ \left\{\begin{array}{l} r(t)=\int R(\omega) \exp (\mathrm{i} \omega t) \mathrm{d} \omega \\ b(t)=\int B(\omega) \exp (\mathrm{i} \omega t) \mathrm{d} \omega \end{array}\right. $ | (10) |
以上处理过程只是一种理想状况。通常情况下,子波和反射系数的同态谱难以通过一个简单的滤波器进行分离,特别是当数据中存在噪声时,同态反褶积方法在实际应用中效果不理想。
VMD能够自适应地实现信号的频域划分以及各分量的有效分离,并且抗噪性、对信号的敏感度都强于其他模态分解方法[23]。如果可以利用VMD方法更合理地分离同态域子波与反射系数,则可以有效提高同态反褶积的应用效果。
1.2 基于重构能量差的自适应VMD分解VMD方法在应用中,分解层数的确定是一个复杂的过程,通常需要进行多次实验。针对此问题,本文提出一种基于分解前、后能量差的自适应变分模态分解算法。如果分解层数过多,处理后信号与原始信号的能量差值会发生突变,因此通过判断能量差值是否发生突变以自适应确定分解层数。
信号的能量可表示为
| $ E=\sqrt{\frac{\sum\limits_{i=1}^N \mu^2(i)}{N}} $ | (11) |
式中:μ为信号序列;N为序列长度。当分解层数为k时,定义各模态分量能量之和与原始信号能量的相对能量差及其变化率分别为
| $ \rho_k=\frac{\left|\sum\limits_{j=1}^k E_j-E_{\mathrm{s}}\right|}{E_{\mathrm{s}}} $ | (12) |
| $ \rho_k^{\prime}=\frac{\rho_k-\rho_k-1}{\rho_k} $ | (13) |
式中:Ej为第j个模态分量的能量;Es为原始信号的能量。ρ′最大值对应了能量差值最不稳定的分层参数,可以将其作为分层参数选择的标志。
数据在重构过程中存在能量损耗现象,分解的层数越多损耗越严重,通过对ρ求导数,找到求导后的最大值,就可以确定最佳分解层数。
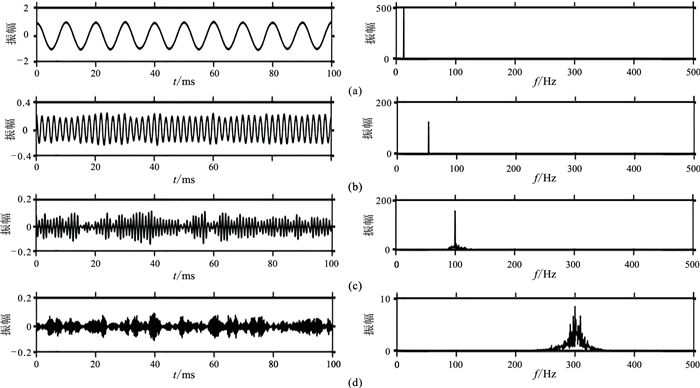
为验证上述方法的可行性,采用三个单频谐波合成的信号(图 1)进行实验。单频信号频率分别为10、50、100 Hz,合成信号的能量为508.7350。
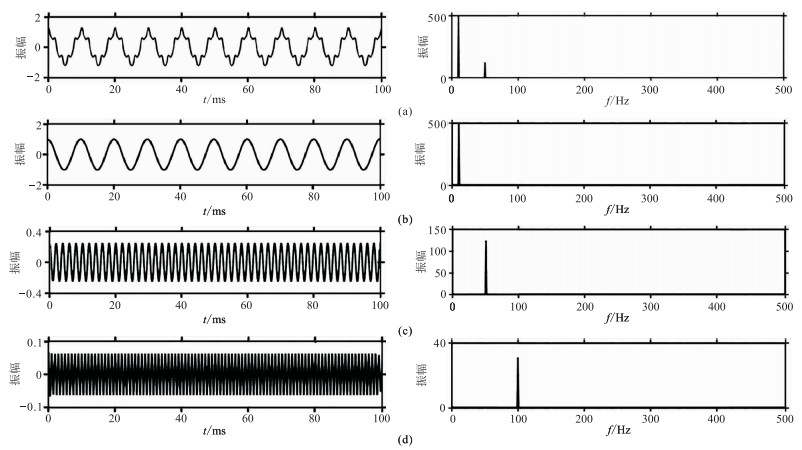
|
图 1 合成信号(左)及其频谱(右) (a)合成信号;(b)信号一;(c)信号二;(d)信号三 |
根据式(12)、式(13)计算能量差和能量差的变化率,可以自动确定最佳分解层数。对信号进行1层分解,相当于信号没有变化,因此不对1层分解进行分析。将2~5层分解结果进行统计,结果如表 1所示。
|
|
表 1 合成信号不同层数分解结果统计 |
由表 1可知,在分解层数由3变化到4时,信号能量差具有较大值,差值变化率为最大值。表明分解4层时,重构信号与原始信号能量差值发生突变,因此图 1a数据分解三层最合适。
图 2和图 3分别为图 1a信号的3层和4层模态(IMF)分解结果。在按照4层进行分解时,信号出现了能量畸变,分解出的信号不是期望信号(图 3)。因此当分解层数过多时,会造成分解过度、模态混叠,出现信号杂乱现象(如图 3中IMF3),不合适的分解层数将无法保证分解结果的可靠性。如按照本文方法确定的层数进行分解,能得到最优结果。
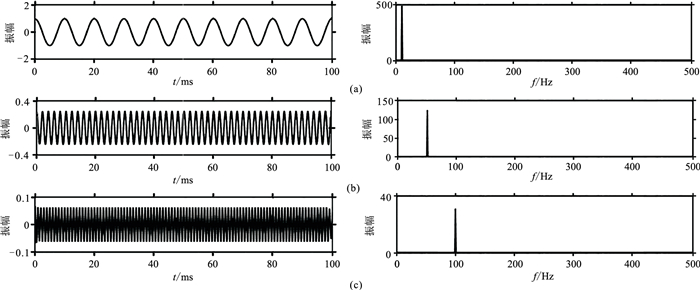
|
图 2 3层VMD结果 (a)IMF1;(b)IMF2;(c)IMF3。左为时域波形;右为频谱。 |
|
图 3 4层VMD结果 (a)IMF1;(b)IMF2;(c)IMF3;(d)IMF4。左为时域波形;右为频谱。 |
基于VMD方法分离同态域的子波与反射系数的同态反褶积方法实现步骤如图 4所示。

|
图 4 基于VMD的同态反褶积流程 |
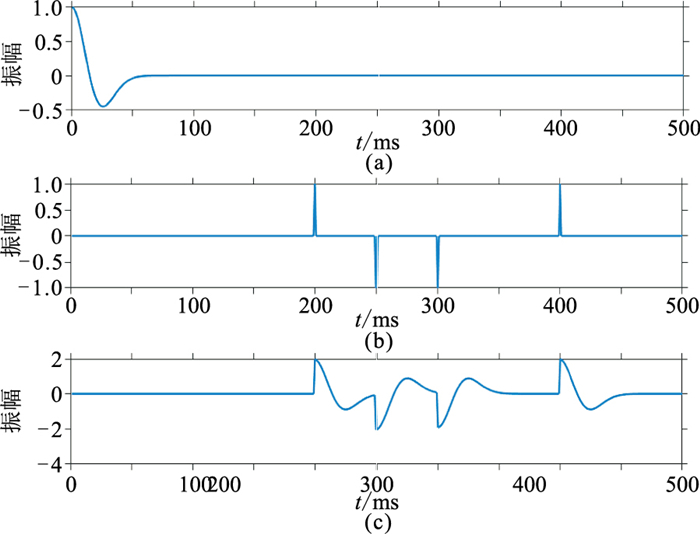
为了更好地说明本文方法的基本步骤,采用主频为15 Hz的零相位Ricker子波合成采样间隔为1 ms、样点数为500的单道地震记录进行反褶积处理(图 5)。
|
图 5 合成的单道地震记录 (a)子波;(b)反射系数;(c)褶积结果 |
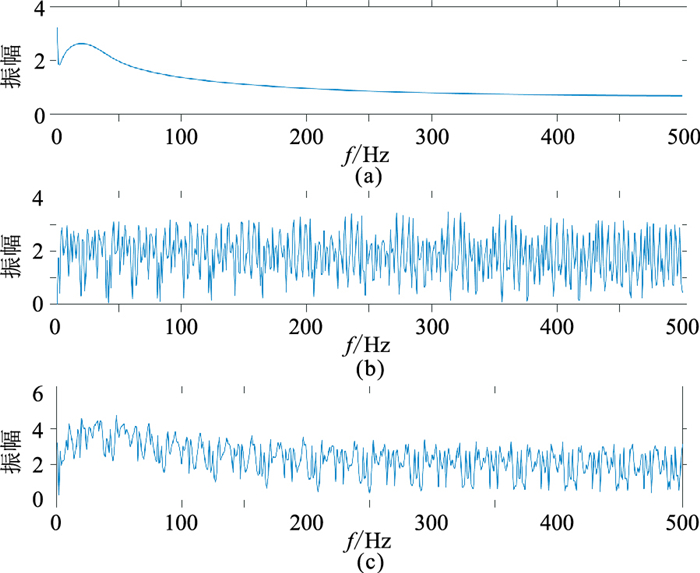
首先对图 5数据进行傅里叶变换,得到数据的频谱,再对频谱分别取对数,将子波与反射系数在频率域的相乘关系转换为相加关系(图 6)。由图 6可以看出,图 6a的子波信息为低频信息,而图 6b的反射系数为高频信息。
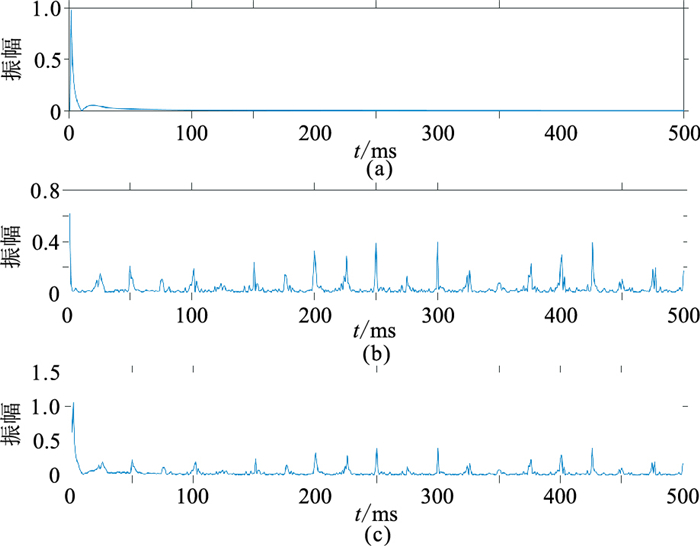
对图 6c的对数谱做傅里叶反变换转换到同态域(图 7),图 7c对应的地震数据的同态谱结果可以看作子波同态谱(图 7a)与反射系数同态谱(图 7b)相加的结果。
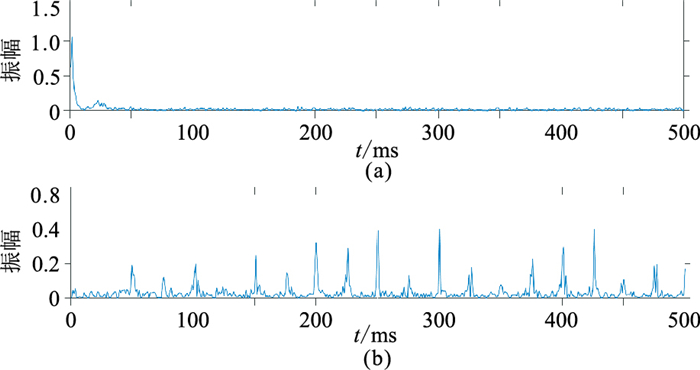
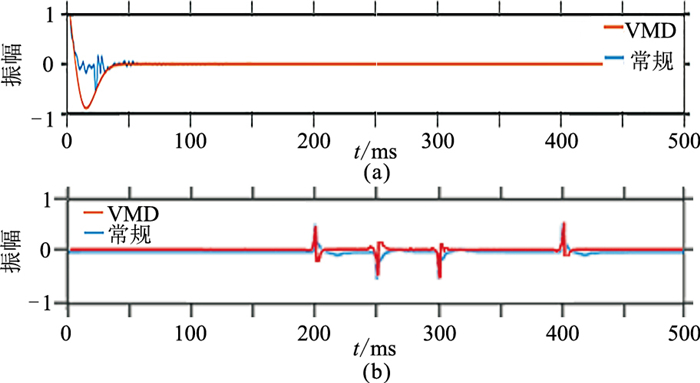
应用本文方法分离的同态域反射系数和子波如图 8所示。与图 7a、图 7b对比可以看出,本文方法分离出的子波形态与实际子波形态基本一致,反射系数位置也比较准确,证明了VMD方法可在同态域有效分离子波与反射系数信息。与常规同态反褶积相比,经过本文方法处理后,原始记录的分辨率大幅提高(图 9)。
|
图 8 图 7c数据VMD法分离结果 (a)子波;(b)反射系数 |
|
图 9 本文方法与常规同态反褶积分离出子波(a)和反射系数(b)对比 |
图 5~图 9使用了一个简单的合成记录对基于VMD的同态反褶积方法实现过程进行了说明。在反褶积过程中,子波随时间和空间变化会对反褶积效果有很大的影响。
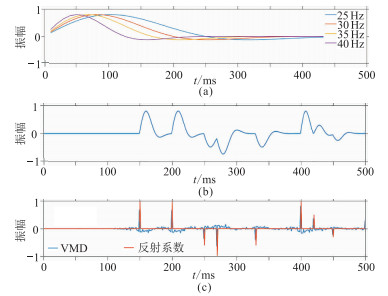
使用一维合成记录验证本文方法对时变子波的适用性。采用最小相位时变子波(图 10a)与反射系数褶积合成地震记录(101~200 ms,主频为40 Hz;201~300 ms,主频为35 Hz;301~400 ms,主频为30 Hz;401~500 ms,主频为25 Hz),结果如图 10b所示。图 10c为本文方法处理结果与实际反射系数对比,可以看出,分离出反射系数与实际反射系数位置基本吻合,而常规反褶积方法难以做到。
|
图 10 时变子波合成记录的本文方法处理结果 (a)不同主频的子波;(b)合成地震记录;(c)本文方法处理结果与理论反射系数的对比 |
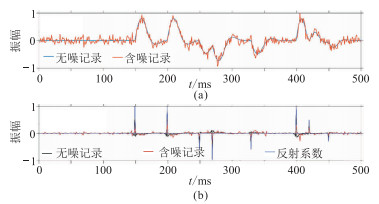
为测试方法的抗噪声能力,在图 10b合成记录中加入高斯噪声,合成了信噪比为5的记录(图 11a)。本文方法对含噪记录的处理结果如图 11b所示。可以看出,噪声虽然对处理结果有所影响,但影响很小,不但分离出了统计子波,分离的反射系数与实际位置基本吻合,而且提高了地震记录的分辨率。
|
图 11 含噪时变子波合成记录本文方法处理结果 (a)含噪合成记录;(b)含噪、无噪合成记录处理结果与反射系数的对比 |
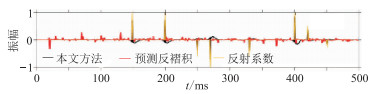
对比本文方法与预测反褶积在处理时变子波记录的结果(图 12)可见:预测反褶积对实际数据分辨率有所提高,但无法准确恢复反射系数的位置,处理效果较差;本文的基于VMD的同态反褶积方法可以较准确地突出反射系数位置,有效压制噪声,提高分辨率。
|
图 12 常规预测反褶积与本文方法处理结果的对比 |
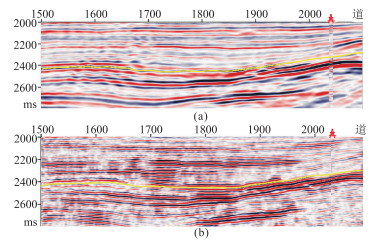
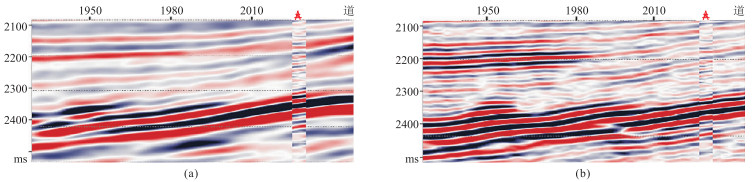
为了验证本文的基于VMD的同态反褶积方法的实用性,对实际叠后数据进行处理,结果如图 13所示。由图可以看出,经本文方法处理后的剖面,同相轴明显变细、数量增多、同相轴连续性增强,同时目的层位处理前后振幅无明显变化,能够显著提升地震记录剖面的分辨率。对比图 13的井位处的放大显示(图 14)可见:本文方法处理结果可以清晰追踪原始剖面中无法分辨的薄层,与测井数据合成记录保持一致,证明了本文方法高分辨处理结果的正确性,为后续解释提供了资料基础。
|
图 13 本文方法实际数据处理结果 (a)原始剖面;(b)本文方法处理剖面。黄色曲线为目的层位,井位处为使用测井数据制作的合成记录 |
|
图 14 图 13井位处的放大显示对比 (a)原始剖面;(b)本文方法处理剖面。井位处为测井数据合成记录。 |
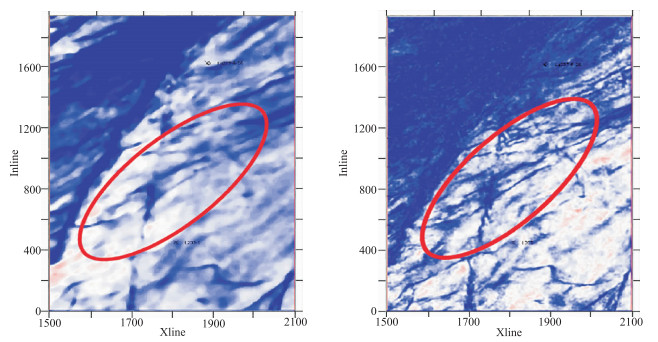
对比本文方法实际数据处理前、后时间切片(图 15)可以看出,横向分辨率大大提高,断点更加清晰,断层更加连续,尤其红色椭圆内,原本分辨不出的断层也能清晰刻画,这证明了本文方法是一种适用性强的高分辨率处理方法。
|
图 15 本文方法处理前(左)、后(右)的时间切片对比 |
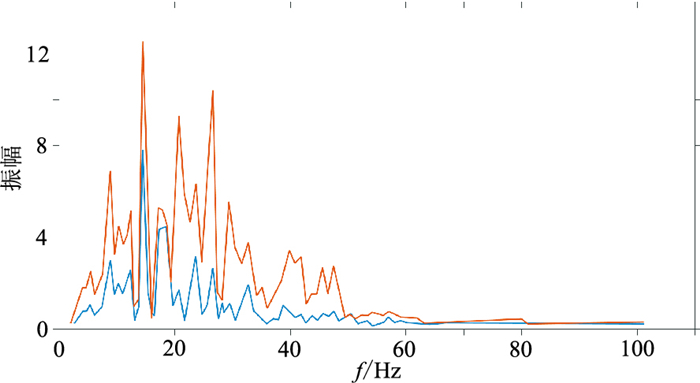
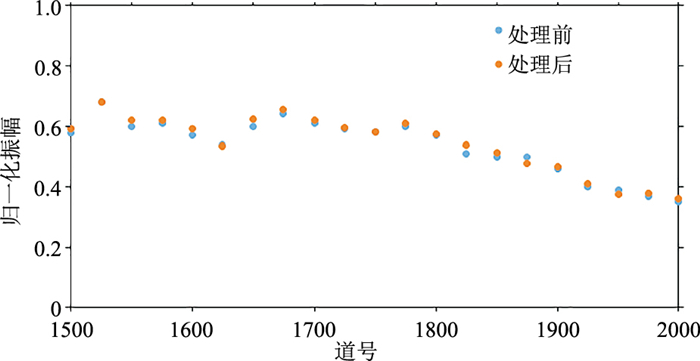
图 16为图 13剖面目的层的频谱曲线,可以看出,经本文方法处理,在一定程度上拓宽了频带,提升了主频。提取本文方法处理前(图 13a)、后(图 13b)目的层振幅曲线(图 17)可见,本文方法在拓宽地震数据频带的基础上,处理前、后振幅曲线基本一致。
|
图 16 原始地震剖面(蓝色)与本文方法(红色)处理结果的频谱对比 |
|
图 17 本文方法处理前、后沿目的层的振幅曲线对比 |
本文提出了一种使用VMD算法对同态域地震信号进行高分辨率处理的方法。该方法能够较好地分离地震子波与反射系数,有效提高地震资料的分辨率。得出以下几点结论:
(1) 针对VMD算法分解层数不易确定的问题,采用了重构后数据与原数据能量差作为标准,实现了分解层数的自动确定;
(2) 对时变子波合成记录可以较好地分离子波与反射系数,表明本文方法对时变子波具有较好的适应能力;
(3) 应用本文方法对实际资料处理,结果与测井数据合成记录一致,提高了地震分辨率,有利于后续薄层、断层的解释。
| [1] |
RAMACHANDRAN G N, RAMAN S. Syntheses for the deconvolution of the Patterson function, Ι: General principles[J]. Acta Crystallographica, 1959, 12(12): 957-964. DOI:10.1107/S0365110X59002778 |
| [2] |
ULRYCH T J. Application of homomorphic deconvolution to seismology[J]. Geophysics, 1971, 36(4): 650-660. DOI:10.1190/1.1440202 |
| [3] |
乌尔里克 T J, 刘颂威. 同态反褶积在地震学中的应用[J]. 石油地球物理勘探, 1979, 14(4): 61-74. ULRYCH T J, LIU Songwei. Application of homomorphic deconvolution in seismology[J]. Oil Geophysical Prospecting, 1979, 14(4): 61-74. DOI:10.13810/j.cnki.issn.1000-7210.1979.04.009 |
| [4] |
凌云, 俞寿朋, 周熙襄. 零相位同态反褶积[J]. 石油地球物理勘探, 1995, 30(3): 299-309. LING Yun, YU Shoupeng, ZHOU Xixiang. Zero-phase homomorphic deconvolution[J]. Oil Geophysical Prospecting, 1995, 30(3): 299-309. DOI:10.13810/j.cnki.issn.1000-7210.1995.03.005 |
| [5] |
郭向宇, 周兴元, 董敏煜. 混合相位子波的相位估算及校正[J]. 石油地球物理勘探, 1998, 33(2): 214-221. GUO Xiangyu, ZHOU Xingyuan, DONG Minyu. Estimation and correction of mixed-phase wavelet phase[J]. Oil Geophysical Prospecting, 1998, 33(2): 214-221. DOI:10.13810/j.cnki.issn.1000-7210.1998.02.009 |
| [6] |
王君, 周兴元, 曹孟起. 同态反褶积的改进与应用[J]. 石油地球物理勘探, 2003, 38(增刊1): 27-30. WANG Jun, ZHOU Xingyuan, CAO Mengqi. Improvement and application of homomorphic deconvolution[J]. Oil Geophysical Prospecting, 2003, 38(S1): 27-30. DOI:10.13810/j.cnki.issn.1000-7210.2003.s1.005 |
| [7] |
LIAO B Y, SHEU T W, YEH Y T, et al. A rupture model for the 1999 Chi-Chi earthquake from inversion of teleseismic data using the hybrid homomorphic deconvolution method[J]. Pure and Applied Geophy-sics, 2013, 170(3): 391-407. DOI:10.1007/s00024-012-0498-0 |
| [8] |
王丹, 莫瀚宁. 基于同态法子波提取的管道泄漏定位研究[J]. 石化技术, 2018, 25(10): 93-94, 96. WANG Dan, MO Hanning. Research on pipeline leakage location based on homomorphic wavelet extraction[J]. Petrochemical Industry Technology, 2018, 25(10): 93-94, 96. DOI:10.3969/j.issn.1006-0235.2018.10.072 |
| [9] |
DE MACEDO I A S, DE FIGUEIREDO J J S, DE SOUSA M C, et al. Estimation of the seismic wavelet through homomorphic deconvolution and well log data: application on well-to-seismic tie procedure[J]. Geophysical Prospecting, 2020, 68(4): 1328-1340. DOI:10.1111/1365-2478.12908 |
| [10] |
HERNÁNDEZ C. Homomorphic deconvolution applied to foetal heart rate signals-homomorphische ent-konvolution auf Foetus-Herzrhythmussignale angewandt[J]. Biomedical Engineering/Biomedizinische Technik, 1982, 27(5): 118-123. DOI:10.1515/bmte.1982.27.5.118 |
| [11] |
PARK Y, CHOI A, KIM K. Parametric estimations based on homomorphic deconvolution for time of flight in sound source localization system[J]. Sensors, 2020, 20(3): 925. DOI:10.3390/s20030925 |
| [12] |
JIN D J, ROGERS J R. Homomorphic deconvolution[J]. Geophysics, 1983, 48(7): 1014-1016. DOI:10.1190/1.1441512 |
| [13] |
HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-955. DOI:10.1098/rspa.1998.0193 |
| [14] |
WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [15] |
YEH J R, SHIEH J S, HUANG N E. Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156. DOI:10.1142/S1793536910000422 |
| [16] |
蔡俊雄, 赵迎, 乐友喜. CEEMD在地震数据去噪中的运用[C]. 2016中国地球科学联合学术年会论文集(三十九), 2016, 83. CAI Junxiong, ZHAO Ying, LE Youxi. Application of CEEMD in seismic data denoising[C]. Proceedings of 2016 China Earth Science Joint Academic Annual Conference (39), 2016, 83. |
| [17] |
JEGADEESHWARAN R, SUGUMARAN V, SOMAN K P. Vibration based fault diagnosis of a hydraulic brake system using variational mode decomposition (VMD)[J]. Structural Durability and Health Monitoring, 2014, 10(1): 81-97. |
| [18] |
方江雄, 温志平, 顾华奇, 等. 基于变分模态分解的地震随机噪声压制方法[J]. 石油地球物理勘探, 2019, 54(4): 757-767. FANG Jiangxiong, WEN Zhiping, GU Huaqi, et al. Seismic random noise attenuation based on variational mode decomposition[J]. Oil Geophysical Prospecting, 2019, 54(4): 757-767. DOI:10.13810/j.cnki.issn.1000-7210.2019.04.005 |
| [19] |
武迪, 宋维琪, 刘军, 等. 变分模态分解与包络导数算子结合的时频分析方法及溶洞储层预测[J]. 石油地球物理勘探, 2021, 56(2): 346-355. WU Di, SONG Weiqi, LIU Jun, et al. Seismic time-frequency analysis based on VMD and envelope deri-vyative operator for fractured-vuggy reservoir prediction[J]. Oil Geophysical Prospecting, 2021, 56(2): 346-355. DOI:10.13810/j.cnki.issn.1000-7210.2021.02.017 |
| [20] |
胡瑞卿, 何俊杰, 李华飞, 等. 时频域变分模态分解地震资料去噪方法[J]. 石油地球物理勘探, 2021, 56(2): 257-264. HU Ruiqing, HE Junjie, LI Huafei, et al. Seismic data de-noising method based on VMD in time-frequency domain[J]. Oil Geophysical Prospecting, 2021, 56(2): 257-264. DOI:10.13810/j.cnki.issn.1000-7210.2021.02.006 |
| [21] |
李华, 伍星, 刘韬, 等. 基于信息熵优化变分模态分解的滚动轴承故障特征提取[J]. 振动与冲击, 2018, 37(23): 219-225. LI Hua, WU Xing, LIU Tao, et al. Bearing fault feature extraction based on VMD optimized with information entropy[J]. Journal of Vibration and Shock, 2018, 37(23): 219-225. DOI:10.13465/j.cnki.jvs.2018.23.030 |
| [22] |
马洪斌. 基于变分模态分解的滚动轴承故障检测方法研究[D]. 北京: 北京交通大学, 2018. MA Hongbin. Research on Rolling Bearing Fault Detection Method Based on Variational Mode Decomposition[D]. Beijing Jiaotong University, Beijing, 2018. |
| [23] |
赵昕海, 张术臣, 李志深, 等. 基于VMD的故障特征信号提取方法[J]. 振动、测试与诊断, 2018, 38(1): 11-19. ZHAO Xinhai, ZHANG Shuchen, LI Zhishen, et al. Fault feature signal extraction method based on VMD[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(1): 11-19. DOI:10.16450/j.cnki.issn.1004-6801.2018.01.002 |



 潘树林, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院,610500。Email:
潘树林, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院,610500。Email: