2. 中国石油勘探开发研究院,北京 100083
2. Research Institute of Petroleum Exploration and Development, PetroChina, Beijing 100083, China
由于不同时期沉积地层的岩石性质变化一般较大,形成强反射界面;而同期地层内不同小层的岩石性质变化通常较小,形成弱反射界面。当弱反射界面距强反射界面较近时,地震数据中的弱反射信号往往会被其附近的强反射信号所掩盖,使地震数据的分辨能力降低,导致小层划分困难。
为了识别弱反射界面的地震反射信号,传统方法最常见思路为通过对地震记录进行分解后将强反射界面对应的分量剔除,以突出小层之间界面对应的弱反射信号。匹配追踪算法是研究最多的技术之一,它对信号进行自适应的分解,实现强反射背景的匹配追踪和识别[1-5];子波分解和重构技术[6-12]通过将地震数据分解为不同主频的地震子波集合,将强反射信号对应分量去除后,再进行信号重构,实现去除强反射的目的;基于奇异值分解的波形分解技术[13-15]也是相同的思路,只是信号分解的方法不同;田亚军等[16]提出了采用AIDNN和U-net两个深度神经网络的地震强反射剥离方法。以上方法都要求正确提取地震子波。如果预测的地震子波不准确,“减去法”会存在子波残留,引入虚假的弱信号。Guo等[17]提出使用反Q滤波方法对目标层的弱反射信号和相位进行补偿以增强能量。
近年来,随着计算机性能的大幅提升,神经网络算法被广泛地应用到石油勘探领域。一方面,将机器学习应用到初至拾取[18-20]和层位拾取[21],以提高工作效率;另一方面,由于神经网络强大的拟合能力,避免了求解极其复杂的非线性映射问题,它在地震资料的处理、解释中被广泛应用,尤其是在地震反演[22-25]中。长短期记忆(LSTM)循环神经网络[26]是一种在时间序列分析中得到广泛应用的模型,已经应用于岩相预测[27]、速度谱自动拾取[28]、测井曲线重构[29]、地震数据初至拾取[30]、沉积微相的智能化识别[31]等方面。
针对弱信号增强中“减去法”的局限性,本文提出了一种基于“升弱降强”的新思路。通过对反射系数进行分数次幂运算,获得拟反射系数序列;用原始反射系数和拟反射系数计算合成地震记录和拟合成地震记录,生成训练样本集;然后训练LSTM网络,建立合成地震记录与拟合成地震记录的映射关系;最后将该网络应用于地震数据,增强弱地震反射信号。本文方法不是消除强地震信号,而是通过构建一种幂次反射系数模型缩小弱反射系数与强反射系数的相对差异,从而突出弱反射信号。
1 方法原理 1.1 拟合成地震记录在地震剖面上,对应强反射界面和弱反射界面的分别是强同相轴和弱同相轴,反射信号能量的大小取决于反射系数的大小及其组合。任意一个地震反射界面的反射系数与地震子波褶积可以得到一个同相轴。当界面相距较近时,弱同相轴被强同相轴掩盖的程度取决于它们振幅绝对值之比,而不是振幅的绝对值。为了减小强、弱同相轴的振幅的比值,本文提出利用分数次幂运算对原始反射系数序列进行重构,得到拟反射系数序列。
设原始反射系数序列为r =(r1,r2,…,rN),拟反射系数序列为R =(R1,R2,…,RN),则
| $ R_n=\operatorname{sign}\left(r_n\right)\left|r_n\right|^{\frac{j_1}{j_2}} $ | (1) |
式中:n=1,2,…,N,N为反射系数个数;j1/j2为分数次幂,其中j1、j2为正整数。
假设反射系数|r1|<|r2|,当幂指数j1/j2<1时,有
| $ \left(\frac{\left|r_2\right|}{\left|r_1\right|}\right)^{\frac{j_1}{j_2}}<\frac{\left|r_2\right|}{\left|r_1\right|} $ | (2) |
则强、弱反射系数绝对值的比值降低,可以减小强、弱反射系数绝对值之间的差异。当幂指数j1/j2>1时,强、弱反射系数绝对值的比值增大,相对增强了强反射系数。本文应用拟反射系数序列可以对反射系数进行自由缩放。合成地震记录s和拟合成地震记录S可以分别表示为地震子波w与反射系数序列r、拟反射系数序列R的褶积,即
| $ \left\{\begin{array}{l} \boldsymbol{s}=\boldsymbol{w} * \boldsymbol{r} \\ \boldsymbol{S}=\boldsymbol{w} * \boldsymbol{R} \end{array}\right. $ | (3) |
为保持处理前、后数据的值域的统一性,对合成记录和拟合成地震记录进行标准化处理
| $ \left\{ \begin{array}{*{35}{l}} s_{n}^{\prime }=\frac{{{s}_{n}}-{{\mu }_{\boldsymbol{s}}}}{{{\delta }_{\boldsymbol{s}}}} \\ S_{n}^{\prime }=\frac{{{S}_{n}}-{{\mu }_{\boldsymbol{S}}}}{{{\delta }_{\boldsymbol{S}}}} \\ \end{array} \right. $ | (4) |
式中:s′、S′分别为标准化后的合成记录和拟合成记录;μs、μS分别为s、S的均值;δs、δS分别为s、S的标准差。
1.2 长短期记忆循环神经网络循环神经网络(RNN)允许数据在重复网络结构中不断循环,可以让先前步骤中的预测结果加入到当前步骤的运算中,使RNN具备了长期记忆功能。因此,不仅当前步骤的输入会影响RNN的输出,过去所有步骤的输入都会影响RNN的输出。
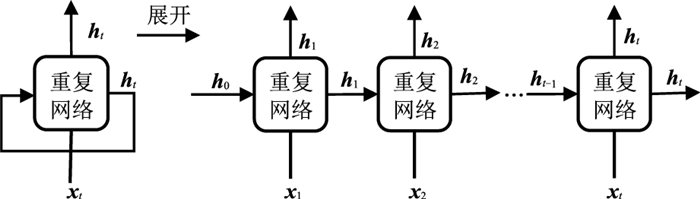
图 1为一个标准的RNN模型,对于给定的序列x =(x1,x2,…,xM)(M为序列长度),RNN可以通过迭代
| $ {\mathit{\boldsymbol{h}}_t} = \tanh \left( {{\mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{xh}}}}{\mathit{\boldsymbol{x}}_t} + {\mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{hh}}}}{\mathit{\boldsymbol{h}}_t} + {\mathit{\boldsymbol{b}}_\mathit{\boldsymbol{h}}}} \right) $ | (5) |
|
图 1 标准RNN及其展开示意图 |
给出一个隐藏状态ht。式中:xt为由x分割的第t个子向量;Wxh、Whh分别为输入层、隐藏层的权重系数矩阵;bh为隐藏层的偏置向量。隐藏层以双曲正切函数tanh为激活函数。
RNN存在梯度消失和梯度爆炸问题,因此提出了LSTM网络。LSTM网络除了增加了一个tanh函数层之外,还同时增加了三个门层,即遗忘门、输入门、输出门[32](图 2)。

|
图 2 LSTM网络单元结构示意图 |
遗忘门决定上一时刻的细胞状态Ct-1中哪些被忘记,哪些被保留到当前时刻的细胞状态Ct,遗忘门的状态ft的值域为0~1,可表示为
| $ {\mathit{\boldsymbol{f}}_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{xf}}}}{\mathit{\boldsymbol{x}}_t} + {\mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{hf}}}}{\mathit{\boldsymbol{h}}_{t - 1}} + {\mathit{\boldsymbol{b}}_\mathit{\boldsymbol{f}}}} \right) $ | (6) |
式中:Wxf、Whf分别为遗忘门中输入层、隐藏层的权重系数矩阵;σ为Sigmoid激活函数;bf为遗忘门状态f的偏置向量。
输入门决定输入信息中哪些信息加入当前时刻的细胞状态值Ct,由2个模块构成,即用于确定信息更新状态的模块和用tanh函数确定当前时刻更新的候选信息的模块。输入门的状态it和候选更新状态
| $ \left\{\begin{array}{l} \boldsymbol{i}_t=\sigma\left(\boldsymbol{W}_{\boldsymbol{x i}} \boldsymbol{x}_t+\boldsymbol{W}_{\boldsymbol{h i}} \boldsymbol{h}_{t-1}+\boldsymbol{b}_i\right) \\ \widetilde{\boldsymbol{C}}_t=\tanh \left(\boldsymbol{W}_{\boldsymbol{x c}} \boldsymbol{x}_t+\boldsymbol{W}_{\boldsymbol{h C}} \boldsymbol{h}_{t-1}+\boldsymbol{b}_\boldsymbol{C}\right) \end{array}\right. $ | (7) |
式中:Wxi、Whi分别为输入门中输入层、隐藏层的权重系数矩阵;Wxc、WhC分别为候选更新状态中输入层、隐藏层的权重系数矩阵;bi、bC分别i、C的偏置向量。
当前时刻单元状态Ct的计算式为
| $ \boldsymbol{C}_t=\boldsymbol{C}_{t-1} \odot \boldsymbol{f}_t+\boldsymbol{i}_t \odot \widetilde{\boldsymbol{C}}_t $ | (8) |
式中“⊙”表示向量中元素按位相乘。
输出门用于将当前细胞状态和它生成的LSTM网络状态输出。输出门的状态和隐藏状态为
| $ \left\{\begin{array}{l} \boldsymbol{o}_t=\sigma\left(\boldsymbol{W}_{\boldsymbol{x} \boldsymbol{o}} \boldsymbol{x}_t+\boldsymbol{W}_{\boldsymbol{h o}} \boldsymbol{h}_{t-1}+\boldsymbol{b}_{\boldsymbol{o}}\right) \\ \boldsymbol{h}_t=\boldsymbol{o}_t \odot \tanh \left(\boldsymbol{C}_t\right) \end{array}\right. $ | (9) |
式中:Wxo、Who分别为输出门中输出层、隐藏层的权重系数矩阵;bo为输出门状态o的偏置向量。
1.3 网络训练一般情况下,制作训练LSTM的训练集使用的是同一时间序列。本文的训练集中,使用原始合成地震记录作为输入序列,拟合成地震记录作为目标输出序列。假设合成地震记录的样点数同样为N,则标准化后的合成地震记录s′ =(s′1, s′n, …s′N)。根据LSTM数据输入的要求,将合成地震记录分割为L个向量,分割的向量长度为N-L+1,则分割后的输入数据为
| $ \boldsymbol{X}=\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_L\right) $ | (10) |
| $ \boldsymbol{x}_l=\left(s_l^{\prime}, s_{l+1}^{\prime}, \cdots, s_{N-L+l}^{\prime}\right) $ | (11) |
式中:1≤l≤L;1<L<N。X经过隐藏层的输出为
| $ \left\{\begin{array}{l} \boldsymbol{P}=\left(p_1, p_2, \cdots, p_L\right) \\ p_t=\boldsymbol{W}_{\boldsymbol{h p}} \boldsymbol{h}_t+b_p \end{array}\right. $ | (12) |
式中:Whp和bp分别为输出单元的权重系数矩阵和偏置;t为1~L之间的整数。与之对应的目标输出为
| $ \boldsymbol{Y}=\left(\boldsymbol{y}_1, \boldsymbol{y}_2, \cdots, \boldsymbol{y}_L\right) $ | (13) |
| $ \boldsymbol{y}_l=\left(S_l^{\prime}, S_{l+1}^{\prime}, \cdots, S_{N-L+l}^{\prime}\right) $ | (14) |
与xl对应的拟合成地震记录yl中有N-L+1个数据,预测值只有一个,因此只可以选择数据中的任意1个样点进行拟合,定义为第k(1≤k≤L-1)个样点
| $ \boldsymbol{Y}^k=\left(y_1^k, y_2^k, \cdots, y_L^k\right) $ | (15) |
选用均方根误差作为网络的损失函数,定义为
| $ {\rm{ Loss }} = \sqrt {\frac{{\sum\limits_{l = 1}^L {{{\left( {{p_l} - y_l^k} \right)}^2}} }}{L}} $ | (16) |
地震数据服从广义高斯概率分布,但不同数据的值域不同,严重影响LSTM网络的输出结果,因此将输入LSTM网络的地震数据进行标准化
| $ d_n^\prime = \frac{{{d_n} - {\mu _\mathit{\boldsymbol{d}}}}}{{{\delta _\mathit{\boldsymbol{d}}}}} $ | (17) |
式中:dn和d′n分别为标准化前、后地震数据d和d′的第n个样点;μd、δd分别为d的均值和标准差。
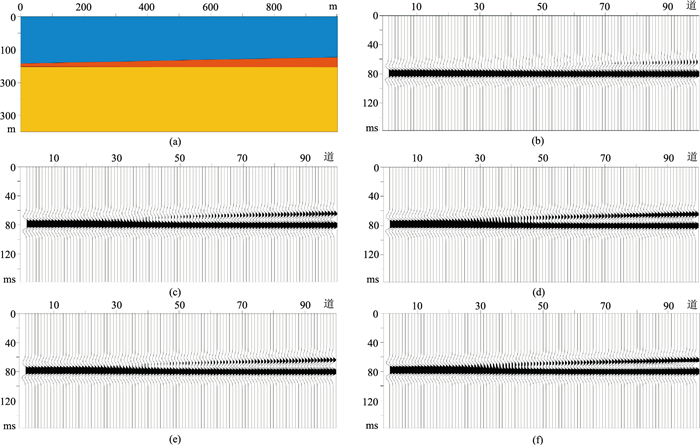
2 模型实验首先用正演模型(图 3a)验证本文算法的可行性。模型宽度为1000 m,道间距为10 m,包含三层,其中中间层的厚度由10 m线性增大到30 m,各层的速度和密度如表 1所示。垂直入射情况下,上层与中间层的反射系数为0.05,中间层与下层的反射系数为0.2。本文选用主频为35 Hz的Ricker子波[33]与反射系数褶积合成地震记录(图 3b),两个拟地震记录剖面是地震子波分别与1/2次幂、1/3次幂拟反射系数序列的褶积(图 3c、图 3d)。为了保证次幂运算前、后数据分布的一致性,需对地震记录进行标准化处理。
|
图 3 模型数据测试结果 (a)地层模型;(b)合成剖面;(c)1/2次幂拟合成剖面;(d)1/3次幂拟合成剖面;(e)1/2次幂弱反射增强结果;(f)1/3次幂弱反射增强结果 |
|
|
表 1 模型参数 |
相邻两道合成地震记录对应的中间层的厚度差为0.2 m。由图 3b可以看出,弱反射系数界面对应的同相轴在第75道便无法识别。使用模型反射系数序列的1/2次幂与Ricker子波褶积,其合成记录剖面在第45道就弱到无法识别(图 3c)。使用模型反射系数序列的1/3次幂与Ricker子波褶积,其合成记录剖面在第25道才被强反射淹没(图 3d)。与原始合成地震记录(图 3b)相比,使用拟反射系数序列计算得到的地震合成记录(图 3c、图 3d)中弱反射同相轴的能量得到增强,分辨率分别提高了6和10 m。
从图 3b、图 3c的地震剖面中的相同位置选取5道数据分别作为输入数据和标签,制作训练集,其中选取的每次输入的数据长度为40 ms(20个样点),将最终训练结果与标签的均方根误差作为训练集误差。用图 3b所示地震剖面作为验证集,将预测结果(图 3e)与对应数据(图 3c)的均方根误差作为验证集误差。同样对图 3b、图 3d所示地震剖面进行相同处理,预测结果如图 3f所示。对比图 3e与图 3c、图 3f与图 3d可见,预测结果与模拟数据的误差极小。
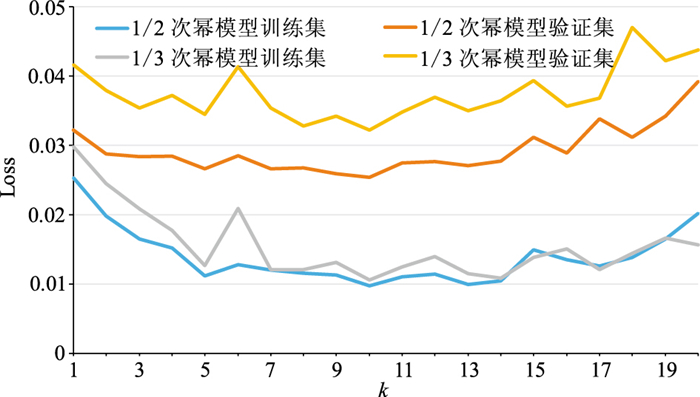
1/2、1/3次幂弱反射增强LSTM网络训练集、验证集误差曲线如图 4所示,可以看出式(15)中选用不同的k值(不同采样点)最终计算得到的均方根误差不同,用分割窗口中部对应元素作为标签,拟合误差较小;1/2、1/3次幂LSTM网络的训练集误差相差不大,但后者的验证集误差较大。
|
图 4 模型数据1/2、1/3次幂弱反射增强LSTM网络训练集、验证集误差曲线 |
四川盆地下志留统龙马溪组(LMX)海相页岩气已经进入大规模开发阶段。龙马溪组龙一段1亚段可再细分为LMX11-1、LMX11-2、LMX11-3、LMX11-44个小层,其中LMX11-1~LMX11-3开发效果好[34]。由于小层间的物性差异远小于龙马溪组与五峰组物性差异,LMX11-3顶界在地震剖面上不易识别。
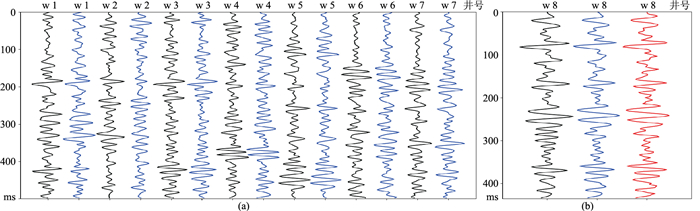
工区内目的层地震数据主频为35 Hz,因此将Ricker子波的主频也设定为35 Hz。工区附近有8口井,用7口井的数据制作1/2次幂弱反射增强LSTM网络训练集(图 5a),剩下的一口井的数据作为验证集(图 5b)。为了防止过拟合,设置当误差小于0.1后停止训练。训练集的均方根误差为0.09,验证集均方根误差为0.21。
|
图 5 测井数据测试结果
(a)训练集;(b)测试集预测结果 黑色曲线为原始合成地震记录;蓝色曲线为1/2次幂拟合成地震记录;红色曲线为RNN模型的输出结果。 |
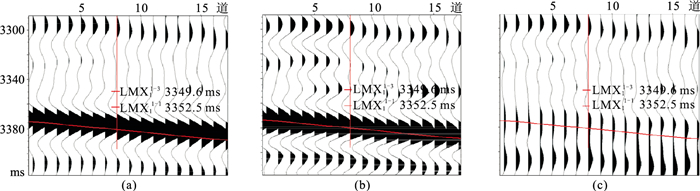
图 6a为实际地震剖面,其中强同相轴为龙马溪组底的反射,优质储层顶界(LMX11-3顶)反射被强反射掩盖而不能识别。图中井筒标注了LMX11-1和LMX11-3顶界在井震标定后对应的时间。将训练好的LSTM网络应用于该剖面,结果如图 6b所示,可见本文方法处理剖面可以识别LMX11-3顶。LMX11-1顶界位于波谷的最小值处,更易拾取。由某商业软件去强反射后的地震剖面(图 6c)可以看出,虽然强反射被有效地压制了,但LMX11-3底界对应的地震响应仍然较弱,无法识别。使用本文方法可以计算得到的优质储层顶界(LMX11-3顶)与底界之差可以得到时间厚度数据,结合速度数据,可以计算储层的实际厚度,厚度较大位置的井产量更高,因此本文方法为布井提供了指导。
|
图 6 四川盆地应用实例
(a)原始地震剖面;(b)本文方法处理的地震剖面;(c)商业软件去强反射后的地震剖面 上、下红色短线分别为钻井数据标定的LMX11-3顶和LMX11-1顶,红色长斜线为龙马溪组底强反射。 |
为了进一步展示本文方法的适用性,使用长庆油田X工区地震数据进行测试。该工区具有鲜明的河控三角洲前积反射特征(图 7a)。Forest1和Fo-rest2为不同前积期沉积体的分界面。C73为长73底界对应的反射,为该区强反射界面。由于本区相邻的前积体部分区域的的弹性参数差别不大,出现部分区域反射信号弱、同相轴不连续等问题。

|
图 7 长庆油田实际数据应用 (a)原始地震剖面;(b)本文方法处理后的地震剖面 |
相对于原始剖面(图 7a),本文方法处理后的地震剖面(图 7b)中能量更加均衡,其中强反射信号减弱,弱反射信号明显增强,原本因为反射能量较弱而不能显示的同相轴也突显出来,原先不连续的同相轴更加连续(红色箭头所示),为后期层位拾取提供了可靠的资料基础。
4 结束语本文提出的基于“升弱降强”思路的分数次幂弱反射增强方法,缩小了弱反射信号与强反射信号的相对差异,避免了“减去法”中强子波残余形成的虚假弱反射。本文使用测井反射系数合成地震记录与拟合成地震记录构建训练集,采用LSTM网络拟合二者的映射关系。模型数据测试表明:LSTM网络模型可以有效地建立合成地震记录与拟合成地震记录之间的映射关系,并且具有泛化能力,可以直接拓展应用于地震数据;避免了直接从地震数据中提取反射系数序列,既减小了计算量,又避免了提取的反射系数误差大的问题。
对于在原始地震剖面中小层界面对应的同相轴难以识别的问题,本文方法可以有效增强弱反射,提高地震数据对弱反射界面的识别能力,为小层划分提供了一种可行方案,有着广泛的应用前景。
| [1] |
刘杰, 张忠涛, 刘道理, 等. 强反射背景下沉积体边界检测及流体识别方法[J]. 石油物探, 2016, 55(1): 142-149. LIU Jie, ZHANG Zhongtao, LIU Daoli, et al. Sediment boundary identification and fluid detection for the seismic data with strong background reflections[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 142-149. |
| [2] |
WANG Y H. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics, 2007, 72(1): V13-V20. DOI:10.1190/1.2387109 |
| [3] |
何峰, 翁斌, 韩刚, 等. 一种基于地震约束的井控匹配追踪煤层强反射消除技术[J]. 中国海上油气, 2019, 31(1): 61-66. HE Feng, WENG Bin, HAN Gang, et al. A seismic constraint-based technology for elimination of strong coal seam reflection via well-control and matching pursuit[J]. China Offshore Oil and Gas, 2019, 31(1): 61-66. |
| [4] |
李海山, 杨午阳, 田军, 等. 匹配追踪煤层强反射分离方法[J]. 石油地球物理勘探, 2014, 49(5): 866-870. LI Haishan, YANG Wuyang, TIAN Jun, et al. Coal seam strong reflection separation with matching pursuit[J]. Oil Geophysical Prospecting, 2014, 49(5): 866-870. |
| [5] |
许璐, 吴笑荷, 张明振, 等. 基于局部频率约束的动态匹配追踪强反射识别与分离方法[J]. 石油地球物理勘探, 2019, 54(3): 587-593. XU Lu, WU Xiaohe, ZHANG Mingzhen, et al. Strong reflection identification and separation based on the local-frequency-constrained dynamic matching pursuit[J]. Oil Geophysical Prospecting, 2019, 54(3): 587-593. |
| [6] |
汲生珍, 邬兴威, 夏东领. 子波分解与重构技术在储层预测中的应用[J]. 石油天然气学报, 2013, 35(11): 66-69. JI Shengzhen, WU Xingwei, XIA Dongling. Application of wavelet decomposition and reconstruction technique in reservoir prediction[J]. Journal of Oil and Gas Technology, 2013, 35(11): 66-69. |
| [7] |
AN P. Application of multi-wavelet seismic trace decomposition and reconstruction to seismic data interpretation and reservoir characterization[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 973-977.
|
| [8] |
BEAR L K, PAVLIS G L. Multi-channel estimation of time residuals from broadband seismic data using multi-wavelets[J]. Bulletin of the Seismological Society of America, 1999, 89(3): 681-692. DOI:10.1785/BSSA0890030681 |
| [9] |
LEBRUN J, VETTERLI M. Balanced multiwavelets theory and design[J]. IEEE Transactions on Signal Processing, 1998, 46(4): 1119-1125. DOI:10.1109/78.668561 |
| [10] |
陈人杰, 童思友, 刘怀山, 等. 基于子波分解与重构的储层预测技术[J]. 海洋地质前沿, 2014, 30(1): 55-61. CHEN Renjie, TONG Siyou, LIU Huaishan, et al. Reservoir prediction technology based on wavelet decomposition and reconstruction[J]. Marine Geology Frontiers, 2014, 30(1): 55-61. |
| [11] |
佘刚, 周小鹰, 王箭波. 多子波分解与重构法砂岩储层预测[J]. 西南石油大学学报(自然科学版), 2013, 35(1): 19-27. SHE Gang, ZHOU Xiaoying, WANG Jianbo. Prediction of sand reservoir with multi-wavelet seismic trace decomposition and reconstruction[J]. Journal of Southwest Petroleum University (Science & Techno-logy Edition), 2013, 35(1): 19-27. |
| [12] |
赵爽, 李仲东, 许红梅, 等. 多子波分解技术检测含煤砂岩储层[J]. 天然气工业, 2007(9): 44-47. ZHAO Shuang, LI Zhongdong, XU Hongmei, et al. Using multiple wavelet decomposition technique to detect the sandstone reservoir with coal layer[J]. Na-tural Gas Industry, 2007(9): 44-47. |
| [13] |
AN P. Case studies on stratigraphic interpretation and sand mapping using volume-based seismic waveform decomposition[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 496-499.
|
| [14] |
AN P. Case studies on oil and water wells separation and gas sand prediction in a coal formation using wavelet selection and volume-based seismic waveform decomposition[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 498-502.
|
| [15] |
谢春临, 黄伟, 关晓巍, 等. 波形分解技术在强反射背景下薄砂层识别中的应用[J]. 石油地球物理勘探, 2017, 52(3): 516-520. XIE Chunlin, HUANG Wei, GUAN Xiaowei, et al. Thin sand identification under strong reflection with volume-based waveform decomposition[J]. Oil Geophysical Prospecting, 2017, 52(3): 516-520. |
| [16] |
田亚军, 高静怀, 王大兴, 等. 基于深度神经网络的地震强反射剥离方法[J]. 地球物理学报, 2021, 64(8): 2780-2794. TIAN Yajun, GAO Jinghuai, WANG Daxing, et al. Removing strong seismic reflection based on the deep neural network[J]. Chinese Journal of Geophysics, 2021, 64(8): 2780-2794. |
| [17] |
GUO J, WANG Y H. Recovery of a target reflection underneath coal seams[J]. Journal of Geophysics & Engineering, 2004, 1(1): 46-50. |
| [18] |
宋建国, 李赋真, 徐维秀, 等. 改进的神经网络级联相关算法及其在初至拾取中的应用[J]. 石油地球物理勘探, 2018, 53(1): 8-16. SONG Jianguo, LI Fuzhen, XU Weixiu, et al. An improved neural-network cascade-correlation algorithm and its application in seismic first break picking[J]. Oil Geophysical Prospecting, 2018, 53(1): 8-16. |
| [19] |
庄东海, 肖春燕, 颜永宁. 利用人工神经网络自动拾取地震记录初至[J]. 石油地球物理勘探, 1994, 29(5): 659-664. ZHUANG Donghai, XIAO Chunyan, YAN Yongning. Seismic first arrivel pickup using artificial neural network[J]. Oil Geophysical Prospecting, 1994, 29(5): 659-664. |
| [20] |
于子叶, 储日升, 盛敏汉. 深度神经网络拾取地震P和S波到时[J]. 地球物理学报, 2018, 61(12): 4873-4886. YU Ziye, CHU Risheng, SHENG Minhan. Pick onset time of P and S phase by deep neural network[J]. Chinese Journal of Geophysics, 2018, 61(12): 4873-4886. |
| [21] |
姚姚. 用人工神经网络实现同相轴自动拾取[J]. 石油地球物理勘探, 1994, 29(1): 111-116. YAO Yao. Automatic seismic event pickup using artificial nerve network[J]. Oil Geophysical Prospecting, 1994, 29(1): 111-116. |
| [22] |
戴前伟, 江沸菠, 董莉. 基于汉南—奎因信息准则的电阻率层析成像径向基神经网络反演[J]. 地球物理学报, 2014, 57(4): 1335-1344. DAI Qianwei, JIANG Feibo, DONG Li. RBFNN inversion for electrical resistivity tomography based on Hannan-Quinn criterion[J]. Chinese Journal of Geophysics, 2014, 57(4): 1335-1344. |
| [23] |
陆文凯, 李衍达, 牟永光. 误差反传播神经网络法地震反演[J]. 地球物理学报, 1996, 39(增刊1): 292-301. LU Wenkai, LI Yanda, MU Yongguang. Seismic inversion using error-back-propagation neural network[J]. Chinese Journal of Geophysics, 1996, 39(S1): 292-301. |
| [24] |
吴媚, 符力耘, 李维新. 高分辨率非线性储层物性参数反演方法和应用[J]. 地球物理学报, 2008, 51(2): 546-557. WU Mei, FU Liyun, LI Weixin. A high-resolution nonli-near inversion method of reservoir parameters and its application to oil/gas exploration[J]. Chinese Journal of Geophysics, 2008, 51(2): 546-557. |
| [25] |
张繁昌, 刘汉卿, 钮学民, 等. 褶积神经网络高分辨率地震反演[J]. 石油地球物理勘探, 2014, 49(6): 1165-1169. ZHANG Fanchang, LIU Hanqing, NIU Xuemin, et al. High resolution seismic inversion by convolutional neural network[J]. Oil Geophysical Prospecting, 2014, 49(6): 1165-1169. |
| [26] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. |
| [27] |
熊玄辰, 曹俊兴, 周鹏, 等. 基于双向长短期记忆神经网络的岩相预测方法[J]. 成都理工大学学报(自然科学版), 2021, 48(2): 226-234. XIONG Xuanchen, CAO Junxing, ZHOU Peng, et al. Lithofacies prediction method based on bidirectional long short memory neural network[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2021, 48(2): 226-234. |
| [28] |
张昊, 朱培民, 顾元, 等. 基于深度学习的地震速度谱自动拾取方法[J]. 石油物探, 2019, 58(5): 724-733. ZHANG Hao, ZHU Peimin, GU Yuan, et al. Velocity auto-picking from seismic velocity spectra based on deep learning[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 724-733. |
| [29] |
王俊, 曹俊兴, 尤加春. 基于GRU神经网络的测井曲线重构[J]. 石油地球物理勘探, 2020, 55(3): 510-520. WANG Jun, CAO Junxing, YOU Jiachun. Reconstruction of logging traces based on GRU neural network[J]. Oil Geophysical Prospecting, 2020, 55(3): 510-520. |
| [30] |
邓飞, 蒋沛凡, 蒋先艺, 等. 应用图像语义分割网络的微地震事件识别和初至拾取方法[J]. 石油地球物理勘探, 2022, 57(5): 1011-1019. DENG Fei, JIANG Peifan, JIANG Xianyi, et al. Microseismic event recognition and first break picking method based on image semantic segmentation network[J]. Oil Geophysical Prospecting, 2022, 57(5): 1011-1019. |
| [31] |
罗仁泽, 周洋, 康丽侠, 等. 基于DMC-BiLSTM的沉积微相智能识别方法[J]. 石油物探, 2022, 61(2): 253-261. LUO Renze, ZHOU Yang, KANG Lixia, et al. Intelligent identification of sedimentary microfacies based on DMC-BiLSTM[J]. Geophysical Prospecting for Petroleum, 2022, 61(2): 253-261. |
| [32] |
GRAVES A, MOHAMED A R, HINTON G. Speech recognition with deep recurrent neural networks[C]. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 2013, 6645-6649.
|
| [33] |
RICKER N. The form and laws of propagation of seismic wavelets[J]. Geophysics, 1953, 18(1): 10-40. |
| [34] |
MA X H, XIE J, YONG R, et al. Geological characte-ristics and high production control factors of shale gas reservoirs in Silurian Longmaxi Formation, southern Sichuan Basin, SW China[J]. Petroleum Exploration and Development, 2020, 47(5): 901-915. |



 郑晓东, 北京市海淀区学院路20号中国石油勘探开发研究院物探技术研究所,100083。Email:
郑晓东, 北京市海淀区学院路20号中国石油勘探开发研究院物探技术研究所,100083。Email: