②. 中国石油大港油田公司勘探开发研究院, 天津 300280
②. Exploration & Development Research Institute, Dagang Oilfield Company, PetroChina, Tianjin 300280, China
随着油气勘探不断深入,全球油气资源勘探重点已经转向复杂油气藏和非常规油气藏,对地震成像要求越来越高。影响成像精度主要有三方面的因素:叠前数据体的质量、速度建模的精度、偏移成像方法[1-2]。但受复杂地表和地下地质条件的影响,地震数据通常信噪比、分辨率较低,因此叠前数据质量并不高。所以,寻找合适的偏移方法以及建立准确的速度模型才是提高成像质量的关键[3-4]。
叠前深度偏移速度建模一般分为两个阶段:初始速度模型建立和速度模型优化。初始速度模型的建立需要综合考虑地质、测井、地震等多种资料信息,建立相对准确的初始速度模型是速度建模的基础,并且对速度场的下一步优化及速度收敛具有重要的影响[5-6]。目前,建立深度域初始速度模型的方法比较多,最早的是利用Dix公式将叠加速度转化为深度域层速度,但是该公式是建立在水平层状介质的基础上,对于复杂地质构造,误差较大[7]。Clapp等[8]针对Dix公式应用的假设条件,提出了一种改进的Dix约束层速度反演方法,在一定程度上不受水平层状介质条件约束,但当地下介质横向速度变化比较大时仍然存在较大的误差。目前实际地震数据处理中,经常利用这两种方法先得到初始层速度场,然后对初始速度模型不断优化。
目前,模型优化常用的方法可分为两大类:偏移速度分析和旅行时反演。在地震资料处理中,Kirchhoff积分法叠前深度偏移技术应用广泛,因此基于叠前深度偏移共成像点道集的层析成像建模方法是目前研究较多、应用也较广泛的方法之一[9-11]。随着物探技术以及计算机技术的不断发展,基于波动方程的叠前深度偏移技术的应用越来越多,同时基于波动理论的很多方法包括共聚焦点速度分析、基于共反射点角道集的偏移速度分析、全波形反演等速度建模方法也被提出并得到应用[12-14],但是由于运算效率的影响,这些方法尚并得到大规模的工业化应用。
网格层析是一种利用全局优化技术进行速度误差求取的技术,在实际数据处理中得到了广泛应用。近年来,许多专家学者对基于层位的层析反演和基于网格的层析反演技术优势进行了分析,通过拾取速度纵向变化明显的地震层位,从浅至深逐层约束网格层析反演,可以较好地解决纵、横向构造变化带来的影响,改善了网格层析速度建模技术在复杂构造区块中的应用效果。本文在该技术思路基础上,利用GeoEast-Diva深度域速度建模软件,对非洲尼日尔AG区块地震资料开展了基于层位约束的网格层析速度建模技术应用研究。实际应用结果表明,层位约束的网格层析技术反演精度高、收敛速度快,是一种非常实用的高效、高精度速度建模工具。
1 网格层析建模技术 1.1 基本原理网格层析速度建模方法是一种基于射线理论的高精度速度建模方法,该方法将介质离散成网格单元,在每一个三维空间网格体内更新速度,通过三维网格射线追踪,建立层析反演方程。速度反演过程就是线性方程组的求解过程,利用射线追踪计算灵敏度矩阵和旅行时残差,并通过旅行时残差更新速度模型。
网格层析技术首先在叠前深度偏移道集上求取剩余深度差。对于倾角为α的反射界面,在共成像点(CIP)道集上,入射角β对应的偏移深度为
| $Z_\alpha=Z_0 \sqrt{\gamma^2+\left(\gamma^2-1\right) \tan ^2 \beta} $ | (1) |
式中:Z0为零炮检距的偏移深度;γ为Z0与真实深度的比值。根据式(1),道集的剩余深度差可表示为
| $ \Delta Z=Z_0\left[\sqrt{\gamma^2+\left(\gamma^2-1\right) \tan ^2 \beta}-1\right] $ | (2) |
剩余深度差通常与旅行时残差一一对应,二者对应为
| $ \Delta t=2 s \Delta Z \cos \alpha \cos \beta $ | (3) |
式中s为慢度。
根据参考模型和真实模型的慢度差Δs沿射线l的积分得到实际数据与参考模型的旅行时残差
| $ \Delta t=\int_l \Delta s \mathrm{~d} l $ | (4) |
对式(4)进行网格离散化,可以得到层析反演方程
| $ \boldsymbol{L} \Delta \boldsymbol{s}=\Delta t $ | (5) |
式中:L为灵敏度矩阵;Δs为慢度变化量的离散形式;Δt为旅行时残差向量。
为了降低反演的多解性,加入正则化项,式(4)可变为
| $ \left[\begin{array}{c} \boldsymbol{L} \\ \boldsymbol{\mu} \boldsymbol{\varGamma} \end{array}\right] \Delta \boldsymbol{s}=\left[\begin{array}{c} \Delta \boldsymbol{t} \\ 0 \end{array}\right] $ | (6) |
式中:μ、Γ分别为网格内的射线覆盖次数和横向正则化矩阵。求解上式就可得到慢度变化量,再通过迭代就可得到层析反演的速度模型。
纯数据驱动的网格层析反演流程通常可分为以下四步:①求取地层斜率;②剩余深度差拾取;③将拾取的剩余深度差进行优化;④建立和求解层析反演方程。
1.2 初始速度模型建立实际地震资料处理过程中,通常利用均方根速度场,采用约束速度反演方法得到初始层速度模型。具体实现步骤如下:首先,建立初始的低频趋势模型速度场,对于每一个反演的垂向函数,假设局部变化是一维模型,那么可以利用最小二乘法原理求解反问题;其次,为了减少噪声对速度反演的影响,可以通过加权函数进行约束,其主要由三项构成,分别是均方根速度误差项、速度趋势模型误差项以及阻尼能量项,以此提高方法的稳定性[15-16]。
2 基于层位约束的网格层析反演 2.1 层位拾取及构造模型建立对于复杂构造区地震资料,尤其是低信噪比资料,直接采用网格层析得到的速度模型成像效果并不理想。为了提高网格层析反演的精度,本文采用基于层位约束的网格层析反演技术进行精细速度建模。首先,在叠前时间偏移成果上拾取层位(图 1a),选取大套标志层对层间速度进行约束;其次,根据拾取的层位构建块体模型,生成时间域的块体结构模型(图 1b);然后,利用初始层速度将模型及层位转到深度域;最后,利用层位模型对网格层析进行约束。

|
图 1 叠前时间偏移剖面层位拾取结果(a)及建立的块体结构模型(b) |
获得层位模型后,根据精细分析的叠前时间偏移均方根速度场,利用约束速度反演得到初始层速度并进行叠前深度偏移,获得初始的叠前深度偏移剖面和成像道集,然后分别拾取地层倾角和剩余深度差。由于地层倾角和剩余深度差的拾取质量直接影响网格层析反演方程的稳定性和可靠性,进而影响速度模型的精度,因此前期处理时一定要仔细分析数据的拾取质量、做好质控。
地层倾角拾取是基于多道相似的相干体技术,通过定义一个矩形时窗,以分析点为中心,在设置的倾角范围内,按照设定的倾角间隔求取地震数据的相似性,相似性最大所对应的倾角就是分析点的倾角。具体做法是在初始的叠前深度偏移剖面上,利用最小二乘法搜索离散的局部地层斜率(地层倾角的正切值),分别获得Inline方向和Crossline方向的两个三维离散地层斜率数据体,然后对离散数据体进行插值平滑得到最终的数据体。通过拾取地层倾角、分析倾角场拾取质量因子,可以为下一步拾取残差提供基础信息。在前期网格层析处理中由于数据精度不高,可采用大分析时窗和大尺度平滑参数,保证背景信息正确,随着迭代进行,减小分析时窗,优化局部信息。图 2是拾取的地层倾角和拾取质量因子。拾取质量因子从0到1,值越高,代表同相轴连续性越强,拾取的地层倾角越可靠。

|
图 2 拾取的地层倾角剖面(a)和质量因子剖面(b) |
根据共成像点道集相似度计算共成像点道集中的剩余深度差,即不同炮检距和零炮检距的偏移深度差。拾取剩余深度差时可以定义相似度阈值和拾取质量因子阈值,小于阈值的同相轴被认为不可靠而不予拾取,从而确保拾取较可靠的有效信息。
网格层析速度建模方法其实就是通过校正共成像点道集的深度差来修正速度模型。所以,剩余深度差的拾取精度直接决定了网格层析的精度[17]。在实际处理中主要可以通过以下方法提高剩余深度差的拾取质量:①对偏移道集进行去噪等处理,提高资料的信噪比;②设置剩余深度差的拾取范围,确保拾取正确、合理的剩余深度差;③对纵、横向变化剧烈的层位进行层位约束控制;④对拾取的剩余深度差进行优化,去除拾取有误的结果。
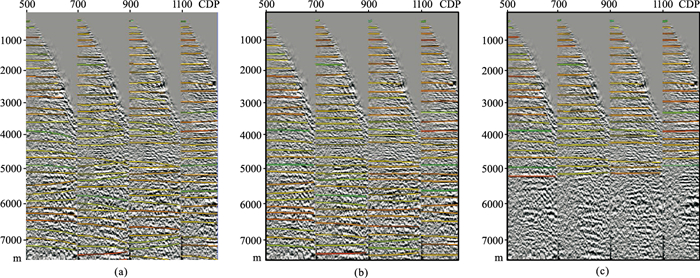
图 3a是在叠前深度偏移共成像点道集上的拾取结果,图 3b是优化后的拾取结果,图 3c是输入结构模型和层位,利用层位约束后的拾取结果。可以看出,优化后能基本丢掉一些不合理的拾取结果,但是并不能消除深层资料信噪比低带来的错误拾取结果,从而造成深层速度异常。加入层位约束后,可以有效消除深层低信噪比资料的错误拾取结果,从而避免深层速度异常,消除构造假象。
|
图 3 深度偏移道集拾取结果 (a)初始拾取结果;(b)优化结果;(c)层位约束后 |
网格层析首先精细反演浅层、中深层速度,避免深层的剩余深度差拾取误差导致网格层析反演速度异常或错误,然后再对深层速度进行沿层约束更新,最终得到一个精确的速度模型。
网格层析反演包括两部分:即层析反演方程的建立和求解。通过将优化的成像道集的剩余深度差按照射线路径进行射线追踪建立层析反演方程,然后迭代求解得到速度变化量,从而不断更新速度模型[18]。网格层析利用离散的网格代替地下连续介质,虽然这种做法可以实现三维网格全局速度修正迭代,但事实上并不能充分考虑地下地层的分布规律,尤其是在复杂构造区,网格分布并不能真实、完全表征地下介质的分布特征,从而降低了速度模型反演的精度[19]。本文采用层位约束网格层析反演技术对实际资料进行处理,具体做法是:①首先采用大网格反演全局网格层析低频分量,并对反演结果进行一定尺度的平滑,在层析迭代过程中,逐步减小层析反演的网格尺寸和速度平滑尺度,确保整体背景成像合理;②在整体背景成像合理的基础上,沿地层倾角场约束反演,使反演的速度模型与整体构造背景一致;③加入拾取的层位和结构模型约束网格层析反演,最终得到精确的速度模型。
3 实际应用效果为测试GeoEast-Diva建模软件层位约束的网格层析建模技术的普适性,选取非洲尼日尔AG区块进行测试。区块内沙丘起伏变化较大,地层吸收衰减严重,高大沙丘使得地表条件复杂。另外,该区浅层断层比较丰富,速度横向变化剧烈,地下地质条件复杂,目标是提高深层底劈成像质量。
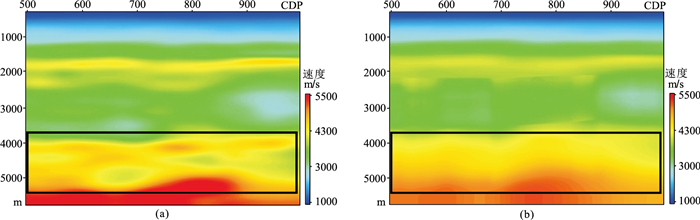
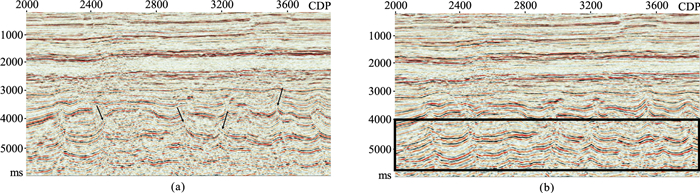
本文采用GeoEast-Diva建模软件层位约束的网格层析建模技术和GeoEast-Kirchhoff叠前深度偏移技术联合进行处理。图 4a和图 5a是无层位约束时,仅利用网格层析得到的速度模型及其叠前深度偏移结果。由速度模型可以看出,从浅层到深层都出现局部速度异常,尤其是深层局部速度纵、横向变化剧烈(图 4a方框所示),导致偏移结果上同相轴扭曲严重,出现了虚假构造(图 5a方框所示);图 4b和图 5b是利用层位约束的网格层析建模方法得到的速度模型及其叠前深度偏移结果。层位约束后,速度模型纵、横向变化相对均匀,有效消除了速度局部异常现象,消除了叠前深度偏移剖面上的同相轴扭曲现象,大幅度提高了深层的成像质量(方框所示)。与叠前时间偏移结果(图 6a)相比,叠前深度偏移结果(图 6b)有效消除了叠前时间偏移同相轴交叉的构造假象(箭头所示),断裂刻画相对更清晰,有效改善了深层底劈构造(黑框所示)的成像质量。
|
图 4 层位约束前(a)、后(b)网格层析的速度模型的对比 |

|
图 5 层位约束前(a)、后(b)网格层析速度模型的叠前深度偏移剖面对比 |
|
图 6 叠前时间(a)与深度(b)偏移剖面对比 |
针对实际工区地震资料深层信噪比低、速度横向变化剧烈,同时缺乏钻井、测井资料数据,本文基于GeoEast-Diva速度建模软件,大幅度提高了深层底劈成像质量以及断裂成像精度,为后续构造解释提供较好的资料基础。得到以下认识:
(1) 层位约束的网格层析速度建模方法,依靠数据驱动结合层位约束,体现了处理、解释一体化思想,可以有效降低速度层析反演的多解性,消除虚假构造、提高模型精度;
(2) GeoEast-Diva速度建模软件集成层位模型创建、网格层析、沿层层析等优点,结合GPU-Kirchhoff叠前深度偏移技术,可以实现快速有效的速度建模反演迭代,极大地提高了叠前深度偏移的效率。实际数据处理效果说明该软件是一种非常实用的高精度建模工具。
在本文完成过程中,东方地球物理公司物探技术研发中心姜绍辉老师等给予了大力支持,在此表示衷心感谢!
| [1] |
马彦彦, 李国发, 张星宇, 等. 叠前深度偏移速度建模方法分析[J]. 石油地球物理勘探, 2014, 49(4): 687-693. MA Yanyan, LI Guofa, ZHANG Xingyu, et al. Strategy of velocity model building in prestack depth migration[J]. Oil Geophysical Prospecting, 2014, 49(4): 687-693. |
| [2] |
LI G F, CAO M Q, ZHOU H. Effects of near-surface absorption on reflection characteristics of continental interbedded strata: the Dagang Oilfield as an example[J]. Acta Geologica Sinica, 2010, 84(5): 1306-1314. DOI:10.1111/j.1755-6724.2010.00299.x |
| [3] |
刘文卿, 王西文, 刘洪, 等. 盐下构造速度建模与逆时偏移成像研究及应用[J]. 地球物理学报, 2013, 56(2): 616-625. LIU Wenqing, WANG Xiwen, LIU Hong, et al. Application of velocity modeling and reverse time migration to subsalt structure[J]. Chinese Journal of Geophysics, 2013, 56(2): 616-625. |
| [4] |
杨哲, 王小卫, 胡自多, 等. 基于束偏移的地层倾角约束网格层析建模[J]. 石油地球物理勘探, 2018, 53(增刊1): 75-82. YANG Zhe, WANG Xiaowei, HU Ziduo, et al. Formation-dip-constrained grid tomography velocity mode-ling based on Gaussian beam migration[J]. Oil Geophysical Prospecting, 2018, 53(S1): 75-82. |
| [5] |
谷延斌, 张旭东, 姚征, 等. 网格层析和高斯束偏移在深度域速度建模中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 112-116. GU Yanbin, ZHANG Xudong, YAO Zheng, et al. Application of the grid tomography and Gauss beam migration in velocity modelling in the depth domain[J]. Oil Geophysical Prospecting, 2018, 53(S1): 112-116. |
| [6] |
潘兴祥, 秦宁, 曲志鹏, 等. 叠前深度偏移层析速度建模及应用[J]. 地球物理学进展, 2013, 28(6): 3080-3085. PAN Xingxiang, QIN Ning, QU Zhipeng, et al. Tomography velocity modeling and application of prestack depth migration[J]. Progress in Geophysics, 2013, 28(6): 3080-3085. |
| [7] |
HEWITT DIX C. Seismic velocities from surface measurements[J]. Geophysics, 1955, 20(1): 68-86. |
| [8] |
CLAPP R, SAVA P, CLEARBOUT J F. Interval velocities estimation with a null space[R]. Stanford Exploration Project Report, 1998, 147-156.
|
| [9] |
胡英, 张研, 陈立康, 等. 速度建模的影响因素与技术对策[J]. 石油物探, 2006, 45(5): 503-507. HU Ying, ZHANG Yan, CHEN Likang, et al. Influencing factors and technical strategies for velocity modeling[J]. Geophysical Prospecting for Petroleum, 2006, 45(5): 503-507. |
| [10] |
LAFOND C F, LEVANDER A R. Migration moveout analysis and depth focusing[J]. Geophysics, 1993, 58(1): 91-100. |
| [11] |
李慧, 成德安, 金婧. 网格层析成像速度建模方法与应用[J]. 石油地球物理勘探, 2013, 48(增刊1): 12-16. LI Hui, CHENG Dean, JIN Jing. Velocity model building based on grid tomography[J]. Oil Geophysical Prospecting, 2013, 48(S1): 12-16. |
| [12] |
辛可锋, 王华忠, 马在田. 基于共聚焦点技术的成像速度建模方法研究[J]. 石油地球物理勘探, 2004, 39(5): 519-525. XIN Kefeng, WANG Huazhong, MA Zaitian. Imaging velocity model-building method based on common focus point technique[J]. Oil Geophysical Prospecting, 2004, 39(5): 519-525. |
| [13] |
王非翊, 张凯, 李振春, 等. VTI介质各向异性参数角道集层析反演[J]. 石油地球物理勘探, 2019, 54(5): 1057-1066. WANG Feiyi, ZHANG Kai, LI Zhenchun, et al. VTI medium anisotropic parameter tomography inversion based on angle domain common imaging gathers[J]. Oil Geophysical Prospecting, 2019, 54(5): 1057-1066. |
| [14] |
张子良, 李振春, 张凯, 等. 地质模型约束的全波形速度建模反演及在复杂断块区的应用[J]. 石油地球物理勘探, 2020, 55(3): 599-606. ZHANG Ziliang, LI Zhenchun, ZHANG Kai, et al. Research of geological model-constrained FWI and application in complex fault-block zones[J]. Oil Geophysical Prospecting, 2020, 55(3): 599-606. |
| [15] |
王小卫, 姚姚, 刘文卿, 等. 波动方程叠前偏移在碳酸盐岩成像中的应用研究[J]. 天然气地球科学, 2011, 22(5): 874-877. WANG Xiaowei, YAO Yao, LIU Wenqing, et al. Application of wave equation prestack migration in carbonate imaging[J]. Natural Gas Geoscience, 2011, 22(5): 874-877. |
| [16] |
袁刚, 冯心远, 蒋波, 等. 约束层析反演及其在地震速度计算中的应用[J]. 石油物探, 2013, 52(1): 55-59. YUAN Gang, FENG Xinyuan, JIANG Bo, et al. Constrained tomography inversion and its application in seismic velocity computation[J]. Geophysical Prospecting for Petroleum, 2013, 52(1): 55-59. |
| [17] |
杨午阳, 张厚柱, 撒利明, 等. 逆时偏移关键问题探讨[J]. 石油地球物理勘探, 2016, 51(6): 1251-1262. YANG Wuyang, ZHANG Houzhu, SA Liming, et al. Some issues about reverse time migration[J]. Oil Geophysical Prospecting, 2016, 51(6): 1251-1262. |
| [18] |
肖艳玲, 范旭, 王晓涛, 等. 网格层析速度反演技术在齐古背斜叠前深度偏移中的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 98-103. XIAO Yanling, FAN Xu, WANG Xiaotao, et al. Mesh tomographic velocity inversion for the prestack depth migration of the Qigu anticline[J]. Oil Geophysical Prospecting, 2017, 52(S2): 98-103. |
| [19] |
王兆旗, 叶月明, 庄锡进, 等. 层控网格层析速度建模技术在陆上盐丘区的应用[J]. 天然气地球科学, 2016, 27(11): 2070-2076. WANG Zhaoqi, YE Yueming, ZHUANG Xijin, et al. Application of layer-constrained grid tomographic velocity modeling in onshore salt domes area[J]. Natural Gas Geoscience, 2016, 27(11): 2070-2076. |



 徐兴荣, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院地震资料处理解释中心, 730020。Email:
徐兴荣, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院地震资料处理解释中心, 730020。Email: 