②. 中油国际勘探开发有限公司, 北京 100034
②. China National Oil and Gas Exploration and Deve-lopment Corporation, CNPC, Beijing 100034, China
随着地震勘探的难度不断加大,叠前保真成像要求数据尽可能规则,即在合适观测孔径内的采样尽量是等间隔、无空间假频。然而,在实际采集过程中,由于地表条件等常常造成地震道缺失、炮检点分布不规则、覆盖次数不均匀等现象,从而导致实际资料存在严重的空间假频,偏移时会产生划弧和成像振幅畸变、同相轴不连续等现象,难以满足勘探要求。因此,数据规则化[1-5]是地震数据处理最基础且非常重要的一环。目前规则化方法主要分为以下三大类。一类是基于信号分析理论的插值规则化方法,它假设地震同相轴是线性可预测的,其思路是采用多种约束条件下的反演方法重建规则数据的傅里叶谱。第二类是基于模型的规则化方法,此类方法的核心思想是借助速度模型或速度假设条件将非规则数据体映射到规则的数据体,模型精度对规则化效果影响比较大。第三类规则化方法是稀疏域压缩感知类重建方法,其核心思想是利用非规则采集数据的随机性和冗余性,选择合理的稀疏域表达,获得信号的压缩识别,然后进行稀疏反变换实现信号的插值,同时实现噪声压制。但变换域的选择、随机采样的方式和冗余度的估计皆存在潜在风险,有可能损失有效信息和增加错误信息。张岩等[6]提出了联合小波域与深度学习的地震数据规则化方法,虽然可以精确表示地震数据的纹理特征,但在样本有限的情况下难以取得理想效果。目前,抗假频数据规则化、叠前三维地震数据体的五维重建等已经成为改善成像质量、提高资料保真性及保幅性的关键处理环节。地震数据插值方法正在往高维拓展,研究高效、高精度、抗噪、抗假频的数据插值方法,提高地震数据的横向连续性,已成为插值重建方法发展趋势。在诸多方法中,傅里叶数据重建[7]是常用的地震数据插值方法,其基本思路就是把数据变换到频率—波数域,估算出稀疏谱,再反变换到时空域,生成无假频的时空域数据。
GeoEast系统五维插值技术利用傅里叶重构技术[8-11],能够同时进行五个维度的规则化处理,使得空间方向不均匀采样数据得到规则化重建,从而改善炮检距、覆盖次数等属性的均匀性。尼日尔Agadem区块由采集参数不同的三个工区组成,各工区地震数据的方位角、面元尺寸、覆盖次数和采集年度都有不同,原始资料能量不均衡,部分炮检距缺失,数据信噪比低。应用GeoEast系统五维规则化模块后,有效地解决了浅层数据缺失问题,同时提高了深层资料的信噪比。
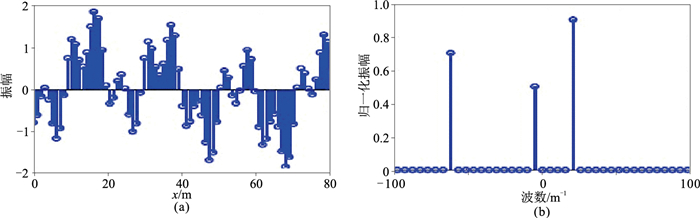
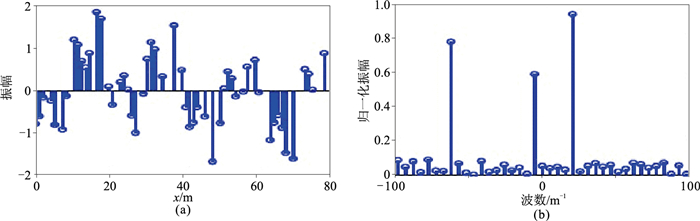
1 不规则地震数据分类及频谱泄漏现象[12-15]图 1a为规则采样的3个有效谐波的叠加信号,利用离散傅里叶变换(DFT)将其转换至波数域(图 1b)。在波数域只有相应的3个波数的谐波信号,其余波数的信号能量都是0,表明规则采样的信号有且仅有3个谐波信号,与理论期望值一致。而对图 2a的不规则采样数据,同样利用DFT将其转换至波数域(图 2b),可以看出,虽然也有3个能量较强的谐波信号,但其余波数信号的能量并不全为0,说明对非规则采样的输入信号进行DFT存在由非正交基导致的能量泄漏。因此,规则化的过程实质上就是一个能量反泄漏过程[16-20]。
|
图 1 规则采样谐波信号(a)及其DFT谱(b) |
|
图 2 不规则采样谐波信号(a)及其DFT谱(b) |
地震数据的频谱估计可以分为两类,一类是基于反演理论,另一类是基于相关理论。基于相关理论的方法包括反泄漏傅里叶变换(Antileakage Fourier Transform,ALFT)、凸集投影(POCS)、匹配追踪(MP)等方法。Xu等[21]提出的ALFT法运用迭代傅里叶变换实现插值,是用阈值方法去掉小的傅里叶系数得到最大的傅里叶系数[22-25]。在地震数据重建中常用的ALFT能够压制能量谱泄漏,使得重建结果在有限频宽内保持数据信号不受损失并压制高频信号的假频现象。
反泄漏傅里叶算法[21]主要是通过估计不规则采样地震数据的傅里叶系数来达到减少波数泄漏的目的。野外三维地震采集数据包括炮点、检波点坐标和时间。在时间维度上,地震记录的采样是规则的,可以用FFT(快速傅里叶变换)将数据转换到频率域。因此,在对数据进行规则化时,主要考虑在空间维度上的不规则性。空间维度可以选择炮检域(炮点x坐标、炮点y坐标、检波点x坐标、检波点y坐标),也可以选择CDP域(CDP的x坐标、CDP的y坐标、x方向炮检距、y方向炮检距)。以x方向坐标维度为例,非规则采样数据f傅里叶变换可表示为
| $\hat{f}(k)=\frac{1}{\Delta X} \sum\limits_{l=1}^N w\left(x_l\right) f\left(x_l\right) \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} k x_l}$ | (1) |
式中:w(xl)为积分权值,xl为第l个样点位置;ΔX=
ALFT算法通过估计所有波数成分k的傅里叶系数来完成。首先,选取谱能量最大的分量
| $f^k\left(x_l\right)=\hat{f}_{\max }(k) \mathrm{e}^{\mathrm{i} 2 {\rm{ \mathsf{ π} }} k x_l}$ | (2) |
式中fk(xl)为k波数分量对应输入数据。再从原始数据中减去
| $f^{\mathrm{u}}\left(x_l\right)=f\left(x_l\right)-f^k\left(x_l\right)$ | (3) |
将相减之后的数据重复式(1)~式(3)运算,反复迭代,直到傅里叶系数中能量最大的成分小于给定的阈值为止。
将所有最大能量成分反变换后,就得到了规则化后的数据[26-29]。
2.2 反泄漏傅里叶变换数据规则化实现步骤利用ALFT技术进行地震数据规则化的基本步骤[28]主要有以下几步:
(1) 对数据进行离散傅里叶变换;
(2) 对傅里叶谱计算权重(先验值),并将权重应用在频谱的全频带上;
(3) 选取加权后最大能量的傅里叶谱成分;
(4) 将该傅里叶谱成分(未加权)加入“估算谱”;
(5) 对该傅里叶谱成分(未加权)进行反傅里叶变换,并按照输入位置输出迭代结果;
(6) 从原始输入数据中减去该次迭代结果;
(7) 重复步骤(1)~步骤(6),直到达到设定迭代次数或者式(3)达到预设值;
(8) 对最终“估算谱”进行反傅里叶变换, 输出到期望位置。
GeoEast系统一般选择在炮检域进行插值,可以加密炮线、检波线或缩小面元。对于宽方位、高密度的采集数据,可以在OVT域规则化处理,将炮检中点规则化到CMP面元中心。
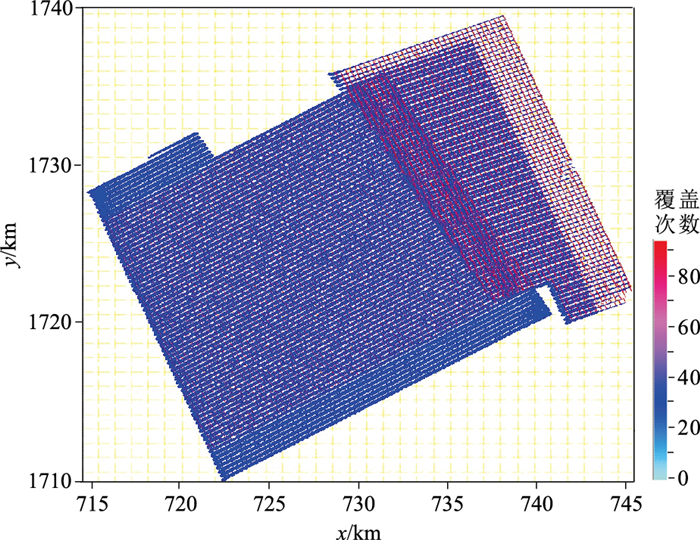
3 实例分析 3.1 三维连片数据分析如图 3所示,三维连片区块位于尼日尔东南部的Termit盆地,由采集参数不同的三个工区组成(表 1)。3个工区地震资料的方位角、面元尺寸、覆盖次数和采集年度都有不同,各区块间原始资料能量不均衡,部分炮检距缺失,数据信噪比低,成像效果不够理想。受地表条件的限制,炮、检线不完全正交,既有64次满覆盖,也有96次满覆盖。
|
图 3 连片工区位置图 |
|
|
表 1 三个工区采集参数 |
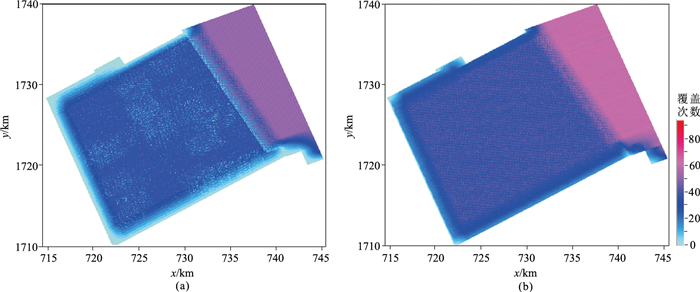
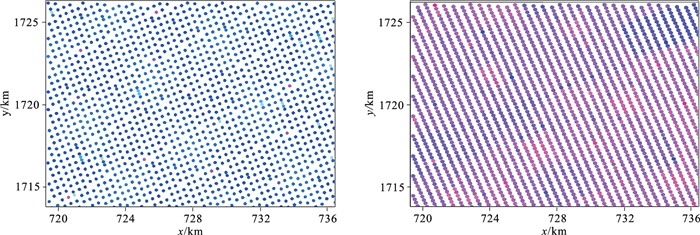
GeoEast五维规则化模块提供了规则化和插值两种选项,因为尼日尔连片数据区块间资料品质差别较大,完全重构结果不理想,所以选择了极坐标系统下的五维插值,将炮检距以200m、方位角以20°为间隔分组,插值后输出数据是由输入数据和重建的缺失地震道合并而成,既不改变原有地震数据信息,又重建了缺失数据,如图 4和图 5所示。插值后数据统一到96次满覆盖,整体面元分布均匀。
|
图 4 五维规则化前(左)、后(右)覆盖次数 |
|
图 5 数据规则化前(左)、后(右)的面元分布(局部放大) |
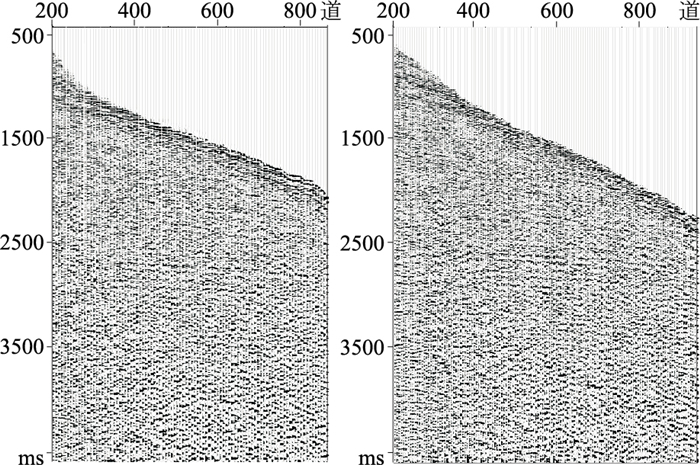
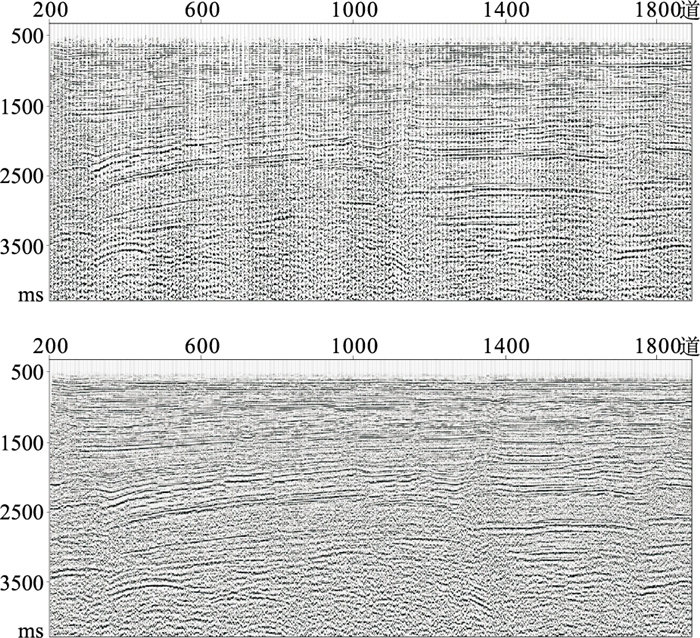
对比插值前、后CDP道集(图 6)和叠加剖面(图 7)可见:五维空间插值后,解决了覆盖次数变化大的问题,插值后剖面成像整体效果得到改善,浅层尤其明显,有效解决了数据缺失问题;因为在傅里叶变换域优先搜索能量最强的有效信号,而干扰波则会呈现杂乱的低能量的频谱,所以不会被反变换回时间—空间域,叠加剖面的信噪比得到了提高。插值前覆盖次数变化较大,尤其是拼接处,插值后整体数据覆盖次数比较均匀,偏移时能有效减弱划弧现象,偏移噪声明显减弱,信噪比得到提高(图 8)。红框所示区域连续性增强,中、浅层成像效果进一步改善;蓝色椭圆所示区域为目的层,同相轴更聚焦,划弧现象减弱。
|
图 6 五维插值前(左)、后(右)的道集对比 |
|
图 7 五维规则化前(上)、后(下)的叠加剖面对比 |

|
图 8 五维规则化前(上)、后(下)叠前时间偏移剖面对比 |
五维插值规则化算法复杂,在Agadem区块的处理过程中,由于工区多、面积大、数据量大,为满足五维插值需求,GeoEast系统五维插值规则化模块(BinRegular5D)使用基于多核通用处理器(GPP)并行框架机制,不仅具有高效的计算能力,而且具有容错能力,解决了项目时间紧的问题。
4 结论通过尼日尔Agadem区块应用GeoEast系统五维规则化技术,得到如下认识:
(1) GeoEast五维规则化技术可以有效地解决Agadem连片区块由采集因素导致的缺道、覆盖次数不均匀等问题,提高地震资料的信噪比,减少了偏移划弧;
(2) GeoEast五维规则化技术可以适用于任意观测系统,充分利用地震数据五个维度的信息,根据不同的数据选择插值或者规则化,保真能力比较卓越;
(3) GeoEast五维规则化模块使用GPP并行框架机制,解决了五维插值规则化算法效率低的问题,能够满足工业生产需求。
| [1] |
王伟, 陈双廷, 王宝彬, 等. 五维规则化技术研究与应用[J]. 石油地球物理勘探, 2017, 52(增刊1): 28-33. WANG Wei, CHEN Shuangting, WANG Baobin, et al. Application of 5D regularization in seismic data processing[J]. Oil Geophysical Prospecting, 2017, 52(S1): 28-33. |
| [2] |
曹国滨. 频率—空间域数据规则化压制采集脚印技术研究[J]. 石油物探, 2010, 49(4): 359-363. CAO Guobin. Study of suppressing acquisition footprint by data regularization in frequency-space domain[J]. Geophysical Prospecting for Petroleum, 2010, 49(4): 359-363. |
| [3] |
辛可锋, 王华忠, 王成礼, 等. 叠前地震数据的规则化[J]. 石油地球物理勘探, 2002, 37(4): 311-317. XIN Kefeng, WANG Huazhong, WANG Chengli, et al. Regularization of pre-stack seismic data[J]. Oil Geophysical Prospecting, 2002, 37(4): 311-317. |
| [4] |
石颖, 张振, 王建民, 等. 地震数据反假频规则化方法研究[J]. 地球物理学进展, 2013, 28(1): 250-256. SHI Ying, ZHANG Zhen, WANG Jianmin, et al. Investigation on anti-aliasing regularization approach for seismic data[J]. Progress in Geophysics, 2013, 28(1): 250-256. |
| [5] |
PIEPRZAK A, MCCLEAN J. Trace interpolation of severely aliased events[C]. SEG Technical Program Expanded Abstracts, 1988, 7: 658-660.
|
| [6] |
张岩, 李杰, 王斌, 等. 基于联合小波域深度学习的地震数据规则化方法[J]. 石油地球物理勘探, 2022, 57(4): 777-788. ZHANG Yan, LI Jie, WANG Bin, et al. Seismic data regularization based on deep learning combining wavelet domain[J]. Oil Geophysical Prospecting, 2022, 57(4): 777-788. |
| [7] |
段文胜, 王鹏, 党青宁, 等. 应用匹配追踪傅里叶插值技术实现OVT域连片处理[J]. 石油地球物理勘探, 2017, 52(4): 669-677. DUAN Wensheng, WANG Peng, DANG Qingning, et al. 5D data regularization based on matching pursuit Fourier interpolation for the OVT domain data merging processing[J]. Oil Geophysical Prospecting, 2017, 52(4): 669-677. |
| [8] |
李国发. f-k域与f-x域联合实现道内插[J]. 石油地球物理勘探, 1995, 30(5): 693-701, 718. LI Guofa. Joint trace interpolation in f-k and f-x domains[J]. Oil Geophysical Prospecting, 1995, 30(5): 693-701. |
| [9] |
LIU Y, SERGEY F. Seismic data interpolation beyond aliasing using regularized nonstationary auto regression[J]. Geophysics, 2011, 76(5): V69-V77. DOI:10.1190/geo2010-0231.1 |
| [10] |
RONEN J. Wave-equation trace interpolation[J]. Geophysics, 1987, 52(7): 973-984. DOI:10.1190/1.1442366 |
| [11] |
刘喜武, 刘洪, 刘彬. 反假频非均匀地震数据重建方法研究[J]. 地球物理学报, 2004, 47(2): 299-305. LIU Xiwu, LIU Hong, LIU Bin. A study on algorithm for reconstruction of de-alias uneven seismic data[J]. Chinese Journal of Geophysics, 2004, 47(2): 299-305. |
| [12] |
高建军, 陈小宏, 王芳芳, 等. 不规则地震道数据规则化重建方法研究[J]. 地球物理学进展, 2011, 26(3): 983-991. GAO Jianjun, CHEN Xiaohong, WANG Fangfang, et al. Study on regularized reconstruction of uneven seismic traces[J]. Progress in Geophysics, 2011, 26(3): 983-991. |
| [13] |
薛亚茹, 陈健升, 钱步仁. 高阶3D Radon变换及其数据重建应用[J]. 中国石油大学学报(自然科学版), 2016, 40(3): 69-76. XUE Yaru, CHEN Jiansheng, QIAN Buren. High order 3D Radon transform and its application in data reconstruction[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016, 40(3): 69-76. |
| [14] |
魏小强, 雷秀丽, 马庆珍. 基于多道奇异谱分析的三维地震数据规则化方法[J]. 石油地球物理勘探, 2014, 49(5): 846-850. WEI Xiaoqiang, LEI Xiuli, MA Qingzhen. 3D seismic data regularization based on multichannel singular spectrum analysis[J]. Oil Geophysical Prospecting, 2014, 49(5): 846-850. |
| [15] |
WANG B F, CHEN X H, LI J Y, et al. An improved weighted projection onto convex sets method for seismic data interpolation and denoising[J]. IEEE Journal of Selected Topics in Applied Earth Observation and Remote Sensing, 2016, 9(1): 228-235. |
| [16] |
郭念民, 李海山, 冯雪梅, 等. 非抽样离散小波变换叠前地震数据重建方法[J]. 石油地球物理勘探, 2014, 49(3): 508-516. GUO Nianmin, LI Haishan, FENG Xuemei, et al. Pre-stack seismic data reconstruction based on the undecimated wavelet transform[J]. Oil Geophysical Prospecting, 2014, 49(3): 508-516. |
| [17] |
孟小红, 郭良辉, 张致付, 等. 基于非均匀快速傅里叶变换的最小二乘反演地震数据重建[J]. 地球物理学报, 2008, 51(1): 235-241. MENG Xiaohong, GUO Lianghui, ZHANG Zhifu, et al. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform[J]. Chinese Journal of Geophysics, 2008, 51(1): 235-241. |
| [18] |
王棣, 马秀红, 崔兴福, 等. 偏移距规则化技术在叠前时间偏移中的应用[J]. 勘探地球物理进展, 2009, 32(1): 44-47. WANG Di, MA Xiuhong, CUI Xingfu, et al. Application of prestack offset regularization in prestack time migration[J]. Progress in Exploration Geophysics, 2009, 32(1): 44-47. |
| [19] |
郭树祥. 埕岛桩海地区连片地震资料的数据规则化处理[J]. 石油物探, 2008, 47(4): 387-392. GUO Shuxiang. Seismic data regularization by merging processing in Chengdao-Zhuanghai area[J]. Geophysical Prospecting for Petroleum, 2008, 47(4): 387-392. |
| [20] |
高彩霞. 波动方程叠前成像数据规则化技术研究与应用[J]. 石油天然气学报, 2010, 32(6): 271-273. GAO Caixia. Technical study and application of wave equation prestack imaging data rules[J]. Journal of Oil and Gas Technology, 2010, 32(6): 271-273. |
| [21] |
XU S, ZHANG Y, PHAM D, et al. Antileakage Fourier transfrom for seismic data regularization[J]. Geophysics, 2005, 70(4): V87-V95. |
| [22] |
苏世龙, 王永明, 黄志. 两种数据规则化地震处理技术应用探讨[J]. 勘探地球物理进展, 2010, 33(3): 200-206. SU Shilong, WANG Yongming, HUANG Zhi. Application of two data regularization in seismic data processing[J]. Progress in Exploration Geophysics, 2010, 33(3): 200-206. |
| [23] |
宜明理, 严又生, 魏新, 等. F-K域抗假频道内插[J]. 石油物探, 2001, 40(2): 36-41. YI Mingli, YAN Yousheng, WEI Xin, et al. Using anti-alias trace interpolation in F-K domain[J]. Geophysical Prospecting for Petroleum, 2001, 40(2): 36-41. |
| [24] |
渥·伊尔玛兹. 地震资料分析[M]. 北京: 石油工业出版社, 2006.
|
| [25] |
ZWARTJES P M, SACCHI D M. Fourier reconstruction of non-uniformly sampled, aliased seismic data[J]. Geophysics, 2007, 72(1): V21-V32. |
| [26] |
凌云研究组. 叠前相对保持振幅、频率、相位和波形的地震数据处理与评价研究[J]. 石油地球物理勘探, 2004, 39(5): 543-552. LING Yun Research Group. Study of seismic data processing and appreciation based on prestack relative preservation of amplitude, frequency, phase and waveform[J]. Oil Geophysical Prospecting, 2004, 39(5): 543-552. |
| [27] |
徐兴荣, 苏勤, 王劲松, 等. 加权MPFI方法及其在三维连片处理中的应用[J]. 岩性油气藏, 2019, 31(1): 122-129. XU Xingrong, SU Qin, WANG Jinsong, et al. Weighted MPFI method and its application in 3D joint processing[J]. Lithologic Reservoirs, 2019, 31(1): 122-129. |
| [28] |
凌越, 刘伟明, 肖明图, 等. 改进的匹配追踪数据规则化方法[J]. 石油地球物理勘探, 2020, 55(增刊): 25-32. LING Yue, LIU Weiming, XIAO Mingtu, et al. The improved seismic data regularization method based on matching pursuit theory[J]. Oil Geophysical Prospecting, 2020, 55(S): 25-32. |
| [29] |
马渊明, 王飞, 柴军丽, 等. GeoEast系统叠前五维插值规则化技术[J]. 石油工业计算机应用, 2018, 26(2-4): 27-30. MA Yuanming, WANG Fei, CHAI Junli, et al. Pre-stack 5D interpolation regularization technology of GeoEast system[J]. Computer Applications of Petroleum, 2018, 26(2-4): 27-30. |



 王艳香, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email:
王艳香, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email: 