②. 中海石油(中国)海南分公司, 海南海口 570311;
③. 上海青凤致远地球物理地质勘探科技有限公司, 上海 200093
②. Hainan Branch, CNOOC (China), Haikou, Hainan 570311, China;
③. Shanghai Qingfeng Zhiyuan Geophysics & Geology, Co. Ltd., Shanghai 200093, China
随着海上OBC/OBN地震资料的大规模采集,处理炮检点不在同一水平面上的资料成为了重要研究内容。常规的方式是首先对数据进行静校正处理,将炮检点坐标校正到同一水平面,然后进行常规水平地表处理。在炮检点高程差较大时,静校正通常会引入较大的误差,影响后续成像的效果。减小这种误差的方法是进行波动方程基准面校正处理[1-3],如杨锴等[1-2]利用波动方程将不同高度炮检点波场延拓到同一水平面,再进行后续水平地表的处理。另外一种处理方式为直接进行不在同一基准面的偏移成像,即起伏地表偏移。如文献[4-5]研究了起伏地表Kirchhoff积分叠前时间偏移;文献[6-8]研究了起伏地表Kirchhoff叠前深度偏移技术;文献[9-11]中,研究人员深入分析了起伏地表高斯束偏移;文献[12-17]针对起伏地表炮域单程波偏移成像提出了不同的实现方法。在炮域单程波偏移的基础上,研究人员推广了逆时偏移的起伏地表实现[18-21]。曲英铭[22]对近年来直接从起伏地表进行偏移成像的方法进行了全面调研,进一步指出了起伏地表进行直接偏移的重要性。可以看出,无论是Kirchhoff偏移、高斯束偏移还是炮域单程波和逆时偏移,研究者们均已经提出了相应的起伏地表实现方案。
双平方根方程偏移[23-28]又称为沉降观测偏移,其实现过程相当于炮检点同步沉降到成像点处进行成像。由于该方法计算效率和精度较高、偏移孔径无需人为选择、偏移角度道集容易输出,是工业界一种重要的成像方法。近年来,业界对该方法进行了大量研究,扩展了其适用范围。迄今为止,还没有相关文献研究基于该成像算子的起伏地表成像方法。OBC/OBN数据可以视为一种特殊的起伏地表数据,炮点和检波点分别位于两个不同的基准面上。本文研究OBC/OBN数据的双平方根方程偏移方法,以期改善OBC/OBN数据的成像效果。
首先回顾双平方根方程的基本推导;然后分析OBC/OBN采集情况下实现起伏地表偏移的方法,分析该方法对于OBN数据镜偏移的适用性;最后,将本文方法用于OBC/OBN成像处理测试,用理论数据和实际资料验证方法的正确性。
1 双平方根偏移算子根据Claerbout的傍轴波动方程理论[23],炮点和检波点波场分别向地下沉降,旅行时满足
| $ \frac{\partial t_{\mathrm{s}}}{\partial z_{\mathrm{s}}}=-\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{s}}, z\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{s}}}\right)^2\right]^{\frac{1}{2}} $ | (1) |
| $\frac{\partial t_{\mathrm{g}}}{\partial z_{\mathrm{g}}}=-\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{g}}, z\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{g}}}\right)^2\right]^{\frac{1}{2}} $ | (2) |
式中: ts、tg分别表示炮点和检波点波场旅行时; t为波场传播总时间; zs、zg分别表示炮点和检波点延拓深度;
| $ \begin{aligned} \frac{\partial t}{\partial z}=\frac{\partial t}{\partial z_{\mathrm{s}}}+\frac{\partial t}{\partial z_{\mathrm{g}}}= & -\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{s}}, z_{\mathrm{s}}\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{s}}}\right)^2\right]^{\frac{1}{2}} \\ & -\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{g}}, z_{\mathrm{g}}\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{g}}}\right)^2\right]^{\frac{1}{2}} \end{aligned} $ | (3) |
进而得到DSR方程
| $ \begin{aligned} & \frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{g}}, z\right)}{\partial z}=-\frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{g}}, z\right)}{\partial t} \frac{\partial t}{\partial z} \\ & =\left\{\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{s}}, z\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{s}}}\right)^2\right]^{\frac{1}{2}}+\right. \\ & \left.\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{g}}, z\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{g}}}\right)^2\right]^{\frac{1}{2}}\right\} \frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{g}}, z\right)}{\partial t} \end{aligned} $ | (4) |
式中P(t,Xs,Xg,z) 为t时刻空间位置(Xs,Xg,z)对应的波场。
式(4)即为以炮检点坐标表示的DSR延拓方程。为了计算方便,该方程通常在中点—半炮检距域实现。令M、H分别表示炮检中点和半炮检距,有
| $ \left\{\begin{array}{l} \boldsymbol{M}=\frac{1}{2}\left(\boldsymbol{X}_{\mathrm{g}}+\boldsymbol{X}_{\mathrm{s}}\right) \\ \boldsymbol{H}=\frac{1}{2}\left(\boldsymbol{X}_{\mathrm{g}}-\boldsymbol{X}_{\mathrm{s}}\right) \end{array}\right. $ | (5) |
则式(4)可以表示为
| $ \begin{aligned} & \frac{\partial P(t, \boldsymbol{M}, \boldsymbol{H}, z)}{\partial z} \\ & =\left\{\left[\frac{1}{v^2(\boldsymbol{M}-\boldsymbol{H}, z)}-\frac{1}{4}\left(\frac{\partial t}{\partial \boldsymbol{M}}-\frac{\partial t}{\partial \boldsymbol{H}}\right)^2\right]^{\frac{1}{2}}+\right. \\ & \left.\left[\frac{1}{v^2(\boldsymbol{M}+\boldsymbol{H}, z)}-\frac{1}{4}\left(\frac{\partial t}{\partial \boldsymbol{M}}+\frac{\partial t}{\partial \boldsymbol{H}}\right)^2\right]^{\frac{1}{2}}\right\} \times \\ & \frac{\partial P(t, \boldsymbol{M}, \boldsymbol{H}, z)}{\partial t} \\ & \end{aligned} $ | (6) |
式(6)即为经典的中点—半炮检距域表示的DSR方程。
2 OBC/OBN数据双平方根偏移及镜偏移对于OBC/OBN观测数据,炮点位于海平面,检波点位于海底,炮检点位于两个基准面,不满足同时沉降。设海底深度为zb,根据式(1),先将炮点沉降到海底深度zb,其沉降公式为
| $ \begin{aligned} & \frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{g}}, z\right)}{\partial z}=-\frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{g}}, z\right)}{\partial t} \frac{\partial t}{\partial z} \\ & =\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{s}}, z\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{s}}}\right)^2\right]^{\frac{1}{2}} \frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{g}}, z\right)}{\partial t} \end{aligned} $ | (7) |
在炮点波场到达海底zb后,炮检点波场同步进行沉降,则最终波场延拓公式为
| $ \left\{\begin{array}{l} \frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{g}}, z\right)}{\partial z}=\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{s}}, z\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{s}}}\right)^2\right]^{\frac{1}{2}} \times \\ \frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{g}}, z\right)}{\partial t} ~~~~z <z_{\mathrm{b}}~~~~(8\mathrm{a})\\ \frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{b}}, z\right)}{\partial z}=\left\{\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{s}}, z\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{s}}}\right)^2\right]^{\frac{1}{2}}+\right. \\ \left.\left[\frac{1}{v^2\left(\boldsymbol{X}_{\mathrm{g}}, z\right)}-\left(\frac{\partial t}{\partial \boldsymbol{X}_{\mathrm{g}}}\right)^2\right]^{\frac{1}{2}}\right\} \frac{\partial P\left(t, \boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{\mathrm{g}}, z\right)}{\partial t} \quad \text { 其他 } \end{array}\right.\\ ~~~~~~~~~~~~(8\mathrm{b}) $ |
在中点—半炮检距域,根据式(5),式(8)可以表述为
| $ \left\{\begin{array}{l} \frac{\partial P(t, \boldsymbol{M}, \boldsymbol{H}, z)}{\partial z}=\left[\frac{1}{v^2(\boldsymbol{M}-\boldsymbol{H}, z)}-\right. \\ \left.\frac{1}{4}\left(\frac{\partial t}{\partial \boldsymbol{M}}-\frac{\partial t}{\partial \boldsymbol{H}}\right)^2\right]^{\frac{1}{2}} \frac{\partial P(t, \boldsymbol{M}, \boldsymbol{H}, z)}{\partial t} \quad z <z_b ~~~~(9\mathrm{a})\\ \frac{\partial P(t, \boldsymbol{M}, \boldsymbol{H}, z)}{\partial z}=\left\{\left[\frac{1}{v^2(\boldsymbol{M}-\boldsymbol{H}, z)}-\right.\right. \\ \left.\frac{1}{4}\left(\frac{\partial t}{\partial \boldsymbol{M}}-\frac{\partial t}{\partial \boldsymbol{H}}\right)^2\right]^{\frac{1}{2}}+\left[\frac{1}{v^2(\boldsymbol{M}+\boldsymbol{H}, z)}-\right. \\ \left.\left.\frac{1}{4}\left(\frac{\partial t}{\partial \boldsymbol{M}}+\frac{\partial t}{\partial \boldsymbol{H}}\right)^2\right]^{\frac{1}{2}}\right\} \frac{\partial P(t, \boldsymbol{M}, \boldsymbol{H}, z)}{\partial t} \quad \text { 其他 }~~~~(9\mathrm{b}) \end{array}\right. $ |
将式(9)分解为背景场和散射场,分别在背景介质和扰动介质中传播,可以得到不同精度的外推方程。式(7)或者式(8)中,在海底面之上波场延拓为单平方根方程延拓,实现炮点的独立沉降; 到达海底面之后,炮检点同步延拓,为双平方根方程延拓,本文称之为单/双平方根方程混合延拓。
对于OBN数据单/双平方根方程混合延拓成像条件,在海底之上不需要成像,到达海底之后与常规DSR成像条件一样。根据零时间零炮检距成像条件
| $ P\left(t=0, \boldsymbol{K}_{\mathrm{m}}, \boldsymbol{H}=0, z\right)=\int \mathrm{d} \omega \int \mathrm{d} \boldsymbol{K}_{\mathrm{h}} P\left(\omega, \boldsymbol{K}_{\mathrm{m}}, \boldsymbol{K}_{\mathrm{h}}, z\right) $ | (10) |
实现成像值提取,完成上行波叠前深度偏移。式中;Km为中心点M对应的波数;Kh为半炮检距H对应的波数。
与常规的先静校正再偏移方法相比,本文方法一方面避免了静校正引入的旅行时误差,提高了波场传播的准确性;另一方面,本文方法在海水中只需要进行单平方根方程延拓,并且不需要提取成像值,计算量更小,具有更高的计算效率。这两点在海水较深时优势更为明显。
对于OBN采集数据,由于接收点较为稀疏,上行波对于浅层构造照明不足,采集脚印明显。解决OBN中浅层成像差的主要方法为利用下行波进行镜偏移,减小中浅层的采集脚印影响,改善成像效果。显然,对于镜偏移,仍旧为双基准面成像问题,用同样的方法可以实现OBN数据的镜偏移。
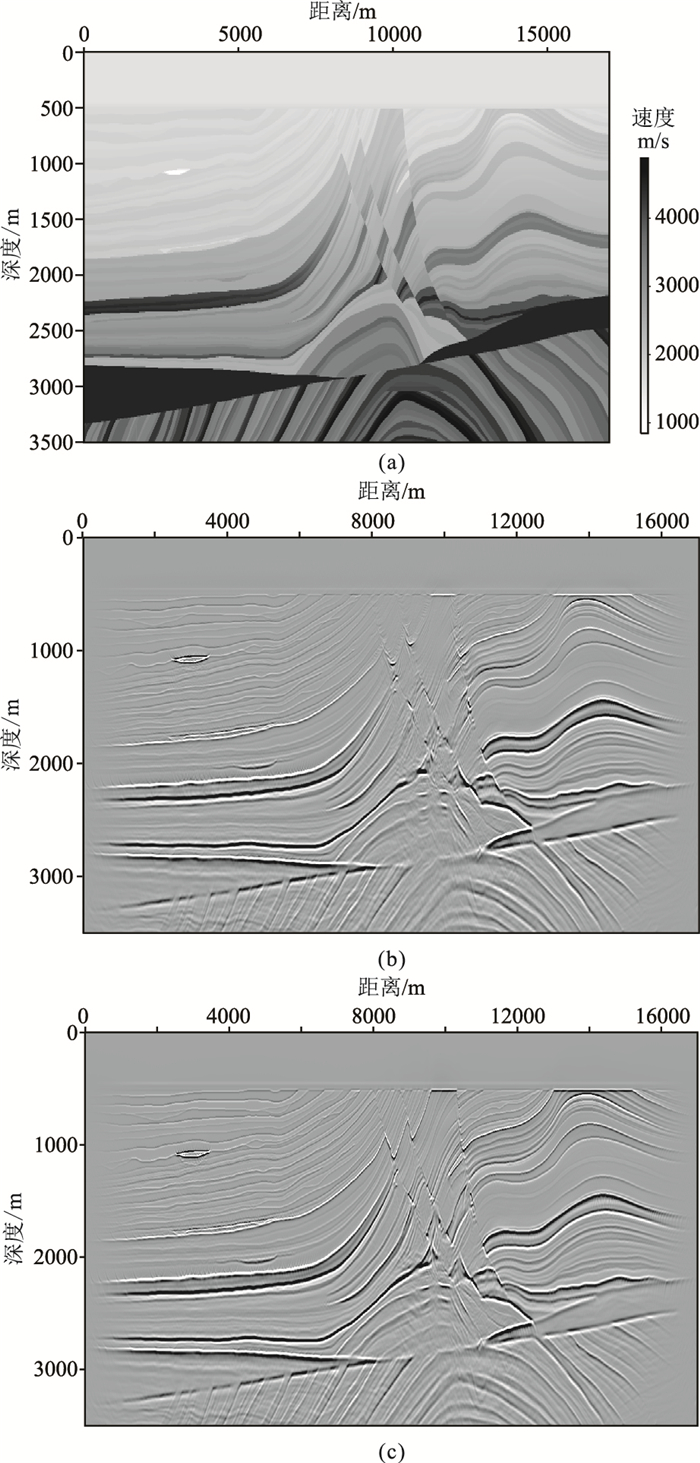
3 理论数据及实际数据测试首先选用Marmousi模型模拟的OBN数据进行本文方法测试。该模型数据共计340炮,记录长度为4s,时间采样间隔为0.5ms。单边接收,每炮241道,炮检距为50m,道间距为12.5m,接收点位于海底处(450m)。成像中心点间距为6.25m,半炮检距间距为50m。图 1为Marmousi速度模型及采用不同方法获得的偏移剖面。对比图 1b和图 1c可以看出,采用本文方法偏移,对于中间复杂构造能够更好地成像,断层更加清晰,陡倾角地层能够更好地成像。
|
图 1 Marmousi模型偏移效果对比 (a)速度模型;(b)先将数据校正到同一平面再进行常规偏移剖面;(c)直接进行单/双平方根混合延拓偏移剖面 |
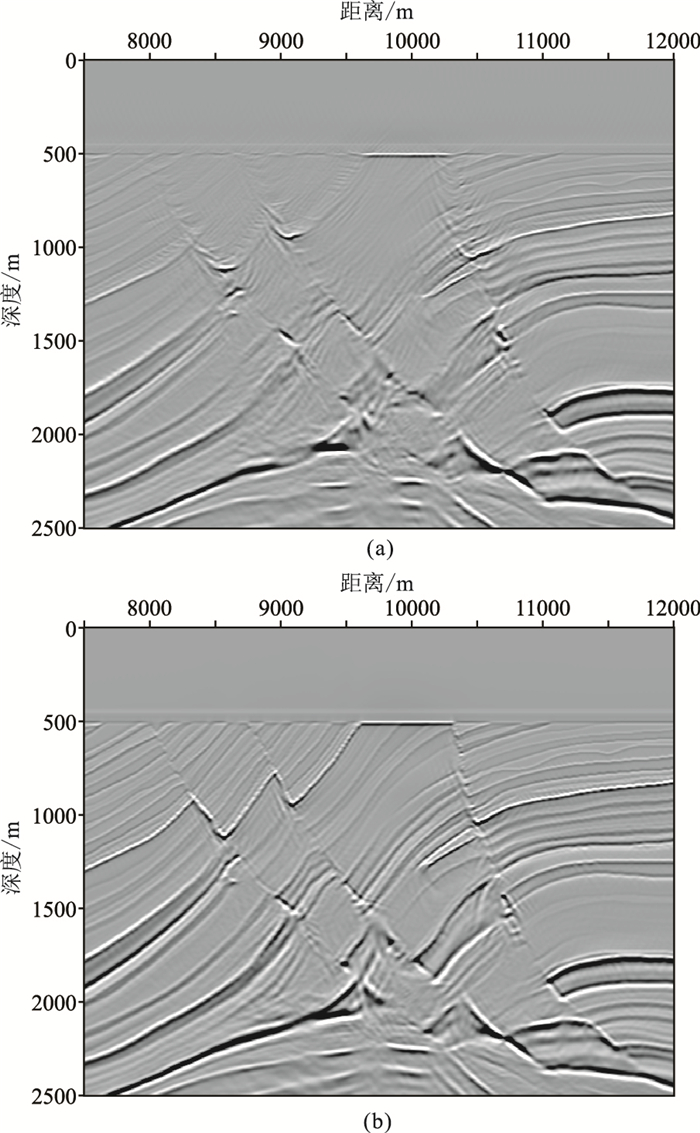
图 2为图 1成像剖面中间部分中浅层放大显示对比。其中图 2a对应图 1b成像剖面中间复杂构造区域放大,图 2b对应图 1c成像剖面中间复杂构造区域放大显示。对比图 2a和图 2b可以看出,由于静校正引入的误差,海底面已经无法清晰成像,造成海底面引入人为起伏和断续(图 2a);而基于本文方法的海底面能够清晰成像,海底面刻画效果更好(图 2b)。对比图 2a和图 2b中间部分,先静校正造成的成像误差较大,倾斜层无法准确成像,偏移画弧明显; 而本文方法能够清晰成像,断层刻画清晰,绕射波很好地归位。上述结果验证了本文方法的正确性。
表 1列出了Marmousi模型数据先进行静校正再偏移成像和本文单/双平方根混合延拓直接偏移方法计算耗时对比,计算硬件均为单节点,处理器为Intel Xeon Gold 6258R,内存为256GB。常规方法仅偏移计算耗时就需要40s,而本文方法由于海水层仅需要进行单平方根延拓,并且不需要提取成像值,偏移计算仅需要32s。本文仅统计了偏移成像计算时间,没有统计常规方法需要提前进行静校正运算的耗时。偏移计算耗时比受海水深度和成像偏移深度比控制,海水越深,加速比越高。
|
|
表 1 Marmousi模型常规偏移和本文偏移方法计算耗时对比 |
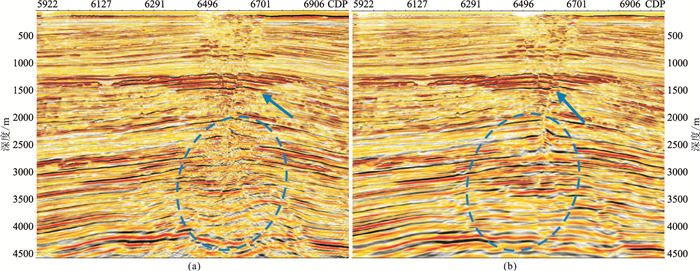
为了验证本文方法在实际资料处理中的有效性,将它应用于中国南海A探区进行测试、对比。该研究区海底深度约70m,OBN观测线距为200m,OBN间距为50m,地表炮检距为50m。对于该数据,分别用常规Kirchhoff积分偏移和本文方法进行偏移成像,比较两种方法的成像结果。图 3为该数据Inline方向成像剖面对比,在蓝色箭头位置,本文方法对于断层刻画更为清晰,断层更为干脆。图中蓝色圆圈标注区域,本文方法成像信噪比更高,成像结果更加符合地质逻辑。
|
图 3 Kirchhoff PSDM剖面(a)与双基准面成像剖面(b)对比(Inline方向) |
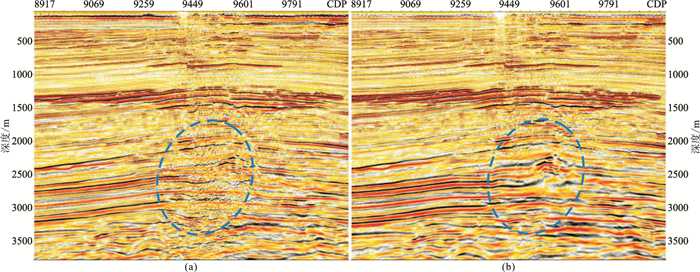
图 4为该探区Crossline方向成像剖面对比,与图 3类似,本文方法成像效果明显优于Kirchhoff积分深度偏移剖面,尤其是图中蓝色椭圆标注的复杂构造区域,图 4a成像已经无法准确聚焦,成像信噪比较低,而本文方法仍旧能够很好归位,成像质量更高(图 4b)。
|
图 4 Kirchhoff PSDM镜偏移剖面(a)与双基准面成像剖面(b)对比(Crossline方向) |
本文给出了单、双平方根方程混合延拓实现OBC/OBN数据偏移的适用方法。该方法在深度延拓到海底面之前通过单平方根方程的方式进行炮点波场的延拓,延拓深度超过海底深度之后,采用传统双平方根方程延拓,并根据常规双平方根方程零时间零炮检距成像条件进行成像。本文方法拓展了双平方根算子成像的适用范围,提高了该算子在OBC/OBN资料的延拓精度,提高了延拓效率,改善了OBC/OBN数据的成像效果。OBC/OBN理论数据测试表明,本文方法能够显著改善复杂构造的成像效果。中国南海M区实际数据成像对比测试表明,本文方法较常规Kirchhoff偏移效果有较大改善,复杂构造成像质量更高。
| [1] |
杨锴, 王华忠, 程玖兵, 等. 非水平观测面有限差分法叠前波动方程基准面校正[J]. 石油地球物理勘探, 2002, 37(2): 154-162. YANG Kai, WANG Huazhong, CHENG Jiubing, et al. Prestack wave equation datum correction from non-flat surface with finite-difference scheme[J]. Oil Geophysical Prospecting, 2002, 37(2): 154-162. DOI:10.3321/j.issn:1000-7210.2002.02.011 |
| [2] |
杨锴, 程玖兵, 刘玉柱, 等. 三维波动方程基准面校正方法的应用研究[J]. 地球物理学报, 2007, 50(4): 1232-1240. YANG Kai, CHENG Jiubing, LIU Yuzhu, et al. A study on the application of the 3-D wave-equation-datuming[J]. Chinese Journal of Geophysics, 2007, 50(4): 1232-1240. DOI:10.3321/j.issn:0001-5733.2007.04.033 |
| [3] |
LIU W G, ZHAO B, ZHOU H W, et al. Wave-equation global datuming based on the double square root operator[J]. Geophysics, 2011, 76(3): U35-U43. |
| [4] |
ZHANG J F, XU J C, ZHANG H. Migration from 3D irregular surfaces: a prestack time migration approach[J]. Geophysics, 2012, 77(5): S117-S129. DOI:10.1190/geo2011-0447.1 |
| [5] |
刘国峰, 刘洪, 李博, 等. 山地地震资料叠前时间偏移方法及其GPU实现[J]. 地球物理学报, 2009, 52(12): 3101-3108. LIU Guofeng, LIU Hong, LI Bo, et al. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation[J]. Chinese Journal of Geophysics, 2009, 52(12): 3101-3108. DOI:10.3969/j.issn.0001-5733.2009.12.019 |
| [6] |
GRAY S H, MARFURT K J. Migration from topog raphy: improving the near-surface image[J]. Canadian Journal of Exploration Geophysics, 1995, 31(1-2): 18-24. |
| [7] |
JÄGER C. HERTWECK T, SPINNER M. True-amplitude Kirchhoff migration from topography[C]. SEG Technical Program Expanded Abstracts, 2003, 22: 909-912.
|
| [8] |
刘少勇, 王华忠, 张兵. 起伏地表Kirchhoff积分法叠前深度偏移方法研究与应用[J]. 岩性油气藏, 2010, F07: 49-54. LIU Shaoyong, WANG Huazhong, ZHANG Bing. Kirchhoff integral PSDM for rugged topography: technology and applications[J]. Northwest Oil & Gas Exploration, 2010, F07: 49-54. DOI:10.3969/j.issn.1673-8926.2010.z1.011 |
| [9] |
岳玉波, 李振春, 钱忠平, 等. 复杂地表条件下保幅高斯束偏移[J]. 地球物理学报, 2012, 55(4): 1376-1383. YUE Yubo, LI Zhenchun, QIAN Zhongping, et al. Amplitude-preserved Gaussian beam migration under complex topographic conditions[J]. Chinese Journal of Geophysics, 2012, 55(4): 1376-1383. |
| [10] |
杨继东, 黄建平, 王欣, 等. 复杂地表条件下叠前菲涅尔束偏移方法[J]. 地球物理学报, 2015, 58(10): 3758-3770. YANG Jidong, HUANG Jianping, WANG Xin, et al. Prestack Fresnel beam migration method under complex topographic conditions[J]. Chinese Journal of Geophysics, 2015, 58(10): 3758-3770. DOI:10.6038/cjg20151026 |
| [11] |
黄建平, 袁茂林, 段新意, 等. 一种解耦的起伏地表弹性波高斯束偏移方法[J]. 石油地球物理勘探, 2015, 50(3): 460-468. HUANG Jianping, YUAN Maolin, DUAN Xinyi, et al. Decoupled elastic Gaussian beam migration for rugged topography[J]. Oil Geophysical Prospecting, 2015, 50(3): 460-468. |
| [12] |
BEASLEY C, LYNN W. The zero velocity layer: migration from irregular surfaces[J]. Geophysics, 1992, 57(11): 1435-1443. DOI:10.1190/1.1443211 |
| [13] |
RESHEF M. Depth migration from irregular surfaces with the depth extrapolation methods[J]. Geophy-sics, 1991, 56(1): 119-122. |
| [14] |
雷秀丽, 李振春, 孔雪, 等. 起伏地表条件下基于复Pade逼近的叠前深度偏移[J]. 地球物理学进展, 2012, 27(5): 2100-2106. LEI Xiuli, LI Zhenchun, KONG Xue, et al. Prestack depth migration using complex Pade approximations for irregular surfaces[J]. Progress in Geophysics, 2012, 27(5): 2100-2106. |
| [15] |
何英, 王华忠, 马在田, 等. 复杂地形条件下波动方程叠前深度成像[J]. 勘探地球物理进展, 2002, 25(3): 13-19. HE Ying, WANG Huazhong, MA Zaitian, et al. Pre-stack wave equation depth migration for irregular topography[J]. Progress in Exploration Geophysics, 2002, 25(3): 13-19. |
| [16] |
王成祥, 赵波, 张关泉. 基于起伏地表的混合法叠前深度偏移[J]. 石油地球物理勘探, 2002, 37(3): 219-223. WANG Chengxiang, ZHAO Bo, ZHANG Guanquan. Rugged surface oriented hybrid pre-stack depth migration[J]. Oil Geophysical Prospecting, 2002, 37(3): 219-223. |
| [17] |
叶月明, 李振春, 仝兆岐, 等. 双复杂介质条件下频率空间域有限差分法保幅偏移[J]. 地球物理学报, 2008, 51(5): 1511-1519. YE Yueming, LI Zhenchun, TONG Zhaoqi, et al. Preserved-amplitude migration with dual-complexity[J]. Chinese Journal of Geophysics, 2008, 51(5): 1511-1519. |
| [18] |
刘红伟, 刘洪, 李博, 等. 起伏地表叠前逆时偏移理论及GPU加速技术[J]. 地球物理学报, 2011, 54(7): 1883-1892. LIU Hongwei, LIU Hong, LI Bo, et al. Pre-stack reverse time migration for rugged topography and GPU acceleration technology[J]. Chinese Journal of Geophysics, 2011, 54(7): 1883-1892. |
| [19] |
孔祥宁, 段心标, 刘守伟, 等. 起伏地表叠前逆时偏移的实现及应用[J]. 地球物理学进展, 2014, 29(3): 1168-1172. KONG Xiangning, DUAN Xinbiao, LIU Shouwei, et al. Reverse time migration from rugged datum: technology and applications[J]. Progress in Geophysics, 2014, 29(3): 1168-1172. |
| [20] |
SHRAGGE J. Reverse time migration from topography[J]. Geophysics, 2014, 79(4): S141-S152. |
| [21] |
QU Y M, LI J L. Q-compensated reverse time migration in viscoacoustic media including surface topography[J]. Geophysics, 2019, 84(4): S201-S217. |
| [22] |
曲英铭. 起伏地表直接成像技术研究进展[J]. 石油物探, 2019, 58(5): 625-644. QU Yingming. Research progress of topographic ima-ging methods[J]. Geophysical Prospecting for Pe-troleum, 2019, 58(5): 625-644. |
| [23] |
CLAERBOUT J F. Imaging the Earth' s Interior[M]. Blackwell Scientific Publication, Oxford[England]Boston, 1985.
|
| [24] |
程玖兵, 王华忠, 马在田. 双平方根方程三维叠前深度偏移[J]. 地球物理学报, 2003, 46(5): 676-683. CHENG Jiubing, WANG Huazhong, MA Zaitian. Dou-ble square root equation 3D prestack depth migration[J]. Chinese Journal of Geophysics, 2003, 46(5): 676-683. |
| [25] |
吴成梁, 王田珍, 王华忠, 等. VTI介质全三维双平方根偏移方法研究及其实际资料应用[C]. CPS/SEG北京2018国际地球物理会议, 北京, 2018, 545-548. WU Chengliang, WANG Tianzhen, WANG Huazhong, et al. Full 3D double square root migration method for VTI media and its application in real data[C]. CPS/SEG Beijing International Geophysical Conference, Beijing, China, 2018, 545-548. |
| [26] |
李江, 李庆春. VTI介质角度域叠前深度偏移[J]. 石油地球物理勘探, 2019, 54(2): 330-340. LI Jiang, LI Qingchun. Angle-domain prestack depth migration in VTI media[J]. Oil Geophysical Prospecting, 2019, 54(2): 330-340. |
| [27] |
ZHANG Y, SUN J C, GRAY S H. Aliasing in wavefield extrapolation prestack migration[J]. Geophy-sics, 2003, 68(2): 629-633. |
| [28] |
赫建伟, 邓勇, 任婷, 等. 黏声介质全三维双平方根方程叠前深度偏移及其在海上数据中的应用[J]. 石油地球物理勘探, 2018, 53(6): 1210-1217. HE Jianwei, DENG Yong, REN Ting, et al. Full 3D double-square-root prestack depth migration in visco-acoustic medium and its application in offshore seismic data[J]. Oil Geophysical Prospecting, 2018, 53(6): 1210-1217. |



 欧阳敏, 海南省海口市秀英区西海岸荣城铂郡大厦, 570311。Email:
欧阳敏, 海南省海口市秀英区西海岸荣城铂郡大厦, 570311。Email: